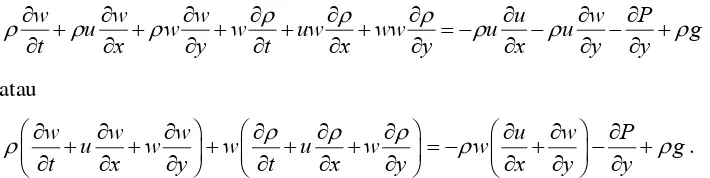Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam

FORMULASI HAMILTONIAN UNTUK MENGGAMBARKAN

GERAK GELOMBANG INTERNAL PADA LAUT DALAM

RINA PRASTIWI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PERYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2009

ABSTRACT

RINA PRASTIWI. Hamiltonian Formulation for Internal Waves Motion in Deep Ocean. Supervised by JAHARUDDIN and ALI KUSNANTO.

The ocean is considered as layers of water with different densities. Internal waves are waves occured under surface of the ocean that caused by density difference in each fluid layer. Interfacial wave is one of internal waves between two layers of fluid. In this thesis, the series expansion of the Hamiltonian is used to derive the model equation for the wave motion at the interface between fluids in the case when the lower layer has infinite depth and the upper layer has a certain depth. In the formulation, Hamiltonian is defined as the sum of kinetic and potential energy. The Hamiltonian system is obtained from reduction of kinetic energy by using the Dirichlet-Neumann operator. The coefficients of Hamiltonian equation depend on the density and the depth of fluids. Assuming the interfacial wave as solitary wave, its motion equation could be used as to predict the amplitude and the phase speed of the wave. The result of numerical simulation shows that Hamiltonian remains unchanged for a long period of time, in other words, it is consistent in time.

RINGKASAN

RINA PRASTIWI. Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.

Laut dapat dianggap terdiri dari lapisan-lapisan air yang memiliki rapat massa yang berbeda. Perbedaan rapat massa air laut dapat disebabkan oleh perbedaan kadar garam dan temperatur pada setiap lapisan air laut. Akibat perbedaaan rapat massa ini, maka muncul suatu gelombang. Gelombang internal adalah suatu gelombang yang terjadi di bawah permukaan, yang merupakan batas dua lapisan air laut karena adanya perbedaan rapat massa pada setiap lapisan air laut. Pada penelitian ini akan dibatasi pada fluida dua lapisan dengan kedalaman yang cukup besar. Diasumsikan bahwa kedua lapisan fluida ini masing-masing mempunyai rapat massa yang konstan dan berupa fluida ideal, yaitu fluida yang tak mampat (incompressiable) dan tak kental (inviscid). Gelombang interfacial terjadi pada batas kedua lapisan fluida (interface).

Persamaan gerak gelombang internal pada laut dalam yang diasumsikan pada fluida dua lapisan diformulasikan menggunakan formulasi Hamiltonian yang melibatkan operator Dirichlet-Neumann. Domain fluida dua lapisan dibatasi oleh lapisan atas mempunyai ketebalan yang berhingga dan lapisan bawah mempunyai ketebalan yang cukup besar. Ketebalan yang cukup besar ini dapat dilihat dari perbandingan amplitudo gelombang dengan kedalaman fluida, yaitu nilai amplitudo gelombang jauh lebih kecil dari kedalaman fluida. Untuk menentukan persamaan Hamiltonian yang eksplisit dibutuhkan asumsi gelombang panjang dan amplitudo kecil.

Persamaan gerak gelombang interfacial yang diperoleh berupa sistem Hamiltonian dengan Hamiltonian yang bergantung pada simpangan gelombang interfacial dan kecepatan partikel fluida untuk arah horizontal. Berdasarkan sistem Hamiltonian ini diperoleh persamaan gerak gelombang yang merambat dalam dua arah. Selanjutnya dengan menggunakan definisi transformasi untuk simpangan gelombang yang bergerak dalam arah kanan dan arah kiri, diperoleh persamaan gerak gelombang interfacial yang berupa sistem Hamiltonian dengan Hamiltoniannya yang bergantung pada simpangan gelombang yang bergerak dalam arah kanan dan arah kiri. Untuk menentukan persamaan gelombang interfacial yang merambat hanya dalam satu arah digunakan asumsi simpangan gelombang yang merambat dalam arah kiri sangat kecil sehingga diperoleh persamaan gerak gelombang interfacial yang merambat dalam satu arah, yaitu arah kanan.

Berdasarkan penyelesaian persamaan gerak gelombang soliter interfacial dapat disimpulkan apabila rapat massa fluida lapisan atas sangat kecil maka kecepatan phase gelombang yang dihasilkan tinggi. Jika rapat massa fluida lapisan atas mendekati nilai rapat massa fluida lapisan bawah, maka kecepatan phase gelombang yang dihasilkan semakin rendah atau mencapai nol. Nilai amplitudo gelombang soliter interfacial bernilai negatif. Dengan kata lain gelombang soliter interfacial yang terjadi berupa depresi. Dengan menyubstitusikan penyelesaian persamaan gerak gelombang soliter interfacial ke dalam persamaan Hamiltonian yang bergantung pada simpangan gelombang yang bergerak dalam arah kanan diperoleh nilai Hamiltonian yang tetap atau tidak berubah terhadap waktu.

© Hak Cipta milik IPB, tahun 2009

Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah.

b. Pengutipan tersebut tidak merugikan kepentingan yang wajar IPB.

FORMULASI HAMILTONIAN UNTUK MENGGAMBARKAN

GERAK GELOMBANG INTERNAL PADA LAUT DALAM

RINA PRASTIWI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCA SARJANA

INSTITUT PERTANIAN BOGOR

Judul Tesis : Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam

Nama : Rina Prastiwi

NIM : G551070381

Disetujui Komisi Pembimbing

Dr. Jaharuddin, M.S. Drs. Ali Kusnanto, M.Si.

Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

PRAKATA

Segala puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan segala rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan tesis yang berjudul “Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam”.

Penulis menyadari bahwa dalam penyusunan tesis ini masih banyak terdapat kekurangan, hal ini karena pengetahuan yang dimiliki oleh penulis sangat terbatas. Dalam kesempatan ini penulis mengucapkan terimakasih yang sebesar-besarnya kepada yang terhormat

1. Bapak Bapak Dr. Jaharuddin, M.S. dan Bapak Drs. Ali Kusnanto, M.Si. selaku pembimbing, pendidik dan pengajar yang dengan penuh kesabaran memberikan bimbingan, arahan, nasehat serta motivasi kepada penulis.

2. Ibu Dr. Ir. Endar H. Nugrahani, M.S. selaku penguji, pendidik dan pengajar yang telah memberikan saran dan kritikannya kepada penulis.

3. Departemaen Agama RI yang telah memberikan beasiswa kepada penulis untuk melanjutkan Sekolah Pascasarjana pada Institut Pertanian Bogor periode 2007 s.d 2009.

4. Ketua Departemen, ketua Program Studi dan seluruh staf pengajar, serta staf administrasi Fakultas Matematika dan Ilmu Pengetahuan Alam yang turut membantu proses penyelesaian tesis ini.

5. Kepala sekolah dan seluruh staf pengajar MTs Al-Islamiyah Srengseng yang turut mendoakan dan memotivasi penulis dalam menyelesaikan tesis ini. 6. Suami, anak dan kedua orang tua yang senantiasa mendoakan penulis di setiap

waktu dalam menyelesaikan tesis ini.

7. Seluruh teman-teman yang turut membantu dalam penyelesaian tesis ini. Penulis doakan semoga segala bantuan, bimbingan dan pengarahan yang diberikan mendapat ganjaran yang berlipat ganda dari Allah SWT, dan semoga tesis ini bermanfaat bagi kita semua. Amiin.

FORMULASI HAMILTONIAN UNTUK MENGGAMBARKAN

GERAK GELOMBANG INTERNAL PADA LAUT DALAM

RINA PRASTIWI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PERYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2009

ABSTRACT

RINA PRASTIWI. Hamiltonian Formulation for Internal Waves Motion in Deep Ocean. Supervised by JAHARUDDIN and ALI KUSNANTO.

The ocean is considered as layers of water with different densities. Internal waves are waves occured under surface of the ocean that caused by density difference in each fluid layer. Interfacial wave is one of internal waves between two layers of fluid. In this thesis, the series expansion of the Hamiltonian is used to derive the model equation for the wave motion at the interface between fluids in the case when the lower layer has infinite depth and the upper layer has a certain depth. In the formulation, Hamiltonian is defined as the sum of kinetic and potential energy. The Hamiltonian system is obtained from reduction of kinetic energy by using the Dirichlet-Neumann operator. The coefficients of Hamiltonian equation depend on the density and the depth of fluids. Assuming the interfacial wave as solitary wave, its motion equation could be used as to predict the amplitude and the phase speed of the wave. The result of numerical simulation shows that Hamiltonian remains unchanged for a long period of time, in other words, it is consistent in time.

RINGKASAN

RINA PRASTIWI. Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.

Laut dapat dianggap terdiri dari lapisan-lapisan air yang memiliki rapat massa yang berbeda. Perbedaan rapat massa air laut dapat disebabkan oleh perbedaan kadar garam dan temperatur pada setiap lapisan air laut. Akibat perbedaaan rapat massa ini, maka muncul suatu gelombang. Gelombang internal adalah suatu gelombang yang terjadi di bawah permukaan, yang merupakan batas dua lapisan air laut karena adanya perbedaan rapat massa pada setiap lapisan air laut. Pada penelitian ini akan dibatasi pada fluida dua lapisan dengan kedalaman yang cukup besar. Diasumsikan bahwa kedua lapisan fluida ini masing-masing mempunyai rapat massa yang konstan dan berupa fluida ideal, yaitu fluida yang tak mampat (incompressiable) dan tak kental (inviscid). Gelombang interfacial terjadi pada batas kedua lapisan fluida (interface).

Persamaan gerak gelombang internal pada laut dalam yang diasumsikan pada fluida dua lapisan diformulasikan menggunakan formulasi Hamiltonian yang melibatkan operator Dirichlet-Neumann. Domain fluida dua lapisan dibatasi oleh lapisan atas mempunyai ketebalan yang berhingga dan lapisan bawah mempunyai ketebalan yang cukup besar. Ketebalan yang cukup besar ini dapat dilihat dari perbandingan amplitudo gelombang dengan kedalaman fluida, yaitu nilai amplitudo gelombang jauh lebih kecil dari kedalaman fluida. Untuk menentukan persamaan Hamiltonian yang eksplisit dibutuhkan asumsi gelombang panjang dan amplitudo kecil.

Persamaan gerak gelombang interfacial yang diperoleh berupa sistem Hamiltonian dengan Hamiltonian yang bergantung pada simpangan gelombang interfacial dan kecepatan partikel fluida untuk arah horizontal. Berdasarkan sistem Hamiltonian ini diperoleh persamaan gerak gelombang yang merambat dalam dua arah. Selanjutnya dengan menggunakan definisi transformasi untuk simpangan gelombang yang bergerak dalam arah kanan dan arah kiri, diperoleh persamaan gerak gelombang interfacial yang berupa sistem Hamiltonian dengan Hamiltoniannya yang bergantung pada simpangan gelombang yang bergerak dalam arah kanan dan arah kiri. Untuk menentukan persamaan gelombang interfacial yang merambat hanya dalam satu arah digunakan asumsi simpangan gelombang yang merambat dalam arah kiri sangat kecil sehingga diperoleh persamaan gerak gelombang interfacial yang merambat dalam satu arah, yaitu arah kanan.

Berdasarkan penyelesaian persamaan gerak gelombang soliter interfacial dapat disimpulkan apabila rapat massa fluida lapisan atas sangat kecil maka kecepatan phase gelombang yang dihasilkan tinggi. Jika rapat massa fluida lapisan atas mendekati nilai rapat massa fluida lapisan bawah, maka kecepatan phase gelombang yang dihasilkan semakin rendah atau mencapai nol. Nilai amplitudo gelombang soliter interfacial bernilai negatif. Dengan kata lain gelombang soliter interfacial yang terjadi berupa depresi. Dengan menyubstitusikan penyelesaian persamaan gerak gelombang soliter interfacial ke dalam persamaan Hamiltonian yang bergantung pada simpangan gelombang yang bergerak dalam arah kanan diperoleh nilai Hamiltonian yang tetap atau tidak berubah terhadap waktu.

© Hak Cipta milik IPB, tahun 2009

Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah.

b. Pengutipan tersebut tidak merugikan kepentingan yang wajar IPB.

FORMULASI HAMILTONIAN UNTUK MENGGAMBARKAN

GERAK GELOMBANG INTERNAL PADA LAUT DALAM

RINA PRASTIWI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCA SARJANA

INSTITUT PERTANIAN BOGOR

Judul Tesis : Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam

Nama : Rina Prastiwi

NIM : G551070381

Disetujui Komisi Pembimbing

Dr. Jaharuddin, M.S. Drs. Ali Kusnanto, M.Si.

Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

PRAKATA

Segala puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan segala rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan tesis yang berjudul “Formulasi Hamiltonian untuk Menggambarkan Gerak Gelombang Internal pada Laut Dalam”.

Penulis menyadari bahwa dalam penyusunan tesis ini masih banyak terdapat kekurangan, hal ini karena pengetahuan yang dimiliki oleh penulis sangat terbatas. Dalam kesempatan ini penulis mengucapkan terimakasih yang sebesar-besarnya kepada yang terhormat

1. Bapak Bapak Dr. Jaharuddin, M.S. dan Bapak Drs. Ali Kusnanto, M.Si. selaku pembimbing, pendidik dan pengajar yang dengan penuh kesabaran memberikan bimbingan, arahan, nasehat serta motivasi kepada penulis.

2. Ibu Dr. Ir. Endar H. Nugrahani, M.S. selaku penguji, pendidik dan pengajar yang telah memberikan saran dan kritikannya kepada penulis.

3. Departemaen Agama RI yang telah memberikan beasiswa kepada penulis untuk melanjutkan Sekolah Pascasarjana pada Institut Pertanian Bogor periode 2007 s.d 2009.

4. Ketua Departemen, ketua Program Studi dan seluruh staf pengajar, serta staf administrasi Fakultas Matematika dan Ilmu Pengetahuan Alam yang turut membantu proses penyelesaian tesis ini.

5. Kepala sekolah dan seluruh staf pengajar MTs Al-Islamiyah Srengseng yang turut mendoakan dan memotivasi penulis dalam menyelesaikan tesis ini. 6. Suami, anak dan kedua orang tua yang senantiasa mendoakan penulis di setiap

waktu dalam menyelesaikan tesis ini.

7. Seluruh teman-teman yang turut membantu dalam penyelesaian tesis ini. Penulis doakan semoga segala bantuan, bimbingan dan pengarahan yang diberikan mendapat ganjaran yang berlipat ganda dari Allah SWT, dan semoga tesis ini bermanfaat bagi kita semua. Amiin.

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 14 Oktober 1981 dari bapak Sakimin dan ibu Nazimah. Penulis merupakan anak pertama dari tiga bersaudara.

Tahun 1999 penulis lulus dari SMU Negeri 47 Jakarta dan lulus seleksi masuk Universitas Negeri Jakarta melalui jalur Ujian Masuk Perguruan Tinggi Negeri (UMPTN) pada Jurusan Pendidikan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam dan selesai pada tahun 2004.

DAFTAR ISI

Halaman

DAFTAR GAMBAR ………... xiii

DAFTAR LAMPIRAN ………... xiv

I PENDAHULUAN ………... 1

1.1 Latar Belakang ………... 1.2 Tujuan Penelitian ………...

1 2

II LANDASAN TEORI ………... 3

2.1 Persamaan Dasar Fluida ……….... 2.2 Sistem Hamiltonian ………...

3 6 III METODOLOGI PENELITIAN ………... 9 IV HASIL DAN PEMBAHASAN ………... 11

4.1 Formulasi Hamiltonian ……….. 4.2 Gerak Gelombang Interfacial ……… 4.3 Gelombang Soliter Interfacial ………

11 13 18 V SIMPULAN DAN SARAN ... 22

5.1 Simpulan ……….. 5.2 Saran ………

DAFTAR GAMBAR

Halaman 1 Domain fluida dua lapisan .... 5 2 Hubungan kecepatan phase gelombang terhadap perbandingan

DAFTAR LAMPIRAN

Halaman Lampiran 1 Penurunan Persamaan (2.1), (2.2), (2.3), (2.6), (2.7), (2.8) dan

(2.11) ……….. 26

Lampiran 2 Penurunan Persamaan (4.8), (4.9), (4.10) dan (4.11) ………... 35 Lampiran 3 Penurunan Persamaan (4.14), (4.15), (4.23), (4.25), (4.28),

I PENDAHULUAN

1.1Latar Belakang

Sebagian besar wilayah bumi merupakan lautan. Laut dapat dianggap terdiri dari lapisan-lapisan air yang memiliki rapat massa yang berbeda. Akibat perbedaaan rapat massa ini, maka muncul suatu gelombang. Gelombang yang dapat diamati secara langsung adalah gelombang permukaan. Gelombang permukaan adalah suatu gelombang yang terjadi di permukaan, yang merupakan batas antara air dan udara karena rapat massa air berbeda dengan rapat massa udara. Selain itu ada juga gelombang yang tidak dapat diamati secara langsung karena terjadinya di bawah permukaan. Gelombang semacam ini disebut gelombang internal. Gelombang internal adalah suatu gelombang yang terjadi di bawah permukaan, yang merupakan batas dua lapisan air laut karena adanya perbedaan rapat massa pada setiap lapisan air laut. Perbedaan rapat massa air laut dapat disebabkan oleh perbedaan kadar garam dan temperatur pada setiap lapisan air laut.

Pada penelitian ini akan dibatasi pada fluida dua lapisan dengan kedalaman yang cukup besar. Diasumsikan bahwa kedua lapisan fluida ini masing-masing mempunyai rapat massa yang konstan dan berupa fluida ideal, yaitu fluida yang tak mampat (incompressiable) dan tak kental (inviscid). Gelombang interfacial terjadi pada batas kedua lapisan fluida (interface). Contoh gelombang interfacial adalah gelombang yang terjadi pada percampuran air dan minyak dalam pipa, aliran lumpur di suatu perairan dan lain-lain. Persamaan gerak pada fluida dua lapisan diformulasikan menggunakan formulasi Hamiltonian yang melibatkan operator Dirichlet-Neumann dengan asumsi gelombang panjang dan amplitudo kecil.

internal pada fluida dua lapisan yang masing-masing berupa fluida ideal dengan batas atas berupa permukaan bebas dan batas bawah berupa dasar rata. Mereka menurunkan persamaan gerak gelombang internal dengan menggunakan formulasi Lagrange. Formulasi Hamiltonian pada fluida dua lapisan dengan batas atas dan batas bawah berupa permukaan rata telah dibahas oleh Benjamin dan Bridges (1997).

Penaksiran tentang gerak gelombang internal di laut berguna untuk merencanakan pembangunan tiang-tiang pancang penyangga anjungan minyak di tempat yang berpotensi terjadinya gelombang internal. Osborne dan Burch (1980) melaporkan bahwa gelombang internal telah merusak tiang penyangga anjungan minyak di Laut Andaman. Selain itu, gelombang internal berguna untuk pelayaran kapal selam. Informasi tentang kekuatan gelombang internal perlu diketahui guna menghindari tumbukan kapal selam dengan gelombang tersebut.

1.2Tujuan Penelitian

Berdasarkan latar belakang di atas, maka tujuan penelitian adalah :

1 Menggunakan formulasi Hamiltonian untuk memformulasikan gerak gelombang interfacial pada fluida dua lapisan dengan lapisan atas dibatasi oleh permukaan rata dan lapisan bawah memiliki ketebalan yang cukup besar.

2 Menentukan persamaan gerak gelombang interfacial yang merambat hanya dalam satu arah berdasarkan sistem Hamiltonian yang diperoleh.

II LANDASAN TEORI

Pada bab ini akan diuraikan beberapa konsep yang mendasari penelitian ini. Konsep dinamika fluida yang disajikan berdasarkan Ambrosi (2000) dan teori sistem Hamiltonian dirangkum dari Groesen dan Jager (1994) dan Jaharuddin (2004).

2.1 Persamaan Dasar Fluida

Persamaan dasar fluida diperoleh dengan menggunakan dua hukum yang mempengaruhi setiap gerak partikel fluida, yaitu hukum kekekalan massa dan hukum kekekalan momentum. Misalkan partikel-partikel fluida yang ditinjau memiliki rapat massa





x,y,t



dan diasumsikan bergerak dalam dua dimensi sehingga x merupakan koordinat untuk partikel fluida yang bergerak dalam arah horizontal, y merupakan koordinat untuk partikel fluida yang bergerak dalam arah vertikal dan t merupakan waktu. Kecepatan gerak partikel fluida untuk arah horizontal dinotasikan oleh u dan arah vertikal oleh w.

Menurut hukum kekekalan massa, laju perubahan massa dalam suatu bidang adalah selisih antara massa yang masuk dan massa yang keluar pada bidang tersebut. Jika digunakan asumsi fluida tak mampat (incompressible), maka didapatkan persamaan kontinuitas berbentuk:

0

 

 x y

t u w

 ,

0

  _y

x w

u . (2.1)

Menurut hukum kekekalan momentum, laju kesetimbangan momentum dalam suatu bidang adalah selisih antara momentum yang masuk dengan yang keluar ditambah dengan gaya-gaya yang bekerja pada bidang tersebut. Dalam kesetimbangan momentum, tekanan P dan gravitasi g mempengaruhi gaya pada permukaan fluida. Jadi persamaan momentum pada arah horizontal (arah sumbu -x) adalah

(u_t uu_x wu_y) P_x 0

     , (2.2)

dan persamaan momentum pada arah vertikal (arah sumbu -y) adalah (w_t uw_x ww_y) P_y g 0

Selanjutnya akan dibahas syarat batas yang harus dipenuhi gerak partikel fluida, yaitu syarat batas kinematik yang disebabkan oleh adanya gerak partikel fluida dan syarat batas dinamik yang disebabkan oleh gaya-gaya yang bekerja pada fluida. Misalkan fluida dibatasi oleh batas bawah yang rata di y = -h dan batas atas y



₀

 

x t, , maka berlaku syarat batas berikut:

0t u 0x w

    di y



₀

 

x t, , w = 0 di y = -h,

p = 0 di y



₀

 

x t, . (2.4) Berdasarkan asumsi fluida tak berotasi (irrotational) diperoleh adanya suatu fungsi skalar  yang disebut kecepatan potensial dan memenuhi





( , ) _x, _y

q u w      .

Dengan demikian persamaan dasar fluida ideal yang tak berotasi berbentuk persamaaan Laplace berikut

0

  _yy

xx 

 . (2.5)

Selanjutnya akan dibahas syarat batas yang harus dipenuhi gerak partikel fluida, yaitu syarat batas kinematik yang disebabkan oleh adanya gerak partikel fluida dan syarat batas dinamik yang disebabkan oleh tekanan partikel fluida. Misalkan fluida dibatasi oleh batas bawah yang rata di y = -h dan batas atas

 

0 ,

y



x t , maka berlaku syarat batas berikut. Syarat batas kinematiknya berbentuk:

0t x 0x y 0

     di y₀

 

x,t , (2.6) 0



y

 di y = -h, (2.7)

dan syarat batas dinamik berbentuk



2 2



0 1

0, 2

t x y g

 _   _  

 

atau

2 0 1

0. 2

t g

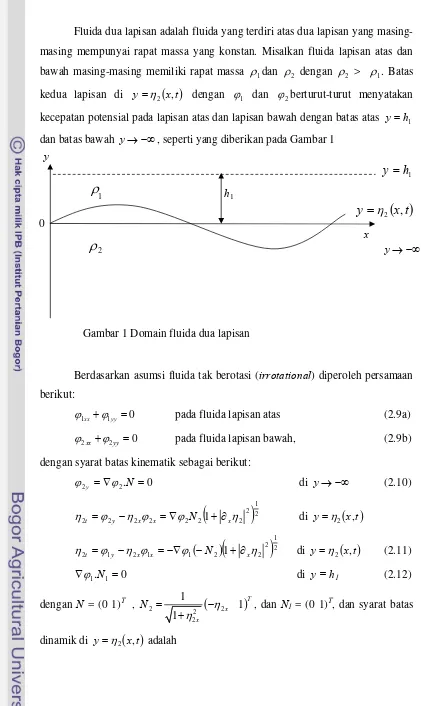
Fluida dua lapisan adalah fluida yang terdiri atas dua lapisan yang masing-masing mempunyai rapat massa yang konstan. Misalkan fluida lapisan atas dan bawah masing-masing memiliki rapat massa



₁dan



₂ dengan



₂ >



₁. Batas kedua lapisan di y



2

 

x,t dengan



1 dan



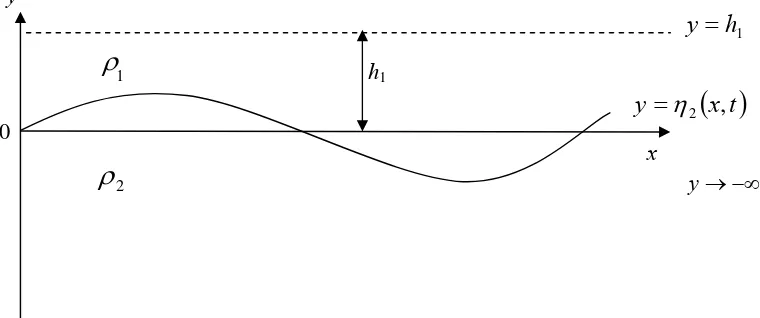
2berturut-turut menyatakan

kecepatan potensial pada lapisan atas dan lapisan bawah dengan batas atas yh₁

dan batas bawah y , seperti yang diberikan pada Gambar 1

Berdasarkan asumsi fluida tak berotasi (irrotational) diperoleh persamaan berikut:

1xx 1yy 0

   pada fluida lapisan atas (2.9a) 2xx 2yy 0

   pada fluida lapisan bawah, (2.9b) dengan syarat batas kinematik sebagai berikut:

0 . 2 2y  N 

 di y  (2.10)





2

1 2 2 2

2 2

2 2

2









1





_t  _y  _{x x}  N  _x di y



2

 

x,t









2

1 2 2 2

1 1

2 1

2









1





_t  _y  _{x x}  N  _x di y



2

 

x,t (2.11)

0 . 1

1 





N di y = h1 (2.12)

dengan N = (0 1)T , ₂



₂



2

2

1

1 1

T x x

N





 

 , dan N1= (0 1)

T

, dan syarat batas

dinamik di y



2

 

x,t adalah [image:31.612.133.513.213.372.2]

y

Gambar 1 Domain fluida dua lapisan

x 0

2



h1

1

h

y



y 

 

x

t

y





₂

,

1

      _{  }        _{  } 2 2 1 1 1 2 2 2 2 2 2 1 2

1 _{     }



 _t g _t g

diy



2

 

x,t . (2.13)

Penurunan persamaan (2.1) – (2.11) dapat dilihat pada Lampiran 1.

Persamaan dasar (2.9) – (2.13) di atas akan diformulasikan menjadi suatu sistem Hamiltonian. Konsep sistem Hamiltonian diberikan berikut ini.

2.2 Sistem Hamiltonian

Didefinisikan fungsional pada ruang M, yaitu pemetaaan H : MR dengan

 

( , , _x, _xx,...) H v h x v v v dx









vM , (2.14)

dan h adalah fungsi sembarang dari v beserta turunannya. Turunan variasi dari fungsional H terhadap v didefinisikan sebagai berikut. Jika terdapat operator simetri miring  di ruang M sehingga untuk setiap bilangan real  berlaku





    

 s sdx

v H d d 0 | ) (  _

 sM, (2.15)

maka  disebut turunan variasi dari H terhadap v, ditulis dengan notasi

vH

 (Groesen dan Jager 1994). Turunan variasi _vH dapat ditentukan dengan cara berikut. Perhatikan fungsional

( ) ( , , _{x x}, _{xx xx},...) H v s h x v s v s v s dx





 



   . (2.16)

Misalkan rv



s, maka diperoleh



                  dx d dr r h d dr r h d dr r h d dH xx xx x x ...









=



                 dx s r h s r h s r h xx xx x x ... =



                 sdx r h dx d r h dx d r h x x ... 2 .

... 2 2                       xx x v v h dx d v h dx d v H H



(2.17)

Selanjutnya operator : MM disebut operator simetri miring, jika

s v s

v,    , , v,sM (2.18)

dengan .,. adalah notasi untuk perkalian dalam. Pada penelitian ini perkalian dalam yang digunakan berbentuk



    vsdx s

v, . v,sM (2.19)

Suatu persamaan diferensial parsial dikatakan sebagai sistem Hamiltonian jika terdapat fungsional H dan operator simetri miring  sehingga persamaan diferensial parsial tersebut dapat ditulis dalam bentuk

H

v _v

t 

 . (2.20)

Hamiltonian H merupakan besaran yang tetap, artinya jika v(x,t) merupakan penyelesaian dari sistem Hamiltonian (2.20), maka nilai H(v(x,t)) tidak berubah terhadap waktu. Penjelasan mengenai hal ini adalah sebagai berikut

Jika rv_tv, maka

 





0 ) ( ,      t r dr r dH t x v H dt d = 0 ) (    



r dr r dH = 0 ) (  



d r dH =



 



0 ,  _

 H v xt v

d d

t , (2.21)

sehingga diperoleh ,

v t

dH

H v

dt    . (2.22)

Jika persamaan (2.20) disubstitusikan ke persamaan (2.22), maka diperoleh H H dt dH v v   

 , . (2.23)

Karena  operator simetri miring, maka



vH,



vH 0 sehingga

0



dt dH

Hal ini menunjukan bahwa nilai H (v(x, t)) tidak berubah terhadap waktu t.

Berikut ini akan dibahas sistem persamaan diferensial parsial yang merupakan sistem Hamiltonian.

Definisikan fungsional H yaitu pemetaan H M: M Rdengan

 

( , , _x, _xx,...) H v h x v v v dx









,

dan hadalah fungsi sembarang dari v beserta turunannya. Turunan variasi dari fungsional Hterhadap v, yaitu



_vHmemenuhi

0

( ) | _v , ,

d

H v s H s s M

d       .

Suatu sistem persamaan diferensial parsial dikatakan sistem Hamiltonian, jika terdapat fungsional H dan operator simetri miring sehingga sistem persamaan diferensial parsial tersebut dapat ditulis dalam bentuk

1 2

1 2

v t

v

H v

v _H

 

 

  _{ }

 _{ } 

 

  _{ },

dengan berupa matriks berorde 2.

Sebagai contoh, sistem persamaan diferensial parsial

1 2

1 2

,

v t

v

H v

v _H

 

 

  _{ }

 _{ } 

 

  _{ } dengan

0 0

x x



 

  _ 

 ,

merupakan suatu sistem Hamiltonian, karena  operator simetri miring. Jika dua vektor v dan y memenuhi vB y. , dengan B suatu matriks, maka hubungan sistem Hamiltonian kedua vektor tersebut diberikan pada proposisi berikut.

Proposisi 1

Misalkan y memenuhi persamaan   _ty _yH Jika v memenuhi vB y. , maka   _tv



_vH, dengan

* B B

   ,

 

 

H v H y .

III METODOLOGI PENELITIAN

Penelitian ini dimulai dengan mempelajari dan menurunkan ulang persamaan dasar untuk fluida ideal beserta syarat batas fluida. Persamaan dasar untuk fluida ideal diperoleh berdasarkan hukum kekekalan massa dan hukum kekekalan momentum. Syarat batas untuk gerak partikel fluida adalah syarat batas kinematik dan syarat batas dinamik. Syarat batas kinematik terjadi karena gerak partikel fluida dan syarat batas dinamik terjadi karena adanya gaya-gaya yang bekerja pada fluida. Setelah itu, kedua persamaan tersebut dan syarat batasnya digunakan untuk menurunkan persamaan dasar fluida dua lapisan. Diasumsikan bahwa domain fluida dua lapisan dibatasi oleh lapisan atas berupa permukaan rata dan lapisan bawah mempunyai ketebalan yang cukup besar. Persamaaan gerak yang diperoleh pada fluida dua lapisan lebih sederhana. Formulasinya yang eksplisit dan sederhana memungkinkan diperolehnya pemahaman masalah gelombang interfacial.

Persamaan gerak pada fluida dua lapisan diformulasikan menggunakan formulasi Hamiltonian. Hamiltonian didefinisikan sebagai energi total, yaitu penjumlahan energi kinetik dengan energi potensial. Energi kinetik tidak secara eksplisit dinyatakan dalam peubah fisis sehingga energi kinetik direduksi menggunakan operator Dirichlet-Neumann. Selanjutnya, dengan asumsi gelombang panjang dan amplitudo kecil diperoleh sistem persamaan tak linear bagi gerak gelombang interfacial dalam sistem Hamiltonian.

IV HASIL DAN PEMBAHASAN

Berikut ini persamaan dasar fluida dua lapisan yang telah diperoleh pada bagian sebelumnya akan diformulasikan menjadi suatu sistem Hamiltonian. Pembahasan masalah ini berdasarkan rujukan Craig, Guyenne, dan Kalisch (2005). Hamiltonian H didefinisikan sebagai energi total, yaitu penjumlahan energi kinetik K dan energi potensial P yang dinyatakan oleh

H = K + P. (4.1)

4.1 Formulasi Hamiltonian

Energi kinetik K dan energi potensial P berturut-turut didefinisikan sebagai berikut:

2 1

2 2

( )

2 2

2 2 1 1

1 1

2 2

x h

h

K dydx dydx





   





 

 

 



฀ ฀

(4.2)

2 1

2 2

( )

2 1

( )

x h

h x

P g ydydx g ydydx





 





 



 

฀ ฀

= 2

2 2 1

1

( )( )

2g x   dx



฀

. (4.3)

Misalkan ₁

 

₁



 



2 , x  x x

  dan ₂

 

₂



 



2 , x  x x

  . Didefinisikan

operator Dirichlet- Neumann untuk domain fluida di batas kedua lapisan sebagai berikut:

 



2



12

2 2 2 2. 2 1 x 2

G     N   (4.4)

 



2



1₂

1 2 1 1. 2 1 x 2

G     N   , (4.5)

dengan ₂



₂



2 2

1

1 1

T x x

N





 

 yakni vektor normal satuan di y



2

 

x t, . Jadi

energi kinetik pada persamaan (4.2) dapat dinyatakan sebagai berikut

 

 

2 2 2 2 2 1 1 1 2 1

1 1

2 2

K  _



 G



 



G



 _dx

 



฀

. (4.6) Berdasarkan definisi operator Dirichlet- Neumann, syarat batas kinematik pada persamaan (2.11) dapat dinyatakan oleh:

 

2t G2 2 2

 

2t G1 2 1



 



 , (4.7)

dengan penyelesaian masing-masing berbentuk   ₁ G₁1

 

 

_{2 2t}dan

 

1

2 G2

 

2 2t



  . Selanjutnya, didefinisikan Lagrangian LKP, maka dengan menggunakan persamaan (4.3) dan (4.6) diperoleh:

 

 



  

1 1

2 2 2 2 2 2 2 1 2 1 2 2 2

2 1 2 1 ( , ) ( ) 2 1 . 2

t t t t t

L G G dx

g x dx

                  





฀ ฀ (4.8)

Definisikan peubah

 

2

2 x _tL







, diperoleh

 

1

 

1

 

2 x 2G2 2 2t 1G1 2 2t



_





 

_





 

=



₂₂

 

x  



_{1 1}, (4.9) dan berdasarkan persamaan (4.7) dan (4.9) diperoleh

 



 

 



1 2 2 1 2 2 2 1 2 2 G    G   G  

 



 

 



2 2 2 2 1 2 1 2 2 1 G    G  G 

    , (4.10)

sehingga Hamiltonian H pada persamaan (4.1) menjadi





 



 

 





 







1

2 2 2 1 2 2 1 2 1 2 2 2 2 2 2

2 2 1 1 , 2 1 . 2

H G G G G dx

g dx                  





฀ ฀ (4.11)

Jadi sistem persamaan bagi gerak gelombang interfacial dinyatakan dalam sistem Hamiltonian berikut: 2 2 2 2 0 1 1 0 t H H              _{  } _ _      _{ },

atau dapat ditulis sebagai berikut: 2

2

t  H

 

2 2

t  H

   , (4.12)

Nilai H yang diberikan pada persamaan (4.11) masih sulit ditentukan, karena masih bergantung pada ₂ yang tidak dinyatakan secara eksplisit. Penurunan persamaaan (4.8) - (4.11) dapat dilihat pada Lampiran 2.

4.2 Gerak Gelombang Interfacial

Sistem Hamiltonian yang diperoleh pada bagian sebelumnya akan digunakan untuk mendapatkan persamaan gerak gelombang interfacial antar fluida yang lapisan bawahnya mempunyai ketebalan yang cukup besar dan lapisan atasnya mempunyai ketebalan yang berhingga. Berdasarkan persamaan gerak gelombang interfacial akan diformulasikan gerak gelombang soliter interfacial. Penurunan persamaan gerak gelombang interfacial dilakukan dengan asumsi, perbandingan amplitudo dan ketebalan lapisan atas dengan perbandingan ketebalan lapisan atas dan panjang gelombang memiliki orde yang sama. Dengan kata lain, amplitudo dan panjang gelombang interfacial yang ditinjau memiliki nilai yang sebanding, sehingga diperkenalkan parameter kecil



pada penskalaan berikut:

'

x 



x, 2

2'  



 , ₂'₂, (4.13)

dimana



฀



h₁/



 

฀ a h/ ₁



฀ 1.

Parameter dan penskalaan pada persamaan (4.13) akan diaplikasikan pada bentuk Hamiltonian pada persamaan (4.11). Agar bentuk Hamiltonian H dinyatakan secara eksplisit, maka operator Dirichlet-Neumann pada persamaaan (4.4) dan (4.5) dinyatakan dalam uraian deret Taylor yang masing-masing berbentuk:

 



2 3



2 2 2 2 2

G



 D D D



 D



D O



D ,

 

 



 

 







1 2 1 2 1 2 1

2 3 2

tanh tanh tanh

,

G D h D D D D h D D h D

O D

  



  

 (4.14)

 

3





2 2' ' ' 2' ' ' 2' '

G   D  D  D  D  D , (4.15)

dan

 





₃ 2









1 2 1

1 2 1

' ' '

' ' tanh '

' tanh ' ' ' tanh '

D D

G D h D

D h D D h D



   

  

 

  _ _

 

Uraian deret Taylor dari

 

' 1 2

G  terhadap



adalah

G₁

 

₂' 2



h D₁ '2



3



D'₂'D'



O

 

4 , (4.16) dengan D



D'.

Selanjutnya, tuliskan Hamiltonian H pada persamaan (4.11) sebagai berikut





 

1



 



2





2 2 2 1 2 2 2 2 2 2 1

1 1

,

2 2

H   



 G  B G   dx



g   dx

฀ ฀

, (4.17) dengan operator B berikut

 

 

2 1 2 1 2 2

B



G







G



.

Berdasarkan persamaan (4.15) dan (4.16), operator B menjadi





2 2 3 3

2 1 ' 2 ' 2' ' 1 ' 1 ' 2' ' ' 2' ' B  h D   D D  D   D D D  D

(4.18) sehingga invers dari operator B adalah





1

2 2 3 3

2 1 2 2 1 1 2 2

1

' ' ' ' ' ' ' ' ' ' '

B

h D D D D D D D D

         

 _

    .

Kemudian, uraian deret Taylor dari B1 terhadap



adalah





 

2

1 1 2

2 2

1 1

3

2 ' 2 ' 2 2 ' 4 2 2

2 1 2 1 2 1 2 1 2

3 ₃ 1

3

4 ' 2 2 ' 2

3 1 2 1 2 1 2 1 2 2

4 _{4 4 ' 2 6 3 3}

1 1 2 1 2 1 2

' 1

' _'

' ' ' ' ' '

'

2 ' ' 2 ' '

1

' 2 ' ' '

D h B

D _D

D D D D D D h

D

D D h D D h

o

D D D h D h



  _

        



     

 

    

 _{ }

   



 _ 

 

 

_{ } 

 









 

2

1 1 2

2 2 1 1

' 2

3

2 2 2

2 2

1 3

1 2

3 1 2 2 2

2 1 3 4 ' 1 ' ' ' ' ' ' ' ' 2 ' ' ' ' h D B D D D

D D D D

D h D D D O D                  _{ }             _{ }           _ _  _{ }     (4.20)

Jika persamaan (4.15), (4.16) dan (4.20) digunakan, maka diperoleh bentuk

 

' 1

 

' 2 1 2 12 2 2 2 3

 

4

1 2 2 2 2

1 1 1

' '

' h D D ' '

D h D D

G  B G      O 

  

 _{  }_{ } _{ }

 

 

sehingga

 

 

2 2 2 2

1 2

' 1 ' 1 2 3

2 1 2 2 2 2 2 2 2

1 1 1

' '

' h D D ' '

D h D D

G B G   

           _ _{ } _  _      _{ }    (4.21) Jika persamaan (4.21) digunakan, maka bentuk H pada persamaan (4.17) menjadi









2 2 2 2

1 2 3

1 2

2 2 2 2 2

1 1 1

2

2 2 1

' ' ' ' ' 1 , 2 1 2

h D D

D h D D

H dx g dx                    _ _  _ _      





฀ ฀ (4.22)

Selanjutnya, misalkan ₂ dan turunan-turunannya terhadap x menuju nol di x , dan notasikan '

2 ' 2

x x

u      , maka diperoleh









 

2 2

2 2

1 2 1

2 2 1 2 2

1 1 2 2 3 2 1 ,

2 2 2

. 2

x

h h

H u u dx g dx u udx

u dx O

           _{ }        









฀ ฀ ฀ ฀ (4.23)

Penurunan persamaan (4.15) dan (4.23) dapat dilihat pada Lampiran 3. Dengan demikian sistem Hamiltonian pada persamaan (4.12) menjadi

1 2

t  xuH



   

2

1

tu



x



 H



dengan Hamiltonian H diberikan pada persamaan (4.23).

Dengan menggunakan rumus turunan variasi dan Hamiltonian H pada persamaan (4.23) terhadap ₂ dan u , maka persamaan (4.24) menjadi

2

1 2 1

2 2 2

1 1 1

( )

t x x x x

h h

u  u  u

  

  

         ,



2 1



2 1

tu g x u ux



  



       . (4.25)

Persamaan (4.23) merupakan persamaan gerak gelombang interfacial yang merambat dalam dua arah. Penurunan persamaan (4.25) dapat dilihat pada Lampiran 3.

Berikut ini akan dibahas persamaan gerak interfacial yang merambat hanya dalam satu arah. Untuk membahas gerak gelombang tersebut, maka didefinisikan transformasi berikut:

















1 2 1 1

4 4

1 1 2 1 ₂

1 2 1 1

4 4

1 1 2 1

4 4 , 4 4 g h h g r

s _{g h} u

h g       _        _                      _    _    (4.26)

dengan r dan s masing-masing menyatakan simpangan gelombang yang bergerak dalam arah kanan dan kiri. Dengan menggunakan proposisi 1 pada bagian landasan teori, maka sistem Hamiltonian pada persamaan (4.24) menjadi

tr  x rH

   

ts  x sH

    , (4.27)

dengan

 











    









2 2

1 2 1 1

2 2

1 2 1 1 2 2

1 2 1 2 1

2

1 1

2

1 2 1 3 2 2 3 4 1 1 2 , 2 2 2 2 2 2 4 1

2 2 4

x

gh r rs s

H r s dx

gh r rs s

dx g

h

r s r s dx h

g

Penurunan persamaan (4.28) dapat dilihat pada Lampiran 3.

Selanjutnya asumsikan bahwa gelombang yang ditinjau hanya merambat dalam satu arah sehingga dimisalkan _s฀O

 

2 _{. Jadi Hamiltonian H pada persamaan} (4.28) menjadi













2 2

1 2 1 2 2 1 1 2 1

2

1 1 1

2

1 2 1 3 4

1 1

4 2 4

1

.

2 2 4

x

gh h g

H r dx r rdx

h g r dx h                      







฀ ฀ ฀ (4.29)

Dengan menggunakan rumus turunan variasi terhadap Hamiltonian H pada persamaan (4.29), maka diperoleh persamaan gerak gelombang r sebagai berikut













2

1 2 1 2 1 1 2 1

2

1 1 1

1 2 1 4 1 1 2 3 2 . 4

t x x x

x

gh h g

r r r

h g r r h                           (4.30)

Selanjutnya gunakan penskalaan 0

X  x c t t   ,

dengan ₀ 1



2 1



1 gh

c  





 ,

maka persamaan (4.30) menjadi









2

1 2 1 1 2 1

2 1 ₄

2

1 1 1 1

3 2

2 X X 4 X

g g

h

r r r r

h h            

      . (4.31)

Penurunan persamaan (4.29), (4.30) dan (4.31) dapat dilihat di Lampiran 3. Persamaan (4.31) dapat dinyatakan dalam bentuk

 

0

X XX

r_ 



rr 



H r  , (4.32)

dengan 4 1



2 1



1 1 3 2 4 g h         ,





2

1 2 1 2 1 2 1 1 2 g h h       

 . (4.33)

 

1

 

2

ikX

XX X

r k r e dk

 









H F ,

dengan F merupakan transformasi Fourier yang diberikan berikut

 

ikX

X X

r r e dX 







F .

Penurunan persamaan (4.32) dapat dilihat pada Lampiran 4.

4.3 Gelombang Soliter Interfacial

Misalkan penyelesaian persamaan (4.32) diasumsikan dalam bentuk gelombang berjalan, yaitu

( )

r r  , (4.34)

dengan  X c₁ .

Jika persamaan (4.34) disubstitusikan ke dalam persamaan (4.32), maka diperoleh

1 ( ) 0

c r_ rr_  r_

   H  .

Kemudian setiap ruas diintegralkan terhadap  , diperoleh 2

1 ( ) 0

2

c r r  r_

   H  . (4.35)

Selanjutnya, jika transformasi Fourier dilakukan pada persamaan (4.35), kemudian menggunakan teorema konvolusi (Kreyzig 1993), maka diperoleh

1

( ) ( ) ( ') ( ')

2

c  k r k  r k r k k dk 



  



   _(4.36)

Penurunan persamaan (4.36) dapat dilihat pada Lampiran 4. Misalkan penyelesaian persamaan integral (4.36) dalam bentuk

1

( ) exp( )

2

r k  ab b k , (4.37)

dengan a dan b yang akan ditentukan berikut ini.

Substitusikan persamaan (4.37) ke dalam persamaan (4.36), diperoleh ruas kanan persamaan (4.36) dalam bentuk

 

2 2 1

exp

8 a b b k b k

  _ 

 

  ,



1



 

exp 2

c k

ab b k





.

Berdasarkan kedua bentuk di atas dan persamaan (4.36), diperoleh



  

2 2

 

1

1

exp exp

2 8

ab

c k b k a b k b k

b 

  

  _  _

  . (4.38)

Persamaan (4.38) terpenuhi, jika 2 2

8 2

ab a b

 _{ }

dan 2 2

1 1

8 2

ab

a b c

b

 _

sehingga diperoleh 1 4c a



 b 4

a  

 .

Selanjutnya, gunakan balikan transformasi Fourier dari persamaan (4.37), diperoleh

1

( ) ( ) exp( )

2

r  r k ik dk 









 _{, (4.39)}

yang merupakan penyelesaian persamaan (4.35).

Jika persamaan (4.37) disubstitusikan ke dalam persamaan (4.39), dan menggunakan rumus integral kompleks

2 ₂

1 2

exp( )

2

b b k ik dk

b 

 





 





,

maka diperoleh penyelesaian persamaan (4.32) berbentuk 2

2 ₂

( ) ab ,

r

b 





 (4.40)

dengan _a 4c1 

 b 4

a  

 . (4.41)

Berdasarkan persamaan (4.33) diperoleh bahwa μ selalu bernilai negatif, sehingga dari persamaan (4.41) dapat disimpulkan bahwa amplitudo gelombang soliter interfacial bernilai negatif. Dengan kata lain gelombang soliter interfacial yang terjadi berupa depresi. Selanjutnya, berdasarkan persamaan (4.41) dan



pada persamaan (4.33), diperoleh





1 2

1

10 1 2

c p p

p b

  ,

dengan 1 2 p 



 .

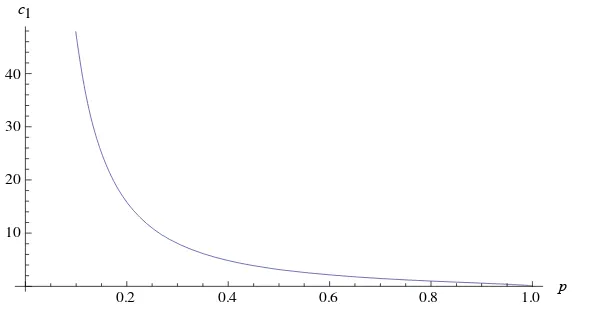
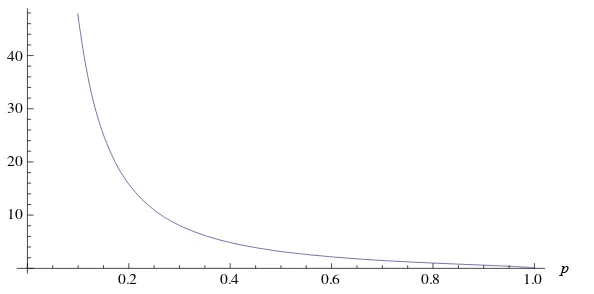
Hubungan kecepatan phase gelombang dan perbandingan rapat massa kedua lapisan diberikan pada Gambar 2 dengan b = 1 dan g = 10.

0.2 0.4 0.6 0.8 1.0 p

10 20 30 40

[image:46.612.164.464.292.449.2]

c₁

Gambar 2 Hubungan kecepatan phase gelombang terhadap perbandingan rapat massa

Dari Gambar 2 dapat dilihat bahwa apabila rapat massa fluida lapisan atas sangat kecil maka kecepatan phase gelombang yang dihasilkan tinggi. Jika rapat massa fluida lapisan atas mendekati nilai rapat massa fluida lapisan bawah, maka kecepatan phase gelombang yang dihasilkan semakin rendah atau mencapai nol.

Jika persamaan (4.33) dan (4.41) disubstitusikan ke dalam persamaan (4.40), maka diperoleh Gambar 3 berikut.

4 2 0 2 4 7

6 5 4 3 2 1 0

t



82

3

4

5

4

3

t

2 

[image:47.612.131.450.79.269.2]

1

Gambar 3 Gelombang soliter untuk persamaan gerak gelombang interfacial.

Gambar 3 membuktikan bahwa gelombang soliter interfacial yang terjadi berupa depresi.

Selanjutnya, persamaan (4.40) disubstitusikan ke persamaan (4.29), maka diperoleh nilai Hamiltonian H yang tetap, yaitu 6 x 10-7 atau tidak berubah terhadap waktu t, seperti diperlihatkan pada Gambar 4.

0 10 20 30 40 50

0.006 0.008 0.010 0.012 0.014

t

H

Gambar 4 Hubungan nilai Hamiltonian H terhadap waktu t

[image:47.612.151.468.407.623.2]

V SIMPULAN DAN SARAN

5.1 Simpulan

Persamaan gerak gelombang internal pada laut dalam dengan menggunakan formulasi Hamiltonian diturunkan dengan asumsi domain fluida dua lapisan dibatasi oleh lapisan atas mempunyai ketebalan yang berhingga dan lapisan bawah mempunyai ketebalan yang cukup besar. Ketebalan yang cukup besar didasarkan pada perbandingan amplitudo gelombang yang ditinjau dengan kedalaman fluida. Amplitudo gelombang yang ditinjau jauh lebih kecil dari kedalaman fluida. Selain itu dibutuhkan pula asumsi gelombang panjang untuk penyederhanaan formulasi Hamiltonian.

Formulasi gerak gelombang interfacial yang diperoleh berupa sistem Hamiltonian dengan energi total (Hamiltonian) bergantung pada simpangan gelombang interfacial dan kecepatan partikel fluida dalam arah horizontal. Sistem Hamiltonian yang diperoleh ini berupa persamaan gerak gelombang yang merambat dalam dua arah, tetapi masih tergantung pada kecepatan partikel fluida dalam arah horizontal, dimana besaran ini masih sulit ditentukan. Oleh karena itu diperkenalkan suatu transformasi yang mengubah besaran tersebut menjadi besaran simpangan gelombang yang bergerak ke arah kanan dan kiri sehingga sistem Hamiltonian yang diperoleh memiliki Hamiltonian yang bergantung pada simpangan gelombang yang bergerak dalam arah kanan dan arah kiri. Jika simpangan gelombang yang bergerak dalam arah kiri di asumsikan sangat kecil, maka diperoleh persamaan gerak gelombang interfacial yang merambat hanya dalam satu arah. Hamiltonian dari sistem Hamiltonian ini merupakan besaran yang tetap atau tidak mengalami perubahan pada setiap waktu.

gerak gelombang interfacial bergantung pada kondisi fisis fluida, yaitu rapat massa kedua lapisan dan ketebalan lapisan atas.

Berdasarkan simulasi numerik diperoleh bahwa apabila rapat massa fluida lapisan atas jauh lebih kecil dibanding rapat massa lapisan bawah, maka kecepatan phase gelombang yang dihasilkan besar. Jika rapat massa fluida lapisan atas mendekati rapat massa fluida lapisan bawah, maka kecepatan phase gelombang yang dihasilkan sangat kecil. Selanjutnya, gelombang soliter interfacial yang terjadi berupa depresi.

5.2 Saran

DAFTAR PUSTAKA

Ambrosi D. 2000. Hamiltonian Formulation for Surface Waves in a Layered Fluid. Wave Motion 31:71-76.

Benjamin TB, Bridges TJ. 1997. Reappraisal of The Kelvin-Helmholtz Problem. I. Hamiltonian Structure. J. Fluid Mech 333:301-325.

Choi W, Camassa R. 1996. Weakly Nonlinear Internal Waves in a Two Fluid System. J. Fluid Mech 313:83-103.

Craig W, Guyenne P, Kalisch H. 2005. Hamiltonian Long-wave Expansions for Free Surfaces and Interfaces. Wiley Periodical, Inc 58:1587-1642.

Groesen EV, de Jager EM. 1994. Mathematical Structures in Continuous Dynamical System, in Series: Studies in Mathematical Physics. Amsterdam:North-Holland, Elsevier.

Jaharuddin. 2004. Gelombang Soliter di Selat Lombok dan Simulasi Numerik Fenomena Morning Glory [disertasi]. Bandung:Program Pascasarjana, Institut Teknologi Bandung.

Kreyzig, E. 1993. Matematika Teknik Lanjut. Gramedia Pustaka Utama.Jakarta. Osborne AR, Burch TL. 1980. Internal Solitons in The Andaman Sea. Science

208:451-460.

Lampiran 1 Penurunan Persamaan (2.1), (2.2), (2.3), (2.6), (2.7), (2.8) dan (2.11)

Penurunan persamaan (2.1)

Dari Gambar 5, diperoleh laju perubahan massa dinyatakan sebagai berikut:



x x x





y y y



x y u u y w w x

t

 _{   }

 



       



atau



ux ux x





wy wy y



t x y

 

 

    

 _{ }

   .

Untuk  x 0 dan  y 0diperoleh

   









, 0,0

y y y

x x x

x y

w w

u u

Lim

t x y

 

 

  

  

 _{ } 

 _{   }

 

 _   _

 

atau

u w

t x y

  

 _{ } _

   . (1)

Jika dinotasikan , x y

      _{ } 

 , q



u w,



, dan turunan total  terhadap t adalah

D

u w

Dt t x y

 _  _  _ 

   ,

maka persamaan (1) menjadi

 

D

q Dt

 _{  }

฀ , (2)

y u_x



_{u y}

x x 



x w

y



x w_yy 

y

[image:52.612.149.379.131.277.2]

dengan q u w x y

 

  

 

฀ .

Dengan menggunakan asumsi fluida tak termampatkan, yaitu fluida mengalir tanpa mengalami perubahan volume dan rapat massa, maka diperoleh

0 D

Dt  _

, (3)

sehingga dari persamaan (2) diperoleh  ฀q 0 atau 0

x y

u w  . (4)

Persamaan (3) dan (4) dapat ditulis 0

 

 _{x y}

t u w



0

  _y

x w

u .

Penurunan persamaan (2.2)

Dari Gambar 6, laju perubahan momentum dalam elemen luas pada komponen-x adalah













,

x x x y y y

x x x

u

x y uu u u y wu wu x

t

P P y

 _{   }

 





       



  

atau



uux u ux x





wuy wuy y





Px Px x



u

t x y x

 

 

      

 _{  }

    .

y u u_x 



_{u u y}

x x 



x w u

y 



x w u _yy  

y

[image:53.612.165.352.355.519.2]

x Gambar 6 Kesetimbangan momentum

Untuk  x 0 dan  y 0diperoleh

   













, 0,0

y y y

x x x x x x

x y

wu wu

uu u u P P

u

Lim

t x y x

 

 

   

  

 _{  } 

 _{    }

 

 _    _

 

atau



uu





wu



u P

t x y x







 

 _{   }

   

atau

u u u u w P

u u u uu w u wu

t t x x x y y y x

  

            �