Geometri dalam Ruang, Vektor

(1)

Kecepatan, Percepatan dan Kelengkungan

Geometri dalam Ruang, Vektor

Zahnur@informatika.unsyiah.ac.id

Prodi Matematika FMIPA Unsyiah

September 15, 2011

(2)

Pengertian

Contoh

Rumus-rumus Lain untuk Kelengkungan

Komponen Normal dan Komponen Singgung pada Percepatan

Kelengkungan(curvature) adalah suatu bilangan yang

menyatakan seberapa tajam suatu kurva melengkung. Sebuah garis mempunyai kelengkungan 0, sementara sebuah kurva yang melengkung tajam tentu mempunyai kelengkungan yang besar.

42. Sebuah bola kecil digelindingkan pada sebuah meja men-datar yang mempunyai tinggi 4 kaki dengan laju 20 kaki per detik. Pada sudut berapakah dan pada laju berapakah bola ini akan menyentuh lantai?

43. Sebuah kaleng terbuka pada salah satu ujungnya dan ditempelkan pada tepi roda berputar vertikal beIjari-jari 60 em, di mana bagian kaleng yang terbuka menghadap ke pusat roda. Di dalarn kaleng tersebut diletakkan sebuah kelereng. Berapakah Jaju sudut yang harns dijaga agar kelereng tersebut tidak jatuh? (Lihat Soal 44 untuk nilai g.)

44. Sebuah benda dengan mass a rn berputar pada orbit melingkar dengan jari-jari r pada laju konstas v mengelilingi sebuah benda yang massanya M. Dari Contoh 3,

v2

a = la(t)1 = orlr(t)1 =

-r

sementara dari Hukum Newton ten tang Kuadrat Invers, F = rna = GrnM/? atau

k

a = r2 (k adalah konstanta)

Misalkan T adalah waktu yang dibutuhkan untuk melakukan satu revolusi, R '" 3960 mil (jari-jari bumi), g '" 32,17 kaki per detik2

'" 980 em per detik2

(pereepatan gravitasi di permukaan bumi).

Gunakan fakta-fakta ini untuk menunjukkan yang berikut: (a) v2 = ~

r

(b) T2 =

(4:

2 }3

(c) k = gR2

(Hukum Ketiga Kepler ten tang orbit melingkar)

[g 45. Terapkan hasil dari Soal 44 untuk kasus burni dan sebuah satelit dengan menentukan hal-hal berikut ini:

SUBBAB 13.5 Kelengkungan dan Percepatan 195

(a) laju satelit yang mengorbit (mengelilingi) bumi 200 mil di atas permukaan bumi.

(b) jarak dari pusat burni ke sebuah satelit komunikasi yang berada

pada orbit sinkron (synchronous orbit), yaitu satelit tersebut akan senantiasa berada tepat di atas suatu titik di bumi yang sarna.

[g 46. Bulan mengorbit burni setiap 27,32 hari. Tentukan jarak dari bumi ke bulan dalam mil (lihat Soal 44).

ICASI47. Gambarlah lintasan kepala dari ret) = (4 cos t)i + (3 sin t)j,

r'(t), dan r"(t), 0 :0; t :0; nl2. Pada grafik-grafik ini, tampilkan vektor-vektor yang bersesuaian untuk

(a) t = nl6

(c) t = nl3, dan

(b) t = nl4

(d) t = nl2,

buatlah ilustrasi yang menunjukkan bahwa r'(t) akan mengarah garis singgung lintasan tersebut dan bahwa r"(t) akan mengarah sisi eekung lintasan tersebut.

ICASI48. Gambarlah lintasan kepala dari ret) = (a cos t)i + (b sin t)j,

r'(t), dan r"(t) , 0 :0; t :0; 2n, untuk beberapa nilai a dan b. Buatlah

sebuah dugaan tentang Iintasan ini dan buktikan dugaan Anda.

ICASI 49. Misalkan ret) = (3 cos t - cos 3t)i + (3 sin t - sin 3t)j. Gambarlah lintasan kepaJa dari ret), r'(t), dan r"(t) , untuk 0 :0; t :0; n. Kemudian, dengan menggunakan grafik-grafik ini, tunjukkan vektor-vektor yang bersesuaian untuk

(a) t = nl6

(c) t = nl2, dan

(b) t = nl3 (d) t = 2n13.

Jawaban Telaah Ulang Konsep: 1. fungsi bernilai-vektor dari sebuah peubah real 2. f dan g kontinu di c; f'(t)i + g'(t)j

3. posisi 4. r'(t); r"(t); garis singgung; eekung

13.5 Kelengkungan dan Percepatan

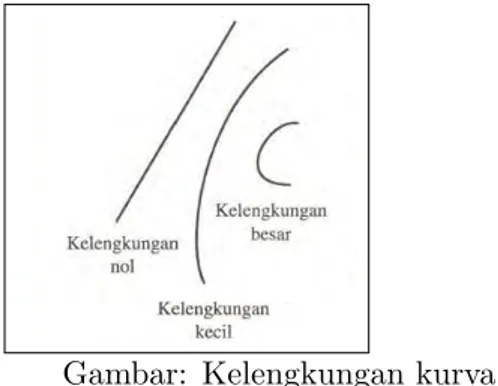
Kita akan mempelajari suatu bilangan yang disebut kelengkungan (curvature), yang mengukur seberapa tajam suatu kurva melengkung. Sebuah garis mempunyai kelengkungan 0, semen tara sebuah kurva yang melengkung tajam tentu mempunyai kelengkungan yang besar (Gambar 1). Agar sampai ke suatu definisi yang tepat, kita harus mengingat kembali beberapa gagasan terdahulu dan memperkenalkan beberapa gagasan baru.

Gambar 1

c

Kelengkungan besar Kelengkungan kecil

Untuk a :,; t:'; b, misalkan ret) = f(t)i + g(t)j = (f(t), g(t» adalah vektor posisi untuk titik P = pet) pad a bidang. Kita andaikan r'(t) ada dan kontinu, dan r'(t)

*"

°

pada selang (a, b). Maka (lihat Subbab 6.4), ketika t meningkat, P akan membentuk sebuah kurva mulus (Gambar 2), dan panjang lintasan s = h(t) dari Pea) ke pet) dinyatakan dengan

s = h(t) =

L

~[J'(u)f

+ [g'(U)]2 du =

L

Ir'(u)1 du Laju titik yang bergerak adalah

ds

dt = Ir'(t)1 = Iv(t)1

Karena r'(t)

*"

0, maka Iv(t)1 > 0, sehingga s akan meningkat ketika t meningkat. Berdasarkan Teorema Fungsi lovers (Teorema 7.2B), s = h(t) mempunyai invers t = h-1(s) dan

dt ds

1 ds/dt Iv(t)1

Misalkan T(t), yang disebut vektor singgung satuan (unit tangent vector) di pet), didefinisikan sebagai

Gambar: Kelengkungan kurva

(3)

Pengertian

Contoh

Komponen Normal dan Komponen Singgung pada Percepatan Untuka≤t≤b, misalkan r(t) =f(t)i+g(t)j=hf(t), g(t)i

adalah vektor posisi untuk titikP =P(t) pada bidang. Kita andaikanr0(t) ada dan kontinu, danr0(t)6= 0 pada selang (a, b).

Maka ketikatmeningkat,P akan membentuk sebuah kurva

mulus dan panjang lintasans=h(t) dari P(a) ke P(t) dinyatakan dengan s=h(t) = Z t a p [f0(u)]2_{+ [}_g0₍_u_)]2_du₌ Z t a |r0(u)|du

196 BAS 13 Geometri pada Bidang, Vektor

y ~ PCb)

"

_{""" Pet)}

S~

= n\t)~ Pea) r(t) x Gambar 2 y x Vektor singgung satuan T(t)

Gambar 3 y x Gambar 4 Lingkaran

\

_a

\

Gambar 5 r'(t) v(t) T(t) = Ir'(t)1 = Iv(t)1

Ketika pet) bergerak di sepanjang kurva, vektor satuan T(t) akan mengubah arahnya (Gambar

3). Tingkat perubahan T terhadap panjang busur s, dalam hal ini d Tlds, disebut vektor

kelengkungan (curvature vector) di P. Akhimya, kita mendefinisikan kelengkungan 1C(kappa) di P sebagai besaran dari dTlds, yaitu 1C = IdTldsl. Maka, berdasarkan Aturan Rantai,

dT dT

dt T'(t)

ds dt ds Iv(t)1

Jadi,

1C =

IdTl

= IT'(t)1 = IT'(t)1

ds Iv(t)1 Ir'(t)1

8eberapa Contoh Penting Untuk meyakinkan Anda bahwa definisi tentang kelengkungan di atas masuk akal, kita akan melihat beberapa ilustrasi berikut ini.

CONTOH 1 Tunjukkan bahwa kelengkungan dari sebuah garis identik dengan nol.

Penyeiesaian Hal ini segera dapat dibuktikan berdasarkan fakta bahwa T adalah sebuah

vektor konstan. Tetapi untuk mengilustrasikan metode-metode vektor, kita akan melihat sebuah

demonstrasi aljabar. Misalkan P dan Q adalah dua titik tetap pada suatu garis, dan rnisalkan

a =

oP

dan b = PQ. Maka sebuah bentuk vektor untuk persamaan garis tersebut dapat ditulis

sebagai (Gambar 4) Jadi, r = ret) = a + tb vet)

=

r'(t)

=

b T(t) = b Ibl IT'(t)1 = ~ = 0 Iv(t)1 Ibl

•

CONTOH 2 Tunjukkan bahwa pada tiap titik, kelengkungan sebuah lingkaran dengan

jari-jari a adalah 1C = 1/a (Gambar 5).

Penyeiesaian Kita dapat menganggap bahwa lingkaran tersebut berpusat di titik asal. Maka

persamaan vektomya dapat dituliskan dengan

Jadi,

ret) = a cos ti + a sin tj

vet) = r'(t) = -a sin ti + a cos tj

Iv(t)1 = [a2 sin2

t + a2 cos2

t] 112 = a

v(t) vet)

T(t) = Iv(t)1 = ----;; = -sin ti + cos tj

1C= IT'(t)1 = I-cos ti - sin tjl = .!.

Iv(t)1 a a

Karena 1C adalah kebalikan dari jari-jari, maka semakin besar suatu lingkaran, semakin kecil

kelengkungannya. •

Contoh tentang lingkaran ini membawa kita ke beberapa gagasan baru. Andaikan P adalah

sebuah titik pada sebuah kurva di mana 1C *-O. Perhatikan lingkaran berikut di mana garis Gambar: Kelengkungan kurva

(4)

Pengertian

Contoh

Laju titik yang bergerak adalah

ds

dt =|r

0₍_t₎_|₌_|v₍_t₎_|

Karenar0(t)6= 0, maka |v(t)|>0, sehingga sakan meningkat

ketikat meningkat.

Selanjutnya,s=h(t) mempunyai invers t=h−1(s) dan

dt ds = 1 ds/dt = 1 |v(t)|

(5)

Pengertian

Contoh

MisalkanT(t), yang disebut vektor singgung satuan (unit

tangent vector) diP(t), didefinisikan T(t) = r

0₍_t₎

|r0₍_t₎_| =

v(t) |v(t)|

KetikaP(t) bergerak di sepanjang kurva, vektor satuanT(t)

akan mengubah arahnya. Tingkat perubahanTterhadap

panjang busurs, dalam hal inidT/ds, disebutvektor

kelengkungan(curvature vector) di P.

y ~ PCb)

"

_{""" Pet)}

S~

\

_a

\

Ketika pet) bergerak di sepanjang kurva, vektor satuan T(t) akan mengubah arahnya (Gambar

3). Tingkat perubahan T terhadap panjang busur s, dalam hal ini d Tlds, disebut vektor

kelengkungan (curvature vector) di P. Akhimya, kita mendefinisikan kelengkungan 1C(kappa) di P sebagai besaran dari dTlds, yaitu 1C = IdTldsl. Maka, berdasarkan Aturan Rantai,

dT dT

dt T'(t)

ds dt ds Iv(t)1

Jadi,

1C =

IdTl

= IT'(t)1 = IT'(t)1

ds Iv(t)1 Ir'(t)1

8eberapa Contoh Penting Untuk meyakinkan Anda bahwa definisi tentang kelengkungan di atas masuk akal, kita akan melihat beberapa ilustrasi berikut ini.

demonstrasi aljabar. Misalkan P dan Q adalah dua titik tetap pada suatu garis, dan rnisalkan

a =

oP

dan b = PQ. Maka sebuah bentuk vektor untuk persamaan garis tersebut dapat ditulis

sebagai (Gambar 4) Jadi, r = ret) = a + tb vet)

=

r'(t)

=

b T(t) = b Ibl IT'(t)1 = ~ = 0 Iv(t)1 Ibl

•

jari-jari a adalah 1C = 1/a (Gambar 5).

Jadi,

ret) = a cos ti + a sin tj

vet) = r'(t) = -a sin ti + a cos tj

Iv(t)1 = [a2 sin2

t + a2 cos2

t] 112 = a

v(t) vet)

1C= IT'(t)1 = I-cos ti - sin tjl = .!.

Iv(t)1 a a

sebuah titik pada sebuah kurva di mana 1C *-O. Perhatikan lingkaran berikut di mana garis

Gambar: Vektor singgung satuanT(t)

(6)

Pengertian

Contoh

Kelengkunganκ (kappa) di P didefinisikan sebagai besaran

daridT/ds, yaitu κ=|dT/ds|. Maka, berdasarkan Aturan Rantai, dT ds = dT dt dt ds = T0(t) |v(t)| Jadi κ= dT ds = |T 0₍_t₎_| |v(t)| = |T0(t)| |r0₍_t₎_|

(7)

Pengertian

Contoh

Contoh 1

Tunjukkan bahwa pada tiap titik, kelengkungan sebuah lingkaran dengan jari-jaria adalahκ= 1/a.

y ~ PCb)

"

_{""" Pet)}

S~

\

_a

\

Ketika pet) bergerak di sepanjang kurva, vektor satuan T(t) akan mengubah arahnya (Gambar

3). Tingkat perubahan T terhadap panjang busur s, dalam hal ini d Tlds, disebut vektor

kelengkungan (curvature vector) di P. Akhimya, kita mendefinisikan kelengkungan 1C(kappa) di P sebagai besaran dari dTlds, yaitu 1C = IdTldsl. Maka, berdasarkan Aturan Rantai,

dT dT

dt T'(t)

ds dt ds Iv(t)1

Jadi,

1C =

IdTl

= IT'(t)1 = IT'(t)1 ds Iv(t)1 Ir'(t)1

8eberapa Contoh Penting Untuk meyakinkan Anda bahwa definisi tentang kelengkungan

di atas masuk akal, kita akan melihat beberapa ilustrasi berikut ini.

demonstrasi aljabar. Misalkan P dan Q adalah dua titik tetap pada suatu garis, dan rnisalkan a =

oP

dan b =

PQ.

Maka sebuah bentuk vektor untuk persamaan garis tersebut dapat ditulis

sebagai (Gambar 4) Jadi, r

=

ret)

=

a + tb vet)

=

r'(t)

=

b T(t)

=

b Ibl IT'(t)1 = ~ = 0 Iv(t)1 Ibl

•

jari-jari a adalah 1C = 1/a (Gambar 5).

Jadi,

ret) = a cos ti + a sin tj

vet) = r'(t) = -a sin ti + a cos tj

Iv(t)1 = [a2 _sin2 _t_{+ a}2 _cos2 _t]₁₁₂_{= a} v(t) vet)

1C= IT'(t)1 = I-cos ti - sin tjl =

.!.

Iv(t)1 a a

sebuah titik pada sebuah kurva di mana 1C *-O. Perhatikan lingkaran berikut di mana garis

(8)

Pengertian

Contoh

Komponen Normal dan Komponen Singgung pada Percepatan Penyelesaian.

Kita dapat menganggap bahwa lingkaran tersebut berpusat di titik asal. Maka persamaan vektorya dapat dituliskan dengan

r(t) =acosti+asintj Jadi v(t) = r0(t) =−asinti+acostj |v(t)| = [a2sin2t+a2cos2t]1/2=a T(t) = v(t) |v(t)| = v(t) a =−sinti+ costj κ = |T 0₍_t₎_| |v(t)| = | −costi−sintj| a = 1 a

Karenaκ adalah kebalikan dari jari-jari, maka semakin besar

suatu lingkaran, semakin kecil kelengkungannya.

(9)

Pengertian

Contoh

Komponen Normal dan Komponen Singgung pada Percepatan Kelengkungan pada lingkaran ini memberikan kita ke beberapa

gagasan baru kelengkungan pada kurva. Perhatikan lingkaran berikut dimana garis singgung terhadap suatu kurva berada di

titikP dan mempunyai kelengkungan yang sarna di titik

tersebut. Pusat lingkaran tersebut akan terletak di sisi cekung

kurva tersebut. Lingkaran ini disebutlingkaran

kelengkungan(circle of curvature) ataulingkaran oskulasi

(osculating circle), jari-jarinyaR= 1/κdisebutjari-jari

kelengkungan(radius of curvature), dan pusatnya disebut

pusat kelengkungan(center of curvature).

(10)

Pengertian

Contoh

Lingkaran kelengkungan

Kurva

Gambar 6

SUBBAB 13.5 Kelengkungan dan Percepatan 197

singgung terhadap suatu kurva berada di titik P dan mempunyai kelengkungan yang sarna di

titik tersebut. Pusat lingkaran tersebut akan terletak di sisi cekung kurva tersebut. Lingkaran ini disebut Iingkaran kelengkungan (circle of curvature) atau Iingkaran oskulasi (osculating circle), jari-jarinya R = 11K" disebut jari-jari kelengkungan (radius of curvature), dan pusatnya disebut pusat kelengkungan (center of curvature). Gagasan ini diilustrasikan pada Gambar 6.

CONTOH 3 Tentukan kelengkungan dan jari-jari kelengkungan untuk hiposikloid r = 8 cos3 t i + 8 sin3 t j

di titik-titik P dan Q, di mana masing-masing t = n!12 dan t = 3n14. Kemudian sketsalah grafik hiposikloid ini yang menunjukkan lingkaran kelengkungan di titik P dan Q.

Peny.eiesaian Untuk 0 < t < n, t f:. rcI2,

vet) = r'(t) = -24 cos2 _t_{sin t}_i₊₂₄_sin2 _t_{cos t}_j

Iv(t)1 = 241sin t cos tl

. 2 . 2

T( t = -) sm t cos t. 1+ sm t cos t . J

Isin t cos tl Isin t cos tl

{ -eo, ti Hin ~ j 0< t <-n = n 2 cos tl - sm tJ - < t < n 2 {,in Ii + eos Ij o < t < -n T'(t) = _n 2 -sin ti - cos tj - < t < n 2 K(t) = IT'(t)1 = 1

Iv(t)1 241sin t cos tl 121sin 2tl Jadi, di P kita mempunyai

K"C~)

= -12-sin-(;-2-'

-~""7)

dan di Q kita mempunyai

1

6 dan

dan

RC:)

= 12

Grafik hiposikloid dan lingkaran-lingkaran kelengkungan tersebut ditunjukkan pada Gambar 7.

Lingkaran kelengkungan di Q Gambar 7 Lingkaran kelengkungan di P P 8 10 x

(11)

Pengertian

Contoh

Contoh 2

Tentukan kelengkungan dan jari-jari kelengkungan untuk hiposikloid

r(t) = 8 cos3ti+ 8 sin3tj

di titik-titikP danQ, di mana masing-masing t=π/12 dan

t= 3π/4.

(12)

Pengertian

Contoh

Untuk 0< t < π,t6=π/2,

v(t) = r0(t) =−24 cos2tsinti+ 24 sin2tcostj

(13)

Pengertian

Contoh

Jadi, diP kita mempunyai

κ(π/12) = 1 12|sin 2· π 12| = 1 6 dan R π 12 = 6

dan diQ kita mempunyai

κ(3π/4) = 1 12|sin 2·3π₄ | = 1 12 dan R 3π 4 = 12 Zahnur@informatika.unsyiah.ac.id Geometri dalam Ruang, Vektor

(14)

Pengertian Contoh

Misalkanφmelambangkan sudut yang diukur berlawanan arah

jarum jam dariike T. Maka, T = cosφi+ sinφj, sehingga

dT

dφ =−sinφi+ cosφj

dT

dφ adalah sebuah vektor satuan (panjang 1) danT.

dT dφ = 0. Di samping itu, κ= dT ds = dT dφ dφ ds = dT dφ dφ ds akibatnya κ= dφ ds

Rumus untukκ ini membantu pemahaman intuitif kita

mengenai kelengkungan, yaitu mengukur tingkat perubahanφ

terhadaps.

(15)

Pengertian Contoh

(16)

Pengertian Contoh

Teorema

Tinjau sebuah kurva dengan persamaan vektor

r(t) =f(t)i+g(t)j, yakni, dengan menggunakan persamaan parametrikx=f(t) dan y=g(t), maka

κ= |x

0_y00₋_x00_y0_| [(x0)2_{+ (}_y0₎2_]3/2_]

Secara khusus jika kurva tersebut mempunyai grafiky=g(x)

maka

κ= |y

00_| [1 + (y0₎2_]3/2_]

Bagian,utama menunjukan pendiferensialan terhadapt pada

rumus pertama, dan terhadapx pada rumus kedua.

(17)

Pengertian Contoh

Contoh 3

Tentukan kelengkungan elips

x= 3 cost, y = 2 sint

pada titik yang berhubungan dengant= 0 dan t=π/2, yaitu

di (3,0) dan (0,2). Sketsalah elips tersebut yang menunjukkan lingkaran kelengkungan yang bersesuaian.

(18)

Pengertian Contoh

Dari persamaan-persamaan berikut,

x0=−3 sint, y0 = 2 cost x00=−3 cost, y00=−2 sint Jadi κ=κ(t) = |x 0_y00₋_x00_y0_| [(x0)2_{+ (}_y0₎2_]3/2_] = 6 sin2t+ 6 cos2t [9 sin2t+ 4 cos2_t_]3/2 = 6 [5 sin2t+ 4]3/2 Akibatnya κ(0) = 6 43/2 = 3 4 κ(π/2) = 6 93/2 = 2 9 Zahnur@informatika.unsyiah.ac.id Geometri dalam Ruang, Vektor

(19)

Pengertian Contoh

(20)

Pengertian Contoh

MisalkanP=P(t) adalah sebuah titik pada sebuah kurva

mulus. Definisikan sebuah vektor baruN=N(t), disebut

vektor normal satuan(unit normal vector) di titikP, dengan

N= dT/ds |dT/ds| = 1 κ dT ds maka dT ds =κN

SekarangT= cosφi+ sinφj, maka

dT ds = dT dφ dφ ds = (−sinφi+ cosφj) dφ ds

di manaT·N= 0. Jadi, Nadalah sebuah vektor satuan yang

tegak lurus terhadapTdan mengarah ke sisi cekung kurva.

(21)

Pengertian Contoh

Vektor kecepatanvmemenuhi

v=|v|T= ds dtT maka a = dv dt = d2s dt2T+ ds dt dT dt = d 2_s dt2T+ ds dt dT ds ds dt Jadi a= d 2_s dt2T+ ds dt 2 κN

(22)

Pengertian Contoh

(23)

Pengertian Contoh

Contoh 4

Sebuah partikel bergerak sedemikian rupa sehingga vektor posisinya adalahr(t) =t2i+₃1t3j, t≥0. Nyatakan a(t) dalam

bentukTdan Ndan hitunglah ketikat= 2.

(24)

Pengertian Contoh

Penyelesaian. v(t) = 2ti+t2j ds dt = |v(t)|= p 4t2₊_t4 ₌_tp_{4 +}_t2 d2s dt2 = 4 + 2t2 √ 4 +t2 κ ds dt 2 = |x 0_y00₋_x00_y0_| [(x0)2_{+ (}_y0₎2_]3/2 ds dt 2 = |x 0_y00₋_x00_y0_| ds/dt = |(2t)(2t)−(t 2₎₍₂₎_| t√4 +t2 = 2t2 t√4 +t2 = 2t √ 4 +t2

(25)

Pengertian Contoh

Penyelesaian. Jadi a(t) = d 2_s dt2T+ ds dt 2 κN = 4 + 2t 2 √ 4 +t2T+ 2t √ 4 +t2N dan a(2) = √12 8T+ 4 √ 8N= 3 √ 2T+√2N