PENGANTAR PERSAMAAN
DIFERENSIAL PARSIAL
UNTUK SAINS DAN TEKNIK
Komputasi Metode Beda Hingga untuk Tipe Parabolik dan Hiperbolik Menggunakan FreeMat/MATLAB
Dr. Putu Harry Gunawan
12016
Diterbitkan secara mandiri melalui Nulisbuku.com 1Corresponding author. Tel.+6287 762 434 081.
Email: phgunawan@telkomuniversity.ac.id; harry.gunawan.putu@gmail.com Computational Sciences, School of Computing, Telkom University.
Pengantar Persamaan Diferensial Parsial untuk Sains dan Teknik
Hak cipta c�2016 oleh Dr. Putu Harry Gunawan Desain Cover: Dr. Putu Harry Gunawan
Editor Tulisan: Friska Fristella, S.Si., M.Si., M.Sc. Penerbit: www.nulisbuku.com
ILP Center Lt. 3S01 Jl. Raya Pasar Minggu No. 39A Pancoran, Jakarta Selatan 12780
Kata Pengantar
Puji syukur penulis panjatkan ke hadapan Tuhan Yang Maha Esa, karena berkat dan rahmat Beliau, buku ini dapat diselesaikan dan diterbitkan tepat waktu. Buku ini merupakan pengantar persamaan diferensial parsial (PDP) untuk level strata 1 dan yang setara. Materi yang disampaikan pada buku ini merupakan bagian terkecil dari materi PDP keseluruhan. Hanya PDP tipe parabolik dan hiperbolik berdimensi satu (1D) dan dua (2D) saja yang akan dibahas. Algoritma dan contoh program dengan bahasa pemrograman gratis FreeMat (mirip MATLAB) juga dibahas. Kode program Freemat mirip dengan MATLAB, sehingga pembaca dapat menjalankan kode program pada dua perangkat lunak yang berbeda.
Penulis mengucapkan terima kasih banyak atas masukan dan saran yang sudah diberikan oleh beberapa kolega untuk memperbaiki dan meningkatkan kualitas isi dari buku ini. Terima kasih juga saya ucapkan kepada jurusan Ilmu Komputasi, Telkom University, karena memberikan kesempatan kepada penulis untuk dapat mengajar PDP sehingga muncul ide untuk membuat buku ini.
Terakhir tapi bukan yang paling akhir, penulis mengucapkan terima kasih banyak kepada orangtua dan saudara-saudara yang senantiasa memberikan doa yang tidak mungkin penulis dapat membalasnya. Penulis juga membe-rikan kesempatan kepada pembaca untuk membemembe-rikan masukan, pertanyaan atau ide jika ada yang perlu diperbaiki dari segala sisi buku ini. Silakan meng-irimkan email kephgunawan@telkomuniversity.ac.iduntuk saran dan per-tanyaan.
Dr. Putu Harry Gunawan 2016
Bab 0:
Daftar Isi
Kata Pengantar i
Daftar Isi iii
Daftar Gambar vii
Daftar Algoritma xi
Daftar Program FreeMat/MATLAB xiii
1 Tentang Buku 1 1.1 Motivasi . . . 1 1.2 Panduan Pembaca . . . 3 1.3 Catatan . . . 3 2 Pengantar PDP 5 2.1 Konsep Dasar PDP . . . 5 2.1.1 Kehomogenan . . . 8 2.1.2 Orde . . . 9 2.1.3 Kelinieran . . . 9 2.2 Klasifikasi PDP . . . 10 2.3 Aplikasi PDP . . . 11 2.4 Latihan . . . 16 Daftar Pustaka . . . 17
Bab 0: Daftar Isi
3 Separasi Variabel 19
3.1 Masalah Nilai Eigen . . . 19
3.2 Separasi Variabel untuk Persamaan Panas . . . 20
3.3 Koefisien Fourier . . . 26
3.4 Separasi Variabel untuk Persamaan Gelombang . . . 29
3.5 Latihan . . . 32
Daftar Pustaka . . . 35
4 Metode Beda Hingga untuk 1D Parabolik 37 4.1 Masalah Persamaan Panas 1D . . . 37
4.2 Skema Numerik . . . 38
4.3 Program FreeMat/MATLAB . . . 43
4.4 Latihan . . . 46
Daftar Pustaka . . . 48
5 Metode Beda Hingga untuk 1D Hiperbolik 51 5.1 Masalah Persamaan Gelombang 1D . . . 51
5.2 Skema Numerik . . . 52
5.3 Program FreeMat/MATLAB . . . 57
5.4 Latihan . . . 60
Daftar Pustaka . . . 62
6 Metode Beda Hingga 2D Parabolik 65 6.1 Masalah Persamaan Panas 2D . . . 65
6.2 Skema Numerik . . . 67
6.3 Program FreeMat/MATLAB . . . 70
6.4 Latihan . . . 73
Daftar Pustaka . . . 75
7 Metode Beda Hingga 2D Hiperbolik 79 7.1 Masalah Persamaan Gelombang 2D . . . 79
7.2 Skema Numerik . . . 80
7.3 Program FreeMat/MATLAB . . . 85
7.3.1 Batas Dirichlet . . . 89
Bab 0: Daftar Isi
7.3.2 Batas Neumann . . . 91
7.4 Latihan . . . 95
Daftar Pustaka . . . 95
8 Implementasi PDP 97 8.1 Aliran Air Tanah (Groundwater flow) . . . 97
8.1.1 ModelGroundwater flow. . . 97
8.1.2 Program FreeMat/MATLAB . . . 100
Daftar Pustaka . . . 101
8.2 Gelombang Air . . . 103
8.2.1 Model SWE dan Gelombang . . . 103
8.2.2 Program FreeMat/MATLAB . . . 105
Daftar Pustaka . . . 113
Daftar Pustaka Lengkap 115
Tentang Penulis 121
Bab 0: Daftar Isi
Daftar Gambar
1.1 Flowchart pembahasan materi PDP . . . 2
2.1 Sketsa masalah difusi. . . 12
2.2 Gangguan vertikal senar . . . 13
2.3 Peregangan senar dengan sudut kecil . . . 14
3.1 Konfigurasi fisik sebuah batang besi dengan panjangL[Gun16]. 21 3.2 Solusi dari persamaan panas denganf(x) = 3 sin(πx)+5 sin(4πx) untukt= 0,0.01 dan 0.1. . . 25
3.3 Solusi dari persamaan panas denganf(x) = 1 . . . 28
3.4 Solusiu(x, t) pada Contoh 3.4.1 untuk (x, t)∈([0,1]×[0,3]). . 32
3.5 Solusi dari persamaan gelombangu(x, t) pada Contoh 3.4.2 un-tuk (x, t)∈([0,1]×[0,3]). . . 33
4.1 Partisi domain perhitunganΩsatu-dimensi. . . 38
4.2 Bentuk jaring titik-titik diskrit domain waktu dan spasial. . . . 39
4.3 Stencil untuk skema explicit FTCS (Forward Time Central Space). . . 40
4.4 Perbandingan numerik persamaan panas stabil dan tidak stabil 41 4.5 Hasil plot program untuk Contoh 4.2.2 dengan waktu t = 0 (atas) sebagai nilai awal dant= 40×Δt(bawah) sebagai nilai akhir. . . 47
Bab 0: Daftar Gambar
5.1 Bentuk jaring titik-titik diskrit domain waktu dan spasial un-tuk (5.2.1). . . 53 5.2 Perbandingan hasil numerik persamaan gelombang stabil dan
tidak stabil . . . 57 5.3 Hasil dari simulasi numerik dengan menggunakan Δt = 5×
10−2dari awal sampai waktu akhirt= 60Δt. . . 61 6.1 Contoh penyebaran panas pada wajan yang panaskan. . . 66 6.2 Daerah perhitungan dalam dua-dimensi. Daerah dalam
dino-tasikan dengan ¯Ωdan daerah batas /boundarydengan ∂Ω. . . 66 6.3 Daerah diskrit untuk spasial 2D yaituxdany. . . 67 6.4 Perbandingan hasil numerik 2D persaman panas stabil dan
ti-dak stabil . . . 69 6.5 Hasil simulasi numerik 2D persamaan panas . . . 74 6.6 Posisi awal domain bentukL. . . 76 6.7 Sebaran panas pada titik-titik diskrit domain bentuk L pada
waktu akhir t= 0.025 (atas) dant= 0.25 (bawah). . . 77
7.1 Alat musik gendang menghasilkan suara dari vibrasi selaput gendang. . . 79 7.2 Daerah diskrit untuk spasial 2D yaituxdany. . . 81 7.3 Perbandingan hasil numerik 2D persamaan gelombang stabil
dan tidak stabil . . . 83 7.4 Hasil simulasi numerik 2D persamaan gelombang dengan syarat
batasDirichlet . . . 89 7.5 Hasil simulasi numerik 2D persamaan gelombang dengan syarat
batasDirichlet . . . 90 7.6 Gelombang yang ditimbulkan oleh tetesan air. . . 91 7.7 Ilustrasi vektor normaln(x) pada daerah batas. . . 92 7.8 Hasil simulasi numerik 2D persamaan gelombang batasNeumman 93 7.9 Hasil simulasi numerik 2D persamaan gelombang batasNeumman 94 8.1 Ilustrasi air tanah. . . 98
Bab 0: Daftar Gambar
8.2 Terjadi aliran air tanah karena turunnya ketinggian air sungai. 99
8.3 Hasil simulasi numerik pada model aliran air tanah. . . 102
8.4 Ilustrasi linier SWE. . . 104
8.5 Hasil simulasi numerik standing wave. . . 108
8.6 Hasil simulasi numerik dam-break. . . 111
8.7 Hasil simulasi numerikbreaking wave. . . 114
Bab 0: Daftar Gambar
Daftar Algoritma
1 Algoritma persamaan panas 1D. . . 44
2 Algoritma persamaan gelombang 1D. . . 58
3 Algoritma persamaan panas 2D. . . 71
Bab 0: Daftar Algoritma
Daftar Program
4.1 Kode FreeMat/MATLAB untuk persamaan panas 1D . . . 46
5.1 Kode FreeMat/MATLAB untuk persamaan gelombang 1D . . . 60
6.1 Kode FreeMat/MATLAB untuk persamaan panas 2D . . . 73
7.1 Kode FreeMat/MATLAB untuk persamaan gelombang 2D . . . 88
8.1 Kode FreeMat/MATLAB untuk model aliran air tanah . . . . 101 8.2 Kode FreeMat/MATLAB untuk persamaan gelombang air
ka-susstanding wave. . . 107 8.3 Kode FreeMat/MATLAB untuk persamaan gelombang air
ka-sus dam-break . . . 110 8.4 Kode FreeMat/MATLAB untuk persamaan gelombang air
Bab 0: Daftar Program
Bab 1
Tentang Buku
1.1
Motivasi
Buku ini ditulis sebagai catatan kuliah Persamaan Differensial Parsial (PDP) di jurusan S1 Ilmu Komputasi, Telkom University. Dalam bab-bab selanjut-nya, mulai dari konsep dasar PDP, pencarian solusi analitik dengan menggu-nakan separasi variabel, sampai solusi numerik dengan metode beda hingga (finite difference method) pada PDP tipe parabolik dan hiperbolik akan dije-laskan. Untuk tipe parabolik dan hiperbolik, Algoritma dan contoh program komputer menggunakan bahasa pemrograman FreeMat (open source) yang mirip dengan MATLAB (berbayar). Perlu diketahui bahwa MATLAB ada-lah perangkat lunak yang berbayar dan membutuhkan license. Sedangkan FreeMat adalah perangkat lunakopen softwareyang bebas kita unduh tanpa menggunakan license. Untuk melihat FreeMat lebih jauh, silakan kunjungi webistehttp://freemat.sourceforge.net/.
Tidak memungkiri bahwa buku ini merupakan bagian yang sangat kecil dari materi PDP yang sebenarnya. Beberapa hal menarik pada materi kuliah PDP lainnya seperti solusi PDP tipe Eliptik, pembahasan konservasi massa, metode karakteristik, dan lain sebagainya tidak dibahas dalam buku ini. Bu-ku ini dirancang untuk mahasiswa s1 jurusan teknik dengan memperkenalkan
Bab 1: Tentang Buku
notasi-notasi matematika yang biasanya digunakan untuk memodelkan PDP. Mengingat bahwa materi PDP sangat luas, maka penulis hanya memberikan beberapa materi khusus untuk tipe PDP. Pada PDP tipe parabolik, persama-an konduktivitas ppersama-anas 1D dpersama-an 2D saja ypersama-ang akpersama-an dibahas. Sedpersama-angkpersama-an pada tipe hiperbolik, hanya persamaan gelombang orde dua 1D dan 2D yang akan dikupas lebih detail.
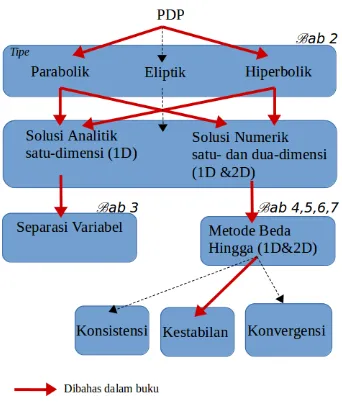
Gambar 1.1: Alur atau flowchart materi yang akan dijelaskan pada buku ini. Panah bergaris tebal menyatakan materi yang akan dibahas pada buku. Sedangkan panah bergaris putus-putus menyatakan materi yang berkaitan dengan PDP, akan tetapi tidak dibahas dalam buku.
Bab 1: Tentang Buku
Penulis membuat buku ini ditujukan kepada semua kalangan pembaca, dalam hal ini, bisa dari kalangan praktisi dan ilmuwan. Secara khusus, target pembaca buku ini adalah mahasiswa atau peneliti yang bekerja dengan PDP di jurusan teknik maupun sains, khususnya Matematika dan Fisika. Tidak menutup kemungkinan buku ini juga dapat digunakan sebagai pegangan dosen dalam mengajar pengantar PDP di jurusan yang menyediakan mata kuliah ini. Bagan atau flowchart untuk memandu pembaca dalam menggunakan buku ini dapat dilihat pada Gambar 1.1.
1.2
Panduan Pembaca
Pada Bab 2, konsep dasar dari PDP seperti klasifikasi, orde, dan linierias ak-an diberikak-an. Beberapa apliaksi dari PDP juga diberikak-an untuk menambah pengetahuan pembaca dalam memodelkan fenomena alam menjadi persama-an PDP. Bab 3 bercerita tentpersama-ang bagaimpersama-ana mencari solusi persama-analitik dengpersama-an menggunakan metode separasi variabel. Dalam hal ini, digunakan asumsi bahwa nilai awal diberikan oleh sebuah fungsi smooth yakni sinusoidal. Bab 4 membahas metode numerik untuk mencari solusi dari persamaan konduk-tivitas panas. Metode numerik yang diusulkan adalah metode beda hingga. Algoritma secara umum beserta contoh numerik dengan menggunakan baha-sa pemrograman FreeMat/MATLAB juga diberikan. Metode numerik untuk persamaan gelombang dengan menggunakan metode beda hingga, beserta al-goritma dan contoh kode program dalam FreeMat/MATLAB dipaparkan pa-da Bab 5.
Metode numerik untuk PDP tentang persamaan panas dan gelombang dua-dimensi diberikan pada Bab 6 dan 7 secara berurutan. Terakhir, bebe-rapa contoh proyek dalam pemodelan PDP dibahas pada Bab 8.
1.3
Catatan
Sebagian dari bab-bab yang ada di buku ini dibahas dengan sangat sing-kat. Mengingat buku ini tidak hanya diperuntukkan untuk matematikawan,
Bab 1: Tentang Buku
banyak beberapa lema tidak dibuktikan secara rinci. Untuk itu, penulis me-nyarankan untuk melihat beberapa pustaka yang penulis gunakan.
Dalam pembahasan bab metode numerik, penulis menyertakan algoritma yang dapat diimplementasikan ke bahasa pemrograman yang pembaca kua-sai atau pahami. Pada buku ini hanya diberikan contoh program kompu-ter dengan menggunakan bahasa pemrograman FreeMat/MATLAB. Kode program yang ada pada buku ini dapat diunduh pada tautan berikut ini https://bcomps.telkomuniversity.ac.id/putu-harry-gunawan/. Akan tetapi, penulis menyarankan pembaca untuk mencoba menulis program Fre-eMat/MATLAB sendiri. Hal ini akan mempermudah pembaca untuk mema-hami keseluruhan kode program.
Teknik mengkoding dalam semua program FreeMat/MATLAB yang ada di buku ini belum seluruhnya optimal dari sisi fungsi-fungsi yang dimiliki oleh FreeMat/MATLAB. Hal ini dikarenakan kode program disesuaikan dengan algoritma umum yang dapat diimplementasikan pada bahasa pemrograman lainnya seperti Fortran, C/C++, Python, dll. Sehingga, penulis memberikan kesempatan pembaca untuk dapat mengimprovisasi program yang ada pada buku ini, sesuai dengan teknik pemrograman atau penggunaan fungsi-fungsi yang ada atau pembaca kuasai.
Bab 2
Pengantar PDP
2.1
Konsep Dasar PDP
Definisi 2.1.1(PDP). Persamaan diferensial parsial (PDP) merupakan se-buah persamaan yang memfokuskan pada hubungan antara sebuah fungsi yang belum diketahuiu(x1, x2,· · ·, xn)berdimensin≥2,danturunan parsial fungsi terhadap variabel-variabel bebasnya [TW04]. Bentuk umum dari PDP diberikan sebagai berikut:
F � x1, x2,· · ·xn, u, ∂u ∂x1,· · · , ∂u ∂xn, ∂2u ∂x1x1,· · ·, ∂2u ∂x1xn,· · · � = 0.
PDP biasanya memiliki variabel bebas untuk ruang dan/atau waktu. Va-riabel bebas untuk ruang biasanya dinotasikan sebagai (x, y, z) atau dengan tambahan variabel waktu menjadi (x, y, z, t). Berikut beberapa contoh PDP sederhana denganusebagai fungsi yang belum diketahui (unknown function) dan hanya memiliki dua variabel bebas:
∂2u ∂2x+ ∂2u ∂2y = 0, (2.1.1) ∂u ∂t −α ∂2u ∂2x= 0, (2.1.2)
Bab 2: Pengantar PDP
∂2u
∂2t −c 2∂2u
∂2x= 0, (2.1.3)
dengan∂u/∂t,∂2u/∂x2menyatakan turunan partial terhadap variabel waktu orde satu dan ruang orde dua secara berurutan.
Persamaan (2.1.1-2.1.3) merupakan persamaan diferensial parsial satu-dimensi mengacu pada domain spasial. Persamaan (2.1.1) secara umum dike-nal dengan nama persamaanLaplace, persamaan (2.1.2) adalah persamaan difusi atau konduktivitas panas, dan persamaan (2.1.3) dikenal sebagai persamaan gelombang. Biasanya, dalam beberapa kajian pustaka, secara singkat PDP dapat juga ditulis dalam bentuk:
uxx+uyy= 0, (2.1.4)
ut−αuxx= 0, (2.1.5)
utt−c2uxx= 0, (2.1.6) dengan subscript menyatakan turunan parsial. Beberapa contoh lain PDP yang terkenal selain tiga contoh diatas adalah
ut+ux= 0, persamaan transport (2.1.7)
ut+ux−αuxx= 0, persamaan reaksi-difusi (2.1.8) ut+uux= 0, persamaan inviscid Burger (2.1.9) uxx+uyy=f(x, y), persamaan Poisson (2.1.10) ut+uux+uxxx = 0, persamaan KdV (2.1.11) iut+uxx= 0. persamaan Schr¨odinger (2.1.12) Selain contoh diatas, beberapa referensi di dalam buku atau jurnal saintifik, biasanya menggunakan notasi-notasi seperti berikut ini:
• Gradiengrad(u) =∇u:
Notasi untuk menyatakan vektor gradien dari suatu fungsiu(x1, x2,· · · , xn)
Bab 2: Pengantar PDP
pada n-dimensi ruang Euclidean. Contohnya:
∇u(x1, x2,· · · , xn) = � ∂ ∂x1, ∂ ∂x2,· · · , ∂ ∂xn � u. Misalkan terdapat persamaanu(x, y), maka∇u(x, y) = (ux, uy).
• Divergent div(u) =∇·u:
Notasi untuk menyatakan divergensi (divergence) dari suatu fungsi ber-dimensi nu(x1, x2,· · · , xn) pada n-dimensi ruang Euclidean (yaitu jum-lah dari suku-suku vektor gradiennya). Contohnya:
∇·u(x1, x2,· · ·, xn) = � ∂ ∂x1 + ∂ ∂x2 +· · ·+ ∂ ∂xn � u. Misalkan terdapat persamaanu(x, y, z), maka didapat
·u(x, y, z) = �∂u ∂x+ ∂u ∂y + ∂u ∂z � .
• Laplace operator Δu=∇2u=
∇·∇u:
Notasi untuk menyatakan turunan orde dua u(x1, x2,· · ·, xn) pada n-dimensi ruang Euclidean. Contohnya:
Δu(x1, x2,· · · , xn) = � ∂2 ∂x2 1 + ∂ 2 ∂x2 2 +· · ·+ ∂ 2 ∂x2 n � u. Misalkan terdapat persamaanu(x, y, z), maka didapat
Δu(x, y, z) = �∂2u ∂x2+ ∂2u ∂y2 + ∂2u ∂z2 � .
Secara umum, solusi PDP adalah nontrivial, akan tetapi ketika sebu-ah solusi ditemukan, akan sangat mudsebu-ah untuk membuktikan apaksebu-ah fung-si tersebut merupakan solufung-si atau bukan. Sebagai contoh, untuk melihat u(x, t) =et−xmerupakan solusi dari persamaan gelombang (2.1.6), secara se-derhananya fungsi tersebut kita substitusikan ke dalam persamaan, sehingga
Bab 3
Separasi Variabel
3.1
Masalah Nilai Eigen
Dalam subbab ini, akan dibahas mengenai masalah nilai eigen berkaitan
de-ngan operator kontinu L. Subbab ini hanya akan memberikan definisi dan
lema sebagai senjata/alat yang dapat digunakan dalam mencari solusi PDP dengan metode separasi variabel. Bukti dari lema tidak akan dibahas dengan detail. Jika pembaca tertarik untuk melihat bukti dari lema-lema yang dibe-rikan, pembaca disarankan untuk membaca pustaka yang dilampirkan pada catatan setelah lema dipaparkan.
Definisi 3.1.1. Bilangan riil λdisebut nilai eigen berkaitan dengan masalah nilai batas
−u��(x) =f(x), x∈(0, L), u(0) =u(L) = 0 (3.1.1)
jika
Lu=λu (3.1.2)
untuk fungsi tak nol u ∈ C2
0((0,1)) dan Lu = −u��. Fungsi u selanjutnya
Bab 3: Separasi Variabel
Lema 3.1.2. Nilai dan fungsi eigen dari masalah (3.1.2) diberikan sebagai berikut λk = � kπ L �2 f or k= 1,2,· · ·, (3.1.3) and uk(x) = sin �kπx L � (3.1.4) Bukti. Bukti dari lema ini dapat ditemukan di buku [TW04] untuk lebih leng-kapnya.
Lema 3.1.3. Fungsi eigen{sin�kπLx�}k≥1 memenuhi persamaan berikut
<sin �kπx L � ,sin�mπx L � >= 0 k�=m, 1/2 k=m,, (3.1.5)
dengan<·,·>menyatakan hasil kali dalam (inner product).
Bukti. Bukti dari lema ini dapat ditemukan di [TW04] untuk lebih jelasnya.
3.2
Separasi Variabel untuk Persamaan Panas
Sebuah batang besi tipis dengan panjangLdipanaskan dengan api di bagian
tengah besi sedangkan ujung kiri dan kanan besi dipertahankan dalam suhu
dingin yakni 00C (lihat Gambar 3.1). Sehingga nantinya dapat diamati bahwa
besarnya temperatur di daerah tengah besi akan lebih besar dibandingkan dengan daerah lainnya. Selanjutnya, pada waktu tertentu atau waktu akhir pengamatan, api dipadamkan dan pengamatan dilanjutkan dengan mengukur penyebaran panas dari tengah ke bagian lainnya selama proses pendinginan.
Asumsikan sebuah batang besi memiliki panjangL= 1 m, maka formulasi
matematika dari penyebaran panas dalam sebuah domainΩ= [0 : 1] adalah
sebagai berikut
Bab 3: Separasi Variabel Lebih jelasnya, dari Lema 3.1.3,kita peroleh
<sin �kπx L � ,sin�mπx L � >= 0 k�=m, 1/2 k=m. (3.3.2)
Dengan mengggunakan properti dasar di atas, kita dapat dengan mudah
me-nentukan koefisien{Ak} sehingga
f(x) = ∞ � k=1 Aksin � kπx L � . (3.3.3)
Untuk setiap indexm≥1, kita ambil nilai hasil kali dalammfungsi eigen
dengan sin�mπx L
�
. Kemudian menggunakan (3.3.2) akan diperoleh < f(x),sin�mπx L � >=Ak<sin �kπx L � ,sin�mπx L � >= Am 2 . (3.3.4)
Sehingga kita peroleh
Ak = 2< f(x),sin�mπx L
�
> dan k= 1,2,· · · . (3.3.5)
Koefisien inilah yang kita sebut sebagai koefisien Fourier (Fourier coefficient)
dan deret yang bersesuaian disebut sebagai deret Fourier (Fourier series).
Terakhir, solusi umumnya adalah u(x, t) = ∞ � k=1 Ake−(kπLx) 2t sin �kπx L � , (3.3.6)
dengan Ak merupakan koefisien yang didapat dari (3.3.5). Mari kita lihat
contoh sebelumnya pada kasus persamaan panas.
Contoh 3.3.1. Diberikan kembali fungsi awal temperatur pada sebuah
ba-tang kawat tipis yaitu f(x) = 1 dengan panjang kawat L = 1 m. Dengan
Bab 3: Separasi Variabel menggunakan (3.3.5), kita peroleh
Ak = 2 � 1 0 (1) sin(kπx)dx= 2 kπ(1−cos(kπ)). (3.3.7) Sehingga didapat Ak = 4 kπ fork= 1,3,5,· · ·, 0 fork= 2,4,6,· · ·, (3.3.8) dan 1 = 4 π ∞ � k=1 1 2k−1sin((2k−1)πx). (3.3.9)
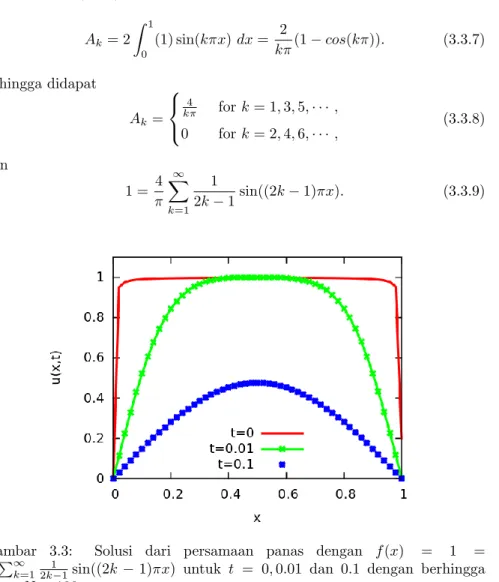
Gambar 3.3: Solusi dari persamaan panas dengan f(x) = 1 =
4
π
�∞
k=1 1
2k−1sin((2k−1)πx) untuk t = 0,0.01 dan 0.1 dengan berhingga
deretN = 100.
Jadi solusi umumnya adalah u(x, t) = 4 π ∞ � k=1 1 2k−1e −((2k−1)π)2tsin((2k −1)πx). (3.3.10)
Bab 5
Metode Beda Hingga
untuk 1D Hiperbolik
5.1
Masalah Persamaan Gelombang 1D
Mengingat kembali persamaan (2.3.8) yang ada pada Subbab 2.3, jika gaya badan (body forces) per unit massa hanya merupakan gaya gravitasi, maka
Q(x, t) = −g pada persamaan (2.3.8). Seringkali, gaya ini sangat kecil ji-ka dibandingji-kan dengan gaya tarik senar (ρ0q << |T0∂2u/∂x2|) dan dapat diabaikan. Sehingga menurut [Hab12], gaya badan diberikanQ(x, t) = 0,
∂2u(x, t) ∂t2 = T0 ρ0 ∂2u(x, t) ∂x2 , (5.1.1)
atau dapat ditulis sebagai
∂2u(x, t)
∂t2 =c
2∂2u(x, t)
Bab 5: Metode Beda Hingga untuk 1D Hiperbolik
n= 0 dengan
vk0=f(xk), k∈M+{0, M}. (5.2.3)
Sedangkan, untuk mencari nilai pada level waktu n = 1, kita dapat meng-gunakan expansi Taylor orde dua terhadap waktu dan persamaanut=g(x)
pada (5.1.5) yaitu u(x,Δt) =u(x,0) + (Δt)ut(x,0) + Δt2 2 utt(x,0) +O � (Δt)3� =f(x) + (Δt)g(x) +Δt 2 2 f ��(x) +O�(Δt)3�.
denganf��(x) dapat dicari melalui persamaan (5.1.3) yaituutt(x,0) =uxx(x,0) =
f��(x).
Sehingga kita dapat menghitung nilai v1
k untuk menghampiri u(xk,Δt) dengan v1 k−v0k Δt =g(xj) + Δt 2Δx2(v 0 k−1−2v0k+vnk−1), k∈M. (5.2.4) Jadi, dapat kita urutkan langkah-langkah pengerjaan skema eksplisit un-tuk menghampiri persamaan gelombang (5.1.3-5.1.5) sebagai berikut:
1. Hitung (5.2.3) untuk mencari nilaiv pada level waktu 0. 2. Hitung (5.2.4) untuk mencari nilaiv pada level waktu 1.
3. Hitung (5.2.1) untuk mencari nilai v pada daerah dalam perhitungan dan level waktun≥2.
4. Hitung (4.2.2) untuk mencari nilai batas.
Algoritma dari skema eksplisit beda hingga persamaan gelombang dapat di-lihat pada Algoritma (2) di subbab berikutnya.
Lema 5.2.1. Skema numerik eksplisit (5.2.1-5.2.4) untuk menghampiri solusi persaman panas (5.1.3-5.1.5) akan stabil jika dan hanya jika memenuhi
cΔt
Δx ≤1. (5.2.5)
Bab 5: Metode Beda Hingga untuk 1D Hiperbolik 0 0.2 0.4 0.6 0.8 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 t=60 xΔ t t=0 t=7 xΔ t t=10 xΔ t t=13 xΔ t x v(x,t) 0 0.2 0.4 0.6 0.8 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 t=60 xΔ t t=0 t=7 xΔ t t=10 xΔ t t=13 xΔ t x v(x,t)
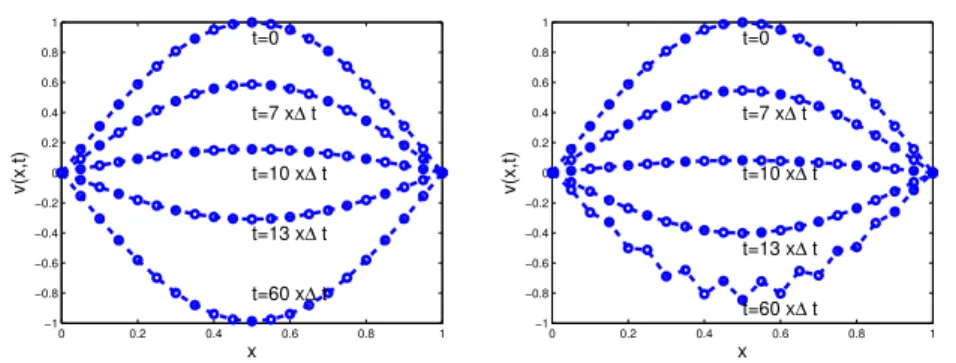
Gambar 5.2: Perbandingan hasil numerik dengan menggunakanΔt= 5×10−2 (kiri) danΔt= 5.26×10−2(kanan).
kiri skema numerik eksplisit stabil dengan menggunakan Δt = 5×10−2 se-dangkan di kanan, skema numerik menghasilkan osilasi yang artinya skema numerik tidak stabil denganΔt= 5.26×10−2.
Sesuai dengan Lema 5.2.5, dengan Δt= 5×10−2 danΔx= 1/20, maka
cΔt
Δx = 1 sehingga skema stabil. Sebaliknya, dengan Δt = 5.26×10−
2 dan
Δx= 1/20, maka cΔΔxt = 1.108>1 sehingga skema pastinya tidak stabil.
5.3
Program FreeMat/MATLAB
Berikut akan diberikan algoritma untuk menghitung solusi persamaan gelom-bang dengan menggunakan metode beda hingga skema eksplisit. Algoritma 2, dibentuk agar sesuai dengan bahasa pemrograman yang pembaca kuasai (contoh Fortran, C/C++, Python, FreeMat/MATLAB dll).
Berikut diberikan kode dari program komputer sesuai dengan Algoritma 2 menggunakan bahasa pemrograman FreeMat/MATLAB. Catatan bahwa, pada Algoritma 2 indeks untuk larik/arrays dimulai dari k = 0 sampai de-ngan k =M. Akan tetapi, bahasa pemrograman FreeMat/MATLAB tidak mendukung adanya indeks 0, indeks dimulai dari 1. Sehingga perlu dilakukan pengaturan untuk menyamakan program FreeMat/MATLAB dengan Algori-tma 2.
Bab 5: Metode Beda Hingga untuk 1D Hiperbolik
Algoritma 2Algoritma persamaan gelombang 1D.
1: procedureWave1D(f(x), g(x), M, L, c, T,Δt, a=b= 0) 2: Start 3: Definedx=L/M,r=c2 Δt 2 (Δx)2 4: For k= 0 :M do 5: x[k] =k×dx, vold2[k] =f(x[k]), � n=0 6: EndFor 7: For k= 1 :M −1 do 8: vold[k] = vold2[k] + Δtg(x[k]) + r
2(vold2[k+ 1]−2vold2[k] +vold2[k−1]) � n=1 9: EndFor 10: time=0 11: while time < T do 12: time=time+Δt 13: Fork= 1 :M −1do 14: v[k] = 2vold[k] − vold2[k] +
r(vold[k+ 1]−2vold[k] +vold[k−1])
15: EndFor
16: v[0] = 0 =v[M]
17: For k= 0 :M do
18: vold2[k] =vold[k] � update nilaivkn−1
19: vold[k] =v[k] � update nilaivnk
20: EndFor
21: end while
22: OUTPUTv[0 :M]; Plot(x, v) 23: End
24: end procedure
Bab 7
Metode Beda Hingga 2D
Hiperbolik
7.1
Masalah Persamaan Gelombang 2D
Gambar 7.1: Alat musik gendang menghasilkan suara dari vibrasi selaput gendang.
Gendang merupakan salah satu alat musik yang banyak ditemukan di ber-bagai daerah di Indonesia. Gendang sendiri memiliki bentuk, ukuran dan bahan yang sangat beragam sesuai dengan kebudayaan yang ada pada daerah masing-masing (lihat Gambar 7.1). Bagaimana gendang dimainkan? dengan memberikan gangguan pada kulit/selaput gendang, maka selaput gendang
Bab 7: Metode Beda Hingga 2D Hiperbolik akan bervibrasi sehingga suara akan terdengar.
Vibrasi dari selaput gendang dapat dimodelkan dengan PDP yaitu per-samaan gelombang. Misalkan notasi untuk seluruh daerah perhitunganΩ=
�¯
Ω∪∂Ω�∈[0, Lx]×[0, Ly], dengan ¯Ω=∈(0, Lx)×(0, Ly) menyatakan dae-rah dalam dan∂Ωmenyatakan daerah batas (lihat Gambar 6.2). Persamaan konduktivitas panas dua-dimensi diberikan sebagai berikut:
∂2u(x, y, t) ∂t2 =c 2�∂2u(x, y, t) ∂x2 + ∂2u(x, y, t) ∂y2 � , (x, y)∈Ω¯, t >0 (7.1.1) u(x, y,0) =f(x, y), ut(x, y,0) =g(x, y), (x, y)∈Ω (7.1.2) u(x, y, t) = 0, (x, y)∈∂Ω, t≥0 (7.1.3)
dengan u(x, y, t) menyatakan ketinggian gelombang pada posisi (x, y) dan waktut. Kecepatan gelombang dinotasikan sebagai suatu konstantac. Solusi analitik dari persamaan diatas dapat ditemukan pada pustaka [Asm05], dan [Hab12].
7.2
Skema Numerik
Sejalan dengan skema numerik untuk persamaan panas 2D pada Bab 6, ma-ka penggunaan notasi ama-kan disamama-kan. Untuk membentuk skema numerik dengan menggunakan metode beda hingga, tentu saja kita harus membentuk daerah diskrit dari masalah PDP (7.1.1-7.1.3). Untuk daerah spasial, anda-ikan kita memiliki daerah seperti pada Gambar 6.2, maka dengan memben-tuk daerah diskrit, daerah dibagi-bagi menjadi persegi-persegi yang memiliki ukuranΔx×Δy, seperti ditunjukkan pada Gambar 7.2.
Andaikan kita membagi daerah spasial perhitungan arahxsebanyakMx partisi dan arahy sebanyakMy partisi dengan (Mx, My)∈Z+, maka diskrit domain dalam dapat kita notasikan dengan ¯Mx= 1,2,· · ·Mx−1 dan ¯My = 1,2,· · ·My−1. Ingat bahwa, grid batas 0 dan Mx atau My tidak termasuk dalam diskrit domain dalam, jadi untuk diskrit keseluruhan domain (dalam + batas) didefinisikan sebagaiM=�M¯x+{0, Mx}�×�M¯y+{0, My}�.
Bab 7: Metode Beda Hingga 2D Hiperbolik diurutkan menjadi:
1. Hitung (7.2.3) untukn= 0. 2. Hitung (7.2.4) untukn= 1. 3. Hitung (7.2.2) untukn≥2.
Berikut akan diberikan contoh masalah gelombang dengan menggunakan ske-ma numerik beda hingga serta menggunakan dua nilai Δtyang berbeda.
Contoh 7.2.1. Misalkan diberikan masalah gelombang pada domain Ω = [0,1]×[0,1] seperti berikut ∂2u(x, y, t) ∂t2 =c 2�∂2u(x, y, t) ∂x2 + ∂2u(x, y, t) ∂y2 � , (x, y)∈Ω¯, t >0 (7.2.5) u(x, y,0) =f(x, y), ut(x, y,0) =g(x, y), (x, y)∈Ω (7.2.6) u(x, y, t) =h(x, y), (x, y)∈∂Ω, t≥0 (7.2.7) dengan c= 1,f(x, y) = max(0,1−20((x−0.5)2+ (y −0.5)2)) dang(x, y) =
h(x, y) = 0. Menggunakan Mx = My = 20 sebagai partisi spasial, maka hasil plot menggunakan dua langkah waktu berbedaΔt=ds/√2 danΔt=
ds/√1.5 denganΔs=Δx=Δy, dapat dilihat pada Gambar 7.3.
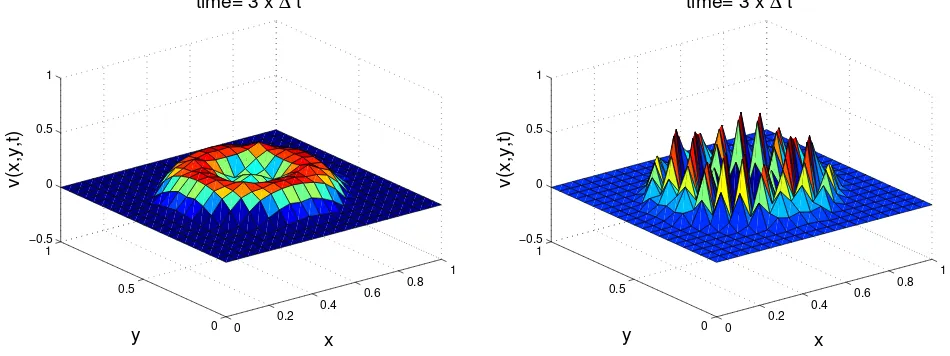
0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 3 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 3 x Δ t y v(x,y,t)
Gambar 7.3: Perbandingan hasil numerik dengan menggunakanΔt=Δs/√2 (kiri) danΔt=Δs/√1.5 (kanan).
Bab 7: Metode Beda Hingga 2D Hiperbolik
7.3
Program FreeMat/MATLAB
Untuk membuat program menggunakan bahasa pemrograman komputer, per-hatikan Algoritma 4 berikut ini. Algoritma 4 dapat diaplikasikan sesuai de-ngan bahasa pemrograman yang ada seperti Fortran, C/C++, Python, dll, untuk mengerjakan Contoh 7.2.1.
Pada Algoritma 4, baris (4-9) menyatakan definisi dari xk dan yl. Ba-ris (10-14) digunakan untuk mendefinisikan nilai awal yaitu pada persamaan 7.2.3. Di sini,v0
k,l dinotasikan denganvold2[k][l] yang selanjutnya akan digu-nakan untuk menyatakan level waktun−1. Baris (15-20) mempresentasikan persamaan (7.2.4) untuk menghitung level waktu n= 1 yaituvold[k][l] yang berikutnya akan digunakan untuk menyatakan level waktun.
Selanjutnya baris (22-41) menyatakan perulangan waktu untuk menyele-saikan masalah sampai waktu akhir T yang ditentukan. Dalam perulangan waktu, baris (23) digunakan untuk memperbarui nilai waktu, baris (24-28) ditujukan untuk menghitung nilai vn+1k,l , dan baris (30-35) digunakan untuk menghitung nilai batas. Prosedur update untuk level waktu n−1 dan n
diberikan pada baris (36-40).
%---% Program FreeMat for the 2D wave problem by PHN
%
% u_tt = c^2 (u_xx + u_yy), (x,y) \in (0,1)^2
% u(x,y,0)=f(x,y), u_t(x,y,0)=g(x,y)
% u(x,0,t)=u(x,L_y,t)=0
% u(0,y,t)=u(L_x,y,t)=0
%---clc;
clear all; % clear all variables in memory
close all;
f= @(x,y) max(0,1-20*((x-0.5)^2 + (y-0.5)^2));% fungsi f(x,y) g= @(x,y) 0;
h= @(x,y) 0; %Batas Dirichlet
Lx = 1; % set panjang domain x
Ly = 1; % set panjang domain y
Mx = 20; % set titik grid x
My = 20; % set titik grid y
dx = Lx/ Mx; % set spasial step dx
dy = Ly/ My; % set spasial step dy
ds = dx; % set ds=dx=dy
Bab 7: Metode Beda Hingga 2D Hiperbolik
7.3.1
Batas Dirichlet
Untuk syarat batas Dirichlet, nilai batas diberikan dengan sebuah fungsi
h(x, y). Sebagai contoh sebelumnya, PDP yang diberikan adalah PDP de-ngan syarat batas Dirichlet yaituh(x, y) = 0 sehinggau(x, y, t) = 0, (x, y)∈
∂Ω, t≥0. 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 0 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 3 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 6 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 9 x Δ t y v(x,y,t)
Gambar 7.4: Plot hasil simulasi persamaan panas 2D dengan deret waktu
t= 0×Δtsampai dengant= 9×Δt, dengan kenaikant= 3×Δtuntuk tiap gambarnya.
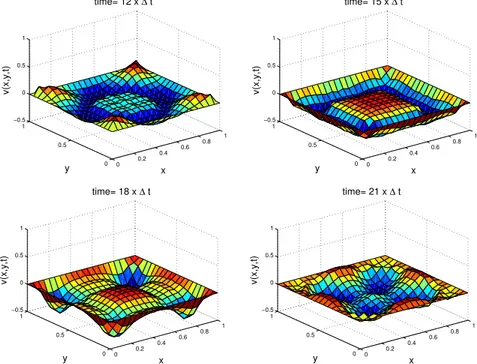
Hasil simulasi numerik dengan syarat batas Dirichlet dapat dilihat pada Gambar 7.4. Dengan menggunakan syarat batas h(x, y) = 0, terlihat bahwa vibrasi hanya terjadi pada daerah dalam setelah gangguan diberikan. Simulasi di atas analogi dengan alat musik gendang yang diberikan gangguan pada daerah tengah. Sedangkan daerah pinggir gendang, kulit atau selaput yang menghasilkan suara pada gendang terikat dengan kencang. Ilustrasi dapat
Bab 7: Metode Beda Hingga 2D Hiperbolik ] 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 12 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 15 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 18 x Δ t y v(x,y,t) 0 0.2 0.4 0.6 0.8 1 0 0.5 1 −0.5 0 0.5 1 x time= 21 x Δ t y v(x,y,t)
Gambar 7.5: Plot hasil simulasi persamaan panas 2D dengan deret waktu
t= 12×Δt sampai dengan t= 21×Δt, dengan kelipatant= 3×Δt untuk tiap gambarnya.
Bab 8
Implementasi PDP
8.1
Aliran Air Tanah (
Groundwater
fl
ow
)
8.1.1
Model
Groundwater
fl
ow
Bab ini akan membahas model sederhana berupa model aliran air tanah be-serta metode numerik untuk menghampiri solusi model. Misalkan terdapat aliran air tanah pada lapisan dalam tanah seperti pada Gambar 8.1. Sesuai dengan sumber acuan di buku [Vre12], persamaan massa pada kolom tanah sama dengan persamaan massa untuk suatu aliran sungai, sehingga persama-an massa dapat ditulis sebagai berikut:
∂h ∂t + ∂(hu) ∂x = w p (8.1.1) dengan
h= ketebalan air tanah,
u= kecepatan rata-rata aliran air tanah,
w= air hujan dalam volum per luas area,
p= porositas tanah.
huj-Bab 8: Implementasi PDP dengan D adalah konstanta difusi berdimensi m2/s. Persamaan ini mirip
dengan persamaan konduktivitas panas seperti yang sudah dibahas pada Su-bbab 2.3. Persamaan (8.1.4) merupakan PDP orde satu terhadap waktu t
dan orde dua terhadap spasialx.
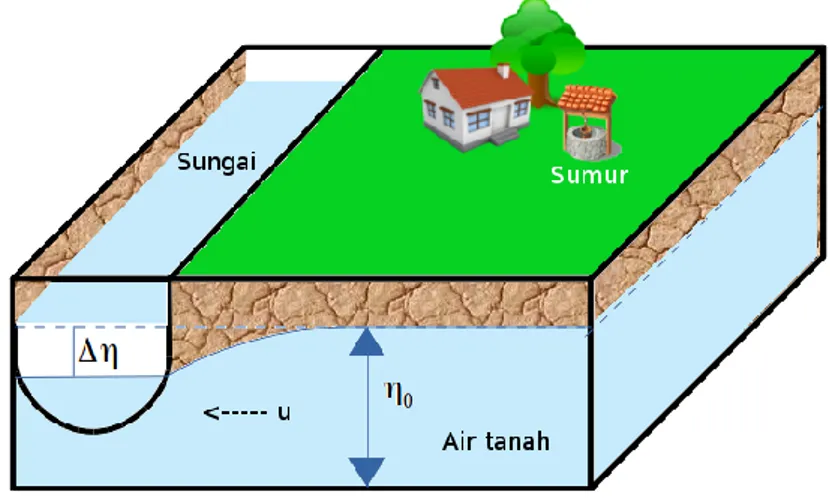
Gambar 8.2: Terjadi aliran air tanah karena turunnya ketinggian air sungai. Berikut akan diberikan satu contoh kasus, yang diambil dari buku [Vre12].
Contoh 8.1.1. Andaikan lapisan air tanah berada di dekat sebuah sungai. Pada keadaan awal, semuanya dianggap setimbang (tidak ada hujan, per-mukaan air tanah lurus horisontal). Pada sesuatu keadaan, perper-mukaan air sungai tiba-tiba menjadi rendah (yang pada akhirnya akan segera mempe-ngaruhi permukaan air tanah) dan pada ketinggian yang rendah tersebut air sungai menjadi konstan lagi. Sehingga akan terjadi aliran air tanah menuju sungai sebagaimana diakibatkan oleh kemiringan permukaan air (Pers. 8.1.2), lihat Gambar 8.2.
Selanjutnya, kita misalkan panjang domain air tanah sebelah kanan su-ngai adalahL= 200 m. Level air sungai pada awalnya terletak di 10 m, lalu tiba-tiba jatuh ke level 0 m. Dan tetap berada di level 0 sampai pada waktu tertentu. Misalkan besaran difusi diberikan konstanD= 10−3. Dengan
Daftar Pustaka Lengkap
[Asm05] N.H. Asmar. Partial Differential Equations with Fourier Series and Boundary Value Problems. Pearson Prentice Hall, 2005.isbn: 9780131480964.
[CY98] Yong-Sik Cho and SUNG BUM YOON. “A modified leap-frog scheme for linear shallow-water equations”. In:Coastal Enginee-ring Journal 40.02 (1998), pp. 191–205.
[DD91] R.G. Dean and R.A. Dalrymple. Water Wave Mechanics for Engineers and Scientists. Advanced series on ocean engineering. World Scientific, 1991.isbn: 9789810204211.
[DG14] David Doyen and Putu Harry Gunawan. “An explicit staggered
finite volume scheme for the shallow water equations”. In:Finite Volumes for Complex Applications VII-Methods and Theoretical Aspects. Springer, 2014, pp. 227–235.
[GR13] Edwige Godlewski and Pierre-Arnaud Raviart. Numerical app-roximation of hyperbolic systems of conservation laws. Vol. 118. Springer Science & Business Media, 2013.
[Gun16] P.H. Gunawan. “Scientific Parallel Computing for 1D Heat
Di-ffusion Problem Based on OpenMP”. In:Information and Com-munication Technology (ICoICT ), 2016 4th International Con-ference on. IEEE. 2016.
Bab 8: Daftar Pustaka Lengkap [Hab12] Richard Haberman. Applied Partial Differential Equations with
Fourier Series and Boundary Valve Problems. Pearson Higher Ed, 2012.
[Han+05] Emmanuel Hanert et al. “An efficient Eulerianfinite element me-thod for the shallow water equations”. In:Ocean Modelling 10.1 (2005), pp. 115–136.
[HF01] Joe D Hoffman and Steven Frankel.Numerical methods for engi-neers and scientists. CRC press, 2001.
[K¨am09] Jochen K¨ampf.Ocean Modelling for Beginners: Using Open-Source Software. Springer Science & Business Media, 2009.
[K¨am10] Jochen K¨ampf. Advanced Ocean Modelling: Using Open-source Software. Springer Science & Business Media, 2010.
[LC08] Jichun Li and Yi-Tung Chen.Computational partial differential equations using MATLAB. Crc Press, 2008.
[LeV02] Randall J LeVeque. Finite volume methods for hyperbolic pro-blems. Vol. 31. Cambridge university press, 2002.
[LL92] Randall J LeVeque and Randall J Leveque.Numerical methods for conservation laws. Vol. 132. Springer, 1992.
[LY90] Randall J LeVeque and Helen C Yee. “A study of numerical me-thods for hyperbolic conservation laws with stiff source terms”. In:Journal of computational physics 86.1 (1990), pp. 187–210. [MQS99] Edie Miglio, Alfio Quarteroni, and Fausto Saleri. “Finite element
approximation of quasi-3D shallow water equations”. In: Compu-ter methods in applied mechanics and engineering 174.3 (1999), pp. 355–369.
[MRTB05] Robert MM Mattheij, Sjoerd W Rienstra, and Jan HM ten Thi-je Boonkkamp.Partial differential equations: modeling, analysis, computation. Siam, 2005.
[Str92] Walter A Strauss. Partial differential equations. Vol. 92. Wiley New York, 1992.
Bab 8: Daftar Pustaka Lengkap [Tho13] James William Thomas.Numerical partial differential equations:
finite difference methods. Vol. 22. Springer Science & Business Media, 2013.
[TRA05] A Tokgozlu, M Rasulov, and Z Aslan. “Modeling and Classifi -cation of Mountain Waves”. In: Technical Soaring 29.1 (2005), pp. 22–30.
[TTI97] Mark Taylor, Joseph Tribbia, and Mohamed Iskandarani. “The spectral element method for the shallow water equations on the sphere”. In:Journal of Computational Physics130.1 (1997), pp. 92– 108.
[TW04] Aslak Tveito and Ragnar Winther. Introduction to partial
di-fferential equations: a computational approach. Vol. 29. Springer Science & Business Media, 2004.
[Vre12] Cornelis B Vreugdenhil. Computational hydraulics: an introdu-ction. Springer Science & Business Media, 2012.
[Vre13] Cornelis Boudewijn Vreugdenhil.Numerical methods for shallow-waterflow. Vol. 13. Springer Science & Business Media, 2013. [WA95] Herbert F Wang and Mary P Anderson. Introduction to
gro-undwater modeling: finite difference andfinite element methods. Academic Press, 1995.
Bab 8: Daftar Pustaka Lengkap
Tentang Penulis
Dr. Putu Harry Gunawan, S.Si., M.Si., M.Sc., lahir di Singaraja - Bali merupakan anak pertama dari empat bersaudara. Mengenyam pendidikan S1 ju-rusan Matematika Komputasi di Univeritas Udaya-na dan mendapatkan beasiswa double degree pro-gram S2 jurusan Sains Komputasi ITB dan Kana-zawa University, Jepang. Lanjut studi S3, beasis-wa double degree Indonesia Prancis diraih dengan mengambil jurusanApplied Mathematics, ITB dan Universite Paris-est, France. Penulis kini aktif seba-gai pengajar dan peneliti di jurusan Computational Sciences, School of Computing, Telkom University. Penulis tertarik pada pe-nelitian di bidang Computational Fluid Dynamics, pemodelan dan simulasi Matematika & Fisika.