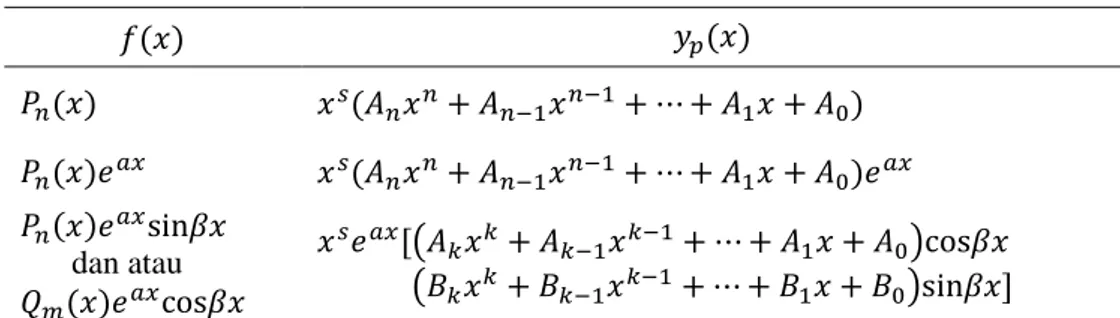METODE BEDA HINGGA UNTUK PERSAMAAN
DIFERENSIAL BIASA ORDE DUA LINEAR
DENGAN SYARAT BATAS DIRICHLET
GALUH MAHARANI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2016
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Metode Beda Hingga untuk Persamaan Diferensial Biasa Orde Dua Linear dengan Syarat Batas Dirichlet adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Agustus 2016
Galuh Maharani
ABSTRAK
GALUH MAHARANI. Metode Beda Hingga untuk Persamaan Diferensial Biasa Orde Dua Linear dengan Syarat Batas Dirichlet. Dibimbing oleh ELIS KHATIZAH dan ALI KUSNANTO.
Persamaan diferensial dapat digunakan untuk memodelkan suatu fenomena dinamis. Seringkali model tersebut sangat kompleks yang mengakibatkan penyelesaian persamaan diferensial secara analitik sulit dilakukan sehingga dibutuhkan suatu pendekatan numerik untuk mencari solusi persamaan. Secara umum pendekatan numerik menggunakan prinsip hampiran sehingga hasil solusi numerik akan memiliki selisih nilai dengan hasil solusi analitik. Karya ilmiah ini berfokus pada penyelesaian persamaan diferensial biasa orde dua linear secara numerik menggunakan metode beda hingga. Solusi khusus dalam penelitian ini diperoleh dengan menggunakan syarat batas Dirichlet yang menspesifikasi nilai solusi fungsi pada nilai variabel bebas tertentu. Metode beda hingga bekerja dengan mengganti suatu persamaan diferensial dengan syarat batas menjadi sebuah sistem persamaan linear yang dilakukan dengan mendiskretisasi daerah asal dan mengubah turunan pada persamaan dengan hampiran beda hingga pusat. Hasil penelitian menunjukkan bahwa pendekatan secara numerik menggunakan metode beda hingga hasilnya tidak berbeda jauh dengan metode analitik, hal ini terlihat dari nilai MAPE yang memiliki kisaran kurang dari 10% pada setiap kasus.
Kata kunci: persamaan diferensial biasa orde dua linear, syarat batas Dirichlet, metode beda hingga
ABSTRACT
GALUH MAHARANI. Finite Difference Method for Second Order Linear Differential Equation with Dirichlet Boundary Value Problem. Supervised by ELIS KHATIZAH and ALI KUSNANTO.
Differential equation can be used to model a dynamical phenomenon. Oftentimes, the model can be very complex, which causes the solution of the problem using analytical method will be difficult to be done, so using numerical approach to solve the problem seems to be the very feasible method. Generally, numerical method uses approximation principal, it will yield a difference between numerical solution with analytical solution. This research focused on the solution of second order linear differential equation with numerical approach using finite difference method. Explicit solution obtained by using Dirichlet Boundary Value Problem, which specifies solution value function in each independent variable. Finite difference method works by replacing a differential equation with boundary value problem into linear equation systems through discretization of the initial value and change the derivative in the equation by central finite difference approximation. The results of this research shows that approximation using numerical method in solving differential equation problem will obtain a small
deviation with the solution using analytical method, this showed by MAPE value which less than 10% in each case.
Keywords: Dirichlet boundary value problem, finite difference method, second order linear differential equation
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
METODE BEDA HINGGA UNTUK PERSAMAAN
DIFERENSIAL BIASA ORDE DUA LINEAR
DENGAN SYARAT BATAS DIRICHLET
GALUH MAHARANI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2016
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan September 2015 ini ialah mengenai metode numerik beda hingga, dengan judul Metode Beda Hingga untuk Persamaan Diferensial Biasa Orde Dua Linear dengan Syarat Batas Dirichlet. Terima kasih penulis ucapkan kepada:
1 Ibu Elis Khatizah, SSi, MSi dan Bapak Drs Ali Kusnanto, MSi selaku Pembimbing atas ilmu dan masukannya selama masa bimbingan, dan kepada Bapak Dr Ir Fahren Bukhari, MSc selaku Penguji.
2 Ayahanda Djoko Nurprianto dan Ibunda Titi Suryani yang banyak memberikan nasihat, doa serta dukungan. Kakakku Puri Mahestyanti yang selalu menjadi pengingat, pemberi masukan dan pemberi semangat.
3 Keluarga besar Departemen Matematika IPB.
4 Teman-teman seperjuangan Aulia Khoirunnisa, Lina Amalia, Nuzul Farina, dan Novalia Kartika yang selalu mejadi teman positif.
5 Teman-teman terbaik yang selalu memberikan motivasi positif Cynthia, Ghina, Mazaya, Olivia, Ajeng, Claudia, Henysya, dan seluruh Akselerasi 11th(Exelon) serta teman masa kecil Kiki dan Hanna.
6 Rekan-rekan mahasiswa Matematika 49.
7 Teman-teman lainnya yang telah memberikan dukungan moral yang tak bisa disebutkan satu persatu.
8 For Galuh Maharani, thank you for your hardwork. [VIP]. Semoga karya ilmiah ini bermanfaat.
Bogor, Agustus 2016
DAFTAR ISI
DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 2 TINJAUAN PUSTAKA 2HASIL DAN PEMBAHASAN 10
Persamaan Diferensial Biasa Orde Dua Linear Homogen dengan Koefisien
Konstan 10
Persamaan Diferensial Orde Dua Linear Nonhomogen dengan Koefisien
Konstan 13
Persamaan Diferensial Orde Dua Linear Homogen dengan Koefisien Variabel
Jika Salah Satu Solusi Diketahui 17
Persamaan Diferensial Orde Dua Linear Homogen dengan Koefisien Variabel 21 Persamaan Diferensial Orde Dua Linear Nonhomogen dengan Koefisien
Variabel Jika Kedua Solusi Diketahui 25
SIMPULAN DAN SARAN 28
Simpulan 28
Saran 29
DAFTAR PUSTAKA 29
LAMPIRAN 30
DAFTAR TABEL
1 Asumsi awal solusi partikular berdasarkan bentuk 4
2 Nilai MAPE dan interpretasinya 10
3 Eror hasil solusi khusus persamaan (25) pada setiap titik nilai 12 4 Nilai MAPE hasil solusi khusus persamaan (25) pada setiap titik nilai 13 5 Eror hasil solusi khusus persamaan (28) pada setiap titik nilai 16 6 Nilai MAPE hasil solusi khusus persamaan (28) pada setiap titik nilai 17 7 Eror hasil solusi khusus persamaan (35) pada setiap titik nilai 20 8 Nilai MAPE hasil solusi khusus persamaan (35) pada setiap titik nilai 21
9 Persamaan indeks untuk persamaan (43) 23
10 Solusi khusus persamaan (43) pada setiap titik nilai 24 11 Eror hasil solusi khusus persamaan (52) pada setiap titik nilai 27 12 Nilai MAPE hasil solusi khusus persamaan (52) pada setiap titik nilai 28
DAFTAR GAMBAR
1 Plot solusi khusus persamaan (25) metode analitik dan numerik 11 2 Plot solusi khusus persamaan (28) metode analitik dan numerik 15 3 Plot solusi khusus persamaan (35) metode analitik dan numerik 19 4 Plot solusi khusus persamaan (43) metode numerik beda hingga 24 5 Plot solusi khusus persamaan (52) metode analitik dan numerik 26
DAFTAR LAMPIRAN
1 Wronskian untuk memeriksa kebebasan linear 30
2 Hampiran beda hingga pusat 30
3 Penurunan metode variasi parameter untuk persamaan (52) 30 4 Metode beda hingga persamaan diferensial orde dua linear homogen
PENDAHULUAN
Latar Belakang
Hampir seluruh fenomena di alam semesta merupakan suatu hal yang dinamis. Mempelajari suatu fenomena yang dinamis dapat dilakukan dengan memodelkan fenomena tersebut secara matematis, yakni menggunakan persamaan diferensial karena persamaan diferensial dapat menggambarkan tingkat perubahan suatu kejadian. Suatu model persamaan diferensial dapat menggambarkan fenomena dinamis yang terjadi pada kondisi umum namun seringkali ingin diketahui lebih lanjut bagaimana jika fenomena tersebut terjadi pada kondisi tertentu sehingga model persamaan diferensial saja tidak akan cukup untuk menggambarkan fenomena tersebut. Kondisi khusus pada suatu fenomena dapat digambarkan menggunakan suatu syarat batas. Masalah syarat batas pada persamaan diferensial menyebabkan suatu persamaan diferensial memiliki suatu kondisi khusus pada batas ekstrim, yakni pada batas bawah dan batas atas.
Dalam poses memodelkan suatu fenomena, model yang dihasilkan harus dapat dengan tepat menggambarkan fenomena tersebut atau dengan kata lain model yang akurat sangat diutamakan. Biasanya model yang akurat dibentuk dengan menggunakan sedikit asumsi atau bahkan tanpa menggunakan asumsi-asumsi tertentu. Penggunaan sedikit asumsi-asumsi akan menyebabkan model yang dihasilkan menjadi kompleks sehingga menurut LeVeque (2007) untuk menyelesaikan suatu model persamaan diferensial dengan syarat batas atau mencari sebuah fungsi (atau hampiran diskret untuk fungsi tersebut) yang memenuhi hubungan antara turunan-turunan yang dimiliki dan memenuhi kondisi batas dalam suatu daerah asal yang diberikan dapat dilakukan dengan suatu pendekatan numerik. Hal ini terjadi ketika penyelesaian secara analitik tidak mudah untuk dilakukan.
Metode beda hingga merupakan salah satu metode numerik yang didasarkan pada aplikasi ekspansi Taylor untuk menghampiri persamaan diferensial. Metode beda hingga bekerja dengan mengganti daerah asal suatu variabel terikat dalam suatu persamaan diferensial yang terdefinisi dengan titik-titik nilai berhingga dari hampiran variabel bebas. Turunan dalam suatu persamaan diferensial pada setiap titik nilai akan dihampiri dari nilai sekitar menggunakan teorema Taylor (Causon dan Mingham 2010). Proses ini akan menghasilkan beberapa persamaan aljabar yang dapat dengan mudah diselesaikan dengan proses komputasi.
Secara umum metode numerik menggunakan prinsip hampiran sehingga solusi yang dihasilkan berupa nilai yang mendekati solusi analitiknya. Oleh karena itu terdapat selisih nilai antara hasil metode numerik dengan hasil metode analitik yang biasa disebut kesalahan atau galat. Nilai kesalahan yang kecil menjadi indikasi bahwa metode numerik yang digunakan akurat dalam menyelesaikan permasalahan. Dalam karya ilmiah ini akan dibahas penyelesaian persamaan diferensial biasa orde dua linear dengan masalah syarat batas Dirichlet menggunakan metode analitik dan metode numerik beda hingga. Selanjutnya, akan dievaluasi pula keakuratan metode beda hingga dalam menghasilkan solusi dari suatu model persamaan diferensial dengan syarat batas Dirichlet menggunakan nilai MAPE.
2
Tujuan Penelitian Penelitian ini bertujuan untuk:
1 mempelajari penyelesaian analitik masalah nilai batas Dirichlet pada persamaan diferensial biasa orde dua linear homogen dan nonhomogen dengan koefisien konstan dan koefisien variabel,
2 mempelajari penyelesaian numerik masalah nilai batas Dirichlet pada persamaan diferensial biasa orde dua linear menggunakan metode beda hingga,
3 mengevaluasi keakuratan hasil penyelesaian numerik dengan metode beda hingga untuk masalah syarat batas Dirichlet persamaan diferensial biasa orde dua linear.
TINJAUAN PUSTAKA
Persamaan Diferensial Biasa
Persamaan diferensial adalah sebuah persamaan yang menghubungkan turunan dari sebuah fungsi tak diketahui, fugsi itu sendiri, variabel ketika fungsi tersebut terdefinisi, dan konstanta (Farlow 1994). Berdasarkan banyak variabel bebasnya, persamaan diferensial dibagi menjadi dua, yaitu persamaan diferensial biasa yang terdiri atas satu variabel bebas dan persamaan diferensial parsial yang terdiri atas dua atau lebih variabel bebas. Secara umum suatu persamaan diferensial biasa dapat dituliskan dalam bentuk
Suatu persamaan diferensial dapat diklasifikasikan berdasarkan orde, kelinearan, dan kehomogenan persamaan. Orde dari suatu peramaan diferensial ialah orde dari turunan tertinggi persamaan diferensial tersebut, yakni persamaan diferensial dikatakan memiliki orde jika turunan tertinggi pada persamaan diferensial tersebut memiliki orde . Persamaan diferensial diklasifikasikan linear jika persamaan tersebut berupa fungsi linear, yakni tidak terdapat operasi perkalian, pembagian, atau pangkat antara variabel terikat dan turunannya. Persamaan diferensial diklasifikasikan kedalam persamaan homogen jika pada persamaan (1) .
Dalam karya ilmiah ini persamaan diferensial biasa yang dibahas akan difokuskan pada persamaan diferensial orde dua linear yang memiliki bentuk umum
untuk setiap dengan merupakan sebuah fungsi yang kontinu pada selang I. Jika pada persamaan (2) merupakan sebuah konstanta, maka persamaan diferensial dikatakan memiliki koefisien konstan.
Solusi dari suatu persamaan diferensial adalah sebuah fungsi yang dapat disubstitusikan kedalam persamaan sehingga persamaan tersebut berlaku. Solusi dari suatu persamaan diferensial biasa harus saling bebas linear. Menurut Farlow (1994) dua fungsi f dan g dikatakan bebas linear pada selang I jika terdapat dua konstanta tak nol dan yang memenuhi
3 untuk setiap pada selang I. Dua fungsi f dan g dikatakan bergantung linear pada selang I jika kedua fungsi tersebut tidak bebas linear pada selang I atau jika persamaan diatas berlaku untuk setiap pada selang I hanya jika . Kombinasi linier dari semua solusi yang saling bebas linear dari persamaan diferensial biasa disebut solusi umum.
Metode Akar Karakteristik
Pada prinsipnya metode akar karakteristik digunakan untuk mengubah persamaan diferensial biasa linear homogen dengan koefisien konstan menjadi persamaan karakteristik. Misalkan persamaan diferensial biasa orde dua linear koefisien konstan dengan bentuk umum
dengan sebuah konstanta sembarang, . Persamaan (3) merupakan kombinasi linear dan sehingga turunan dari tidak akan merubah bentuk kecuali hanya mengalikannya dengan konstanta. Fungsi yang memenuhi kondisi ini ialah fungsi eksponensial. Misalkan
persamaan (4) merupakan solusi dari (3) jika dan hanya jika
Karena tidak pernah sama dengan nol, persamaan (4) merupakan solusi jika memenuhi
dengan (5) merupakan persamaan karakteristik.
Solusi dari persamaan (5) akan mengandung akar-akar persamaan. Berdasarkan jenis akar yang diperoleh dapat dibedakan menjadi tiga, yakni:
1 Dua akar real berbeda
Jika diskriminan dari persamaan karakteristik lebih dari nol atau , maka solusi dari persamaan diferensial biasa orde dua ialah
dengan √ , √ , dan merupakan konstanta (Farlow 1994).
2 Dua akar real sama
Jika diskriminan dari persamaan karakteristik sama dengan nol atau , maka solusi dari persamaan diferensial biasa orde dua ialah
dengan , dan merupakan konstanta (Farlow 1994).
4
3 Akar kompleks
Jika diskriminan dari persamaan karakteristik kurang dari nol atau , maka solusi dari persamaan diferensial biasa orde dua ialah
( ) ( ) ( ) dengan , √ , dan merupakan konstanta (Farlow 1994).
Metode Koefisien Taktentu
Metode koefisien taktentu digunakan untuk mencari solusi partikular persamaan diferensial biasa nonhomogen koefisien konstan. Metode ini menggunakan asumsi awal untuk memperkirakan bentuk solusi partikular yang akan diperoleh, namun dengan nilai koefisien yang tidak spesifik. Jika nilai koefisien tidak dapat diperoleh setelah mensubstitusikan asumsi awal bentuk solusi partikular ke dalam persamaan diferensial, maka bentuk asumsi awal yang digunakan tidak tepat sehingga asumsi bentuk solusi partikular harus diubah sampai diperoleh nilai koefisien yang spesifik. Perlunya asumsi awal berbentuk solusi partikular menyebabkan metode ini terbatas untuk kelas fungsi tertentu. Pada umumnya fungsi nonhomogen ( ) merupakan fungsi polinom, eksponensial, sinus atau kosinus, atau perkalian dari fungsi-fungsi tersebut yang secara singkat dituliskan pada Tabel 1.
Tabel 1 Asumsi awal solusi partikular berdasarkan bentuk ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) dan atau ( ) ( ) ( ) , dengan penjelasan:
1 jika ( ) merupakan fungsi polinom dan persamaan diferensial biasa merupakan kombinasi linear dari , maka solusi partikular akan merupakan fungsi polinom,
2 jika ( ) merupakan fungsi polinom dan eksponensial dan persamaan diferensial biasa merupakan kombinasi linear dari , maka solusi partikular akan merupakan fungsi polinom dan eksponensial (hal ini berlaku karena turunan dari fungsi eksponensial tetap, hanya berlipat sebesar ),
3 jika ( ) merupakan fungsi sinus atau kosinus dan persamaan diferensial biasa merupakan kombinasi linear dari , maka solusi partikular akan
5 merupakan fungsi polinom dan sinus kosinus karena turunan dari keduanya masih merupakan fungsi sinus atau kosinus.
Metode Reduksi Orde d’Alembert
Metode reduksi orde d’Alembert digunakan untuk mentransformasi persamaan diferensial biasa orde tinggi menjadi sebuah persamaan diferensial biasa dengan orde lebih rendah. Metode reduksi orde dapat digunakan jika salah satu solusi tak nol dari persamaan diferensial biasa tersebut diketahui. Misalkan
merupakan solusi dari persamaan
maka berdasarkan prinsip superposisi, juga merupakan solusi dari persamaan (6) dengan sebuah konstanta sebarang. Solusi lain yang bebas linear terhadap dapat diperoleh jika solusi tersebut tidak dalam bentuk , sehingga konstanta sebarang diganti dengan sebuah fungsi, misal
dengan
∫ ∫
Metode Deret Pangkat dan Deret Frobenius
Metode deret digunakan untuk menyelesaikan persamaan diferensial biasa koefisien variabel. Misalkan suatu persamaan diferensial biasa
dengan dan merupakan fungsi yang terdefinisi disekitar . Jika fungsi dan merupakan fungsi analitik, atau dengan kata lain memiliki ekspansi deret pangkat disekitar , maka merupakan titik regular. Namun, jika setidaknya salah satu fungsi atau tidak analitik disekitar atau dengan kata lain tidak memiliki ekspansi deret pangkat dengan pusat , maka merupakan titik singular.
a Solusi disekitar titik regular
Jika merupakan titik regular, maka setiap solusi dari persamaan (7) dapat direpresentasikaan sebagai deret pangkat dengan pusat .
∑
Perhatikan bahwa untuk kasus ini
∑ ∑ ∑ ∑
6
Solusi dapat diperoleh dengan:
1 mensubstitusikan , dan ke dalam persamaan diferensial, 2 menuliskan ruas kiri persamaan (7) sebagai deret pangkat tunggal,
3 merepresentasikan koefisien deret yang diperoleh menjadi nol. Hal ini akan menghasilkan suatu persamaan rekursif,
4 jika memungkinkan, buat sebuah barisan yang merupakan fungsi dari . Setelah itu akan diperoleh solusi dalam bentuk deret pangkat. Jika solusi deret dapat dituliskan dalam bentuk fungsi dasar, maka solusi tersebut dikatakan dalam bentuk tertutup.
b Solusi disekitar titik regular-singular
Jika fungsi atau tidak analitik di , maka titik merupakan titik singular. Dalam kasus ini jika persamaan (7) dapat dituliskan dalam bentuk
̅ ̅ dengan fungsi ̅ dan ̅ analitik di , maka titik disebut titik regular-singular. Jika persamaan (7) tidak dapat dituliskan dalam bentuk (8), maka titik disebut titik iregular atau essential singularity.
Penyederhanaan pengerjaan dapat dilakukan dengan mengasumsikan . Solusi dapat dicari dalam bentuk
∑ ∑
untuk beberapa nilai r. Deret (9) dinamakan deret Frobenius.
Perhatikan bahwa untuk kasus ini ∑
∑
Solusi dapat diperoleh dengan:
1 mensubstitusikan , dan ke dalam persamaan diferensial, 2 menuliskan ruas kiri persamaan (7) sebagai deret pangkat tunggal,
3 ambil koefisien deret dengan pangkat terendah, kemudian koefisien tersebut disamadengankan dengan nol dan akan diperoleh persamaan kuadratik yang akan menghasilkan nilai dan . Dari nilai dan yang diperoleh, substitusikan ke persamaan indeks sehingga akan diperoleh solusi deret dan .
Dari nilai dan yang diperoleh, dengan , akan terdapat tiga kasus: 1 jika selisih nilai dan bukan bilangan bulat, maka akan diperoleh dua
solusi bebas linear
∑
∑
2 jika selisih nilai dan bilangan bulat tak nol, memiliki nilai yang
lebih besar, maka akan diperoleh dua solusi bebas linear
∑
∑
3 jika selisih nilai dan nol, maka akan diperoleh dua solusi bebas linear
7
∑
∑
Metode Variasi Parameter
Metode variasi parameter digunakan untuk mencari solusi partikular persamaan diferensial biasa nonhomogen. Metode ini dapat digunakan jika dua solusi bebas linear persamaan homogen padanan diketahui. Meskipun metode ini hanya dapat digunakan jika dua solusi bebas linear diketahui, namun metode ini dapat diaplikasikan secara lebih mudah pada persamaan diferensial dengan orde yang tinggi jika dibandingkan dengan metode reduksi orde serta tidak diperlukannya asumsi awal bentuk solusi seperti pada metode koefisien tak tentu. Metode variasi parameter memperoleh solusi partikular dengan mengasumsikan parameter di solusi persamaan homogen padanan adalah suatu fungsi. Misalkan persamaan diferensial biasa orde dua linear nonhomogen
dengan dan fungsi kontinu. Persamaan homogen padanan dari persamaan diferensial (10) ialah
yang memiliki solusi homogen dengan bentuk umum
dengan dan konstanta sembarang. Ide dari metode variasi parameter ialah mengganti konstanta dan pada persamaan (11) dengan fungsi dan untuk solusi partikular sehingga akan diperoleh bentuk umum solusi partikular
Fungsi dan dapat dicari dengan memfokuskan pada dua kondisi. Persamaan (12) merupakan kondisi pertama, yakni bahwa solusi partikular harus memenuhi persamaan diferensial dengan turunan pertamanya
Kondisi kedua yang digunakan Lagrange dalam kasus ini ialah
sehingga turunan kedua menjadi lebih sederhana
substitusikan persamaan (12), (13), dan (15) ke dalam persamaan (10) sehingga akan diperoleh
Persamaan (14) dan (16) akan menghasilkan suatu sistem persamaan linear. Dengan metode Cramer akan diperoleh
dengan (lampiran 1). Solusi partikular persamaan diferensial biasa dinyatakan dalam persamaan (18)
∫
∫
8
Syarat Batas Dirichlet
Ketika suatu persamaan diferensial harus memenuhi kondisi batas pada lebih dari satu nilai variabel bebas, maka persamaan diferensial tersebut dikatakan memiliki masalah nilai batas atau boundary value problem. Pada umumnya kondisi batas yang harus dipenuhi ialah pada dua titik, yakni pada batas bawah dan batas atas. Kondisi batas ketika nilai solusi fungsi dispesifikasi pada nilai variabel bebas tertentu dinamakan syarat batas Dirichlet. Contoh syarat batas Dirichlet ialah
atau
Metode Beda Hingga
Metode beda hingga merupakan sebuah teknik penyelesaian persamaan diferensial biasa yang menghampiri turunan dari fungsi dengan formula hampiran beda hingga hasil ekspansi Taylor yang dievaluasi pada titik-titik diskret hasil diskretisasi daerah asal sehingga menghasilkan solusi berupa nilai-nilai fungsi pada titik-titik diskret. Secara umum terdapat tiga langkah utama metode beda hingga yakni diskretisasi daerah asal, menghampiri turunan fungsi dengan formula beda hingga, dan menyelesaikan persamaan aljabar untuk memperoleh nilai hampiran fungsi pada setiap titik.
Misalkan terdapat persamaan diferensial biasa orde dua linear dengan masalah syarat batas Dirichlet berikut
pada dengan dan .
Menurut Mathews (1987) persamaan (19) dapat diselesaikan menggunakan metode beda hingga dengan tahapan pengerjaan sebagai berikut:
1 Dikretisasi daerah asal.
Diskretisasi daerah asal dilakukan dengan memartisi daerah asal menjadi beberapa titik nilai, seperti . Titik-titik nilai yang dihasilkan akan digunakan untuk mencari nilai fungsi yang merepresentasikan hampiran solusi dari persamaan diferensial. Memartisi daerah asal dapat dilakukan menggunakan uniform Cartesian grid
dengan antar titik yang dihasilkan akan memiliki lebar selang yang seragam. Sebagai contoh misalkan suatu persamaan diferensial memiliki daerah asal yang akan dipartisi menjadi empat bagian. Proses diskretisasi akan menghasilkan lima titik nilai dengan lebar selang seragam, yakni dengan titik-titik nilai yang dihasilkan ialah .
2 Mengubah turunan pada persamaan diferensial dengan hampiran beda hingga pada setiap titik nilai untuk memperoleh beberapa sistem persamaan aljabar. Proses pengubahan turunan dapat dilakukan dengan memanfaatkan formula beda pusat hasil ekspansi Taylor (lampiran 2)
9
dan
Agar penulisan lebih mudah,untuk selanjutnya akan dinotasikan dengan . Substitusi persamaan (20) dan (21) ke persamaan (19)
(
) Selanjutnya, kesalahan dihilangkan dan perubahan penulisan notasi , , sehingga persamaan (22) menjadi
(
) Dengan mengalikan setiap ruas persamaan (23) dengan , dan mengatur menjadi sebuah sistem persamaan linear diperoleh
( ) ( ) untuk , dengan dan .
3 Menyelesaikan sistem persamaan aljabar untuk memperoleh hampiran solusi pada setiap titik.
Sistem persamaan linear aljabar (24) dapat dituliskan dalam bentuk matriks dan vektor [ ] [ ] [ ]
dengan ( ) dan ( ). Selanjutnya dapat diperoleh nilai ,untuk .
MAPE (Mean Absolute Percentage Error)
MAPE (Mean Absolute Percentage Error) digunakan untuk mengukur keakuratan hasil peramalan. Nilai MAPE disajikan dalam bentuk persen. MAPE memiliki formula
∑| ̂ |
10
dengan menyatakan banyaknya ukuran contoh, ̂ menyatakan nilai hasil prediksi pada titik , dan menyatakan nilai pada titik . Tabel 2 mensajikan nilai MAPE dan interpretasinya
Tabel 2 Nilai MAPE dan interpretasinya
MAPE Interpretasi
< 10 Tingkat keakuratan tinggi 10-20 Tingkat keakuratan baik 20-50 Tingkat keakuratan cukup baik
> 50 Tidak akurat
Sumber: Lewis (1982)
HASIL DAN PEMBAHASAN
1 Persamaan Diferensial Biasa Orde Dua Linear Homogen dengan Koefisien Konstan
Berikut ini akan dibahas penyelesaian persamaan diferensial biasa orde dua linear homogen dengan koefisien konstan menggunakan metode analitik akar karakteristik dan menggunakan metode numerik beda hingga. Contoh persamaan diferensial biasa orde dua linear homogen dengan koefisien konstan diberikan pada persamaan (25).
Misalkan persamaan diferensial biasa orde dua linear
dengan syarat batas Dirichlet a Metode Akar Karakteristik
Persamaan karakteristik dari persamaan diferensial (25)
maka diperoleh solusi umum persamaan (25)
Dengan syarat batas , maka
eliminasi persamaan (26) dan (27) menggunakan metode eliminasi Gauss, diperoleh , dan , sehingga solusi khusus persamaan (25)
11 b Metode Beda Hingga
Penyelesaian persamaan diferensial orde dua linear homogen dengan koefisien konstan menggunakan metode numerik beda hingga diawali dengan mendiskretisasi daerah asal , yakni memartisi daerah menjadi beberapa titik nilai dengan . Untuk terdapat 5 titik nilai hasil partisi, untuk terdapat 11 titik nilai dan untuk terdapat 21 titik nilai. Selanjutnya, mengubah turunan pada persamaan (25) dengan hampiran beda hingga pada setiap titik nilai sehingga diperoleh sistem persamaan linear
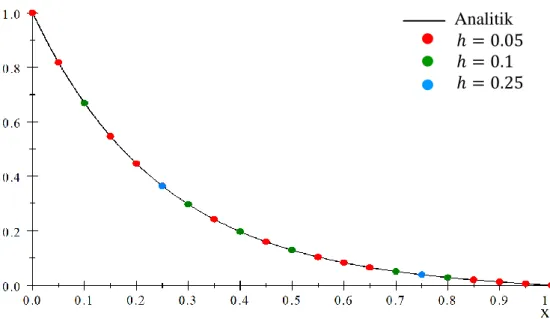
Dengan program MATLAB diperoleh solusi khusus persamaan (25) pada setiap titik nilai. Gambar 1 menunjukkan plot solusi khusus persamaan (25) metode analitik dan metode numerik beda hingga untuk tiga nilai yang berbeda dengan eror untuk masing-masing nilai pada setiap titik nilai ditunjukkan pada Tabel 3 dan nilai MAPE pada setiap titik nilai ditunjukkan pada Tabel 4.
Gambar 1 Plot solusi khusus persamaan (25) metode analitik dan numerik Titik-titik warna pada Gambar 1 menunjukkan hasil pendekatan solusi numerik pada setiap titik nilai hasil diskretisasi dengan metode beda hingga. Titik warna merah menunjukkan hasil pendekatan untuk , titik warna hijau menunjukkan hasil pendekatan untuk , dan titik warna biru menunjukkan hasil pendekatan untuk dengan garis hitam menunjukkan hasil solusi analitik. Pada Gambar 1 terlihat plot solusi numerik metode beda hingga bertumpuk dengan plot solusi analitik metode akar karakteristik untuk setiap nilai . Nilai eror hasil solusi khusus persamaan (25) pada setiap titik nilai diperlihatkan pada Tabel 3.
Analitik
12
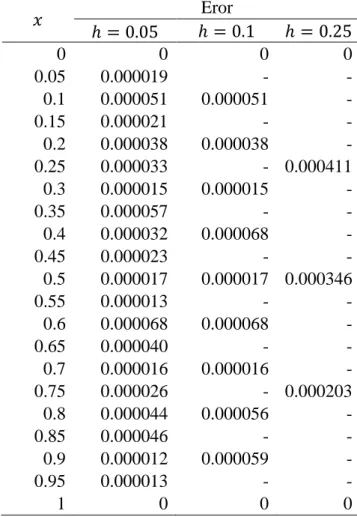
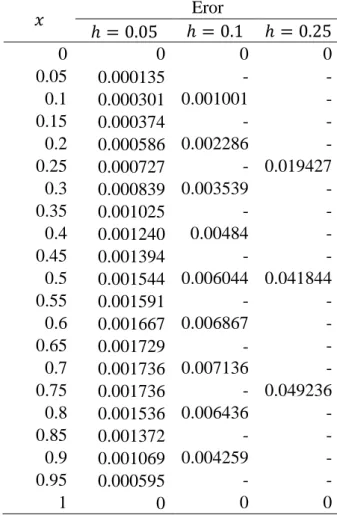
Tabel 3 Eror hasil solusi khusus persamaan (25) pada setiap titik nilai
Eror 0 0 0 0 0.05 0.000019 - - 0.1 0.000051 0.000051 - 0.15 0.000021 - - 0.2 0.000038 0.000038 - 0.25 0.000033 - 0.000411 0.3 0.000015 0.000015 - 0.35 0.000057 - - 0.4 0.000032 0.000068 - 0.45 0.000023 - - 0.5 0.000017 0.000017 0.000346 0.55 0.000013 - - 0.6 0.000068 0.000068 - 0.65 0.000040 - - 0.7 0.000016 0.000016 - 0.75 0.000026 - 0.000203 0.8 0.000044 0.000056 - 0.85 0.000046 - - 0.9 0.000012 0.000059 - 0.95 0.000013 - - 1 0 0 0
Tabel 3 menunjukkan ketika nilai eror hasil solusi khusus persamaan (25) kurang dari 0.0005, ketika lebar selang diperkecil menjadi memiliki eror kurang dari 0.00007, dan ketika lebar selang diperkecil menjadi 0.05 memiliki eror kurang dari 0.00007. Secara umum terlihat pemilihan nilai memengaruhi hasil pendekatan metode beda hingga terhadap solusi analitik, seperti saat , untuk hasil pendekatan metode beda hingga memiliki eror sebesar 0.000346, ketika nilai diperkecil menjadi 0.1, hasil pendekatan metode beda hingga memiliki eror sebesar 0.000017 dan ketika nilai diperkecil kembali menjadi 0.05, hasil pendekatan metode beda hingga memiliki eror 0.000017 sehingga untuk kasus ini hasil pendekatan metode beda hingga secara umum memiliki nilai eror terkecil ketika . Pada Tabel 4 ditunjukkan nilai MAPE hasil solusi khusus persamaan (25) pada setiap titik nilai.
13 Tabel 4 Nilai MAPE hasil solusi khusus persamaan (25) pada setiap titik nilai
MAPE 0 0 % 0 % 0 % 0.05 0.00232 % - - 0.1 0.007572 % 0.007572 % - 0.15 0.00386 % - - 0.2 0.008608 % 0.008608 % - 0.25 0.000915 % - 0.112686 % 0.3 0.004992 % 0.004992 % - 0.35 0.002369 % - - 0.4 0.016285 % 0.034510 % - 0.45 0.001414 % - - 0.5 0.013100 % 0.013100 % 0.267993 % 0.55 0.012939 % - - 0.6 0.008246 % 0.008246 % - 0.65 0.061619 % - - 0.7 0.030746 % 0.030746 % - 0.75 0.066586 % - 0.522982 % 0.8 0.155329 % 0.194864 % - 0.85 0.232085 % - - 0.9 0.333545 % 0.475596 % - 0.95 0.215087 % - - 1 0 % 0 % 0 %
Dari Tabel 4 terlihat solusi khusus persamaan (25) secara keseluruhan memiliki nilai MAPE kurang dari 1% dengan rata-rata nilai MAPE saat sebesar 0.180732%, saat memiliki rata-rata 0.070749% dan rata-rata terkecil terjadi saat yakni sebesar 0.056076% sehingga dapat dikatakan bahwa metode numerik beda hingga memiliki tingkat keakuratan yang tinggi dalam mendekati solusi analitik persamaan (25).
2 Persamaan Diferensial Orde Dua Linear Nonhomogen dengan Koefisien Konstan
Penyelesaian persamaan diferensial orde dua linear nonhomogen dengan koefisien konstan secara analitik yang akan dibahas pada bagian ini dilakukan dengan menyelesaikan persamaan homogen padanan persamaan menggunakan metode akar karakteristik dilanjutkan dengan penyelesaian persamaan partikular menggunakan metode koefisien taktentu. Pada bagian ini akan dibahas pula penyelesaian persamaan diferensial orde dua linear nonhomogen dengan koefisien konstan secara numerik menggunakan metode beda hingga. Contoh dari
14
persamaan diferensial orde dua linear nonhomogen koefisien konstan diberikan pada persamaan (28).
Misalkan persamaan diferensial biasa orde dua linear
dengan syarat batas Dirichlet a Metode Akar Karakteristik dan Koefisien Taktentu
Persamaan homogen padanan dari persamaan (28)
Persamaan karakteristik dari (29)
maka solusi homogen padanan
Persamaan partikular dari persamaan (28)
substitusi persamaan (30), (31), (32) ke persamaan (28)
maka solusi partikular , sehingga diperoleh solusi umum persamaan (28)
Dengan syarat batas , maka
eliminasi persamaan (33) dan (34) menggunakan metode eliminasi Gauss, diperoleh , sehingga solusi khusus persamaan (28)
b Metode Beda Hingga
Penyelesaian menggunakan metode beda hingga untuk menyelesaikan persamaan diferensial orde dua linear nonhomogen dengan koefisien konstan diawali dengan mendiskretisasi daerah asal menjadi beberapa titik nilai dengan . Dalam karya ilmiah ini terdapat tiga nilai yang digunakan yakni , sehingga untuk terdapat 5 titik nilai hasil partisi, untuk terdapat 11 titik nilai dan untuk terdapat 21 titik nilai. Selanjutnya, dilakukan pengubahan turunan pada persamaan
15 (28) dengan hampiran beda hingga pusat pada setiap titik nilai sehingga diperoleh sistem persamaan linear
Solusi khusus persamaan (28) pada setiap titik nilai diperoleh dengan program MATLAB. Gambar 2 menunjukkan plot solusi khusus persamaan (28) metode analitik dan metode numerik beda hingga untuk tiga nilai yang berbeda dengan eror untuk masing-masing nilai pada setiap titik nilai ditunjukkan pada Tabel 5 dan pada Tabel 6 ditunjukkan nilai MAPE pada setiap titik nilai untuk masing-masing nilai .
Gambar 2 Plot solusi khusus persamaan (28) metode analitik dan numerik
Hasil pendekatan solusi numerik pada setiap titik nilai hasil diskretisasi dengan metode beda hingga ditunjukkan dengan plot yang berupa titik-titik diskret pada Gambar 2. Titik warna merah menunjukkan hasil pendekatan untuk , titik warna hijau menunjukkan hasil pendekatan untuk , dan titik warna biru menunjukkan hasil pendekatan untuk dengan garis hitam menunjukkan hasil solusi analitik. Pada Gambar 2 terlihat plot solusi numerik metode beda hingga bertumpuk dengan plot solusi analitik metode akar karakteristik dan koefisien tak tentu untuk nilai sementara ketika plot solusi numerik tidak tepat bertumpuk dengan plot solusi numerik. Nilai eror hasil solusi khusus persamaan (28) pada setiap titik nilai diperlihatkan pada Tabel 5.
Analitik
16
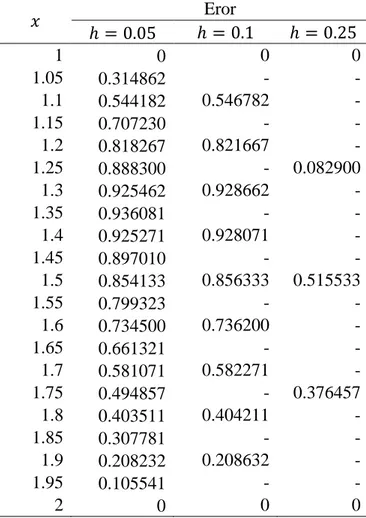
Tabel 5 Eror hasil solusi khusus persamaan (28) pada setiap titik nilai
Eror 0 0 0 0 0.05 0.000135 - - 0.1 0.000301 0.001001 - 0.15 0.000374 - - 0.2 0.000586 0.002286 - 0.25 0.000727 - 0.019427 0.3 0.000839 0.003539 - 0.35 0.001025 - - 0.4 0.001240 0.00484 - 0.45 0.001394 - - 0.5 0.001544 0.006044 0.041844 0.55 0.001591 - - 0.6 0.001667 0.006867 - 0.65 0.001729 - - 0.7 0.001736 0.007136 - 0.75 0.001736 - 0.049236 0.8 0.001536 0.006436 - 0.85 0.001372 - - 0.9 0.001069 0.004259 - 0.95 0.000595 - - 1 0 0 0
Tabel 5 menunjukkan ketika nilai eror hasil solusi khusus persamaan (28) kurang dari 0.05, ketika lebar selang diperkecil menjadi memiliki eror kurang dari 0.008, dan ketika lebar selang diperkecil menjadi 0.05 memiliki eror kurang dari 0.002. Secara umum terlihat pemilihan nilai memengaruhi hasil pendekatan metode beda hingga terhadap solusi analitik, seperti saat , untuk hasil pendekatan metode beda hingga memiliki eror sebesar 0.041844, ketika nilai diperkecil menjadi 0.1, hasil pendekatan metode beda hingga memiliki eror sebesar 0.006044 dan ketika nilai diperkecil kembali menjadi 0.05, hasil pendekatan metode beda hingga memiliki eror 0.001544 sehingga untuk kasus ini hasil pendekatan metode beda hingga secara umum memiliki nilai eror terkecil ketika . Pada Tabel 6 ditunjukkan nilai MAPE hasil solusi khusus persamaan (28) pada setiap titik nilai.
17 Tabel 6 Nilai MAPE hasil solusi khusus persamaan (28) pada setiap titik nilai
MAPE 0 0 % 0 % 0 % 0.05 0.013231 % - - 0.1 0.028789 % 0.095819 % - 0.15 0.035193 % - - 0.2 0.054577 % 0.212847 % - 0.25 0.067161 % - 1.795485 % 0.3 0.077416 % 0.326457 % - 0.35 0.094929 % - - 0.4 0.11611 % 0.453106 % - 0.45 0.132980 % - - 0.5 0.151499 % 0.592954 % 4.104977 % 0.55 0.162312 % - - 0.6 0.179346 % 0.738707 % - 0.65 0.199414 % - - 0.7 0.219535 % 0.902419 % - 0.75 0.247918 % - 7.031075 % 0.8 0.258446 % 1.082857 % - 0.85 0.290607 % - - 0.9 0.321398 % 1.283137 % - 0.95 0.339177 % - - 1 0 % 0 % 0 %
Keakuratan metode beda hingga dalam mendekati solusi analitik persamaan (28) dapat dilihat pada Tabel 6 yang menunjukkan nilai MAPE untuk solusi khusus persamaan (28) dengan rata-rata nilai MAPE untuk sebesar 2.586307%, untuk dan memiliki rata-rata nilai MAPE kurang dari 1% yakni sebesar 0.517119% saat dan 0.142383% saat yang merupakan rata-rata terkecil sehingga dapat dikatakan bahwa metode numerik beda hingga memiliki tingkat keakuratan yang tinggi dalam mendekati solusi analitik persamaan (28).
3 Persamaan Diferensial Orde Dua Linear Homogen dengan Koefisien Variabel Jika Salah Satu Solusi Diketahui
Pada bagian ini akan dibahas metode analitik reduksi orde d’Alembert untuk menyelesaian persamaan diferensial orde dua linear homogen dengan koefisien variabel jika salah satu solusi persamaan sudah diketahui. Selanjutnya, akan dibahas pula penyelesaian menggunakan metode numerik beda hingga. Persamaan diferensial orde dua linear homogen dengan koefisien variabel diberikan pada persamaan (35) dengan salah satu nilai solusi yang telah diketahui.
18
Misalkan adalah solusi dari persamaan diferensial
dengan syarat batas Dirichlet a Metode reduksi orde d’Alembert
Persamaan (35) memiliki bentuk umum
Misalkan
substitusi persamaan (36), (37), (38) ke persamaan (35)
( ) misalkan , , maka persamaan (39) dapat dituliskan menjadi
∫ ∫ | | | | pilih , akan diperoleh
∫
pilih , akan diperoleh
substitusikan persamaan (40) ke persamaan (36), akan diperoleh
dengan | | Jadi , dan bebas linear.
Maka solusi umum persamaan (35)
dengan syarat batas Dirichlet
19 eliminasi persamaan (41) dan (42) menggunakan metode eliminasi Gauss diperoleh , .
Jadi solusi khusus persamaan (35)
b Metode Beda Hingga
Penyelesaian persamaan (35) menggunakan metode numerik beda hingga diawali dengan mendiskretisasi daerah asal , yakni memartisi daerah menjadi beberapa titik nilai dengan . Dalam karya ilmiah ini terdapat tiga nilai yang digunakan yakni , sehingga untuk terdapat 5 titik nilai hasil partisi, untuk terdapat 11 titik nilai dan untuk terdapat 21 titik nilai. Selanjutnya, proses penyelesaian dilakukan dengan mengubah turunan pada persamaan (35) dengan hampiran beda hingga pada setiap titik nilai sehingga diperoleh sistem persamaan linear
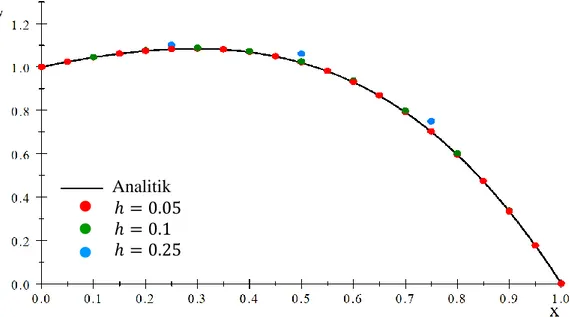
dengan program MATLAB diperoleh solusi khusus persamaan (35) pada setiap titik nilai. Gambar 3 menunjukkan plot solusi khusus persamaan (35) metode analitik dan metode numerik beda hingga untuk tiga nilai yang berbeda dengan eror untuk masing-masing nilai pada setiap titik nilai ditunjukkan pada Tabel 7 dan nilai MAPE pada setiap titik nilai untuk masing-masing nilai ditunjukkan pada Tabel 8.
Gambar 3 Plot solusi khusus persamaan (35) metode analitik dan numerik Analitik
20
Gambar 3 menunjukkan plot solusi analitik yang berupa garis berwarna hitam dan plot hasil pendekatan solusi numerik pada setiap titik nilai hasil diskretisasi dengan metode beda hingga yang berupa titik-titik diskret dengan titik warna merah menunjukkan hasil pendekatan untuk , titik warna hijau menunjukkan hasil pendekatan untuk , dan titik warna biru menunjukkan hasil pendekatan untuk . Pada Gambar 3 terlihat plot solusi analitik tidak tepat bertumpuk dengan plot solusi numerik metode reduksi orde d’Alembert. Nilai eror hasil solusi khusus persamaan (35) pada setiap titik nilai diperlihatkan pada Tabel 7.
Tabel 7 Eror hasil solusi khusus persamaan (35) pada setiap titik nilai
Eror 1 0 0 0 1.05 0.314862 - - 1.1 0.544182 0.546782 - 1.15 0.707230 - - 1.2 0.818267 0.821667 - 1.25 0.888300 - 0.082900 1.3 0.925462 0.928662 - 1.35 0.936081 - - 1.4 0.925271 0.928071 - 1.45 0.897010 - - 1.5 0.854133 0.856333 0.515533 1.55 0.799323 - - 1.6 0.734500 0.736200 - 1.65 0.661321 - - 1.7 0.581071 0.582271 - 1.75 0.494857 - 0.376457 1.8 0.403511 0.404211 - 1.85 0.307781 - - 1.9 0.208232 0.208632 - 1.95 0.105541 - - 2 0 0 0
Tabel 7 menunjukkan nilai eror hasil solusi khusus persamaan (35) pada setiap titik nilai untuk setiap nilai . Pemilihan nilai mempengaruhi hasil pendekatan metode beda hingga terhadap solusi analitik, seperti saat , untuk hasil pendekatan metode beda hingga memiliki eror sebesar 0.515533, ketika nilai diperkecil menjadi 0.1, hasil pendekatan metode beda hingga memiliki eror sebesar 0.856333 dan ketika nilai diperkecil kembali menjadi 0.05, hasil pendekatan metode beda hingga memiliki eror 0.854133. Solusi khusus persamaan (35) hasil pendekatan metode beda hingga secara umum
21 memiliki nilai eror terkecil ketika . Pada Tabel 8 ditunjukkan nilai MAPE hasil solusi khusus persamaan (35) pada setiap titik nilai.
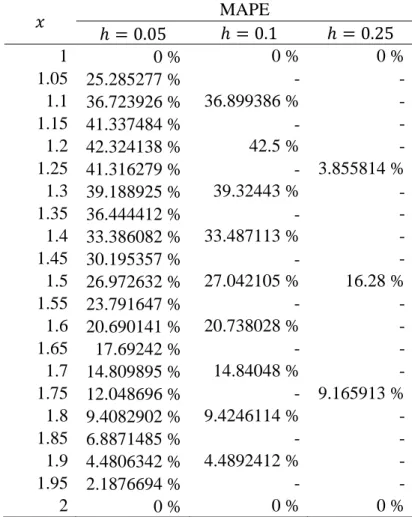
Tabel 8 Nilai MAPE hasil solusi khusus persamaan (35) pada setiap titik nilai
MAPE 1 0 % 0 % 0 % 1.05 25.285277 % - - 1.1 36.723926 % 36.899386 % - 1.15 41.337484 % - - 1.2 42.324138 % 42.5 % - 1.25 41.316279 % - 3.855814 % 1.3 39.188925 % 39.32443 % - 1.35 36.444412 % - - 1.4 33.386082 % 33.487113 % - 1.45 30.195357 % - - 1.5 26.972632 % 27.042105 % 16.28 % 1.55 23.791647 % - - 1.6 20.690141 % 20.738028 % - 1.65 17.69242 % - - 1.7 14.809895 % 14.84048 % - 1.75 12.048696 % - 9.165913 % 1.8 9.4082902 % 9.4246114 % - 1.85 6.8871485 % - - 1.9 4.4806342 % 4.4892412 % - 1.95 2.1876694 % - - 2 0 % 0 % 0 %
Dari Tabel 8 terlihat untuk memiliki rata-rata nilai MAPE lebih dari 10%, yakni untuk secara rata-rata memiliki nilai MAPE sebesar 22.151%, dan untuk memiliki rata-rata nilai MAPE sebesar 20.79504%, sedangkan untuk memiliki rata-rata nilai MAPE kurang dari 10%, yakni sebesar 5.860345%. Dari nilai MAPE yang diperoleh dapat dikatakan bahwa metode beda hingga memiliki tingkat keakuratan yang baik dalam mendekati solusi analitik persamaan (35).
4 Persamaan Diferensial Orde Dua Linear Homogen dengan Koefisien Variabel
Berikut ini akan dibahas penyelesaian persamaan diferensial orde dua linear homogen dengan koefisien variabel menggunakan metode analitik deret dan metode numerik beda hingga. Salah satu contoh persamaan diferensial orde dua linear homogen koefisien variabel ialah persamaan Chebysev yang memiliki
22
bentuk menyerupai persamaan Legandre yang biasa digunakan dalam mekanika quantum. Persamaan Chebysev diberikan pada persamaan (43).
Misalkan persamaan diferensial biasa orde dua linear
| | dengan syarat batas Dirichlet
a Metode Deret
Persamaan (43) merupakan persamaan Chebysev, yang memiliki titik regular singular , dan sehingga penyelesaian secara analitik dapat menggunakan metode deret pangkat.
∑ ∑ ∑ ∑ ∑ ∑ ∑ Substitusi persamaan (44), (45), dan (46) ke persamaan (43), akan diperoleh
∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ dari persamaan (47) diperoleh
23 dan persamaan indeks
Persamaan (48) dan (49) merupakan kasus khusus persamaan (50), yakni ketika dan , maka persamaan (50) dapat dituliskan menjadi
Tabel 9 Persamaan indeks untuk persamaan (43)
Sehingga solusi umum persamaan Chebysev dengan (
) (
) Solusi khusus persamaan (43) tidak dapat diperoleh karena solusi umum tidak dalam bentuk tertutup.
b Metode Beda Hingga
Penyelesaian persamaan diferensial orde dua linear homogen dengan koefisien variabel menggunakan metode numerik beda hingga diawali dengan mendiskretisasi daerah asal , yakni memartisi daerah menjadi beberapa titik nilai dengan . Untuk terdapat 5 titik nilai hasil partisi, untuk terdapat 11 titik nilai dan untuk terdapat 21 titik nilai. Selanjutnya, mengubah turunan pada persamaan (43) dengan hampiran beda hingga pada setiap titik nilai sehingga diperoleh sistem persamaan linear
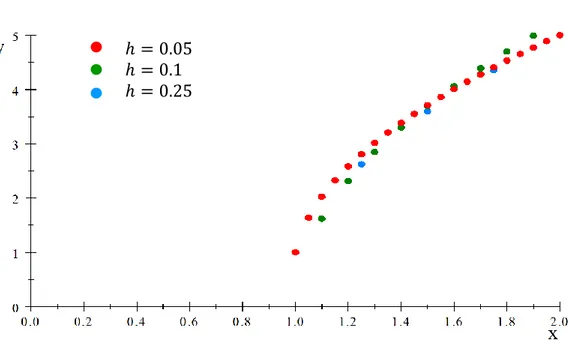
Dengan program MATLAB diperoleh solusi khusus persamaan (43) pada setiap titik nilai. Gambar 4 menunjukkan plot solusi khusus persamaan (43) metode analitik dan metode numerik beda hingga untuk tiga nilai yang berbeda dengan eror untuk masing-masing nilai pada setiap titik nilai ditunjukkan pada Tabel 10.
24
Gambar 4 Plot solusi khusus persamaan (43) metode numerik beda hingga Tabel 10 Solusi khusus persamaan (43) pada setiap titik nilai
Numerik 1 1 0 0 1.05 1.6367 - - 1.1 2.0231 1.6203 - 1.15 2.3249 - - 1.2 2.5815 2.3097 - 1.25 2.8087 - 2.6229 1.3 3.015 2.8452 - 1.35 3.2053 - - 1.4 3.3829 3.2979 - 1.45 3.5502 - - 1.5 3.7088 3.6971 3.5973 1.55 3.8599 - - 1.6 4.0046 4.0581 - 1.65 4.1436 - - 1.7 4.2776 4.39 - 1.75 4.407 - 4.3565 1.8 4.5324 4.699 - 1.85 4.6541 - - 1.9 4.7724 4.9891 - 1.95 4.8877 - - 2 5 0 0
25 Penyelesaian persamaan Chebysev dengan metode deret tidak menghasilkan solusi dalam bentuk tertutup sehingga syarat batas tidak dapat disubstitusikan ke dalam solusi umum untuk memeroleh solusi khusus. Pada Gambar 4 metode beda hingga dapat menggambarkan nilai solusi pada setiap titik diskret hasil metode numerik beda hingga dengan nilai solusi pada setiap titiknya ditunjukkan pada Tabel 10. Secara keseluruhan untuk setiap nilai plot solusi memiliki pola yang sama. Terlihat bahwa nilai yang lebih kecil dapat lebih mulus menunjukkan kurva solusi dibandingkan dengan nilai yang lebih besar. Dari contoh kasus ini dapat dilihat bahwa metode beda hingga mampu memberikan gambaran bentuk kurva solusi ketika metode analitik tidak memungkinkan untuk digunakan dalam menyelesaikan suatu permasalahan, namun pada kasus ini tidak dapat dilihat apakah metode beda hingga akurat dalam mendekati solusi analitik untuk persamaan (43).
5 Persamaan Diferensial Orde Dua Linear Nonhomogen dengan Koefisien Variabel Jika Kedua Solusi Diketahui
Jika solusi persamaan homogen padanan dari persamaan diferensial orde dua linear nonhomogen dengan koefisien variabel diketahui, maka penyelesaian persamaan partikular dapat dilakukan menggunakan metode variasi parameter yang akan dibahas pada bagian ini. Akan dibahas pula metode numerik beda hingga untuk penyelesaian persamaan diferensial orde dua linear nonhomogen dengan koefisien variabel. Contoh persamaan diferensial orde dua linear nonhomogen dengan koefisien variabel diberikan pada persamaan (52) dengan solusi homogen padanan yang telah diketahui.
Misalkan , dan adalah solusi dari persamaan diferensial biasa
dengan syarat batas Dirichlet a Metode Variasi Parameter
Misalkan
dengan metode variasi parameter, misalkan
dapat dicari menggunakan persamaan (18), dari persamaan (17) akan diperoleh
(lampiran 3). Substitusikan persamaan (54) dan (55) ke persamaan (53) akan diperoleh
Sehingga solusi umum persamaan (52)
Dengan syarat batas , maka
26
substitusi persamaan (56) ke persamaan (57) diperoleh
, sehingga solusi khusus persamaan (52)
b Metode Beda Hingga
Penyelesaian persamaan diferensial orde dua linear homogen dengan koefisien konstan menggunakan metode numerik beda hingga diawali dengan mendiskretisasi daerah asal , yakni memartisi daerah menjadi beberapa titik nilai dengan . Untuk terdapat 5 titik nilai hasil partisi, untuk terdapat 11 titik nilai dan untuk terdapat 21 titik nilai. Selanjutnya, mengubah turunan pada persamaan (52) dengan hampiran beda hingga pada setiap titik nilai sehingga diperoleh sistem persamaan linear
Dengan program MATLAB diperoleh solusi khusus persamaan (52) pada setiap titik nilai. Gambar 5 menunjukkan plot solusi khusus persamaan (52) metode analitik dan metode numerik beda hingga untuk tiga nilai yang berbeda dengan eror untuk masing-masing nilai pada setiap titik nilai ditunjukkan pada Tabel 11 dan nilai MAPE pada setiap titik nilai untuk masing-masing nilai ditunjukkan pada Tabel 12.
Gambar 5 Plot solusi khusus persamaan (52) metode analitik dan numerik Gambar 5 menunjukkan plot solusi analitik yang berupa garis berwarna hitam dan plot hasil pendekatan solusi numerik pada setiap titik nilai hasil diskretisasi dengan metode beda hingga yang berupa titik-titik diskret dengan titik warna merah menunjukkan hasil pendekatan untuk , titik warna hijau menunjukkan hasil pendekatan untuk , dan titik warna biru menunjukkan hasil pendekatan untuk . Pada Gambar 5 terlihat plot solusi numerik metode beda hingga bersinggungan dengan plot solusi analitik metode variasi
Analitik
27 parameter untuk setiap nilai dengan nilai eror untuk setiap titik ditunjukkan pada Tabel 11.
Tabel 11 Eror hasil solusi khusus persamaan (52) pada setiap titik nilai
Eror 0 0 0 0 0.05 0.030357 - - 0.1 0.059609 0.059709 - 0.15 0.086659 - - 0.2 0.112430 0.110730 - 0.25 0.130769 - 0.131569 0.3 0.146649 0.146749 - 0.35 0.157672 - - 0.4 0.163577 0.163677 - 0.45 0.164347 - - 0.5 0.160113 0.160212 0.160813 0.55 0.150967 - - 0.6 0.137573 0.137673 - 0.65 0.120377 - - 0.7 0.100320 0.10042 - 0.75 0.078556 - 0.078956 0.8 0.056364 0.056464 - 0.85 0.035372 - - 0.9 0.017474 0.017474 - 0.95 0.004851 - - 1 0 0 0
Pada Tabel 11 terlihat metode beda hingga memiliki nilai eror kurang dari 0.2 secara keseluruhan untuk setiap nilai pada setiap titik nilai. Secara umum terlihat pemilihan nilai mempengaruhi hasil pendekatan metode beda hingga terhadap solusi analitik. Seperti saat , untuk hasil pendekatan metode beda hingga memiliki eror sebesar 0.160813, ketika nilai diperkecil menjadi 0.1, hasil pendekatan metode beda hingga memiliki eror sebesar 0.160212 dan ketika nilai diperkecil kembali menjadi 0.05, hasil pendekatan metode beda hingga memiliki eror 0.160113. Dari Tabel 11 terlihat solusi khusus persamaan (52) hasil pendekatan metode beda hingga secara umum memiliki nilai eror terkecil ketika dengan penjelasan lebih lanjut dapat dilihat pada Tabel 12.
28
Tabel 12 Nilai MAPE hasil solusi khusus persamaan (52) pada setiap titik nilai
MAPE 0 0 % 0 % 0 % 0.05 0.023093 % - - 0.1 3.640494 % 3.646601 % - 0.15 4.400608 % - - 0.2 4.865674 % 4.792103 % - 0.25 4.912189 % - 4.94224 % 0.3 4.849571 % 4.852878 % - 0.35 4.642421 % - - 0.4 4.328218 % 4.330864 % - 0.45 3.938474 % - - 0.5 3.498437 % 3.500622 % 3.513731 % 0.55 3.025129 % - - 0.6 2.541290 % 2.543138 % - 0.65 2.059413 % - - 0.7 1.596294 % 1.597886 % - 0.75 1.167169 % - 1.173112 % 0.8 0.784855 % 0.786247 % - 0.85 0.463231 % - - 0.9 0.215936 % 0.215936 % - 0.95 0.056754 % - - 1 0% 0% 0 %
Pada Tabel 12 terlihat solusi khusus persamaan (52) secara keseluruhan memiliki nilai MAPE kurang dari 10% dengan rata-rata nilai MAPE saat sebesar 2.429012%, saat memiliki rata-rata 2.387843% dan rata-rata terkecil terjadi saat yakni sebesar 1.925817% sehingga dapat dikatakan bahwa metode numerik beda hingga memiliki tingkat keakuratan yang baik dalam mendekati solusi analitik persamaan (52).
SIMPULAN DAN SARAN
Simpulan
Dalam pembahasan pada skripsi ini, dapat ditarik kesimpulan bahwa metode numerik beda hingga dapat digunakan untuk menyelesaikan semua jenis persamaan diferensial biasa orde dua linear. Dalam hal metode analitik tidak dapat menyelesaikan solusi secara eksak, metode beda hingga dapat menyelesaikan persamaan diferensial biasa orde dua linier seperti terlihat pada kasus ketiga yakni
29 metode beda hingga mampu menunjukkan bentuk kurva solusi khusus secara eksplisit. Metode beda hingga juga mengubah suatu persamaan diferensial dengan syarat batas menjadi sebuah sistem persamaan linear yang dapat diselesaikan dengan proses komputasi sederhana. Pemilihan nilai pada metode beda hingga menentukan keakuratan hasil pendekatan solusi, namun pemilihan nilai yang kecil tidak menjamin solusi akan semakin akurat atau akan memiliki eror yang kecil jika dibandingkan dengan metode analitik. Metode beda hingga memiliki nilai MAPE kurang dari 10% untuk semua jenis kasus yang diselesaikan.
Saran
Dalam karya ilmiah ini telah dibahas penyelesaian persamaan diferensial biasa orde dua linier. Metode ini dapat dikembangkan untuk menyelesaikan persamaan diferensial tak linier. Saran dari penulis adalah dapat dilakukan penelitian lebih lanjut untuk menyelesaikan persamaan diferensial biasa orde dua tak linier menggunakan metode beda hingga.
DAFTAR PUSTAKA
Causon D M dan Mingham C G. 2010. Introductory Finite Different Methods Fr
PDEs. Manchester(UK): Ventus Publishing ApS.
Farlow S J. 1994. An Introduction to Differential Equations and Their
Applications. Singapore(SG): McGraw-Hill.
LeVaque R J. 2007. Finite Difference Methods For Ordinary and Partial
Differential Equation. Philadelphia(PA): SIAM.
Lewis C D. 1982. Industrial and business forecasting methods. London: Butterworths.
Mathews J. 1987. Numerical Methods for Mathematics, Science, and Engineering. Ed ke-2. New Jersey(US): Prentice-Hall, Inc.
30
LAMPIRAN
Lampiran 1 Wronskian untuk memeriksa kebebasan linear Misalkan dua fungsi terturunkan dan
| | dinamakan Wronskian dari dan
Lampiran 2 Hampiran beda hingga pusat
Deret Taylor dari fungsi di (atau di sekitar atau yang berpusat di ) memenuhi persamaan ∑ (Varberg et al.2008) Misalkan ekspansi deret Taylor pada
Pada akan diperoleh
Pada akan diperoleh
Untuk k=2, dengan mengurangi persamaan (69) dan (70) akan diperoleh
persamaan (71) dapat dituliskan menjadi
Untuk k=4 dengan menjumlahkan persamaan (69) dan (70) akan diperoleh
persamaan (72) dapat dituliskan menjadi
Lampiran 3 Penurunan metode variasi parameter untuk persamaan (52)
Nilai dapat diperoleh dengan mensubstitusikan solusi homogen persamaan (52) ke persamaan (17), akan diperoleh
31 | | ∫ dengan menggunakan teknik pengintegralan parsial dengan dan diperoleh
Nilai dapat diperoleh dengan mensubstitusikan solusi homogen persamaan (52) ke persamaan (17), akan diperoleh
| | dengan menggunakan teknik pengintegralan parsial dengan ,
dan , diperoleh
[ ∫ ( ∫ )] dengan menggunakan teknik pengintegralan parsial dengan ,
diperoleh
Lampiran 4 Metode beda hingga persamaan diferensial orde dua linear homogen dengan koefisien konstan
Dengan metode beda hingga dari persamaan (25) diperoleh sistem persamaan linear dengan A1=[-2.5 1.25 0; 0.75 -2.5 1.25; 0 0.75 -2.5] A1 = -2.5000 1.2500 0 0.7500 -2.5000 1.2500 0 0.7500 -2.5000 B1=[-0.9; 0; 0]
32 B1 = -0.900 0 0 Y1=inv(A1)*B1 Y1 = 0.3643 0.1286 0.0386 dengan A3=[-2.08 1.1 0 0 0 0 0 0 0; 0.9 -2.08 1.1 0 0 0 0 0 0; 0 0.9 2.08 1.1 0 0 0 0 0; 0 0 0.9 2.08 1.1 0 0 0 0; 0 0 0 0.9 -2.08 1.1 0 0 0; 0 0 0 0 0.9 --2.08 1.1 0 0; 0 0 0 0 0 0.9 --2.08 1.1 0; 0 0 0 0 0 0 0.9 -2.08 1.1; 0 0 0 0 0 0 0 0.9 -2.08] A3 = -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 1.1000 0 0 0 0 0 0 0 0.9000 -2.0800 B3=[-0.75 0 0 0 0 0 0 0 0] B3 = -0.7500 0 0 0 0 0 0 0 0 B3=[-0.9; 0; 0; 0; 0; 0; 0; 0; 0] B3 = -0.9000 0 0 0
33 0 0 0 0 0 Y3=inv(A3)*B3 Y3 = 0.6689 0.4467 0.2974 0.1968 0.1289 0.0827 0.0509 0.0285 0.0123 dengan A2=[-2.02 1.05 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02 1.05; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.95 -2.02] A2 = Columns 1 through 9 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0
34 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 0 0 0 0 0 0 0 0 0.9500 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 10 through 18 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.0500 0 0 0 0 0 0 0 0 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0
35 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 1.0500 0 0 0 0 0 0 0 0.9500 -2.0200 0 0 0 0 0 0 0 0 0.9500 Column 19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.0500 -2.0200 B2=[-0.95; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0] B2 = -0.9500 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
36 0 Y2=inv(A2)*B2 Y2 = 0.8180 0.6689 0.5468 0.4467 0.3647 0.2974 0.2422 0.1969 0.1596 0.1289 0.1036 0.0827 0.0653 0.0509 0.0388 0.0286 0.0199 0.0124 0.0058