persamaan diferensial parsial dari persamaan linear dan kuasi orde pertama sampai materi persamaan Laplace

PERSAMAAN DIFERENSIAL PARSIAL ORDE PERTAMA PERSAMAAN DIFERENSIAL PARSIAL ORDE PERTAMA

BAB III BAB III

TEORI PERSAMAAN LINIER DAN KUASI LINIER ORDE PERTAMA TEORI PERSAMAAN LINIER DAN KUASI LINIER ORDE PERTAMA

Pada bab ini akan kita pelajari persamaan kuasi linier (dan linier) orde pertama. Teori dan

Pada bab ini akan kita pelajari persamaan kuasi linier (dan linier) orde pertama. Teori dan

metode dari solusi masalah nilai awal untuk persamaan tersebut didapatkan sebagai suatu

metode dari solusi masalah nilai awal untuk persamaan tersebut didapatkan sebagai suatu

aplikasi langsung dari teori dan metode dalam kontruksi integral kurva dan permukaan dari

aplikasi langsung dari teori dan metode dalam kontruksi integral kurva dan permukaan dari

medan vektor yang dijelaskan pada Bab II.

medan vektor yang dijelaskan pada Bab II.

Pada bagian 1, kita akan mendefinisikan apa yang dimaksud solusi dari persamaan orde

Pada bagian 1, kita akan mendefinisikan apa yang dimaksud solusi dari persamaan orde

pertama dan kita klasifikasi/kelompokan persamaan orde pertama berdasarkan kelinieritasannya.

pertama dan kita klasifikasi/kelompokan persamaan orde pertama berdasarkan kelinieritasannya.

Pada bagian 2, kita definisikan integral umum dari persamaan kuasi linier orde pertama dan

Pada bagian 2, kita definisikan integral umum dari persamaan kuasi linier orde pertama dan

metode untuk mendapatkannya. Integral umum adalah rumus yang sering menghasilkan solusi

metode untuk mendapatkannya. Integral umum adalah rumus yang sering menghasilkan solusi

dari persamaan. Pada bagian 3, kita akan mendeskripsikan masalah nilai awal untuk persamaan

dari persamaan. Pada bagian 3, kita akan mendeskripsikan masalah nilai awal untuk persamaan

kuasi linier orde pertama dan mendapatkan kondisi dimana terdapat solusi unik/tunggal untuk 

kuasi linier orde pertama dan mendapatkan kondisi dimana terdapat solusi unik/tunggal untuk 

masalah ini. Pada bagian 4, kita akan melihat bagaimana jika kondisi tidak dipenuhi yang

masalah ini. Pada bagian 4, kita akan melihat bagaimana jika kondisi tidak dipenuhi yang

kemudian biasanya tidak terdapat solusi untuk masalah ini, dan pada kasus khusus dimana

kemudian biasanya tidak terdapat solusi untuk masalah ini, dan pada kasus khusus dimana

terdapat solusi, terdapat tak terhingga solusi yang ada. Pada bagian 5, kita mengaplikasikan teori

terdapat solusi, terdapat tak terhingga solusi yang ada. Pada bagian 5, kita mengaplikasikan teori

umum untuk mempelajari hukum konservasi yang merupakan persamaan kuasi linier orde

umum untuk mempelajari hukum konservasi yang merupakan persamaan kuasi linier orde

pertama yang dibangkitkan pada berbagai bagian dari fisika. Solusi dari persamaan tersebut

pertama yang dibangkitkan pada berbagai bagian dari fisika. Solusi dari persamaan tersebut

biasanya mengembangkan diskontinuitas yang disebut shocks atau gelombang shock, yang

biasanya mengembangkan diskontinuitas yang disebut shocks atau gelombang shock, yang

diketahui sebagai fenomena pada gas dinamik. Dua contoh yang ada adalah pada arus lalu lintas

diketahui sebagai fenomena pada gas dinamik. Dua contoh yang ada adalah pada arus lalu lintas

dan gas dinamik, didiskusikan secara detail pada bagian 6. Terakhir, pada bagian 7, kita

dan gas dinamik, didiskusikan secara detail pada bagian 6. Terakhir, pada bagian 7, kita

perlihatkan aplikasi penting dari persamaan linier orde pertama untuk peluang, secara spesifik 

perlihatkan aplikasi penting dari persamaan linier orde pertama untuk peluang, secara spesifik 

untuk mempelajari proses stokastik. Kita diskusikan pada dua contoh yang detail, yaitu mengenai

untuk mempelajari proses stokastik. Kita diskusikan pada dua contoh yang detail, yaitu mengenai

masalah trunking sederhana pada jaringan telepon dan kontrol dari penyakit tropis. Berbagai

masalah trunking sederhana pada jaringan telepon dan kontrol dari penyakit tropis. Berbagai

contoh lain juga dideskripsikan dalam soal-soal pada bagian ini.

1.

1. Persamaan Diferensial Parsial Orde PertamaPersamaan Diferensial Parsial Orde Pertama

Sebuah persamaan diferensial parsial orde pertama dalam dua variabel independen x,y dan

Sebuah persamaan diferensial parsial orde pertama dalam dua variabel independen x,y dan

z yang tidak diketahui adalah persamaan yang dapat dibentuk dalam

z yang tidak diketahui adalah persamaan yang dapat dibentuk dalam

(1.1)

(1.1)

(

(







))

Fungsi

Fungsi













didefinisikan pada suatu domain di

didefinisikan pada suatu domain di





..





digunakan sebagai

digunakan sebagai

kordinat untuk titik-titik di

kordinat untuk titik-titik di





. Solusi persamaan (1.1) di domain

. Solusi persamaan (1.1) di domain



adalah sebuah fungsi

adalah sebuah fungsi





yang terdefinisi dan

yang terdefinisi dan





di

di



sehingga dua kondisi di bawah ini harus dipenuhi:

sehingga dua kondisi di bawah ini harus dipenuhi:

i.

i. Untuk setiap

Untuk setiap





titik 

titik 













terdapat pada domain di fungsi

terdapat pada domain di fungsi



..

ii.

ii. Ketika

Ketika





disubstitusikan ke persamaan (1.1) menghasilkan sebuah persamaan

disubstitusikan ke persamaan (1.1) menghasilkan sebuah persamaan

identitas di

identitas di



untuk setiap

untuk setiap



Persamaan diferensial parsial orde pertama dapat dikelompokan berdasarkan bentuk 

Persamaan diferensial parsial orde pertama dapat dikelompokan berdasarkan bentuk 

istimewa dari fungsi

istimewa dari fungsi



. Pengelompokan persamaan diferensial parsial adalah sebagai berikut:

. Pengelompokan persamaan diferensial parsial adalah sebagai berikut:

1.

1.

Persamaan kuasi linier

Persamaan kuasi linier

Bentuk persamaan kuasi linier adalah

Bentuk persamaan kuasi linier adalah

(1.2)

(1.2)

















Pada persamaan di atas, fungsi

Pada persamaan di atas, fungsi



adalah sebuah fungsi linier pada turunan

adalah sebuah fungsi linier pada turunan





dan

dan





dengan koefisien

dengan koefisien





bergantung pada variabel independen

bergantung pada variabel independen



seperti pada variable

seperti pada variable



yang tidak diketahui.

yang tidak diketahui.

2.

2.

Persamaan hampir linier

Persamaan hampir linier

Bentuk persamaan hampir linier adalah

Bentuk persamaan hampir linier adalah

(1.3)

(1.3)













Pada persamaan di atas, koefisien dari turunan

Pada persamaan di atas, koefisien dari turunan





dan

dan





adalah fungsi variabel independen

adalah fungsi variabel independen



..

3.

3.

Persamaan linier

Persamaan linier

Bentuk persamaan linier adalah

Bentuk persamaan linier adalah

(1.4)

(1.4)













Pada persamaan di atas, fungsi dari

Pada persamaan di atas, fungsi dari



adalah linier pada

adalah linier pada









dan

dan



dengan semua

dengan semua

koefisien hanya bergantung kepada variabel independen

koefisien hanya bergantung kepada variabel independen



dan y.

dan y.

Apabila suatau persamaan tidak memenuhi bentuk di atas maka persamaan disebut persamaan

Apabila suatau persamaan tidak memenuhi bentuk di atas maka persamaan disebut persamaan

non-linier.

Untuk lebih memahami ketiga bentuk pengelompokan yang telah dijelaskan, akan

Untuk lebih memahami ketiga bentuk pengelompokan yang telah dijelaskan, akan

disajikan beberapa contoh bentuk persamaan serta pengelompokan sebagai berikut:

disajikan beberapa contoh bentuk persamaan serta pengelompokan sebagai berikut:

1.

1.

Persamaan diferensial parsial berikut

Persamaan diferensial parsial berikut

(1.6)

(1.6)











memiliki koefisien

memiliki koefisien





berupa fungsi

berupa fungsi



yang

yang bergantung dengan

bergantung dengan variabel z.

variabel z. Persamaan

Persamaan

(1.6) merupakan persamaan kuasi linier.

(1.6) merupakan persamaan kuasi linier.

2.

2.

Persamaan diferensial parsial yang disebut

Persamaan diferensial parsial yang disebut

euler’s relation

euler’s relation

berikut

berikut

(1.7)

(1.7)











dapat kita tulis sebagai

dapat kita tulis sebagai













sehingga memiliki bentuk fungsi F yang linier

sehingga memiliki bentuk fungsi F yang linier

pada

pada









dan

dan



dengan koefisien-koefisien yang bergantung hanya pada variabel

dengan koefisien-koefisien yang bergantung hanya pada variabel



dan

dan



. Sehingga, persamaan (1.7) merupakan persamaan linier.

. Sehingga, persamaan (1.7) merupakan persamaan linier.

3.

3.

Persamaan diferensial parsial berikut

Persamaan diferensial parsial berikut

(1.8)

(1.8)









  



memiliki koefisien

memiliki koefisien





dan

dan





yang bergantung hanya pada variabel

yang bergantung hanya pada variabel



dan

dan



, serta fungsi di

, serta fungsi di

ruas kanan hanya bergantung pada variabel

ruas kanan hanya bergantung pada variabel



yaitu

yaitu





. Sehingga, persamaan (1.8)

. Sehingga, persamaan (1.8)

merupakan persamaan hampir linier.

merupakan persamaan hampir linier.

4.

4.

Persamaan diferensial parsial berikut

Persamaan diferensial parsial berikut

(1.9)

(1.9)











tidak memenuhi ketiga pengelompokan persamaan diferensial yang ada. Sehingga,

tidak memenuhi ketiga pengelompokan persamaan diferensial yang ada. Sehingga,

persamaan (1.9) merupakan persamaan non-linier.

persamaan (1.9) merupakan persamaan non-linier.

Pada bab ini, kita mempelajari persamaan diferensial parsial kuasi linier orde pertama.

Pada bab ini, kita mempelajari persamaan diferensial parsial kuasi linier orde pertama.

Ingat bahwa persamaan linier dan hampir linier adalah kasus khusus dari persamaan kuasi linier.

Ingat bahwa persamaan linier dan hampir linier adalah kasus khusus dari persamaan kuasi linier.

Soal

Soal

1.1

1.1 Misalkan

Misalkan

 f  f 

merupakan fungsi C

merupakan fungsi C

11

pada R

pada R

22

dan perhatikan bahwa untuk beberapa bilangan

dan perhatikan bahwa untuk beberapa bilangan

bulat n

bulat n





1,

1, f 

 f memenuhi kondisi

memenuhi kondisi

(1.12)

(1.12)

 

     







Untuk semua t

Untuk semua t



R

R

11

dan semua (x,y)

dan semua (x,y)



R

R

22

. Maka fungsi tersebut dikatakan homogen pada

. Maka fungsi tersebut dikatakan homogen pada

derajat n.

derajat n.

(a)

--

Contoh fungsi yang homogen pada derajat 1 adalah

Contoh fungsi yang homogen pada derajat 1 adalah

 f 

 f (x,y) = x+y(x,y) = x+y

karena

karena f 

 f 

(tx,ty)=tx+ty= t(x+y)=t

(tx,ty)=tx+ty= t(x+y)=t

11 f  f 

(x,y)

(x,y)

--

Contoh fungsi yang homogen pada derajat 2 adalah

Contoh fungsi yang homogen pada derajat 2 adalah

 f 

 f (x,y)=x(x,y)=x22+y+y22

karena

karena f 

 f 

(tx,ty)=(tx)

(tx,ty)=(tx)

22

+(ty)

+(ty)

22

=t

=t

22

x

x

22

+t

+t

22

y

y

22

=t

=t

22

(x

(x

22

+y

+y

22

)=t

)=t

22 f  f 

(x,y)

(x,y)

--

Contoh fungsi yang homogen pada derajat 3 adalah

Contoh fungsi yang homogen pada derajat 3 adalah

 f 

 f (x,y)=x(x,y)=x33+y+y33

karena

karena f 

 f 

(tx,ty)=(tx)

(tx,ty)=(tx)

33

+(ty)

+(ty)

33

=t

=t

33

x

x

33

+t

+t

33

y

y

33

=t

=t

33

(x

(x

33

+y

+y

33

)=t

)=t

33 f  f 

(x,y)

(x,y)

(b)

(b) Buktikan bahwa jika f homogen pada derajat n maka z=f(x,y) memenuhi persamaan

Buktikan bahwa jika f homogen pada derajat n maka z=f(x,y) memenuhi persamaan

diferensial parsial (1.7) [Petunjuk : Turunkan (1.12) terhadap t dan substitusi t=1.]

diferensial parsial (1.7) [Petunjuk : Turunkan (1.12) terhadap t dan substitusi t=1.]

f homogen pada derajat n artinya f(tx,ty)=t

f homogen pada derajat n artinya f(tx,ty)=t

nn f  f 

(x,y), misalkan

(x,y), misalkan f 

 f 

(x,y)=z maka

(x,y)=z maka f 

 f 

(tx,ty)=t

(tx,ty)=t

nn

zz

apabila masing-masing ruas diturunkan terhadap t akan didapat

apabila masing-masing ruas diturunkan terhadap t akan didapat

 

 

_{ }



   

 

 





apabila disubstitusi t=1 maka akan didapat

apabila disubstitusi t=1 maka akan didapat

  

_{ }

1.2

2.

2. Integral Umum dari Persamaan Kuasi LinierIntegral Umum dari Persamaan Kuasi Linier

Pada persamaan kuasi linier berikut

Pada persamaan kuasi linier berikut

(2.1)

(2.1)

















diasumsikan bahwa fungsi

diasumsikan bahwa fungsi





terdefinisi dan

terdefinisi dan





pada suatu domain

pada suatu domain







dari

dari





dan tidak 

dan tidak 

terhubung secara simultan pada beberapa titik dalam domain. Suatu solusi dari persamaan (2.1)

terhubung secara simultan pada beberapa titik dalam domain. Suatu solusi dari persamaan (2.1)

pada domain

pada domain





dari

dari





adalah fungsi

adalah fungsi





yang terdefinisi dan

yang terdefinisi dan





terdapat pada

terdapat pada





sehingga dua kondisi berikut terpenuhi:

sehingga dua kondisi berikut terpenuhi:

(i)

(i) Untuk setiap

Untuk setiap

 

 





, titik 

, titik 





termasuk domain

termasuk domain







dari fungsi

dari fungsi

P, Q, RP, Q, R..

(ii)

(ii) Saat

Saat z=f(x,y)

 z=f(x,y)

disubstitusikan pada (2.1), hasilnya merupakan identitas pada

disubstitusikan pada (2.1), hasilnya merupakan identitas pada



untuk semua

untuk semua

  





..

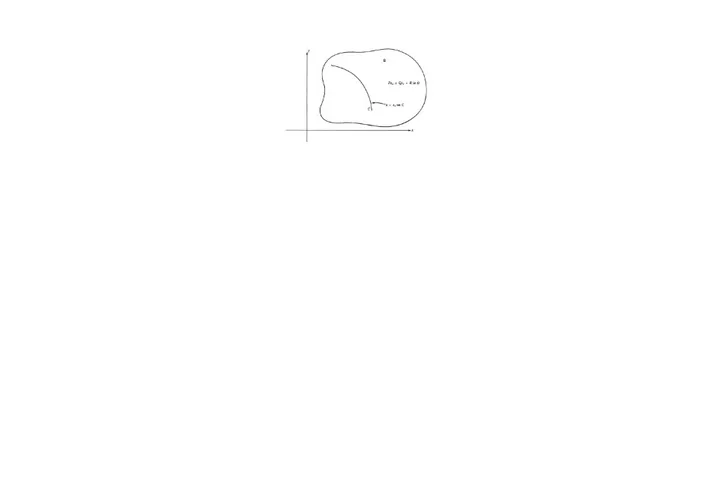
Suatu solusi

Suatu solusi

(2.2)

(2.2)

   

   

 

 

dari persamaan (2.1) dapat dilihat sebagai suatu permukaan dari

dari persamaan (2.1) dapat dilihat sebagai suatu permukaan dari





, yang disebut solusi

, yang disebut solusi

permukaan dari persamaan (2.1). Vektor normal permukaan (2.2) dapat dihitung dengan

permukaan dari persamaan (2.1). Vektor normal permukaan (2.2) dapat dihitung dengan

menggunakan gradien dari fungsi (2.2) pada titik 

menggunakan gradien dari fungsi (2.2) pada titik 





yang hasilnya adalah

yang hasilnya adalah

((



 



)

)





 





. Apabila vektor normal

. Apabila vektor normal





 





dikalikan dengan

dikalikan dengan





hasilnya akan

hasilnya akan

sama dengan nol, sehingga vektor

sama dengan nol, sehingga vektor



ortogonal/ tegak lurus dengan vektor normal

ortogonal/ tegak lurus dengan vektor normal

((



 



)

)

di

di

setiap titik pada persamaan (2.2). Jadi, suatu permukaan S disebut suatu solusi permukaan dari

setiap titik pada persamaan (2.2). Jadi, suatu permukaan S disebut suatu solusi permukaan dari

persamaan (2.1) jika S dapat dinyatakan sebagai persamaan (2.2) dan jika pada setiap titik dari S,

persamaan (2.1) jika S dapat dinyatakan sebagai persamaan (2.2) dan jika pada setiap titik dari S,

vektor

vektor





adalah tangen/ vektor singgung dari S.

adalah tangen/ vektor singgung dari S.

Suatu solusi permukaan dari persamaan (2.1) adalah integral permukaan dari medan vektor

Suatu solusi permukaan dari persamaan (2.1) adalah integral permukaan dari medan vektor





yang dapat dinyatakan sebagai persamaan (2.2). Ini menyatakan bahwa untuk 

yang dapat dinyatakan sebagai persamaan (2.2). Ini menyatakan bahwa untuk 

mencari suatu solusi permukaan dari persamaan (2.1) perlu dicari integral permukaan

mencari suatu solusi permukaan dari persamaan (2.1) perlu dicari integral permukaan



terlebih

terlebih

dahulu atau solusi permukaan dari persamaan diferensial parsial

dahulu atau solusi permukaan dari persamaan diferensial parsial

(2.3)

(2.3)





  



  



  

yang dapat dinyatakan sebagai persamaan (2.2).

yang dapat dinyatakan sebagai persamaan (2.2).

Solusi permukaan dari (2.3) merupakan permukaan ketinggian, yaitu

Solusi permukaan dari (2.3) merupakan permukaan ketinggian, yaitu

(2.4)

dari suatu solusi

dari suatu solusi





dari (2.3). Jika persamaan (2.4) dapat diselesaikan untuk 

dari (2.3). Jika persamaan (2.4) dapat diselesaikan untuk 



dalam

dalam

bentuk 

bentuk 



dan

dan



, maka hasil dari fungsinya adalah solusi dari persamaan (2.1). Sehingga

, maka hasil dari fungsinya adalah solusi dari persamaan (2.1). Sehingga

didapatkan Lemma berikut ini:

didapatkan Lemma berikut ini:

Bukti :

Bukti :

Dari teorema fungsi implisit, didapatkan

Dari teorema fungsi implisit, didapatkan











_











_

dan karena itu, didapat

dan karena itu, didapat

















_







_





Lemma 2.1 memperlihatkan bagaimana mendapatkan solusi persamaan (2.1) dari solusi

Lemma 2.1 memperlihatkan bagaimana mendapatkan solusi persamaan (2.1) dari solusi

persamaan (2.3). Karena kita telah mengetahui solusi umum dari persamaan (2.3), Lemma 2.1

persamaan (2.3). Karena kita telah mengetahui solusi umum dari persamaan (2.3), Lemma 2.1

menghasilkan kelas yang lebih besar dari solusi persamaan (2.1).

menghasilkan kelas yang lebih besar dari solusi persamaan (2.1).

Definisi 2.1 Definisi 2.1

Persamaan (2.5) disebut

Persamaan (2.5) disebut

integral umumintegral umum

dari persamaan (2.1) pada

dari persamaan (2.1) pada







Teorema 2.1

Teorema 2.1

Misalkan

Misalkan





dan

dan





adalah dua solusi yang bebas fungsional dari persamaan

adalah dua solusi yang bebas fungsional dari persamaan

(2.3) pada domain

(2.3) pada domain



pada R

pada R

33

. Misalkan

. Misalkan











merupakan suatu fungsi C

merupakan suatu fungsi C

11

dari dua variabel dan perhatikan permukaan ketinggian

dari dua variabel dan perhatikan permukaan ketinggian

(2.5)

(2.5)















Maka, setiap bagian dari permukaan ini memiliki vektor normal dengan

Maka, setiap bagian dari permukaan ini memiliki vektor normal dengan

komponen tak nol z, persamaan (2.5) mendefinisikan z secara implisit sebagai

komponen tak nol z, persamaan (2.5) mendefinisikan z secara implisit sebagai

suatu fungsi dari x dan y dan fungsi ini adalah suatu solusi dari persamaan

suatu fungsi dari x dan y dan fungsi ini adalah suatu solusi dari persamaan

(2.1)

(2.1)

Lemma 2.1 Lemma 2.1

Misalkan

Misalkan



ada pada

ada pada





̃̃

dan perhatikan bahwa setiap titik pada ketinggian

dan perhatikan bahwa setiap titik pada ketinggian

permukaan (2.4) memenuhi dua kondisi berikut :

permukaan (2.4) memenuhi dua kondisi berikut :

(i)

(i)





  



  



  

(ii)

(ii)





 

 



kemudian persamaan (2.4) menyebabkan definisi

kemudian persamaan (2.4) menyebabkan definisi



sebagai fungsi dari

sebagai fungsi dari



dan

dan



dan fungsi ini memenuhi persamaan diferensial parsial (2.1)

dan fungsi ini memenuhi persamaan diferensial parsial (2.1)

Telah diketahui bahwa tidak setiap solusi dari persamaan (2.1) dapat dihasilkan dari

Telah diketahui bahwa tidak setiap solusi dari persamaan (2.1) dapat dihasilkan dari

integral umum (2.5) seperti yang dijelaskan pada Teorema (2.1). Oleh karena itu, persamaan

integral umum (2.5) seperti yang dijelaskan pada Teorema (2.1). Oleh karena itu, persamaan

(2.5) tidak bisa disebut solusi umum dari persamaan (2.1).

(2.5) tidak bisa disebut solusi umum dari persamaan (2.1).

Pada penggunaannya fungsi

Pada penggunaannya fungsi





dan

dan





yang

yang dihasilkan

dihasilkan dari integral

dari integral umum

umum (2.5) diperoleh

(2.5) diperoleh

dari penyelesaian yang berhubungan dengan sistem persamaan

dari penyelesaian yang berhubungan dengan sistem persamaan

(2.6)

(2.6)



seperti yang sudah dijelaskan pada BAB 2 bagian 2.

seperti yang sudah dijelaskan pada BAB 2 bagian 2.

Untuk lebih memahami materi di atas, perhatikan beberapa contoh berikut:

Untuk lebih memahami materi di atas, perhatikan beberapa contoh berikut:

Contoh 2.1

Contoh 2.1

Carilah integral umum dari

Carilah integral umum dari

(2.7)

(2.7)





  



  

Sistem yang berhubungan dengan persamaan di atas adalah

Sistem yang berhubungan dengan persamaan di atas adalah



Dan dapat diambil

Dan dapat diambil

















. Integral umumnya adalah

. Integral umumnya adalah

(2.8)

(2.8)

  

dimana

dimana



adalah sembarang

adalah sembarang fungsi

fungsi 2

2 variabel pada

variabel pada





. Jika dipilih

. Jika dipilih









    



– – 



, (2.8)

, (2.8)

menjadi

menjadi



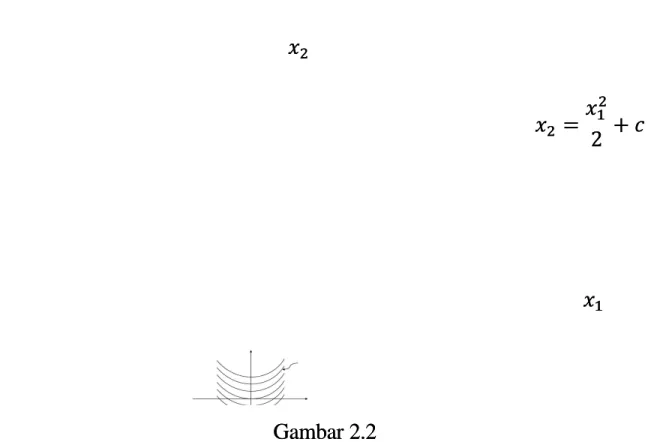
Selesaikan

Selesaikan



sehingga didapatkan

sehingga didapatkan



yang jelas merupakan solusi dari (2.7) pada

yang jelas merupakan solusi dari (2.7) pada





. Jika

. Jika

dipilih

dipilih









    



– – 



,,

akan didapatkan solusi

akan didapatkan solusi









yang terdefinisi pada domain

yang terdefinisi pada domain



atau

atau



. Jika dipilih

. Jika dipilih









    



– – 



maka persamaan (2.8) menjadi

maka persamaan (2.8) menjadi











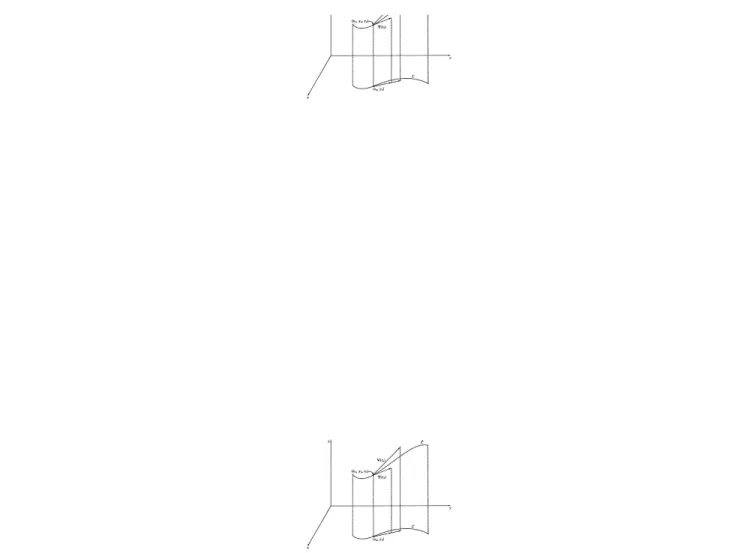
Bagian dari permukaan dengan

Bagian dari permukaan dengan



mendefinisikan z sebagai fungsi dari x dan y,

mendefinisikan z sebagai fungsi dari x dan y,

  

Ini adalah solusi dari (2.7) pada salah satu domain

Perlu diperhatikan bahwa jika salah satu dari integral pertama yang bebas linier secara

Perlu diperhatikan bahwa jika salah satu dari integral pertama yang bebas linier secara

fungsional, misalkan

fungsional, misalkan





, tidak bergantung pada z, maka secara umum, integral umum (2.5) dapat

, tidak bergantung pada z, maka secara umum, integral umum (2.5) dapat

ditulis dalam bentuk 

ditulis dalam bentuk 

(2.9)

(2.9)















Dimana

Dimana



adalah sembarang fungsi 1 variabel pada

adalah sembarang fungsi 1 variabel pada





..

Contoh 2.2

Contoh 2.2

Perhatikan persamaan linier berikut:

Perhatikan persamaan linier berikut:

(2.10)

(2.10)







  



  

Dimana

Dimana



dan

dan



adalah fungsi dari

adalah fungsi dari





dan tidak kosong secara silmultan. Integral umum dari

dan tidak kosong secara silmultan. Integral umum dari

(2.10) adalah sebagai berikut

(2.10) adalah sebagai berikut

(2.11)

(2.11)





Dimana

Dimana



adalah sembarang fungsi 1 variabel pada

adalah sembarang fungsi 1 variabel pada





dan

dan



adalah solusi umum dari

adalah solusi umum dari

persamaan diferensial biasa

persamaan diferensial biasa



 



Tentunya, sistem dari persamaan difernsial biasa yang berhubungan dengan (2.10) adalah

Tentunya, sistem dari persamaan difernsial biasa yang berhubungan dengan (2.10) adalah



 



Dan dua integral pertama yang bebas linier secara fungsional dari sistem ini adalah fungsi

Dan dua integral pertama yang bebas linier secara fungsional dari sistem ini adalah fungsi



Soal Soal

2.1.

2.1. Untuk setiap persamaan berikut tentukan integral umum dan cari tiga solusi yang berbeda.

Untuk setiap persamaan berikut tentukan integral umum dan cari tiga solusi yang berbeda.

Jelaskan pada domain bidang (x,y) yang mana solusi tersebut terdefinisi?

Jelaskan pada domain bidang (x,y) yang mana solusi tersebut terdefinisi?

(a)

(a)









  







  

(b)

(b)





  



  

Jawaban:

Jawaban:

Dari persamaan di atas, nilai

Dari persamaan di atas, nilai

  

..

Untuk mencari

Untuk mencari









,dan

,dan







, selesaikan sistem persamaan berikut:

, selesaikan sistem persamaan berikut:



1.

1. Pilih persamaan

Pilih persamaan









    

    ∫∫  ∫∫  







_







_









Pilih

Pilih





















,

, periksa

periksa apakah

apakah





















merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat











  





Substitusi pada

Substitusi pada



















dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_



_









Jadi,

2.

2. Pilih persamaan

Pilih persamaan

















_{}

_{ }

  ∫

  ∫



_{ ∫∫}

_{}

∫

∫



∫

∫







































Pilih

Pilih









,

, periksa

periksa apakah

apakah









merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat











_







Substitusi pada

Substitusi pada



















dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_



_















Jadi,

Jadi,









,

, merupakan

merupakan solusi.

solusi.

3.

3. Pilih persamaan

Pilih persamaan















  

  ∫∫

_{ ∫∫}

∫∫

_{ ∫∫}

∫∫



∫

∫



































(())







Pilih

Pilih







,

, periksa

periksa apakah

apakah







merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat

















Substitusi pada

Substitusi pada

























dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_



_













Jadi,

Jadi,







,

, merupakan

merupakan solusi.

solusi.

Untuk membuat suatu integral umum, gunakan 2 buah solusi dari 3 solusi yang

Untuk membuat suatu integral umum, gunakan 2 buah solusi dari 3 solusi yang

tersedia, misalkan diambil

tersedia, misalkan diambil





dan

dan





. Lakukan pengecekan terlebih dahulu apakah

. Lakukan pengecekan terlebih dahulu apakah





dan

dan





bebas secara fungsional atau tidak. Cara melakukan pengecekan bebas secara

bebas secara fungsional atau tidak. Cara melakukan pengecekan bebas secara

fungsional adalah dengan menghitung

fungsional adalah dengan menghitung

 

 



  

  



, bila hasilnya bukan nol,

, bila hasilnya bukan nol,

maka

maka





dan

dan





bebas secara fungsional.

bebas secara fungsional.

 

 



  

  







_

 

  



_

 







 

 







  

_{  }

 











Nilainya

Nilainya



. Jadi,

. Jadi,





dan

dan





bebas secara fungsional.

bebas secara fungsional.

Karena

Karena





dan

dan





bebas secara fungsional, kita dapat membentuk suatu integral umum

bebas secara fungsional, kita dapat membentuk suatu integral umum

dari

dari





dan

dan





. Integral umumnya adalah

. Integral umumnya adalah





dengan

dengan



merupakan fungsi

merupakan fungsi





dari dua variabel. Jika diambil

dari dua variabel. Jika diambil

















maka

maka









_{ }







_{ }

















_





































_{}











_{}









sehingga didapatkan

sehingga didapatkan



((





))





yang merupakan solusi dari

yang merupakan solusi dari





  



  

di

di

seluruh

seluruh





..

(c)

(c)









  







 

 

(d)

(d)





  



Jawaban:

Jawaban:

Dari persamaan di atas, nilai

Dari persamaan di atas, nilai

  



..

Untuk mencari

Untuk mencari









,dan

,dan







, selesaikan sistem persamaan berikut:

, selesaikan sistem persamaan berikut:





1.

1. Pilih persamaan

Pilih persamaan













  

  ∫

∫



















Pilih

Pilih







, periksa apakah

, periksa apakah







merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat



















Substitusi pada

Substitusi pada

























dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_



_



_













Jadi,

Jadi,







,

, merupakan

merupakan solusi.

solusi.

2.

2.

Pilih persamaan

Pilih persamaan





















  

  ∫

∫



∫

∫







_





_









Pilih

Pilih











,

, periksa

periksa apakah

apakah











merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat





















Substitusi pada

Substitusi pada

























dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_



_



_























Jadi,

Jadi,











,

, merupakan

merupakan solusi.

solusi.

3.

3.

Pilih persamaan

Pilih persamaan

















_

_









  

  ∫

∫



∫

∫







_



_







Pilih

Pilih











periksa apakah

periksa apakah











merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat























Substitusi pada

Substitusi pada

























dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_



_



_















Jadi,

Jadi,











merupakan solusi.

merupakan solusi.

Untuk membuat suatu integral umum, gunakan 2 buah solusi dari 3 solusi yang

Untuk membuat suatu integral umum, gunakan 2 buah solusi dari 3 solusi yang

tersedia, misalkan diambil

tersedia, misalkan diambil





dan

dan





. Lakukan pengecekan terlebih dahulu apakah

. Lakukan pengecekan terlebih dahulu apakah





dan

dan





bebas secara fungsional atau tidak. Cara melakukan pengecekan bebas secara

bebas secara fungsional atau tidak. Cara melakukan pengecekan bebas secara

fungsional adalah dengan menghitung

fungsional adalah dengan menghitung

 

 



  

  



, bila hasilnya bukan nol,

, bila hasilnya bukan nol,

maka

maka





dan

dan





bebas secara fungsional.

bebas secara fungsional.

 

 



  

  







_

 

  



_

 







 

 







  

 





 













Nilainya

Nilainya



. Jadi,

. Jadi,





dan

dan





bebas secara fungsional.

bebas secara fungsional.

Karena

Karena





dan

dan





bebas secara fungsional, kita dapat membentuk suatu integral umum

bebas secara fungsional, kita dapat membentuk suatu integral umum

dari

dari





dan

dan





. Integral umumnya adalah

. Integral umumnya adalah













dengan

dengan



merupakan fungsi

merupakan fungsi





dari dua variabel. Jika diambil

dari dua variabel. Jika diambil

















maka

maka

















































sehingga didapatkan

sehingga didapatkan











yang merupakan solusi dari

yang merupakan solusi dari









di seluruh

di seluruh





..

(e)

(e)







  



 

 

Jawaban:

Jawaban:

Dari persamaan di atas, nilai

Dari persamaan di atas, nilai

   

..

Untuk mencari

 

 



1.

1. Pilih persamaan

Pilih persamaan

























_{}

_{ }

  

  ∫∫



_{}

_{ ∫∫}







































Pilih

Pilih









, periksa apakah

, periksa apakah









merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat











_







Substitusi pada

Substitusi pada

























dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_





_

















_



Jadi,

2.

2.

Pilih persamaan

Pilih persamaan















 





_{  }





  

  ∫∫∫

∫









_







_







































Pilih

Pilih















,

, periksa

periksa apakah

apakah















merupakan solusi?

merupakan solusi?

Turunkan terhadap

Turunkan terhadap





sehingga didapat

sehingga didapat









  







Substitusi pada

Substitusi pada

























dan periksa apakah bernilai nol atau tidak?

dan periksa apakah bernilai nol atau tidak?

(Bila bernilai nol, maka

(Bila bernilai nol, maka





adalah solusi.)

adalah solusi.)



_{ }



_{ }



_{ }



_



_





_

(()(

)()

)







Jadi,

Jadi,















,

, merupakan

merupakan solusi.

solusi.

3.

3.

Pilih persamaan

Pilih persamaan



















 



_{  }



