Penyelesaian sistem persamaan diferensial linear dengan tranformasi laplace - USD Repository

i

PENYELESAIAN SISTEM PERSAMAAN DIFERENSIAL LINEAR

DENGAN TRANSFORMASI LAPLACE

SKRIPSI

Diajukan untuk memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh:

Hilaria Heparantiza

NIM: 083114002

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

THE SOLUTION OF LINEAR DIFFERENTIAL EQUATION SYSTEM

USING LAPLACE TRANSFORMATION

THESIS

Presented as Partial Fulfillment of the Requirements

To Obtain the SARJANA SAINS Degree

In Mathematics

By:

Hilaria Heparantiza

Student Number: 083114002

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT

SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

vi

Tuhan Yesus Kristus

Bapak dan Mama Tercinta atas Cinta, Kasih Sayang, Doa Serta

Dukungan secara Moril dan Materiil

Kakakku Angela Hadryana

Adikku Yeserika Lindani

Serta Segenap Keluarga

………....

Satu-satunya cara untuk melakukan pekerjaan besar adalah dengan mencintai apa yang Anda lakukan, walaupun sebenarnya anda membencinya.

Hidup ini seperti piano. Berwarna putih dan hitam. Namun, ketika Tuhan yang memainkannya, semuanya menjadi indah.

Sungguh, Allah itu keselamatanku; aku percaya dengan tidak gemetar, Sebab TUHAN ALLAH itu kekuatanku dan mazmurku,

Ia telah menjadi keselamatanku Yes (12:2)

viii ABSTRAK

Persamaan diferensial adalah suatu persamaan yang memuat derivatif atau dife-rensial dari satu atau lebih fungsi. Dalam menyelesaikan persamaan difedife-rensial biasanya terdapat syarat bantu yang disebut syarat awal. Persamaan diferensial dengan syarat awalnya disebut masalah nilai awal. Salah satu metode yang dapat digunakan untuk menyelesaikan masalah nilai awal adalah metode transformasi Laplace. Transformasi Laplace juga dapat digunakan digunakan untuk mencari penyelesaian dari suatu sistem persamaan diferensial dengan koefisien konstan. Metode penyelesaian dengan menggunakan transformasi Laplace adalah dengan mengubah persamaan diferensial dengan parameter t ke dalam persamaan aljabar dengan parameter s. Kemudian sistem tersebut diselesaikan dengan menggunakan eliminasi gauss dan menggunakan invers transformasi Laplace untuk menda-patkan penyelesaian khusus dari sistem persamaan diferensial tersebut.

ix ABSTRACT

The differential equation is an equation that contains the derivative or differential of one or more functions. In solving differential equation, usually there is an aux-iliary condition, called initial conditions. Differential equations with initial conditions are called initial value problem. One of the method that can be used to solve initial value problem in differential equation is Laplace transform method. Laplace transformation also can be used for solving systems of differential equations with constant coefficients. Using this method, the differential equations of the parameter t is change into algebraic equation of the parameter s. Then, the system is solved using Gauss elimination and inverse Laplace transform to obtain a special solution of the system of differential equations.

x

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus, Sang

Pe-nerang dan Juru Selamat, yang senantiasa mencurahkan kasih dan karunia-Nya

kepada penulis sehingga penulis dapat menyelesaikan skripsi ini dengan baik.

Selama penulisan skripsi ini penulis membutuhkan pertolongan dari berbagai

pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin

menyampai-kan ucapan terima kasih kepada:

1. Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing dan selaku

Kaprodi Matematika FST-USD yang dengan rendah hati dan dengan penuh

kesabaran membimbing penulis selama penyusunan skripsi.

2. P. H. Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas Sains dan Teknologi.

3. M.V. Any Herawati, S.Si., M.Si., selaku dosen penguji dan dosen

pembimbing akademik.

4. Dr. Marcellinus Andy Rudhito, S.Pd., M.Si., selaku dosen penguji.

5. C.H. Eny Murwaningtyas, S.Si., M.Si., yang pernah menjadi dosen

pembimbing akademik bagi penulis.

6. Bapak dan Ibu dosen Program Studi Matematika FST-USD yang telah

memberikan bekal ilmu yang sangat berguna bagi penulis.

7. Karyawan sekretariat FST-USD khususnya kepada Bapak Tukija dan Ibu

Linda, serta karyawan perpustakaan USD dan Mas Susilo selaku laboran atas

xi

8. Kedua orang tuaku, Bapak Herman dan Mama Yulianti serta kakakku Angela

Hadryana dan adikku Yeserika Lindani yang senantiasa memberikan

dukungan, kasih sayang, dan doa bagi penulis.

9. Dennis Tri Hassapta atas kasih sayang, perhatian dan dukungan yang selalu

diberikan kepada penulis.

10. Teman-teman Matematika angkatan 2008: Yudit, Nopi, Amel, Marcel, Feny,

Etus, Moyo, Widi, serta kakak dan adik angkatan.

11. Teman-teman kos Aulia: Yudit, Nopi, Ao, Sende, Elvira, Wiwik, dan Tesa.

12. Sahabat seperjuangan: Yudit, Nopi, Amel, Pipot dan Marcel.

13. Teman-teman kos Nuvi: Kak Thea, Pipot dan Lita.

14. Teman-teman KKN XLII kelompok 35 Banaran atas semua pengalaman yang

sudah dilalui bersama.

15. Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu.

Penulis menyadari masih ada kekurangan dalam skripsi ini, untuk itu saran

serta kritik yang membangun sangat diharapkan dalam peningkatan kualitas

skripsi ini, dan akhirnya penulis berharap semoga skripsi ini bermanfaat bagi

semua pihak.

Yogyakarta, 31 Januari 2012

Penulis,

xii

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

PERYATAAN KEASLIAN KARYA ... v

HALAMAN PERSEMBAHAN ... vi

LEMBAR PERYATAAN PERSETUJUAN PUBLIKASI ... vii

ABSTRAK ... viii

ABSTRACT ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 3

C. Pembatasan Masalah ... 3

D. Tujuan Penulisan ... 3

E. Manfaat Penulisan ... 3

F. Metode Penulisan ... 4

xiii

BAB II MASALAH NILAI AWAL DAN SISTEM PERSAMAAN

DIFERENSIAL ... 6

A. Sistem Persamaan Linear ... 6

B. Limit, Fungsi Kontinu dan Fungsi Transenden ... 12

C. Deret Geometrik ... 21

D. Persamaan Diferensial dan Penyelesaiannya ... 25

E. Sistem Persamaan Diferensial ... 30

F. Integral Tentu, Integral Tak Wajar dan Integral Parsial ... 33

BAB III TRANSFORMASI LAPLACE ... 44

A. Transformasi Laplace ... 44

B. Sifat-sifat Transformasi Laplace ... 54

C. Fungsi Khusus Transformasi Laplace ... 63

D. Invers Transformasi Laplace dan Konvolusinya ... 70

BAB IV PENYELESAIAN SISTEM PERSAMAAN DIFERENSIAL LINEAR DENGAN TRANSFORMASI LAPLACE ... 80

A. Penyelesaian Persamaan Diferensial Linear dengan Transformasi Laplace ... 81

B. Penyelesaian Sistem Persamaan Diferensial Linear Orde Pertama dengan Transformasi Laplace ... 97

xiv

D. Penyelesaian Sistem Persamaan Diferensial Linear Orde ke-n

dengan Transformasi Laplace ... 118

BAB V PENUTUP ... 124

A. Kesimpulan ... 124

B. Saran ... 125

xv

DAFTAR TABEL

Halaman

BAB I

PENDAHULUAN

A. LATAR BELAKANG

Sistem merupakan sekumpulan elemen yang saling berkaitan dan saling

mempengaruhi dalam melakukan kegiatan bersama untuk mencapai suatu

tujuan. Sebuah sistem dikatakan linear jika hubungan antara suatu variabel

terhadap variabel lainnya dapat dinyatakan dalam bentuk persamaan linear.

Persamaan dalam sebuah sistem dapat berupa persamaan diferensial.

Persamaan diferensial adalah suatu persamaan yang memuat derivatif

atau diferensial dari satu atau lebih fungsi. Persamaan ini digunakan dalam

berbagai macam bidang. Tidak hanya dalam bidang matematika tetapi juga

dalam bidang ekonomi, fisika, biologi, astronomi, dan yang lainnya.

Persamaan diferensial diklasifikasikan dalam berbagai jenis. Sebuah

persamaan dikatakan persamaan diferensial biasa jika fungsi yang belum

di-ketahui dalam persamaan diferensial bergantung hanya pada satu variabel

be-bas. Sebuah persamaan dikatakan persamaan diferensial parsial jika fungsi

yang belum diketahui bergantung pada dua atau lebih variabel bebas.

Persamaan diferensial juga dapat dibedakan menurut orde atau tingkat. Orde

persamaan diferensial adalah tingkat derivatif tertinggi yang muncul dalam

Sebuah persamaan diferensial dikatakan linear jika dalam persamaaan

diferensial tersebut fungsi yang belum diketahui derivatif-derivatifnya secara

aljabar berderajat satu dan tidak ada hasil kali yang berkaitan dengan fungsi

yang belum diketahui dengan derivatif-derivatifnya. Selain itu, tidak ada

fungsi transendental dari fungsi yang belum diketahui beserta

derivatif-derivatifnya dan yang lainnya. Jika salah satu syarat tidak dipenuhi maka

persamaan tersebut dikatakan tidak linear.

Apabila koefisien-koefisien pada persamaan diferensial linear adalah

konstanta real maka persamaan disebut persamaan diferensial linear dengan

koefisien konstan. Dalam menyelesaikan persamaan diferensial terkadang

terdapat syarat bantu yang mengikutinya. Jika syarat bantu pada persamaan

diferensial yang diketahui berhubungan dengan sebuah nilai tertentu, syarat

itu disebut syarat awal. Persamaan diferensial dengan syarat awalnya disebut

masalah nilai awal.

Salah satu cara penyelesaian masalah nilai awal pada sistem persamaan

diferensial adalah dengan menggunakan metode transformasi Laplace. Metode

ini mentransformasikan masalah nilai awal pada sistem persamaan diferensial

ke dalam masalah aljabar dengan melibatkan suatu variabel. Setelah

ditransformasikan, dari persamaan tersebut ditentukan invers transformasi

Laplacenya untuk mencari penyelesaian dari masalah nilai awal tersebut.

B. RUMUSAN MASALAH

1. Apa yang dimaksud dengan transformasi Laplace dan bagaimana

sifatnya?

2. Bagaimana cara menyelesaikan masalah nilai awal pada persamaan

diferensial dengan menggunakan transformasi Laplace?

3. Bagaimana cara menyelesaikan masalah nilai awal pada sistem

persamaan diferensial dengan menggunakan transformasi Laplace?

C. PEMBATASAN MASALAH

Dalam penulisan karya ilmiah ini, penulis hanya akan membatasi pada

sistem persamaan diferensial hanya sistem persamaan diferensial dengan dua

variabel.

D. TUJUAN PENULISAN

Tujuan dari penulisan ini adalah untuk memahami sifat-sifat dari

transformasi Laplace dan mencari penyelesaian masalah nilai awal pada

sistem persamaan diferensial dengan menggunakan transformasi Laplace.

E. MANFAAT PENULISAN

Manfaat penulisan ini adalah memberikan pemahaman dalam

menyelesaikan masalah nilai awal pada persamaan diferensial dengan

F. METODE PENULISAN

Metode penulisan yang digunakan adalah metode studi pustaka, yaitu

dengan mempelajari buku-buku yang berkaitan dengan topik tansformasi

Laplace dan persamaan diferensial.

G. SISTEMATIKA PENULISAN

BAB I: PENDAHULUAN

Dalam bab I akan dibahas tentang latar belakang masalah,

perumusan masalah, pembatasan masalah, tujuan penulisan,

manfaat penulisan, metode penulisan, dan sistematika penulisan

BAB II: MASALAH NILAI AWAL DAN SISTEM PERSAMAAN

DIFERENSIAL

Dalam bab II akan dibahas tentang sistem persamaan linear, limit,

fungsi kontinu dan fungsi transenden, deret geometrik, persamaan

diferensial dan penyelesaiannya, sistem persamaan diferensial serta

integral tak wajar dan integral parsial.

BAB III: TRANSFORMASI LAPLACE

Dalam bab ini akan dibahas tentang transformasi Laplace,

sifat-sifat transformasi Laplace, fungsi khusus transformasi Laplace

BAB IV: PENYELESAIAN SISTEM PERSAMAAN DIFERENSIAL

LINEAR DENGAN TRANSFORMASI LAPLACE

Dalam bab ini akan dibahas tentang penyelesaian persamaan

diferensial linear dengan transformasi Laplace, penyelesaian sistem

persamaan diferensial linear orde pertama dengan transformasi

Laplace, penyelesaian sistem persamaan diferensial linear orde

kedua dengan transformasi Laplace dan penyelesaian sistem

persamaan diferensial linear orde ke-n dengan transformasi

Laplace.

BAB V: PENUTUP

BAB II

MASALAH NILAI AWAL DAN SISTEM PERSAMAAN DIFERENSIAL

Dalam bab ini akan dibahas mengenai materi-materi yang akan digunakan

dalam pembahasan bab-bab selanjutnya. Materi-materi tersebut antara lain adalah

sistem persamaan linear, limit, fungsi kontinu dan fungsi transenden, deret geometrik,

persamaan diferensial dan penyelesaiannya, sistem persamaan diferensial serta

integral tentu, integral tak wajar dan integral parsial.

A. Sistem Persamaan Linear

Persamaan linear dengan n variabel y₁,y₂,...,y_n dapat dinyatakan dalam

bentuk

b y a y

a y

a_{1 1} _{2 2} ... _{n n} 

di mana a₁,a₂,...,a_n dan b merupakan konstanta real. Suatu sistem dengan m

persamaan linear dan n variabel yang tidak diketahui dapat ditulis sebagai

m n mn m

m

n n

n n

b y a y

a y a

b y a y

a y a

b y a y

a y a

 

 

  

 

 

 

...

... ...

2 2 1 1

2 2

2 22 1 21

1 1

2 12 1 11

 



di mana y₁,y₂,...,y_n adalah variabel yang tidak diketahui. Bilangan aij

merupakan koefisien persamaan ke-i dari variabel ke-j dan bi menyatakan

konstanta di ruas kanan untuk persamaan ke-i. Koefisien tersebut dapat dituliskan

dalam bentuk matriks, yaitu

   

 

   

 

mn m

m

n n

a a

a

a a

a a

  



 

2 1

2 22

21

1 12

11

a a

yang disebut matriks koefisien. Jika suatu koefisien variabel tidak muncul,

maka pada matriks koefisien akan dituliskan sebagai bilangan nol.

Konstanta di ruas kanan dapat dituliskan dalam bentuk, yaitu

   

 

   

 

m

b b b



2 1

yang disebut matriks konstanta. Matriks yang terdiri dari matriks koefisien

dengan menambahkan matriks konstanta pada kolom terakhir disebut dengan

matriks lengkap. Dengan demikian matriks lengkap untuk sistem persamaan

   

 

   

 

m mn m

m

n n

b b b

a a

a

a a

a a

 

 



 

2 1

2 1

2 22

21

1 12

11

a

a

Definisi 2.1.1

Urutan sejumlah bilangan s₁,s₂,,s_n merupakan penyelesaian dari sistem

persamaan (2.1.1) jika y₁s₁,y₂ s₂,,y_n s_n merupakan penyelesaian dari setiap persamaan di dalam sistem tersebut.

Contoh 2.1.1

Sistem persamaan

4 9

3

1 3

4

3 2 1

3 2 1

   

   

y y y

y y y

(2.1.2)

memiliki penyelesaian y₁ 1,y₂ 2 dan y₃ 1 karena nilai-nilai tersebut memenuhi kedua persamaan (2.1.2).

Definisi 2.1.2

Sebuah matriks disebut matriks eselon baris jika memenuhi syarat-syarat

1. Jika sebuah baris tidak seluruhnya terdiri dari nol, maka bilangan taknol

pertama pada baris tersebut adalah 1. Bilangan ini disebut 1 utama.

2. Jika terdapat baris yang seluruhnya terdiri dari angka nol, maka baris

tersebut dikelompokkan di baris paling bawah matriks.

3. Jika terdapat dua baris berurutan yang tidak seluruhnya terdiri dari nol, maka

1 utama pada baris yang lebih rendah terdapat pada kolom yang lebih kanan

dari 1 utama pada baris yang lebih tinggi.

Contoh 2.1.2

Berikut adalah contoh matriks yang sudah dalam bentuk eselon baris

  

 

  



 

5 2 4 1 0 0

6 1 0

3 4 1

,

  

 

  

 

0 0 0

0 1 0

0 1 1

,

  

 

  

 



1 0 0 0

1 6 0 0 0

1 0 0

2 1 0

Definisi 2.1.3

Operasi Baris Elementer pada suatu matriks adalah salah satu operasi:

1. Menukar letak dari dua baris matriks tersebut.

2. Mengalikan suatu baris dengan konstanta tak nol.

3. Mengganti suatu baris dengan hasil penjumlahan baris tersebut dan kelipatan

Salah satu metode yang digunakan untuk meyelesaikan sistem persamaan

linear adalah metode eliminasi Gauss. Metode ini menghasilkan matriks sampai

pada bentuk eselon baris. Prosedur umum untuk metode eliminasi Gauss ini

adalah:

1. Menentukan matriks lengkap dari suatu sistem persamaan linear.

2. Mencari kolom paling kiri yang memuat unsur tak nol.

3. Jika elemen pertama kolom yang diperoleh pada langkah pertama sama

dengan nol maka baris pertama dari matriks ditukar dengan unsur pada kolom

tersebut yang taknol.

4. Setelah elemen pertama dari kolom diperoleh pada langkah pertama tak sama

dengan nol, maka elemen di bawahnya diubah menjadi nol dengan operasi

baris elementer.

Contoh 2.1.3

Selesaikan sistem persamaan linear berikut dengan menggunakan eleminasi

Gauss

. 0 5 6 3

1 3 4 2

9 2

3 2 1

3 2 1

3 2 1

  

  

  

y y y

y y y

Penyelesaian:

Matriks lengkap dari sistem persamaan linear di atas adalah

  

 

  

 

0 1 9 5 -6 3

3 -4 2

2 1 1

Kemudian matriks tersebut di ubah kedalam bentuk eselon baris menjadi

  

 

  

 



3 2 17

-9

1 0 0

2 7 1 0

2 1 1

Sistem yang bersesuaian dengan matriks adalah

3 2 17 2

7 9 2

3 3 2

3 2 1

   

  

y y y

y y y

atau

3 2

1 9 y 2y

y    (2.1.3)

3 2

2 7 2 17

y

y   (2.1.4)

. 3

3 

y (2.1.5)

Dengan mensubstitusikan nilai y3 ke persamaan (2.1.4) diperoleh y₂ 2 dan

dengan mensubstitusikan y2 ke persamaan (2.1.3) diperoleh y1 1. Jadi

B. Limit, Fungsi Kontinu dan Fungsi Transenden

1. Limit

Definisi 2.2.1

Pengertian yang tepat tentang limit mengatakan bahwa f

 

t L

c

t 

lim

berarti bahwa untuk tiap  0 yang diberikan, terdapat  0 yang

berpadanan sedemikian sehingga f

 

x L  asalkan bahwa



   x c

0 yakni

 

     



 x c f x L

0

Contoh 2.2.1

Buktikan bahwa lim



3 7



5.

4  

 t

t

Penyelesaian:

Andaikan  bilangan positif sebarang sedemikian sehingga







     



 4 3 7 5

0 t t









3 4

4 3

4 3

12 3 5

7 3

 

  

  

  

  

     

t t t t t

Andaikan diberikan  0. Jika dipilih , 3



  maka 0 t4 

mengimplikasikan



3t7



5  3t12  3



t4



3t4 3 

Jadi, terbukti bahwa lim



3 7



5.

4  

 t

t

Definisi 2.2.2

Misalkan f didefinisikan pada



c, 



untuk suatu bilangan c, dikatakan

bahwa

 

t L f

t 

lim

jika untuk setiap  0, _{terdapat bilangan} M sedemikian sehingga

 

 



M f t L

t

Contoh 2.2.2

Hitunglah nilai limit dari

4 3 5

2 3 2 lim

3 2 3

 

  

 _{t t}

t t

Penyelesaian:

Untuk menghitung nilai limit, pembilang dan penyebut dibagi dengan

pangkat tertinggi yang muncul yaitu t3, sehingga diperoleh

5 2

1 lim 4 1 lim 3 5 lim

1 lim 2 1 lim 3 2 lim

4 3 5

2 3 2 lim 4 3 5

2 3 2 lim

3 2

3 3

2 3

3 3 3 3

3 3 2

3 3



 

 



 

  

 

 

  

  

  

 

   



t t

t t

t t

t t

t t

t t t

t t t t t

t t

t

t t

t t t

2. Fungsi Kontinu

Definisi 2.2.3

Andaikan f terdefinisi pada suatu selang terbuka yang mengandung c, f

kontinu di c jika

 

t f

 

c f

c

x 

lim

Definisi di atas menyatakan bahwa f kontinu jika syarat-syarat berikut

dipenuhi:

i). f

 

t

c t

lim ada,

iii). f

 

t f

 

c

c

t 

lim .

Jika salah satu dari ketiga syarat tidak dipenuhi, maka f tak kontinu di c.

Contoh 2.2.3

Fungsi f yang didefinisikan

 

1 1

2

  

t t t f

tidak kontinu untuk t 1, karena lim

 

1 2

 

1 1

1 lim

1 2

1 _t t f

t

t

t     

 

 maka f

tidak kontinu di t1.

Definisi 2.2.4

Fungsi f kontinu kanan di a jika f

 

t f

 

a

a

tlim   dan kontinu kiri b jika

 

t f

 

b f

b

t 

lim .

Definisi 2.2.5

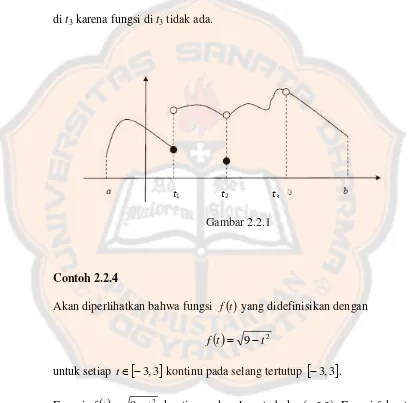
Pada Gambar 2.2.1, fungsi f kontinu pada (a,b) kecuali di titik-titik t1, t2, t3.

Fungsi f tak kontinu di t1 karena f

 

t

t t ₁

lim

 tidak ada, tidak kontinu di t2

karena nilai f

 

t

t t 2

lim

 tidak sama dengan nilai fungsi di t2, dan f tak kontinu

di t3 karena fungsi di t3 tidak ada.

Gambar 2.2.1

Contoh 2.2.4

Akan diperlihatkan bahwa fungsi f

 

t yang didefinisikan dengan

 

2

9 t t

f  

untuk setiap t



3,3



kontinu pada selang tertutup



3,3



.

Fungsi f

 

t  9t2 kontinu pada selang terbuka



3,3



. Fungsi f kontinu kanan di t 3 yaitu lim 0

3 

 

t

dan kontinu kiri di t3 yaitu lim 0

3 



t

. Ini

berarti fungsi f kontinu pada selang tertutup



3,3



.

Definisi 2.2.6

Fungsi f

 

t dikatakan kontinu bagian demi bagian pada interval tertutup

 

a,b jika f kontinu pada setiap titik dalam

 

a,b kecuali untuk sejumlah

berhingga titik-titik di mana f

 

t mempunyai ketakontinuan lompat. Fungsi

 

t

f _{dikatakan kontinu bagian demi bagian pada}

 

0, jika f _kontinu ba-gian demi baba-gian pada

 

0,N untuk setiap N 0.

Contoh 2.2.5

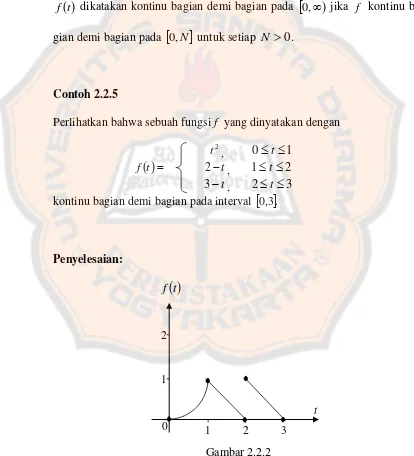
Perlihatkan bahwa sebuah fungsi f yang dinyatakan dengan

 

t 

f

2

t _, 0t 1

t 

2 _, 1t 2

t 

3 _, 2t 3 kontinu bagian demi bagian pada interval

 

0,3.

Penyelesaian:

Gambar 2.2.2

 

t f

t

0 _{1 2 3}

Gambar 2.2.2 tersebut memperlihatkan f

 

t kontinu pada interval

 

0,1,

 

1,2 dan

 

2,3 . Pada titik yang tidak kontinu yaitu untuk t 2, fungsi f

mempunyai ketakkontinuan lompat karena

 

0

lim

2





 f t

t

dan lim

 

1

2





 f t

t

.

Jadi fungsi f kontinu bagian demi bagian pada interval

 

0,3 _.

Contoh 2.2.6

Perlihatkan bahwa fungsi sebuah fungsi f yang dinyatakan dengan

 

t  t2 4t3

f

tidak kontinu bagian demi bagian.

Penyelesaian:

Grafik tersebut di atas memperlihatkan bahwa f(t) kontinu pada interval



,1



dan



3,



tetapi f(t) tidak kontinu pada interval

 

1 ,3 . Untuk

 

0

lim

1 

 f t

t tetapi untuk limt2 f

 

t tidak terdefinisi. Ini berarti bahwa fungsi

tersebut tidak kontinu bagian demi bagian.

3. Fungsi Transenden

Fungsi transenden merupakan fungsi yang tidak dapat dinyatakan sebagai

sejumlah berhingga operasi aljabar atas fungsi konstan y = k dan fungsi

y = x. Fungsi-fungsi transenden antara lain yaitu:

i). Fungsi Logaritma Natural

Contoh: ln y

ii). Fungsi Eksponensial

Contoh: ey,3e5y,dan y

eln .

iii). Fungsi Trigonometri

Contoh: sin y, cos y, dan tan y.

iv). Fungsi Siklometri

Contoh: arc sin y dan arc cos y.

v). Fungsi Hiperbolik

Definisi 2.2.7

Sebuah fungsi f dikatakan berorde eksponensial jika terdapat konstanta α

dan konstanta positif t₀ dan M sedemikian rupa sehingga

 

t M f

et  untuk setiap tt₀

di mana f

 

t terdefinisi.

Contoh 2.2.7

Jika diketahui f

 

t sinbt _maka

 

t e sinbt.

f

et  t

Untuk setiap  0

. 0 sin lim  



 e bt

t t



Ini berarti untuk setiap 0 ada M 0dan t₀ 0 sehingga

 

t e bt M f

et  tsin  untuk tt₀. Jadi f

 

t sinbt berorde eksponensial, dengan konstanta α sama dengan semua bilangan positif.

Contoh 2.2.8

Penyelesaian:

Diketahui bahwa f

 

t et2 maka

 

_{t t}2

t

e e t f

e   .

Untuk setiap  0

  _

 

  

 



 tt

t t t

t e e lime

lim 2 .

Ini berarti bahwa fungsi et2tidak berorde eksponensial karena et2membesar

lebih cepat daripada t

e untuk berapapun nilai α.

C. Deret Geometrik

Definisi 2.3.1

Deret tak berhingga





1 n

n

a konvergen dan mempunyai jumlah S jika

barisan jumlah-jumlah parsial

 

S_n konvergen menuju S atau S_n S

n 

lim . Jika

 

Sn divergen, maka deret tersebut divergen. Deret divergen tidak mempunyai

jumlah.

Contoh 2.3.1





Selidikilah apakah deret tak hingga di atas divergen atau konvergen.

Penyelesaian:

Diketahui bahwa





2

Kemudian an ditulis dalam bentuk pecahan parsial berikut





2

Maka pecahan parsial deret yang diberikan dapat ditulis menjadi









Oleh karena itu,



1



1.

Definisi 2.3.2

Deret berbentuk

... ... 1 3

2

1

1        



 



n

k n

ar ar

ar ar a ar

di mana a0disebut deret geometrik.

Contoh 2.3.2

Deret    

81 4 27

4 9 4 3 4

adalah deret geometrik dengan

3 4



a dan

3 1



r .

Teorema 2.3.1

Deret geometrik konvergen ke

r a S

 

1 jika r 1,dan divergen jika r 1.

Jumlahan parsial n suku pertama adalah





. 1 1

r r a S

n n

  

Bukti:

Deret jumlahan parsial suku pertama adalah:

n n

n n

ar ar

ar ar ar ar rS

ar ar

ar ar ar a S

 

   

     

 

... ...

5 4 3 2

1 4

maka

n r Sehingga diperoleh

D. Persamaan Diferensial dan Penyelesaiannya

Persamaan diferensial adalah suatu persamaan yang memuat derivatif atau

diferensial dari satu atau lebih fungsi. Persamaan diferensial diklasifikasikan

menjadi dua jenis, yaitu persamaan diferensial biasa dan persamaan diferensial

parsial. Jika fungsi yang belum diketahui dalam persamaan diferensial hanya

bergantung pada satu variabel bebas saja, maka persamaan tersebut dikatakan

persamaan diferensial biasa. Jika fungsi yang belum diketahui bergantung pada

dua atau lebih variabel bebas, maka persamaan tersebut dikatakan persamaan

diferensial parsial.

Definisi 2.4.1

Orde suatu persamaan diferensial adalah tingkat derivatif tertinggi yang muncul

dalam persamaan.

Bentuk umum dari persamaan diferensial biasa tingkat ke-n adalah

0 ,...,

, ,

, ₂

2

    

 

n n

dt y d dt

y d dt dy y t F

Bila

dt dy y ,

2 2

dt y d

y , ...,   _n

n n

dt y d

y  maka persamaan di atas dapat ditulis

menjadi

 



t,y,y',y'',...,yn



0

F

Contoh 2.4.1

3 '

''

3 3y y x

y    merupakan persamaan diferensial orde kedua karena pada

persamaan ini tingkat derivatif tertinggi yang muncul adalah dua dan

    x

xe y x y x

y4  2 3  3  _{adalah persamaan diferensial orde keempat.}

Definisi 2.4.2

Sebuah persamaan diferensial biasa orde ke-n dikatakan linear, di mana y adalah

variabel tak bebas dan t adalah variabel bebas dapat ditulis dalam bentuk

 

 

₁ ... ₁

 

 

( )

1

1

0 a t y b t

dt dy t a dt

y d t a dt

y d t

a _{n n n}

n n

n

 

 

 _{ } (2.4.1)

di mana a₀,a₁,...,a_n dan b adalah fungsi-fungsi kontinu pada suatu interval yang

memuat y dan a₀

 

t 0 pada interval itu. Fungsi a_k

 

t disebut fungsi-fungsi

koefisien.

Definisi di atas menyatakan bahwa persamaan diferensial adalah linear jika

syarat-syarat berikut dipenuhi:

i). Fungsi yang belum diketahui dan derivatif-derivatifnya secara aljabar

berderajat satu.

ii). Tidak ada hasil kali yang berkaitan dengan fungsi yang belum diketahui

iii). Tidak ada fungsi transendental dari y dan derivatif-derivatifnya misalnya

y

sin dan y

e .

Jika salah satu syarat tersebut tidak dipenuhi maka persamaan diferensial

tersebut tidak linear atau nonlinear. Persamaan diferensial yang tidak linear

di-sebut persamaan diferensial non linear.

Contoh 2.4.2:

 

t y y

y 3 5 ''3 sin dan y''5y' 6y0 berturut-turut adalah contoh-contoh

persamaan diferensial linear, sedangkan yy'' 5y'6y0 adalah contoh

persamaan diferensial non linear.

Definisi 2.4.3

Jika b

 

t 0untuk setiap t, maka persamaan (2.4.1) menjadi

 

 

... ₁

 

 

0

1 1

1

0       



y t a dt dy t a dt

y d t a dt

y d t

a _{n n n}

n n

n

dan disebut persamaan diferensial linear homogen. Jika b

 

t 0untuk setiap t,

Contoh 2.4.3

Persamaan y3y0adalah persamaan diferensial homogen orde pertama, sedangkan y y2y e3t adalah persamaan diferensial tak homogen orde

kedua. Persamaan ini tak homogen karena b

 

t 0 pada ruas kanan.

Definisi 2.4.4

Jika syarat bantu pada persamaan diferensial yang diketahui berhubungan dengan

sebuah nilai t, syarat itu disebut syarat awal. Persamaan diferensial dengan syarat

awalnya disebut Masalah Nilai Awal (MNA).

Definisi 2.4.5

Masalah nilai awal dari persamaan diferensial orde ke-n dengan n syarat

awal dapat ditulis dalam bentuk

 

 

 

 

n

n

c t y c t y c t y c t

y       0 

1 3

0 2 0 1

0 , , ,...,

yang harus dipenuhi oleh penyelesaian persamaan diferensial dan

derivatif-derivatifnya pada titik awal t₀.

Contoh 2.4.4

 

0 2 ,

3

2  

 y t y dt

dy

adalah contoh masalah nilai awal pada persamaan

 

5 

 

sin 0,

 

1 0, 

 

1 7

t y t t x x

y adalah contoh masalah nilai awal

pada persamaan diferensial di mana titik awalnya adalah t 1.

Definisi 2.4.6

Masalah Nilai Awal untuk persamaan diferensial linear homogen orde ke-n

dengan koefisien konstan terdiri dari penyelesaian persamaan diferensial

0 ... ₁

1 1

1

0       



y a dt dy a dt

y d a dt

y d

a _{n n n}

n n

n

di mana a₀,a₁,...,a_n adalah konstanta dan a₀ 0 dengan syarat awalnya adalah

 

 

 

 

n

n

c t y c t y c t y c t

y       0 

1 3

0 2 0 1

0 , , ,...,

di mana c₁,c₂,...,c_n adalah konstanta.

Contoh 2.4.5

0 6

2 2

 

 y

dt dy dt

y d

dengan syarat y

 

0 6 dan y

 

0 2 adalah contoh masalah

nilai awal untuk persamaan diferensial linear homogen orde kedua.

Definisi 2.4.7

Masalah Nilai Awal untuk persamaan diferensial linear tak homogen orde

ke-n dengan koefisien konstan terdiri dari penyelesaian persamaan diferensial

 

t b y a dt dy a dt

y d a dt

y d

a _{n n n}

n n

n

  



 _{ 1}

1 1

1

di mana a₀,a₁,...,a_n adalah konstanta dan a₀ 0 dengan syarat awalnya adalah

 

 

 

 

n

n

c t y c t y c t y c t

y ₀  ₁,  ₀  ₂,  ₀  ₃,..., 1 ₀ 

di mana c₁,c₂,...,c_n adalah konstanta.

Contoh 2.4.6

t y

y5 sin dengan syarat awalnya y

 

0 0 dan y

 

0 1 adalah contoh masalah nilai awal untuk persamaan diferensial linear tak homogen karena

 

t t b sin .

E. Sistem Persamaan Diferensial

Sistem persamaan diferensial linear adalah persamaan yang melibatkan n

persamaan dengan m fungsi yang tidak diketahui. Sistem persamaan diferensial

linear dapat juga disebut dengan sistem linear. Bentuk umum sistem persamaan

diferensial linear orde pertama dengan dua persamaan dalam fungsi x dan y yang

tidak diketahui adalah

 

 

 

 

 

 

 

b

 

t x b

 

t y F

 

t

dt dy t b dt dx t b

t F y t a x t a dt dy t a dt dx t a

2 4

3 2

1

1 4

3 2

1

 

 

 

 

(2.5.1)

Penyelesaian di atas dinyatakan dalam pasangan terurut dari fungsi real



f,g



demikian sehingga x f

 

t , yg

 

t memenuhi kedua persamaan dari

Contoh 2.5.1

Sebuah sistem persamaan yang didefinisikan dengan

t

e y x dt dy dt

dx

t x dt dy dt dx

   

  

4 3 2

2 3

2 2

adalah sistem persamaan diferensial linear orde pertama dengan koefisien

konstan.

Sistem linear dari dua persamaan diferensial orde kedua dari dua fungsi

yang tidak diketahui x dan y ditulis dalam bentuk

 

 

 

 

 

 

 

 

 

 

 

b

 

t x b

 

t y F

 

t

dt dy t b dt dx t b dt

y d t b dt

x d t b

t F y t a x t a dt dy t a dt dx t a dt

y d t a dt

x d t a

2 6

5 4

3 2 2

2 2 2

1

1 6

5 4

3 2 2

2 2 2

1

 

 

 

 

 

 

(2.5.2)

Penyelesaian di atas dinyatakan dalam pasangan terurut dari fungsi real



f,g



demikian sehingga x f

 

t , yg

 

t memenuhi kedua persamaan dari

sistem (2.5.2) pada interval atb.

Contoh 2.5.2

0

adalah sistem persamaan diferensial linear orde kedua dengan koefisien konstan.

Secara umum sistem persamaan diferensial linear dengan n persamaan

diferensial orde pertama dan n fungsi yang tidak diketahui ditulis dalam bentuk

 

 

 

 

Persamaan diferensial orde ke-n adalah

 

 

₁ ... ₁

 

 

( )

dengan satu fungsi yang tak diketahui y. Didefinisikan

y

Dari persamaan (2.5.4)

dt

Dengan menggunakan persamaan (2.5.4) dan (2.5.5) maka persamaan

 

1 1

 

2 1

 

 

,

1 3 2

2 1

t F y t a y

t a y t a dt dy

y dt dy

y dt dy

y dt dy

n n

n n

n n

 

 

    

 



 (2.5.6)

yang merupakan kasus khusus dari sistem linear pada persamaan (2.5.3) dengan

n persamaan dan n fungsi yang tak diketahui. Jadi suatu persamaan diferensial

linear orde ke-n dari persamaan (2.5.1) dalam satu fungsi yang tidak diketahui

berhubungan erat dengan sistem linear dari n persamaan diferensial orde pertama

dalan n fungsi yang tidak diketahui.

F. Integral Tentu, Integral Tak Wajar dan Integral Parsial

1. Integral Tentu

Definisi 2.6.1

Jika f adalah suatu fungsi yang didefinisikan pada interval tertutup

 

a , . b

Misalkan P adalah partisi dari

 

a ,b dengan titik-titik partisi t0,t1,t2,,tn

dan P max

 

t_i . Integral tentu f dari a ke b adalah

 

 

i

n

i i b

a p

t t f dt

t

f 







 _

1 0

jika limitnya ada. Jika limitnya ada, maka f dikatakan terintegral pada

interval

 

a , . b

Teorema 2.6.1

Jika f kontinu pada seluruh selang

 

a , , maka b f terintegralkan pada

 

a , . b

Bukti:

Menurut Definisi 2.6.1, untuk membutikan Teorema 2.6.1 akan ditunjukan

bahwa untuk sebarang  0, terdapat  sedemikian sehingga

   

_

_

a b t

f t f

    

2



(2.6.2)

dengan t dan t adalah titik-titik dari

 

a , sedemikian sehingga b



    t

t . Pertimbangkan sebarang partisi



t0,t1,t2,,tn



sedemikian

sehingga semua subinterval mempunyai panjang kurang dari  . Pada

subinterval tertutup



ti1,ti



, misalkan mi dan Mi masing-masing

mengatakan batas bawah terbesar dan batas atas terkecil dari nilai f. Maka

dapat dibentuk















_{1 0}



₂



_{2 1}





₁



.

1

1 1

2 2 0 1 1

   

  

 

 

  

 

n n n

n n n

t t M t

t M t t M S

t t m t

t m t t m s

 

Pada interval



t_n1,t_n



, pilih titik t sedemikian sehingga f

 

t dekat ke M_i

dan t sedemikian sehingga f

 

t dekat ke m_i. Dengan demikian

persamaan (2.6.2) menjadi



b a



Dari persamaan (2.6.3) dapat diperoleh



1 1



1 0

 

  2



2 1



 







 1



Dari persamaan (2.6.4)





1 0

   

2 1





1



Teorema 2.6.2

Jika f kontinu bagian demi bagian pada interval tertutup

 

a , maka b f

Bukti:

Karena f kontinu bagian demi bagian, maka f kontinu pada

 

a , kecuali b

pada titik-titik

.

2

1 t t b

t

a   _n 

Berdasarkan Teorema 2.6.1, f terintegral pada selang



t₁,t₂



sedemikian

sehingga f

 

t dt

t

t

2

1



ada. Begitupun juga untuk f

 

t dt

t

t



3

2

, f

 

t dt

t

t

4

3



, ,

 

t dt f

t

n

t

t



_1

ada. Karena f terintegral pada setiap selang



ti,ti_1



di mana

n i1 ,2 , , dan

 

t dt f

 

t dt f

 

t dt f

 

t dt f

n

n

-n t

t t

t t

t t

t









   

1 3

2 2

1 1



maka f

 

t dt

n

t

t



1

ada. Jadi terbukti bahwa f terintegral pada

 

a , . b

2. Integral Tak Wajar

Dalam mendefinisikan integral tentu

 



b a

fungsi f dimisalkan terdefinisi pada interval tertutup

 

a,b . Namun bila

integral tersebut mempunyai batas tak berhingga maka integral tersebut

adalah integral tak wajar. Contoh untuk integral tak wajar tersebut adalah

dt e t



 

0

Definisi 2.6.2

Jika f kontinu untuk setiap t a, maka

 

t dt f

 

t dt f

b

a b a

lim











Bilamana limitnya ada dan nilainya berhingga, integral tak wajar tersebut

konvergen. Jika tidak, integral tak wajar tesebut divergen.

Contoh 2.6.1

Hitunglah



e tdt 



0

, jika ada

Penyelesaian:





_R R



R R

t R t

e dt e dt

e

0 0 0

lim lim

  

   



 



_





1 1 0

1 lim lim

1 lim

  

  

  

    

  

R R R

R R

e e

Jadi

1

0





 

dt e t

Contoh 2.6.2

Hitunglah







0 t 1

dt

, jika ada.

Penyelesaian:





 _

 

 R

R _t

dt t

dt

0

0 1

lim 1

 

 



2 1



lim

1 2 1 1 lim

1 lim

0 2 1 0

2 1

  

    

  

 



 

 

 



 



R t

dt t

R

R

R R

Karena lim



2 1





 R

R adalah tak berhingga maka







0 t 1

dt

divergen.

Teorema 2.6.2

Jika g dan h adalah fungsi real sedemikian sehingga 0g

   

t ht pada

.

  t

a Misalkan h

 

t dt

a





ada dan g terintegral pada setiap subinterval

tertutup berhingga dari at maka g

 

t dt

a





ada.

Bukti:

Misalkan untuk Aa

 



_

 

A

a

dt t g A

G

dan

 





 

.

A

a

dt t h A H

Karena 0g

   

t ht maka G

 

A H

 

A dan kedua fungsi tersebut

meningkat. Oleh karena itu, H

 

A cenderung ke limit L untuk A. Ini

 

A H

 

A L.

G  

Karena G

 

A meningkat dan terbatas ke atas L, maka G

 

A juga konvergen

ke suatu limit untuk A. Ini berarti g

 

t dt

a





ada.

Teorema 2.6.3

Misalkan fungsi real g terintegral pada setiap subinterval berhingga dari

  t

a dan g

 

t dt

0





ada maka g

 

t dt

0





ada.

Bukti:

Perhatikan bahwa

 

t



g

   

t g t



g

 

t

g    .

Maka

 

t dt



g

 

t g

 

t



dt g

 

t dt.

g

b

a b

a b

a







   (2.6.4)

   

t g t g

 

t g

 

t g

 

t

g    2

sehingga

   

t g t g

 

t

g 2

0  

Oleh karena itu

 

 



g t g t



dt g

 

t dt

b

a b

a

2 0



 



Karena g

 

t dt

b

a

2



ada untuk b, maka integral pertama pada ruas

kanan persamaan (2.6.4) juga ada untuk b. Jadi terbukti bahwa

 



b a

dt t

g ada untuk b.

3. Integral Parsial

Misalkan u

 

t u dan v

 

t v maka rumus diferensial hasil kali dua

fungsi adalah

   



u t v t



u

       

t vt u t v t dt

d _

 



atau

   



u

   

t vt



u

   

t vt dt

d t v t

Dengan mengintegralkan dua ruas pada persamaan di atas diperoleh

   

t v t dt u

   

t v t u

   

t vt dt

u





   

Karena dvv

 

t dt dan du u

 

t dt, persamaan di atas dapat ditulis dalam

bentuk

 

t d u

   

t vt v

 

t du

u v





 

Integral di atas adalah integral parsial tak tentu, rumus integral parsial

tentunya adalah

 

t dv u

   

t v t



v

 

t du u

b

a b a b

a





 

Contoh 2.6.3

Tentukanlah





1

0

dt e t t .

Penyelesaian:

Misalkan ut dan dvetdt. Maka u mejadi du dt dan vet.











 



1

1 1

1 0 1

0 1

0 1 0

1

0 1 0 1

0

2 1

1 0



 

 

 

 



 

    

 



 



  









e

e e

e te

e te

e te

dt e t

t t

t t

t t

t

Jadi 1

1

0

2 1 

 _{ }

BAB III

TRANSFORMASI LAPLACE

Pada bab ini akan dibahas suatu metode yang digunakan untuk

menyelesaikan persamaan diferensial dan sistem persamaan diferensial dengan

menggunakan transformasi Laplace. Sebelum dijelaskan bagaimana memperoleh

penyelesaian sistem persamaan diferensial dengan transformasi Laplace, maka

akan dibahas terlebih dahulu tentang transformasi Laplace dan sifat-sifatnya.

A. Transformasi Laplace

Transformasi Laplace adalah salah satu metode untuk menyelesaikan

persamaan diferensial linear baik homogen maupun tak homogen dengan

koe-fisien konstan. Transformasi Laplace sangat berguna dalam menyelesaikan

masalah nilai awal pada persamaan diferensial.

Andaikan f adalah fungsi yang bernilai real dari variabel t maka akan

ditransformasikan oleh Laplace ke dalam fungsi F dari variabel s yang

berni-lai real. Ketika diterapkan ke dalam masalah niberni-lai awal pada persamaan

dife-rensial dalam fungsi yang tidak diketahui dari t, masalah nilai awal tersebut

ditransformasikan ke dalam masalah aljabar dengan melibatkan variabel s.

Definisi 3.1.1:

Bila f(t) adalah fungsi yang terdefinisi pada interval [0,+∞). Maka

 

s

 

f

 

t e f

 

t dt

F



st

   

0

L _(3.1.1)

untuk setiap nilai s di mana integral tak wajar tersebut ada.

Contoh 3.1.1

Tentukan transformasi Laplace dari f

 

t 1 untuk t > 0.

Penyelesaian:

Fungsi f didefinisikan dengan

 

t 1

f , untuk t > 0

Maka

 

   



 

  

      

 

 



 



 

   







s s e

s e

dt e

dt e

sR

R

R st

R R

st R

st

1 lim

lim

1 lim

1 1

0 0

0 L

0 untuk 1

1 lim

> s s

s s e sR

R



   

 

 

 

 

Jadi

 

s

1 1 

Contoh 3.1.2

Penyelesaian:

Fungsi f didefinisikan dengan

Contoh 3.1.3

Jika f

 

t sin bt untuk t > 0, tentukan L



sinbt



.

Penyelesaian:

Fungsi f didefinisikan dengan f

 

t sin bt, untuk t > 0

Maka

 





dt bt e

bt s

F

st

sin sin

0





  L

Selanjutnya akan digunakan integral parsial kedua untuk

menyederhanakannya. Misalkan usinbtdan dvestdt. Sehingga u

menjadi du bcosbtdt _dan e st s

v1  . Dengan demikian











cos



untuk 0 lim

cos lim

0

cos 1

lim sin

1 lim

sin lim

sin

0 0

0 0

0

 

 

  

 

  

 

 









  

  

 

 

 

  

s dt

bt e

s b

dt bt e

s b

dt bt b e s bt

e s

dt bt e

bt

R st R

R st R

R

st R

R st

R R

st R

L

Karena masih memuat integral, akan digunakan integral parsial kedua.

Misalkan ucosbt _dan dvestdt. Sehingga dubsinbtdtdan

st

e s









Menurut Definisi 3.1.1, sin

0

sehingga









Teorema 3.1.1