BAB 3 RESPONS SINUSOIDAL PADA RANGKAIAN SERI RL DAN RC

BAB 3

RESPONS SINUSOIDAL PADA RANGKAIAN SERI RL DAN RC

3.1 Respons Sinusoidal Pada Rangkaian RL Seri

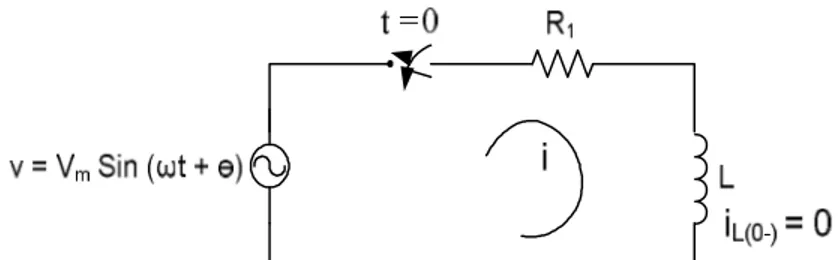
Perhatikan rangkaian di bawah ini :

Gambar 3.1 Rangkaian RL dengan sumber tegangan v = Vm sin (ωt + )

Rangkaian di atas memiliki sumber tegangan v = Vm sin (ωt + θ) di mana θ memiliki harga dari 0

→

2π rad/det. Bilamana saklar ditutup pada saat t = 0, maka persamaan tegangan pada rangkaian adalah :

 dt V sin



t



di L i . R _m (3.1) Penyelesaian umum persamaan ini adalah :

iiss itr (3.2)

di mana dalam hal ini :

itr = ic = penyelesaian komplementer iss = ip = penyelesaian partikular

Adapun penyelesaian komplementer dari Persamaan (3.1) adalah :

0 dt di L Ri c c   atau : dt di L Ri c c  atau : dt L R di di c c _ atau : L t K' R ) i ( Ln _c  

atau : t L R t L R ' K ' K t L R c K i       atau : t L R c K i    _(3.3)

misalkan penyelesaian partikular adalah :

                                       ) c )...( t ( sin B ) t ( cos A dt i d ) b ..( ... ) t ( cos B ) t ( sin A dt di ) a ( ... ... ) t ( sin B ) t ( cos A i 2 2 2 p 2 p p (3.4)

Bilamana persamaan (3.1) dideferensialkan satu kali maka :

) t ( cos Vm dt i d L dt di R 2 2       (3.5)

Bilamana harga-harga dari Persamaan (3.4) disubsitusikan ke Persamaan (3.5) dengan mengambil i = ip, maka akan diperoleh :



Asin( t ) Bcos( t )



L



Acos( t ) Bsin( t )



Vmcos( t )

R        2   2     

dengan menyamakan koefisien persamaan ini maka didapat : R LA Vm B : maka Vm LA BR2      L RA B : maka 0 LB RA 2        sehingga diperoleh : 2 2 2 R L LVm A : didapat maka L RA R LA Vm           

dan selanjutnya didapat :

2 2 2 R L RVm B    

dan seterusnya bilamana harga-harga A dan B disubsitusikan ke dalam Persamaan (3.4a) diperoleh : ) t sin( R L RVm ) t cos( R L LVm ip _{2 2 2 2 2 2}              (3.6) melihat segi tiga impedansi dari RL seri :



Gambar 3.2 Segitiga impedansi RL seri

maka terlihat bahwa :

2L2 R2 R Z R cos      (3.7) 2L2 R2 L Z L sin        (3.8) R L tan 1    (3.9)

Persamaan (3.6) dapat dibuat menjadi :

) t sin( R L RVm ) t cos( R L LVm i 2 2 2 2 2 2 p              ) t sin( cos R L R R L Vm ) t cos( sin R L L R L Vm i 2 2 2 2 2 2 2 2 2 2 2 2 p                                    sehingga : ) t sin( cos R L Vm ) t cos( sin R L Vm i 2 2 2 2 2 2 p               atau :



     



 

 sin( t )cos cos( t )sin

R L Vm i 2 2 2 p mengingat :              

t ) sin( t )cos cos( t )sin

( sin maka : ) t ( sin R L Vm i 2 2 2 p      (3.10) sehingga dengan demikian :

p c i i i  atau : ) t ( sin R L Vm K i 2 2 2 t L R            (3.11)

Karena pada t = 0- arus pada rangkaian : i(0-) = iL(0-) = 0, dan karena sifat dari L yang tidak dapat berubah dengan seketika, maka pada t = 0, arus pada rangkaian adalah i(0) = 0 dan kalau harga ini disubsitusikan ke dalam persamaan (3.11) akan diperoleh :

) 0 . ( sin R L Vm K 0 i 2 2 2 0 . L R             sehingga diperoleh : ) ( sin R L Vm K 2 2 2 _    

apabila harga K ini disubsitusikan ke Persamaan (3.11) maka diperoleh :

) t ( sin R L Vm ) ( sin R L Vm i 2 2 2 t L R 2 2 2 _   _{ }       (3.12)

Bilamana Persamaan (3.9) disubsitusikan ke dalam persamaan ini, maka di dapat bentuk persamaan arus pada rangkaian setelah saklar ditutup :

) R L tan t ( sin R L Vm ) R L tan ( sin R L Vm i 1 2 2 2 1 2 2 2 t L R                 _           (3.13) Contoh :

Jawab :

Sewaktu rangkaian dihubungkan dengan sumber tegangan v dimana θ = 0 persamaan tegangan pada rangkaian :

v dt di L i R   atau : dt 500sin500t di 2 , 0 i 50   (*)

Adapun penyelesaian komplementer dari persamaan di atas adalah :

0 dt di 2 , 0 i 50 c c   atau : dt di 2 , 0 i 50 c c  atau : dt 250dt di_c  

kalau diintegralkan akan diperoleh :

' K t 250 ) i ( Ln c   atau : t 250 ' K ' K t 250 c i     karena : _K' _K , maka : ic K 250t    _(**)

Misalkan persamaan partikular (i = ip) adalah

) t 500 ( cos B 500 ) t 500 ( sin A 500 dt di : maka ) t 500 ( sin B ) t 500 ( cos A i_p     p     (***)

maka persamaan (*) untuk i = ip adalah

t 500 sin 150 dt di 2 , 0 i 50 _p p  atau : t 500 sin 750 i 250 dt di p p  

kemudian subsitusikan ip dan dt di_p

ke dalam persamaan di atas, maka diperoleh : t 500 sin 750 ) t 50 sin T 500 cos A ( 250 t 500 cos B 500 t 500 sin A 500      atau :



250B500A



sin500t



500B250A



cos500t750sin500t

dengan menyamakan koefisien ini di dapat :

250B – 500A = 750 dan 500B+250A = 0 maka diperoleh : A = -1,2 dan B = 0,6

Harga A dan B yang diperoleh disubsitusikan ke persamaan (***) : t 500 cos 2 , 1 t 500 sin 6 , 0 t 500 sin 6 , 0 t 500 cos 2 , 1 i_p     Mengingat : ) t ( sin d c ) t cos( b ) t ( sin a       2  2   di mana : d c tan dan ; sin b cos a d ; cos b sin a c_{      } 1 maka : ip 1,31sin(500t63,4) _(****) sehingga i = (**) + (****) atau : i = Kε-250.t + 1,34 sin (250.t-63,40) (*****)

Pada saat t = 0- diketahui iL(0-) = 0, dan karena sifat dari L yang tidak dapat berubah dengan seketika, pada saat t = 0, arus i(0) = 0 sehingga :

i(0) = 0 = Kε-250.0 + 1,34 sin (250.0-63,40)

Maka diperoleh : K = 1,19, harga K yang diperoleh disubsitusikan ke persamaan (*****), sehingga di dapat persamaan arus pada rangkain bila saklar ditutup adalah :

mp t

sin 1,19.

3.2 Response Sinusoidal Pada RC Seri

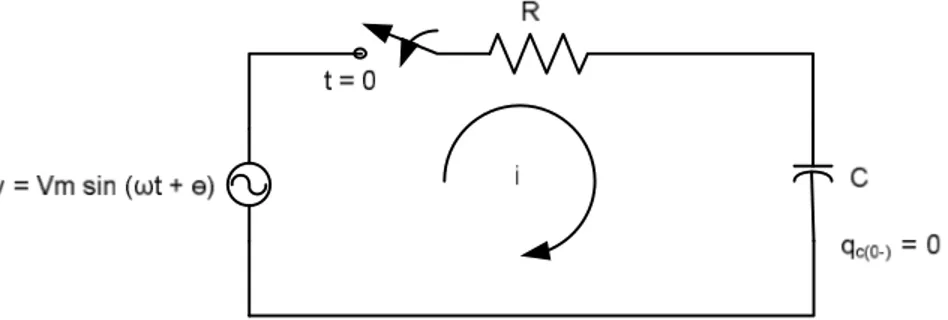
Perhatikan gambar di bawah ini :

Gambar 3.3 Rangkaian RC dengan sumber tegangan v = Vm sin (ωt + θ)

Pada saat t = 0 saklar di tutup sehingga rangakaian terhubung dengan sumber tegangan v = Vm sin (ωt + θ) di mana harga θ dari 0 →2π.rad/det.

Setelah saklar di tutup maka persamaan tegangan pada rangkaian adalah : C idt Vmsin( t )

1 i.

R 

_

  

(3.14)

bila dideferensialkan satu kali :

C Vmcos( t ) i dt di R     (3.15) sesuai Persamaan (3.2), maka penyelesaian Persamaan (3.14) ini adalah :

iiss itr

dimana :

itr = ic = penyelesaian komplementer iss = ip = penyelesaian partikular

Adapun penyelesaian komplementer dari Persamaan (3.15) untuk i = ic adalah :

RC i dt di : atau 0 C i dt di R c  c  c  c atau : RC dt i di c c _

kalau diintegralkan :

 

K' RC t i Ln c   atau : RC t ' K ' K RC t c i         karena : εK' = K, maka : RC t c K. i   _(3.16)

selanjutnya Persamaan (3.15) untuk i = ip adalah :

C Vmcos



t



i dt di R p p (3.17) Misalkan penyelesaian partikular sesuai Persamaan (3.4) yaitu :









 









 



t



Bsin



t



...

 

c sin A dt i d b ... ... t cos B t sin A dt di a ... ... ... t sin B t cos A i 2 2 p 2 p p                              

Bilamana harga-harga Persamaan (3.4) disubsitusikan ke Persamaan (3.5) maka diperoleh :







  







Acos



t



Bsin



t





Vmcos



t



C 1 t sin A R atau :



 



                         cos( t ) Vmcos t C A RB ) t sin( RA C B

dengan menyamakan koefisien ruas kiri dan ruas kanan maka diperoleh :



Vm RB



A : didapat maka Vm C A RB RC B A : didapat maka 0 RA C B                           

dari kedua persamaan ini diperoleh :

2 2 2 2 2 2 2 2 2 R C 1 Vm R C B dan R C 1 CVm A        

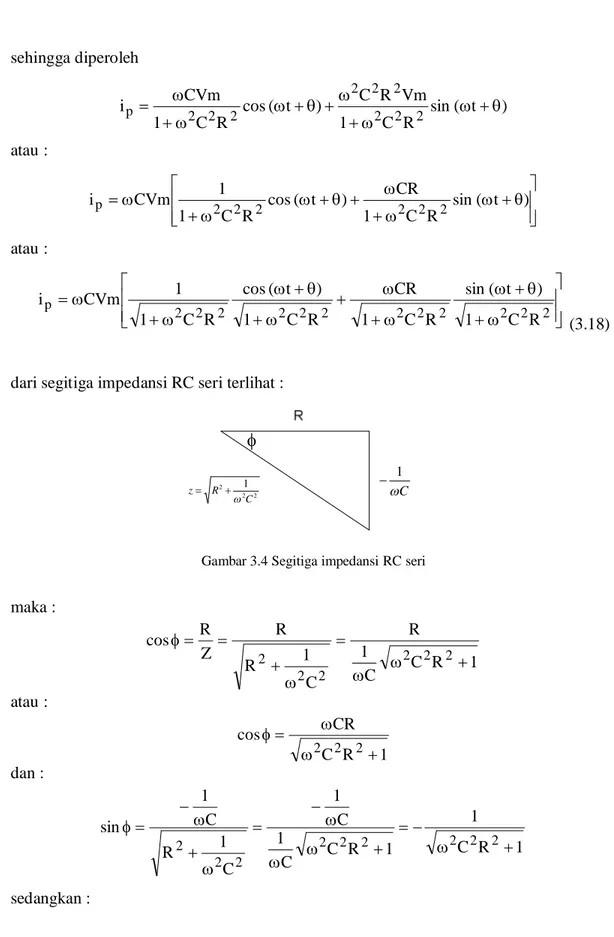
ip= A cos (ωt + θ) + B sin (ωt + θ) sehingga diperoleh ) t ( sin R C 1 Vm R C ) t ( cos R C 1 CVm i 2 2 2 2 2 2 2 2 2 p              atau :                       sin ( t ) R C 1 CR ) t ( cos R C 1 1 CVm i 2 2 2 2 2 2 p atau :                           2 2 2 2 2 2 2 2 2 2 2 2 p R C 1 ) t ( sin R C 1 CR R C 1 ) t ( cos R C 1 1 CVm i (3.18)

dari segitiga impedansi RC seri terlihat :

2 2 2 1 C R z    C 1 



Gambar 3.4 Segitiga impedansi RC seri

maka : 1 R C C 1 R C 1 R R Z R cos 2 2 2 2 2 2 _{ }        atau : 1 R C CR cos 2 2 2 _     dan : 1 R C 1 1 R C C 1 C 1 C 1 R C 1 sin 2 2 2 2 2 2 2 2 2                 sedangkan :

ωCR 1 tan : maka . R ωC 1 tan  1     

jika besaran cos  dan sin  disubstitusikan kedalam Persamaan (3.18) akan diperoleh :

                        cos 1 R C ) t ( sin sin 1 R C ) t ( cos CVm i 2 2 2 2 2 2 p atau :



     



  

 sin( t )cos cos( t )sin

1 R C CVm i 2 2 2 p mengingat :        

 ) sin cos cos sin

( sin maka :              

t ) sin( t )cos cos( t )sin

( sin sehingga : ) t ( sin 1 R C CVm i 2 2 2 p      (3.19) maka, dengan demikian :

) t ( sin 1 R C CVm . K i i i 2 2 2 RC t p c           (3.20) untuk mencari harga K, maka Persamaan (79) pada t = 0 adalah :



    i .d0 Vmsin( .0 ) C 1 i . R _{(0) (0)} maka :  R sin Vm i₍₀₎

kemudian, jika Persamaan (3.20) dibuat pada t = 0, akan diperoleh : ) 0 . ( sin 1 R C CVm . K sin R Vm i 2 2 2 RC 0 ) 0 (            maka diperoleh : ) ( sin 1 R C CVm sin R Vm K 2 2 2 _      

Bilamana harga K ini disubstitusikan kedalam Persamaan (3.20) akan diperoleh persamaan arus yang mengalir pada rangkaian :

) t ( sin 1 R C CVm . ) ( sin 1 R C CVm sin R Vm i 2 2 2 RC t 2 2 2 _{ }                       karena : ωCR 1 tan 1     , maka : ) ωCR 1 1 tan t ( sin 1 2 R 2 C 2 CVm RC t . ) ωCR 1 1 tan ( sin 1 2 R 2 C 2 CVm sin R Vm i                            (3.21) Contoh :

Perhatikan rangkaian di bawah ini :

volt ) t 500 ( sin 250 v   100 R F 25 C  0 ) 0 ( q_c  

Pada saat t = 0, dan  = 0 saklar ditutup sehingga rangkaian terhubung ke sumber tegangan v, carilah bentuk persamaan arus i pada rangkaian.

Jawab :

Adapun persamaan tegangan pada rangkaian setelah saklar ditutup adalah :

C idt 250sin500t 1 i . R 

_

 (a) atau : t 500 sin 250 dt i 10 . 25 1 i . 100  _6

_

 atau : t 500 sin 5 , 2 dt i 400 i

_



bila dideferensialkan satu kali :

dt 400.i 1250cos500t di

 

(b)

Untuk mencari penyelesaian komplementer maka Persamaan (b) disamakan dengan nol dimana i = ic.

0 i . 400 dt di c c _{ } atau : dt 400 i di c c _

kemudian diintegralkan hasilnya adalah :

' K t 400 ) i ( Ln _c   atau : t 400 ' K ' K t 400 c . i     karena : K' K, maka : t 400 c K. i  

Misalkan penyelesaian partikular adalah :

ip Acos500tBsin500t _(c) t 500 cos B 500 t 500 sin A 500 dt di_p    (d)

selanjutnya Persamaan (b) untuk : i = ip, adalah :

dt 400.i 1250cos500t di p p   (e)

selanjutnya bilamana harga-harga i dan p dt

di_p

pada persamaan (c) dan (d) disubstitusikan kedalam persamaan (e), maka diperoleh :

t 500 cos 1250 ) t 500 sin B 400 t 500 cos A 400 ( ) t 500 cos B 500 t 500 sin A 500 (     atau : t 500 cos 1250 t 500 cos ) A 400 B 500 ( t 500 sin ) B 400 A 500 (     maka diperoleh : 0 ) B 400 A 500 (   _dan (500B400A)1250 maka diperoleh : A = 1,22 dan B = 1,525

Harga A dan B ini disubtitusikan kedalam persamaan (c), maka diperoleh : t 500 sin 525 , 1 t 500 cos 22 , 1 i_p   atau :

) 3 , 51 t 500 ( cos 953 , 1 i_p    karena : p c i i i  atau : iK.400t 1,953cos(500t51,3) (f) Pada saat t = 0, maka persamaan (a) didapat :



    i.d0 250sin500.0 makai 0 C 1 i . R (0) (0)

sehingga persamaan (f) untuk t = 0 adalah :

) 3 , 51 0 . 500 ( cos 953 , 1 . K 0 i₍₀₎   400t   

maka diperoleh : K = -1,22,kemudian harga K ini disubstitusikan ke persamaan (f), maka diperoleh persamaan arus pada rangkaian setelah saklar ditutup adalah :

. Amp ) 3 , 51 t . 500 ( cos 953 , 1 . 22 , 1 i 400t        Contoh :

Perhatikan rangkaian di bawah ini :

100 R F 25 C t = 0 C 10 . 5 q_c(0) 3 volt ) t 500 ( sin 250 v -+ i

Pada saat t = 0, dan  = 45o saklar ditutup, carilah bentuk persamaan arus pada rangkaian.

Jawab :

Sebelum saklar kapasitor memiliki muatan qc(0-) = 5.10-3 C, berarti pada terminal kapasitor telah ada tegangan sebesar :

volt 200 10 . 25 10 . 5 C q v ₆ 3 ) 0 ( c ) 0 ( c       

C idt 250sin(500t 45 ) 1 i . R 

_

   (a) atau : ) 45 t 500 ( sin 250 dt i 10 . 25 1 i . 100  _6

_

   atau : t 500 sin 5 , 2 dt i 400 i

_



bila dideferensialkan satu kali :

dt 400.i 1250cos(500t 45 ) di     (b)

Untuk mencari penyelesaian komplementer ic, maka Persamaan (b) disamakan dengan nol dengan menggantikan i = ic.

0 i . 400 dt di c c _{ } atau : dt 400 i di c c _

jika diintegralkan hasilnya adalah :

' K t 400 ) i ( Ln _c   atau : t 400 ' K ' K t 400 c . i _  _{ } karena : K' K_{, maka :} t 400 c K. i   _(c)

Untuk mendapatkan penyelesaian partikular ip, maka dimisalkan :

ip Acos(500t45)Bsin(500t45) _(d) sehingga : dt 500Asin(500t 45 ) 500Bcos(500t 45 ) di_p        (e)

selanjutnya dengan membuat i = ip pada persamaan (b) dan mensubstitusikan persamaan (d) dan (e) ke dalamnya akan diperoleh :

) 45 t 500 ( cos 1250 ) 45 t 500 ( sin B 400 ) 45 t 500 ( cos A 400 ) 45 t 500 ( cos B 500 ) 45 t 500 ( sin A 500                atau :

) 45 t 500 ( cos 1250 ) 45 t 500 ( cos ) A 400 B 500 ( ) 45 t 500 ( sin ) B 400 A 500 (          

dengan menyamakan koefisien didapat :

0 ) B 400 A 500 (   dan : 1250 ) A 400 B 500 (   atau diperoleh : A = 1,22 dan B = 1,525

harga-harga A dan B ini disubtitusikan kedalam persamaan (d), maka diperoleh : ) 45 t 500 ( sin 525 , 1 ) 45 t 500 ( cos 22 , 1 i_p       atau : ip 1,953sin (500t83,67) _(f) karena : p c i i i  maka diperoleh : iK.400t 1,953sin (500t83,67) (g)

Pada saat t = 0- pada kapasitor telah ada tegangan sebesar vc(0-) = 200 volt dan karena sifat dari kapasitor yang tidak dapat berubah dengan seketika, maka pada t = 0, tegangan pada kapasitor juga sebesar vc(0) = 200 volt. Selanjutnya harga sesaat dari sumber tegangan pada saat t = 0 adalah :

volt 77 , 176 ) 45 0 . 500 ( sin 250 v₍₀₎    

maka melihat dari plaritas sumber dan kapasitor, kedua tegangan ini v(0) dan vc(0) saling menguatkan, sehingga pada saat t = 0, kedua tegangan ini menghasilkan arus pada rangkaian sebesar : . Amp 76 , 3 100 200 77 , 176 R v v i₍₀₎  (0) c(0)   

maka pada saat t = 0, persamaan (g) menjadi :

) 67 , 83 0 . 500 ( cos 953 , 1 . K 76 , 3 i₍₀₎   400t   

maka dengan menyelesaikan persamaan ini di dapat K = 1,82. Kemudian harga K ini disubstitusikan ke persamaan (g), sehingga diperoleh bentuk persamaan arus pada rangkaian apabila saklar ditutup adalah :

. Amp ) 67 , 83 t . 500 ( cos 953 , 1 . 82 , 1 i 400t    3.3 Soal Latihan

1. Rangkaian seperti di bawah ini :

V ) 6 t 10 sin( 10 v 4 

Carilah bentuk persamaan arus i setelah saklar ditutup.

2. Rangkaian seperti di bawah ini :

V ) 6 t 10 sin( 5 v 5 

Carilah bentuk persamaan arus i setelah saklar ditutup.

V ) 30 t 1000 ( sin 10 v  