PENERAPAN TRANSFORMASI LAPLACE DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL
LINEAR PADA RANGKAIAN SERI RLC
SKRIPSI
SITI FATIMAH AISYAH 130803020
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
2017
PENERAPAN TRANSFORMASI LAPLACE DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL
LINEAR PADA RANGKAIAN SERI RLC
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat Mencapai gelar Sarjana Sains
SITI FATIMAH AISYAH 130803020
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : Penerapan Transformasi Laplace Dalam
Menyelesaikan Persamaan Diferensial Linear Pada Rangkaian Seri RLC.
Kategori : Skripsi
Nama : Siti Fatimah Aisyah
Nomor Induk Mahasiswa : 130803020
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, 18 April 2017
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Asima Manurung, S.Si. M. Si Drs. Agus Salim Harahap, M.Si NIP. 197303151999032001 NIP.195408281981031004 Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
Dr. Suyanto, M. Kom NIP. 195908131986011 002
PERNYATAAN
PENERAPAN TRANSFORMASI LAPLACE DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL
LINEAR PADA RANGKAIAN SERI RLC
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing – masing disebutkan sumbernya.
Medan, 18 April 2017
SITI FATIMAH AISYAH 130803020
PENGHARGAAN
Puji dan syukur penulis ucapkan kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpah karunia- Nya Penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Penerapan Transformasi Laplace Dalam Menyelesaikan Persamaan Diferensial Linear Pada Rangkaian Seri RLC. Shalawat dan salam penulis ucapkan kepada Rasulullahshalallahu’ Alaihi wa sallam, keluarga, para sahabat, dan orang-orang yang mengikutinya.
Terima kasih penulis sampaikan kepada Bapak Drs. Agus Salim Harahap, M.Si selaku pembimbing 1 dan Ibu Asima Manurung, S.Si, M.Si selaku pembimbing 2 yang telah meluangkan waktu dan pikirannya, memberikan pengarahan, saran dan kritik terkait penulisan skripsi ini.
Terima kasih sebesar-besarnya penulis sampaikan kepada kedua orang tua atas do’a dan dukungannya kepada penulis baik secara moril ataupun materi, kepada abang Indra sastra winata yang telah memberikan motivasi kepada penulis sehingga terselesaikan skripsi ini.
Terimakasih penulis sampaikan kepada bapak Drs. Ujian sinulingga, M.Si selaku penguji 1 dan bapak Prof. Dr. Tulus, M.Si. selaku penguji 2 yang telah meluangkan waktu, pikiran dan memberikan kritik maupun saran untuk perbaikan skripsi ini dan sebagai pembelajaran bagi penulis.
Terima kasih penulis sampaikan kepada seluruh dosen Matematika USU yang telah memberi ilmu kepada penulis selama masa perkuliahan, Dekan dan Wakil Dekan FMIPA USU, serta seluruh staf administrasi FMIPA USU.
Terima kasih juga penulis ucapkan kepada teman-teman yang telah memberikan do’a dan motivasi kepada penulis dalam mengerjakan skripsi ini. Semoga Tuhan Yang Maha Esa membalas kebaikan teman-teman semua.
vi
PENERAPAN TRANSFORMASI LAPLACE DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL
LINEAR PADA RANGKAIAN SERI RLC
ABSTRAK
Penelitian ini bertujuan untuk mengetahui bagaimana bentuk karakteristik arus dan tegangan yang dihasilkan dari persamaan diferensial pada rangkaian seri RLC orde satu dan dua dengan menggunakan metode transformasi Laplace dan transformasi Laplace invers. Analisis rangkaian dilakukan dengan menerapkan hukum Kirchoff dan hukum Ohm lalu diselesaikan dengan transformasi Laplace dan inversnya. Penyelesaian ini adalah dengan menstrasformasikan persamaan rangkaian dalam fungsi waktu ke dalam kawasan frekuensi . Rangkaian seri RLC adalah rangkaian yang terdiri dari resistor R, induktor L, dan kapasitor C yang terhubung secara seri. Penamaan RLC disebabkan nama yang menjadi simbol listrik pada kapasitansi, induktansi dan resistansi. Untuk rangkaian orde satu bentuk karakteristik alami yang dihasilkan adalah bentuk eksponensial menurun dan bentuk karakteristik alami dari rangkaian orde dua, yaitu: teredam berlebih (Over Damped), terdeam kritis (Critically Damped), dan kurang teredam (Under Damped). Dengan mengubah nilai resistor (R) dan capasitor (C) diperoleh bentuk tanggapan alami yang berbeda dengan seiring berjalannya waktu tanggapan tersebut akan menghilang atau menuju nol yang merupakan tanggapan transien (sementara).
Kata kunci: Rangkaian RLC, trasformasi Laplace, invers transformasi, hukum Kirchoff, hukum Ohm.
LAPLACE TRANSFORMATION APPLICATION IN COMPLETING THE LINEAR DIFFERENTIAL
EQUATION IN RLC SERIES CIRCUIT
ABSTRACT
This study aimed to determine how the characteristic form of current and voltage generated from the differential equations in series RLC series of order one and two by using Laplace transform method and Laplace inverse transformation. The circuit analysis is carried out by applying Kirchoff's law and Ohm's law and is solved by Laplace transformation and its inverse. The solution is to menstrasform the circuit equation in the time function into the frequency region . RLC series circuit is a circuit consisting of resistor R, inductor L, and capacitor C are connected in series. The naming of the RLC is due to the name being the electrical symbol on capacitance, inductance and resistance. For the first order sequence the resulting natural characteristic form is the decreased exponential shape and the natural characteristic form of the second order circuit, namely: Overdamped, Critically Damped, and Under Damped. By changing the resistor value (R) and capasitor (C), there is a different natural response form as over time the response will disappear or toward zero which is a transient response.
Keywords: Circuit RLC, Laplace transformation, transform Laplace invers, Kirchoff law, Ohm law.
viii
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR viii
DAFTAR LAMPIRAN ix
BAB 1 PENDAHULUAN 1.1 Latar Belakang 1
1.2 Rumusan Masalah 2
1.3 Batasan Masalah 2
1.4 Tujuan Penelitian 3
1.5 Manfaat Penelitian 3
1.6 Metodologi Penelitian 3
BAB 2 TINJAUAN PUSTAKA 2.1 Persamaan Diferensial 5
2.1.1 Persamaan Diferensial Linear 5
2.1.2 Persamaan Diferensial Orde Satu 6
2.1.3 Persamaan Diferensial Orde Dua 8
2.2 Rangkaian Listrik 10
2.2.1 Rangkaian Transien 10
2.2.2 Hukum – Hukum Rangkaian Listrik 10
2.2.3 Elemen Resistor, Induktor, Kapasitor, dalam Rangkaian Seri dan Paralel 12
2.2.4 Tanggapan Rangkaian RLC Seri 15
2.3 Integral Parsial 17
2.4 Transformasi Laplace 17
2.4.1 Trasformasi Laplace Dari Turunan 18 2.4.2 Transformasi Laplace Invers 19 2.4.3 Transformasi Laplace Dalam Ekspansi
Pecahan parsial
20
2.5 Masalah Nilai Awal 21
BAB 3 METODE PENELITIAN Halaman
BAB 4 HASIL dan PEMBAHASAN
4.1 Tanggapan Alami Rangkaian Orde Satu 24 4.2 Tanggapan Alami Rangkaian Orde Dua 28
BAB 5 KESIMPULAN dan SARAN
5.1 Kesimpulan 38
5.2 Saran 38
DAFTAR PUSTAKA 39
TABEL TRANSFORMASI LAPLACE 40
x
DAFTAR GAMBAR
Nomor Gambar
Judul Halaman
2.1 Simpul Arus Sederhana 11
2.2 Kombinasi Rangkaian N buah resistor 12
2.3 Rangkaian Ekivalen resistor 12
2.4 Kombinasi Rangkaian N buah Induktor 13
2.5 Rangkaian Ekivalen N buah induktor 14
2.6 Rangkaian Seri RLC 15
4.1 Rangkaian RL 24
4.2 Rangakaian Ekivalen RL 25
4.3 Tanggapan Rangkaian RL Seri 26
4.4 Rangkaian RC Kombinasi Seri dan Paralel 27
4.5 Rangkaian Ekivalen RC 27
4.6 Tanggapan Rangkaian RC Sebagai 28
4.7 Rangkaian RLC Seri 29
4.8 Tanggapan Rangkaian Kurang Teredam 31
4.9 Rangkaian RLC Seri 32
4.10 Rangkaian Ekivalen RLC Seri 32
4.11 Tanggapan Rangkaian RLC Seri Teredam Berlebih 34
4.12 Rangkaian RLC Kombinasi Seri dan Paralel 35
4.13 Rangkain Ekivalen RLC Seri 35
4.14 Tanggapan Rangkaian RLC Seri Teredam Kritis 37
DAFTAR LAMPIRAN
Nomor Lampi
Judul Halaman
1 Tabel Transformasi Laplace 40
vi
PENERAPAN TRANSFORMASI LAPLACE DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL
LINEAR PADA RANGKAIAN SERI RLC
ABSTRAK
Penelitian ini bertujuan untuk mengetahui bagaimana bentuk karakteristik arus dan tegangan yang dihasilkan dari persamaan diferensial pada rangkaian seri RLC orde satu dan dua dengan menggunakan metode transformasi Laplace dan transformasi Laplace invers. Analisis rangkaian dilakukan dengan menerapkan hukum Kirchoff dan hukum Ohm lalu diselesaikan dengan transformasi Laplace dan inversnya. Penyelesaian ini adalah dengan menstrasformasikan persamaan rangkaian dalam fungsi waktu ke dalam kawasan frekuensi . Rangkaian seri RLC adalah rangkaian yang terdiri dari resistor R, induktor L, dan kapasitor C yang terhubung secara seri. Penamaan RLC disebabkan nama yang menjadi simbol listrik pada kapasitansi, induktansi dan resistansi. Untuk rangkaian orde satu bentuk karakteristik alami yang dihasilkan adalah bentuk eksponensial menurun dan bentuk karakteristik alami dari rangkaian orde dua, yaitu: teredam berlebih (Over Damped), terdeam kritis (Critically Damped), dan kurang teredam (Under Damped). Dengan mengubah nilai resistor (R) dan capasitor (C) diperoleh bentuk tanggapan alami yang berbeda dengan seiring berjalannya waktu tanggapan tersebut akan menghilang atau menuju nol yang merupakan tanggapan transien (sementara).
Kata kunci: Rangkaian RLC, trasformasi Laplace, invers transformasi, hukum Kirchoff, hukum Ohm.
LAPLACE TRANSFORMATION APPLICATION IN COMPLETING THE LINEAR DIFFERENTIAL
EQUATION IN RLC SERIES CIRCUIT
ABSTRACT
This study aimed to determine how the characteristic form of current and voltage generated from the differential equations in series RLC series of order one and two by using Laplace transform method and Laplace inverse transformation. The circuit analysis is carried out by applying Kirchoff's law and Ohm's law and is solved by Laplace transformation and its inverse. The solution is to menstrasform the circuit equation in the time function into the frequency region . RLC series circuit is a circuit consisting of resistor R, inductor L, and capacitor C are connected in series. The naming of the RLC is due to the name being the electrical symbol on capacitance, inductance and resistance. For the first order sequence the resulting natural characteristic form is the decreased exponential shape and the natural characteristic form of the second order circuit, namely: Overdamped, Critically Damped, and Under Damped. By changing the resistor value (R) and capasitor (C), there is a different natural response form as over time the response will disappear or toward zero which is a transient response.
Keywords: Circuit RLC, Laplace transformation, transform Laplace invers, Kirchoff law, Ohm law.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Dalam kehidupan sehari – hari, terdapat banyak sekali permasalahan yang melibatkan matematika, baik dalam bidang ekonomi, politik, kimia, fisika dan bidang lainnya.
Objek (masalah) tersebut diidentifikasi, dirumuskan dan dimodelkan untuk kemudian dicari solusinya. Salah satu model matematika yang banyak digunakan dalam berbagai permasalahan di bidang lain adalah berbentuk persamaan diferensial. Persamaan diferensial dibagi menjadi dua jenis, yaitu persamaan diferensial linear dan nonlinear.
Dalam penelitian ini, penulis membahas persamaan diferensial linear.
Persamaan diferensial adalah salah satu ilmu matematika yang banyak digunakan untuk menjelaskan masalah – masalah fisis. Masalah - masalah fisis tersebut dapat dimodelkan dalam bentuk persamaan diferensial. Jika model matematika berbentuk persamaan diferensial, maka masalahnya adalah bagaimana menentukan solusi persamaan diferensial itu.
Salah satu metode yang digunakan untuk menyelesaikan persamaan diferensial linear maupun menyelesaikan masalah nilai awal pada persamaan diferensial linear adalah dengan menggunakan metode transformasi Laplace. Metode transformasi Lapace adalah salah satu metode untuk menyelesaikan masalah nilai awal pada persamaan diferensial linear koefiesien konstan dengan cara mengubah variabel menjadi variabel yang berbentuk persamaan aljabar atau dengan menggunakan tabel yang memuat transformasi Laplace.
Metode ini pertama kali diperkenalkan oleh Pierre Simon Marquas de Laplace (1749 - 1827), seorang matematikawan Perancis dan seorang guru besar di Paris.
Keunggulan transformasi Laplace adalah bahwa masalah nilai awal persamaan diferensial linear dapat diselesaikan secara langsung tanpa terlebih dahulu menentukan solusi umumnya atau persamaan – persamaan non homogen dapat diselesaikan tanpa terlebih dahulu menyelesaikan persamaan homogenya.
Metode transformasi Laplace, seperti halnya metode lain dalam menyelesaikan masalah nilai awal, juga dapat diterapkan pada masalah – masalah yang melibatkan sistem persamaan diferensial, salah satunya di bidang fisika mengenai rangkaian seri RLC. Rangkaian seri RLC adalah rangkaian yang terdiri dari resistor (R), induktor (L), dan kapasitor (C) yang disusun secara seri. Pada rangkaian seri RLC dapat diterapkan transformasi Laplace untuk memperoleh solusi khususnya dengan cara mengubah variabel waktu dalam rangkaian seri RLC menjadi variable frekuensi dengan transformasi.
Dalam menganalisis rangkaiannya dapat diterapkan hukum Kirchoff dan hukum Ohm dengan memperhatikan karakteristik yang ditimbulkan dari rangkaian. Dalam sistem rangkaian orde satu bentuk karakteristik dari tanggapan alami berbentuk fungsi eksponensial. Dan untuk sistem orde dua terdapat tiga karakteristik yang diperoleh dari rangkaian yaitu: teredam berlebih (Over Damped), teredam kritis (Critically Damped), dan kurang teredam (Under Damped). Dengan menggunakan metode transformasi Laplace dan invers transformasi dapat diperoleh bentuk karakteristik dari sistem rangkaian tersebut. Berdasarkan latar belakang tersebut, penulis memilih judul penelitian sebagai “Penerapan Transformasi Laplace Dalam Menyelesaikan Persamaan Diferensial Linear Pada Rangkaian Seri RLC.”
1.2 Perumusan Masalah
Rumusan masalah yang akan dibahas dalam penelitian ini adalah:
1. Bagaimana menyelesaikan persamaan diferensial linear orde satu dan dua pada rangkaian seri RLC dengan kondisi awal yang diberikan menggunakan metode tarnsformasi Laplace.
2. Bagaimana bentuk karakteristik sebagai tanggapan arus dan tegangan yang dihasilkan dari persamaan diferensial linear orde satu dan dua pada rangkaian seri RLC.
1.3 Batasan Masalah
Persamaan diferensial yang diselesaikan dengan transformasi Laplace adalah persamaan diferensial linear orde satu dan dua koefisien konstan pada rangkaian seri RLC.
3
1.4 Tujuan Penelitian Tujuan penelitian ini adalah
1 Menjelaskan metode transformasi Laplace dan transformasi invers dan aplikasinya pada rangkaian seri RLC.
2 Mengetahui bagaimana bentuk karakteristik tanggapan arus dan tegangan yang dihasilkan pada rangkaian seri RLC.
1.5 Manfaat Penelitian
Manfaat dari penulisan skripsi ini adalah :
1. Sebagai salah satu cara pemecahan masalah persamaan diferensial linear orde satu dan dua koefisien konstan dengan nilai awal yang diberikan.
2. Mengetahui bagaimana bentuk karakteristik arus dan tegangan yang dihasilkan pada rangkaian seri RLC.
1.6 Metodologi Penelitian
Penelitian ini adalah penelitian studi literatur yang bersumber dari buku – buku dan jurnal dengan menggunakan metode transformasi Laplace, adapun langkah – langkahnya sebagai berikut:
1. Memodelkan sistem rangkaian orde satu (RL dan RC) ke dalam bentuk persamaan diferensial linear.
2. Memodelkan sistem rangkaian orde dua (RLC) ke dalam bentuk persamaan diferensial linear.
3. Mentransformasikan persamaan diferensial yang berada dalam kawasan waktu ke kawasan frekuensi dengan menggunakan transformasi Laplace.
4. Mengambil transformasi Laplace invers pada persamaan diferensial rangkaian orde satu dan dua.
5. Memperoleh solusinya dalam bentuk tanggapan arus dan tegangan.
6. Visualisasi penggambaran model dari persamaan diferensial pada rangkaian sistem orde satu dan dua digunakan bantuan Software Maple 18.
7. Menyelesaikan contoh kasus.
8. Mengambil kesimpulan.
5
BAB 2
TINJAUAN PUSTAKA
2.1 Persamaan Diferensial
Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen , suatu variabel dependen , dan satu atau lebih turunan dari terhadap (K.A. Stroud. 2003).
Contoh :
2.1.1 Persamaan Diferensial Linear
Secara umum persamaan diferensial linear orde koefisien konstan dituliskan sebagai:
Di mana dan koefisien tergantung hanya pada variabel . Dengan kata lain, persamaan ini tidak tergantung pada atau pada turunan dari .
Contoh persamaan diferensial linear
2.1.2 Persamaan Diferensial Orde Satu
Bentuk standar dari persamaan diferensial orde satu dalam fungsi adalah
Persamaan diferensial orde satu diklasifikasikan berdasarkan cara penyelesaiannya menjadi tiga macam:
1. Persamaan Diferensial Terpisah Bentuk umum persamaan diferensial terpisah
Solusinya dicari dengan pengintegralan langsung terhadap
∫ ∫
2. Persamaan Homogen Orde Satu
Persamaan diferensial orde satu homogen ditulis dalam bentuk atau
Persamaan homogen dapat diselesaikan dengan metode substitusi menjadi persamaan yang dapat dipisahkan dengan mensubstitusikan dimana adalah fungsi dari .
Sehingga Diferensialkan terhadap (dengan menggunakan aturan hasil kali)
7
Persamaan yang dihasilkan dalam variable dan dapat diselesaikan dengan metode pemisahan variabel dan mengintegrasi pada kedua sisi persamaan yang terpisah,
Contoh:
Solusi
Dengan mensubstitusi dalam persamaan diperoleh
Sehingga persamaannya menjadi
∫
∫
Dengan mensubstitusikan dalam persamaan yang terakhir diperoleh
( )
3. Persamaan Diferensial Linear Orde Satu Persamaan diferensial linear orde satu memiliki bentuk
Dimana dan adalah fungsi dari (konstanta). Untuk menyelesaikan persamaan seperti ini, dikalikan kedua sisi dengan faktor integrasi yang berbentuk
∫
Yang bergantung pada dan independen terhadap . sehingga dengan mengalikan kedua sisi persamaan dengan faktor integrasi diperoleh
Yang menghasikan persamaan eksak sehingga dapat diselesaikan dengan metode pemisahan variabel. Prosedur selanjutnya untuk persamaan dapat ditulis
Persamaan ini dapat diselesaikan dengan melakukan integrasi pada kedua sisi, dan kemudian menyelesaikannya untuk memperoleh persamaan untuk .
Contoh
solusi
∫ ∫
{ }
∫
2.1.3 Persamaan Diferensial Orde Dua
persamaan diferensial orde dua dapat ditulis dalam bentuk
(2.2) Dimana , , dan adalah koefisien konstanta. Dan adalah suatu fungsi yang diketahui. Persamaan diferensial orde dua dapat ditulis dalam bentuk persamaan kuadrat sebagai.
9
Yang diperoleh dengan menuliskan
Persamaan kuadrat disebut juga persamaan karakteristik. Berdasarkan akar – akar dari persamaan kuadrat, penyelesaiannya dibedakan atas tiga tipe yaitu:
1. Akar – akar Real yang Tidak Sama
Apabila akar – akar dari persamaan kuadrat diperoleh dalam bentuk real dan berbeda dimana:
Maka solusinya diperoleh dalam bentuk
(2.3) Dimana dan adalah konstanta sembarang dan dan adalah akar – akar persamaan kuadrat.
2. Akar – akar Real yang Sama
Apabila akar – akar dari persamaan kuadrat diperoleh dalam bentuk real dan sama dimana:
Maka Solusinya diperoleh dalam bentuk
3. Akar – akar Kompleks
Apabila akar – akar dari persamaan kuadrat diperoleh dalam bentuk kompleks dimana:
Maka Solusinya diperoleh dalam bentuk
(2.5)
2.2 Rangkaian Listrik
Rangkaian listrik adalah suatu kumpulan elemen atau komponen listrik yang saling dihubungkan dengan cara – cara tertentu dan paling sedikit mempunyai satu lintasan tertutup. Adapun komponen listrik terdiri dari tiga macam yaitu:
1. Resistor (R) yang berfungsi sebagai penghambat arus dalam rangkaian.
2. Induktor (L) dapat menyimpan energi dalam bentuk medan magnet.
3. Kapasitor (C) menyimpan energi dalam bentuk medan listrik.
2.2.1 Rangkaian Transien
Dalam analisis transien terdapat tiga macam komponen listrik beserta sifatnya yang akan menimbulkan karakteristik baru dalam rangkaian. Resistor yang bersifat membuang energi dalam bentuk panas, induktor yang bersifat menyimpan arus bolak- balik atau alternating current (ac), dan kapasitor yang bersifat menyimpan tegangan searah atau direct current (dc), akan menimbulkan adanya sifat sementara (transien) dalam rangkaian. Dalam kondisi sementara ini, sebelum diterapkan sumber-sumber bebas dari luar, tanggapan rangkaian disebut dengan tanggapan sementara. Setelah lenyapnya tanggapan sementara, rangkaian dikatakan dalam keadaan mantap (steady state). Tanggapan yang diakibatkan oleh sumber-sumber bebas dari luar dinamakan dengan tanggapan paksa. Kombinasi dari tanggapan transien dengan tanggapan paksa merupakan tanggapan lengkap rangkaian.
2.2.2 Hukum – Hukum Rangkaian listrik 1. Hukum Arus Kirchhoff (HAK)
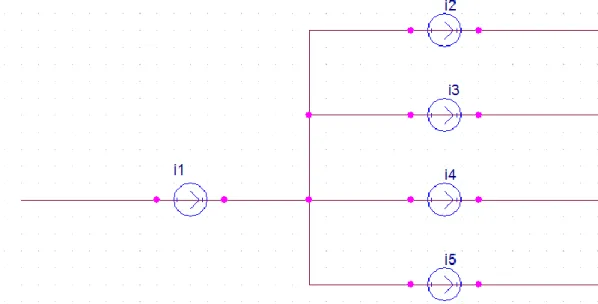
Hukum arus Kirchhoff menyatakan bahwa jumlah aljabar dari arus – arus yang memasuki setiap node/simpul rangkaian adalah nol (William H, 2005). Arus yang menuju node dinyatakan positif dan yang meninggalkan node dinyatakan negatif. Untuk memberi gambaran mengenai hukum arus Kirchhoff dengan gambar sebagai berikut:
11
Gambar 2.1 Simpul Arus Sederhana
Berdasarkan hukum arus Kirchhoff pada rangkaian diperoleh persamaan =0
Atau
2. Hukum Tegangan Kirchhoff (HTK)
Hukum tegangan Kirchhoff menyatakan bahwa penjumlahan aljabar dari tegangan disekeliling suatu lintasan tertutup sama dengan nol (William H, 2005).
3. Hukum Ohm
Hukum Ohm menyatakan bahwa tegangan V yang melewati suatu penghantar berbanding lurus degan arus I dari elemen rangkaian yang ditulis sebagai (Zainuddin Zukhri, 2007).
2.2.3 Elemen Resistor, Induktor, dan Kapasitor dalam Hubungan Seri dan Paralel
1. Resistor dalam Hubungan Seri dan Parallel
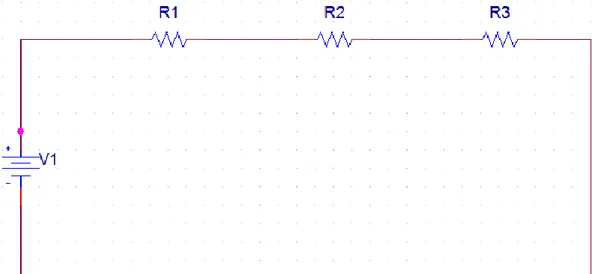
Gambar 2. 2 Kombinasi Rangkaian N Buah Resitor
Gambar 2.3 Rangkaian Ekivalen Resistor
Dalam praktiknya kita bisa saja menggantikan suatu kombinasi resistor yang terlalu rumit dengan sebuah resistor ekivalen. Kombinasi dari N buah resistor yang terhubung seri dapat disederhanakan dengan mengantikan N buah resistor dengan sebuah resistor ekivalen (Req). Resistansi ekivalen untuk N buah resistor yang terhubung seri adalah:
∑ (2.6)
13
Proses penyederhanaan yang serupa juga dapat diaplikasikan untuk rangkaian paralel.
Sebuah rangkaian yang mengandung N buah resistor dalam hubungan paralel adalah.
Yang dapat ditulis sebagai
Untuk kasus dimana hanya terdapat dua buah resistor yang terhubung paralel.
Persamaannya dapat di rumuskan sebagai:
2. Induktor dalam Hubungan Seri dan Paralel
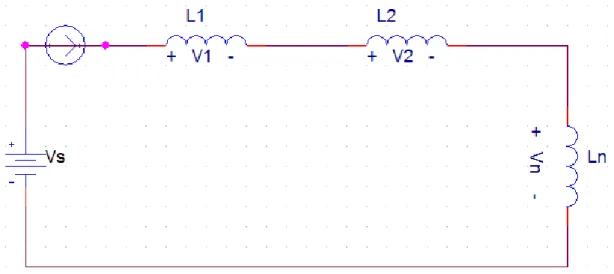
Kombinasi dari N buah induktor yang terhubung seri pada gambar dapat diganti denga sebuah rangkaian induktor ekivalen, dengan induktansi Leq untuk menggantikan kombinasi seri tersebut. Dengan menerapakan HTK (hukum tegangan Kirchhoof atau Kirchoof voltage law) pada rangkaian aslinya.
Gambar 2.4 Rangkaian Kombinasi N Buah Induktor
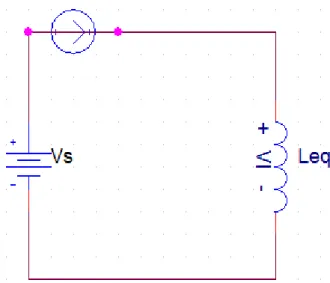
Gambar 4.5 Rangkaian Ekivalen N Buah Induktor
∑
∑
∑
untuk rangkaian ekivalen, KVL (kirchooff voltage law) menghasilkan
Untuk kasus dua induktor yang terhubung paralel
(2.8)
3. Kapasitor dalam Hubungan Seri dan Paralel
Kombinasi dari N buah kapasitor yang terhubung seri membentuk kombinasi yang sama dengan konduktansi – konduktansi atau resistor – resistor paralel.
Untuk kasus dua kapasitor yang terhubung seri. Persamaan yang diperoleh adalah
15
Untuk rangkaian N buah kapasitor yang terhubung paralel yaitu
(2.10)
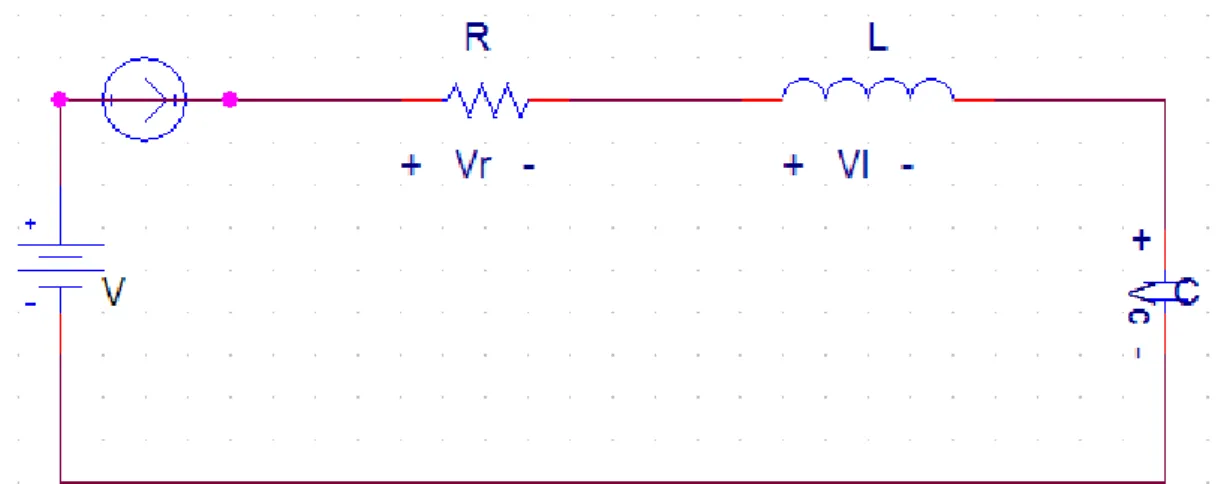
2.2.4 Tanggapan Rangkaian RLC Seri
Pada rangkaian listrik, terdapat 3 respon yang dikenal, yaitu respon alami yang kurang teredam (underdamped), teredam kritis (crititically damped), dan sangat teredam (overdamped), karena yang akan dibicarakan adalah arus, maka, respon yang dimaksud adalah respon arus. Secara matematis dalam ilmu rangkaian listrik dapat dijelaskan 3 respon ini. Suatu rangkaian listrik sederhana yang terdiri dari komponen aktif R, juga komponen pasif L dan C dirangkai secara seri pada gambar dengan menerapkan hukum tegangan Kirchhoff pada gambar maka diperoleh persamaan arus, sebagai:
Gambar 2.6 Rangkaian RCL Seri
∫
Persamaan derajat kedua diperoleh dengan mendiferensiasikan terhadap fungsi waktu sebagai:
Dengan menggunakan persamaan diferensial orde dua dan pemisalan , maka
( )
Persamaan terakhir yang diperoleh dikenal sebagai persamaan karakteristik atau persamaan pelengkap (auxiliary). Karena persamaan ini adalah sebuah persamaan kuadrat, maka persamaan tersebut memiliki dua buah pemecahan yang diidentifikasikan sebagai dan
√(
)
√ Dengan sebagai parameter frekuensi resonansi
√
Dan sebagai parameter frekuensi neper atau koefisien redaman eksponensial
Terdapat tiga kondisi yang di peroleh yaitu:
Untuk merupakan kondisi teredam kritis
bentuk umum tanggapan teredam kritis (crititially damped) adalah (2.11)
Untuk merupakan kondisi kurang teredam (under damped) bentuk umum tanggapan kurang teredam adalah
(2.12) Dengan sebagai bilangan radix
√
Untuk merupakan kondisi teredam berlebih (over damped)
17
bentuk umum tanggapan teredam berlebih
(2.13) konstanta didapat dengan menggunakan kondisi awal (initial condition) (Hayt dkk. 2005).
2.3 Integral Parsial
Jika dan adalah fungsi dari , maka diketahui bahwa
∫
∫ Dan dengan mengatur kembali suku – sukunya, diperoleh
∫
∫ Rumus sederhananya diperoleh
∫ ∫ (2.14)
2.4 Transformasi Laplace
Transformasi Laplace adalah suatu metode operasional yang dapat digunakan secara mudah untuk menyelesaikan persamaan diferensial linier. Transformasi Laplace juga dapat digunakan untuk mengubah persamaan diferensial kedalam bentuk persamaan aljabar, sehinnga mengurangi kerumitan penggunaan bentuk eksponensial menjadi bentuk ekspresi persamaan aljabar.
Jika adalah suatu pernyataan dalam yang terdefinisi untuk maka transformasi Laplace dari dinotasikan dengan { } atau didefenisikan sebagai:
{ } ∫
Dimana adalah suatu variabel yang nilai – nilainya dipilih sedemikian rupa agar intrgral infinitnya konvergen. Pemusatan terjadi ketika limit
∫
Eksis. Jika limit ini tidak eksis, integral tak wajar tersebut divergen dan tidak memiliki transformasi laplace.
2.4.1 Transformasi Laplace Dari Turunan 1. Turunan Pertama
{ } ∫
Bukti:
{ } ∫
Dengan menggunakan integral parsial diperoleh
{ } ∫
∫
[ ] ∫
[ ] ∫
( )
{ } (2.20)
19
2. Turunan Kedua { } ∫
Bukti:
Dengan menggunakan integral parsial dan hasil dari turunan pertama diperoleh { } ∫
= [ ] ∫ = ( ) { }
= [ ]
{ } = (2.21) Secara umum turunan ke – adalah sebagai berikut:
{ } { } (2.22)
2.4.2 Transformasi Laplace Invers
Jika transformasi laplace suatu fungsi adalah , yaitu { } , maka disebut invers transformasi Laplace dari yang ditulis sebagai:
{ } . (2.23)
Sifat – sifat transformasi Laplace invers adalah sebagai berikut
1. Transformasi invers dari suatu jumlah atau selisih dari pernyataan adalah jumlah atau selisih dari masing – masing transformasi invers itu sendiri. yang ditulis sebagai:
{ } { } { }
2. Transformasi invers dari suatu pernyataan yang dikalikan dengan suatu konstanta adalah konstanta tersebut dikalikan dengan transformasi invers dari pernyataan tersebut, dengan kata lain:
{ } { } di mana adalah konstanta.
2.4.3 Transformasi Laplace dalam Ekpansi Pecahan Parsial
Di dalam penggunaannya, transformasi Laplace sering kali melibatkan bentuk
dengan banyak fraksi, di mana P(s) dan Q(s) merupakan suku polinomial. Solusinya ialah dengan cara mengetahui bagaimana fraksi – fraksi yang terlibat/dihasilkan diubah dalam bentuk fraksi pecahan (parcial fraction). Jika
dengan penyebut
Maka, terdapat tiga penyelesaiannya.
1. Akar – akar Real yang Tidak Sama
Untuk setiap faktor dari P(s) yang linear dalam bentuk dan diperoleh bentuk pecahan parsialnya sebagai
(2.25)
Dengan dan sebagai konstanta.
21
2. Akar – akar Real yang Sama
Untuk setiap faktor dari P(s) yang linear dalam bentuk diperoleh bentuk pecahan parsialnya sebagai
Dengan , , , dan adalah konstanta yang belum diketahui nilainya.
3. Akar – akar Kompleks
Untuk setiap faktor dari P(s) dalam bentuk
Maka, pecahan parsialnya dapat ditulis dalam bentuk
2.5 Masalah Nilai Awal (Initial Value Problem) Masalah nilai awal untuk persamaan diferensial order
( ) yaitu menentukan solusi persamaan diferensial pada interval I yang memenuhi syarat awal di subset dari real
di mana adalah konstanta yang diberikan (Baiduri, 2002).
BAB 3
METODE PENELITIAN
3.1 Langkah – Langkah Metode Penelitian
Peranan metode penelitian dalam suatu penelitian sangat penting. Sehingga dengan metode penelitian dapat mencapai tujuan penelitian yang telah ditetapkan dan agar penelitian yang telah dilakukan berjalan dengan lancar. Melalui metode penelitian, masalah yang dihadapi dapat diatasi dan dipecahkan.
Langkah – langkah yang dilakukan pada penelitian ini meliputi beberapa hal yaitu:
1. Pemilihan Masalah
Yang menjadi permasalahan dalam penelitian ini adalah bagaimana menyelesaikan sistem persamaan diferensial pada rangkaian seri RLC dengan menggunakan metode transformasi Laplace dan inversnya.
2. Merumuskan Masalah
Perumusan masalah diperlukan untuk membatasi permasalahan sehingga diperoleh bahan kajian yang jelas. Sehingga akan lebih mudah untuk menentukan langkah dalam memecahkan masalah tersebut.
3. Studi Pustaka
Setelah diperoleh masalah untuk diteliti, peneliti mengadakan studi pustaka. Studi pustaka adalah penelahan sumber pustaka yang relevan, digunakan untuk mengumpulkan data informasi yang diperlukan dalam penelitian. Studi pustaka diawali dengan mengumpulkan sumber pustaka yang berupa buku atau literatur, jurnal, skripsi dan sebagainya. Setelah pustaka terkumpul dilanjutkan dengan pemahaman isi sumber pustaka tersebut yang pada akhirnya sumber pustaka ini dijadikan landasan untuk menganalisis permasalahan.
23
4. Memecahkan Masalah
Setelah permasalahan dirumuskan dan sumber pustaka terkumpul, langkah selanjutnya adalah pemecahan masalah melalui pengkajian secara teoritis yang selanjutnya disususn secara rinci dalam bentuk pembahasan.
Dalam pemecahan masalah dilakukan langkah – langkah sebagai berikut:
a. Memodelkan permasalahan rangkaian secara matematis, dalam hal ini dimodelkan dalam bentuk persamaan diferensial linear.
b. Mengambil transformasi Lapalce dan inversnya dalam persamaan diferensial yang diperoleh.
c. Mengetahui bagaimana bentuk karakteristik rangkaian orde satu dan dua.
5. Menarik Kesimpulan
Langkah terakhir dalam kegiatan penelitian ini adalah menarik kesimpulan dari keseluruhan permasalahan yang telah dirumuskan dengan berdasarkan pada landasan teori dan hasil pemecahan masalah.
BAB 4
HASIL DAN PEMBAHASAN
4.1 Tanggapan Alami Rangkaian Orde Satu
Tanggapan alami adalah solusi homogen dari persamaan diferensial homogen pada rangkaian.
1. Tanggapan Alami Rangkaian RL
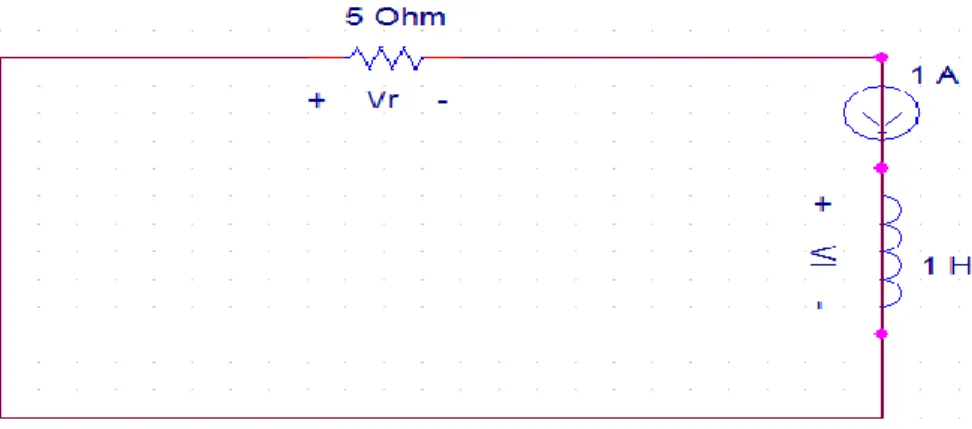
Sebuah rangkaian RL bersifat resistif (memuat resistor - resitor) dihubungkan secara seri dengan sebuah induktor tanpa sumber sebagaimana terlihat pada gambar berikut:
Gambar 4.1 Rangkaian RL
Analisis rangkaian dilakukan dengan menghitung nilai-nilai ekivalen resistor yang terhubung seri dan paralel sebagai
Rangkaian ekivalennya diperoleh sebagai berikut:
25
Gambar 4.2 Rangkaian Ekivalen RL
Pada rangkaian ekivalen ini di berikan arus awal yang melewati induktor sebesar . Akan ditentukan bagaimana bentuk karakteristik tanggapan arus yang dihasilkan dari rangkaian tersebut.
Pada waktu aplikasi HTK dan hukum Ohm memberikan sistem persamaan rangkaian orde satu sebagai:
Dengan menyederhanakan persamaan rangkaian dan mensubstitusikan nilai – nilai elemen rangkaian dalam persamaan diferensial diperoleh
Dengan mengambil transformasi Lapalce di kedua sisi dari persamaan diferensial dan mensubstitusikan nilai arus awal yang diberikan pada persamaan diferensial diperoleh
[ ]
Untuk memperoleh bentuk arus dalam fungsi waktu dengan mengambil transformasi Laplace invers dari persamaan diperoleh
Adapun gambar grafiknya sebagai berikut:
Gambar 4.3 Tanggapan Rangkaian RL Seri Sebagai
pada gambar 4.3., menunjukkan bahwa bentuk tanggapan alami rangkaian RL teredam kritis pada 1 konstanta waktu tanggapan ini menghilang dengan seiring berjalannya waktu atau menuju nol yang merupakan tanggapan transien (sementara).
2. Tanggapan Alami Rangkaian RC
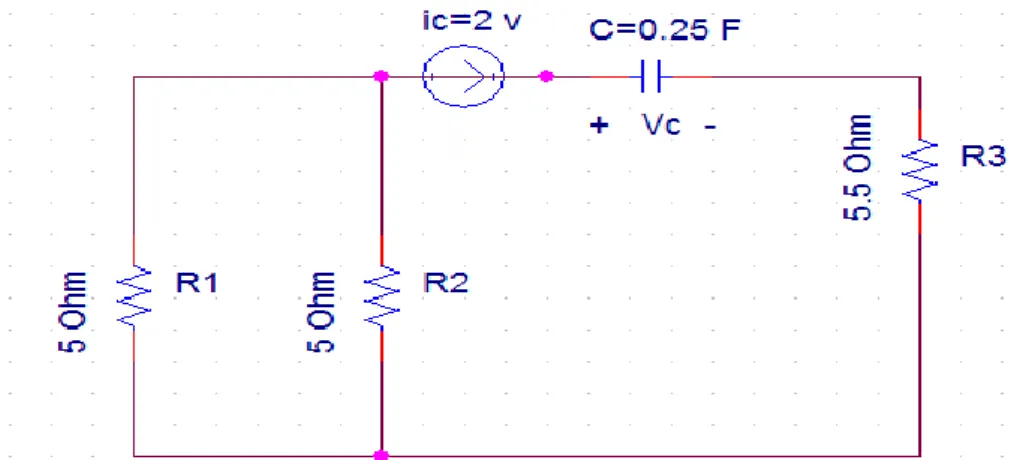
Beberapa resistor dihubungkan dengan kapasitor sebagaimana terlihat pada gambar berikut
Gambar 4.4 Rangkaian RC Kombinasi Seri dan Paralel
27
Analisis rangkaian dilakukan dengan menghitung nilai-nilai ekivalen resistor yang terhubung seri dan paralel sebagai
Dengan rangkaian ekivalennya sebagai berikut
Gambar 4.5 Rangkaian RC Ekivalen
Dengan nilai arus awal yang melewati kapasitor yang menyebabkan timbulnya tegangan pada kedua ujung kapasitor pada rangkaian sebesar . Akan ditentukan bagaimana bentuk karakteristik tegangan yang dihasilkan dari rangkaian tersebut.
Pada waktu aplikasi HAK pada rangkaian ekivalen diperoleh persamaan arus sebagai
Dengan menyederhanakan persamaan akan menghasilkan
Dengan mengambil transformasi Laplace di kedua sisi dari persamaan diferensial rangkaian dan mensubstitusikan nilai–nilai elemen rangkaian dan kondisi awal yang diberikan pada persamaan diferensial diperoleh
[ ]
Dengan mengambil transformasi Laplace invers dari persamaan diperoleh tegangan kapasitor dalam fungsi waktu sebagai berikut
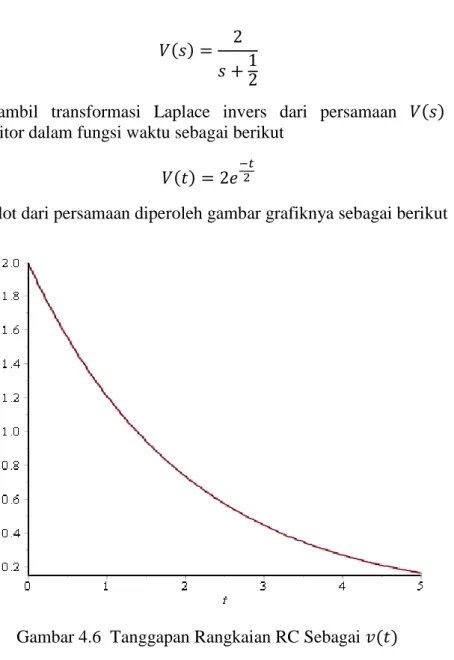
Adapun hasil plot dari persamaan diperoleh gambar grafiknya sebagai berikut
Gambar 4.6 Tanggapan Rangkaian RC Sebagai
Pada gambar 4.6., menunujukkan bahwa bentuk tanggapan alami rangkaian RC merupakan bentuk eksponensial menurun dengan seiring berjalannya waktu sampai 5 konstanta waktu tegangan akan hilang atau menuju nol yang merupakan tanggapan transien (sementara).
4.2 Tanggapan Alami Rangkaian Orde Dua 1. Tanggapan Rangkaian Kurang Teredam
Diberikan gambar rangkaian RLC dengan nilai arus awal yang melewati induktor dan nilai arus awal yang melintasi kedua ujung kapasitor diberikan sebagai:
29
Gambar 4.7 Rangkaian RLC Seri
Aplikasi HTK pada waktu memberikan persamaan integral diferensial karakteristik untuk rangkaian jenis ini sebagai
∫
Mendiferensialkan persamaan terhadap fungsi waktu diperoleh persamaan diferensial orde dua homogen yang linear.
Akan ditentukan bagaimana bentuk karakteristik tanggapan arus yang dihasilkan dari rangkaian. Nilai-nilai parameter frekuensi redaman eksponensial, frekuensi resonansi, dan frekuensi alami diberikan sebagai
√ √
√ √
Berdasarkan nilai-nilai parameter diperoleh yang mengindikasikan kondisi kurang teredam sesuai dengan persamaan (2.12).
Dengan mengambil transformasi Laplace di kedua sisi dari persamaan diferensial dan mensubstitusikan nilai-nilai elemen rangkaian dan kondisi awal yang diberikan pada persamaan diferensial diperoleh
[ ] [ ]
Dengan menggunakan penyelesaian kuadrat pada penyebutnya diperoleh
Dengan mengambil transformasi Laplace invers dari persamaan diperoleh tanggapan arus sebagai
{
} {
} Manipulasi pembilangnya sebagai
{
} {
} {
}
Hasil plot dari persamaan diperoleh gambar grafiknya sebagai berikut
31
Gambar 4.8 Tanggapan Rangkaian RLC Kurang Teredam
Pada gambar 4.8., menunjukkan bahwa bentuk tanggapan alami rangkaian RLC kurang teredam bersifat sinusoida dengan seiring berjalannya waktu tanggapan arus akan hilang atau menuju nol yang merupakan tanggapan transien (sementara).
2. Tanggapan Teredam Berlebih
Diberikan gambar rangkaian RLC dengan nilai arus awal yang melewati induktor dan nilai arus awal yang melintasi kedua ujung kapasitor sebagai
Gambar 4.9 Rangkaian RLC Seri
Analisis rangkaian dilakukan dengan menghitung nilai-nilai tahanan (R) yang terhubung seri.
Dengan gambar rangkaian ekivalennya sebagai berikut
Gambar 4.10 Rangkaian Ekivalen RLC Seri
Aplikasi HTK pada waktu memberikan persamaan diferensial orde dua sebagaimana tanggapan kurang teredam sebagai berikut:
33
Akan ditentukan bagaimana bentuk karakteristik arus yang dihsilkan dari rangkaian.
Nilai frekuensi redaman eksponensial dan frekuensi resonansi adalah
√ √ Berdasarkan nilai-nilai parameter diperoleh
Yang mengindikasikan kondisi teredam berlebih sesuai dengan persamaan (2.13).
Dengan mengambil transformasi Laplace di kedua sisi dari persamaan diferensial dan mesubstitusikan nilai-nilai elemen rangkaian dan kondisi awal yang diberikan pada persamaan diferensial diperoleh
[ ] [ ]
Dengan menggunakan cara alternatif untuk memperoleh konstanta A dan B
Maka diperoleh
Dengan mengambil transformasi Laplace invers dari persamaan diperoleh {
} {
}
Merupakan bentuk tanggapan teredam berlebih sesuai dengan persamaan (2.13) dengan nilai akar-akarnya sebagai berikut:
√ dan
Hasil plot dari persamaan diperoleh gambar grafiknya sebagai
Gambar 4.11 Tanggapan Rangkaian RLC Seri Teredam Berlebih
Pada gambar 4.11., menunjukkan bahwa bentuk tanggapan alami rangkaian RLC teredam berlebih dengan seiring berjalannya waktu sampai 3 konstanta waktu tanggapannya akan menghilang atau menuju nol. Tanggapan ini merupakan tanggapan transien (sementara).
35
3. Tanggapan Teredam Kritis
Diberikan gambar rangkaian RLC sebagai berikut dengan arus awal yang melewati induktor dan arus awal yang melintasi kedua ujung kapasitor diberikan
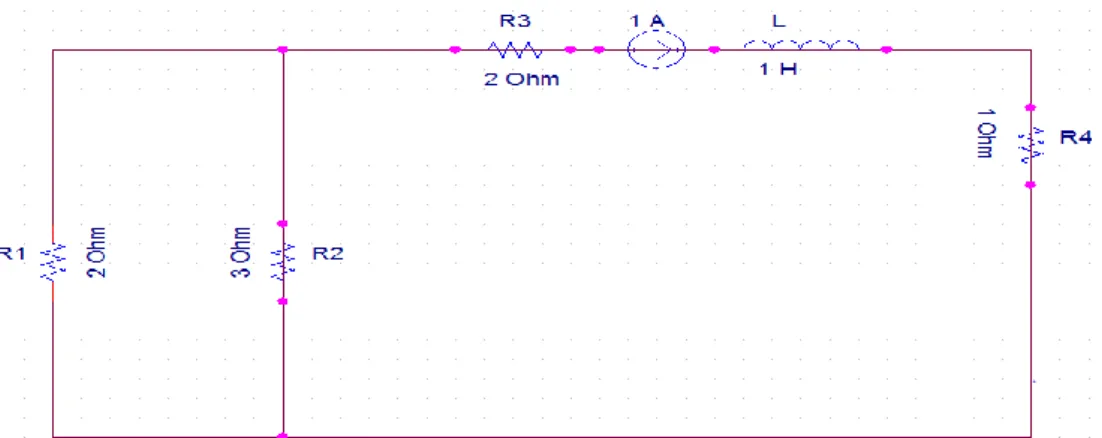
Gambar 4.12 Rangkaian RLC Kombinasi Seri dan Paralel
Analisis rangkaian dilakukan dengan menghitung nilai-nilai resitor yang terhubung paralel dan seri sebagai:
Diperoleh gambar rangkaian ekivalennya sebagai:
Gambar 4. 13 Rangkaian Ekivalen RLC Seri
Aplikasi HTK pada waktu memberikan persamaan diferensial orde dua sebagaimana tanggapan kurang teredam sebagai berikut:
Akan ditentukan bagaimana bentuk karakteristik tanggapan arus yang dihasilkan dari persamaan rangkaian. Nilai-nilai parameter frekuensi peredam eksponensial dan frekuensi resonansi diberikan sebagai
√ √ Berdasarkan harga-harga parameter diperoleh
Mengindikasikan kondisi teredam kritis sesuai dengan persamaan (2.11).
Dengan mengambil transformasi Laplace di kedua sisi dari persamaan diferensial dan mensubstitusikan nilai-nilai elemen rangkaian dan kondisi awal yang diberikan pada persamaan diferensial diperoleh
[ ] [ ]
Dengan cara alternatif diperoleh
37
Dengan mengambil transformasi Laplace invers dari persamaan diperoleh {
} { }
Yang merupakan bentuk umum tanggapan teredam kritis dengan gambar hasil plot sebagai berikut
Gambar 4.14 Tanggapan Rangkaian RLC Seri Teredam Kritis
Pada gambar 4.14., menunjukkan bahwa bentuk tanggapan alami rangkaian RLC teredam kritis dengan seiring berjalannya waktu sampai pada 2 konstatanta waktu tanggapannya menghilang atau menuju nol yang merupakan tanggapan transien (sementara).
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Berdasarkan pembahasan yang telah dibuat, diperoleh kesimpulan antara lain:
1. Karakteristik tanggapan alami dari persamaan diferensial pada rangkaian orde satu diperoleh dalam bentuk fungsi eksponensial menurun dengan seiring berjalannya waktu, tanggapan arus akan menghilang atau menuju nol. Arus ini bersifat transien (sementara).
2. Karakteristik tanggapan alami dari persamaan diferensial pada rangkaian orde dua terdapat tiga jenis, yaitu: teredam berlebih (Overdamped), teredam kritis (Crititially damped), dan kurang teredam (Under damped). Dengan menaikkan nilai tahanan (R) dan menurunkan nilai kapasitor (C) pada rangkaian seri RLC menyebabkan bentuk tanggapan alami berubah-ubah dengan seiring berjalannya waktu tanggapan alami tersebut akan menghilang atau menuju nol yang merupakan tanggapan transien (sementara).
5.2 Saran
Dalam penelitian ini membatasi penyelesaian persoalan persamaan diferensial linear orde dua dengan transformasi Laplace yang diaplikasikan pada rangkaian listrik RLC.
Ada banyak metode lain yang dapat digunakan untuk penelitian selanjutnya.
Diharapkan menggunakan metode lain dalam hal rangkaian yang berbeda.
39
DAFTAR PUSTAKA
Arifin Syamsul. 2013. Metode Transformasi Laplace Matriks Dan Penerapannya Pada Sistem Pegas Massa. [Skripsi]. Yogyakarta: Universitas Islam Negeri Sunan Kalijaga, Program Pascasarjana.
Baiduri. 2002. Persamaan Diferensial dan Matematika Model. Malang: UMM Press.
Bronson Richard., Costa Gabriel., 2007. Persamaan Differensial schaum outline, Edisi Ketiga, Penerbit Erlangga. Jakarta. hlm:155-156.
K. A. Stroud 2003. Matematika Teknik Edisi Kelima, Jilid I, Penerbit Erlangga. Jakarta.
hlm:348-352.
Santoso Widiarti. 1988. Persamaan Diferensial Biasa dengan penerapan modern Edisi Kedua, Penerbit Erlangga. Jakarta. hlm:116.
Sears dan Zemansky. 2003. Fisika Universitas Edisi Kesepuluh, Penerbit Erlangga.
Jakarta.
Sudirham Sudaryatno. 2013. Analisis Rangkaian Listrik. Jilid II. hlm:55-56.
Wlliam H., Jack E.Kemmerly., Steven M. Durbin., 2005 Rangkaian Listrik Edisi Keenam, Jilid I, Penerbit Erlangga. Jakarta.
Yuni Yulida. Juni 2012. Metode Dekomposisi Adomian Laplace Untuk Solusi Persamaan Diferensial Nonlinear Koefisien Fungsi. Jurnal Matematika Murni dan Terapan . Vol 6:1. hlm 18-20.
Zukhri Zainuddin. 2007. Analisis Rangkaian, Edisi kedua, Penerbit Graha Ilmu.
Jakarta.
TABEL TRANSFORMASI LAPLACE
1
41
Sumber: Richard Bronson 2007