PEMBAHASAN
1.1 Pengertian bilangan jam atau modulo
Bilangan adalah suatu konsep matematika yang digunakan untuk pencacahan dan pengukuran. Dalam bilangan tersebut ada banyak macam macam bilangan, diantaranya adalah aritmatika jam/modulo.
Untuk memudahkam penjelasan definisi tersebut maka perlu diilustrasikan sebuah bilangan jam tertentu.
Modulo adalah sebuah operasi bilangan yang menghasilkan sisa pembagian dari suatu bilangan terhadap bilangan lainnya. Misalkan dua bilangan a dan b, a modulo b (disingkat a mod b) adalah bilangan-bilangan bulat sisa pembagian a oleh b. Misalnya, “1 mod 3”, “4 mod 3”, dan “7 mod 3” memiliki hasil 1, karena ketiga bilangan tersebut memiliki sisa 1 jika di bagi oleh 3, sedangkan “9 mod 3” sama dengan 0. Penerapan operasi modulus dalam teori bilangan tergolong aritmatika modulo.
Bilangan modulo adalah bilangan yang banyak bilanganya terbatas. Maksudnya bilangan yang banyak bilanganya terbatas ini adalah angka-angka yang terdapat pada permukaan sebuah jam. Pada aritmatika jam angka-angka yang dapat dipergunakan adalah persis sama dengan angka-angka pada jam tersebut dan tidak mengenal adanya bilangan negatif.
1.1.1 Teori Dasar Aritmetika Modulo
Misalkan a adalah bilangan bulat dan m adalah bilangan bulat > 0. Operasi a mod m (dibaca “a modulo m”) memberikan sisa jika a dibagi dengan m
Notasi: a mod m = r sedemikian sehingga a = mq + r, dengan 0 <= r < m
Bilangan m disebut modulus atau modulo, dan hasil aritmetika modulo m terletak di dalam himpunan {0, 1, 2, …, m – 1}
Kegiatan pengayaan yang dapat dilaksanakan dalam pembelajaran matematika di sekolah dasar yang berkenaan dengan kongruensi adalah pembelajaran aritmatika jam. Sebagai contoh, Jika sekarang adalah pukul 07.00 maka pukul berapa jam kemudian? Untuk menentukan 8 jam setelah pukul 09.00 kita dapat menggunakan gambar jam dan akan kita peroleh 8 jam setelah pukul 09.00 adalah pukul 05.00. Masalah ini kita tulis 9 + 8 = 5, di mana lambang menunjukkan penjumlahan jam. Hasil ini dapat pula diperoleh dengan menggunakan penjumlahan biasa 9 + 8 = 17, kemudian 17 dibagi oleh 12 dan kita pilih sisa pembagian itu sebagai jawabannya, yaitu 5. Dengan demikian, untuk memperoleh hasil penjumlahan dua buah bilangan dalam jam 12-an, kita jumlahkan bilangan-bilangan itu dengan cara biasa, kemudian cari sisa hasil pembagiannya oleh 12.
Bilangan jam dapat dibedakan atas dua hal yaitu:
Contoh :
a. Modulo 4
Angka yang digunakan , 0,1,2,3
b. Modulo 5
Angka yang digunakan 0,1,2,3,4
2. Bilangan yang dimulai dengan angka satu dan diakhiri dengan angka nol
Contoh :
a. Modulo 2 hanya memuat 2 angka yaitu : 1 dan 0 b. Modulo 3 hanya memuat 3 angka yaitu : 1, 2 darn 0 c. Modulo 4 hanya memuat 4 angka yaitu : 1, 2, 3 dan 0 d. Modulo 5 hanya memuat 5 angka yaitu : 1, 2, 3, 4 dan 0 e. Modulo 6 hanya memuat 6 angka yaitu : 1, 2, 3, 4, 5 dan 0
2.1 Operasi operasi bilangan modulo
Pada umumnya bilangan modulo yang sering digunakan adalah bilangan modulo yang dimulai dengan angka satu dan diakhiri dengan angka nol.
Contoh :
Pada modulo 5 berapakah 3 + 4 ? Jawab :
Putarlah jarum jam sebanyak 4 langkah dari 3 ke kanan. Langkah jarum berhenti pada angka 2.
Jadi, 3 + 4 = 2 pada modulo 5
2.1.1 Operasi penjumlahan (Z, +)
Z ={0,1,2,3, …} Diberikan (Z,+) maka ∀a,b,c ϵ z berlaku :
a. Close a + b Zϵ
Contoh :
1.) Pada Modulo 4 (Z4)
3 + 4 = . . . . ? => 3 + 4 = 7 = 3 (mod 4) 2 + 4 = . . . . ? => 2 + 4 = 6 = 2 (mod 4)
2.) Pada modulo 5 (Z5)
3 + 4 = . . . . ? => 3 + 4 = 7 = 2 (mod 5) 2 + 4 = . . . . ? => 2 + 4 = 6 = 1 (mod 5) 3 + 6 = . . . . ? => 2 + 6 = 8 = 3 (mod 5)
b. Asosiatif, a + (b + c) = (a + b) + c
Contoh :
1.) Pada modulo 6 (Z6)
7 + (4 + 9) = (7 + 4) + 9 20 = 20
= 2 (mod 6)
2.) Pada modulo 7 (Z7)
11 + (7 + 13) = (11 + 7) + 13 31 = 31
Untuk membuktikan sifat close, asosiatif, elemen identitas, invers, dan komutatif dari
Untuk menyelidiki berlaku tidaknya sifat assosiatifnya, Cukup dengan memberikan satu contoh saja (1 + 2) + 3 = 3 + 3 = 2 1 + (2 + 3) = 1 + 1 = 2. Terlihat pada {Z4,+) berlaku sifat assosiatif. Untuk menyelidiki elemen identitasnya kita perhatikan perhitungan penjumlahan di atas dan kita tulis lagi sebagai berikut:
0 + 0 = 0 1 + 0 = 1 2 + 0= 2 3 + 0 = 3
0 + 1 = 1 1 + 1 = 2 2 + 1= 3 3 + 1 = 0
0 + 2 = 2 1 + 2 = 3 2 + 2= 0 3 + 2 = 1
0 + 3 = 3 1 + 3 = 0 2 + 3= 1 3 + 3 = 2
Setelah memperhatikan bilangan yang tertulis tebal dapat disimpulkan unsur identitas bilangan modulo 4 adalah bilangan 0. Untuk mengetahui tentang elemen inversnya kita perhatikan table penjumlahan dan kita tulis lagi sebagai berikut:
0 + 0 = 0 1 + 0 = 1 2 + 0= 2 3 + 0 = 3
0 + 1 = 1 1 + 1 = 2 2 + 1= 3 3 + 1 = 0
0 + 2 = 2 1 + 2 = 3 2 + 2= 0 3 + 2 = 1
0 + 3 = 3 1 + 3 = 0 2 + 3= 1 3 + 3 = 2
Dengan memperhatikan bilangan yang tertulis tebal dapat kita ketahui invers dari setiap elemen pada modulo 4 tersebut. Yaitu invers 0 adalah 0, inversnya 1 adalah 3, inversnya 2 adalah 2, dan inversnya 3 adalah 1.
Dari penyelidikan dapat disimpulkan bahwa operasi penjumlahan pada bilangan modulo 4 memiliki sifat-sifat closed, komutatif, assosiatif, elemen identitas,dan setiap elemen memiliki invers, sehingga dapata katakana group Abel.
e. Komutatif, a x b = b x a
Untuk membuktikan sifat-sifat perkalian yaitu; close, asosiatif, elemen identitas, invers, dan komutatif.
0 x 0 = 0 1 x 0 = 0 2 x 0 = 0 3 x 0 = 0
0 x 1 = 0 1 x 1 = 1 2 x 1 = 2 3 x 1 = 3
0 x 2 = 0 1 x 2 = 2 2 x 2 = 0 3 x 2 = 2
0 x 3 = 0 1 x 3 = 3 2 x 3 = 2 3 x 3 = 1
Berdasarkan perhitungan tersebut terlihat bahwa dalam modulo 4 berlaku sifat-sifat: close, komutatif. Untuk menyelidiki berlaku tidaknya system asosiatif, cukup dengan mem-berikan satu contoh saja ( 1 x 2) x 3 = 2 x 3 = 2 dan 1 x (2 x 3) = 1 x 2 = 2. Terlihat pada ( Z4,
x) berlaku sifat asosiatif. Selanjutnya perhatikan perhitungan perkalian bilangan modulo 4 berikut:
0 x 0 = 0 1 x 0 = 0 2 x 0 = 0 3 x 0 = 0
0 x 1 = 0 1 x 1 = 1 2 x 1 = 2 3 x 1 = 3
0 x 2 = 0 1 x 2 = 2 2 x 2 = 0 3 x 2 = 2
0 x 3 = 0 1 x 3 = 3 2 x 3 = 2 3 x 3 = 1
Setelah memperhatikan bilangan yang tertulis tebal dapat disimpulkan unsur identitas bilangan modulo 4 adalah bilangan 1. Kemudian perhatikan perhitungan perkalian bilangan modulo 4 dan tulis lagi sebagai berikut:
0 x 0 = 0 1 x 0 = 0 2 x 0 = 0 3 x 0 = 0
0 x 1 = 0 1 x 1 = 1 2 x 1 = 2 3 x 1 = 3
0 x 2 = 0 1 x 2 = 2 2 x 2 = 0 3 x 2 = 2
0 x 3 = 0 1 x 3 = 3 2 x 3 = 2 3 x 3 = 1
Dengan memperhatikan bilangan yang tertulis tebal dapat diketahui invers dari elemen pada bilangan modulo 4 tersebut yaitu inversnya 1 adalah 1 dan 3 inversnya 3. Sedangkan 0 dan 2 tidak memiliki invers.
Dari proses penyelidikan dapat disimpulkan bahwa operasi perkalian pada modulo 4 merupakan system matematika yang memiliki sifat close, komutatif, assosiatif, memiliki ele-men identitas tetapi tidak setiap eleele-men bilangan modulo 4 meiliki invers sehingga belum da-pat dikatakan grup Abel.
2.2 Aplikasi Bilangan jam atau modulo
Teori bilangan merupakan bagian dari matematika yang tergolong sudah tua usianya. Namun demikian, akhir-akhir ini Teori Bilangan menjadi dasar dari pengembangan beberapa cabang matematika seperti cryptografi (tulisan rahasia/sandi) dan ilmu pengetahuan komputer
sebagai salah satu pengembangan dalam matematika terapan. Sistem modulo merupakan bagian yang cukup penting dalam Teori Bilangan.
Salah satu penggunaan sistem modulo yang sangat menarik adalah untuk menentukan hari . Baik hari yang telah lampau ataupun yang akan datang.
Syaratnya adalah tanggal, bulan dan tahun yang akan dicari hari diketahui dengan pasti. Sering kita alami kejadian untuk menentukan hari suatu tanggal yang kita anggap begitu bersejarah bagi kita tak berhasil kita ingat dengan benar. Mau melihat kalendar sudah lama dirobek atau bahkan sudah tidak ada lagi. Karena kesulitan mencari kalender tahun- tahun yang telah lampau untuk menentukan hari tanggal yang penting adalah suatu permasalahan yang harus dicari penyelesaiana atau jawabannya secara umum dan matematis. Oleh karena itu, berikut ini akan disajikan beberapa cara yang mudah dan sederhana untuk keperluan itu.
Cara yang akan sajikan di bawah ini tidak hanya dipakai untuk mengingat hari yang telah lampau, melainkan juga untuk menentukan hari yang akan datang.
2.2.1 Aplikasi bilangan jam atau modulo Menentukan hari
Pandang himpunan H = {Minggu, Senin, Selasa, Rabu, Kamis, Jum’at, Sabtu}. Dengan menggunakan tiga pengertian pokok, yakni:
1. Sistem modulo 7. 2. Tahun biasa= 365 hari.
3. Tahun kabisat = 366 hari (tahun yang bilangannya habis dibagi empat).
Maka akan muncul rumus-rumus yang dapat dipakai untuk mencari hari dari tanggal, bulan, dan tahun yang diinginkan. Pada prinsipnya jumlah semua hari dari Kalendar Masehi dimulai dari tanggal 1 bulan Januari tahun 1 sampai dengan tanggal x bulan y tahun z yang akan dicari harinya, dihitung kemudian hasilnya dibagi dengan 7. Dengan beberapa percobaan yang nanti akan kami uraikan, ternyata apabila sisanya nol jatuh pada hari sabtu, bila sisanya 1 jatuh pada hari Minggu dan seterusnya akhirnya bila sisanya 6 jatuh pada hari Jum’at, seperti pada tabel berikut ini.
Perlu diketahui bahwa jumlah hari tahun biasa = 365 hari,
berarti 365 = 1 (modulus 7), sedangkan jumlah hari tahun kabisat = 366 hari, berarti 366 = 2 (modulus 7).
Suatu tahun tertentu dapat dinyatakan sebagai jumlahan tahun biasa dan tahun kabisat, sehingga jumlah harinya juga dapat dihitung.
Misal A tahun = B tahun biasa + C tahun kabisat.
Dengan sedikit gambaran di atas maka untuk menentukan hari tertentu dapat dipergunakan beberapa cara sebagai berikut.
Cara I :
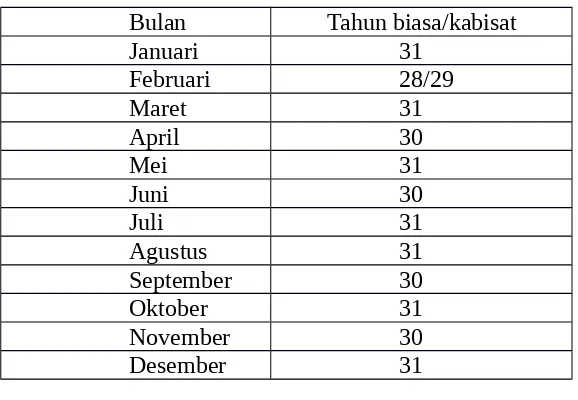
Tabel 2. Jumlah hari tiap-tiap bulan
Bulan Tahun biasa/kabisat
sehingga, U + V – W = 1945 + 486 – 136 = 2295 = 6 (modulo 7)
a.) Kemerdekaan Republik Indonesia 17 agustus 1945 jatuh pada hari apa ? Dengan menggunakan cara 2 : jatuh pada hari Jum’at
2.4.2 Aplikasi bilangan jam atau modulo Menentukan jam
Di setiap jam dinding yang normal, ada terdapat 12 angka. Yaitu 1, 2, 3, 4, … 12. Pada jam digital, angka 12 diganti dengan angka 0. Sehingga angka-angka yang tersedia adalah 0, 1, 2, 3 … 11. Walaupun jam digital bisa di-setting sehingga menunjukkan angka 0, 1, 2, 3 … 23, banyak orang lebih memilih memakai setting 12-jam, yaitu 0, 1, 2, 3, .. 11. Begitu pula para matematikawan. Mereka lebih suka memakai angka 0, 1, 2, 3, … 11. Jangan tanya kenapa.
Di dalam artikel ini, semua jam akan mengikuti sistem 12-jam ala matematikawan, yaitu jam dinding dengan angka 0, 1, 2, 3 … 11. Angka 0 berada di posisi angka 12. Agara lebih mudah dipahami, perhatikan gambar berikut :
X + Y + Z = S (modulus 7)
Kita tahu bahwa dalam 12 jam, jarum jam akan kembali ke posisinya semula, yaitu 0. Kita katakan bahwa jarum jam akan membutuhkan 12 jam untuk melakukan satu “putaran penuh”. Dengan kata lain, satu putaran penuh = 12 jam. Sekarang, seperti layaknya kebiasaan di dunia matematika yang membosankan, akan kita lakukan ritual simbolisasi
a = menyatakan waktu. Untuk masa lalu diberi tanda negatif (-) dan untuk masa yang akan datang tidak diberi tanda, alias positif (+).
q = menyatakan banyaknya putaran
d = menyatakan waktu yang diperlukan untuk melakukan satu “putaran penuh”. Dengan demikian d = 12.
r = menyatakan sisa waktu setelah berputar-putar.
Contoh :
1. Bila sekarang jarum jam tepat menunjukkan pada angka 0. Dalam 32 jam mendatang, ke angka berapakah jarum jam akan menunjuk?
2. Bila sekarang jarum jam tepat menunjukkan pada angka 0. Empat jam yang lalu, di angka berapakah jarum jam menunjuk?
Pembahasan
1. Waktu yang dimiliki adalah 32 jam (di masa yang akan datang). Dengan demikian a = 32.
Dalam 32 jam, jarum jam melakukan dua kali putaran penuh. Dengan demikian q = 2.
Karena jarum jam berputar dua kali, maka waktu yang habis untuk berputar-putar adalah 24 jam. Sisanya adalah 8 jam. Dengan demikian r = 8.
Secara matematis dapat dituliskan 32 = 2.12 + 8
2. Waktu yang dimiliki adalah 4 jam (di masa lampau). Dengan demikian a = -4.
Dalam 4 jam (ke belakang), jarum jam belum melakukan satu kalipun putaran penuh. Dengan demikian q = 0.
Secara matematis dapat dituliskan -4 = 0.12 + -4
Karena jam kita tidak memiliki angka -4, maka kita harus mengubahnya menjadi suatu angka yang “dikenali” oleh jam kita. Karena kita tahu dalam 12 jam, si jarum pasti akan kembali ke posisinya semula, maka jam -4 akan menunjukkan angka yang sama dengan jam -4 + 12 alias 8. Dengan
PENUTUP
2.3 Kesimpulan
Bahwa pada bilangan modulo sifat-sifat dari penjumlahan adalah closed, assosiatif, komutatif, elemen identitas 0 dan inversnya di setiap elemen bilangan memiliki invers sehingga disebut group Abel.
DAFTAR PUSTAKA
Dedi Heryadi. 2007. Matematika. Jakarta: Yudhistira.
Sartono. 2008. Matematika Ib. Jakarta: Erlangga
Sunardi,dkk. 2008. Matematika II. Jakarta: Bumi Aksara.
https://books.google.co.id/books?