MATEMATIKA DISKRET – Srava Chrisdes 1 1 1 1
ALJABAR BOOLEAN
9.1. Definisi Aljabar Boolean
Aljabar Boolean merupakan aljabar yang berhubungan dengan variabel-variabel biner (0 atau 1) dan operasi-operasi logik. Variabel-variabel diperlihatkan dengan huruf-huruf alfabet dan tiga operasi dasar, yakni AND, OR, dan NOT (komplemen).
AND dinotasikan 𝑥 ∗ 𝑦 atau 𝑥𝑦 OR dinotasikan 𝑥 + 𝑦
NOT (komplemen) dinotasikan 𝑥′ atau 𝑥 Perhatikan tabel berikut.
Tabel AND
𝒙 𝒚 𝒙𝒚
1 1 1
1 0 0
0 1 0
0 0 0
Tabel OR
𝒙 𝒚 𝒙 + 𝒚
1 1 1
1 0 1
0 1 1
0 0 0
Tabel NOT (Komplemen)
𝒙 𝒙 ′
1 0
0 1
Contoh 1:
Tentukan nilai dari 1 ∙ 0 + (0 + 1)′ ! Jawab:
1 ∙ 0 + (0 + 1)′ = 0 + 1′ = 0 + 0 = 0
Selanjutnya, lihat definisi formal mengenai aljabar Boolean berikut.
Misalkan B adalah himpunan yang didefinisikan pada dua operasi biner (+ dan *) dan sebuah operasi unar („), serta menggunakan dua elemen 0 dan 1, maka (B, +, *, „) disebut aljabar Boolean jika memenuhi aksioma-aksioma berikut untuk setiap elemen 𝑥, 𝑦, dan 𝑧 dari himpunan B.
MATEMATIKA DISKRET – Srava Chrisdes 2 2 2 2
Hukum Komutatif 𝑥 + 𝑦 = 𝑦 + 𝑥 𝑥𝑦 = 𝑦𝑥
Hukum Asosiatif 𝑥 + 𝑦 + 𝑧 = 𝑥 + (𝑦 + 𝑧) 𝑥𝑦 𝑧 = 𝑥(𝑦𝑧) Hukum Distributif 𝑥 + 𝑦𝑧 = 𝑥 + 𝑦 (𝑥 + 𝑧) 𝑥 𝑦 + 𝑧 = 𝑥𝑦 + (𝑥𝑧)
Hukum Identitas 𝑥 + 0 = 𝑥 𝑥 ∙ 1 = 𝑥
Hukum Komplemen 𝑥 + 𝑥′ = 1 𝑥 ∙ 𝑥′ = 0
9.2. Definisi Ekspresi Boolean
Misalkan B = {0, 1}. Maka, Bn { 𝑥1, 𝑥2, … , 𝑥𝑛 |𝑥𝑖 ∈ B untuk 1 ≤ 𝑖 ≤ 𝑛} adalah suatu himpunan dari semua 𝑛-tupel yang mungkin atas 0 dan 1. Suatu fungsi dari B ke B ini n disebut sebagai fungsi Boolean atau ekspresi Boolean.
Contoh 2:
Tentukan nilai dari ekspresi Boolean berikut: 𝐸(𝑥, 𝑦, 𝑧) = 𝑥𝑦 + 𝑧′ ! Jawab:
𝒙 𝒚 𝒛 𝒙𝒚 𝒛′ 𝑬
1 1 1 1 0 1
1 1 0 1 1 1
1 0 1 0 0 0
1 0 0 0 1 1
0 1 1 0 0 0
0 1 0 0 1 1
0 0 1 0 0 0
0 0 0 0 1 1
Contoh 3:
Tentukan nilai dari ekspresi Boolean berikut: 𝐸(𝑥, 𝑦, 𝑧) = 𝑥𝑦𝑧′ + 𝑥𝑦′𝑧′ + 𝑥𝑦′𝑧 + 𝑥′𝑦𝑧′ ! Jawab:
𝒙 𝒚 𝒛 𝒙𝒚𝒛′ 𝒙𝒚′𝒛′ 𝒙𝒚′𝒛 𝒙′𝒚𝒛′ 𝑬
1 1 1 0 0 0 0 0
1 1 0 1 0 0 0 1
1 0 1 0 0 1 0 1
1 0 0 0 1 0 0 1
0 1 1 0 0 0 0 0
0 1 0 0 0 0 1 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0
Berikutnya akan diberikan contoh bagaimana mencari ekspresi Boolean jika diketahui nilainya.
Contoh 4:
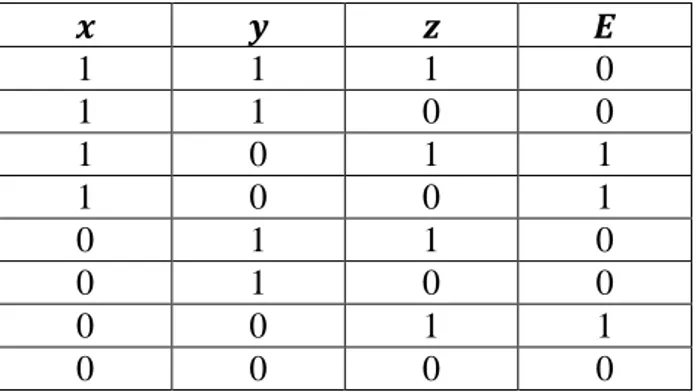
Carilah ekspresi Boolean dari 𝑥, 𝑦, dan 𝑧 yang diberikan dalam tabel berikut:
MATEMATIKA DISKRET – Srava Chrisdes 3 3 3 3
𝒙 𝒚 𝒛 𝑬
1 1 1 0
1 1 0 0
1 0 1 1
1 0 0 1
0 1 1 0
0 1 0 0
0 0 1 1
0 0 0 0
Jawab:
Untuk mengetahui ekspresi Boolean, fokus pada angka “1” dalam kolom 𝐸, yaitu baris ketiga, baris keempat, dan baris ketujuh.
Baris ke-3 : 𝑥 = 1, 𝑦 = 0, 𝑧 = 1 → ketiganya menghasilkan 𝐸 = 1 sehingga diperoleh 𝑥𝑦′𝑧
Baris ke-4 : 𝑥 = 1, 𝑦 = 0, 𝑧 = 0 → ketiganya menghasilkan 𝐸 = 1 sehingga diperoleh 𝑥𝑦′𝑧′
Baris ke-7 : 𝑥 = 0, 𝑦 = 0, 𝑧 = 1 → ketiganya menghasilkan 𝐸 = 1 sehingga diperoleh 𝑥′𝑦′𝑧
Dengan demikian, 𝐸(𝑥, 𝑦, 𝑧) = 𝑥𝑦′𝑧 + 𝑥𝑦′𝑧′ + 𝑥′𝑦′𝑧.
9.3. Tabel Identitas Boolean
Selain kelima aksioma yang telah dipaparkan pada Subbab 9.1, aljabar Boolean juga memiliki beberapa hukum lainnya. Perhatikan Tabel Identitas Boolean berikut.
Tabel Identitas Boolean
Hukum Idempoten 𝑥 + 𝑥 = 𝑥 𝑥𝑥 = 𝑥
Hukum Dominasi 𝑥 + 1 = 1 𝑥 ∙ 0 = 0
Hukum Absorpsi 𝑥 + 𝑥𝑦 = 𝑥 𝑥 𝑥 + 𝑦 = 𝑥
Hukum Involusi (𝑥′)′ = 𝑥
Hukum De Morgan (𝑥 + 𝑦)′ = 𝑥′𝑦′ (𝑥𝑦)′ = 𝑥′ + 𝑦′
9.4. Dualitas
Dalam aljabar Boolean, ada istilah dualitas. Untuk mencari bentuk dual dari suatu aljabar Boolean, dapat diperoleh dengan:
“+” diubah menjadi “*”
“*” diubah menjadi “+”
“1” diubah menjadi “0”
“0” diubah menjadi “1”
MATEMATIKA DISKRET – Srava Chrisdes 4 4 4 4 Jika terdapat variabel seperti 𝑥 atau 𝑥′ pada suatu aljabar Boolean, maka bentuk tersebut tetap dalam bentuk dualnya.
Contoh 5:
Buktikan bahwa (𝑥 ∙ 𝑥 + 𝑦 ∙ 0 ) ′ = 𝑥′ , dan tuliskanlah bentuk dualnya!
Jawab:
x x y0
x
x 0
(Hukum Dominasi)
x x
(Hukum Identitas)
x
(Hukum Idempoten)
Bentuk dualnya:
x
x
y1 x
9.5. Bentuk Normal Disjungtif (Disjungtive Normal Form)
Suatu variabel Boolean (atau komplemennya) disebut sebagai literal. Contoh literal adalah 𝑥, 𝑥′, 𝑦′, 𝑧, dan sebagainya.
Suatu minterm atau perkalian dasar adalah hasil kali dari n literal dengan satu literal mewakili satu variabel (n bilangan asli). Contoh minterm adalah 𝑥′, 𝑥𝑦, 𝑥′𝑦, 𝑥𝑦𝑧′, 𝑦′𝑧, dan sebagainya. Contoh yang bukan minterm antara lain 𝑥𝑥′, 𝑥𝑦𝑥′𝑧, 𝑥𝑦𝑥𝑦, dan sebagainya.
Perhatikan contoh berikut untuk memahami perbedaan antara variabel biasa dengan literal.
Diberikan ekspresi Boolean
𝐸 𝑥, 𝑦, 𝑧 = 𝑥𝑧′ + 𝑥′𝑦
Ekspresi Boolean di atas memiliki 3 variabel (𝑥, 𝑦, 𝑧), 4 literal (𝑥, 𝑥′, 𝑦, 𝑧′), dan 2 minterm (𝑥𝑧′, 𝑥′𝑦). [Pahami perbedaan antara variabel biasa dan literal.]
Ekspresi Boolean disebut bentuk normal disjungtif (dnf) jika merupakan suatu minterm atau penjumlahan 2/lebih minterm yang masing-masing mintermnya tidak terkandung dalam minterm lainnya. Bentuk normal disjungtif pada suatu ekspresi Boolean juga sering disebut sebagai ekspansi sum-of-products (SoP).
Ekspresi Boolean dnf yang setiap mintermnya mengandung semua variabel disebut bentuk lengkap normal disjungtif (full dnf).
Sebagai contoh,
1( , , )
E x y z x y → dnf / SoP
2( , , )
E x y z xzx yz xy z → dnf / SoP
3( , , )
E x y z xzy z xyz → bukan dnf karena xz terkandung dalam xyz
4( , , )
E x y z xyzx yz x y z → full dnf / SoP Contoh 6:
Nyatakanlah ekspresi Boolean E x y z( , , )(xy z) menjadi bentuk dnf dan full dnf!
Jawab:
MATEMATIKA DISKRET – Srava Chrisdes 5 5 5 5 (dengan Hukum de Morgan)
(dengan Hukum Distributif) ( , , ) ( )
(dilanjutkan den
( )
gan Hukum Identitas) E x y z xy z
x y z
x z yz dnf
[Perhatikan minterm x z belum ada variabel y, dan minterm y z belum ada variabel x.]
(dengan Hukum Komplemen) (dengan Hukum Di
1 1
( ) ( )
stributif)
(karena ada minterm yang sama, gunakan Hukum Idempo ( ,
t )
) ,
en x y
x z y z
x y y z x x y z
E x
x yz xy z
x yz y z
z x y z
x y z xyz full dnf
Perlu diperhatikan bahwa semua ekspresi Boolean yang full dnf, pasti dnf. Namun, ekspresi Boolean yang dnf belum tentu full dnf.
Apabila ekspresi Boolean sudah diketahui dalam bentuk normal disjungtif, maka bentuk dualnya akan disebut sebagai bentuk normal konjungtif (conjungtive normal form – cnf), atau sering juga disebut ekspansi product-of-sums (PoS).
Contoh 7:
Nyatakanlah ekspresi Boolean E x y z( , , )(xy z) menjadi bentuk cnf!
Jawab:
Berdasarkan Contoh 6, telah diketahui bahwa full dnf-nya adalah:
( , , )
E x y z x yz x y z xy z
Maka, dengan menggunakan teknik dualitas, bentuk cnf dari E x y z( , , )(xy z) adalah:
(x y z) (x y z) (x y z) 9.6. Gerbang Logika
Gerbang logika merupakan pembentuk sistem elektronika digital yang berfungsi mengubah satu atau beberapa input menjadi suatu sinyal output logis.
Gerbang logika beroperasi berdasarkan sistem bilangan biner, yaitu hanya memiliki dua kode simbol yakni 0 dan 1.
Tabel Gerbang Logika
Nama Gerbang Gerbang Lambang
NOT 𝐸 = 𝑥′
OR 𝐸 = 𝑥 + 𝑦
AND 𝐸 = 𝑥𝑦
MATEMATIKA DISKRET – Srava Chrisdes 6 6 6 6
NOR (not or) 𝐸 = (𝑥 + 𝑦)′
NAND (not and) 𝐸 = (𝑥𝑦)′
XOR (exclusive or) 𝐸 = 𝑥 ⊕ 𝑦
Contoh 8:
Buatlah rangkaian gerbang logika dari 𝐸(𝑥, 𝑦) = 𝑥 + 𝑦 𝑥′ ! Jawab:
Apabila gerbang diawali dengan n input, bisa digambarkan seperti berikut ini.
Contoh 9:
Diketahui rangkaian gerbang logika berikut:
Tentukan ekspresi Boolean dari rangkaian gerbang logika di atas!
Jawab:
𝐸
𝑥′
𝑥 + 𝑦
MATEMATIKA DISKRET – Srava Chrisdes 7 7 7 7 1
2 E
3 5
4
1: 𝑥 + 𝑦 + 𝑧 ; 2: 𝑥′ ; 3: 𝑦′ ; 4: 𝑧′ ; 5: 𝑥′𝑦′𝑧′
Jadi, ekspresi Booleannya adalah 𝐸 = 𝑥 + 𝑦 + 𝑧 𝑥′𝑦′𝑧′.
9.7. Penyederhanaan Ekspresi Boolean
Ekspresi Boolean dikatakan dnf minimal jika ekspresi Boolean dnf tersebut tidak dapat disederhanakan lagi. Sebagai contoh,
1( , , )
E x y z xzy z → dnf minimal
2( , , )
E x y z xyx y → dnf, tapi bukan dnf minimal
3( , , )
E x y z xyzx y z → full dnf, dan dnf minimal
4( , , )
E x y z x yz x y z x y z → full dnf, tapi bukan dnf minimal
Ada dua cara yang dapat digunakan untuk menyederhanakan ekspresi Boolean menjadi dnf minimal, yaitu:
1) dengan metode konsensus, dan 2) dengan peta Karnaugh.
A. Metode Konsensus
Misalkan 𝑃1 dan 𝑃2 adalah suatu minterm sedemikian sehingga tepat satu variabel (misal 𝑎) muncul dengan komplemennya (misal 𝑎′) pada salah satu dari 𝑃1 atau 𝑃2. Maka, yang disebut konsensus dari 𝑃1 dan 𝑃2 adalah hasil kali (tanpa pengulangan) dari literal 𝑃1 dan literal 𝑃2 setelah 𝑎 dan 𝑎′ dihilangkan. Sebagai contoh,
𝑥𝑦′ dan 𝑦 → konsensusnya 𝑥
𝑥𝑦′ dan 𝑥′𝑦 → tidak memiliki konsensus; karena ada lebih dari satu variabel yang muncul dengan komplemennya, yaitu variabel 𝑥 dan variabel 𝑦
𝑥′𝑧′ dan 𝑥′𝑦′𝑧 → konsensusnya 𝑥′𝑦′
𝑥′𝑦′ dan 𝑥′𝑦′z → tidak memiliki konsensus; karena tidak ada variabel yang muncul dengan komplemennya
Contoh 10:
Tentukan dnf minimal dari E x y z( , , )xyzxy z x y z xyzx yz dengan metode konsensus!
Jawab:
MATEMATIKA DISKRET – Srava Chrisdes 8 8 8 8 𝑥
𝑥′
𝑦 𝑦′
𝑥
𝑥′
’ 𝑦𝑧
’
𝑦𝑧′
’
𝑦′𝑧′
’
𝑦′𝑧 ( , , )
E x y z xyzxy z x y z xyzx yz
karena 𝑥𝑦𝑧 dan 𝑥𝑦′𝑧 berkonsensus 𝑥𝑧, lalu 𝑥𝑦𝑧′ dan 𝑥′𝑦𝑧′ berkonsensus 𝑦𝑧′, maka:
( , , ) xyz xy z xz x y z xyz x yz yz E x y z
karena 𝑥𝑧 terkandung dalam 𝑥𝑦𝑧, maka 𝑥𝑧 + 𝑥𝑦𝑧 = 𝑥𝑧 1 + 𝑦 = 𝑥𝑧 karena 𝑥𝑧 terkandung dalam 𝑥𝑦′𝑧, maka 𝑥𝑧 + 𝑥𝑦′𝑧 = 𝑥𝑧 1 + 𝑦′ = 𝑥𝑧 ( , , ) xz x y z
E x y z xyzx yz yz
karena 𝑦𝑧′ terkandung dalam 𝑥𝑦𝑧′, maka 𝑦𝑧′ + 𝑥𝑦𝑧′ = 𝑦𝑧′ 1 + 𝑥 = 𝑦𝑧′
karena 𝑦𝑧′ terkandung dalam 𝑥′𝑦𝑧′, maka 𝑦𝑧′ + 𝑥′𝑦𝑧′ = 𝑦𝑧′ 1 + 𝑥′ = 𝑦𝑧′
( , , ) xz x y z y E x y z z
karena 𝑥𝑧 dan 𝑥′𝑦′𝑧 berkonsensus 𝑦′𝑧, maka:
( , , ) xz x y z y z yz E x y z
karena 𝑦′𝑧 terkandung dalam 𝑥′𝑦′𝑧, maka 𝑦′𝑧 + 𝑥′𝑦′𝑧 = 𝑦′𝑧 1 + 𝑥′ = 𝑦′𝑧 ( , , ) x
E x y z zyzyz
Jadi, dnf minimal dari E x y z( , , )xyzxy z x y z xyzx yz adalah:
( , , )
E x y z xzy z yz
Jika suatu ekspresi Boolean merupakan dnf minimal, maka setiap mintermnya disebut sebagai prime implikan. Sebagai contoh, perhatikan kembali Contoh 10 di atas. Ekspresi Boolean
( , , )
E x y z xyzxy z x y z xyzx yz memiliki dnf minimal
( , , )
E x y z xzy z yz sehingga prime implikannya adalah xz , y z , dan yz.
B. Peta Karnaugh
Peta Karnaugh dua variabel adalah sebagai berikut.
Peta Karnaugh tiga variabel adalah sebagai berikut.
dengan
area 𝑥 mencakup sel: 𝑥𝑦𝑧, 𝑥𝑦𝑧′, 𝑥𝑦′𝑧′, dan 𝑥𝑦′𝑧;
area 𝑥′ mencakup sel: 𝑥′𝑦𝑧, 𝑥′𝑦𝑧′, 𝑥′𝑦′𝑧′, dan 𝑥′𝑦′𝑧;
area 𝑦 mencakup sel: 𝑥𝑦𝑧, 𝑥𝑦𝑧′, 𝑥′𝑦𝑧, dan 𝑥′𝑦𝑧′;
area 𝑦′ mencakup sel: 𝑥𝑦′𝑧′, 𝑥𝑦′𝑧, 𝑥′𝑦′𝑧′, dan 𝑥′𝑦′𝑧;
area 𝑧 mencakup sel: 𝑥𝑦𝑧, 𝑥′𝑦𝑧, 𝑥𝑦′𝑧, dan 𝑥′𝑦′𝑧;
area 𝑧′ mencakup sel: 𝑥𝑦𝑧′, 𝑥𝑦′𝑧′, 𝑥′𝑦𝑧′, dan 𝑥′𝑦′𝑧′.
MATEMATIKA DISKRET – Srava Chrisdes 9 9 9 9 𝑦′
’ 𝑦
’
𝑥′
’ 𝑥 𝑥′
’ 𝑥
𝑦′
’ 𝑦
’
𝑦′
’
𝑦′
’ 𝑦
’
𝑦
’
Ada beberapa aturan dalam membuat blok pada peta Karnaugh, yaitu:
a) Blok yang diperbolehkan adalah secara horizontal atau vertikal, tidak boleh secara diagonal.
b) Semua sel yang terisi “1” harus masuk dalam blok dan banyaknya blok yang dibuat harus seminim mungkin.
c) Utamakan membuat blok yang bisa mencakup “1” lebih banyak.
d) Jumlah “1” yang diperbolehkan dalam setiap bloknya adalah 2, 4, 8, atau 16 (jika ekspresi Booleannya memiliki empat variabel).
Perlu diperhatikan bahwa jika semua sel pada peta Karnaugh terisi “1”, maka 𝐸 = 1.
Dalam bab ini, penggunaan peta Karnaugh hanya dibatasi untuk 2 dan 3 variabel.
Contoh 11:
Tentukan peta Karnaugh dari:
a. 𝐸 𝑥, 𝑦 = 𝑥𝑦 + 𝑥′𝑦 b. 𝐸 𝑥, 𝑦 = 𝑥𝑦′ + 𝑥′𝑦 Jawab:
a. b.
Contoh 12:
Tentukan dnf minimal dari 𝐸 𝑥, 𝑦 = 𝑥𝑦′ + 𝑥′𝑦 + 𝑥′𝑦′ dengan menggunakan peta Karnaugh!
Jawab:
Peta Karnaughnya:
Dengan memperhatikan aturan dalam membuat blok, maka blok yang bisa dilakukan adalah sebagai berikut:
Blok vertikal: berada dalam area 𝑥 𝑥′ 𝑦′, sehingga didapatlah 𝑦′.
Blok horizontal: berada dalam area 𝑥′𝑦 𝑦′, sehingga didapatlah 𝑥′.
Maka, dnf minimal dari 𝐸 𝑥, 𝑦 = 𝑥𝑦′ + 𝑥′𝑦 + 𝑥′𝑦′ adalah:
𝐸 𝑥, 𝑦 = 𝑥′ + 𝑦′
𝑥
𝑥′
’ 𝑥
𝑥′
’
MATEMATIKA DISKRET – Srava Chrisdes 10 10 10 10 𝑥′
’ 𝑥
𝑦𝑧
’
𝑦𝑧′
’
𝑦′𝑧′
’
𝑦′𝑧 𝑥′
’ 𝑥
𝑦𝑧
’
𝑦𝑧′
’
𝑦′𝑧′
’
𝑦′𝑧 Contoh 13:
Tentukan dnf minimal dari
𝐸 𝑥, 𝑦 = 𝑥𝑦𝑧 + 𝑥𝑦𝑧′ + 𝑥𝑦′𝑧 + 𝑥𝑦′𝑧′ + 𝑥′𝑦𝑧 + 𝑥′𝑦′𝑧 + 𝑥′𝑦′𝑧′
dengan menggunakan peta Karnaugh!
Jawab:
Peta Karnaughnya:
Dengan memperhatikan aturan dalam membuat blok, maka blok yang bisa dilakukan adalah sebagai berikut:
Blok merah : berada dalam area 𝑥 𝑦 𝑦′ 𝑧 𝑧′, sehingga didapatlah 𝑥.
Blok hijau : berada dalam area 𝑥 𝑥′ 𝑦′ 𝑧 𝑧′, sehingga didapatlah 𝑦′.
Blok hitam
putus-putus : berada dalam area 𝑥 𝑥′ 𝑦 𝑦′ 𝑧, sehingga didapatlah 𝑧.
Maka, dnf minimal dari 𝐸 𝑥, 𝑦 = 𝑥𝑦𝑧 + 𝑥𝑦𝑧′ + 𝑥𝑦′𝑧 + 𝑥𝑦′𝑧′ + 𝑥′𝑦𝑧 + 𝑥′𝑦′𝑧 + 𝑥′𝑦′𝑧′
adalah:
𝐸 𝑥, 𝑦, 𝑧 = 𝑥 + 𝑦′ + 𝑧
1 1
1
1 1
1 1
1 1
1
1 1
1 1
MATEMATIKA DISKRET – Srava Chrisdes 11 11 11 11 L A T I H A N S O A L
1. Gunakan tabel untuk mencari nilai dari ekspresi Boolean berikut:
a. E x y z( , , )xy(xyz) b. E x y z( , , ) y xz( x z )
2. Carilah ekspresi Boolean dari variabel 𝑥, 𝑦, dan 𝑧 pada tabel berikut:
𝒙 𝒚 𝒛 𝑬
1 1 1 1
1 1 0 0
1 0 1 1
1 0 0 0
0 1 1 1
0 1 0 0
0 0 1 1
0 0 0 0
3. Buktikan bahwa
x
x
y1 x!
4. Diketahui ekspresi-ekspresi Boolean sebagai berikut:
a. E x y z( , , )(xy z) b. E x y z( , , )(xy z) y c. E x y z( , , )(xy) ( x z)
Tentukanlah: (i) gambar rangkaian gerbang logikanya!
(ii) dnf dan full dnf-nya!
5. Tentukan dnf minimal dari ekspresi Boolean berikut dengan konsensus dan Karnaugh:
a. E x y z( , , )x yz x y z
b. E x y z( , , )xyzxyzx yz x yz
c. E x y z( , , )xyzxy z xy z x yz x y z
6. Tuliskanlah ekspresi Boolean dari masing-masing rangkaian gerbang logika berikut:
a.
MATEMATIKA DISKRET – Srava Chrisdes 12 12 12 12 b.
c.