Optimasi pemotongan rol kertas dua dimensi dengan menggunakan program linear

(1)

i

DENGAN MENGGUNAKAN PROGRAM LINEAR

Tugas Akhir

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Andreas Irawan Susanto

NIM : 133114020

PROGRAM STUDI MATEMATIKA, JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(2)

ii

DIMENSIONAL USING LINEAR PROGRAMING

A Thesis

Presented as a Partial Fulfillment of the

Requirements to Obtain the Degree of Sarjana Sains

Mathematics Study Program

Written by:

Andreas Irawan Susanto

Student Number: 133114020

MATHEMATICS STUDY PROGRAM

DEPARTMENT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

(3)

(4)

(5)

v

HALAMAN PERSEMBAHAN

Skripsi ini saya persembahkan kepada:

 Tuhan Yesus Kristus atas segala Berkat dan Kasih-Nya disepanjang hidup saya.

 Papa dan Mama Tercinta yaitu Liem Kwan Seng dan Suwarni.

 Adik saya yaitu Elvika Kumalasari Susanto.

 Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku dosen pembimbing skripsi saya.

Serahkanlah Perbuatanmu Kepada TUHAN,

Maka Terlaksanalah Segala Rencanamu

(6)

(7)

vii

Industri kertas melakukan proses pemotongan kertas untuk menghasilkan

berbagai jenis ukuran lembaran kertas. Proses pemotongan rol kertas dilakukan

menggunakan mesin. Proses pemotongan ini harus dilakukan dengan optimal.

Apabila tidak dilakukan dengan optimal maka akan menimbulkan sisa

pemotongan kertas. Sisa kertas ini disebabkan oleh beberapa faktor yang salah

satu di antaranya adalah ukuran rol kertas tidak sesuai dengan ukuran lembaran

kertas produksi.

Proses pengoptimalan sisa pemotongan kertas menggunakan ilmu

matematika, yaitu program linear. Pada tugas akhir ini dibahas masalah

pen-goptimalan pemotongan kertas berupa Mixed Integer Non Linear Programing

(MINLP). MINLP dapat diselesaikan dengan cara merubah masalah MINLP

ke-bentuk Mixed Integer Linear Programing (MILP). Proses pengubahan ini

dil-akukan dengan cara memasukkan nilai dari salah satu variabel keputusan.Variabel

keputusan tersebut adalah banyaknya pola pemotongan. Oleh sebab itu banyaknya

pola pemotongan juga dicari terlebih dahulu.

Semua proses tersebut dilakukan pada MATLAB dengan membuat

program dan GUI MATLAB. Tujuan dibuat GUI MATLAB adalah

mempermudah setiap orang menggunakan program yang telah dibuat. Terdapat

juga contoh kasus dengan delapan jenis kertas produksi. Hasil yang diperoleh

adalah cara pemotongan tiap rol, panjang setiap jenis kertas produksi yang telah

dipotong dan sisa minimum pemotongan kertas.

Kata Kunci: Pemotongan Kertas, Pola Pemotongan Kertas, Program Linear,

Mixed Integer Non Linear Programing (MINLP), Mixed Integer Linear

(8)

viii

The cutting paper industry process produces various types of paper sheet

sizes. The paper rolls cutting process is done using the machine. This cutting

process should be done optimally. If not done optimally, it will make lots of

waste. The waste could be caused by several factors, one of the factors is the size

of the paper roll size which is not matching to the size of the paper sheet

production.

Linear program can be used to optimize the paper cutting process. This

thesis discusses about problem of optimation cutting paper with Mixed Integer

Non-Linear Programming (MINLP). MINLP can be solved with converted

MINLP become Mixed Integer Linear Programing (MILP). This conversion

pro-cess is done by inputting the value of one of the decision variables. The

deci-sion variable is the number of cutting patterns. Therefore, the number of cutting

patterns should be known.

All these processes were done in MATLAB by creating a program and

GUI MATLAB. The purpose of the GUI MATLAB was to help everyone to use

the program they had created. There were also cases provided with eight types of

production paper cases. The results obtained were how to cut each roll, the length

of each type of production paper that has been cut and the minimum remaining

paper.

Keywords: Paper Cutting, Paper Cutting Pattern, Linear Program, Mixed Integer

Non Linear Programing (MINLP), Mixed Integer Linear Programing (MILP),

(9)

(10)

x

Puji dan syukur penulis haturkan kepada Tuhan Yang Maha Esa karena atas

berkat dan kasih-Nya penulis dapat menyelesaikan tugas akhir ini dengan baik.

Tugas akhir dibuat sebagai salah satu syarat untuk memperoleh gelar sarjana

Matematika pada Fakultas Sains dan Teknologi Universitas Sanata Dharma

Yogyakarta. Penulis mendapat banyak dukungan dan bantuan dalam proses

menyelesaikan tugas akhir ini. Oleh karena itu, penulis ingin menyampaikan

terima kasih kepada:

1. Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku Ketua Program Studi dan

dosen pembimbing tugas akhir yang penuh sabar membimbing,

meluangkan waktu, tenaga, dan pikiran serta memberikan masukan,

arahan, dan nasihat kepada penulis.

2. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dekan Fakultas

Sains dan Teknologi.

3. Ibu M. V. Any Herawati, S.Si., M.Si., selaku wakil kepala program studi

Matematika dan Dosen Pembimbing Akademik yang selalu memberikan

arahan dalam menjalani perkuliahan.

4. Romo Prof. Dr. Frans Susilo, S.J., Bapak Dr. rer. nat. Herry P. Suryawan,

S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak YG. Hartono,

S.Si., M.Sc., Ph.D., Ibu M. V. Any Herawati, S.Si., M.Sc., dan Ibu Lusia

Krismiyati Budiasih, S.Si., M.Si., selaku dosen program studi matematika

yang telah membimbing, memberikan ilmu dan pengalaman selama masa

perkuliahan.

5. Kedua orang tua saya yaitu Liem Kwan Seng dan Suwarni yang selalu

mendoakan, mendukung, memberi semangat dan motivasi dalam

me-nyelesaikan tugas akhir ini.

6. Adik saya yaitu Elvika Kumalasari Susanto yang selalu menemani dan

menghibur dalam menyelesaikan tugas akhir ini.

7. Teman-teman Program Sudi Matematika Angkatan 2013: Bintang, Agung,

(11)

(12)

xii

HALAMAN JUDUL ... ii

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ... vi

ABSTRAK ... vii

ABSTRACT ... viii

LEMBAR PERNYATAAN PERSETUJUAN ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

BAB I ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 3

C. Batasan Masalah ... 3

D. Metode Penulisan ... 3

E. Tujuan Penulisan ... 3

F. Manfaat Penulisan ... 3

G. Sistematika Penulisan ... 4

BAB II ... 5

A. Program Linear dan Program Linear Bulat ... 5

B. Metode Pencabangan dan Pembatasan (Branch and Bound Method) ... 8

(13)

xiii

BAB III ... 22

A. Masalah Sisa Pemotongan (Trims Loss Problem) ... 22

B. Mencari Banyaknya Pola Pemotongan ... 22

C. Model Matematika ... 54

BAB IV ... 66

BAB V ... 76

A. Kesimpulan ... 76

B. Saran ... 76

DAFTAR PUSTAKA ... 78

(14)

1 BAB I

PENDAHULUAN

A. Latar Belakang

Dalam suatu proses produksi orang menginginkan suatu hal yang optimal,

oleh karena itu orang ingin meminimalkan kerugian dalam proses produksi,

khususnya pada proses pemotongan material. Sering kita jumpai sisa pemotongan

yang tidak dapat digunakan lagi. Hal tersebut terjadi dikarenakan ukuran material

utamanya tidak bersesuaian dengan yang diharapkan dalam proses. Masalah

tersebut sering dikenal sebagai masalah sisa pemotongan (trim loss) yang berarti

masalah yang timbul karena hasil pemotongan yang tidak optimal.

Masalah sisa pemotongan selain memboroskan bahan baku juga dapat

membuang-buang waktu. Misalnya saja dalam memproduksi kertas, jika

pemotongannya tidak optimal maka banyak bahan baku yang harus didaur ulang

sehingga proses pemotongan kertas adalah hal yang penting dalam memproduksi

kertas. Pemotongan kertas memiliki tiga tahap, yang pertama pemotongan dari rol

besar ke rol yang lebih kecil, yang kedua pemotongan dari rol yang kecil menjadi

lembaran kertas yang memiliki ukuran besar dan yang ketiga pemotongan dari

lembaran kertas yang besar menjadi lembaran kertas yang lebih kecil lagi.

Dalam tugas akhir ini, akan dibahas mengenai bagaimana cara

mengoptimalkan proses produksi kertas, khususnya pemotongan kertas pada tahap

kedua yaitu pemotongan dari rol kecil ke lembaran kertas yang ukuran besar. Pada

pemotongan kertas tahap kedua masalah sisa pemotongan juga sering terjadi.

Masalah tersebut adalah masalah meminimumkan sisa kertas dengan

banyaknya permintaan yang beragam mengenai ukuran kertas yang disediakan

suatu pabrik. Sisa kertas ini ada karena ukuran kertas yang diminta tidak sesuai

dengan panjang dan lebar rol kertas yang ada. Pada tugas akhir ini pemotongan

kertas menggunakan mesin pemotong kertas dengan memperhatikan ukuran

pan-jang dan lebar kertas Mesin tersebut memiliki tujuh pisau yang terdiri dari dua

(15)

Gambar 1.1 Operasi Mesin Pemotong

Pada dasarnya terdapat tiga faktor yang menyebabkan adanya masalah sisa

pemotongan pada pemotongan kertas tahap kedua. Pertama dalam setiap proses

produksi ukuran rol memiliki panjang dan lebar yang sama, akan tetapi terdapat

permintaan yang beragam mengenai ukuran panjang dan lembaran kertas yang

sudah disediakan suatu pabrik. Kedua adalah ketika kita mengubah pola

pemotongan kertas sebab setiap kombinasi pola memiliki hasil sisa kertas yang

berbeda. Ketiga mengenai pola pemotongan, dalam sekali pemotongan terkadang

dapat dihasilkan dua jenis produk bahkan lebih sehingga dapat mengakibatkan

adanya permintaan yang sudah terpenuhi dan adanya permintaaan yang belum

terpenuhi bahkan ada produksi yang melebihi permintaan.

Permasalahan sisa pemotongan tersebut dapat dilihat sebagai masalah

Program Linear. Masalah tersebut dapat juga dipandang sebagai permasalahan

integer linear programming (ILP) atau mixed integer linear programming

(MILP). Pada tugas akhir ini penyelesaian menggunakan program komputer yaitu

Matlab. Pada program Matlab juga dibuat Graphical User Interface (GUI) untuk

memudahkan dalam menjalankannya.

Rol Kertas

Pisau Horisontal

(16)

B. Rumusan Masalah

Masalah yang dirumuskan pada tugas akhir ini adalah

1. Bagaimana bentuk Program Linear dari data yang akan dirumuskan?

2. Bagaimana cara penyelesaian dari masalah Program Linear yang didapat?

3. Bagaimana membuat program pada Matlab?

C. Batasan Masalah

Batasan yang ada dalam tugas akhir ini adalah

1. Mesin yang digunakan hanya ada satu mesin pemotong kertas.

2. Setiap rol memiliki panjang yang sama.

3. Pada tugas akhir ini jenis kertas permintaan dibatasi maksimal delapan

jenis kertas karena pertimbangan waktu komputasi.

D. Metode Penulisan

Metode yang digunakan penulis dalam penulisan tugas akhir ini adalah

metode studi pustaka dengan membaca dan mempelajari buku-buku serta

jurnal-jurnal yang berhubungan dengan Program Linear dan masalah sisa pemotongan.

E. Tujuan Penulisan

Tujuan dari penulisan tugas akhir ini adalah

1. Membuat model persamaan linear dari data yang didapat

2. Membuat progam masalah pemotongan kertas pada Matlab

3. Mengoptimalkan masalah pemotongan rol kertas

F. Manfaat Penulisan

Manfaat penulisan tugas akhir ini adalah untuk membantu menyelesaikan

masalah sisa pemotongan yang sering terjadi pada industri pemotongan kertas

dengan adanya permintaan yang banyak dari konsumen dan dengan adanya

program komputer yang dibuat dapat memudahkan orang menyelesaikan masalah

(17)

G. Sistematika Penulisan

BAB I PENDAHULUAN

A. Latar Belakang

B. Rumusan Masalah

C. Batasan Masalah

D. Tujuan Penulisan

E. Manfaat Penulisan

F. Metode Penulisan

G. Sistematika Penulisan

BAB II PROGRAM LINEAR

A. Program Linear dan Program Linear Bulat

B. Metode Pencabangan dan Pembatasan (Branch and Bound

Method)

C. Program Linear Biner

D. Program Linear Campuran (Mixed Integer Linear Programing)

BAB III MASALAH SISA PEMOTONGAN

A. Masalah Sisa Pemotongan (Trims Loss Problem)

B. Mencari Banyaknya Pola Pemotongan

C. Model Matematika

BAB IV PENYELESAIAN MASALAH PEMOTONGAN ROL KERTAS

DENGAN MENGGUNAKAN PROGRAM MATLAB

BAB V PENUTUP

A. Kesimpulan

B. Saran

(18)

5 BAB II

PROGRAM LINEAR

A. Program Linear dan Program Linear Bulat

Istilah Program Linear mulai dikenal pada tahun 1950-an, akan tetapi

masalah Program Linear sudah mulai ada sejak tahun 1940-an di Departemen

Pertahanan Inggris dan Amerika untuk menjawab masalah optimisasi perencanaan

operasi perang melawan Jerman dalam Perang Dunia ke-II. Pada tahun 1947 teori

dan teknik Simpleks dikembangkan oleh Dantzig dan para pakar lainnya. Sejak

itu, para ahli dari berbagai bidang ilmu pengetahuan, terutama dalam bidang

matematika dan ekonomi, telah mengembangkan teori dalam Program Linear dan

penerapan aplikasi dari Program Linear. Masalah Program Linear adalah

mengoptimalkan suatu fungsi tujuan dengan adanya batas kendala-kendala berupa

persamaan atau pertidaksamaan. Pada zaman sekarang Program Linear digunakan

di berbagai bidang seperti, industri, ekonomi, bisnis, dan lain-lain.

Selanjutnya akan dilihat beberapa asumsi yang terdapat pada masalah

Program Linear sebagai berikut

1. Proporsionalitas

Setiap variabel yang terdapat pada fungsi tujuan atau fungsi kendala haruslah

sebanding. Misalnya, untuk membuat sebuah kursi dibutuhkan waktu selama 4

jam, jadi untuk membuat 2 kursi dibutuhkan waktu selama 8 jam.

2. Aditivitas

Kontribusi dari setiap variabel dari fungsi tujuan atau fungsi kendala tidak

ter-gantung dari nilai-nilai variabel lainnya. Contohnya untuk membeli 1

mang-kok bakso dibutuhkan 1000 dan untuk membeli 1 es jeruk 500 sehingga

total-nya 1500. Sedangkan untuk memebeli 2 mangkok bakso dibutuhkan 2000 dan

1 es jeruk 500 sehingga totalnya 2000. Jadi tidak harus memebeli 2 mangkok

(19)

3. Divisibility

Variabel keputusan dapat berupa bilangan pecahan. Namun, dengan

menggunakan teknik khusus yang disebut integer programing (Program

Linear bulat) dapat menghasilkan variabel keputusan yang bernilai bulat.

4. Kepastian

Setiap parameter (koefisien fungsi tujuan, koefisien kendala, dan nilai di sisi

kanan) diketahui dengan pasti dan tidak berubah selama periode analisis.

Secara umum masalah Program Linear dapat dirumuskan sebagai berikut:

Maksimumkan atau Minimumkan

titik layak dan himpunan semua titik-titik layak tersebut disebut daerah layak.

Solusi dari Program Linear haruslah titik di daerah layak.

Secara umum rumus tersebut dapat ditulis secara lebih ringkas menjadi

Maksimumkan atau Minimumkan (1)

∑

Kendala (2)

∑

(20)

(3) Bagian (3) menunjukkan bahwa setiap variabel keputusan haruslah bernilai

tidak negatif. Konstanta disebut koefisien teknis, disebut koefisien ongkos,

dan disebut suku tetap di ruas kanan.

Rumus Program Linear juga bisa ditulis dalam bentuk matrik sebagai

Menggunakan matrik untuk masalah Program Linear bertujuan agar dalam

proses pembuatan program lebih mudah serta menghemat simbol.

Selanjutnya akan dilihat bagaimana jika hasil dari Program Linear harus

bulat atau yang sering disebut Program Linear bulat. Misalnya saja pada masalah

pemotongan kertas pasti banyak kertas yang dihasilkan haruslah utuh sehingga

nilai desimal pada variabel keputusan harus dihindari. Untuk menghilangkan nilai

desimal maka rumusan Program Linear dapat diubah menjadi seperti berikut:

(21)

[ ] [ ] [

]

Perbedaan rumus Program Linear bulat hanya terletak pada variabel

keputusan sehingga kendalanya ditambah dengan setiap anggota haruslah

bilangan bulat positif. Program Linear bulat ini dapat diselesaikan dengan

berbagai cara salah satunya dengan metode pencabangan dan pembatasan. Metode

pencabangan dan pembatasan akan dibahas pada subbab selanjutnya.

B. Metode Pencabangan dan Pembatasan (Branch and Bound Method)

Metode pencabangan dan pembatasan berkembang pada tahun 1960 dan

dikembangkan oleh A. Land dan G. Doig untuk menyelesaikan program bilangan

bulat dan program bilangan bulat campuran. Metode pencabangan dan

pembatasan merupakan metode yang sering digunakan untuk menyelesaikan

masalah Program Linear bulat. Pada Metode pencabangan dan pembatasan

memiliki tiga hal penting yaitu:

1. Pencabangan (Branching)

Pencabangan dilakukan jika masih terdapat variabel keputusan yang harus

bernilai bulat namun memiliki solusi yang tidak bulat. Pencabangan dilakukan

dengan cara menambahkan kendala baru pada masalah awal. Kendala baru

yang ditambahkan merupakan pembulatan ke atas dan ke bawah dari solusi

yang masih berbentuk pecahan. Penambahan kendala ini bertujuan untuk

membuat variabel keputusan yang belum bernilai bulat supaya bernilai bulat.

Proses seperti ini dilakukan terus menerus sampai semua cabang

menghasilkan solusi bulat.

2. Pembatasan (Bound)

Pada metode pencabangan dan pembatasan terdapat dua batas yaitu batas atas

(upper bound) dan batas bawah (lower bound). Langkah ini bertujuan untuk

membatasi solusi sehingga didapat solusi yang optimal. Pada masalah

(22)

dan pada masalah minimum batas bawah merupakan solusi dari masalah

Program Linear bulat.

3. Penghentian Cabang (Fathoming)

Pencabangan pada metode pencabangan dan pembatasan akan berhenti jika

 Tidak memiliki daerah layak (infeasible).

 Semua variabel keputusan yang harus bernilai bulat sudah memenuhi syarat yaitu sudah menjadi bilangan bulat.

 Pada masalah maksimum, penghentian pencabangan pada suatu sub masalah dilakukan jika batas atas dari sub masalah tersebut tidak lebih

besar atau sama dengan batas bawah.

 Pada masalah minimum penghentian pencabangan pada suatu sub masalah dilakukan jika batas bawah tidak lebih kecil atau sama dengan

batas atas.

Kondisi optimal pada metode pencabangan dan pembatasan terjadi jika

tidak ada lagi sub masalah yang perlu dicabangkan lagi.

Pencabangan dan pembatasan memiliki cara kerja sebagai berikut

1. Selesaikan Program Linear tanpa memperhatikan kendala bilangan bulatnya.

Jika penyelesaian yang didapat merupakan bilangan bulat maka solusi optimal

sudah didapat. Jika ada variabel keputusan yang belum bulat maka

pencabangan dilakukan.

2. Tambahkan kendala pada variabel keputusan yang tidak menghasilkan

bilangan bulat. Penambahan kendala hanya menambah satu demi satu kendala.

Penambahan kendala ini berakibat terbentuknya dua sub masalah baru.

3. Menyelesaikan setiap Program Linear dengan batas baru tetapi fungsi tujuan

sama.

4. Jika masih terdapat variabel keputusan yang belum bulat maka lakukan

pencabangan kembali dan jika semua variabel keputusan sudah bulat maka

pencabangan dihentikan sehingga solusi yang didapat menjadi kandidat solusi

optimal.

Untuk melihat cara kerja pencabangan dan pembatasan diambil contoh

(23)

Contoh 2.1

Langkah 2. (Pencabangan). Pada kondisi ini variabel keputusan haruslah bulat

maka pencabangan dilakukan. Pada kondisi ini kendalanya bertambah atau

(24)

Langkah 3. (Penyelesaian). Penyelesaian untuk masalah LP2 adalah

z=23

Langkah 4. Pada kondisi ini sudah terlihat bahwa variabel keputusan sudah bulat

semuanya sehingga kita dapat menyimpan solusi ini sebagai kandidat solusi

opti-mal.

, z=23.33

Langkah 4. Pada kondisi ini terlihat bahwa variabel keputusan masih belum

bulat sehingga harus dilakukan pencabangan kembali.

, z=22.55

Langkah 4. Pada kondisi ini terlihat bahwa variabel keputusan masih belum

(25)

Langkah 3. (Penyelesaian). Penyelesaian untuk masalah LP5 tidak ada sebab pada

kasus ini tidak terdapat daerah layak.

Langkah 4. Pada kondisi seperti ini pencabangan dihentikan sebab tidak terdapat

solusi sama sekali.

, � .

Langkah 4. Pada kondisi ini sudah terlihat bahwa variabel keputusan sudah bulat

semuanya sehingga kita dapat menyimpan solusi ini sebagai kandidat solusi

opti-mal.

Sub LP7, masalah LP7. Maksimumkan

(26)

Kendala

Langkah 3. (Penyelesaian). Penyelesaian untuk masalah LP7 tidak ada sebab pada

kasus ini tidak terdapat daerah layak.

Langkah 4. Pada kondisi seperti ini pencabangan dihentikan sebab tidak terdapat

solusi sama sekali.

Semua pencabangan sudah dihentikan sehingga tinggal dipilih solusi

optimal dari kandidat solusi yang ada dan didapat dengan nilai

(27)

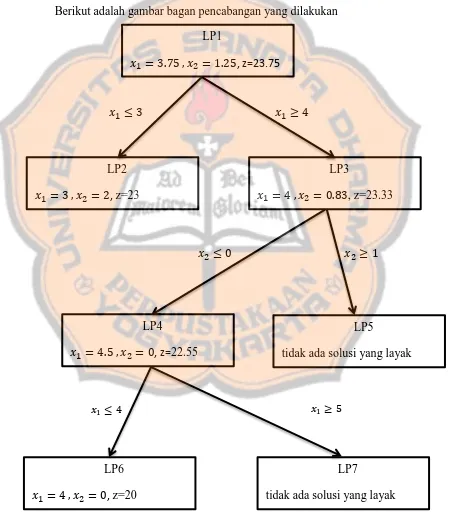
Berikut adalah gambar bagan pencabangan yang dilakukan

LP1

, z=23.75

LP2

, z=23

LP3

, z=23.33

LP7

tidak ada solusi yang layak LP6

, z=20

LP5

tidak ada solusi yang layak LP4

, z=22.55

(28)

C. Program Linear Biner

Pada Program Linear biner setiap variabel keputusan hanya dapat

mengambil nilai 0 atau 1. Pada dunia nyata masalah Program Linear biner seperti

pilihan ya atau tidak, 0 untuk pilihan tidak dan 1 untuk pilihan ya. Program Linear

biner ini dapat diselesaikan dengan metode pencabangan dan pembatasan.

Pada masalah Program Linear biner metode pencabangan dan pembatasan

bekerja seperti menyelesaikan Program Linear bulat. Berikut adalah langkah

menyelesaikan Program Linear biner:

1. Langkah pertama adalah melihat variabel keputusan pada fungsi tujuan. Jika

masalah minimum maka variabel keputusan yang memiliki nilai kecil

dilakukan pencabangan. Jika masalah maksimum maka variabel keputusan

yang memiliki nilai besar dilakukan pencabangan.

2. Pencabangan ini akan menghasilkan dua sub masalah baru.

3. Menyelesaikan setiap Program Linear. Jika solusi belum berada di daerah

layak maka lakukan pencabangan lagi.

Contoh 2.2

Langkah pertama, mencari variabel keputusan yang memiliki koefisien

paling besar pada fungsi tujuan. Terlihat bahwa memiliki nilai terbesar yaitu 6.

Ambil nilai sebagai LP1 dengan nilai , dan solusi

ini berada di daerah yang tidak layak sehingga dilakukan pencabangan kembali.

Langkah selanjutnya melihat kembali nilai terbesar kedua dari koefisien

variabel keputusan pada fungsi tujuan. Terlihat bahwa memiliki nilai 5,

(29)

dan . Pada LP2 yaitu pencabangan dengan menambah kendala

diperoleh kandidat solusi optimal yaitu , dengan nilai

� dan berada pada daerah layak. Pada LP3 yaitu pencabangan dengan menambah kendala tetap dihasilkan solusi yang sama sehingga

pencabangan dihentikan.

Semua pencabangan telah dihentikan sehingga dapat dilihat solusi yang

paling optimal dari kandidat solusi yang ada dan diperoleh solusi optimal adalah

, � .

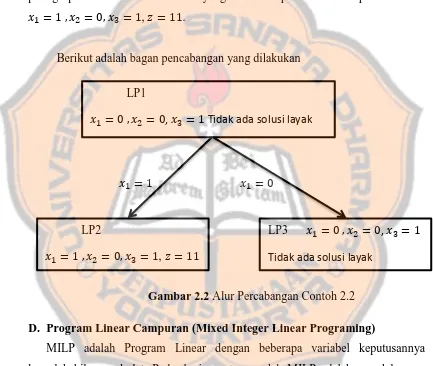
Berikut adalah bagan pencabangan yang dilakukan

D. Program Linear Campuran (Mixed Integer Linear Programing)

MILP adalah Program Linear dengan beberapa variabel keputusannya

haruslah bilangan bulat. Pada dunia nyata masalah MILP adalah masalah yang

paling sering. Masalah MILP dapat diselesaikan dengan menggunakan metode

pencabangan dan pembatasan. Metode pencabangan dan pembatasan merupakan

metode yang efisien secara komputasi.

Selanjutnya akan dilihat algoritma pencabangan dan pembatasan untuk

menyelesaikan MILP LP1

, Tidak ada solusi layak

LP2

, �

LP3 ,

Tidak ada solusi layak

(30)

1. Inisialisasi

Mengatur batas atas dan batas bawah dari solusi optimal dan selanjutnya

memilih penyelesaian MILP pada daerah layak.

2. Cabang (Brancing)

Menyelesaikan setiap Program Linear dengan batas baru tetapi fungsi tujuan

sama. Misalkan variabel berada pada interval [a,b] dan merupakan batas

yang harus bilangan bulat maka batas baru yang bisa dibentuk adalah

. 3. Penyelesaian

Menyelesaikan masalah selanjutnya pada cabang yang lain.

4. Pembaharuan Batas

Jika nilai z yang kita peroleh pada cabang yang baru lebih optimal daripada

sebelumnya maka cabang ini menjadi kandidat sebagai solusi optimal.

5. Pemotongan

Jika penyelesaian yang diperoleh berada di daerah layak bukan berarti

pen-cabangan berhenti, mungkin bisa ada penpen-cabangan lebih lanjut. Jika pada

per-soalan tidak terdapat penyelesaian pada daerah layakanya maka pencabangan

dihentikan atau dipotong.

6. Optimal

Jika terdapat pencabangan yang belum terselesaikan kita lanjutkan pada

langkah ke-3. Jika semua pencabangan telah dihentikan maka dari kandidat

penyelesaian yang telah diperoleh dipilih kandidat penyelesaian yang paling

optimal.

Metode pencabangan dan pembatasan akan menghasilkan solusi optimal

jika:

1. Sub masalah berada di daerah yang tidak layak.

2. Penyelesaian sudah berada pada batas-batanya (memenuhi daerah layak) dan

memenuhi kondisi bilangan bulat untuk variabel keputusan yang ditetapkan.

3. Batas bawah yang diperoleh lebih besar dari batas atas.

Berikut adalah contoh metode pencabangan dan pembatasan untuk

(31)

Contoh 2.3

Contoh 2.3 adalah contoh masalah MILP sebab variabel keputusan pada dan

haruslah bernilai bulat dan variabel keputusan dan tidak harus bernilai bulat.

Langkah 1. (Inisialisasi). Dipilih batas atas dan batas bawah . Pada

kondi-si ini disebut sebagai masalah P0

Minimum

(32)

Langkah 3. (Penyelesaian). Penyelesaian untuk masalah P1 adalah

Langkah 4. (Pembaharuan Batas). Pada kondisi ini sudah memenuhi kendala awal

yaitu , . Nilai dari fungsi tujuan adalah 1.5 lebih kecil dari pada batas atas yang dimiliki sehingga nilai batas atas diubah dari ∞ ke 1.5, dan nilai ini disimpan sebagai kandidat optimal.

Langkah 3. (Penyelesaian). Penyelesaian untuk masalah P2 adalah

Langkah 4. (Pembaharuan Batas). Pada kondisi ini nilai dari bukan bilangan

bulat. Fungsi tujuannya bernilai 0.5 berada diantara batas bawah 0 dan batas atas

1.5 maka batas bawah di perbaruhi dari 0 menjadi 0.5 (sehingga solusi optimal

yang akan didapat harus berada pada interval 0.5 sampai 1.5). Selanjutnya

pen-cabangan akan dilakukan pada variabel menjadi dua masalah sebagai berikut:

(33)

Langkah 3. (Penyelesaian). Pada masalah P3 tidak terdapat daerah layak.

Langkah 4. (Pembaharuan Batas). Tidak ada yang dilakukan pada langkah ini

se-hingga dilanjutkan pada langkah selanjutnya.

Langkah 5. (Cutting). Pada kondisi ini tidak terdapat penyelesaian optimal

Sub LP4,masalah P4. Minimum

Kendala

Langkah 3. (Penyelesaian). P4 memiliki daerah layak sehingga dapat dicari

so-lusinya dan diperoleh

Langkah 4. (Pembaharuan Batas). Tidak ada yang dilakukan pada langkah ini

Langkah 5. (Pemotongan). Pada kondisi ini variabel tidak bilangan bulat dan

nilai solusi optimalnya lebih optimal pada masalah sebelumnya maka dilanjutkan

langkah selanjutnya.

Langkah 6. (Optimasi). Pada kondisi ini tidak terdapat pencabangan lebih lanjut

sehingga solusi optimal diperoleh yaitu:

(34)

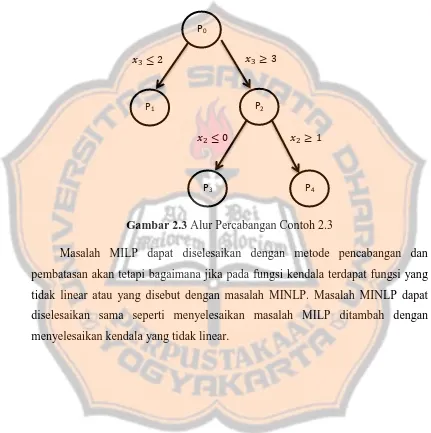
Untuk melihat proses pencabangan yang dilakukan, dapat dilihat pada

gambar 2.3.

Masalah MILP dapat diselesaikan dengan metode pencabangan dan

pembatasan akan tetapi bagaimana jika pada fungsi kendala terdapat fungsi yang

tidak linear atau yang disebut dengan masalah MINLP. Masalah MINLP dapat

diselesaikan sama seperti menyelesaikan masalah MILP ditambah dengan

menyelesaikan kendala yang tidak linear.

P0

P1 P2

P3 P4

Gambar 2.3 Alur Percabangan Contoh 2.3

(35)

22 BAB III

MASALAH SISA PEMOTONGAN

A. Masalah Sisa Pemotongan (Trims Loss Problem)

Dalam dunia industri, khususnya industri kertas masalah meminimalkan sisa

pemotongan kertas merupakan salah satu faktor terpenting. Terjadinya sisa

pemotongan ini dapat disebabkan oleh beberapa hal, salah satu diantaranya adalah

lebar dan panjang kertas permintaan tidak sesuai dengan rol kertas produksi.

Meminimumkan sisa pemotongan juga tergantung pada pola pemotongan yang

merupakan kombinasi dari lembaran kertas permintaan yang dipotong pada waktu

yang sama.

Pada tugas akhir ini akan dibahas mengenai bagaimana meminimalkan sisa

pemotongan dari rol kertas ke lembaran kertas. Masalah utama dari pemotongan

dari rol kertas ke lembaran kertas adalah bagimana memenuhi banyaknya

permintaan yang ada dengan meminimalkan sisa pemotongan kertas dengan

berbagai ukuran kertas yang diminta. Proses pemotongan kertas dari rol kertas

produksi ke lembaran kertas disebut masalah pemotongan dua dimensi. Hal

tersebut dikarenakan dalam memotong rol kertas produksi harus memperhatikan

panjang dan lebar rol kertas produksi serta ukuran kertas permintaan yang ada.

Pada proses produksi rol kertas produksi memiliki panjang yang

berbeda-beda, akan tetapi pada tugas akhir ini panjang dan lebar rol kertas produksi

diang-gap sama. Panjang dan lebar rol kertas produksi memiliki batas atas dan batas

bawah pemotongan. Lebar rol kertas produksi digunakan untuk membuat pola

pemotongan. Banyaknya pola pemotongan merupakan salah satu faktor dalam

meminimalkan sisa pemotongan, oleh sebab itu pada subbab selanjutnya akan

dibahas mengenai bagaimana cara mencari banyaknya pola pemotongan.

B. Mencari Banyaknya Pola Pemotongan

Pola pemotongan merupakan suatu pilihan dalam miminimalkan sisa

pemotongan dan memenuhi jumlah permintaan. Pada masalah nyata yang

(36)

semua kombinasi dari setiap jenis kertas yang ada dan harus memperhatikan

jumlah lebar setiap jenis kertas yang dipotong tidak melebihi lebar dari rol kertas.

Pada pemotongan rol kertas, lebar rol kertas dapat dibatasi dengan batas

maksimum pemotongan rol kertas dan batas minimum lebar pemotongan rol

kertas.

Contoh 3.1

Misalnya saja terdapat lebar lembaran kertas permintaan (pada tugas akhir

ini disebut dengan bi) dengan ukuran 3 cm dan 5 cm. Itu berarti jenis kertas

pertama (b1) memiliki lebar 3 cm dan kertas jenis kedua (b2) memiliki lebar 5 cm.

Terdapat juga batas atas pemotongan dari lebar rol kertas produksi (pada tugas

akhir disebut dengan ) dengan lebar 16 cm dan batas bawah pemotongan

dari lebar rol kertas produksi (pada tugas akhir disebut dengan ) dengan lebar

14 cm. dan digunakan untuk membuat batas pemotongan lebar rol

ker-tas. Pembuatan batas ini bertujuan supaya tidak banyak kertas yang terbuang.

Pa-da contoh 3.1 mencari pola pemotongan dengan manual Pa-dan pola yang diperoleh

dapat dilihat pada Tabel 3.1.

Tabel 3.1 Banyaknya pola pemotongan dengan nilai sisa

(37)

Pola pemotongan ke-1 menghasilkan 2 kertas dengan lebar 3 cm dan

menghasilkan 2 kertas dengan lebar 5 cm. Total lebar kertas yang dipotong adalah

16 cm dan tidak menghasilkan sisa pemotongan sebab lebar rol kertas (16 cm)

sama dengan pola pemotongan (16 cm). Pola pemotongan ke-2 menghasilkan 5

kertas dengan lebar 3 cm dan tidak menghasilkan kertas dengan lebar 5 cm. Total

lebar kertas yang dipotong adalah 16 cm dan menghasilkan sisa pemotongan

sebanyak 1 cm sebab lebar rol kertas (16 cm) dikurangkan dengan lebar pola

pemotongan (15 cm). Menggunakan cara yang sama diperoleh pola ke-3 dan pola

ke-4.

Pada proses pemotongan rol kertas ke lembaran kertas banyaknya pola

pemotongan yang terdapat tergantung pada mesin yang digunakan. Pada kasus ini,

pola pemotongan kertas menggunakan mesin pemotong kertas yang dapat dilihat

pada Gambar 3.1. Mesin pemotong kertas pada Gambar 3.1, terlihat bahwa

banyaknya lembaran kertas yang dapat dihasilkan dalam sekali proses

pemotongan hanya empat lembaran kertas. Sebab ujung kanan dan ujung kiri pada

pisau vertikal digunakan untuk merapikan sisi kanan dan kiri dari rol kertas.

Gambar 3.1 Gambar Mesin Pemotong Rol Kertas

Pisau Horisontal

(38)

Pada mesin pemotong kertas juga terlihat bahwa pisau vertikal hanya bisa

memotong maksimal empat bagian ( ), sehingga tidak boleh melebihi empat,

oleh sebab itu pola pemotongan kedua harus dihilangkan. Pola pemotongan kedua

dihilangkan sebab pada pola pemotongan kedua menghasilkan 5 kertas dengan

lebar 3 cm.

Pada dunia nyata jenis ukuran kertas permintaan beragam bisa lebih dari dua

jenis kertas. Jika kita mencoba satu demi satu kemungkinan pasti memakan waktu

yang lama. Pada tugas akhir ini masalah tersebut akan diselesaikan menggunakan

algoritma pemecah eksplisit. Berikut ini adalah sebuah algoritma pemecahan

eksplisit yang digunakan untuk menghasilkan semua pola pemotongan layak yang

disebut . Jumlah setiap kolom dari unsur-unsur pada kurang dari atau sama

(39)

[ Berikut adalah langkah-langkah dari algoritma pemecah eksplisit untuk

menentukan pola pemotongan yang layak.

Kelompok 0 Langkah 0.0. j = 1

Pada kelompok 1 akan membuat nilai pada j bertambah 1 pada langkah 1.0

(40)

Langkah 2.3.

Langkah 2.4.

{ ⌊ ⌋}

Langkah 3.0. misalkan i = r

Pada kelompok 2, pada langkah 2.0 memberikan nilai awal untuk dan

langkah 2.1 memberikan nilai awal untuk . Pada langkah 2.2 sampai langkah

2.4 nilai berjalan dari i=1 sampai i= r. Langkah 2.2 mencari nilai dari

dengan cara nilai ditambah dengan nilai . Langkah 2.3 mencari nilai dari

dengan cara nilai ditambah dengan nilai . Langkah 2.4 akan

menghasilkan nilai yang merupakan sisa kertas yang dapat dipotong oleh

pisau vertikal. Langkah 3.0 bertujuan untuk mengganti nilai i dengan nilai r

(banyak jenis kertas).

Kelompok 3 Langkah 4.0. Jika lanjutkan ke

langkah 6.0

Kelompok 3, pada langkah 4.0 merupakan langkah untuk melihat nilai dari

setiap unsur dari apakah melebihi atau sama dengan yang kita dapatkan

di langkah 2.4, jika iya berarti lanjut ke langkah 6.0 dan jika tidak lanjut ke

langkah 4.0. langkah ini bertujuan untuk melihat apakah pisau vertikal pada mesin

pemotong kertas tidak memotong lebih dari nilai yang sudah kita tentukan.

Kelompok 4 Langkah 4.1.

Langkah 4.2. Jika lanjutkan ke

langkah 2.0

Kelompok 4, pada langkah 4.1 digunakan untuk mengganti nilai dengan

(41)

sudah melebihi batas bawah lebar rol kertas yang harus dipotong atau belum. Jika

sudah maka lanjut ke langkah 2.0.

Kelompok 5 Langkah 5.0. Didapat pola pemotongan baru

Langkah 5.1. lanjutkan ke langkah 1.0

Kelompok 5, pada langkah 5.0 merupakan pola baru yang diperoleh.

Langkah 5.1 merupakan perintah untuk memulai mencari pola pemotongan yang

baru.

Langkah 6.1.

Langkah 6.2. Jika lanjutkan ke langkah

4.0

Kelompok 6, pada langkah 6.0 digunakan untuk mengganti nilai dengan

nilai 0 sebab akan dilihat berapa banyak kertas ke-i yang dapat dipotong pada saat

itu. Langkah 6.1 digunakan untuk memperbarui nilai i. Langkah 6.2 digunakan

untuk melihat nilai i yang sudah diperbaharui pada langkah sebelumnya. Jika nilai

i lebih dari 0 maka kembali pada langkah 4.0, dan jika nilai i kurang dari atau

sama dengan 0 maka lanjut ke langkah selanjutnya.

Kelompok 7, pada langkah 7.0 merupakan langkah untuk melihat berapa

banyak pola pemotongan yang dapat dilakukan. Jika sudah sampai pada langkah

7.0 maka algoritma pemecah eksplisit ini berhenti. Jika ingin melihat pola

(42)

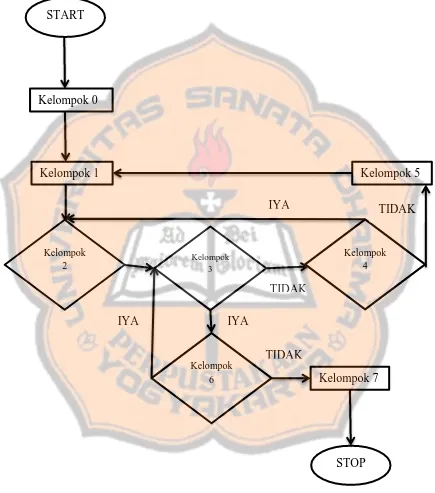
Selanjutnya untuk mempermudahkan melihat pola dari langkah-langkah di

atas, dibuat diagram sebagai berikut:

Gambar 3.2 Diagram Alur Pembuatan Pola Pemotongan

TIDAK Kelompok 1

START

STOP

Kelompok 3

Kelompok 4

Kelompok 6

Kelompok 0

Kelompok 5

Kelompok 7 IYA

TIDAK IYA

IYA

TIDAK

(43)

Contoh 3.2

Misalkan terdapat dua jenis pesanan kertas produk. Pada jenis pertama

memiliki lebar 23 cm dan panjang 30 cm. Pada jenis kedua memiliki lebar 26 cm

dan panjang 32 cm. Rol mempunyai lebar maksimum pemotongan ( ) adalah

96 cm dan lebar minimum pemotongan ( ) adalah 92 cm. Nilai yang

dipilih adalah 4. Selanjutnya akan dicari banyaknya pola pemotongan yang

mungkin dari kasus tersebut dengan algoritma diatas.

Kelompok 0 Langkah 0.0. j = 1

Langkah 0.1.

[ ]

Langkah 1.1.

[ ]

Langkah 2.1.

Pada langkah 2.2 sampai 2.4

dihitung untuk i=1 dan i=2

Langkah 2.2.

Langkah 2.3.

(44)

Langkah 2.4.

{

{ ⌊ ⌋}}

{ { ⌊ _⌋}}

{

{ ⌊ ⌋}}

{ { ⌊ _⌋}}

Langkah 3.0. misalkan

langkah 6.0

maka tidak

lanjut ke langkah 6.0

langkah 2.0

(45)

[ ] maka lanjut ke langkah 2.0

Langkah 2.1.

Langkah 2.2.

Langkah 2.3.

Langkah 2. 4.

{

{ ⌊ ⌋}}

{ {

}}

{

(46)

{ {

}}

langkah 6.0

maka tidak

langkah 2.0

[ ] maka

Langkah 2.1.

Langkah 2.2.

(47)

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

maka tidak

(48)

langkah 2.0

[ ] maka

Langkah 2.1.

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

(49)

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

maka lanjut

ke langkah 6.0

Langkah 6.1.

4.0

maka lanjut ke langkah 4.0

langkah 6.0

maka tidak

(50)

langkah 2.0

[ ] maka

Langkah 2.1.

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

(51)

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

maka tidak

langkah 2.0

[ ] maka

Langkah 2.1.

(52)

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

(53)

langkah 2.0

[ ] maka

Langkah 2.1.

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

(54)

{ {

}}

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

maka tidak

Langkah 6.1.

4.0

langkah 6.0

maka lanjut

(55)

langkah 2.0

[ ] maka

Langkah 2.1.

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

(56)

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

maka tidak

langkah 2.0

[ ] maka

Langkah 2.1.

(57)

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

(58)

ke langkah 6.0

Langkah 6.1.

4.0

langkah 6.0

maka lanjut

ke langkah 6.0

langkah 2.0

[ ] maka

Langkah 2.1.

(59)

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

(60)

langkah 2.0

[ ] maka

tidak lanjut ke langkah 2.0

Kelompok 5 Langkah 5.0. Didapat pola pemotongan baru .

[ ]

akan tetapi pola ini memiliki lebar

diantara 92 cm dan 96 cm maka

pola ini harus dieliminasi

Langkah 1.1.

[ ]

(61)

Langkah 2.2.

Langkah 2.3.

Langkah 2.4.

{

{ ⌊ ⌋}}

{ {

}}

{

{ ⌊ ⌋}}

{ {

}}

(62)

maka lanjut

ke langkah 6.0

Langkah 6.1.

4.0

langkah 6.0

maka tidak

langkah 2.0

[ ] maka

tidak lanjut ke langkah 2.0

Kelompok 5 Langkah 5.0. Didapat pola pemotongan baru .

[ ]

akan tetapi pola ini memiliki lebar

(63)

ini harus dieliminasi

Langkah 1.1.

[ ]

Langkah 2.1.

Langkah 2.2.

Langkah 2.3.

Langkah 2. 4.

{

{ ⌊ ⌋}}

{ {

(64)

{

{ ⌊ ⌋}}

{ {

}}

langkah 6.0

maka lanjut

ke langkah 6.0

Langkah 6.1.

4.0

langkah 6.0

maka lanjut

(65)

Langkah 6.1.

4.0

maka tidak lanjut ke

langkah 4.0

Pola pemotongan yang didapat adalah sebagai berikut

Tabel 3.3. Banyaknya Pola Pemotongan dari algoritma

Pola

ke

Lebar lembaran kertas permintaan

(bi)

Total

lebar

23 cm (b1) 26 cm (b2)

1 3 1 95 cm

(66)

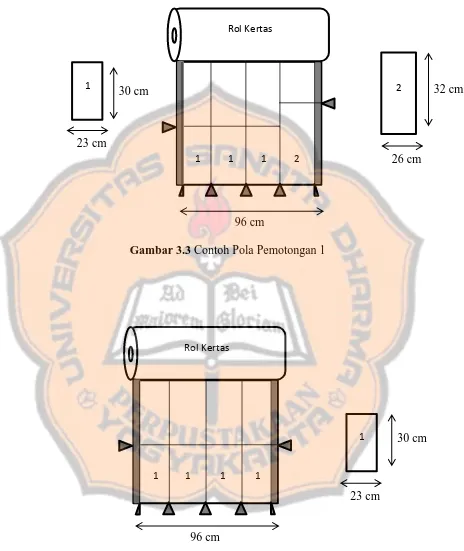
Gambar 3.3 Contoh Pola Pemotongan 1

Gambar 3.4 Contoh Pola Pemotongan 2 1

23 cm cm

30 cm cm

2

26 cm cm

32 cm cm

1

23 cm cm

30 cm cm

Rol Kertas

96 cm

1 1

Rol Kertas

96 cm

(67)

Pada Tabel 3.3 terlihat bahwa terdapat jumlah pola pemotongan sebanyak

dua (J= 2) yang terdiri dari pola pertama yaitu lembaran kertas permintaan

pertama (lebar 23 cm) dipotong sebanyak tiga kali dan lembaran kertas

permintaan kedua (lebar 26 cm) dipotong sebanyak satu kali serta pola kedua

yaitu lembaran kertas permintaan pertama (lebar 23 cm) dipotong sebanyak empat

kali dan lembaran kertas permintaan kedua (lebar 26 cm) tidak dipotong.

C. Model Matematika

Setelah menemukan pola pemotongan yang layak maka langkah selanjutnya

adalah membuat sebuah model matematika. Membuat model matematika

merupakan langkah yang penting dalam menyelesaikan masalah matematika di

dunia nyata. Khususnya pada masalah sisa pemotongan kertas dari rol kertas

produksi ke lembaran kertas, langkah awalnya adalah dengan mendefinisikan

parameter, langkah selanjutnya adalah membuat variabel keputusan atau variabel

yang akan kita cari, dan dilanjutkan dengan membuat fungsi tujuan dengan

kendala-kendala yang ada. Pada tugas akhir ini terdapat beberapa parameter,

variabel keputusan, fungsi tujuan dan kendala seperti berikut:

Tabel 3.4. Parameter dari Model Matematika

Parameter Keterangan

Panjang rol kertas

Panjang minimum permintaan dari produk ke-i

Panjang maksimum permintaan dari produk ke-i

Panjang minimum dari pola pemotongan

Banyaknya rol kertas

Banyaknya pola pemotongan

Banyaknya produk

Sisa panjang rol kertas ketika mengganti ke rol kertas berikutnya

(68)

Lebar produk ke-i

Panjang produk ke-i

Tabel 3.5. Variabel Keputusan dari Model Matematika

Variabel

Keputusan

Keterangan

Banyaknya kertas dari produk ke-i pada pola pemotongan ke-j

Panjang pola pemotongan ke-j pada rol kertas ke-k

Banyaknya pemotongan produk ke-i pada pola

pemotongan ke-j dalam rol kertas ke-k

Total panjang pemotongan pada produk ke-i

1 jika pemotongan pola ke-j menggunakan rol kertas ke-k

dan 0 untuk selainnya

1 jika rol kertas ke-k digunakan dan 0 untuk selainya

Jumlah dari produk ke-i yang di bawah batas atas

Jumlah dari produk ke-i yang melebihi batas atas

Kendala (1) akan dicari fungsi tujuan yang merupakan minimum dari sisa

pemotongan kertas, dengan cara menghitung total luas kertas yang digunakan

(∑ ) dikurangi dengan total luas kertas produksi (∑ ) lalu

ditambah dengan kerugian akibat produksi yang berlebih (∑ ). Jadi didapat

fungsi tujuan sebagai berikut:

Minimum

∑ ∑ ∑ (1)

Kendala (2) akan dicari kendala-kendala yang mempengaruhi saat

meminimalkan fungsi tujuan. Kendala pertama adalah total pola pemotongan

panjang disetiap rol kertas produksi ( ) ditambah dengan sisa panjang rol ( )

kertas produksi tidak boleh melebihi panjang rol kertas produksi ( ).

(69)

Kendala (3) menunjukkan bahwa jika panjang pola pemotongan ke-j pada

rol kertas ke-k ( ) digunakan maka nilai dari yj,k adalah1. Jika tidak digunakan

makan nilai dari yj,kadalah0.

(3)

Kendala (4) panjang pola pemotongan ke-j pada rol kertas ke-k ( ) harus

melebihi panjang minimum dari pola pemotongan ( ).

(4)

Kendala (5) panjang total masing-masing produk ( ) harus sama dengan

hasil kali dari banyaknya kertas dari produk ke-i pada pola pemotongan ke-j ( ),

panjang produk ke-i ( ), dengan banyaknya pemotongan produk ke-i pada pola

pemotongan ke-j dalam rol kertas ke-k ( ).

∑ ∑ (5)

Kendala (6), panjang total pola pemotongan masing-masing produk ( )

harus melebihi batas minimum permintaan dari masing-masing produk yang

bersesuaian ( ).

(6)

Kendala (7), menujukkan bahwa dalam memproduksi kertas permintaan,

konsumen bersedia menerima kelebihan kertas selama tidak melebihi batas atas

permintaan konsumen. Jika memproduksi lebih dari batas atas permintaan maka

dapat mengakibatkan kerugian.

(7)

Kendala (8), menunjukkan panjang kertas permintaan disetiap pola

pemotongan ( ) tidak melebihi panjang pola pemotongan ( ).

(8)

Kendala (9), menunjukkan bahwa rol kertas produksi harus digunakan

secara berurutan.

(9)

Dimana

(70)

Kendala (5) adalah kendala yang menyebabkan sistem persamaan ini

menjadi non-linear, sebab variabel keputusan dan berada dalam satu

operasi perkalian. Sehingga masalah yang didapat adalah masalah yang berbentuk

MINLP. Untuk membuat masalah MINLP menjadi masalah MILP maka pada

kendala (5) dapat dimemasukkan nilai dari variabel yang didapat pada Tabel

3.4. Setelah dimasukan nilai variabel pada kendala (5) maka masalah MINLP

sudah menjadi masalah MILP.

Contoh 3.3

Misalkan panjang rol kertas (L) adalah 160 cm, lebar rol kertas (W) adalah

96 cm, banyaknya rol kertas yang ada (r) adalah 2 rol kertas, sisa panjang rol

kertas ketika mengganti ke rol kertas berikutnya (S) adalah 30 cm, panjang

minimum dari pola pemotongan ( ) adalah 130 cm dan berikut adalah Tabel

spesifikasi jenis dan permintaan kertas.

Tabel 3.6. Ukuran lembaran kertas produksi dan batas permintaan

konsumen

Langkah selanjutnya adalah mengubah kendala dan memasukan nilai yang

diketahui sesuai contoh 3.3 seperti berikut:

Kendala (1) atau fungsi tujuan adalah

(71)

Minimum ∑ ∑ ∑

Minimum

Kendala (2) dibagi menjadi 2 karena nilai dari variabel k adalah 2.

∑

 Kendala (2) dengan nilai variabel

∑

 Kendala (2) dengan nilai variabel

∑

Kendala (3) dibagi menjadi 4 sebab nilai dari variabel k adalah 2 dan nilai

dari variabel j adalah 2.

 Kendala (3) dengan nilai variabel dan nilai variabel

Kendala (4) dibagi menjadi 4 sebab nilai dari variabel k adalah 2 dan nilai dari

(72)

Kendala (5) dibagi menjadi 2 sebab nilai dari variabel i adalah 2.

∑ ∑

Kendala (6) dibagi menjadi 2 sebab nilai dari variabel i adalah 2

(73)

Kendala (7) dibagi menjadi 2 sebab nilai dari variabel i adalah 2

Kendala (8) dibagi menjadi 8 sebab nilai dari variabel i adalah 2, nilai dari

(74)

 Kendala (8) dengan nilai variabel , nilai variabel , dan nilai variabel .

Kendala (9)

Dengan menggunakan program Matlab diperoleh hasil sebagai berikut

Tabel 3.7. Hasil dari variabel

k=1 k=2

1 1

Pada Tabel 3.7 terlihat bahwa nilai adalah 1 dan nilai adalah 1,

sehingga rol kertas mentah yang digunakan pada kasus ini sebanyak 2 rol.

j=1 j=2

(75)

k=2 1 0

Pada Tabel 3.8 terlihat bahwa nilai adalah 1 berarti pada rol kertas ke-1

digunakan pola pemotongan ke-2 dan nilai adalah 1 berarti pada rol kertas

ke-2 digunakan pola pemotongan ke-1.

i=1 i=2

840 96

Pada Tabel 3.9 terlihat bahwa nilai adalah 840 berarti total panjang

pemotongan pada produk ke 1 adalah 840 dan nilai adalah 96 berarti total

panjang pemotongan pada produk ke-2 adalah 96.

i=1 i=2

60 0

Pada Tabel 3.10 terlihat bahwa nilai adalah 60 berarti jumlah dari produk

ke-1 yang di bawah batas atas adalah 60 dan nilai adalah 0 berarti jumlah dari

produk ke-2 yang di bawah batas atas tidak ada.

i=1 i=2

(76)

Pada Tabel 3.11 terlihat bahwa nilai adalah 0 berarti jumlah dari produk

ke-1 yang melebihi batas atas tidak ada dan nilai adalah 4 berarti jumlah dari

produk ke-2 yang melebihi batas atas adalah 4.

j=1 j=2

k=1 0 130

k=2 130 0

Pada Tabel 3.12 terlihat bahwa nilai adalah 130 berarti panjang pola

pemotongan ke-2 pada rol kertas ke-1 adalah 130 dan nilai adalah 130 berarti

panjang pola pemotongan ke-1 pada rol kertas ke-2 adalah 130.

i=1 i=2

j=1 0 0

j=2 0 4

Pada Tabel 3.13 terlihat bahwa nilai adalah 4 berarti banyaknya

pemotongan produk ke-1 pada pola pemotongan ke-2 dalam rol kertas ke-1

adalah 4.

i=1 i=2

j=1 4 3

(77)

Pada Tabel 3.14 terlihat bahwa nilai adalah 4 berarti banyaknya

pemotongan produk ke-1 pada pola pemotongan ke-1 dalam rol kertas ke-2 adalah

4 dan nilai adalah 3 berarti banyaknya pemotongan produk ke-2 pada pola

pemotongan ke-1 dalam rol kertas ke-2 adalah 3. Didapat juga nilai Z adalah 2576

yang berarti sisa pemotongan kertas adalah 2576 .

Untuk melihat apakah hasil program ini benar atau tidak maka digunakan

program LiPS sebagai pembandingnya. Program LiPS adalah program yang

digunakan untuk menyelesaikan masalah Program Linear. Berikut adalah hasil

(78)

Tabel 15. Hasil pada program LiPS

nilainya adalah 2576. Terlihat bahwa nilai solusi minimal pada program

MATLAB dan LiPS sama akan tetapi variabel keputusan yang di peroleh berbeda.

Ini menunjukkan bahwa solusi pada contoh kasus ini tidak hanya terdapat satu

penyelesaian saja. Solusi yang tidak tunggal ini sangat menguntungkan sebab kita

dapat memilih mau menggunakan cara yang mana dengan hasil sisa pemotongan

(79)

BAB IV

PENYELESAIAN MASALAH PEMOTONGAN ROL KERTAS DENGAN

MENGGUNAKAN PROGRAM MATLAB

Pada bab ini akan dibahas mengenai penyelesaian masalah pemotongan rol

kertas yang didapat dan cara menggunakan program MATLAB yang telah dibuat.

Berikut adalah contoh kasus yang diselesaikan menggunakan program GUI

MATLAB:

Terdapat rol kertas produksi (r) sebanyak 12 rol kertas, dengan ukuran lebar

rol kertas adalah 96, lebar minimum pemotongan rol kertas adalah 89, panjang rol

kertas produksi adalah 525.500 cm, panjang minimum dari pola pemotongan

( ) adalah 100.000 cm, sisa panjang rol kertas ketika harus mengganti ke rol

kertas berikutnya (S) adalah 3.500 cm, dan berikut adalah tabel spesifikasi jenis

dan permintaan kertas.

Tabel 4.1 Ukuran lembaran kertas produksi dan batas permintaan

konsumen

Selanjutnya akan dilihat cara menggunakan aplikasi yang sudah dibuat oleh

penulis. Aplikasi ini dibuat dengan Graphical User Interface (GUI) MATLAB.

Selanjutnya akan dijelaskan mengenai cara menggunakan aplikasi yang telah

dibuat.

Pertama buka aplikasi GUI MATLAB yang sudah dibuat sehingga terlihat