BAB 2
LANDASAN TEORI
Bab ini berisi teori dasar yang dipakai dalam melakukan perancangan program serta untuk membuat aplikasi peramalan persediaan barang dengan Holt-Winters guna optimasi pendistribusian barang dengan Saving Method.
2.1. Peramalan
2.1.1. Definisi Peramalan
Peramalan (forecasting) adalah suatu kegiatan untuk memperkirakan apa yang terjadi pada masa yang akan datang (Sofjan Assauri, 1984, p1). Sedangkan menurut Sugiarto dan Harijono (2000, p1) peramalan merupakan studi terhadap data historis untuk menentukan hubungan, kecenderungan dari pola yang sistematis.
Menurut Levine, Stephan, Krehbiel, dan Barenson (2002, p654) menyatakan bahwa peramalan adalah sebuah teknik yang dapat digunakan untuk membantu perencanaan untuk kebutuhan masa depan berdasarkan pengalaman masa lalu.
2.1.2. Kegunaan dan Peran Peramalan
Peramalan diperlukan karena adanya perbedaan waktu antara kesadaran akan dibutuhkannya suatu kebijakan baru dengan waktu pelaksanaan kebijakan tersebut. Jadi dalam menentukan kebijakan itu perlu diperkirakan kesempatan atau peluang yang ada, dan ancaman yang mungkin terjadi.
Kegunaan peramalan terlihat pada saat pengambilan keputusan. Setiap orang selalu dihadapkan pada masalah pengambilan keputusan. Keputusan yang baik adalah keputusan yang didasarkan pertimbangan apa yang akan terjadi pada waktu keputusan itu dilaksanakan. Apabila kurang tepat ramalan yang disusun atau dibuat, maka makin kurang baiklah keputusan yang diambil.
2.1.3. Jenis-Jenis Peramalan
Pada umumnya peramalan dapat dibedakan dari beberapa segi tergantung cara melihatnya. Apabila dilihat dari sifat penyusunannya, maka peramalan dapat dibedakan atas dua macam sebagai berikut.
1. Peramalan yang subjektif, yaitu peramalan yang didasarkan atas perasaan atau intuisi dari orang yang menyusunnya. Dalam hal ini pandangan atau ”judgement” dari orang yang menyusunnya sangat menentukkan baik tidaknya hasil ramalan. 2. Peramalan yang objektif, adalah peramalan yang didasarkan atas data relevan pada
masa lalu, dengan menggunakan teknik–teknik dan metode–metode dalam penganalisaan data tersebut.
Selain itu, jika dilihat dari jangka waktu ramalan yang disusun, maka peramalan dapat dibedakan atas dua macam pula sebagai berikut.
1. Peramalan jangka panjang, yaitu peramalan yang dilakukan untuk penyusunan hasil ramalan yang jangka waktunya lebih dari satu setengah tahun atau tiga semester. Peramalan seperti ini misalnya diperlukan dalam penyusunan rencana
pembangunan suatu negara atau daerah, corporate planning, rencana investasi atau rencana ekspansi dari suatu perusahaan.
2. Peramalan jangka pendek, yaitu peramalan yang dilakukan untuk penyusunan hasil ramalan dengan jangka waktu yang kurang dari satu setengah tahun, atau tiga semester. Peramalan seperti ini diperlukan dalam penyusunan rencana tahunan, rencana kerja operasional, dan anggaran, contohnya penyusunan rencana produksi, rencana penjualan, rencana pengadaan, rencana persediaan, anggaran produksi, anggaran pemasaran, dan anggaran perusahaan.
2.2. Metode Peramalan
Metode peramalan adalah cara memperkirakan secara kuantitatif apa yang akan terjadi pada masa depan, berdasarkan data yang relevan pada masa lalu. Karena metode peramalan skripsi ini berdasarkan atas data yang relevan pada masa lalu, maka digunakan peramalan objektif dengan jenis metode peramalan kuantitatif.
Metode peramalan dapat digunakan untuk membantu dalam pendekatan analisis terhadap tingkah laku atau pola dari data yang lalu. Metode tersebut memberikan cara pemikiran, pengerjaan dan pemecahan yang sistematis dan pragmatis, serta memberikan tingkat keyakinan yang lebih besar atas ketepatan hasil ramalan yang dibuat, atau yang disusun.
2.2.1 Jenis–Jenis Metode Peramalan
Levine, Stephan, Krebhbiel, dan Barenson (2002, p655) mengatakan ada dua pendekatan umum untuk jenis metode peramalan yaitu kualitatif dan kuantitatif. Metode
peramalan kualitatif penting saat data historis tidak tersedia, namun metode ini bersifat sangat subjektif dan membutuhkan penilaian dari pakar. Adapun peramalan kuantitatif menggunakan data historis yang ada. Tujuan metode ini adalah mempelajari apa yang telah terjadi di masa lalu untuk meramalkan nilai-nilai yang akan datang.
2.2.2. Metode Peramalan Kuantitatif
Menurut Makridakis, Wheelwright, dan McGee (1999, p19-20), peramalan kuantitatif dapat diterapkan bila terdapat tiga kondisi sebagai berikut.
1. Tersedia informasi tentang masa lalu dengan jumlah minimal sesuai dengan metode peramalan yang digunakan
2. Informasi tersebut dapat dikuantitatifkan dalam bentuk data numerik sendiri mempunyai empat ukuran variabel atau skala.
a. Skala Nominal: hanya untuk membedakan kelopok mana yang menjadi objek penelitian
b. Skala Ordinal: mengelompokan responden dalam kategori tertentu dan mengurutkannya
c. Skala Interval: dapat menentukan jarak dua titik dalam variabel yang digunakan
d. Skala Rasio: selain membedakan, juga memberikan urutan, menentukan jarak, dan memiliki titik asal.
3. Dapat diasumsikan bahwa beberapa aspek pola masa lalu akan terus berlanjut pada masa mendatang.
Menurut Assauri(1984, p4), metode peramalan kuantitatif dapat dibedakan atas dua kategori sebagai berikut.
1. Metode peramalan yang didasarkan atas penggunaan analisis pola hubungan antara variable yang akan diperiksa dengan variabel waktu, yang merupakan deret waktu atau time series.
2. Metode peramalan yang didasarkan atas penggunaan analisis pola hubungan antara variabel yang akan diperkirakan dengan variabel lain yang mempengaruhinya, yang bukan waktu, yang disebut metode korelasi atau sebab akibat (causal methods).
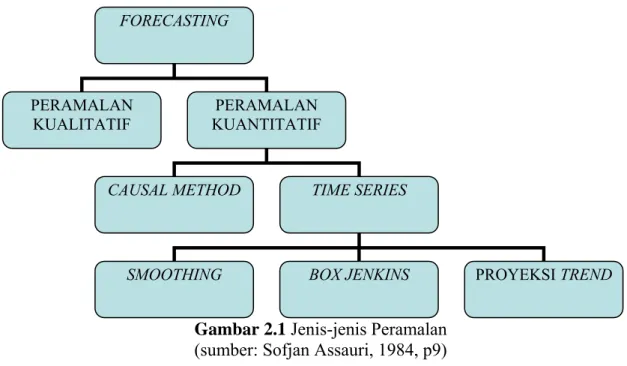
Metode-metode peramalan dengan menggunakan analisis pola hubungan antara variabel yang akan diperkirakan dengan variabel waktu, atau analisis deret waktu, dibagi menjadi tiga hal:
1. metode smoothing, yang mencakup metode data lampau (past data), metode rata-rata kumulatif, metode rata-rata bergerak (moving average) dan metode “exponential smoothing”.
2. metode Box Jenkins.
Gambar 2.1 Jenis-jenis Peramalan (sumber: Sofjan Assauri, 1984, p9) 2.3. Time Series
Model deret berkala melakukan pendugaan masa depan berdasarkan nilai masa lalu dari suatu variabel untuk menemukan pola dalam deret data historis dan mengekstrapolasikan pola tersebut ke masa depan. Di lain pihak, model kausal mengasumsikan bahwa variabel terikat yang diramalkan menunjukkan hubungan sebab akibat dengan satu atau lebih variabel bebas, dengan maksud untuk menemukan bentuk hubungan tersebut dan menggunakannya untuk meramalkan nilai mendatang dari variabel tak bebas (Makridakis et al.,1999, p37).
Langkah penting untuk memilih metode time series yang tepat adalah dengan mempertimbangkan jenis pola data, sehingga metode yang paling tepat dengan pola data tersebut dipertimbangkan. Pola data untuk deret time series dibedakan menjadi pola horizon, pola musiman, pola siklis, dan pola trend. Pola horizon terjadi manakala data berfluktuasi disekitar nilai rata-rata yang konstan. Pola musiman terjadi bilamana suatu deret time series dipengaruhi faktor musiman (misalnya kuartal, bulan, atau hari-hari
FORECASTING
PERAMALAN KUALITATIF
PERAMALAN KUANTITATIF
CAUSAL METHOD TIME SERIES
tertentu). Pola siklis terjadi bilamana datanya dipengaruhi oleh fluktuasi ekonomi jangka panjang seperti yang berhubungan dengan business cycle. Sedangkan pola trend terjadi bilamana terdapat kecenderungan kenaikan atau penurunan jangka panjang dalam data.
2.3.1. Holt
Peramalan dengan penghalusan eksponen sederhana dilakukan jika data tida mengandung komponen trend dan musiman, sedangkan jika mengandung komponen trend tetapi tidak mengandung komponen musiman, maka harus digunakan metode Holt, yaitu metode penghalusan eksponensial dengan dua kali pembobotan.
Metode ini pada awalnya digunakan untuk data bulanan yang tidak memiliki komponen musiman, dan dalam pengembangannya dapat digunakan untuk data tahunan dengan proses analisisnya mengadapsi proses untuk data bulanan. Misalkan x1, x2, . . . , xnsampel data deret waktu bulanan tanpa komponen musiman. Jika dideskripsikan:
mt : taksiran rata-rata pada bulan yang sama (current mean) untuk bulan ke-t, t = 1 , 2 ,… , 12.
Tt: taksiran pola trend pada bulan ke-t, t = 1 , 2 , … , 12 maka formulasi pembobotannya adalah:
mt= αxt+ (1 – α) (mt-1 − Tt-1) persamaan (2.1) Tt = γ(mt– mt-1) + (1 – γ)Tt-1
0 < α , γ < 1 , konstanta riil, xt pengamatan terakhir bulan ke-t
Peramalan nilai data waktu ke-t dengan lead time k dihitung dengan persamaan:
k t
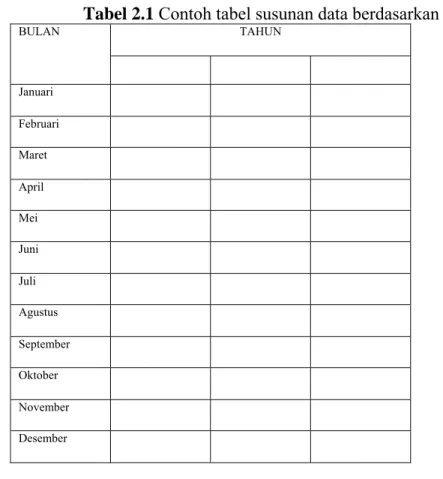
Perhitungan nilai α dan γ berdasarkan data sampel secara “manual” sebagai berikut: 1. Susun nilai data berdasarkan bulan yang sama seperti tabel berikut:
Tabel 2.1 Contoh tabel susunan data berdasarkan bulan
BULAN TAHUN Januari Februari Maret April Mei Juni Juli Agustus September Oktober November Desember
2. rata-rata data pada bulan yang sama untuk setiap bulan, mt, t : 1 , 2 , ... , 12 3. tentukan model trend pada bulan yang sama untuk setiap setiap bulan, dan hitung 4. nilai ramalan untuk pengamatan terakhir bulan ke-t, Tt, t : 1 , 2, … , 12
5. tentukan nilai-nilai pengamatan terakhir bulan ke-t, xt, t : 1 , 2 , … , 12 6. bangun formulasi pembobotan seperti pada persamaan (2.1).
7. lakukan proses iterasi seperti pada penghalusan eksponen sederhana untuk persamaan (2.1).
2.3.2. Winters
Metode ini merupakan penghalusan eksponensial juga, dan digunakan jika data memiliki komponen musiman, tetapi tidak memiliki komponen trend. Metode ini digunakan jika data adalah data bulanan, sebab musiman hanya dideskripsikan pada data bulanan. Secara umum, yang dimaksud dengan musiman adalah komponen siklis dengan periode 12 bulan.
Konsepsi perhitungan metode Winters identik dengan metode Holt, yaitu penghalusan eksponensial dengan dua kali pembobotan. Misalkan x1 , x2 , . . . , xn , sampel data deret waktu yang memiliki komponen musiman, tetapi tidak memiliki komponen trend. Selanjutnya jika didefinisikan (Mulyana, 2004,p62):
mt: taksiran rata-rata pada bulan yang sama untuk bulan ke-t, t : 1, 2, …, 12 st : taksiran faktor musiman pada bulan ke-t, t = 1, 2, …, 12
dan komponen musimannya multiplikatif dengan persamaan :
t t t t t ms x = +ε , ε : kekeliruan acak maka formulasi pembobotannya :
(
)
1 12 1 − − − + = t t t t m s x m α α persamaan (2.3)(
1−)
−12 + = t t t t s m x s δ δdan nilai ramalan untuk lead time h, dihitung dengan formulasi :
h t t h t m s x+ = −12+ Sedangkan jika aditif dengan persamaan
t t t t t m s x = + +ε , ε kekeliruan acak
maka formulasi pembobotannya
(
− −12) (
+ 1−)
−1 = t t t t x s m m α α persamaan (2.4)(
−) (
+ 1−)
−12 = t t t t x m s s δ δdan nilai ramalan untuk lead time h, dihitung dengan formulasi
h t t h t m s xˆ+ = + −12+
Pada formulasi pembobotan, xt pengamatan terakhir pada bulan ke-t , α dan δ konstanta
riil, 0 < α , δ < 1 . Sedangkan nilai lead time h = 1, 2, . . . , 12.
2.3.3. Holt-Winters
Metode peramalan Holt-Winters merupakan gabungan dari dari metode Holt dan metode Winters, digunakan untuk peramalan jika data memiliki komponen trend dan musiman. Metode Holt-Winters merupakan pengembangan dari metode Holt di mana metode Holt merupakan metode pemulusan dengan dua parameter (pemulusan ganda) untuk tipe data yang mengandung kecenderungan (trend)
Untuk deret data musiman, metode Holt-Winters merupakan pendekatan pemulusan yang paling banyak digunakan. Terdapat pendekatan pemulusan musiman yang lain namun jarang digunakan.
Kelemahan utama dari metode Holt-Winters yang menghambat penggunanya secara meluas adalah bahwa metode ini memerlukan tiga parameter pemulusan (α,β, dan γ). Karena setiap parameter ini dapat bernilai antara 0 hingga 1, maka kombinasi yang harus dicobakan sebelum nilai α,β, dan γ yang optimal dapat ditentukan. Salah satu masalah dalam penggunaan metode ini adalah dalam menentukan nilai yang optimal untuk α,β, dan γ tersebut yang akan meminimumkan nilai MSE (Mean Squared Error)
atau MAPE (Mean Absolute Percentage Error). Pendekatan yang dilakukan untuk menentukan nilai ini biasanya secara coba dan salah (trial and error). Namun hal ini memakan banyak waktu (Makridakis et al., 1999, p127).
Metode Holt-Winters memiliki dua tipe yaitu aditif dan multiplikatif. a. Metode Holt-Winters Aditif
Menurut Montgomery, Johnson, dan Gardiner dalam buku mereka ”Forecasting and Time Series Analysis – second edition”:
Model musiman aditif cocok untuk peramalan deret berkala (time series) di mana amplitudo (atau ketinggian) pola musimannya tidak bergantung pada rata-rata level atau tingkatan dari deret data (Montgomery, Johnson&Gardiner, 1990, p146).
Metode ini memiliki empat persamaan sebagai berikut. Pemulusan Keseluruhan (Level)
Lt = α(Yt – St-s) + (1- α)(Lt-1 + Tt-1) Pemulusan Trend Tt = β(Lt – Lt-1) + (1- β)Tt-1 Pemulusan Musiman St = γ(Yt – Lt) + (1 – γ)St-s Ramalan Ft+p = (Lt +Tt.p) + St-s+p Keterangan:
Lt = nilai pemulusan atau estimasi nilai tingkatan/level ke-t.
α = konstanta/koefisien pemulusan untuk level.
β = konstanta/koefisien pemulusan untuk estimasi trend. Tt = estimasi trend.
γ = konstanta/koefisien pemulusan untuk estimasi musiman. St = estimasi musiman.
p = banyaknya periode yang akan diramal ke depan. s = panjang musim.
Ft+p = nilai peramalan selama p periode ke depan (Yˆ ) t+p
b. Metode Holt-Winters Multiplikatif
Menurut Montgomery, Johnson, dan Gardiner dalam buku mereka ”Forecasting and Time Series Analysis – second edition”:
Model musiman multiplikatif cocok untuk peramalan deret berkala (time series) di mana amplitudo (atau ketinggian dari pola musimannya proposional dengan rata-rata level atau tingkatan dari deret data (Montgomery, Johnson&Gardiner, 1990, p138).
Seperti halnya pada metode Holt-Winters aditif, metode Holt-Winters multiplikatif juga memiliki empat persamaan dengan sedikit perbedaan berikut ini.
Pemulusan Keseluruhan (Level) Lt = α s t t S Y − + (1- α)(Lt-1 + Tt-1) Pemulusan Trend Tt = β(Lt – Lt-1) + (1- β)Tt-1
Pemulusan Musiman St = γ t t L Y + (1 – γ)St-s Ramalan Ft+p = (Lt + Tt.p) + St-s+p Keterangan:
Lt = nilai pemulusan atau estimasi nilai tingkatan/level ke-t.
α = konstanta/koefisien pemulusan untuk level.
Yt = nilai pengamatan atau nilai yang sebenarnya pada waktu ke-t.
β = konstanta/koefisien pemulusan untuk estimasi trend. Tt = estimasi trend.
γ = konstanta/koefisien pemulusan untuk estimasi musiman. St = estimasi musiman.
p = banyaknya periode yang akan diramal ke depan. s = panjang musim.
Ft+p = nilai peramalan selama p periode ke depan (Yˆ ) t+p
Seperti halnya pada metode Holt-Winters aditif, besarnya koefisien α, β, dan γ pada metode Holt-Winters multiplikatif memiliki jarak (range) dari 0,1 s/d 0,9. Pemilihan pemakaian besarnya bobot koefisien pemulusan α,β, dan γ dapat dilakukan secara subyektif atau dengan melihat tingkat kesalahan/error pengukuran peramalan seperti MAPE (Mean Absolute Percentage Error) yang dihasilkan berbeda-beda pada masing-masing besarnya α,β, dan γ. Hal tersebut dapat dilakukan secara coba dan salah (trial and error).
Begitu pula halnya untuk penentuan nilai awal Lt, Tt, dan St, pada
Holt-Winters multiplikatif juga memiliki cara penentuan dengan pendekatan nilai yang sama dengan Holt-Winters aditif, di mana perkiraan awal nilai level sama dengan nilai awal data. Lalu trend kemudian diperkirakan sama dengan nol (0), dan musiman yang masing-masing ditentukan sama dengan satu (1,0). Hal ini berlaku hanya untuk satu masa awal periode musiman pada data.
2.4. Ukuran Ketepatan Ramalan
Dalam semua situasi peramalan mengandung derajat ketidakpastian. Fakta ini dengan memasukkan unsur kesalahan (error) dalam perumusan sebuah peramalan deret waktu. Sumber penyimpangan dalam peramalan bukan hanya disebabkan unsur error, tetapi ketidakmampuan suatu model peramalan mengenai unsur yang lain dalam deret data juga mempengaruhi besarnya penyimpangan dalam peramalan. Jadi besarnya penyimpangan hasil ramalan dapat disebabkan oleh besarnya faktor yang tidak diduga (outliers), tidak ada metode peramalan mampu menghasilkan peramalan yang akurat, atau juga disebabkan metode peramalan yang digunakan tidak dapat memprediksi dengan tepat komponen trend, komponen musiman, atau komponen siklus yang mungkin terdapat dalam deret data, yang berarti metode yang digunakan tidak tepat (Bowerman dan O’Connel,1987).
Jika Xi merupakan data aktual untuk periode i dan Fi merupakan ramalan (atau
nilai kecocokan, fitted value) untuk periode yang sama, maka kesalahan didefinisikan sebagai.
Jika terdapat nilai pengamatan dan ramalan untuk n periode waktu, maka akan terdapat n buah galat dan ukuran statistik yang dapat didefinisikan sebagai berikut :
1. Galat Nilai Menengah (Mean Error)
∑
= = n i i n e ME 12. Galat Nilai Menengah Absolut (Mean Absolute Error)
∑
= = n i i n e MAE 13. Galat Jumlah Kuadrat (Sum of Squared Error)
∑
= = n i i e SSE 1 24. Galat Nilai Menengah Kuadrat (Mean Squared Error)
∑
= = n i i n e MSE 1 25. Galat Deviasi Standar (Standart Deviation of Error)
) 2 ( 1 2 − =
∑
= n e SDE n i iSelain ukuran ketepatan yang telah disebutkan di atas, ada lagi ukuran ketepatan yang sering digunakan untuk mengetahui ketepatan suatu metode peramalan dalam memodelkan data deret waktu yaitu nilai MAPE (Mean Absolute Percentage Error), MSD (Mean Squared Deviation) dan MAD (Mean Absolute Deviaton).
MAPE merupakan ukuran ketepatan relatif yang digunakan untuk mengetahui persentase penyimpangan hasil ramalan, dengan persamaan sebagai berikut.
% 100 | ˆ | 1 X n x x x MAPE t n t t t t
∑
= − =MAD menyatakan penyimpangan ramalan dalam unit yang sama pada data, dengan merata-ratakan nilai absolute error (penyimpangan) seluruh hasil ramalan. Nilai absolute berguna untuk menghindari nilai penyimpangan positif dan penyimpangan negatif saling meniadakan. Persamaanya adalah sebagai berikut.
n x x MAD n t t t
∑
= − = 1 | ˆ |MSD merupakan ukuran penyimpangan ramalan dengan merata-ratakan kuadrat error (penyimpangan) semua ramalan. MSD menghindarai nilai penyimpangan positif dan penyimpangan negatif saling meniadakan adalah dengan mengkuadratkan nilai kesalahan tersebut. Persamaanya adalah sebagai berikut.
n x x MSD n t t t
∑
= − = 1 2 ) ˆ ( Di mana :xt: nilai aktual periode t
t
xˆ : nilai ramalan periode t n : jumlah periode ramalan
2. 5. Optimasi
Dalam matematika, istilah optimasi atau program matematika berhubungan dengan masalah pencarian nilai minimum atau maksimum dari fungsi riil dengan memilih nilai dari variabel secara sistematis dari himpunan yang ada. Masalah ini dapat direpresentasikan sebagai berikut.
Diberikan sebuah fungsi f : A → R dari himpunan bilangan A ke himpunan bilangan riil. Akan dicari x0 dari himpunan A dimana f(x0) ≤ f(x) untuk semua x pada A
(”minimalisasi”) atau f(x0)≥f(x) untuk semua x pada A (“maksimalisasi”).
Secara khusus, A adalah himpunan bagian dari dimensi Euclid Rn. Pada A terdapat beberapa kendala berupa persamaan atau pertidaksamaan yang harus dipenuhi oleh anggota himpunan A. Domain dari himpunan A disebut ruang cari dan elemen-elemen dari himpunan A disebut solusi kandidat atau feasible solution. Fungsi f disebut objective function atau cost function. Sebuah solusi kandidat paling minimal atau paling maksimal dari sebuah objective function disebut solusi optimal.
Pada umumnya, pada objective function yang bersifat konveks terdapat lokal minima atau maksima, dimana local minimum x* didefinisikan sebagai berikut.
||x-x*|| ≤ δ , di mana δ > 0 Sehingga
f(x*) ≤ f(x)
Local maxima didefinisikan dengan cara yang sama. Untuk mengatasi hal itu, maka dikenal istilah global opmitzation yang dapat mencari solusi yang konvergen pada permasalahan non konveks dalam waktu yang terbatas.
2.6. Vehicle Routing Problem
Vehicle Routing Problem (VRP) pertama kali diutarakan oleh Dantzig dan Ramser. VRP adalah permasalahan kompleks dari optimisasi kombinatorial, yang merupakan gabungan dari dua permasalahan, yaitu Travelling Salesman Problem (TSP) dan Bin Packing Problem (BPP). VRP merupakan NP-Hard (non-deterministic polynomial-time Hard), sehingga permasalahan ini sulit dipecahkan.
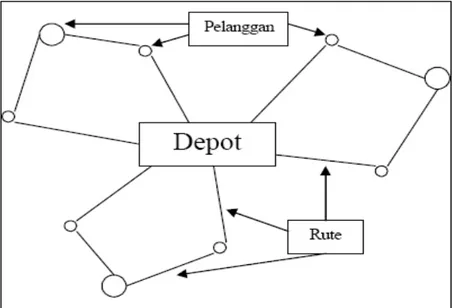
VRP berhubungan dengan pengiriman dan/atau pengambilan barang. Masalah kritis dalam VRP adalah rute dan pengaturan kendaraan pengangkut yang ada sehingga dapat melayani permintaan pelanggan seefisien mungkin berdasarkan kriteria-kriteria yang ada. Sebuah rute adalah serangkaian lokasi yang harus dikunjungi kendaraan pengangkut untuk menyelesaikan pelayanannya, misalnya pelayanan pengiriman barang. Penyelesaian VRP menghasilkan rute, dan dapat juga menghasilkan penjadwalan kendaraan-kendaraan pengangkut dalam rute yang terbentuk.
Permasalahan dalam Vehicle Routing dapat dibedakan menjadi dua, yaitu permasalahan statis dan dinamis. Pada permasalahan statis, permintaan pelanggan telah diketahui sebelumnya. Sedangkan pada permasalahan dinamis, sebagian ataupun seluruh permintaan pelanggan diketahui ketika kendaraan pengangkut sudah mulai beroperasi, yaitu ketika rute telah diatur, ataupun ada perubahan di tengah perjalanan.
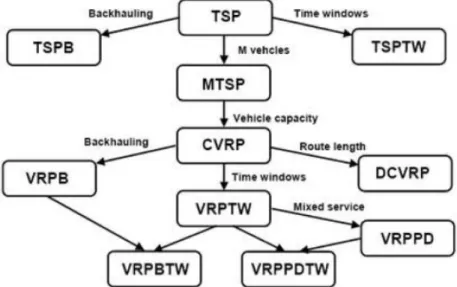
Gambar 2.2 Hubungan VRP dengan TSP dan perkembangannya (sumber : Massimo Paoluci, 2001, p10)
VRP adalah generalisasi dari TSP. Maka, TSP adalah sebuah VRP tanpa batasan seperti depot, pelanggan dan permintaan. M-TSP adalah VRP dengan sebuah depot dan m kendaraan pengangkut, termasuk bila tidak ada permintaan dari pelanggan. M-TSP adalah transformasi dari TSP dengan memperbanyak jumlah depot.
Pada kenyataanya, Vehicle Routing digambarkan dengan jaringan jalan, yang kemudian, dituangkan dalam sebuah graf, baik graf berarah G = (V,A), graf tidak berarah G = (V,E) maupun graf campuran G = (V, A ∪ E). Penggunaan bentuk graf ini disesuaikan dengan daerah yang akan dikunjungi kendaraan pengangkut. Graf tak berarah digunakan jaringan jalan skala besar, meliputi negara, dan negara bagian atau provinsi. Sedangkan graf berarah digunakan untuk jaringan jalan skala kecil, misal untuk menggambarkan jalan-jalan dalam satu kota.
Verteks menggambarkan depot, pelanggan ataupun persimpangan jalan. Himpunan verteks dilambangkan dengan V = (v0, .... vn). Verteks v0 mewakili pusat, di
Sedangkan verteks lainnya melambangkan kota atau pelanggan, yang memiliki permintaan di node. arc atau edge menggambarkan jalan-jalan yang ada. Edge dapat bersifat berarah (i,j) ε A, di mana A = {(vi,vj): i ≠ j, vi,vj ε V} dan tidak berarah e ε E. Biaya dan jarak perjalanan dilambangkan oleh cij, yang didefinisikan pada A, sedangkan
waktu non-negatif dilambangkan oleh tij, yang juga didefinisikan pada A.
Setiap verteks vi dalam V diasosiasikan dengan sejumlah barang qi, yang akan
diantarkan oleh satu kendaraan. VRP bertujuan untuk menentukan sejumlah k rute kendaraan dengan total biaya yang minimum, bermula dan berakhir di sebuah depot. Adapun setiap verteks dalam V dikunjungi tepat sekali oleh satu kendaraan jadi biaya dari solusi masalah ini S adalah : Fvrp(S) =
∑
= k i i R C 1 ) ( .
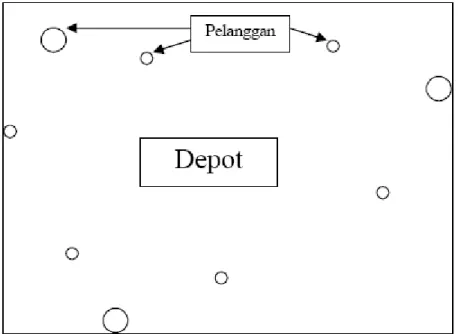
Gambar 2.3. Contoh visualisasi input dari Vehicle Routing Problem (sumber: Massimo Paolucci, 2001, p2)
5 Lokasi permintaan Simpul Garis Campuran 6 Jaringan yang mendasari Tidak berarah Berarah Campuran Euclid 7 Batas kapasitas kendaraan pengangkut Semuanya sama Jalur yang berbeda Kapasitas tak terbatas 8 Rute maksimum Sama untuk semua rute
Berbeda untuk setiap rute Tidak ditentukan
9 Sistem
pengoperasian Pengambilan saja Pengiriman saja
Pengambilan dan pengiriman 10 Biaya Variabel atau biaya rute
Biaya tetap pengoperasian atau biaya tetap kendaraaan pengangkut
Biaya pengangkutan umum 11 Tujuan Meminimalkan biaya total rute
Meminimalkan jumlah kendaraan pengangkut yang diperlukan
Meminimalkan fungsi kegunaan berdasarkan pada pelayanan dan kenyamanan
Meminimalkan fungsi kegunaan berdasarkan pada prioritas pelanggan
2.7. Metode Savings
Clarke dan Wright (1964) menemukan sebuah metode sederhana untuk mengoptimalkan rute pengiriman, di mana terdapat banyak kendaran pengangkut dengan berbagai kapasitas yang berasal dari satu pusat yang akan mengirimkan barang-barang ke banyak tempat. Rute terpendek antara dua titik diberikan pada sistem. Tujuan yang ingin dicapai adalah bagaimana mengalokasikan kendaraan pengangkut, sehingga semua barang dapat terikirim dengan biaya pengiriman serta operasional minimal. Sebenarnya, prosedur sederhana, tetapi sangat efektif dalam menghasilkan solusi yang
Gambar 2.4. Salah satu output dari persoalan VRP dari input gambar 2.3 (sumber: Massimo Paolucci, 2001, p5)
Pada perkembangannya, VRP memiliki beberapa karakteristik sehingga dapat dibagi-bagi dalam beberapa kategori masalah, seperti yang dapat ditunjukan dalam tabel 2.2. Kategori ini dibuat oleh Bodin dan Golden (1981), yang memamparkan berbagai karakteristik umum, yang akan membedakan VRP. Keseluruhan tabel memberikan gambaran singkat tentang masalah routing.
Tabel 2.2 Kategori masalah dalam VRP (sumber: Titiporn Thammapimokkul, 2001, p16) No Karakteristik Varian yang Mungkin
1 Jumlah Kendaraan Pengangkut
Satu kendaraan pengangkut Multi kendaraan pengangkut 2 Tipe kendaraan
pengangkut
Homogen (satu tipe kendaraan pengangkut) Heterogen (multi tipe kendaraan pengangkut) 3 Tempat asal
kendaraan (pusat)
Satu pusat Multi pusat
4 Tipe Permintaan Permintaan deterministik (telah diketahui sebelumnya)
Permintaan stochastic
Permintaan kepuasan sebagian
mendekati optimal. Cara heuristic ini disebut metode Savings, di mana terjadi perubahan prosedur dalam setiap langkah sehingga menghasilkan yang lebih baik. Langkah-langkahnya adalah sebagai berikut.
1. Pertama, setiap rute menghubungkan pusat dengan satu pelanggan
2. Kemudian, hubungkan setiap dua pelanggan dalam satu rute jika total permintaanya tidak melebihi kapasitas kendaraan pengangkut. Dengan algoritma ini, dihitung biayanya dan dipilih yang terbesar.
3. Kemudian, rute diperluas lagi dengan mengkombinasikan rute-rute yang ada, penghitungan biaya dilakukan dan biaya terbesar dipilih.
4. Lakukan langkah ini berulang-ulang hingga permintaan melebihi kapasitas kendaraan pengangkut.
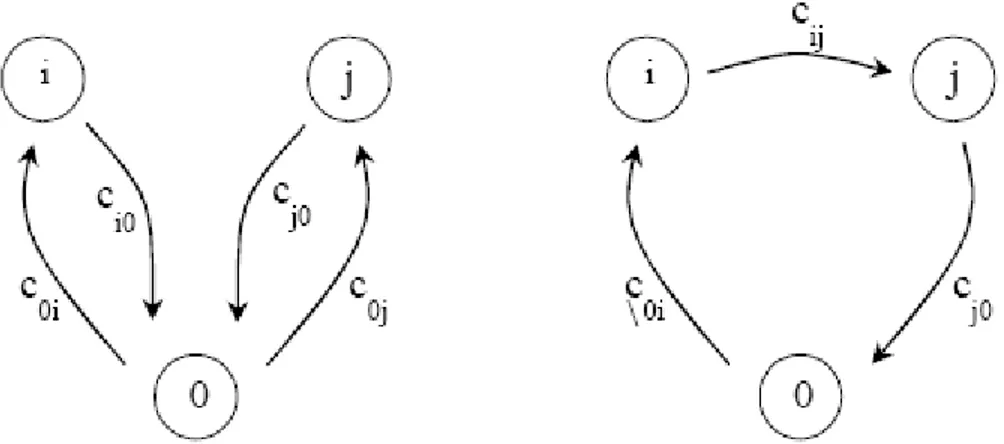
Dalam algoritma Savings, kombinasi dari dua pelanggan i dan j ke dalam satu rute dirumuskan sebagai berikut
ij oj io
ij c c c
S = + +
Di mana cij menyatakan biaya rute dari pelanggan i ke j. Pelanggan “0” merupakan
pusat atau awal rute. Contoh ilustrasi digambarkan dalam Gambar 2.5.
Gambar 2.5. Ilustrasi dari Savings yang telah dihitung (sumber: Titiporn Thammapimookkul, 2001)
Dari prosedur sebelumnya, algoritma dapat digambarkan sebagai berikut 1. Pertama, setiap n kendaraan pengangkut melayani satu pelanggan
2. Untuk setiap pasangan simpul i,j,i,…j (baik pelanggan pertama ataupun terakhir dari siklus yang berbeda) hitung savings dengan menggabungkan siklus dengan edge (i,j) : Sij = cio + coj – cij
3. Urutkan savings dari besar ke kecil
4. Ambil edge (i,j) dari bagian paling atas daftar savings. Gabungkan dua siklus yang terpisah dengan edge (i,j), jika
a. Simpul-simpul dimiliki oleh siklus terpisah
b. Permintaan tidak melebihi kapasitas maksimal dari kendaraan pengangkut c. i dan j adalah pelanggan pertama atau terakhir dari siklus
5. Ulangi langkah keempat sehingga semua data pada daftar savings telah dikerjakan atau kapasitas kendaraan pengangkut sudah penuh untuk melayani pelanggan selanjutnya
Contoh :
Berikut adalah sebuah graf lengkap dengan pusat 0 dan akan mengirimkan barang ke 9 pelanggan dengan kapasitas kendaraan pengangkut = K = 40
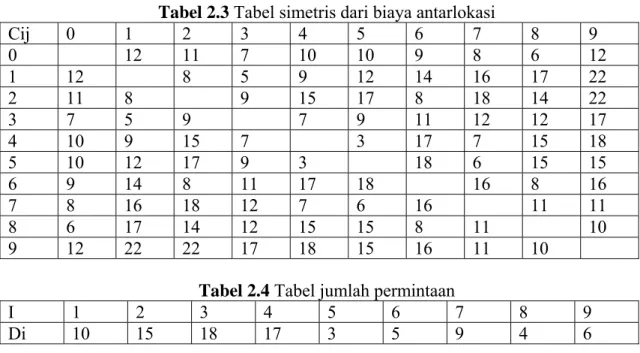
Tabel 2.3 Tabel simetris dari biaya antarlokasi Cij 0 1 2 3 4 5 6 7 8 9 0 12 11 7 10 10 9 8 6 12 1 12 8 5 9 12 14 16 17 22 2 11 8 9 15 17 8 18 14 22 3 7 5 9 7 9 11 12 12 17 4 10 9 15 7 3 17 7 15 18 5 10 12 17 9 3 18 6 15 15 6 9 14 8 11 17 18 16 8 16 7 8 16 18 12 7 6 16 11 11 8 6 17 14 12 15 15 8 11 10 9 12 22 22 17 18 15 16 11 10
Tabel 2.4 Tabel jumlah permintaan
I 1 2 3 4 5 6 7 8 9 Di 10 15 18 17 3 5 9 4 6
Langkah kerja penyelesaian masalah di atas adalah sebagai berikut.
1. dengan menghitung Sij – cio + coj – cij, maka diperoleh tabel saving pada tabel 2.4.
Tabel 2.5 tabel saving setelah diurutkan
Sij 1 2 3 4 5 6 7 8 9 1 15 14 13 10 7 4 1 2 2 9 6 4 12 1 3 1 3 10 8 5 3 1 2 4 17 2 11 1 4 5 1 12 1 7 6 1 7 5 7 3 9 8 8
2. urutkan savings dari besar ke kecil (4,5) = 10+10-3 = 17
(1,2) = 12+11-8 = 15
… (1,3), (1,4), (2,6), (5,7), (4,7), (1,5), (3,4), (2,3), (7,9), (3,5), (8,9), (1,6), (5,9), (6,8), (2,4), dan seterusnya
3. Cari rutenya
Solusi inisialisasi : siklus 0-1-0, 0-2-0, … , 0-9-0
Edge (4,5) : Gabungkan siklus 0-4-0 dengan 0-5-0. Hasil = 0-4-5-0, maka simpan d4+d5
= 20 < K
Edge (1,2) : Gabungkan siklus 0-1-0 dengan 0-2-0. Hasil 0-1-2-0, maka simpan d1 + d2
= 25 < K
~Edge (1,3) : Gabungkan siklus 0-1-2-0 dengan 0-3-0, tetapi ternyata melebihi batas kapasitas, karena d1 + d2 + d3 = 43 > K (tidak memungkinkan)
~Edge (1,4) : Gabungkan siklus 0-1-2-0 dengan 0-4-0, tetapi ternyata melebihi batas kapasitas, karena d1 + d2 + d4 = 43 > K (tidak memungkinkan)
Edge (2,6) : simpul 2 sudah termasuk dalam siklus 0-1-2, maka gabungkan siklus 0-1-2-0 dengan 0-1-2-0-6-0-1-2-0. Hasil : 0-1-2-0-1-2-6-0-1-2-0, maka simpan d1 + d2 + d6 = 30 < K
Edge (5,7) : Simpul 5 sudah termasuk dalam siklus 4-5-0, maka gabungkan siklus 0-4-5-0 dan 0-7-0. Hasil : 0-4-5-7-0, maka simpan d4 + d5 + d7 = 29 < K
~Edge (4,7) : Termasuk siklus 0-4-5-7-0 (tidak memungkinkan)
~Edge (1,5) : Simpul 5 merupakan bagian dalam siklus 0-4-5-7-0 (di bagian tengah), sehingga tidak mungkin bercabang ke lokasi lain (tidak memungkinkan) ~Edge (3,4) : Gabungkan siklus 0-3-0 dengan 0-4-5-7-0, tetapi batas kapasitas :
d3+d4+d5+d7 = 47 > K (tidak memungkinkan)
Edge (7,9) : Simpul 7 sudah termasuk dalam siklus 0-4-5-7-0, maka gabungkan siklus 0-4-5-7-0 dengan 0-9-0. Hasil 0-4-5-7-9-0, maka simpan d4+d5 +d7+d9 = 35
< K
~Edge (3,5) : Simpul 5 merupakan bagian dalam siklus 0-4-5-7-9-0 (tidak memungkinkan)
Edge (8,9) : Simpul 9 sudah termasuk dalam siklus 0-4-5-7-9-0, maka gabungkan siklus 0-4-5-7-9-0 dengan 0-8-0. Hasil : 0-4-5-7-9-8-0, maka simpan d4 +
d5+d7+d9+d8 = 39 < K.
Edge (1,6) : baik simpul 1 maupun simpul 6 sudah termasuk ke dalam siklus Edge (5,9) : baik simpul 5 maupun simpul 9 sudah termasuk ke dalam siklus
~Edge (6,8) : gabungkan siklus 0-1-2-6-0 dengan 0-4-5-7-9-8-0, tetapi ternyata melebihi kapasitas, karena (d1+d2+d6) + (d4+d5+d7+d9+d8) = 69 > K (tidak
memungkinkan) 4. Diperoleh 3 rute, yaitu
RUTE MUATAN BIAYA 0-3-0 18 14
0-1-2-6-0 30 37
0-4-5-7-9-8-0 39 46
5. Graf yang terbentuk
2.8. Software Engineering (Rekayasa Piranti Lunak)
Menurut Fritz Bauer (Pressman, 2005, p53), rekayasa piranti lunak adalah penetapan dan pemakaian prinsip-prinsip rekayasa dengan tujuan mendapatkan piranti lunak yang ekonomis, terpercaya, dan bekerja efisien pada mesin yang sebenarnya (computer).
Menurut Pressman (2005, p54), rekayasa piranti lunak terbagi menjadi 3 lapisan yang mampu mengontrol kualitas dari piranti lunak yaitu :
a. Proses (Process)
Proses merupakan lapisan dasar dalam rekayasa piranti lunak. Proses dari rekayasa piranti lunak adalah perekat yang menyatukan lapisan-lapisan teknologi dan memungkinkan pengembangan yang rasional dan periodik dari piranti lunak komputer.
b. Metode (Methods)
Metode dari rekayasa piranti lunak menyediakan secara teknis bagaimana membangun sebuah piranti lunak. Metode meliputi sekumpulan tugas yang luas,
termasuk di dalamnya analisis kebutuhan, perancangan, konstruksi program, pengujian, dan pemeliharaan. Metode dari rekayasa piranti lunak bergantung pada sekumpulan prinsip dasar masing-masing area teknologi dan memasukkan pemodelan aktivitas, serta teknik deskriptif lainnya.
c. Alat Bantu (Tools)
Alat bantu dari rekayasa piranti lunak menyediakan dukungan otomatis atau semi otomatis untuk proses dan metode. Ketika alat bantu diintegrasi, informasi akan diciptakan oleh sebuah alat bantu yang dapat digunakan oleh lainnya, sebuah system untuk mendukung pengembangan piranti lunak, yang juga disebut computer-aided software engineering (CASE). CASE menggabungkan piranti lunak, perangkat keras, dan database piranti lunak untuk menciptakan lingkungan rekayasa piranti lunak yang sejalan dengan CAD / CAE (computer-aided design / engineering) untuk perangkat keras.
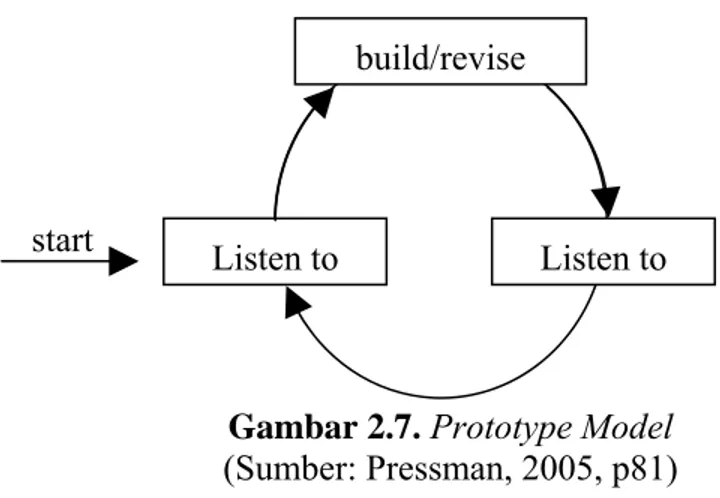
Model rekayasa piranti lunak yang digunakan adalah yang seringkali disebut sebagai prototype model. Model ini memberikan pendekatan-pendekatan yang sistematis dan berurutan (sequential) dalam pengembangan suatu software. Tahapan-tahapan yang terdapat dalam prototype model adalah sebagai berikut.
Gambar 2.7. Prototype Model (Sumber: Pressman, 2005, p81)
Proses prototype model seperti yang telah digambarkan diatas akan dijelaskan berikut ini.
• Pengumpulan kebutuhan
Developer dan client bertemu dan menentukan tujuan umum, kebutuhan yang diketahui dan gambaran bagian-bagian yang akan dibutuhkan berikutnya. Detail kebutuhan mungkin tidak dibicarakan pada awal pengumpulan kebutuhan. • Perancangan
Perancangan dilakukan cepat dan rancangan memiliki semua aspek software yang diketahui, dan rancangan ini menjadi dasar pembuatan prototype.
• Evaluasi prototype
Client mengevaluasi prototype yang dibuat dan digunakan untuk memperjelas kebutuhan software
Listen to
build/revise
Listen to start
2.9. Diagram Alir (Flowchart)
Diagram alir (flowchart) adalah representasi grafis dari serangkaian aktivitas operasi, pergerakan, inspeksi, delay, keputusan dan penyimpanan dari sebuah proses. Diagram alir menggunakan simbol-simbol untuk merepresentasikan jenis proses atau proses yang sedang berjalan. Bentuk yang sudah distandarisasi menyediakan metode yang umum dipakai oleh banyak orang1 untuk memvisualisasikan masalah dengan cara yang sama dan lebih mudah (Hansen, 2005).
2.10. State Transition Diagram (STD)
State Transition Diagram merupakan sebuah modeling tool yang digunakan untuk mendeskripsikan system yang memiliki ketergantungan terhadap waktu. STD merupakan suatu kumpulan keadaan atau atribut yang mencirikan suatu keadaan pada waktu tertentu (Kowal, 1992). Arti dari notasi STD adalah sebagai berikut.
1. State
State merepresentasikan reaksi yang ditampilkan ketika suatu tindakan dilakukan. Ada 2 jenis state, yaitu: state awal dan state akhir. State akhir dapat berupa beberapa state, sedangkan state awal tidak lebih dari satu.
2. Arrow
Arrow sering disebut juga dengan transisi state yang diberi label dengan ekspresi aturan. Label tersebut menunjukan kejadian yang menyebabkan transisi terjadi.
3. Condition dan action
Condition adalah suatu event pada lingkungan eksternal yang dapat dideteksi oleh sistem, sedangkan action adalah aksi yang dilakukan oleh sistem bila terjadi perubahan state atau merupakan reaksi terhadap kondisi. Aksi akan menghasilkan keluaran/tampilan.