MODEL PROBABILISTIK UNTUK KEBIJAKAN PENAMBAHAN PERSEDIAAN BARANG DAN STRATEGI PRODUKSI

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana

Program Studi Matematika

Oleh:

ALBERTUS AAN OKY DWI HATMOKO 023114010

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SANATA DHARMA

YOGYAKARTA 2007

tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta,……….

Penulis

kekuatan itulah yang akan menjadi penolongmu disaat kamu

jatuh

.

Skripsi ini kupersembahkan untuk

Tuhan yang tetap menyayangiku dengan segala kekurangan dan dosaku,

kedua Orangtuaku, adikku Siska, kakakku Oki,

dan untuk ijoep yang tersayang,

serta semua teman – temanku

.

barang dibutuhkan dua komponen penyusun yang saling berhubungan yaitu komponen utama dan komponen pelengkap. Perusahaan tersebut hanya mampu memproduksi salah satu komponen, sehingga perlu memesan komponen pelengkapnya dari perusahaan lain. Ada dua masalah yang dihadapi oleh pihak perusahaan perakitan dan penyuplai. Masalah yang dihadapi oleh perusahaan perakitan adalah bagaimana membuat suatu kebijakan pemesanan untuk menentukan jumlah barang yang akan dipesan. Sedangkan masalah yang dihadapi oleh penyuplai adalah bagaimana penyuplai mampu membuat suatu strategi produksi untuk memenuhi permintaan perusahaan perakitan dengan baik.

Kedua masalah yang dihadapi oleh perusahaan perakitan dan penyuplai tersebut dapat dimodelkan dengan distribusi multinomial. Tahap penyelesaiannya adalah dengan membuat model multinomial dari masalah tersebut kemudian mencari solusinya dengan program linear bilangan bulat.

assembling process of a goods assembling company, those are primary component and supplement component. The company is able to produce one component so it needs to order the supplement component from another company. These are two problems, which are faced by the assembling company and the supplier company. The problem from the assembling company side is how to make ordering policy to determine the number of the ordering of goods. Where as, problem from supplier company side is how it can make producing strategy to fulfill the assembling company request well.

The two problems, which are faced by the assembling company and the supplier company can be put into multinomial distribution model. The finding phases are by making multinomial model of the problems then find the solution using integer programming.

yang telah diberikan sehingga penulis dapat menyelesaikan skripsi ini.

Dalam proses penulisan skripsi ini banyak hambatan yang dialami oleh penulis. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu penulis ingin mengucapkan terima kasih kepada:

1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, selaku dosen pembimbing akademik sekaligus dosen pembimbing skripsi yang telah meluangkan waktu, pikiran, serta nasihatnya sehingga penulis dapat sampai pada tahap penyusunan skripsi ini.

2. Bapak Y.G. Hartono, M.Sc, selaku Ketua Program Studi Matematika FMIPA USD Yogyakarta yang telah memberikan banyak saran.

3. Bapak dan Ibu Dosen FMIPA yang telah memberikan pengetahuan yang sangat berguna bagi penulis.

4. Mas Tukijo dan Ibu Linda yang telah memberikan pelayanan adminitrasi dan urusan – urusan akademik kepada penulis.

5. Perpustakaan USD dan Staf yang telah memberikan fasilitas dan kemudahan kepada penulis.

6. Orang tuaku, adikku Siska dan kakakku Oki yang selalu memberikan dukungan dalam segala hal.

Imut, Ridwan Man, terima kasih atas persahabatan yang kalian berikan untuk penulis.

9. Teman – teman angkatan 2002 tanpa terkecuali yang sudah memberikan segala keceriaan dan dukungan kepada penulis.

10. Teman – teman di kost zenifara dan pak Mardi serta teman – teman dari kost ijo yang telah memberikan humor – humor yang lucu.

11. Bonang, Shiro, Masao, Gepeng, Kriwil, Punk yang telah memberikan persahabatan yang hangat sejak SMA.

12. Seluruh teman – teman di FMIPA. 13. Teman – teman KKN kelompok 42.

Yogyakarta, April 2006

penulis

HALAMAN PERSETUJUAN PEMBIMBING………... ii

HALAMAN PENGESAHAN……….. iii

PERNYATAAN KEASLIAAN KARYA……… iv

HALAMAN PERSEMBAHAN……….. v

ABSTRAK……….. vi

ABSTRACT……… vii

KATA PENGANTAR……… viii

DAFTAR ISI……….. x

BAB I PENDAHULUAN……… 1

A. Latar Belakang………. 1

B. Rumusan Masalah……… 3

C. Pembatasan Masalah………... 3

D. Tujuan Penulisan………. 4

E. Metode Penulisan……….... 4

F. Manfaat Penulisan………... 4

G. Sistematika Penulisan………. 5

BAB II DASAR – DASAR TEORI PROBABILITAS dan PROGRAM LINIER BILANGAN BULAT……… 6

A. Peluang Bersyarat……….. 6

B. Variabel Random………... 8

C. Independensi Variabel Random……… 17

D. Distribusi Marginal………... 20

E. Variansi dan Kovariansi……….... 23

F. Program Linear Bilangan Bulat……… 26

BAB III MODEL PROBABILISTIK UNTUK KEBIJAKAN PENAMBAHAN PERSEDIAAN BARANG DAN STRATEGI PRODUKSI………. 29

A. Produksi Barang dan Model Multinomial……… 29

B. Model Probabilistik untuk Persediaan Lengan Piston dalam Kondisi Aman………... 31

C. Perbandingan Tiga Kebijakan Pemesanan Barang………… 38

1. Kebijakan Pemesanan 1……….. 40

2. Kebijakan Pemesanan 2……….. 41

3. Kebijakan Pemesanan 3……….. 42

4. Perbandingan Ketiga Kebijakan………. 43

5. Kesimpulan dari Ketiga Kebijakan……… 45

D. Variabel Jumlah Produksi Piston………. 48

E. Masalah Produksi Yang Dihadapi Penyuplai……… 50

1. Seleksi Ukuran Target Oleh Penyuplai………... 51

2. Seleksi Target dan Siklus Waktu……… 60

F. Nilai Fungsi Penyuplai………. 73

BAB IV APLIKASI MODEL PROBABILISTIK……… 76

BAB V PENUTUP……… 91

DAFTAR PUSTAKA……… 93

A. Latar Belakang Masalah

Dalam kasus nyata, penentuan jumlah persediaan barang yang ada di gudang merupakan masalah yang sangat rumit. Masalah - masalah tersebut sering dialami oleh suatu perusahaan perakitan barang yang memerlukan dua jenis komponen barang untuk dirakit menjadi suatu produk. Lebih khusus lagi perusahaan perakitan barang tersebut hanya mampu memproduksi salah satu komponen barang yang disebut sebagai barang utama, sehingga dalam proses perakitan barang perusahaan tersebut perlu memesan komponen lain ( yang disebut barang pelengkap ) dari perusahaan penyuplai.

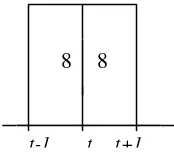
Pada saat proses perakitan barang tersebut perusahaan perakitan barang harus mampu menentukan berapa jumlah barang pelengkap yang ada di dalam gudang. Jumlah persediaan barang pelengkap yang ada di dalam gudang harus sesuai dengan jumlah produksi barang utama sehingga semua jenis barang utama yang telah diproduksi dapat segera dicocokkan dengan barang pelengkap untuk dirakit menjadi satu produk. Untuk memesan barang pelengkap dari penyuplai yang sesuai dengan jumlah barang utama maka perusahaan tersebut harus merancang suatu kebijakan pemesanan barang. Dengan kebijakan pemesanan barang, perusahaan tersebut dapat memesan barang pelengkap pada saat t dan datang pada saat . Supaya proses perakitan barang berjalan dengan lancar maka pihak peruasahaan perakitan barang harus menjalin kerjasama yang baik dengan pihak

4

+ t

penyuplai. Hal ini disebabkan karena pihak penyuplai harus mampu memenuhi permintaan barang pelengkap yang dipesan oleh perusahaan perakitan. Dalam upaya memenuhi permintaan tersebut penyuplai harus mampu merancang suatu strategi produksi mengenai pemilihan ukuran target dan penentuan berapa kali dilakukan proses produksi pada target yang sudah dipilih. Masalah persediaan barang utama dan strategi produksi penyuplai tersebut dapat didekati dengan menggunakan model distribusi multinomial.

Proses produksi barang utama memiliki karakteristik sebagai berikut:

1. Satu barang utama harus sesuai dengan satu tipe barang pelengkap yang dipesan,

2. Jenis barang utama dapat dibagi kedalam k- kategori yang berbeda, 3. Jenis barang utama independen satu dengan yang lainnya,

4. Jumlah barang utama yang diproduksi setiap harinya telah diketahui. Distribusi perakitan ukuran barang utama dapat dimodelkan dengan distribusi multinomial yaitu :

1. adalah variebel acak yang menyatakan jumlah barang utama dalam jenis kategori tertentu i yang diproduksi pada saat t.

( )

t

i

Χ

2. adalah jumlah barang utama jenis i yang diproduksi pada saat t,

rea-lisasi dari .

( )

t xi

( )

t

i

Χ

Berdasarkan asumsi independensi, distribusi probabilitas bersama dari jenis kategori barang utama yang diproduksi pada saat t dapat dirumuskan menjadi:

( ) ( )

( )

(

)

( ) ( )

( )

( )

!

!

!

!

,

,

,

2 1 2

1

t

x

t

x

t

x

t

n

t

x

t

x

t

x

P

k k

L

L

=

( ) ( ) x (t

k t x t

x k

p p

p 1 2 L

2 1

n(t) adalah jumlah barang yang diproduksi sampai saat ke- t, adalah proporsi barang utama jenis i. Pada saat perakitan nilai pasti dari mungkin tidak dapat

diketahui, sehingga diasumsikan diduga dengan untuk i=1,…,k.

i

p

i

p

i

p pˆ_i

B. Rumusan Masalah

Permasalahan yang akan dibahas dalam skripsi ini dapat dirumuskan sebagai berikut:

1. Bagaimana membuat model matematis untuk kebijakan penambahan persediaan barang?

2. Bagaimana membuat model matematis untuk menentukan strategi produksi?

3. Bagaimana aplikasi model matematis untuk masalah – masalah praktis?

C. Pembatasan Masalah

Dalam skripsi ini dibatasi oleh beberapa hal sebagai berikut:

1. Teori probabilitas hanya dibahas sebatas yang terkait langsung dengan permasalahan sedangkan hal – hal yang sifatnya elementer tidak dibahas. 2. Pembahasan masalah dibatasi pada penggunaan variabel random diskrit. 3. Pembahasan mengenai strategi produksi menggunakan pendekatan

distribusi multinomial.

D. Tujuan Penulisan

Skripsi ini bertujuan untuk memenuhi salah satu persyaratan untuk mem-peroleh gelar sarjana sains dalam bidang matematika. Selain itu skripsi ini bertu-juan membuat model matematis untuk:

1. Merumuskan teknik-teknik penambahan persediaan barang.

2. Merumuskan strategi produksi yang harus dimiliki oleh penyuplai barang sehingga dapat memenuhi permintaan perusahaan perakitan barang.

E. Metode Penulisan

Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dengan menggunakan buku-buku, jurnal-jurnal, dan makalah-makalah yang telah dipu-blikasikan, sehingga tidak ditemukan hal baru.

F. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah:

1. Memberikan informasi mengenai kebijakan penambahan persediaan barang dan strategi produksi.

2. Dapat menggunakan distribusi multinomial dalam masalah pemilihan target produksi.

G. Sistematika Penulisan

Bab I. Pendahuluan, pada bagian ini akan dibahas tentang latar belakang masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, metode penulisan, manfaat penulisan, dan sistematika penulisan skripsi ini.

Bab II. Dasar – Dasar Teori Probabilitas dan Program Linier Bilangan bulat, pada bagian ini akan dibahas tentang probabilitas bersyarat, variabel random, independensi variabel random, distribusi marginal, variansi dan kovariansi, program linear bilangan bulat.

Bab III. Model Probabilistik untuk Kebijakan Penambahan Persediaan Barang dan Strategi Produksi, pada bagian ini akan dibahas tentang produksi barang dan model multinomial, model probabilistik untuk persediaan lengan piston dalam kondisi aman, perbandingan tiga kebijakan pemesanan barang, variabel jumlah produksi piston, masalah produksi yang dihadapi penyuplai, masalah seleksi target, nilai fungsi penyuplai.

Bab IV. Aplikasi Model Probabilistik,pada bagian ini akan dibahas penyelesaiaan masalah kebijakan penambahan persediaan rantai dan strategi produksi pada proses perakitan gear rantai.

A. Peluang Bersyarat

Probabilitas suatu kejadian A terjadi dipengaruhi oleh kejadian lain, misal kejadian B, dapat digunakan untuk menentukan tingkat persediaan piston dalam gudang cukup tersedia. Bila tingkat persediaan aman pada masing – masing kategori ukuran diameter lengan piston telah diketahui maka probabilitas tingkat persediaan piston dalam gudang cukup tersedia dapat dicari. Dengan kata lain probabilitas persediaan piston dalam gudang cukup tersedia bersyarat persediaan aman pada masing – masing kategori ukuran diameter lengan piston.

Definisi 2.1.1 Peluang bersyarat

Peluang bersyarat B, bila A diketahui dinotasikan dengan P

(

B|A

)

, didefinisikan

sebagai

(

)

(

( )

)

A P

B A P A B

P | = ∩ , jika P

( )

A >0.

Misalkan bahwa ruang contoh S adalah populasi sarjana di suatu kota. Populasi sarjana tersebut dikelompokkan berdasarkan jenis kelamin dan status pekerjaan:

Bekerja Menganggur

Laki –laki 460 40

Perempuan 140 260

Misalkan akan diambil secara acak seorang diantara mereka untuk ditugaskan mempublikasikan pentingnya didirikan industri – industri baru di kota tersebut. Perhatikan kejadian – kejadian berikut:

M = yang terpilih laki – laki

=

E yang terpilih telah bekerja.

Dengan menggunakan ruang contoh yang dipersempit E, diperoleh

(

)

30 23 600 460

|E = =

M

P .

Misalkan n

( )

A melambangkan banyaknya unsur dalam himpunan A maka

(

) (

( )

)

(

( ) ( )

) ( )

(

( )

)

E P

M E P S

n E n

S n M E n E

n M E n E M

P | = ∩ = ∩ = ∩ , dalam hal ini

dan dihitung dari ruang contoh S.

(

E M

)

P ∩

( )

E

P

( )

3 2 900

600 ₌

=

E

P dan

(

)

45 23 900

460₌

=

∩M

E

P sehingga

(

)

30 23 3 2

45 23

|E = =

M

P sama seperti yang telah

diperoleh sebelumnya. Contoh 2.1.1

Dilakukan percobaan pengambilan dua kartu berturut – turut dengan pengembalian, artinya setelah diambil dan dicatat hasilnya kartu tersebut dikembalikan lagi. Perhatikan dua kejadian berikut:

=

A kartu pertama sebuah kartu as

=

B kartu kedua sebuah kartu sekop.

(

)

( )

4 1 52 13 dan

4 1 52 13

|A = = P B = =

B P

Jadi P

(

B|A

) (

=P B

)

, jika persamaan ini dipenuhi kejadian A dan kejadian B disebut kejadian bebas.Dalam percobaan pengambilan dua kartu pada contoh 2.1.1, telah ditunjukkan bahwa P

(

B|A

) ( )

=P B =14. Dan

(

)

( )

13 1 52

4 dan

13 1 52

4

|B = = P A = =

A

P perhitungan tersebut menunjukkan

bahwa P

(

A|B

) (

=P A

)

.

Definisi 2.1.2 dua kejadian saling bebas

Dua kejadian A dan kejadian B dikatakan bebas bila

(

B A

) ( )

P B P

(

A B

) ( )

P A

P | = atau | = .

Bila hal tersebut tidak dipenuhi, A dan B dikatakan tidak bebas.

B. Variabel random

Aturan pemetaan yang memetakan setiap anggota dari suatu himpunan tertentu ke bilangan real dapat digunakan untuk menentukan banyaknya piston dalam kategori diameter tertentu i yang diproduksi pada hari ke – t. Misalkan adalah suatu variabel random yang menyatakan banyaknya piston dalam kategori diameter tertentu i yang diproduksi pada hari ke – t. Jika diambil sembarang elemen dalam

( )

t X_i

( )

t

X_i misal x_i

( )

t , berarti x_i

( )

t adalah banyaknya piston berukuan i yang diproduksi pada hari ke – t, sebagai contoh

.

( )

1 50lenganpiston

1 =

x

Variabel random, misalkan X adalah suatu fungsi yang didefinisikan pada ruang sampel S, yang memetakan setiap elemen e∈S ke bilangan real, X

( )

e = X .

Huruf Kapital seperti X, Y, dan Z digunakan sebagai lambang variabel random, sedangkan haruf – huruf kecil yang bersesuaian x, y, dan z melambangkan nilai variabel random yang mungkin. Variabel random terdiri atas dua macam yaitu variabel random diskrit dan variabel random kontinu.

Definisi 2.2.2 variabel random diskrit

Variabel random diskret adalah variabel random yang didefinisikan pada suatu ruang sampel diskrit.

Contoh 2.2.1 variabel random diskrit

Banyaknya piston dalam jenis kategori diameter tertentu i yang diproduksi pada hari ke – t.

Definisi 2.2.3 fungsi probabilitas diskrit

Fungsi f

( ) (

x =P X =x

)

, x=x1,x2,x3,... yang menyatakan probabilitas untuk semua kemungkinan nilai variabel random diskrit X disebut fungsi probabilitas diskrit. Jadi f adalah fungsi probabilitas diskret jika memenuhi sifat – sifat berikut:

1. f

( )

xi ≥0

2.

∑

( )

∀

=

i x

i

x

f 1

Contoh fungsi probabilitas diskrit adalah distribusi probabilitas binomial dan distribusi probabilitas multinomial.

Suatu percobaan dapat terdiri atas beberapa ulangan, dan masing – masing mempunyai dua kemungkinan hasil yang dapat dikategorikan sebagai sukses dan gagal. Misalnya saja dalam pelemparan sekeping uang logam sebanyak 5 kali, hasil setiap ulangan adalah mungkin muncul sisi gambar atau sisi angka. Dapat ditentukan salah satu dari dua kemungkinan sebagai sukses. Percobaan demikian disebut sebagai percobaan binomial.

Percobaan binomial dalah percobaan yang memiliki ciri – ciri: 1. Percobaan terdiri atas n ulangan.

2. Dalam setiap ulangan, hasilnya dapat digolongkan sebagai sukses atau gagal. 3. Peluang sukses yang dilambangkan dengan p, untuk setiap ulangan adalah

sama, tidak berubah – ubah.

4. Ulangan - ulangan tersebut bersifat bebas satu sama lain. Definisi 2.2.4 distribusi probabilitas binomial

Suatu percobaan adalah distribusi binomial apabila masing – masing adalah variabel random yang saling bebas dan mempunyai dua kemungkinan hasil

yaitu sukses atau gagal maka merupakan variabel random yang

berdistribusi binomial yaitu:

n

X X1,...

∑

=

= n

i i

X X

1

(

)

p

(

p

)

x n

x n p n x

b ; , _⎟⎟ x1− n x untuk =0,1,2,...,

⎠ ⎞ ⎜⎜ ⎝ ⎛

= −

Percobaan multinomial adalah generalisasi dari percobaan binomial, contohnya pengambilan kartu dengan pengembalian merupakan percobaan multinomial jika yang diamati adalah keempat macam kartu yang ada.

Secara umum, bila setiap ulangan dapat menghasilkan satu di antara k

kemungkinan hasil percobaan , masing – masing dengan peluang

maka distribusi multinomial memberikan peluang terjadinya

kali kejadian , kali kejadian ,…, kali kejadian dalam n ulangan

yang bebas, dengan

k

E E E1, 2,...,

k

p p

p1, 2,...,; x1

1

E x₂ E₂ x_k Ek

n x x

x1+ 2+...+ _k = distribusi peluang bersama ini dilambangkan dengan f

(

x1,x2,..,xk;p1,p2,...,pk,n

)

. Jelas bahwa

karena hasil yang muncul dari setiap ulangan pasti salah satu di antara k kemungkinan hasil.

1 ..

2

1+p + + pk =

p

Diketahui bahwa ulangan satu dengan yang lainnya saling bebas, maka sembarang urutan yang menghasilkan sebanyak , sebanyak ,….,

sebanyak akan terjadi dengan peluang . Banyaknya urutan yang menghasilkan kejadian yang sama seperti di atas sama dengan sekatan n benda ke dalam k kelompok dengan dalam kelompok pertama, dalam kelompok kedua,…, dalam kelompok ke – k.Ini sama halnya dengan

1

E x₁ E₂ x₂ E_k

k

x xk

k x x

p p p1 2...

2 1

1

x x₂

k

x

! !... !

! ,...,

, _{2 1 2}

1 k x x xk

n x

x x

n

= ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

Bila setiap ulangan menghasilkan salah satu dari k hasil percobaan , dengan peluang , maka distribusi probabilitas bagi variabel random

, yang menyatakan berapa kali terjadi dalam n ulangan yang bebas, adalah

k

E E E1, 2,...,

k

p p p1, 2,...,

k

X X

X1, 2,..., E1,E2,...,Ek

(

)

xk

k x x

n k

k p p p

x x x n n p p p x x x f ... ,..., , , ,..., , ; ,..,

, 1 2

2 1 2 1 2 1 2 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = dengan ! !... !. ! ,..., , dan , 1 , 3 2 1 2 1 1

1 x x x

n x x x n p n x n k i i k i

i ⎟⎟=

⎠ ⎞ ⎜⎜ ⎝ ⎛ = =

∑

∑

= = . Contoh 2.2.2

Di sebuah kota pada saat sabtu malam, channel 12 memiliki 50% penonton, channel 10 memiliki 30% penonton, channel 3 memiliki 20% penonton. Tentukan probabilitas dari 8 pemirsa televisi, yang dipilih secara random pada sabtu malam, 5 akan menonton channel 12, 2 akan menonton channel 10, dan 1 akan menonton channel 3.

Jawab

Diketahui 8x1=5,x2 =2,x3 =1,p1=0.5,p2 =0.3,p3 =0.2,dann=

(

)

(

)

( ) ( ) ( )

0945 . 0 2 . 0 3 . 0 5 . 0 ! 1 !. 2 !. 5 ! 8 8 ; 2 . 0 , 3 . 0 , 5 . 0 , 1 , 2 , 5 ... ! !... ! ! , ,..., , ; ,.., , 2 5 2 1 2 1 2 1 2 1 2 1 = = = f p p p x x x n n p p p x x x

f xk

k x x k k k

Fungsi distribusi kumulatif suatu variabel random diskret X didefinisikan sebagai seringkali fungsi

( )

=

∑

( ) (

= ≤

)

∀ ∈ℜ

≤

x x X P t f x

F

x t

, F

( )

x disebut fungsi

distribusi.

Definisi 2.2.7 variabel random kontinu

Variabel random kontinu adalah suatu variabel random yang didefinisikan pada ruang sampel kontinu.

Contoh 2.2.3 variabel random kontinu

Percobaan mengamati daya tahan hidup ( dalam satuan waktu ) lampu. Definisi 2.2.8 fungsi densitas kontinu

Jika X adalah variabel random kontinu maka suatu kejadian akan berkaitan dengan suatu interval nilai. Probabilitas variabel random X akan terletak antara a

dan b atau P

(

a≤ X ≤b

)

dapat diperoleh dengan mengandaikan ada fungsi f

( )

x

sedemikian hingga luas daerah dibawah kurva fungsi f

( )

x pada interval

[ ]

sama dengan , jadi . Fungsi probabilitas

variabel random kontinu disebut juga fungsi densitas. Suatu fungsi

b a,

(

a X b

)

P ≤ ≤

(

≤ ≤

)

=

∫

(

b

a

dx x f b X a

P

)

( )

x f

merupakan fungsi densitas kontinu jika memenuhi sifat berikut: 1. f

( )

x ≥0, ∀x∈ℜ

2.

∫

( )

∞

∞ −

=1

dx x f

Contoh fungsi distribusi kontinu yang popular adalah distribusi Normal.

Variabel random X dukatakan berdistribusi normal dengan mean μ dan simpangan baku σ bila fungsi densitasnya berbentuk

(

)

2

2 1

2 1 ,

; ⎟⎠

⎞ ⎜ ⎝ ⎛ − −

= σ

μ

πσ σ

μ

x

e x

f , untuk −∞<x<∞

dengan π =3,14159 dan e=2,71828.

Secara khusus, bila variabel random berdistribusi normal dengan μ =0danσ =1 maka distribusinya disebut distribusi normal standar.

dx e x

z 2

2 1

0 2

1 −

∫

_π .

Andaikan adalah variabel – variabel random yang berdistribusi

bebas stokastik identik dengan

n

X X X1, 2,...,

( )

X_i =μ

E dan variansi

( )

=σ2<∞ i

X

Var , maka

n X Zn σ

μ

−

−

=

berdistribusi normal, rumus tersebut adalah teorema limit pusat. 3. Pendekatan Normal untuk Distribusi Binomial

Teorema limit pusat dapat digunakan untuk memperkirakan probabilitas beberapa variabel random diskret, jika probabilitas yang berdasarkan distribusi yang sebenarnya sukar dihitung untuk ukuran sampael n yang besar, misalnya pendekatan untuk distribusi binomial.

hanya untuk beberapa nilai n yang terbatas. Jika nilai n sangat besar maka perhitungan akan menjadi sukar dan juga tidak tersedia dalam tabel.

Sebagai alternatif, Y dapat dipandang, banyaknya sukses dalam n ulangan, sebagai jumlah suatu sampel yang terdiri dari nilai 0 dan 1, yaitu

. dengan

∑

=

= n

i i

X Y

1

⎩ ⎨

⎧ −

=

selainnya ,

0

sukses ulangan

jika ,

1 ke i

X_i

dan , dengan , adalah variabel random yang saling bebas ( karena ulangannya saling bebas ). Dengan demikian untuk n yang besar, menurut teorema limit pusat porsi ulangan sukses

i

X i=1,2,3,....,n

X X n n

Y n

i i =

=

∑

=1

1

akan memiliki distribusi sampling yang mendekati distribusi normal dengan dan variansi

( )

X p

E i = Var

( )

Xi n= p

(

1−p

)

.

Pendekatan normal ini sangat baik jika p dekat dengan 0.5 karena distribusi binomial simetrik jika p = 0.5. Keakuratan yang diperlukan dalam sembarang pendekatan tergantung pada penerapannya. Sebagai petunjuk umum pendekatan normal dapat dipakai jika np≥5dann

(

1−p

)

≥5.

Contoh 2.2.4

Andaikan diketahui bahwa 45% dari masyarakat setuju dengan hukuman mati. Jika 160 orang diwawancarai, tentukan probabilitas bahwa lebih dari separuh masyarakat akan setuju dengan hukuman mati.

Y dipandang sebagai banyaknya orang yang setuju ( kejadian sukses ) dari antara

n = 160 orang, yaitu

dengan

∑

=

= n

i i

X Y

1

(

)

⎩ ⎨

⎧ −

=

selainnya ,

0

sukses setuju

orang jika ,

1 ke i

X_i

dan , adalah variabel random yang saling bebas (pendapat seseorang tidak tergantung dari yang lain ). Jika menggunakan distribusi binomial diperoleh:

160 ,..., 2 , 1 dengan

, i=

X_i

(

)

(

) (

)

i

i

i

i Y

P −

=

− ⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ − =

>

∑

80 80

1

45 . 0 1 45 . 0 80 1

80

perhitungan dengan cara ini tidak dapat dengan cepat diselesaikan karena melibatkan kombinasi bilangan – bilangan yang besar.

Dengan menggunakan pendekatan normal masalah tersebut dapat disederhanakan. Berdasarkan teorema limit pusat mean distribusi sampling dari Y adalah np=

( )(

160.0.45

)

=72 dan variansi np

(

1−p

) ( )(

= 160.0.45

)(

.1−0.45

)

dengan demikian:

(

)

(

)(

)

_⎟⎟

⎠ ⎞ ⎜

⎜ ⎝

⎛ ₋

> ≈

>

55 . 0 45 . 0 160

72 80

80 P Z

Y

P

Akan tetapi, karena distribusi binomial adalah distribusi diskret dan distribusi normal adalah kontinu, pendekatan akan menjadi lebih baik bila dibuat koreksi kekontinuan. Secara khusus , setiap probabilitas binomial b

(

y;n,p

)

, mempunyai nilai yang sama yaitu berupa luas daerah segi panjang yang tingginya

dan lebarnya interval

[

(

y n p

)

b ; ,

]

5 . 0 , 5 .

0 +

− y

didekati dengan luas daerah dibawah fungsi densitas normal yang berkaitan dengan distribusi binomial

(

)

(

np np p

)

N

Y ~ , 1−

( )

n,p .

(

)

(

)

(

)

0883 . 0 9117 . 0 1

351 . 1 1

80 1

80

= −

=

− − =

≤ − = >

φ

Y P Y

P

Secara umum, bila Y_n ~bin

( )

n,p dana≤b bilangan bulat, maka:

[

]

(

)

(

)

_⎟⎟

⎠ ⎞ ⎜

⎜ ⎝ ⎛

− − − − ⎟ ⎟ ⎠ ⎞ ⎜

⎜ ⎝ ⎛

− − + ≈ ≤ ≤

p np

np a

p np

np b

b Y a

P _n

1 5 . 0 1

5 .

0 _φ

φ .

Definisi 2.2.10 fungsi distribusi kumulatif

Fungsi distribusi kumulatif suatu variabel random kontinu X adalah:

( )

∫

( )

∞ −

= x

dt t f x F

dengan fungsi densitas f

( )

x .

Sesuai dengan batasan masalah, maka konsep – konsep yang akan dibahas pada subbab - subbab berikutnya adalah dalam kerangka variabel random diskrit.

C. Independensi variabel random

Untuk membuat model masalah perakitan barang sebagai model distribusi multinomial, jenis – jenis barang tersebut harus independen satu dengan yang lainnya.

Definisi 2.3.1 distribusi probabilitas bersama

Jika adalah variabel random diskrit maka distribusi probabilitas diskrit bersama adalah

n

X X X1, 2,...,

(

x x xn

) (

P X x X x Xn xn

untuk semua kemungkinan nilai x=

(

x1,x2,...xn

)

dari X.

Pada definisi 2.3.1 X1=x1,X2 =x2,....,Xn =xn merupakan notasi untuk irisan

n buah kejadian

[

X1=x1

] [

∩ X2 =x2

]

∩....∩

[

Xn =xn

]

Contoh 2.3.1

Dua isi bolpen dipilih secara acak dari sebuah kotak yang berisi 3 isi bolpen biru, 2 isi bolpen merah dan 3 isi bolpen hijau. Bila X banyaknya isi bolpen biru dan Y banyaknya isi bolpen merah yang dipilih, tentukan:

a. Fungsi probabilitas bersama f

( )

x,y

b. P

[

(

X,Y

)

∈A

]

dengan A=

{

( )

x,y |x+y≤1

}

Jawab

a. Semua kemungkinan pasangan nilai dari

(

x,y

)

adalah

( ) ( ) ( ) ( ) ( )

0,0, 0,1,1,0,1,1, 0,2 dan

( )

2,0 . Sekarang f

( )

0,1 , misalnya menyatakan

peluang terambilnya isi bolpen biru dan merah. Banyaknya cara mengambil 2

isi bolpen dari 8 isi bolpen adalah 28 ! 6 !. 2

! 8 2 8

= = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

. Banyaknya cara

mengambil 1 isi bolpen dari 2 isi bolpen merah dan 1 isi bolpen dari 3 isi

bolpen hijau adalah 6

! 2 !. 1

! 3 . ! 1 !. 1

! 2 1 3 1

2

= =

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

sehingga f

( )

0,1 =6 28=314.

Tabel 2.3.1

Distribusi Probabilitas bersama bagi contoh 2.3.1 f(x,y) X

1 2 3 Total baris 1

y 2 3

3/28 9/28 3/28 3/14 3/14

1/28

15/28 3/7 1/28 Total kolom 5/14 15/28 3/28 1

b. P

[

(

X,Y

)

∈A

]

=P

(

X +Y ≤1

)

( ) ( ) ( )

14 9

28 9 14

3 28

3

0 , 1 1 , 0 0 , 0

=

+ + =

+ +

= f f f

Variabel random X dan Y dikatakan independen jika untuk semua a,b berlaku:

{

X a Y b

} {

P X a

} {

PY b

}

P ≤ , ≤ = ≤ ≤ 2.3.1 Dengan kata lain X dan Y adalah independen jika untuk semua a dan b, kejadian

adalah independen.

{

X a

}

dan F

{

Y b

Ea = ≤ b = ≤

}

)

Jika dihubungkan dengan fungsi distribusi bersama F dari X dan Y, maka X and Y dikatakan independen apabila:

.

( )

a b F

( ) ( )

a F b a b

F , = _{x y} , untuksemua ,

Ketika X dan Y adalah variabel random diskret, maka kondisi independen menghasilkan:

. 2.3.2

Untuk membuktikan pernyataan tersebut, jika kasusnya diskret. Andaikan fungsi probabilitas bersama p

( )

x,y , sesuai dengan persamaan 2.3.2 maka

{

}

( )

( ) ( )

( )

( )

{

} {

{

X a

} {

P Y b P

a X P b Y P

x p y p

y p x p

y x p b

Y a X P

b

y x a

x y

b

y x a

y x b

y x a

≤ ≤

=

≤ ≤

= = = = ≤ ≤

∑

∑

∑ ∑

∑

}

}

∑

≤ ≤

≤ ≤

≤ ≤

, ,

Teorema 2.3.1

Jika X dan Y adalah variabel random independen, maka fungsi h dan fungsi g

memenuhi:

( ) ( )

[

g X hY

]

E

[

g

( )

X

]

E

[

h

( )

Y

]

E = .

Bukti:

Jika X dan Y adalah variabel random diskret maka:

( ) ( )

[

]

( ) ( ) ( )

( ) ( ) ( ) ( )

( ) ( )

( ) ( )

( )

[

g X

]

E

[

h

( )

Y

]

E

y p y h x p x g

y p x p y h x g

y x p y h x g Y

h X g E

y y

x

x

y x

y x

y x

= = = =

∑

∑

∑∑

∑∑

,

D. Distribusi Marginal

i yang diproduksi pada hari ke – t. Ini berarti terdapat lebih dari satu variabel random karena i dan t berjalan dari 1 sampai n. Untuk mencari distribusi marginal dari variabel random tersebut diberikan definisi :

Definisi 2.4.1 distribusi marginal

Jika X dan Y adalah variabel random diskret dan P

( )

x,y adalah nilai dari distribusi probabilitas bersama

( )

x,y maka distribusi marginal dari X adalah:

( )

=

∑

( )

y

y x p x

g ,

Jika X dan Y adalah variabel random diskret dan P

( )

x,y adalah nilai dari distribusi probabilitas bersama

( )

x,y maka distribusi marginal dari Y adalah:

( )

=

∑

( )

x

y x p y

h ,

Contoh 2.4.1

Sebuah kelompok terdiri dari tiga orang partai republik, dua orang partai demokrat, dan satu orang independent. Sebuah komisi akan dibentuk dari dua orang yang dipilih secara random. Andaikan adalah variabel random jumlah orang dari partai republik dalam komisi dan variabel random jumlah orang dari partai demokrat dalam komisi. Tentukan distribusi probabilitas bersama dari dan , dan tentukan pula distribusi marginal dari .

1

Y

2

Y

1

Y

2

Y Y₁

Jawab

(

) ( )

15 6 15

2 . 3

2 6

0 1 1

2 1

3 1 , 1 1 , 1 ₂

1 = =

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = =

=

= Y p

penyebut diperoleh dari jumlah ruang sampel yaitu dan pembilang diperoleh dari hasil perkalian .

2 6C 0 1 1 2 1

3C, C, C

(

) ( )

15 3 2 6 0 1 0 2 2 3 0 , 2 0 , 2 ₂ 1 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = =

= Y p

Y P

penyebut diperoleh dari jumlah ruang sampel yaitu dan pembilang diperoleh dari hasil perkalian , dan seterusnya seperti pada tabel 2.4.1.

2 6C 0 1 0 2 2

3C , C , C

Tabel 2.4.1 Distribusi probabilitas Y₁ dan Y₂

Y₁

2

Y

0 1 2 Jumlah

0 0 15 3 15 3 15 6 1 15 2 15 6 0 15 8 2 15

1 0 0

15 1 jumlah 15 3 15 9 15 3 1

Distribusi marginal dari atau Y₁

(

p₁

( )

y₁

)

dapat diperoleh dengan menjumlahkan semua nilai dari Y₂:

( ) ( ) ( ) ( )

( ) ( ) ( ) ( )

( ) ( ) ( ) ( )

15 3 0 0 15 3 2 , 2 1 , 2 0 , 2 2 15 9 0 15 6 15 3 2 , 1 1 , 1 0 , 1 1 15 3 15 1 15 2 0 2 , 0 1 , 0 0 , 0 0 1 1 1 = + + = + + = = + + = + + = = + + = + + = p p p p p p p p p p p p

E. Variansi dan Kovariansi

Salah satu nilai harapan yang penting adalah variansi yang merupakan nilai harapan dari fungsi f

( ) (

x = x−μ

)

2, dengan μ=E

( )

X . Dalam kasus nyata dapat diambil contoh misal E

(

X_i

( )

t

)

adalah nilai harapan banyaknya piston dalam jenis kategori diameter tertentu i yang diproduksi pada hari ke – t.

Definisi 2.5.1 variansi

Variansi variabel random X adalah:

( )

[

(

)

]

[ ]

2 2

2 μ μ − = − = X E X E X Var

kegunaan dari variansi adalah untuk mengukur keragaman data. Teorema 2.5.1

Bila a adalah suatu konstanta maka Var

( )

aX =a2VarX Bukti:

( )

[

(

)

]

(

)

[

]

(

)

[

]

(

)

[

]

VarX a X E a X X a E a X a X a E a aX E aX Var 2 2 2 2 2 2 2 2 2 2 2 2 2 2 = − = + − = + − = − = μ μ μ μ μ μ

Definisi 2.5.2 kovariansi

Kovariansi dari dua variabel random X dan Y dinotasikan dengan Kov

(

X,Y

)

:

(

)

[

(

[ ]

)

(

[ ]

)

]

[ ]

[ ] [ ] [ ]

[

]

[ ] [ ] [ ] [ ] [ ] [ ] [ ]

[ ] [ ] [ ]

XY E X EY

Teorema 2.5.2

Mean dan variansi dari distribusi probabilitas binomial adalah:

(

p

)

np dan

np = −

= σ2 1

μ .

Bukti:

a. bukti mean:

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

) (

)

(

)

(

)

(

) (

)

(

)

(

)

(

) (

)

(

)

(

) (

[

) (

)

]

(

)

[( ) ( )]

(

)

[( ) ( )]

(

X x

)

np np P np p p x n np p p x n x n np x x n p p n np x x n p p p n n x x n p p n x x n p p x n p p x x n n x p p x n x p n x b x n x x n x n x x n x n x n x x n x n x x n x n x x n x n x x n x n x x n x x n x n x n x = = = = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = − − − − − − = − − − − = − − − − = − − − = − − = − − = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = =

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

= − − − − = − − − − = = − − = − − = − = − = − − = = 1 . 1 1 1 1 ! 1 1 ! 1 ! 1 ! 1 !. 1 !. 1 ! 1 !. 1 . ! 1 ! 1 !. 1 !. ! !. 1 . ! 1 ! !. ! . 1 . , ; . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 μ μ

b. bukti variansi:

( )

( )

2

(

( )

)

2 2 X E X E X

Var = −

=

σ

misalkan

( )

'

(

( )

)

2 2 2

2 ₌μ ₌μ

X E dan X

( ) ( )

( ) ( )

[

]

( )

(

)

[

X X

]

E

( )

X E X E X X E X E X E X E X E + − = + − = + − = 1 2 2 2

nilai harapan dari

[

X

(

X −1

)

]

adalah:

(

)

[

]

(

)

(

)

(

)( ) ( )

(

)

(

) (

) (

)

(

) (

) (

)

(

)(

) (

)

(

) (

)

(

)

(

) (

[

(

) (

)

)

]

(

)

[( ) ( )]

(

)

(

)

[( ) ( )]

(

)

(

)

[( ) ( )]

(

)

1

(

)

2

2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 1 1 . 1 1 2 2 1 1 2 2 1 1 ! 2 2 ! 2 ! 2 1 ! 2 ! 1 ! 2 1 1 ! 2 ! ! 1 ! 1 ! ! 1 1 ! ! ! 1 1 1 1 p n n p n n p p p x n n n p p x n n n p p x n x n n n x x n p p n n n p p x x n n p p x x n n x p p x x n n x x p p x n x x X X E n x x n x n x x n x n x x n x n x x n x x n x n x x n x n x x n x n x x n x n x − = − = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − = − − − − − − − = − − − − − = − − − = − − − − = − − − = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = −

∑

∑

∑

∑

∑

∑

∑

∑

= − − − − = − − − = − − − = − − = − = − = − = sehingga:

( )

[

(

)

]

( )

(

)

np np p n np p n n X E X X E X E + − = + − = + − = 2 2 2 2 2 1 1 jadi:

(

p

)

np np np p n np np p n − = − = − + − = − = 1 2 2 2 2 2 2 2 ' 2

2 μ μ

F. Program Linear Bilangan Bulat

Ketika mencari penyelesaian suatu masalah program linear terkadang disyaratkan bahwa penyelesaiannya tidak boleh pecahan atau dengan kata lain penyelesaiannya harus merupakan bilangan bulat. Misalkan saja perusahaan penyuplai lengan piston harus menentukan berapa kali memproduksi lengan piston pada suatu target. Pada contoh tersebut perusahaan harus mampu menentukan bilangan bulat yang dapat mewakili berapa kali dilakukan produksi lengan piston pada suatu target tertentu, misalnya hanya dilakukan satu kali proses produksi lengan piston pada suatu target.

Definisi 2.6.1 program linear bilangan bulat

Program linear bilangan bulat adalah program linear dengan kendala tambahan semuanya atau beberapa variabel keputusannya bernilai bulat.

Berdasarkan definisi di atas maka terdapat dua model program linear bilangan bulat yaitu program linear bilangan bulat murni dan program linear bilangan bulat campuran.

2.6.1 Program Linear Bilangan Bulat Murni

Berikut ini diberikan contoh bentuk model program linear bilangan bulat murni: Contoh 2.6.1

Mencari x₁,x₂

bulat bilangan dan

0 0 36 8

49 10

5

3 20 10

2 1

2 1

2 1

2 1

2 1

x x

x x

x x

x x

x x

≥ ≥ ≤ −

≤ +

≤ +

−

Model matematika program linear bilangan bulat murni: Maksimumkan f =cx

Dengan kendala: Ax≤b

x≥0,xbilanganbulat

1 vektor

1 vektor

1 vektor matrik

× =

× =

× =

× =

m n

n n m

b x c A

Definisi 2.6.2 program linear bilangan bulat murni

Program linear bilangan bulat murni adalah program linear dengan kendala tambahan semua variabel keputusannya bernilai bulat.

2.6.2 Program Linear Bilangan Bulat Campuran Contoh 2.6.2

Mencari x1,x2,x3

. 0

bulat dan 0 ,

3 3 2

2 4 3

4 2

3 2 1

3 2 1

3 2

3 2 1

≥ ≥ ≤ − +

≤ + −

≤ + + −

x x x

x x x

x x

x x x

Model matematika program linear bilangan bulat campuran: Maksimumkan f =cx+dy

Dengan kendala: Ax+By≤b

0 y

x 0 x

≥

≥ , bilanganbulat

1 vektor

1 vektor

1 vektor

1 vektor

1 vektor

matrik matrik

× =

× =

× =

× =

× =

× =

× =

m p n

p n

p m

n m

b y x d c B A

Definisi 2.6.3 program linear bilangan bulat

Model probabilistik untuk kebijakan penambahan persediaan barang dan strategi produksi adalah suatu model matematika mengenai berapa banyak persediaan barang yang dimiliki oleh produsen dan berapa banyak barang yang sebaiknya harus disediakan oleh penyuplai. Ini diperlukan supaya pihak perusahaan perakitan barang mengetahui dengan lebih pasti kapan harus memesan barang pelengkap dari penyuplai dan bagaimana penyuplai mampu membuat jadwal produksi barang pelengkap untuk memenuhi permintaan perusahaan perakitan.

A. Produksi Barang dan Model Multinomial

Perusahaan perakitan memproduksi suatu barang utama dengan barang pelengkap dipesan dari penyuplai. Misalnya, diameter barang utama harus sesuai dengan diameter barang pelengkap yang dipesan dari penyuplai. Diameter barang utama bagian luar yang diproduksi bervariasi secara independen dan random.

Perusahaan perakitan barang harus menjamin bahwa persediaan barang pelengkap yang dipesan dari penyuplai cukup tersedia, sehingga setiap barang utama yang diproduksi oleh perusahaan perakitan barang dapat segera dicocokkan dengan barang pelengkap yang dipesan dari penyuplai. Jika barang pelengkap yang akan dicocokkan dengan barang utama tidak tersedia, maka proses perakitan

barang akan terganggu. Untuk memudahkan pembahasan diambil contoh piston sebagai barang utama dan lengan piston sebagai barang pelengkap.

Proses perakitan piston mempunyai karakteristik sebagai berikut:

a. Satu jenis piston dicocokkan dengan satu jenis lengan piston yang dipesan. b. Diameter piston dapat dibagi kedalam k – kategori yang berbeda.

c. Dalam jangka waktu yang lama proporsi diameter piston yang berada pada kategori ke–i

( )

p _i dibatasi oleh waktu, ini menunjukkan bahwa proses berjalan stabil.

d. Diameter piston independen satu dengan yang lainnya.

e. Banyaknya piston n(t) yang diproduksi pada hari ke t≥1 telah diketahui. Distribusi perakitan ukuran piston pada hari ke−t dapat dimodelkan dengan

distribusi multinomial :

a. adalah variabel acak yang menyatakan banyaknya piston dalam jenis kategori diameter tertentu i yang diproduksi pada hari ke-t.

( )

t

i

Χ

b. adalah banyaknya piston berukuran i yang diproduksi pada hari ke–t

sebagai realisasidari

( )

t x_i

( )

t

i

Χ , dimana k x

( )

t

i i

∑

=1 = n(t) dan

∑

= = 1. k

i 1 pi

Model distribusi probabilitas bersama dari diameter piston yang telah diproduksi adalah:

( ) ( )

( )

(

)

( ) ( )

( )

( )

!

!

!

!

,

,

,

2 1 2

1

t

x

t

x

t

x

t

n

t

x

t

x

t

x

P

k k

L

L

=

( ) ( ) x t

k t x t

x _k

p p

p 1 2 L

2 1

( )

(3.1)

n(t) adalah banyaknya piston yang diproduksi sampai hari ke−t, adalah pro-porsi piston berukuran i, nilai pasti dari pada saat perakitan mungkin tidak

da-i

p

i

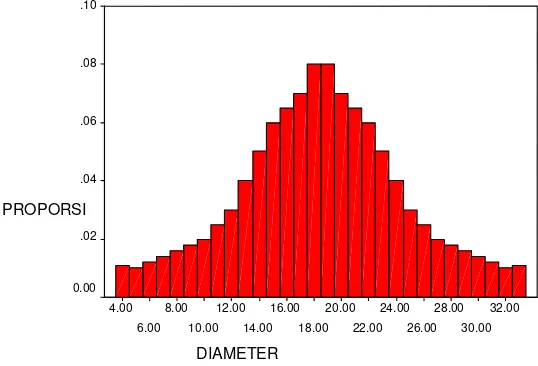
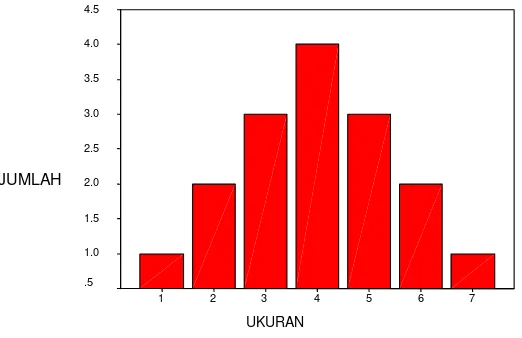
pat diketahui, sehingga diasumsikan diduga dengan untuk i=1,…,k. Contoh histogram frekuensi relatif produksi piston ditunjukkan oleh gambar 3.1, hipotesis distribusi ukuran barang utama dengan k = 30 banyaknya kategori.

i

p pˆi

DIAMETER

32.00 30.00 28.00 26.00 24.00 22.00 20.00 18.00 16.00 14.00 12.00 10.00 8.00 6.00 4.00 .10

.08

.06

.04

.02

0.00

Gambar 3.1 Distribusi ukuran piston

PROPORSI

B. Model Probabilistik untuk Persediaan Lengan Piston dalam Kondisi Aman

Pada bagian ini diasumsikan bahwa banyaknya piston yang diproduksi tiap hari konstan, ini berarti n(t)= n pada hari ke−t. Produsen memesan lengan piston tiap hari, dan kiriman datang dari penyuplai setiap hari. Misalkan 0 di definisikan sebagai banyaknya lengan piston dengan ukuran diameter i yang harus dimiliki produsen dalam persediaannya setiap hari, ( diasumsikan sama untuk setiap hari ). disebut juga persediaan dalam kondisi aman untuk ukuran

diame-ter i, dan

∑

adalah total persediaan aman yang dimiliki dan dimulai pada hari

tertentu. Produsen mengatur tingkat persediaan dalam kondisi aman , dengan

i

s ≥

i

s

i

s

=

k

i 1si

i

tujuan meminimalkan biaya penyimpanan, termasuk biaya perbaikan barang yang rusak ketika barang tersebut disimpan digudang. Secara intuitif produsen menginginkan persediaan dalam kondisi aman sedikit agar mengurangi resiko persediaan kurang dalam berbagai kategori ukuran diameter.

Jika produsen mulai pada hari ke-t dan jumlah lengan piston dalam berbagai macam ukuran i yang ada dalam persediaan telah diketahui dengan pasti ( ) maka probabillitas persediaan cukup pada hari itu adalah:

i

s

) ) ( ,..., )

( ( ) ,..., | cukup persediaan

( s1 sk P X1 t s1 Xk t sk

P = ≤ ≤

berdasarkan persamaan (3.1) maka:

=

( )

( )

( ) ( )

( ) x( )t k t x

s t x s t

x k

k

k k

p p t x t x

n

... ! !...

! ₁

1 1

1

,...., 1

∑

≤ ≤

dengan

∑

_ik₌₁xi

( )

t = n dan

∑

₌

k

i 1pi = 1

jika k besar ( misalkan ), maka akan sulit untuk melakukan perhitungan probabilitas multinomial komulatif secara tepat. Akan tetapi,

30

>

k

( )

( )

(

X t s Xk t sk

)

P

(

X

( )

t s Xk

( )

t sk

)

P 1 ≤ 1,..., ≤ =1− 1 > 1∪....∪ > , bagian kiri persamaan yaitu P

(

X1

( )

t >s1∪....∪Xk

( )

t >sk

)

dapat diubah menjadi bentuk

yang lebih sederhana menjadi:

( )

( )

(

X t s Xk t sk

)

P

(

X

( )

t s

)

P

(

Xk

( )

t sk

)

P 1 > 1∪....∪ > ≤ 1 > 1 +....+ > kemudian diperoleh P

(

X1

( )

t ≤s1,...,Xk

( )

t ≤sk

)

≥1−

[

P

(

X1

( )

t >s1

)

+...+P

(

Xk

( )

t >sk

)

]

dan menghasilkan batas bawah probabilitas persediaan cukup pada hari ke–t, jika tersedia lengan piston di hari pertama. Jadi si

∑

₌

(

( )

>

)

k

resiko paling sedikit satu persediaan kurang yang merupakan jumlah persediaan aman . si

Karena distribusi marginal dari Χi

( )

t adalah distribusi binomial dengan

pa-rameter

(

n,pi

)

maka P

(

Xi

( )

t >si

)

adalah probabilitas binomial. Untuk nilai n

yang cukup besar ( banyaknya piston yang diproduksi setiap hari ), sedemikian hingga dan untuk semua i, distribusi normal merupakan pendekatan yang masuk akal untuk probabilitas binomial, yang ditunjukkan oleh persamaan

5

≥

i

np n

(

1− pi

)

≥5

( )

(

)

(

)

⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − > ≈ > i i i i i i p np np s z P s t X P 1 5 . 0

Persamaan di atas memberikan satu kemungkinan untuk mengatur tingkat persediaan aman dengan menggunakan nilai harapan dan standar deviasi dari

. Jika diandaikan tingkat persediaan aman adalah

i

s

( )

t

i

Χ

( )

(

X t

)

Var

(

X

(

t

))

E

si = i +2 i ( dibulatkan ke bilangan bulat terdekat ), maka

(

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − > ≈ i i p np z P 1 5 . 0 2 ⎟ ⎠ ⎞ ⎜ ⎝

⎛ _{> −} ≈ 5 5 . 0 2 z P

≈P

(

z>1.7764

)

(

>2

)

≈P z

(

<−2

)

≈P z

0228 . 0

≈

menghasilkan P

(

Xi

( )

t >si

)

≈0,0228 untuk semua i. Ini memberikan batas atas untuk probabilitas paling sedikit satu persediaan kurang pada hari tersebut adalah 0.0228k. sama halnya, jika s_i =E

(

X_i

( )

t

)

+3 Var

(

X_i

( )

t

)

( dibulatkan ke bilangan

bulat terdekat ) maka pendekatan normal

( )

(

)

(

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − > ≈ > i i i i i p np np s z P s t X P 1 5 . 0

(

(

)

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − − + > ≈ i i i i i i p np np p np np z P 1 5 . 0 1 3

(

)

(

)

⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − > ≈ i i i i p np p np z P 1 5 . 0 1 3

(

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − > ≈ i i p np z P 1 5 . 0 3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{> −} ≈ 5 5 . 0 3 z P

≈P

(

z>3

)

≈P

(

z<−3

)

≈0.0013

menghasilkan P

(

Xi

( )

t >si

)

≈0.0013 untuk semua i dan P ( probabilitas paling sedikit satu persediaan kurang ) ≤ 0.0013k, dengan k adalah banyaknya kategori. Batas – batas tersebut tergantung pada hari apa dimulainya proses produksi dan jumlah pasti lengan piston berukuran i yang tersedia untuk semua i. Tetapi banyaknya lengan piston yang digunakan setiap hari untuk masing – masing kategori i bersifat acak dan jumlah kedatangan kiriman lengan piston mungkin tidak secara tepat menggantikan banyaknya lengan piston yang telah digunakan. Berarti, jumlah persediaan nyata berfluktuasi pada suatu tingkatan rata – rata tertentu, tergantung bagaimana lengan piston disuplai kembali. Jadi, probabilitas persediaan cukup pada hari t adalah:

i

s

( )

( ) ( )

( )

( )

( )

(

X t y t X t y t X t y t

)

P 1 ≤ 1 , 2 ≤ 2 ,..., _k ≤ _k (3.2) dengan adalah persediaan nyata lengan piston berukuran i yang dimulai pada hari ke–t.

( )

t y_i

Contoh 3.2.1

Diasumsikan bahwa proses perakitan piston produsen dapat dimodelkan dengan distribusi multinomial dan total banyaknya piston yang diproduksi setiap hari te-lah ditentukan sebanyak n

a). tunjukkan bahwa distribusi marginal Xi

( )

t adalah distribusi binomial de-

b). tunjukkan bahwa kovariansi dari X_i

( )

t dan X_j

( )

t adalah

(

n n

)

pipj 2

− untuk

, i

≤

1 j≤k dan i≠ j. Jelaskan mengapa salah satu kemungkinan nilai kovariansi adalah tak nol dan tak negatif.

c). Diberikan kasus sederhana, produsen menentukan n = 10 piston setiap hari dan diameter dibedakan menjadi tiga ukuran kelas ( k = 3 ), dengan probabilitas

5 1 , 5 3 , 5 1 3 2

1= p = p =

p . Cari P

(

2,3,4

)

, cari mean dan variansi dari X₂

( )

t .

Hitung P

(

X2

( )

t =4

)

. Penyelesaian:

a). Telah disebutkan bahwa x_i

( )

t dapat dimodelkan dengan distribusi multinomial

dengan x_i

( )

t adalah realisasi dari X_i

( )

t . Definisi distribusi marginal adalah

jika pasangan variabel random diskret

(

Xi

( )

t ,Xi+1

( )

t

)

mempunyai fungsi

probabilitas bersama f

(

X_i

( )

t ,X_i+1

( )

t

)

maka

(

( )

)

∑

(

( )

( )

)

+ ∀ + = 1 1 , i X i i i

i X t f X t X t

f dan

(

( )

)

∑

(

( )

( )

)

∀ + + + = i X i i i

i X t f X t X t

f _{1 1} , ₁

misalkan X_i

( )

t =X₁ dan X_i+1

( )

t = X₂

(

)

1 2 1

1 2 1 1 2 1 2 1 ... ! !... ! ! ,..., , ~ + + +

= Xk

k X

X

k

k P P P

X X X n X X X f X

dengan

∑

dan =

+ = −

k

i i

k n X

X 1 1

∑

= + = − k i k k P P 1 1 1

( )

∑

(

)

∑

(

)

− = = = 2 1 2 0 2 1 2 1 1

1 , ,

X X n X X X f X X f X f

(

)

(

)

[

(

)

]

( )

(

)

[

]

∑

− = − − − − − − − − = 1 2 2 1 2 1

0 2 1 2

2 1 2 1 1 1 1 ! 1 ! !

! n X

(

)

∑

[

(

)

]

( ) −

=

− −

− − ⎟⎟

⎠ ⎞ ⎜⎜

⎝ ⎛ − −

= 1

2

2 1 2

1

0

2 1 2

2 1 1

1 1

1 !

!

! n X

X

X X n X

X

P P P

X X n P

X n X

n

1

[

(

)

]

1

2 1 2

1 1

1 n X

X

P P P

P X

n ₋

− − + ⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

1

(

)

1

1 1

1

1 n X

X

P P

X

n ₋

− ⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ =

berarti , karena distribusi binomial maka mean dari dan

(

i

i Bin n p

X

X1 = +1~ ,

)

( )

i

i t n p

X = . Var

(

Xi

( )

t

)

=n.pi.

(

1− pi

)

=npiqi.

b). Kov

(

X_i

( ) ( )

t ,X_j t

)

=E

(

X_i

( )

t −μ_i

( )

t

) ( )

(

X_j t −μ_j

( )

t

)

=E

(

Xi

( ) ( )

t Xj t −Xi

( ) ( )

t μj t −Xj

( ) ( )

t μi t +μi

( ) ( )

t μj t

)

=E

(

Xi

( ) ( )

t Xj t

)

−μj

( )

t E

(

Xi

( )

t

)

−μi

( )

t E

(

Xj

( )

t +μi

( ) ( )

t μj t

)

karena E

(

Xi

( )

t

)

=μi

(

t

)

dan E

(

Xj

( )

t

)

=μj

( )

t

=E

(

X_i

( ) ( )

t X_j t

)

−μ