PENYELESAIAN SISTEM PERSAMAAN NON-LINEAR DENGAN METODE NEWTON DAN TERAPANNYA Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh :

Maria Nirmala Anggi Fitra Murti Martosudjito NIM : 033114007

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

Presented As Partial Fulfillment of The Requirement To Obtain The Sarjana Sains Degree in Mathematics

By :

Maria Nirmala Anggi Fitra Murti Martosudjito Student Number : 033114007

STUDY PROGRAM OF MATHEMATICS SCIENCE DEPARTEMENT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY

tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, Desember 2007

Penulis,

Maria Nirmala Anggi Fitra Murti Martosudjito

dan kemudian terbangun ....

Lalu kurasa BERAT dan KELABU semuanya, maka teringatlah aku,

KEGELAPAN adalah juga bagian dari kehidupan ... Bila malam kulewatkan,

dengan penuh KEGELISAHAN,

dan aku sadar ... betapa hidupku penuh dengan ^ BEBAN ^ ...

Lalu sambil merasa ibu bumi masih menyanggaku ... Aku menghela Nafas ...

Maka aku pun merasa pula,

diriku ditopang oleh segala perasaanku, ... GEMBIRA maupun SUSAH ... Bila tidurku lewat,

dalam mimpi menyesakkan ...

dan aku harus berhadapan dengan masalah yang belum ku selesaikan,

yang ingin KU LUPAKAN ... Lalu aku sadar ...

TERANG ataupun GELAP, Harus ku terima semuanya ...

Maka ketika pagi tiba, teristimewa hari ini ...

Aku pun akan menemui diriku “APA ADANYA” dengan penuh PERHATIAN dan CINTA ... dan akan menerima ^ Keterbatasanku ^ ... Aku pun akan mengajak sesamaku,

mengalami apa sesungguhnya MANUSIA itu ...

Ia telah menjadi keselamatanku

(Mzm 118:14)

In times of difficulties don’t ever say “God I have a big problem”

but instead

“Hey problem, I have a big God”

and everything will be alright.

Tugas di hadapan kita tidak akan pernah sebesar

kekuatan di belakang kita

Bila selama ini aku masih bertahan ...

Semua ini aku persembahkan hanya karena cintaku untuk :

Tuhan Yesus dan Bunda Maria,Teman dan Bunda tersayang yang dengan setia mendengarkan

semua kepedihan hatiku

Bapak-Ibuku tercinta.... Aku memang bukan ysng terbaik, tapi ketahuilah bahwa kalianlah

motivasi hidupku ...

Adik-adikku tersayang... Bram dan Christi... Jangan pernah berhenti meraih prestasi ... Do the best that you can do, not for me or our parents but for your life ....

Keluarga Besar Martosudjito dan Keluarga Besar Sudarsono.... Aku bangga

menjadi bagian dari keluarga ini ....

Seseorang yang sudah hadir dan mewarnai hidupku... Di atas semua yang pernah

terjadi di antara kita, baik ataupun buruk, you must know that I’m so glad to have you .... Sahabat-sahabatku ... Aku akan selalu ada untuk kalian... FRIENDS FOREVER ...

dengan m>1 yang dapat dinotasikan dengan F x( )=0. Sistem persamaan non-linear dapat diselesaikan dengan metode numeris, antara lain dengan metode Newton dan metode Turun Tercuram. Metode Newton adalah suatu algoritma iterasi fungsional

yang membangkitkan dengan dan

adalah matriks Jacobian. Apabila nilai awal yang dipilih cukup baik maka iterasi Newton akan konvergen dengan sifat q-kuadratik.

( ) ( 1) ( 1) 1 ( 1)

( ) (

k = k− − k− − k

x x J x F x − )

)

)

1

k≥ J x( )

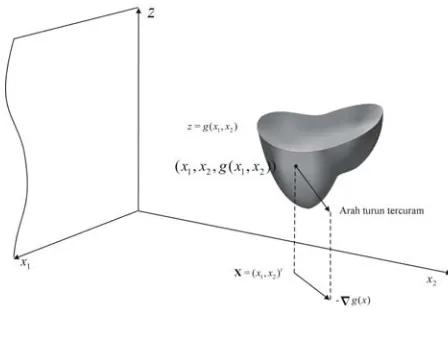
Metode Turun Tercuram merupakan metode optimasi yang akan digunakan untuk mengatasi kelemahan metode Newton. Penyelesaian yang diberikan adalah

dengan , dan adalah

gradien dari . Dalam mencapai konvergensinya, metode Turun Tercuram akan memiliki arah gerak yang zigzag atau vektor-vektor penyelesaiannya akan ortogonal.

(

( )k (k 1) (k 1) (k 1) g λ

− − −

= − ∇

x x x k ≥1

(

2

1

( ) ( )

n i i

g f

=

=

∑

x x ∇g( )x

( )

g x

Metode Newton dan metode Turun Tercuram dapat diaplikasikan dalam bidang fisika, khususnya dalam menghitung konsentrasi unsur dalam sampel.

equations which can be denoted by F x( )=0 in the condition . System of non-linear equations can be solved with numerical methods, for instance Newton Method and Steepest Descent Method. The Newton Method is a functional iteration

procedure generated by in the condition and

the Jacobian matrix . If the selected starting value is sufficiently accurate, the Newton’s Method will converge q-quadratic.

1 m>

( ) ( 1) ( 1) 1 ( 1)

( ) (

k = k− − k− − k

x x J x F x − )

)

)

1 k≥

( )

J x

The Steepest Descent Method is considered as an optimization method which is employed to overcome the weakness of the Newton Method. The given solution is

in the condition , where and

which is defined as the gradient of . To converge, the Steepest Descent Method will have zigzag motion or the vectors of the solution will be orthogonal each other.

(

( )k (k 1) (k 1) (k 1) g λ

− − −

= − ∇

x x x k ≥1

(

2

1

( ) ( )

n i i

g f

=

=

∑

x x

( )

g

∇ x g( )x

The Newton Method and the Steepest Descent Method can be applied to the field of physics, especially to estimate the concentrated subtance that is contained in some sample.

Juru Selamat, sehingga karena kasih dan karunia-Nya skripsi ini dapat terselesaikan tepat waktu.

Dalam penyusunan skripsi ini penulis membutuhkan bantuan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin menyampaikan ucapan terima kasih kepada :

1. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing dan Kaprodi Matematika FST-USD yang dengan rendah hati mau meluangkan banyak waktu luang dan penuh kesabaran telah membimbing selama penyusunan skripsi ini walaupun penulis sering terlambat bahkan kabur dari jadwal bimbingan dengan waktu yang cukup lama.

2. Bapak Sadmoko dan Ibu Darni, untuk semua pelajaran hidup, cinta, kasih sayang, pengorbanan, doa, motivasi dan kepercayaan yang sangat berarti.

3. Bapak Y.G. Hartono, S.Si., M.Sc., yang telah bersedia menjadi dosen penguji dan untuk semua bahan serta chatting sampai tengah malam.

4. Ibu M.V. Any Herawati, S.Si., M.Si., selaku dosen penguji yang telah memberikan nilai yang cukup mengejutkan.

5. Ir. Greg. Heliarko, S.J., S.S., B.S.T., M.Sc., M.A., selaku Dekan FST-USD. 6. Segenap dosen, karyawan sekretariat FST khususnya Bapak Tukija dan Ibu Linda

dan karyawan Perpustakaan Paingan dan Mrican, atas ide, pelayanan dan kesempatan kerja yang pernah diberikan.

9. Herry ‘Pokilz’, yang telah memberikan semangat, kerjaan dan teman tengah malamku yang mau nemenin aku belajar serta curhat lewat rutinitas freetalk kita. 10.Sahabat terbaikku di Matematika’03, Eko, Ridwan ‘Djembat’, Kamto ‘Kambing’,

Koko ‘BruCab’, si putri solo Dewi ‘Cemplux’, si lemot Mekar ‘Kuncup’, si pembuat heboh tapi multitalenta Anin ‘Berukwati’, si panik room Merry, si perkasa Septi ‘Gondeswati’, si feminim dan teman senasib seperjuangan Valent, anak kesasar angkatan Cicil dan si invisible Itha. Terimakasih untuk pelukan, pinjaman bahu untuk menangis dan sandaran hati serta kebersamaan kita selama ini. Tidak akan pernah ku lupakan semua waktu yang pernah kita lewati bersama. 11.Sahabat dan saudaraku, Nela, Teaka ‘si Kecil’ miss Berantakan yang selalu panik,

Uchie ‘my twin’ yang selalu memberikan bantuan dalam segala hal. Kalian selalu ada untukku bahkan di saat paling kelam hidupku.

12.Sahabat-sahabatku, Shindy, yang dari kecil selalu menemani aku, Juna, si cuek yang paling bisa aku ajak bicara dan buat aku tertawa, Ivan ‘Boy’, yang selalu ada kalau aku butuh bantuannya, Sugriwo club, Ikoq ‘Sublek’, Lusi, Agnes ‘Supat’, yang selalu menyemangatiku. Teristimewa untuk Resti ‘adek dan juga sahabatku’, yang selalu dengan setia dan sabar mendengarkan ceritaku. Banyak kisah kebersamaan kita yang tak mungkin dapat ku lupakan dan kamu mengajari aku banyak hal. Terimakasih karena kamu selalu mendukung aku walaupun aku tahu bahwa kamu juga cukup sulit. Maaf, aku pernah membuatmu kecewa.

Hermin, si kembar Rosa-Rosi, Ana, Ribut, Novi, Linda, Nancy, Rinus, Paul dan mbak Niken. Terimakasih atas kebersamaan kita selama ini.

14.Teman-teman selama mengabdi bersama baik di fakultas maupun universitas, crew DEMA 2004 dan DEMA 2005 yang kompak, kakak dan adik angkatan Matematika, Ikom dan Fisika, dan semua kepanitian yang pernah ku ikuti.

15.Carloku tersayang yang dengan setia menemaniku kemanapun aku pergi.

16.Dyan Avando Michael Mendroza Sembiring Meliala, yang mengajariku banyak hal tentang cinta, kesabaran dan pengurbanan bahkan sudah mengisi hidupku dengan penuh warna.

17.Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu.

Tak ada gading yang tak retak, penulis menyadari kekurangan dalam skripsi ini, untuk itu saran serta kritik sangat diharapkan dalam peningkatan kualitas skripsi ini, dan akhirnya penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta, Desember 2007

Penulis,

Maria Nirmala Anggi Fitra Murti Martosudjito

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

PERNYATAAN KEASLIAN KARYA ... iv

HALAMAN PERSEMBAHAN ... v

ABSTRAK ... vii

ABSTRACT ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xii

DAFTAR GAMBAR ... xv

DAFTAR TABEL ... xvi

BAB I PENDAHULUAN ... 1

A. Latar Belakang Masalah ... 1

B. Perumusan Masalah ... 3

C. Batasan Masalah ... 4

D. Tujuan Penulisan ... 4

E. Metode Penulisan ... 4

F. Manfaat Penelitian ... 4

G. Sistematika Penulisan ... 5

C. Penyelesaian Persamaan Non-Linear dengan Iterasi Titik Tetap ... 22

D. Penyelesaian Persamaan Non-Linear dengan Metode Newton- Raphson ... 27

E. Optimasi Fungsi menggunakan Quadratic Fit Line Seach ... 30

BAB III PENYELESAIAN SISTEM PERSAMAAN NON-LINEAR ... 34

A. Sistem Persamaan Non-Linear ... 34

B. Konsep Dasar dan Iterasi Titik Tetap ... 36

C. Metode Newton ... 41

D. Konvergensi Metode Newton ... 62

E. Metode Turun Tercuram ... 67

F. Konvergensi Metode Turun Tercuram ... 85

BAB IV TERAPAN METODE NEWTON DAN METODE TURUN TERCURAM DALAM MENGHITUNG KONSENTRASI UNSUR DALAM SUATU SAMPEL ... 95

A. Metode Penyerapan Cahaya ... 95

B. Terapan Metode Newton dan Metode Turun Tercuram untuk Menghitung Konsentrasi Unsur ... 97

C. Analisis Perhitungan Konsentrasi Unsur dengan Metode Newton dan Metode Turun Tercuram ... 101

2. Pengaruh Nilai Awal terhadap Hasil ... 105

3. Pengaruh Pendekatan Fungsi terhadap Hasil ... 109

a. Metode Newton ... 110

b. Metode Turun Tercuram ... 110

4. Perbandingan Nilai Absorban Hasil Pengukuran dengan Hasil Perhitungan ... 111

5. Konsentrasi Parasetamol dan Kafein yang memenuhi ... 113

BAB V PENUTUP ... 114

A. Kesimpulan ... 114

B. Saran ... 116

DAFTAR PUSTAKA ... 117

LAMPIRAN ... 119

Gambar 2.2.2 ... 18

Gambar 2.5.1 ... 31

Gambar 2.5.2 ... 31

Gambar 2.5.3 ... 32

Gambar 3.3.1 ... 55

Gambar 3.5.1 ... 71

Gambar 3.5.2 ... 78

Gambar 3.6.1 ... 89

Tabel 3.4.1 ... 66

Tabel 3.4.2 ... 67

Tabel 3.5.1 ... 82

Tabel 3.5.2 ... 83

Tabel 3.6.1 ... 91

Tabel 3.6.2 ... 92

Tabel 3.6.3 ... 93

Tabel 4.2.1 ... 98

Tabel 4.2.2 ... 98

Tabel 4.2.3 ... 99

Tabel 4.2.4 ... 100

Tabel 4.2.5 ... 101

Tabel 4.3.1 ... 102

Tabel 4.3.2 ... 103

Tabel 4.3.3 ... 104

Tabel 4.3.4 ... 106

Tabel 4.3.5 ... 107

Tabel 4.3.6 ... 112

Tabel 4.3.7 ... 112

A. Latar Belakang Masalah

Dalam berbagai bidang ilmu pengetahuan sering muncul persoalan yang melibatkan model matematika. Sering kali model matematika yang muncul bukanlah suatu model yang biasa, melainkan suatu model yang rumit bahkan sulit untuk dicari penyelesaiannya. Model matematika ini bisa berupa suatu persamaan atau suatu sistem persamaan. Persamaan bisa dibagi menjadi persamaan linear dan persamaan non-linear. Sistem persamaan juga bisa dibagi menjadi sistem persamaan linear dan sistem persamaan non-linear.

Persamaan linear dengan n variabel bebas x x₁, ₂,…,x_n adalah persamaan yang berbentuk y=a x_{1 1}+a x_{2 2}+…+a x_{n n}. Sedangkan persamaan non-linear merupakan negasi dari persamaan linear. Persamaan non-linear sendiri dibagi menjadi persamaan non-linear satu variabel dan persamaan non-linear dengan n variabel, dengan . Bentuk umum persamaan non-linear dengan satu variabel adalah dengan

1

>

n

0 ) (x =

f f x( ) adalah fungsi non-linear. Sedangkan bentuk umum persamaan non-linear dengan n variabel adalah f(x₁,x₂,…,x_n)=0 dengan

1 2

( , , , _n)

f x x … x adalah fungsi non-linear.

Sistem persamaan linear adalah himpunan n persamaan linear, dengan . Penyelesaian sistem persamaan linear dapat dicari dengan beberapa metode yang sederhana, yaitu seperti metode subsitusi, metode eliminasi dan metode campuran.

1

>

Sistem persamaaan non-linear adalah himpunan n persamaan non-linear, dengan n>1. Sistem persamaan non-linear secara umum berbentuk:

0 ) , , , ( 0 ) , , , ( 0 ) , , , ( 2 1 2 1 2 2 1 1 = = = n n n n x x x f x x x f x x x f … … …

di mana tiap fungsi merupakan pemetaan vektor dari ke . Sistem ini dapat ditulis dalam bentuk lain dengan mendefinisikan fungsi F, yang memetakan ke .

i

f x=(x1,x2,…,xn)t

n n n t n n n n

n f x x x f x x x f x x x

x x

x , , , ) ( ( , , , ), ( , , , ), , ( , , , ))

( _{1 2} … = _{1 1 2} … _{2 1 2} … … _{1 2} …

F

Dengan menggunakan notasi vektor, sistem di atas dapat diasumsikan dengan bentuk F(x) = 0

Secara umum, ada dua metode penyelesaian suatu sistem persamaan yaitu metode analitis dan metode numeris. Metode analitis adalah metode penyelesaian model matematika dengan rumus-rumus aljabar yang sudah baku (lazim). Metode numeris adalah teknik yang digunakan untuk memformulasikan persoalan matematika dengan data numerik.

Sistem persamaan non-linear dapat diselesaikan dengan beberapa metode numeris, salah satunya adalah metode Newton. Metode Newton merupakan perkembangan dari iterasi Titik-Tetap (Fixed-Point) dan metode Newton-Raphson dalam menyelesaikan persamaan non-linear. Langkah awal penyelesaian persamaan non-linear dengan metode Newton-Raphson adalah mencari turunan fungsinya. Tidak jauh berbeda dengan metode Newton-Raphson, langkah awal penyelesaian sistem persamaan non-linear dengan metode Newton adalah mencari turunan parsial semua fungsinya terhadap setiap variabel yang ada dalam sistem tersebut. Semua turunan parsial dalam sistem dibentuk menjadi suatu matriks yang dinamakan matriks Jacobian.

Metode Newton merupakan metode yang paling mudah dan paling sering digunakan akan tetapi mempunyai kelemahan yaitu konvergensinya akan sangat sulit dicapai apabila pendekatan awal tidak baik, artinya terlalu jauh dari nilai yang sebenarnya. Sebagai akibatnya, muncullah suatu metode yang dinamakan Metode Turun Tercuram (Steepest Descent Method). Metode ini dapat mengatasi kelemahan yang muncul pada Metode Newton, maksudnya pendekatan awal apapun yang dipilih akan menyebabkan konvergensinya menjadi lebih cepat.

B. Perumusan Masalah

Berdasarkan uraian yang dikemukakan dalam latar belakang, pokok permasalahan dalam skripsi ini dapat dirumuskan sebagai berikut :

b. Bagaimana mencari penyelesaian sistem persamaan non-linear dengan metode Turun Tercuram?

c. Bagaimana terapan penyelesaian sistem persamaan non-linear di bidang fisika, khususnya dalam masalah menghitung konsentrasi unsur dalam sampel?

C. Batasan Masalah

1. Sistem persamaan non-linear terdiri dari n persamaan dan n variabel.

2. Bahasa pemrograman yang digunakan untuk menyelesaikan sistem persamaan non-linear adalah Matlab.

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah untuk menyelesaikan sistem persamaan non-linear dengan metode Newton dan metode Turun Tercuram untuk mempercepat konvergensinya serta terapannya dalam bidang fisika khususnya dalam masalah menghitung konsentrasi unsur dalam sampel.

E. Metode Penulisan

Metode penulisan skripsi ini adalah dengan menggunakan metode studi pustaka dan analisis data.

F. Manfaat Penulisan

serta terapannya dalam bidang fisika, khususnya dalam masalah menghitung konsentrasi unsur dalam sampel.

G. Sistematika Penulisan

BAB I : PENDAHULUAN

Dalam bab I akan dibahas tentang latar belakang, perumusan masalah, batasan masalah, tujuan penulisan, metode penulisan, manfaat penulisan, dan sistematika penulisan.

BAB II : KONVERGENSI DAN PERSAMAAN NON-LINEAR

Dalam bab II akan dibahas konsep ruang vektor dan matriks, konvergensi, penyelesaian persamaan non-linear dengan iterasi Titik Tetap, penyelesaian persamaan non-linear dengan metode Newton-Raphson serta optimasi fungsi dengan Quadratic Fit Line Search.

BAB III : PENYELESAIAN SISTEM PERSAMAAN NON-LINEAR

BAB IV : TERAPAN METODE NEWTON DAN METODE TURUN TERCURAM DALAM MENGHITUNG KONSENTRASI UNSUR DALAM SUATU SAMPEL

Dalam bab IV akan dibahas tentang metode penyerapan cahaya, terapan metode Newton dan metode Turun Tercuram untuk menghitung konsentrasi unsur serta analisis penghitungan konsentrasi unsur dengan metode Newton dan metode Turun Tercuram

BAB V : PENUTUP

Dalam bab ini akan dibahas konsep ruang vektor dan matriks, konvergensi,

penyelesaian persamaan non-linear dengan iterasi Titik-Tetap dan metode

Newton-Raphson serta optimasi fungsi dengan Quadratic Fit Line Search yang nantinya akan

digunakan untuk memahami metode Newton dan metode Turun Tercuram serta

konvergensinya.

A. Ruang Vektor dan Matriks

Definisi 2.1.1

Misalkan V adalah himpunan di mana didefinisikan operasi-operasi penjumlahan dan

perkalian dengan skalar. Penjumlahan adalah kaidah untuk mengasosiasikan setiap

pasang elemen u dan v di dalam V dengan sebuah elemen u+v, yang dinamakan

jumlah (sum). Perkalian skalar adalah sebuah kaidah untuk mengasosiakan setiap

skalar k dan setiap elemen u di dalam V dengan sebuah elemen ku, yang dinamakan

kelipatan skalar (scalar multiple). Jika aksioma-aksioma berikut dipenuhi oleh

semua elemen u, v, dan w di dalam V dan oleh semua skalar k dan l, maka V

dinamakan ruang vektor dan elemen-elemen di dalam V dinamakan vektor.

(1) Jika u dan v adalah elemen-elemen di dalam V, maka u+v berada di dalam V.

(2) u+ = +v v u

(4) Ada sebuah elemen 0 di dalam V sehingga 0 u+ = + =u 0 u untuk semua u di dalam V.

(5) Untuk setiap u di dalam V, ada sebuah elemen –u di dalam V yang dinamakan

negatif dari u sehingga u+ − = − + =( u) ( u) u 0

k

u

.

(6) Jika k adalah sebarang bilangan real dan u adalah sebarang elemen di dalam V,

maka ku berada di dalam V.

(7) k(u+v)=ku+ v

(8) (k+l)u=ku+l (9) k l( )u =( )kl u

(10) 1u=u

Vektor 0 di dalam Aksioma 4 dinamakan vektor nol (zero vector) untuk V.

Definisi 2.1.2

Hasil kali dalam pada ruang vektor V adalah pemetaan dari V V× ke , dimana V

setiap pasang vektor-vektor u dan v di dalam V dipetakan ke sebuah bilangan real

n

,

u v yang memenuhi syarat berikut:

(1) u u, ≥0 Nonnegatif

(2) u u, =0 jika dan hanya jika u=0 Positif

(3) u+v w, = u w, + v w, Penjumlahan

(4) αu v, =α u v, untuk semua skalar α Homogenitas

Definisi 2.1.3

Hasil kali dalam baku untuk n adalah hasil kali skalar , = T

x y x y

Definisi 2.1.4

Sebuah ruang vektor V dikatakan ruang linear bernorma (normed linear space)

jika untuk setiap vektor v∈V dikaitkan dengan sebuah bilangan real v yang

disebut norma dari v yang memenuhi :

(1) v ≥0 Nonnegatif

(2) v =0 jika dan hanya jika v=0 Positif

(3) αv = α v untuk semua skalar α Homogenitas

(4) v+w ≤ v + w Ketaksamaan segitiga

Teorema 2.1.5 (Pertidaksamaan Cauchy-Schwarz)

Jika u dan v adalah vektor-vektor di dalam sebuah ruang hasil kali dalam V, maka

, ≤ ⋅

u v u v

Bukti:

Bukti teorema 2.1.5 bisa dilihat pada buku karangan Leon, Steven J. (2001). Aljabar

Teorema 2.1.6

Jika V adalah sebuah ruang hasil kali dalam, maka persamaan

, =

v v v untuk semua v∈V

Bukti:

Bukti teorema 2.1.6 bisa dilihat pada buku karangan Leon, Steven J. (2001). Aljabar

Linear dan Aplikasinya (Terjemahan). Edisi kelima. Jakarta : Penerbit Erlangga.

Beberapa contoh norma sebuah vektor

1. Norma Euclidean (Euclidean norm atau l₂ norm) dalam n

(

)

1 1

2

2 2 2 ₂ 2

1 2 2

1

,

n

n i

i

x x x x

=

⎛ ⎞

= + + + =_{⎜ ⎟} =

⎝

∑

⎠

x … x x

i sering disebut juga sebagai panjang vektor.

2. Norma jumlah (norm sum atau l₁ norm) dalam n

1 2 1

1

n

n i

i

x x x

=

= + + + =

∑

x

x …

3. Norma maksimum (max norm atau l_∞ norm) dalam n

{

1 2

}

1

max , , , _n max _i

i n

x x x

∞ = = _{≤ ≤}

x … x

4. Norma l_p (l_p norm) dalam n

1

1

n _p

p i p

i

x

=

⎛ ⎞

= ⎜ ⎟

⎝

∑

⎠

x

Untuk selanjutnya norma yang akan digunakan dalam adalah norma Euclidean

kecuali ada ketentuan khusus dan akan ditulis dengan notasi

n

i .

Definisi 2.1.7

Misalkan adalah vektor-vektor di dalam sebuah ruang hasil kali dalam

V. Jika

1, 2, , n

v v … v

,

i j =

v v 0 bilamana i≠ j, maka

{

v v₁, ₂,…,vn

}

dikatakan sebagai sebuah

himpunan ortogonal dari vektor-vektor.

Definisi 2.1.8

Sebuah himpunan ortonormal dari vektor-vektor adalah sebuah himpunan

ortogonal dari vektor-vektor satuan dengan vektor satuan adalah vektor yang

panjangnya satu.

Himpunan

{

u u₁, ₂,…,un

}

akan menjadi ortonormal jika dan hanya jika

,

i j =δij

u u

di mana

1 jika

0 jika

ij

i j

i j

δ _{= ⎨}⎧ =

Definisi 2.1.9

Sebuah matriks A yang berorde n n× dikatakan nonsingular jika ada sebuah matriks

yang berorde dengan

1 −

A n n× −1 = −1 =

AA A A I. Matriks A−1 dinamakan invers

matriks A. Sebuah matriks yang tidak mempunyai invers disebut matriks singular.

Definisi 2.1.10

Sebuah matriks Q yang berorde n n× dikatakan sebagai matriks ortogonal jika

vektor-vektor kolom dari Q membentuk sebuah himpunan ortonormal di dalam n.

Teorema 2.1.11

Sebuah matriks Q yang berorde n n× adalah ortogonal jika dan hanya jika Q QT =I

Bukti :

Berdasarkan definisi, sebuah matriks Q yang berorde n n× adalah ortogonal jika dan

hanya jika vektor kolom-kolomnya memenuhi

T

i j =δij

q q

Tetapi adalah entri dari . Jadi Q adalah ortogonal jika dan hanya

jika .

T i

q q_j

(

i j,

)

Q QT

T =

Q Q I

Definisi 2.1.12

Misalkan M_n adalah himpunan semua matriks berukuran n×n. Sebuah fungsi :M_n →

i dikatakan suatu norma matriks jika untuk setiap akan

memenuhi kelima aksioma di bawah ini:

, ∈ _n

A B M

(1) A ≥0 Nonnegatif

(1a) 0A = jika dan hanya jika A=0 Positif

(2) cA = c A untuk semua skalar c Homogenitas

(3) A B+ ≤ A + B Ketaksamaan segitiga

(4) AB ≤ A B Submultiplikatif

Beberapa contoh norma matriks

1. Norma untuk l₁ A∈M_n yang didefinisikan dengan

1 , 1

n ij i j

a

=

=

∑

A

2. Norma Euclidean atau norma untuk l₂ A∈M_n yang didefinisikan dengan

1 2 2 2

, 1

n ij i j

a

=

⎛ ⎞

= ⎜ ⎟

⎝

∑

⎠ A

3. Norma l_∞ untuk A∈M_n yang didefinisikan dengan

1 ,maxi j n aij

Untuk selanjutnya norma yang akan digunakan dalam adalah norma Euclidean

kecuali ada ketentuan khusus dan akan ditulis dengan notasi

n

M

i .

B. Konvergensi

Barisan bilangan real adalah suatu fungsi dari ke dalam . Jadi, fungsi

atau

:

f → f n( ) dengan n∈ adalah barisan bilangan real. Biasanya f n( )

dinyatakan dengan s_n. Barisan dengan sn sebagai suku ke-n akan ditulis sn atau

{ }

sn .

Definisi 2.2.1

Misalkan f adalah fungsi yang terdefinisi di dalam himpunan bilangan real X; f

dikatakan mempunyai limitL di x₀, dan ditulis

0

lim ( )

x→x f x =L, jika diberikan sebuah

bilangan ε >0, maka ada sebuah δ >0 sedemikian sehingga f x( )− <L ε bila

x∈X dan 0< −x x₀ <δ.

Definisi 2.2.2

Misalkan f adalah fungsi yang terdefinisi di dalam himpunan bilangan real X dan

0

x ∈X ; f dikatakan kontinu di x₀ jika

0

0

lim ( ) ( )

x→x f x = f x . Fungsi f dikatakan kontinu

Definisi 2.2.3

Barisan

{ }

s_n dikatakan konvergen jika terdapat s∈ dengan sifat, untuk sebarang 0

ε > yang diberikan, terdapat N∈ sehingga untuk semua dengan

berlaku

n∈ n≥

n

s−s <ε. Bilangan s dinamakan limit

{ }

s_n untuk dan ditulis atau disingkat

n→ ∞

lim _n

n→∞s =s limsn =s. Suatu barisan yang tidak mempunyai limit

disebut divergen.

Definisi 2.2.4 (Deret Taylor)

Jika f terdiferensial pada semua tingkat di x=b maka dapat didefinisikan deret

Taylor untuk f di sekitar x=b adalah

( )

2 3

''( ) '''( ) ( )

( ) ( ) '( )( ) ( ) ( ) ( )

2! 3! !

n

n

f b f b f b

f x f b f b x b x b x b x b

n

= + − + − + − + +_… − +_…

Teorema 2.2.5 (Teorema Rolle)

Misalkan f ∈C a b

[ ]

, dan f terdiferensial dalam interval

(

Jika

, maka ada paling sedikit satu bilangan c pada sedemikian

sehingga berlaku .

)

)

,

a b

( )

( )

0

f a = f b =

(

a b,

'( ) 0

f c =

Bukti :

Karena f x( ) kontinu dalam a≤ ≤x b berarti f x( ) mempunyai nilai maksimum M

Karena m<M dan f a( )= f b( ), maka paling sedikit salah satu dari m atau M tidak sama dengan f a( )= f b( ), misalnya M ≠ f a( ). Maka nilai maksimum M tidak pada titik akhir dari

(

a b,

)

, melainkan terletak di x=c,

(

a< <c b

)

dan berarti f c'( )=0.

■

Teorema 2.2.6 (Teorema Nilai Rata-Rata)

Jika f ∈C a b

[ ]

, dan terdifferensial dalam interval

( )

a b, , maka paling sedikit ada

satu nilai c antara a dan b sedemikian hingga berlaku

( ) ( )

'( )

f b f a

f c b a

− ₌

− (2.2.1)

Bukti :

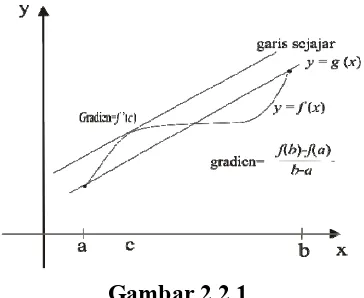
Gambar grafik f sebagai kurva pada bidang dan gambar sebuah garis lurus dari titik

(

, ( )

)

A a f a dan B b f b

(

, ( )

)

(lihat Gambar 2.2.1 ) maka fungsinya

( ) ( )

( ) ( ) f b f a ( )

g x f a x a

b a

−

= + −

− (2.2.2)

Selisih antara grafik f dan g pada x adalah

( ) ( )

( ) ( ) ( ) ( ) ( ) f b f a ( )

h x f x g x f x f a x a

b a

−

= − = − − −

− (2.2.3)

Dari persamaan (2.2.3) maka h a( )=h b( )=0. Oleh karena fungsi-fungsi f x( ) dan

(x−a) adalah kontinu dalam a≤ ≤x b dan terdiferensial dalam , maka menurut teorema 2.2.5, ada (paling sedikit) nilai x yang turunannya = 0 dan misalkan

untuk

a< <x b

Gambar 2.2.1

Dari persamaan (2.2.3) diperoleh

( ) ( ) '( ) '( ) f b f a

h x f x

b a

−

= −

− (2.2.4)

Untuk x=c, maka persamaan (2.2.4) menjadi

( ) ( ) '( ) '( ) f b f a

h c f c

b a

−

= −

−

( ) ( ) 0 f c'( ) f b f a

b a

−

= −

− h c'( )=0

( ) ( ) '( ) f b f a

f c

b a

− =

−

■

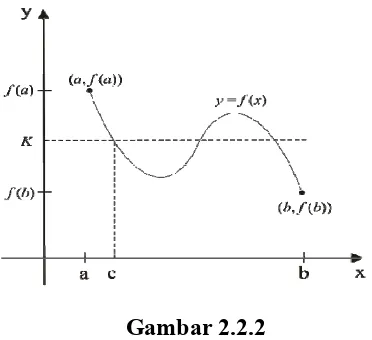
Teorema 2.2.7 (Teorema Nilai Antara)

Jika f ∈C a b

[ ]

, dan K adalah sebuah bilangan yang berada di antara f a( ) dan

( )

Gambar 2.2.2

Bukti:

Dimisalkan f a( )< f b( ) dan m dan M berturut-turut nilai minimum dan maksimum mutlak dari f pada

[

a b,

]

. Maka f

(

[ ]

a b,

)

=

[

m M,

]

karena f kontinu pada

[ ]

a b, . Jadi m≤ f a( )< <c f b( )≤M. Karena pada

[ ]

a b, fungsi f mencapai semua nilai mulai dari m sampai dengan M, maka pasti terdapat K∈

( )

a b, sehingga f c( )=K.

■

Teorema 2.2.8 (Teorema Titik Ekstrem)

Andaikan f didefinisikan pada selang I yang memuat titik c. Jika f c( ) adalah nilai

ekstrim, maka c haruslah berupa suatu titik kritis, yakni c berupa salah satu :

(i) titik ujung dari I

(ii) titik stasioner dari f

(

f c'( )=0

)

atau

Bukti :

Bukti teorema 2.2.8 bisa dilihat pada buku karangan Varberg, Dale, Purcell, Edwin J.

(2001). Kalkulus (Terjemahan). Edisi Tujuh. Jilid Satu. Jakarta : Interaksara.

Teorema 2.2.9 (Perluasaan Teorema Nilai Rata-Rata yang Pertama ke Rumus

Taylor)

Jika f dan f ' kontinu pada

[ ]

a b, dan f ' diferensial pada

( )

a b, , maka ada sebuah

bilangan ξ antara a dan b sedemikian serupa sehingga

2

''( )

( ) ( ) '( )( ) ( )

2!

f

f b = f a + f a b− +a ξ b−a (2.2.5)

Bukti :

Bukti teorema 2.2.9 bisa dilihat pada buku karangan Thomas, George B., Finney,

Ross L. (1986). Kalkulus dan Geometri Analitik (Terjemahan). Edisi keenam. Jilid I.

Jakarta : Penerbit Erlangga.

Lemma 2.2.10

Jika M adalah matriks yang berukuran n n× dengan M <1 maka adalah

nonsingular dan

−

I M

(

)

1 1

1

−

− ≤

− I M

Bukti :

Akan ditunjukkan bahwa I−M adalah nonsingular dan pertidaksamaan (2.2.6) akan diperoleh dengan menunjukkan bahwa deret

1 0

( )

l l

∞

− =

= −

∑

M I M

Jumlah parsial deret tersebut

0

k l k

l= =

∑

S M

yang merupakan bentuk barisan Cauchy di n n×

. Dari pernyataan tersebut maka

untuk semua m>k

1

m l

k m

l k= +

− ≤

∑

S S M

Kemudian, Ml ≤ M l karena i adalah norma matriks yang sudah termasuk norma vektor. Karena itu,

1 1

1

0 1

m k m

l k

k m

l k

− +

= +

⎛ ₋ ⎞

⎜ ⎟

− ≤ = →

⎜ ₋ ⎟

⎝ ⎠

∑

M

S S M M

M

dengan . Oleh sebab itu, barisan konvergen, ditulis S. Karena

, maka didapatkan

,

m k → ∞ S_k

1

k+ = +

M S I S_k M S+ =I S dan sebab itu . Ini

membuktikan bahwa adalah nonsingular dan

(

I M S−

)

=I

−

I M S= −

(

I M

)

−1. Perlu dicatat bahwa

(

)

1

(

)

1

0

1

l l

∞ ₋

− =

− ≤

∑

= −

I M M M

Definisi 2.2.11

B merupakan pendekatan invers dari A jika I BA− <1.

Teorema 2.2.11 (Lemma Banach)

Jika A dan B adalah matriks yang berukuran n n× dan B merupakan pendekatan

invers dari A, maka A dan B keduanya adalah nonsingular dan

1

1

− _≤

− −

B A

I BA ,

1

1

− _≤

− −

A B

I BA (2.2.7)

dan

1

1

− _{− ≤} −

− −

B I BA A B

I BA ,

1

1

− −

− ≤

− −

A I BA A B

I BA (2.2.8)

Bukti :

Misalkan M= −I B A. Berdasarkan dari Lemma 2.2.9, I−M= − −I (I B A)=B A

adalah nonsingular. Oleh karena itu, A dan B keduanya adalah nonsingular. Dari

pertidaksamaan (2.2.6)

(

)

1

1 1 1 1

1 1

−

− − _{= − ≤ =}

− − −

A B I M

M I BA

1 −

B

(2.2.9)

Karena , pertidaksamaan (2.2.9) implikasi dengan bagian pertama

dari (2.2.7). Bagian kedua akan didapatkan dengan cara yang sama dari

.

1 _{( )} − _{= −}

A I M

1 1

( )

− _{= −} −

B A I M

1 1

( )

− _{− = −} −

A B I B A A , A B− −1 =B−1(I B A− )

dan yang akan menggunakan pertidaksamaan (2.2.7).

■

C. Penyelesaian Persamaan Non-Liner dengan Iterasi Titik-Tetap

Persamaan non-linear persamaan non-linear merupakan negasi dari

persamaan linear. Persamaan linear dapat dibedakan menjadi persamaan

non-linear satu variabel dan persamaan non-non-linear dengan n variabel, dengan .

Bentuk umum persamaan non-linear dengan satu variabel adalah , dengan

1

>

n

0 ) (x = f

( )

f x adalah fungsi non-linear. Sedangkan bentuk umum persamaan non-linear

dengan n variabel adalah f(x₁,x₂,…,x_n)=0, dengan f x x( ,_{1 2},…,x_n) adalah fungsi non-linear.

Contoh 2.3.1 :

• Persamaan non-linear satu variabel

0 cos =

− x

x

• Persamaaan non-linear dengan 3-variabel

0 6 cos 2

2 3

2

1 + − + _x − =

ex x

Titik tetap untuk suatu fungsi g adalah titik p dengan . Masalah

mencari akar persamaan dan masalah titik tetap adalah equivalen. Misalkan :

diberikan masalah mencari akar persamaan

( )

g p = p

( ) 0

memiliki titik tetap di p maka fungsi yang didefinsikan dengan

memiliki nilai nol di p.

( ) ( )

g x = −x f x

Teorema 2.3.1

Jika g∈C a b

[ ]

, dan g x( )∈

[ ]

a b, untuk semua x∈

[ ]

a b, maka g memiliki titik tetap

di

[

a b,

]

. Misalkan, ditambahkan, bahwa ada g x'( ) di

( )

a b, dan ada sebuah

konstanta positif k<1 dengan

'( ) 1

g x ≤ <k , untuk semua x∈

( )

a b, (2.3.1)

Maka titik tetap di

[

a b,

]

adalah tunggal.

Bukti :

Jika atau , titik tetap jelas ada. Misalkan tidak maka pasti akan

benar dengan dan

( )

g a =a g b

( )

=b

( )

g a >a g b

( )

<b. Definisikan h x

( )

=g x

( )

−x, maka h akan

kontinu dalam

[

a b,

]

dan

( )

( )

0

h a =g a − >a , h b

( )

=g b

( )

− <b 0

Teorema Nilai Antara berimplikasi dengan ada p∈

( )

a b, sedemikian sehingga

( )

0

h p = . Kemudian, g p

( )

− =p 0 dan p adalah titik tetap dari g.

Misalkan, ditambahkan, dari pertidaksamaan (2.3.1) dan bahwa p dan q

keduanya adalah titik tetap di

[ ]

a b, dengan p≠q. Dari Teorema Nilai Rata-Rata,

( ) ( )

( )

'

g p g q g

p q ξ

−

= −

Maka

( ) ( )

'

( )

p− =q g p −g q = g ξ p− ≤q k p− < −q p q

Kontradiksi. Kontradiksi muncul dari permisalan bahwa p≠q. Oleh karena itu,

dan titik tetap di

[

adalah tunggal.

p=q a b,

]

■

Untuk mendekati titik tetap fungsi g, akan dipilih suatu pendekatan awal (0)

p dan

akan dibangkitkan barisan

{ }

( )

0

n n

p ∞

= dengan maka

( ) ( 1)

(

n n

p =g p − )

(

)

(

)

( ) ( 1) ( 1)

lim n lim n lim n ( )

n n n

p p g p − g p − g

→∞ →∞ →∞

= = = = p

dan penyelesaian x=g x( ) terpenuhi. Teknik ini disebut Iterasi Titik-Tetap atau Iterasi Fungsional.

Teorema 2.3.2 (Teorema Titik-Tetap)

Misalkan g∈C a b

[ ]

, dan g x

( )

∈

[ ]

a b, untuk semua x di

[

. Misalkan,

ditambahkan, bahwa ada ' di

]

,

a b

g

[ ]

a b, dengan

'( ) 1

g x ≤ <k , untuk semua x∈

( )

a b, (2.3.2)

Jika p(0) adalah nilai di

[

a b,

]

, maka barisan yang didefinisikan dengan

(

)

( )n (n 1)

konvergen ke suatu titik tetap secara tunggal di

[ ]

a b, .

Bukti :

Berdasarkan Teorema 2.3.1, ada sebuah titik tetap tunggal p di

[

. Karena g

merupakan pemetaan

[

ke

]

]

,

a b

,

a b

[ ]

a b, , maka barisan

{ }

( )

0

n n

p ∞

= didefinisikan untuk

semua n≥0 dan ( )n

[ ]

,

p ∈ a b untuk semua n. Dengan menggunakan pertidaksamaan

(2.3.2) dan Teorema Nilai Antara, didapatkan

(

)

( )

( )

( ) ( 1) ( 1) ( 1)

'

n n n n

p − =p g p − −g p = g ξ p − − ≤p k p − −p

)

(2.3.3)

dengan ξ∈

(

a b, . Menggunakan pertidaksamaan tersebut akan memberikan

p( )n − ≤p k p(n−1)− ≤p k2 p(n−2)− ≤p …≤kn p(0)−p (2.3.4) Karena k <1,

( ) (0)

lim n lim n 0

n→∞ p − ≤p n→∞k p − =p

dan

{ }

( )

0

n n

p ∞

= konvergen ke p.

■

Akibat 2.3.3

Jika g memenuhi hipotesis Teorema 2.3.2, batas untuk kesalahan (error) yang

terlibat dengan menggunakan p( )n untuk mendekati p diberikan sebagai

{

}

( ) (0) (0)

max ,

n n

p − ≤p k p −a b−p

dan ( ) (0) (1)

1

n

n k

p p p

k

− ≤ −

Bukti :

Batasan pertama menurut pertidaksamaan (2.3.4) :

{

}

( ) (0) (0) (0)

max ,

n n n

p − ≤p k p − ≤p k p −a b−p karena p∈

[ ]

a b, .

Untuk , prosedur akan digunakan untuk bukti Teorema 2.3.2 yang implikasi

dengan 1

n≥

( ) (

)

(n 1) ( )n ( )n (n 1) ( )n (n 1) n (1) (0)

p + −p = g p −g p − ≤k p − p − ≤…≤k p − p

Kemudian, untuk m> ≥n 1

( )m ( )n ( )m (m 1) (m 1) (n 1) ( )

p −p = p −p − + p − − +… p + −p n

( )m (m 1) (m 1) (m 2) (n 1) ( )

p p − p − p − p + p

≤ − + − + +_… − n

1 (1) (0) 2 (1) (0) (1) (0)

m m n

k − p p k − p p k p p

≤ − + − + +_… −

(

2 1

)

(1)

1

n m n

k k k k − − p p

= + + + +_… − (0)

Berdasarkan Teorema 2.3.2, lim ( )m

m→∞p = p, sehingga

( ) ( ) ( ) (1) (0) 0

lim

n m n n

m

i

p p p p k p p k

∞

→∞ ₌

− = − ≤ −

∑

i

Karena adalah barisan geometri dengan konstanta rasio k, maka akan

didapatkan batasan yang kedua sebagai berikut:

0

i i

k

∞

=

∑

( ) (1) (0)

1

n

n k

p p p

k

− ≤ −

− p

D. Penyelesaian Persamaan Non-Linear dengan Metode Newton-Raphson

Metode Newton-Raphson merupakan salah satu metode numerik yang

paling kuat dan paling banyak diketahui untuk menyelesaikan masalah mencari akar

persamaan f x( )=0.

Misalkan f ∈C2

[ ]

a b, . Misalkan x∈

[ ]

a b, akan menjadi pendekatan

untuk p sedemikian sehingga f '( )x ≠0 dan x−p adalah “kecil”. Dengan mempertimbangkan bentuk deret Taylor untuk f x( ) di sekitar x ,

2

( )

( ) ( ) ( ) '( ) ''( ( ))

2

x x

f x ≈ f x + −x x f x + − f ξ x

dengan ξ

( )

x berada di antara x dan x. Karena f p( )=0 dengan x= p, maka persamaan akan menjadi

2

( )

0 ( ) ( ) '( ) ''( ( )

2

p x

)

f x p x f x − f ξ p

≈ + − +

Metode Newton-Raphson diperoleh dari asumsi tersebut, karena p−x kecil, maka

2

(p−x) dapat diabaikan dan akan didapatkan

0≈ f x( ) (+ p−x f) '( )x (2.4.1) Menyelesaikan p dalam persamaan tersebut diberikan dengan

( ) '( )

f x p x

f x ≈ −

Persamaan tersebut merupakan bentuk penyelesaian untuk metode Newton-Raphson

dengan pendekatan awal p(0) dan akan membangkitkan barisan

{ }

( )n

p yang

( 1) ( ) ( 1)

( 1)

( )

'( )

n

n n

n

f p

p p

f p

− −

−

= − , n≥1 (2.4.2)

Teknik-pemberhentian pada metode Newton-Raphson. Pilih toleransi dengan ε >0

dan menyusun p(1),…,p( )n sehingga

( )n (n 1)

p −p − <ε (2.4.3)

( ) ( 1) ( )

n n

n

p p

p ε

−

−

< , p( )n ≠0 (2.4.4)

atau

( )

( n )

f p <ε (2.4.5)

Metode Newton-Raphson adalah teknik iterasi fungsional dengan bentuk

, berlaku

( ) ( 1)

(

n n

p =g p − )

(

)

( 1)

( 1) ( 1)

( 1)

( )

'( )

n

n n

n

f p

g p p

f p

−

− −

−

= − , n≥1

Akan menjadi sangat jelas dari persamaan tersebut bahwa iterasi pada Metode

Newton-Raphson tidak dapat dilanjutkan jika f '(p(n−1))=0.

Teorema 2.4.1

membangkitkan barisan

{ }

( )

1

n n

p ∞

= konvergen ke p untuk beberapa pendekatan awal

[

]

(0) _,

p ∈ p−δ p+δ .

Bukti :

Bukti akan didasarkan dengan menganalisa metode Newton-Raphson sebagai pola

iterasi fungsional p( )n =g p( (n−1)), untuk n≥1, dengan

( )

( )

'( )

f x g x x

f x = − .

Untuk sebuah nilai k di

( )

0,1 , interval

[

p−δ,p+δ

]

sedemikian sehingga g

merupakan pemetaan dari interval

[

p−δ,p+δ

]

ke

[

p−δ,p+δ

]

dan g x'( ) ≤ <k 1

untuk x∈

[

p−δ,p+δ

]

.

Karena f '

( )

p ≠0 dan f ' kontinu , maka ada sebuah δ₁>0 sedemikian sehingga

untuk

'( ) 0

f x ≠ x∈

[

p−δ₁,p+δ₁

] [ ]

⊂ a,b . Kemudian, g didefinisikan dan kontinu pada

[

p−δ₁,p+δ₁

]

. Sehingga

[

]

2

[

]

2

'( ) '( ) ( ) ''( ) ( ) ''( ) '( ) 1

'( ) '( )

f x f x f x f x f x f x

g x

f x f x

−

= − =

untuk x∈

[

p−δ₁,p+δ₁

]

; karena f ∈C2

[ ]

a b, , akan didapatkan

[

]

1

1,

g∈C p−δ p+δ₁ . Berdasarkan asumsi f p( )=0 sehingga

[

]

2

( ) ''( )

'( ) 0

'( )

f p f p g p

f x

Karena g' kontinu , akan implikasi dengan untuk sebuah bilangan positif k<1

maka ada a δ , dengan 0< <δ δ₁ dan

'( )

g x ≤k untuk x∈

[

p−δ,p+δ

]

Akan ditunjukkan bahwa g:

[

p−δ,p+δ

] [

→ p−δ,p+δ

]

. Jika x∈

[

p−δ,p+δ

]

,

Teorema Nilai Rata-Rata akan implikasi dengan untuk sebuah bilangan ξ antara x

dan p, g x( )−g p( ) = g'( )ξ x−p sehingga

( ) ( ) ( ) '( )

g x − =p g x −g p = g ξ x− ≤p k x− < −p x p

Karena x∈

[

p−δ,p+δ

]

, yang diikuti dengan x− <p δ dan g x( )− <p δ. Akan

berimplikasi dengan g:

[

p−δ,p+δ

] [

→ p−δ,p+δ

]

.

Semua kesimpulan yang terdapat pada Teorema 2.3.2 akan dipenuhi untuk

( ) ( )

'( )

f x g x x

f x

= − , sehingga barisan

{ }

( )

1

n n

p ∞

= didefinisikan dengan

(

)

( )n (n 1)

p =g p − untuk n=1, 2, 3,…

konvergen ke p untuk sebuah p(0)∈

[

p−δ,p+δ

]

.

■

E. Optimasi Fungsi menggunakan Metode Quadratic Fit Line Search

Definisi 2.5.1

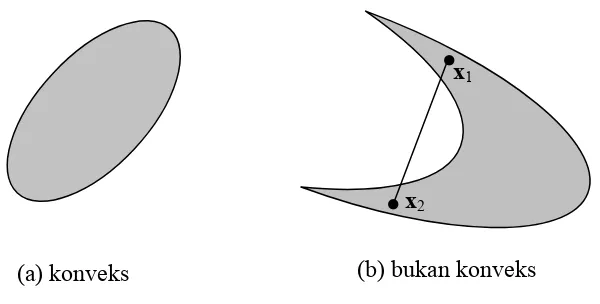
Himpunan S di dikatakan konveks jika setiap garis penghubung antara kedua

nilai yang ada di himpunan berada juga pada himpunan tersebut. Dengan kata lain,

jika dan ada di , maka

n

1

x1

●

●x2

(a) konveks (b) bukan konveks

Gambar 2.5.1 . Ilustrasi dari himpunan konveks

Contoh 2.5.1

Beberapa contoh himpunan konveks.

1. S =

{

(

x x₁, ₂

)

:x₁2+x₂2 ≤4

}

⊂ 2

)

Himpunan ini merepresentasikan nilai yang berada di dalam lingkaran dengan pusat

dan radius 2 seperti pada gambar 2.5.2

(

0, 0

Gambar 2.5.2

2. S =

{

( )

x y, :y≥x2

}

⊂ 2

Himpunan ini mempresentasikan semua nilai yang berada di atas kurva y=x2

Gambar 2.5.3

Definisi 2.5.2 (Quasikonveks)

Misalkan f :S →E₁ dengan S adalah himpunan konveks tak kosong dalam En.

Fungsi f dikatakan quasikonveks jika untuk setiap dan , maka berlaku

pertidaksamaan

1

x x₂ ∈S

{

( ), ( )

}

untuk semua (0,1) maximum

] ) 1 (

[λx₁ + −λ x₂ ≤ f x₁ f x₂ λ∈

f

Fungsi f dikatakan quasikonkav jika – f adalah quasikonveks.

Misalkan akan diminimumkan fungsi kontinu, suatu fungsi quasiconvex

) (λ

θ yang keras (strength) dengan λ ≥0 dan akan diasumsikan tiga nilai

3 2 1

0≤λ <λ <λ sedemikian sehingga θ₁ ≥θ₂ dan θ₂ ≥θ₃ dengan θ_j =θ(λ_j)

dengan j=1,2,3. Jika θ₁ =θ₂ =θ maka akan mudah dipastikan bahwa semuanya adalah penyelesaian minimumnya. Oleh karena itu, misalkan salah satu dari

pertidaksamaan θ₁ ≥θ₂ dan θ₂ ≥θ₃ bernilai benar. Kemudian akan mengarah

kepada kondisi yang dipenuhi oleh pola tiga nilai (Three Point Pattern atau TPP).

Sebagai awalnya, ambil λ₁ =0 dan menghitung nilai percobaan λ yang

dapat merupakan besarnya langkah dari metode line search dalam iterasi berikutnya.

ditemukan dari membagi dua interval

[

λ₁,λ₃

]

secara berulang-ulang sampai

mencapai TPP. Dengan kata lain, jika θ <θ₂ maka dapat ditentukan λ₃ =λ dan λ₃ dapat ditemukan dengan penggandaan interval

[

λ₁,λ₂

]

sampai mencapai TPP.

Akan diberikan tiga titik

(

λ_j,θ_j

)

, j=1,2,3. Dapat disusun sebuah kurva kuadratik yang melalui ketiga titik dan dapat meminimumkan λ dimana harus

terletak dalam (λ₁,λ₃) dengan TPP. Misalkan θ =θ(λ) dan λ_new sebagai peninjauan kembali himpunan dari tiga nilai

(

λ₁,λ₂,λ₃

)

yang diperbaharui adalah

sebagai berikut

i. Kasus I : λ >λ₂

Jika θ ≥θ₂ maka λ_new =

(

λ₁,λ₂,λ

)

. Dengan kata lain, jika θ ≤θ₂ maka

(

λ2,λ,λ3

)

λ_new = . ii. Kasus II : λ <λ₂

Mirip dengan kasus I, jika θ ≥θ₂ maka λnew =

(

λ,λ2,λ3

)

dan jika θ ≤θ2

maka λnew =

(

λ₁,λ,λ₂

)

iii. Kasus III : λ =λ₂

Dalam kasus ini, tidak perlu dicari nilai yang berbeda untuk mencapai TPP.

Jika

(

λ₃ −λ₁

)

≤ε untuk beberapa toleransi konvergensi dengan ε >0 dapat

berhenti untuk menentukan besar langkah. Sebaliknya dapat ditentukan

Dalam Bab III ini akan dibahas tentang beberapa metode untuk

menyelesaikan sistem persamaan non-linear yaitu Metode Newton dan Metode Turun

Tercuram serta konvergensi kedua metode. Di dalam pembahasan kedua metode ini,

pertama penulis akan membahas terlebih dahulu tentang sistem persamaan non-linear

serta Iterasi Titik-Tetap sebagai konsep dasar untuk metode Newton. Kemudian akan

dibahas Metode Newton serta konvergensinya dan yang terakhir Metode

Turun-Tercuram serta konvergensinya. Pengimplementasian penyelesaian sistem persamaan

non-linear dengan Metode Newton dan Metode Turun-Tercuram menggunakan

bahasa pemrograman Matlab.

A. Sistem Persamaan Non-Linear

Sistem persamaaan non-linear adalah himpunan m persamaan non-linear,

dengan m>1. Sistem persamaan non-linear dengan m persamaan dan n variabel

secara umum berbentuk:

0 ) , , , (

0 ) , , , (

0 ) , , , (

2 1

2 1 2

2 1 1

= = =

n m

n n

x x x f

x x x f

x x x f

… … …

Setiap fungsi f_i dengan i=1,2,…,n merupakan pemetaan vektor

t n

x x

x , , , )

( _{1 2} … =

x dari nke . Sistem ini dapat ditulis dalam bentuk lain dengan

mendefinisikan fungsi F yakni pemetaan dari nke n yang dapat ditulis sebagai

t n m

n n

n f x x x f x x x f x x x

x x

x , , , ) ( ( , , , ), ( , , , ), , ( , , , ))

( _{1 2} … = _{1 1 2} … _{2 1 2} … … _{1 2} …

F

Dengan menggunakan notasi vektor, sistem di atas dapat dinyatakan dalam bentuk

F(x) = 0 (3.1.2)

Fungsi f₁,f₂,…,f_m disebut koordinat fungsi F.

Contoh sistem persamaan non-linear

0 20 0 06 . 1 sin ) 1 . 0 ( 81 0 ) cos( 3 3 3 10 3 3 2 2 2 1 2 1 3 2 1 2

1 + + =

= + + + − = − − −

− _x π

e x x x x x x x x (3.1.3)

Sistem persamaan (3.1.3) dalam bentuk persamaan (3.1.2) dengan mendefinisikan

tiga fungsi f₁, f₂ dan f₃dari 3 ke sebagai berikut

0 20 ) , , ( 0 06 . 1 sin ) 1 . 0 ( 81 ) , , ( 0 ) cos( 3 ) , , ( 3 3 10 3 3 2 1 3 3 2 2 2 1 3 2 1 2 2 1 3 2 1 3 2 1 1 2

1 + + =

= = + + + − = = − − = −

− _x π

e x x x f x x x x x x f x x x x x x f x x

Dengan demikian F merupakan fungsi dari 3 → 3 dengan

B. KONSEP DASAR DAN ITERASI TITIK TETAP

Teorema 3.2.1

Jika F terdiferensial dalam suatu himpunan terbuka Ω ⊂ n dan x*∈Ω maka untuk semua x∈Ω yang dekat dengan x* berlaku

∫

′ + − −

=

− 1

0

*) *))( (

* ( *)

( )

(x F x F x t x x x x dt

F

Bukti

Misalkan x*∈Ω dan x∈Ω dengan Ω ⊂ n.

Perhatikan bahwa f(u)=

∫

f′(u)du.

Misalkan *)u=x*+t(x−x maka du=(x−x*)dt

untuk t =0⇒u=x* dan t=1⇒u=x

Sehingga

∫

∫

′ + − − = x ′

x

u u F x

x x x t x F

* 1

0

) ( *)

*))( (

*

( dt d

1 0 * ( * ( *))

)

(u F x x x

F x_x = + −

= t

*)=F(x*+(x−x*))−F(x

*) ( ) (x F x F − =

Definisi 3.2.2

Misalkan

{ }

x( )n ⊂ n dan *x ∈ n

i. x(n) →x* q-kuadratik jika x(n) →x* dan ada sebuah K >0 sedemikian sehingga

2 )

( )

1 (

*

* x x

x

xn+ − ≤ K n −

ii. x(n) →x* q-superlinear dengan q-orde α >1 jika x(n) →x*dan ada sebuah

0

>

K sedemikian sehingga

α

*

* ( )

) 1 (

x x x

xn+ − ≤ K n −

iii. x(n) →x* q-superlinear jika

0 *

* lim

) (

) 1 (

= −

−

+ ∞

→ _{x x}

x x

n n

n

iv. x(n) →x* q-linear dengan q-faktor σ ∈(0,1) jika

*

* ( )

) 1 (

x x x

x n+ − ≤σ n −

Definisi 3.2.3

Misalkan Ω ⊂ n dan G:Ω → n. G memenuhi kondisi kontinu Lipschitz dalam Ω

dengan konstanta Lipschitz γ jika

y x y

G x

Asumsi 3.2.4

1. Persamaaan (3.1.2) mempunyai penyelesaian *x .

2. F′ Ω →: n n× merupakan kontinu Lipshitz dengan konstanta Lipshitz γ .

3. F′(x*) adalah nonsingular.

Dalam hal ini *x adalah akar penyelesaian dari F. Misalkan Β(r) menyatakan suatu

bola dengan radius r di sekitar *x .

{

|

}

dengan * )

(r = x e <r e=x−x

Β

Jika x(k) merupakan iterasi ke-k dari barisan maka e(k) =x(k) −x* merupakan

kesalahan dari iterasi tersebut.

Lemma 3.2.5

Misalkan Asumsi 3.2.4 terpenuhi. Maka ada δ >0 sedemikian sehingga untuk semua )x∈Β(δ

, *) ( 2 )

(x F x

F′ ≤ ′ (3.2.1)

F′(x)−1 ≤2F′(x*)−1 , (3.2.2)

dan

e x F x

F e x

F ( ) 2 ( *) 2

*)

( 1 1 ≤ ≤ ′

′ − −

Bukti

i). Akan dibuktikan bahwa F′(x) ≤2F′(x*)

Karena F′ merupakan kontinu Lipschitz dan x∈Β(δ) maka

δ γ γ γ − ≤ ≤ ≤ ′ −

′ x F x x x e

F( ) ( *) *

Pilih

γ

δ = F′(x*) sedemikian sehingga F′(x)−F′(x*) ≤ F′(x*)−1

*) ( ) ( *) ( ) ( *)

(x F x F x F x F x F′ ≥ ′ − ′ ≥ ′ − ′

) ( *) ( 2 *) ( *)

(x F x F x F x

F′ + ′ = ′ ≥ ′

Sehingga F′(x) ≤2 F′(x*)

ii). Akan dibuktikan bahwa F′(x)−1 ≤2F′(x*)−1

Perlu diingat tentang Lemma Banach bahwa

BA I A B − − ≤ − 1 1

Misalkan A=F′(x*)−1 dan B=F′(x)

1 1 1 *) ( ) ( 1 *) ( ) ( ₋ − − ′ ′ − − ′ ≤ ′ x F x F I x F x F maka 2 1 *) ( ) (

1− I−F′ x F′ x −1 ≤

1 1 1 1 *) ( *) ( *)) ( ) ( ( *) ( *) ( ) ( ′ − = ′ − ′ − ′ ≤ ′ − ≤ ′ − ′

−F x F x F x F x F x F x e F x

Pilih

γ δ

2 *) ( −1 −1 ′

= F x sedemikian sehingga

2 1 *) ( 2 *) ( *) ( ) ( 1 1 1

1 ≤ ′ ′ ≤

′ ′ − − − − − x F x F x F x F I γ

γ (3.2.4)

dengan demikian 1 2 1 1 2 1 1 1 *) ( 2 *) ( 1 *) ( ) ( − − − − _≤ ′ _{= ′} − ′ ≤

′ x F x F x F x

F

iii). Akan dibuktikan F x e F(x) 2F(x*) e 2

*)

( 1 1 ≤ ≤ ′

′ − −

Untuk membuktikan pertidaksamaan tersebut, perlu dicatat bahwa jika x∈Β(δ)

maka x*+te∈Β(δ) untuk semua 0≤t≤1. Dari teorema 3.2.1 dan pertidaksamaan (3.2.1) akan didapatkan

e x F e x F e e x F x F x F x

F( ) ( *) ( ) ( * ) 2 ( *) 2 ( *)

1 0 1 0 �