ESTIMASI MODEL REGRESI SEMIPARAMETRIK BIRESPON MULTIPREDIKTOR BERDASARKAN ESTIMATOR PENALIZED SPLINE SKRIPSI

ESTIMASI MODEL REGRESI SEMIPARAMETRIK

BIRESPON MULTIPREDIKTOR

BERDASARKAN ESTIMATOR

PENALIZED SPLINE

SKRIPSI

DODIK ANDRIANTO

PROGRAM STUDI S-1 STATISTIKA

DEPARTEMEN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

ESTIMASI MODEL REGRESI SEMIPARAMETRIK

BIRESPON MULTIPREDIKTOR

BERDASARKAN ESTIMATOR

PENALIZED SPLINE

SKRIPSI

DODIK ANDRIANTO

PROGRAM STUDI S-1 STATISTIKA

DEPARTEMEN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

PEDOMAN PENGGUNAAN SKRIPSI

KATA PENGANTAR

Alhamdulillahirabbil ’alamin puji syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi dengan judul ”Estimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline”.

Penulis menyadari bahwa skripsi ini tidak terlepas dari bantuan berbagai pihak, oleh karena itu sepantasnya penulis mengucapkan terima kasih kepada:

1. Kedua orang tua tersayang: Ibu Sumarni dan Bapak Subekan, serta keluarga besar penulis yang mendoakan dan telah memberikan semangat, kepercayaan, dan dukungan baik secara materiil maupun moril.

2. Dr. Nur Chamidah, M.Si. dan Dr. Ardi Kurniawan, M.Si. selaku dosen pembimbing yang telah memberikan penjelasan, pengarahan, bimbingan, masukan, saran, dan motivasi kepada penulis untuk terus belajar.

3. Drs. Suliyanto, M.Si. selaku dosen wali selama menjadi mahasiswa yang telah selalu memberikan nasehat, arahan, dukungan, saran, dan motivasi kepada penulis untuk menyelesaikan studi dengan baik serta seluruh dosen statistika yang telah memberikan ilmu pengetahuan selama perkuliahan. 4. Serta pihak yang telah berjasa dalam membantu penulis menyelesaikan

skripsi ini, namun tidak dapat disebutkan satu per satu oleh penulis. Penulis menyadari skripsi ini jauh dari sempurna, baik dari segi penyusunan, bahasa atau penulisan. Oleh karena itu penulis mengharapkan kritik dan saran yang bersifat membangun guna menyempurnakan skripsi ini. Penulis berharap semoga skripsi ini dapat bermanfaat bagi perkembangan ilmu pengetahuan di masa yang akan datang.

Surabaya, 25 Januari 2017 Penulis,

Dodik Andrianto, 2017. Estimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline. Skripsi dibawah bimbingan Dr. Nur Chamidah, M.Si. dan Dr. Ardi Kurniawan, M.Si., Program Studi S-1 Statistika, Departemen Matematika, Fakultas Sains dan Teknologi, Universitas Airlangga, Surabaya.

ABSTRAK

Metode dalam ilmu statistika yang menganalisis pola hubungan secara fungsional antara variabel respon dan variabel prediktor dengan komponen parametrik dan nonparametrik didalamnya yaitu analisis regresi semiparametrik. Estimator dalam regresi noparametrik yang belum banyak dikembangkan salah satunya adalah estimator penalized spline, estimator tersebut dapat digunakan terhadap data yang mengalami peningkatan tajam dengan membebankan penalty pada komponen potongan polinomial (piece wise polinomial) yang memiliki sifat tersegmen yang kontinu. Persoalan dalam kehidupan sehari-hari sering kali memerlukan pemodelan yang melibatkan dua variabel respon dan diantara keduanya terdapat korelasi yang kuat dengan melibatkan lebih dari satu variabel prediktor. Sehingga secara teori menarik untuk megembangkan pengestimasian berdasarkan estimator penalized spline pada model regresi semiparametrik birespon multiprediktor. Tujuan dari penelitian ini adalah mendapatkan bentuk model regresi semiparametrik birespon multiprediktor dengan menggunakan estimator penalized spline dalam mengestimasi kurva regresi nonparametriknya serta mengembangkan pula algoritma dan pemrogramannya untuk implementasi pada data. Data yang digunakan pada pengimplementasian adalah data pasien di RSU Haji Surabaya dengan tekanan darah sistolik dan diastolik sebagai variabel respon, LDL sebagai variabel prediktor komponen parametrik, serta variabel prediktor komponen nonparametriknya adalah berat badan, usia, dan HDL. Hasil estimasi data tekanan darah menggunakan software OSS-R diperoleh nilai MSE dan R-square untuk pemodelan yaitu masing-masing sebesar 136,5604 dan 91,23%.

Dodik Andrianto, 2017. Estimation of Bi-response Multipredictor Semiparametric Regression Model Based on Penalized Spline Estimator.This

skripsi is under supervised by Dr. Nur Chamidah, M.Si. and Dr. Ardi Kurniawan,

M.Si., S-1 Statistics Courses, Mathematics Department, Faculty of Science and Technology, Universitas Airlangga, Surabaya.

ABSTRACT

The methods in statistical science that analyzes the pattern of a functional relationship between the response and the predictor variables with parametric and nonparametric components therein are semiparametric regression analysis. Estimator in nonparametric regression who have developed one of which is the Penalized spline estimator, the estimator can use the data it has increased sharply by imposing a penalty on the component pieces of polynomial (piece wise polynomial) which has the property of segmented continuous. Problems in everyday life often require modeling involving two response variables and between them there is a strong correlation with the involvement of more than one predictor variable. So in theory needs to be developed Penalized spline estimator estimating base on semiparametric regression model bi-response multipredictor. The purpose of this research is to form semiparametric regression model bi-response multipredictor using Penalized spline estimator to estimate the nonparametric regression curve and also develop algorithms and programming to the implementation of the data. Data used in the implementation is data in RSU Haji Surabaya patients with systolic and diastolic blood pressure as the response variable, LDL as a predictor variable component of parametric and nonparametric predictor variable component is the weight, age, and HDL. The estimation results of the blood pressure data using OSS software-R obtained by MSE and R-square for modeling are 136.5604 respectively and 91.23%.

DAFTAR ISI

Halaman

LEMBAR JUDUL ... i

LEMBAR PERNYATAAN ... ii

LEMBAR PENGESAHAN ... iii

LEMBAR PEDOMAN PENGGUNAAN SKRIPSI ... iv

SURAT PERNYATAAN TENTANG ORISIALITAS ... v

KATA PENGANTAR ... vi

ABSTRAK ... vii

ABSTRACT ... viii

DAFTAR ISI ... ix

DAFTAR TABEL ... xii

DAFTAR GAMBAR ... xiii

DAFTAR LAMPIRAN ... xiv

BAB I PENDAHULUAN ... 1

1.1Latar Belakang ... 1

1.2Rumusan Masalah ... 5

1.3Tujuan ... 5

1.4Manfaat ... 5

1.5Batasan Masalah ... 6

BAB II TINJAUAN PUSTAKA ... 7

2.1 Aljabar Matrik ... 7

2.2 Pendekatan Regresi ... 12

2.2.1 Regresi Parametrik ... 12

2.2.2 Regresi Nonparametrik ... 12

2.2.3 Regresi Semiparametrik ... 13

2.3 Regresi Birespon ... 13

2.4 Regresi Multiprediktor ... 14

2.5 Estimator Penalized Spline pada Regresi Nonparametrik... 14

2.7 Pemilihan Titik Knot Optimal ... 19

2.8 Pemilihan Jumlah Titik Knot Optimal ... 19

2.9 Model Semiparametrik Berdasarkan Estimator Penalized Spline dengan Satu Variabel Respon ... 20

2.10 Model Semiparametrik Birespon Berdasarkan Estimator Penalized Spline dengan Satu Variabel Prediktor... 21

2.11 Kasus Homoskedastisitas dan Heteroskedastisitas ... 22

2.12 Estimasi Parameter Weighted Least Square (WLS) ... 23

2.13 Uji Glesjer ... 23

2.14 Uji Korelasi Pearson ... 24

2.15 Open Source Software R(OSS-R) ... 25

2.16 Tekanan Darah ... 28

BAB III METODE PENELITIAN ... 29

3.1 Mengestimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline ... 29

3.2 Membuat Algoritma dan Program Untuk Mengestimasi Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline yang Diterapkan Pada Data Riil atau Data Bangkitan ... 31

3.2.1 Algoritma dan Program untuk Mengestimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline ... 31

3.2.2 Penerapan Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline pada Data Riil ... 36

BAB IV HASIL DAN PEMBAHASAN ... 37

4.1 Estimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline ... 37 4.2 Algoritma dan Program Untuk Mengestimasi Regresi

Penalized Spline yang Diterapkan Pada Data Riil atau Data

Bangkitan ... 47

4.2.1 Algoritma dan Program untuk Mengestimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline ... 47

4.2.2 Penerapan Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline pada Data Riil ... 54

BAB V KESIMPULAN DAN SARAN ... 71

5.1 Kesimpulan ... 71

5.2 Saran ... 72

DAFTAR TABEL

Nomor Judul Tabel Halaman 3.1 Variabel-variabel Penelitian ... 36 4.1 Hasil Kombinasi Orde Polinomial, Jumlah Knot, Titik

Knot, dan Nilai Lambda Optimal, serta GCV Minimum

Prediktor Ke-1 ... 57 4.2 Hasil Kombinasi Orde Polinomial, Jumlah Knot, Titik

Knot, dan Nilai Lambda Optimal, serta GCV Minimum

Prediktor Ke-2 ... 59 4.3 Hasil Kombinasi Orde Polinomial, Jumlah Knot, Titik

Knot, dan Nilai Lambda Optimal, serta GCV Minimum

Prediktor Ke-3 ... 60 4.4 Hasil Kombinasi Orde Polinomial, Jumlah Knot, Titik

DAFTAR GAMBAR

Nomor Judul Gambar Halaman 3.1 Diagram Alir Algoritma dan Program ... 35

4.1 Scatterplot antara Tekanan Darah Sistolik dan Diastolik

dengan Berat Badan ... 55

4.2 Scatterplot antara Tekanan Darah Sistolik dan Diastolik

dengan Usia ... 56

4.3 Scatterplot antara Tekanan Darah Sistolik dan Diastolik

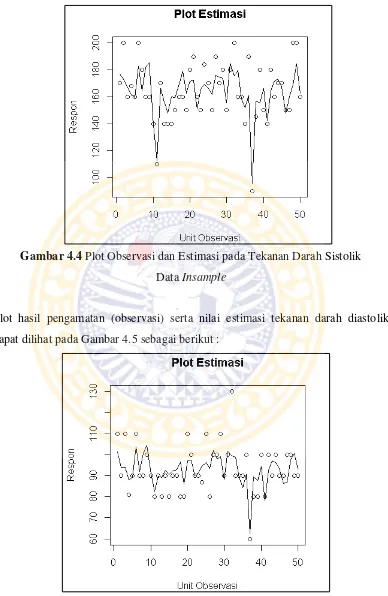
dengan HDL ... 56 4.4 Plot Observasi dan Estimasi pada Tekanan Darah

Sistolik Data Insample ... 68 4.5 Plot Observasi dan Estimasi pada Tekanan Darah

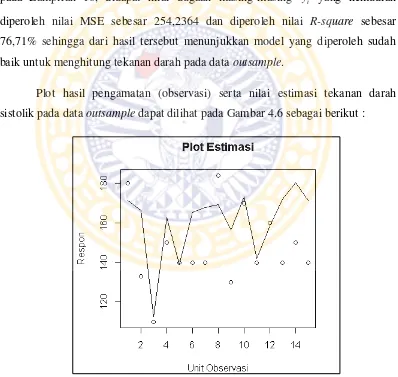
Diastolik Data Insample ... 68 4.6 Plot Observasi dan Estimasi pada Tekanan Darah

Sistolik Data Outsample ... 69 4.7 Plot Observasi dan Estimasi pada Tekanan Darah

DAFTAR LAMPIRAN

Nomor Judul

1 Data Insample Tekanan Darah Pasien dan Variabel Prediktor RSU Haji Surabaya

2 Data Outsample Tekanan Darah Pasien dan Variabel Prediktor RSU Haji Surabaya

3 Program Uji Korelasi Pearson

4 Program Identifikasi Kombiasi Orde Respon, Jumlah Knot, Titik Knot, dan Lambda Optimal Setiap Prediktor

5 Program Estimasi Model Regresi Semiparametrik Birespon Berdasarkan Estimator Penalized Spline (Tanpa Pembobot)

6 Program Uji Glesjer dan Penentuan Matrik Pembobot

7 Program Estimasi Model Regresi Semiparametrik Birespon Berdasarkan Estimator Penalized Spline (dengan Pembobot)

8 Program Estimasi Outsample Model Regresi Semiparametrik Birespon Berdasarkan Estimator Penalized Spline

9 Output Uji Korelasi Pearson

10 Output Indentifikasi Kombiasi Orde Respon, Jumlah Knot, Titik Knot, dan Lambda Optimal Prediktor Ke-1

11 Output Indentifikasi Kombiasi Orde Respon, Jumlah Knot, Titik Knot, dan Lambda Optimal Prediktor Ke-2

12 Output Indentifikasi Kombiasi Orde Respon, Jumlah Knot, Titik Knot, dan Lambda Optimal Prediktor Ke-3

13 Output Estimasi Model Regresi Semiparametrik Birespon Berdasarkan Estimator Penalized Spline (Tanpa Pembobot)

14 Output Uji Glesjer dan Penentuan Matrik Pembobot

BAB I

PENDAHULUAN

1.1 Latar Belakang

Analisis regresi merupakan suatu metode dalam ilmu statistika yang menganalisis pola hubungan secara fungsional antara variabel respon dan variabel prediktor melalui estimasi kurva. Terdapat tiga macam pendekatan dalam mengestimasi fungsi regresi, yaitu pendekatan parametrik, nonparametrik, dan semiparametrik. Pendekatan parametrik digunakan apabila sudah mengasumsikan bentuk tertentu dari pola hubungan antara variabel respon dan variabel prediktor serta terdapat informasi, pengetahuan maupun teori masa lalu tentang karakteristik data yang diteliti, sedangkan pendekatan nonparametrik digunakan karena tidak adanya informasi sebelumnya tentang hubungan antara variabel respon dan variabel prediktor (Ricky, 2014) dan data diharapkan mencari sendiri bentuk estimasinya sehingga dapat dikatakan regresi nonparametrik memiliki fleksibilitas yang lebih besar terhadap data yang diteliti. Dalam beberapa kasus di kehidupan nyata sering diketahui pola kurva antara variabel respon dengan beberapa variabel prediktor karena terdapat informasi sebelumnya tentang hubungan antara keduanya, namun tidak dengan variabel prediktor yang lainnya yang belum diketahui pola hubungannya. Solusi untuk mengetahui model fungsi tersebut adalah dengan mengestimasi fungsi regresi menggunakan pendekatan regresi semiparametrik. Pendekatan regresi semiparametrik digunakan jika pola hubungan antara sekumpulan variabel prediktor terhadap variabel respon ada pola yang diketahui dan ada pula yang pola hubungannya tidak diketahui (Budiantara, 2012).

kelebihan yang berbeda (Wibowo, dkk., 2013). Pendekatan regresi nonparametrik yang cukup populer adalah adalah spline (Andriani, et al., 2015), karena memberikan fleksibilitas yang lebih baik terhadap karakteristik suatu fungsi atau data dengan mulus (smooth) (Ricky, 2014). Keuntugan lain yang dimiliki oleh spline adalah mampu menjelaskan perubahan pola perilaku fungsi dalam sub-interval tertentu dan dapat digunakan untuk mengatasi atau mengurangi pola data yang mengalami peningkatan tajam dengan bantuan titik knot. Griggs (2013) meyatakan bahwa penalized spline lebih cocok digunakan terhadap data yang mengalami peningkatan tajam karena penalized spline membebankan penalty pada komponen potongan polinomial (piece wise polinomial) yang memiliki sifat tersegmen yang kontinu sehingga lebih cocok digunakan untuk lebih mengoptimalkan. Penalized spline adalah salah satu bentuk estimator spline yang diperoleh dengan meminimumkan Penalized Least Square (PLS). Untuk itu ada beberapa hal yang perlu dipertimbangkan, yaitu titik dan jumlah knot, fungsi dasar spline, serta derajat bebas dan matrik penalty (Montoya, et al., 2014).

Beberapa penelitian terkait regresi berdasarkan estimator penalized spline antara lain adalah Andriani, et al. (2015) dan Pütz (2016), kedua penelitian tersebut menggunakan pendekatan nonparametrik dalam mengestimasi model, namun pada kehidupan nyata sering kali ditemukan kasus dengan adanya pola hubungan yang diketahui antara sekumpulan variabel prediktor terhadap variabel respon dan ada pula pola yang tidak dapat diketahui sehingga diperlukan pengembangan penelitian yaitu dengan pendekatan regresi semiparametrik. Penelitian terkait model regresi semiparametrik berdasarkan estimator penalized spline salah satunya adalah Salam (2013), yang mengestimasi model regresi semiparametrik berdasarkan estimator penalized spline dengan menggunakan metode likelihood maximum penalized, namun hanya menggunakan satu variabel respon.

multirespon berdasarkan estimator spline truncated telah banyak dilakukan, antara lain adalah Oktaviana (2011), Setyawan (2011), Juliandari (2014) dan Wulandari (2014), namun penelitian yang menyangkut estimator penalized spline dengan respon lebih dari satu belum banyak dikembangkan. Tujuan pemodelan regresi multirespon adalah untuk mendapatkan model yang lebih baik dari pemodelan respon tunggal, dengan model regresi yang tidak hanya mempertimbangkan pengaruh prediktor terhadap respon, akan tetapi juga hubungan antar respon (Fernandes, 2014). Penelitian dengan menggunakan regresi birespon berdasarkan estimator penalized spline antara lain adalah Yolandika (2011) yaitu dengan menggunakan pendekatan noparametrik, namun seperti halnya permasalahan pada regresi dengan respon tunggal maka diperlukan pengembangan penelitian yaitu dengan pendekatan regresi semiparametrik. Selain itu, terdapat penelitian dari Chamidah dan Eridani (2015) mengenai regresi semiparametrik birespon berdasarkan estimator penalized spline, penelitian tersebut menggunakan satu variabel prediktor pada komponen parametrik dan satu variabel prediktor pula pada komponen nonparametrik sedangkan pada sebagian besar kasus dalam kehidupan nyata variabel respon tidak hanya dipengaruhi oleh satu variabel prediktor saja, jika hanya menggunakan satu variabel saja maka kemungkinan variabel prediktor tersebut belum dapat mewakili faktor yang mempengaruhi variabel respon yang diteliti.

statistika yang digunakan dalam penelitian adalah Open Source Software R (OSS-R).

Teori yang dibahas mengenai estimasi model regresi semiparametrik birespon multiprediktor berdasarkan estimator penalized spline diterapkan pada data tekanan darah dengan variabel respon pertama yaitu tekanan darah sistolik dan variabel respon kedua yaitu tekanan darah diastolik. Tekanan darah sangatlah penting karena merupakan kekuatan pendorong bagi darah agar dapat beredar ke seluruh tubuh untuk memberikan darah segar yang mengandung oksigen dan nutrisi ke organ-organ tubuh. Tekanan darah bervariasi untuk berbagai alasan, seperti usia, berat badan, kandungan lemak darah, dan lain sebagainya. Faktor resiko tekanan darah yang tinggi diantaranya adalah hipertensi, stroke, dan jantung koroner. Penyakit-penyakit tersebut termasuk dalam penyakit tidak menular yang saat ini sangat mengkhawatirkan dan telah menjadi masalah utama dalam kesehatan masyarakat yang ada di Indonesia maupun di beberapa negara yang ada di dunia. Sehingga perlu adanya pengawasan yang lebih dalam dunia kesehatan terhadap tingkat tekanan darah. Penelitian yang membahas mengenai tekanan darah sistolik dan diastolik salah satunya adalah Mersi dan Andrianto (2016) menganalisis pengaruh LDL terhadap tekanan darah dengan pendekatan regresi nonparametrik berdasarkan estimator penalized spline, namun penelitian yang dilakukan masih menggunakan analisis unirespon yaitu dengan memodelkan masing-masing tekanan darah sistolik dan diastolik terhadap LDL dan hanya melibatkan satu variabel prediktor kompoen nonparametrik. Persoalan tersebut melibatkan dua variabel respon dan diantara keduanya terdapat korelasi yang kuat sehingga untuk selanjutya membutuhkan pemodelan dengan analisis regresi semiparameterik birespon multiprediktor.

1.2 Rumusan Masalah

Berdasarkan latar belakang, maka pemasalahan yang dibahas dalam skripsi ini adalah :

1. Bagaimana mengestimasi model regresi semiparametrik birespon multiprediktor berdasarkan estimator penalized spline?

2. Bagaimana membuat algoritma dan program untuk mengestimasi regresi semiparametrik birespon multiprediktor berdasarkan estimator penalized spline menggunakan software OSS-R yang diterapkan pada data riil atau data bangkitan?

1.3 Tujuan Penelitian

Berdasarkan rumusan masalah, maka tujuan penelitian dalam skripsi ini adalah :

1. Mengestimasi model regresi semiparametrik birespon multiprediktor berdasarkan estimator penalized spline.

2. Membuat algoritma dan program untuk mengestimasi regresi semiparametrik birespon multiprediktor berdasarkan estimator penalized spline menggunakan software OSS-R yang diterapkan pada data riil atau data bangkitan.

1.4 Manfaat Penelitian

Berdasarkan latar belakang, maka manfaat penelitian dalam skripsi ini adalah :

1. Menambah wawasan dan pengetahuan tentang estimasi model regresi semiparametrik birespon multiprediktor berdasarkan estimator penalized spline.

spline menggunakan software OSS-R dan penerapan pada data riil atau data bangkitan.

1.5 Batasan Masalah

BAB II

TINJAUAN PUSTAKA

Pada bab ini akan dibahas mengenai beberapa tinjauan pustaka yang akan digunakan untuk pembahasan pada bab-bab berikutnya. Pada BAB I sebelumnya telah diuraikan tentang tujuan dari penulisan skripsi ini. Berdasarkan tujuan tersebut maka akan dibahas mengenai matrik, regresi semiparametrik, regresi birespon, regresi multiprediktor, estimator penalized spline, kuantil, pemilihan titik knot optimal, pemilihan jumlah titik knot optimal, model semiparametrik berdasarkan estimator penalized spline dengan satu variabel respon, model semiparametrik birespon berdasarkan estimator penalized spline dengan satu variabel prediktor, kasus heteroskedastisitas dan homoskedastisitas, estimasi parameter Weighted Least Square (WLS), uji glesjer, uji korelasi pearson, OSS-R.

2.1 Aljabar Matrik

Matrik adalah susunan bilangan atau variabel dalam bentuk persegi panjang atau persegi. Bilangan-bilangan dalam susunan tersebut dinamakan entri matrik. Ukuran matrik dijelaskan dengan menyatakan banyaknya baris dan banyaknya kolom yang terdapat dalam matrik tersebut, sehingga suatu matrik dengan m baris dan n kolom dikatakan sebagai matrik dengan ukuran (ordo) m x n. Bentuk umum matrik yang berukuran m x n adalah sebagai berikut:

11 12 1

sebuah elemen dari matrik A. Beberapa operasi pada matrik adalah sebagai berikut:

a. Matrik Partisi

Partisi matrik A menjadi empat submatrik (persegi atau persegi panjang) sebagai berikut:

11 12

dipartisi sehingga submatrik conformal, maka perkalian AB dapat dinyatakan sebagai berikut:

11 12 11 12

Apabila B diganti oleh vektor b yang dipartisi menjadi dua himpunan dari elemen-elemen, jika A dipartisi menjadi dua himpunan dari kolom-kolom, maka menjadi

b. Perkalian

Jika A adalah matrik berordo m x n dan B adalah matrik berordo n x p. Hasil

dua buah matrik dapat terjadi jika dan hanya jika banyaknya kolom dari matrik A

sama dengan banyaknya baris dari matrik B. Perkalian yang melibatkan vektor mengikuti aturan yang sama untuk matrik. Misalkan A adalah matrik berordo mxn,vektor b berdimensi px1, vektor c berdimensi px1. Kemudian Ab adalah vektor kolom berdimensi nx1, T

T

bc adalah matrik berukuran pxp. karena b cT adalah jumlah perkalian berukuran (1 x 1), maka sama dengan T

Jika j adalah vektor berdimensi nx1 yang semua elemennya 1, maka

(

)

c. Transpose

Jika matrik A=

( )

a_ij , maka transpose dari A didefinisikan sebagai

A . Notasi ini menunjukkan bahwa elemen pada baris ke-i dan kolom ke-j dari matrik A merupakan baris j dan kolom i dari matrik AT. Jika matrik A berordo mxn. Jika A adalah sembarang matrik, maka

( )

AT T =A. Salah satu sifat transpose yang digunakan adalah

( )

AB T =B AT T dengan syarat matrik

A dan B masing-masing merupakan matrik yang memenuhi sifat perkalian. Jika A

adalah matrik partisi 11 12

21 22

A A , maka transpose matrik partisi

11 12 vektor partisi 1

sebuah matrik B berukuran nxn sedemikian hingga AB = I disebut invers kanan dari A dengan I merupakan matrik identitas. Jika AB = BA = I maka matrik B

disebut invers kanan dan invers kiri dari matrik A dan matrik A dikatakan invertibel. Jika matrik A dan B masing-masing merupakan matrik yang invertibel dan AB terdefinisi maka

( )

AB −1=B A−1 −1. Jika A adalah matrik simetri dan nonsingular dan dipartisi menjadi 11 12

21 22

sedemikian hingga, maka 1 11

Trace A=

( )

a_ij berukuran nxn adalah fungsi skalar yang didefinisikan sebagai

jumlah dari elemen-elemen diagonal dari A, yaitu tr(A)

1

f. Turunan Fungsi Vektor dan Matrik

Misalkan T T

dari suatu konstanta,

1

g. Matrik Kovariansi

Variansi σ σ₁2, ₂2,...,σ2_p dari y y₁, ₂,...,y_p dan kovariansi σ_ij untuk semua i≠ j merupakan elemen-elemen dari matrik kovariansi yang dinotasikan dengan Σ yaitu

Baris ke-i dariΣ mengandung variansi y_idan kovariansi y_idengan tiap variabel y yang lain. Supaya konsisten dengan notasi σ_ijdigunakan σ_ii =σ_i2, i=1, 2,...,p untuk varians. Varians terdapat pada diagonal Σ, dan kovariansi berada diselain diagonal tersebut.

2.2 Pendekatan Regresi

2.2.1 Regresi Parametrik

Regresi parametrik digunakan untuk mengetahui pola hubungan antara variabel respon dengan variabel prediktor yang diasumsikan telah diketahui bentuk fungsinya. Salah satu bentuk regresi parametrik dapat dinyatakan sebagai model regresi linier berganda yang secara umum dapat dituliskan dalam notasi matrik sebagai berikut :

i i i

y = X β ε+

dengan ymerupakan vektor dari variabel respon yang berukuran nx1, X merupakan matriks dari variabel prediktor yang diasumsikan tetap berukuran nxp,

βmerupakan vektor parameter yang berukuran px1, dan ε adalah residual acak,

dengan 2

~IIDN(0, )

ε σ .

(Ruppert, et al., 2003)

2.2.2 Regresi Nonparametrik

Regresi nonparametrik merupakan salah satu pendekatan dalam analisis regresi yang digunakan apabila kurva regresinya tidak diasumsikan memiliki bentuk tertentu. Dalam regresi nonparametrik, kurva regresi hanya diasumsikan halus (smooth), sehingga pendekatan regresi nonparametrik memiliki fleksibilitas yang tinggi karena data diharapkan mencari sendiri bentuk estimasi kurva regresi tanpa dipengaruhi oleh faktor subyektivitas peneliti.

Jika diberikan pasangan data

(

t y_i, _i

)

dengan i =1, 2,...,n dan pola hubungan antara variabel response dengan variabel prediktor tidak diketahui bentuknya, maka dapat digunakan pendekatan regresi nonparametrik. Secara umum, model regresi nonparametrik adalah

( )

i i i

y = f t + ε , i=1, 2,...,n

dengan y_i merupakan variabel response, f t

( )

_i adalah persamaan kurva regresi yang tidak diasumsikan mengikuti bentuk tertentu dengan t_i sebagai variabel prediktor, sedangkan ε_i adalah error berdistribusi normal independen dengan (2.1)

mean 0 dan variansi σ2 (Eubank, 1999). Terdapat beberapa teknik untuk mengestimasi kurva regresi dalam regresi nonparametrik, diantaranya yaitu regresi spline, kernel, deret fourir dan lain-lain.

2.2.3 Pendekatan Regresi Semiparametrik

Pendekatan regresi tidak hanya parametrik dan nonparametrik, terdapat pula golongan statistikawan, yang memandang kurva regresi dapat diklasifikasikan kedalam dua komponen, yaitu komponen parametrik (bentuk fungsinya diketahui) dan komponen nonparametrik (bentuk fungsinya tidak diketahui). Pandangan ini memberikan pendekatan regresi semiparametrik, (Budiantara, 2012).

Analisis regresi semiparametrik merupakan gabungan dari regresi parametrik dan regresi nonparametrik, sehingga estimasi model semiparametrik ekuivalen dengan estimasi parameter-parameter pada komponen parametrik dan estimasi kurva pada komponen nonparametrik. Misalkan terdapat data berpasangan

(

y_i, , x t_{i i}

)

, dan hubungan antara y_i, x_i, dan t_i diasumsikan mengikuti model regresi semiparametrik sebagai berikut :

( )

i Xi f i i

Y = β + t +ε dengan i=1, 2,...,n

dengan Y_iadalah variabel respon pada pengamatan ke −i, X_i adalah komponen parametrik, f t( )_i adalah fungsi regresi nonparametrik dan ε adalah residual acak, dengan 2

~IIDN(0, )

ε σ .

(Ruppert, et al., 2003)

2.3 Regresi Birepson

Regresi birespon merupakan suatu analisis model regresi yang melibatkan dua variabel respon dalam estimasi data. Secara umum model regresi birespon dapat dinyatakan dalam persamaan (2.4) sebagai berikut:

( ) ,

i = ti +εi

Y f

   dengan i=1, 2,...,n

(2.3)

denganY_ij =(Y , Y_i(1) _i(2))T adalah dua respon yang saling berkorelasi dan

(1) (1)

( )t_i =(f ( ),t_i f ( ))t_i T

f

 adalah fungsi regresi dalam model, dan

(1) (2)

( , )T

i i i

ε = ε ε



adalah residual pengukuran dengan mean 0

 dan variansi

∑

i , dengan matrik

variansi-covariansi sebagai berikut :

(1)

(Welsh and Yee, 2006)

2.4 Regresi Multiprediktor

Model aditif mempunyai variabel respon y yang bergantung pada penjumlahan beberapa fungsi dari variabel prediktor x, sehingga model regresi multiprediktor dapat dituliskan sebagai berikut :

1

dengan ε_i adalah residual acak yang diasumsikan berdistribusi identik dan independen dengan mean nol dan variansi σ2

.

(Wood and Agustin, 2002)

2.5 Estimator Penalized Spline Pada Regresi Nonparametrik

Estimator penalized spline dengan multiprediktor menggunakan model aditif dengan variabel respon y yang bergantung pada penjumlahan beberapa variabel prediktor x, dengan mengikuti bentuk model sebagai berikut :

( )

dengan f_j adalah fungsi regresi prada prediktor ke-j yang belum diketahui bentuknya, yi adalah variabel respon pengamatan ke−i, xji adalah variabel

prediktor ke-j pada pengamatan ke−i, dan ε_i adalah error random dengan mean 0 dan variansi 2

I σ .

Menurut Ruppert (2003), estimator penalized spline adalah suatu fungsi f yang dinyatakan sebagai berikut :

0 merupakan suatu fungsi yang didefinisikan sebagai berikut :

(

( )

)

p adalah orde polinomial, k_j adalah banyaknya knot untuk prediktor ke-j, dan h adalah indeks fungsi basis berupa bilangan bulat positif, dan

(

)

(

( )

)

( )

Penalized spline merupakan potongan-potongan polinomial dengan segmen-segmen yang berbeda digabungkan bersama menjadi titik knot

1, 2, , k

ξ ξ … ξ . Pada penalized spline, titik knot ditentukan berdasarkan sampel kuantil dari nilai unique (tunggal) suatu variabel indepeden

{ }

1

n i _i

x ₌ . Fungsi regresi nonparametrik degan orde p _{dan titik-titik knots} ξ ξ1, 2,…, ξk dinyatakan dalam

persamaan (2.6) sebagai berikut :

(2.6)

(2.7)

0 1 ( )

dari fungsi pada persamaan (2.9) dapat dirubah menjadi bentuk matrik seperti persamaan (2.10) sehingga didapatkan model linier campuran

( )

dan estimator penalized spline dapat dituliskan sebagai ˆ

ˆ y=Xβ

Estimator penalized spline diperoleh dengan meminimumkan fungsi Penalized Least Square (PLS) yang merupakan ukuran standart dari kesesuaian terhadap

data yang terdiri dari least square

( )

1

dan ukuran kemulusan

alami 2_{( )}

∑

, yang dituliskan dalam persamaan (2.12) sebagai berikut :

( )

dengan λ_j adalah suatu parameter penghalus dari variabel prediktor ke-j, k adalah jumlah knot, dan p adalah orde polinomial. Langkah-langkah selanjutnya untuk meminimumkan fungsi PLS adalah sebagai berikut :

1. Mengubah 1 2

∑

kedalam bentuk matrik

2. Mengubah 2_{( )}

∑

kedalam bentuk matrik

2 2 2 2

Jika diasumsikan terdapat matrik D_j yang merupakan suatu matrik diagonal, didefinisikan sebagai berikut :

11

∑

dituliskan dalam bentuk matrik, sebagai

berikut :

Matrik fungsi PLS yang diperoleh dari menggabungkan fungsi persamaan dapat ditulis sebagai berikut :

Nilai 𝜷𝜷� dapat diperoleh dengan meminimumkan persamaan L. Syarat perlu agar persamaan L minimum adalah turunan pertama sama dengan nol, L 0

β ∂

=

∂ ,

sehingga diperoleh persamaan (2.17) sebagai berikut :

1

 menghasilkan bentuk estimator penalized

spline f x_j( _j) dari variabel prediktor ke-j menjadi persamaan (2.18) sebagai berikut :

(Ruppert, et al., 2003)

2.6 Kuantil

Ukuran lokasi yang menjelaskan atau menunjukkan lokasi sebagian data relatif terhadap keseluruhan data disebut fraktil atau kuantil. Menurut Walpole (1997), kuantil adalah nilai-nilai yang dibawahnya terdapat sejumlah pecahan atau persentase tertentu dari seluruh pengamatan. Beberapa kuantil yang sering dibahas diantaranya adalah persentil, desil, dan kuartil.

Nilai-nilai yang membagi segugus pengamatan menjadi 100 bagian yang sama disebut persentil dan umumnya dinotasikan dengan P P₁, ₂,,P₉₉. Notasi P₁ berarti bahwa 1% dari seluruh data terletak di bawah P₁, 2% terletak di bawah P₂ dan seterusnya sampai P₉₉ yang menyatakan bahwa 99% terletak di bawah P₉₉. Nilai-nilai yang membagi jajaran data menjadi 10 bagian yang sama dinamakan desil. Nilai-nilai tersebut dinotasikan dengan D D₁, ₂,,D₉ yang berarti bahwa 10% data terletak di bawah D₁, 20% terletak di bawah D₂, dan seterusnya sampai

9

D yang berarti bahwa 90% data terletak di bawah D₉. Nilai-nilai yang membagi data menjadi 4 bagian yang sama disebut kuartil dan dinotasikan dengan

(2.17)

𝑄𝑄1,𝑄𝑄2,𝑄𝑄3. Notasi 𝑄𝑄1 berarti bahwa 25% data terletak di bawah 𝑄𝑄1, 50% data

terletak di bawah 𝑄𝑄2, dan 75% data terletak di bawah 𝑄𝑄3. Persentil ke-50, desil

kelima, dan kuartil kedua dari suatu data dapat pula disebut median karena median merupakan nilai-nilai yang membagi data menjadi 2 bagian yang sama.

(Walpole, et al., 2012).

2.7 Pemilihan Titik Knot Optimal

Parameter λ merupakan pengontrol keseimbangan antara kemulusan fungsi terhadap data. Jika λ _{besar maka estimasi fungsi yang diperoleh akan} semakin halus, dan sebaiknya jika λ _{kecil maka estimasi fungsi yang diperoleh} akan semakin kasar. Salah satu metode yang digunakan sebagai kriteria untuk menentukan parameter penghalus λ optimum adalah dengan menentukan nilai Generalized Cross Validation (GCV) yang minimum. Metode GCV dapat didefinisikan sebagai berikut :

1 2

(Ruppert, et al., 2003)

2.8 Pemilihan Jumlah Titik Knot Optimal

Pemilihan jumlah dan titik knot optimal perlu dilakukan untuk mengestimasi fungsi spline. Jumlah knot (K) merupakan banyaknya titik knot atau banyaknya titik perubahan perilaku fungsi pada interval yang berlainan. Ruppert (2002) menyatakan bahwa titik knot terletak pada sampel kuantil dari nilai-nilai unique (tunggal) variabel prediktor

{ }

t_i n_i=1. Salah satu metode yang dapat digunakan untuk menentukan jumlah dan lokasi titik knot optimal adalah metode full-search. Algoritma dari metode full-search yang didasarkan pada kriteria Generalized Cross Validation (GCV) adalah:

a. Membandingkan nilai GCV

( )

λ pada K =1 dan K =2.

i. Apabila nilai GCV

( )

λ pada K =1 lebih kecil dari nilai GCV

( )

λ pada

2

K = , maka algoritma berhenti dengan memilih jumlah knot optimal yaitu K =1.

ii. Apabila nilai GCV

( )

λ pada K =1 lebih besar dari nilai GCV

( )

λ pada

2

K = , maka algoritma ini akan dilanjutkan dengan membandingkan nilai GCV

( )

λ untuk K =2 dan K =3.

b. Membandingkan nilai GCV

( )

λ pada K =2 dan K =3.

i. Apabila nilai GCV

( )

λ pada K =2 lebih kecil dari nilai GCV

( )

λ pada 3

K = , maka algoritma berhenti dengan memilih jumlah knot optimal yaitu K =2.

ii. Apabila nilai GCV

( )

λ pada K =2 lebih besar dari nilai GCV

( )

λ pada 3

K = , maka algoritma ini akan dilanjutkan dengan membandingkan nilai GCV

( )

λ untuk K =3 dan K =4.

Membandingkan nilai GCV

( )

λ pada K =3 dan K =4 yang dilakukan dengan cara yang sama seperti di atas, demikian seterusnya hingga diperoleh nilai GCV

( )

λ yang minimum.

(Ruppert, et al., 2003)

2.9 Model Semiparametrik Berdasarkan Estimator Penalized Spline dengan Satu Variabel Respon

Model regresi semiparametrik berdasarkan estimator penalized spline, diberikan dalam bentuk model sebagai berikut :

( )

T

= β f Z+ +

y X ε

(

0, 1, 2,...,

)

T k

β β β β =

β merupakan vektor (k+1)×1 untuk parameter yang tidak diketahui, f adalah vektor dari fungsi regresi yang bentuk kurvanya tidak diketahui atau merupakan fungsi yang mulus atau dengan kata lain f atau f z( )_i licin (smooth) yaitu _{0 1}

1

ε adalah vektor dari error random independen dengan mean nol dan varians σ2

. (Salam, 2013)

2.10 Model Semiparametrik Birespon Berdasarkan Estimator Penalized Spline dengan Satu Variabel Prediktor

Model regresi semiparametrik birespon berdasarkan estimator penalized spline, diberikan n data observasi (y_i1,y_i2, , )x t_{i i} dengan y_ij menunjukkan observasi ke−i pada respon ke−j memeuhi model regresi semiparametrik multirespon sebagai berikut :

( ) , 1, 2,...,

 berturut-turut adalah respon dan error untuk

observasi ke−i. ( )g t_i

 merupakan fungsi dari rata-rata populasi yang diasumsikan

smooth. XT_i =(1 x_i1 ... x_iq)T

   adalah komponen parametrik dari fungsi yang

diasumsikan diketahui untuk observasi ke−i dan a=

(

a a₀, ,...,₁ a_q

)

T

 yang

merupakan koefisien dari variabel prediktor parametrik. Persamaan (2.20) mengandung XT_ia

 sebagai komponen parametrik dan ( )g ti

 merupakan

komponen nonparametik. Berdasarkan persamaan (2.20), fungsi g t( )_i

 diestimasi

Estimasi α dan β dengan meminimumkan kriteria Penalized Least Square (PLS) sebagai berikut :

2

dengan λ adalah parameter penghalus, dan K adalah titik knot dan p merupakan orde polinomial.

(Chamidah and Eridani, 2015)

2.11 Kasus Homoskedastisitas dan Heteroskedastisitas

Salah satu asumsi dalam analisis regresi adalah homoskedastisitas yang berarti bahwa variansi dari setiap ε_i tidak tergantung pada variabel pedictor. Variansi dari setiap ε_i bernilai sama untuk semua variabel pedictor, sehingga nilai dari variansi residual bersifat konstan atau var( )ε_i =E(ε_i2)=σ2,

1, 2, 3,...,

i= n. Pelanggaran terhadap asumsi ini disebut heteroskedastisitas yang berarti bahwa variansi dari setiap error bersifat tidak konstan. Dalam analisis regresi, heteroskedastisitas dinyatakan sebagai berikut:

2

i i i

var_ε x _= σ , i=1, 2,,n

Persamaan (2.18) juga dapat dinotasikan dalam model di bawah ini.

2

2.12 Estimasi Parameter Weighted Least Square (WLS)

Untuk mengilustrasikan metode Weighted Least Square (WLS), digunakan model dua variabel. Metode kuadrat terkecil tanpa pembobot yaitu Ordinary Least Square (OLS) mengasumsikan bahwa terdapat variansi konstan dalam error yang pada umumnya disebut keadaan homoskedastisitas. Untuk mengestimasi parameter fungsi yang diminimumkan yakni :

(

) (

T

)

T

y y

ε ε = − βX − βX

  _{   }

sedangkan metode WLS meminimumkan jumlah kuadrat error terboboti dapat digunakan ketika asumsi variansi konstan dalam error dilanggar atau dalam kata lain disebut heteroskedastisitas (Greene, 2003) yang dirumuskan sebagai berikut :

(

) (

T

)

matrik variansi-kovariansi dari ε

 atau y_ dengan syarat X, yang dinotasikan

Persamaan (2.18) selanjutnya diturunkan terhadap β

 sedemikian sehingga

diperoleh estimator WLS sebagai berikut:

1

( T )− T y

β = X WX X W

 

Pada metode OLS, pembobot W merupakan matrik identitas.

(Maziyya dkk.,2015)

2.13 Uji Glesjer

Untuk mendeteksi terjadinya heteroskedastisitas bisa dilakukan dengan beberapa uji diantaranya Uji korelasi Rank-Spearmen, Uji Park, Uji Glesjer, Uji Goldfeld-Quandt (Gujarati, 2004). Uji glesjer merupakan pengujian yang sangat popular untuk melihat terjadinya gejala heteroskedastisitas. Uji glesjer dilakukan dengan cara meregresikan harga mutlak residual dengan variabel prediktornya.

(2.24)

(2.25)

( )

i g xi i

ε = +ε

Hipotesis untuk uji glesjer adalah sebagai berikut :

2 2 2 2

0: 1 2 ... n

H σ =σ = =σ =σ

1:

H minimal ada satu σ_i2 ≠σ2, dengan i=1, 2,...,n Statistik uji :

(

)

(

)

akan terjadi kasus heteroskedastisitas jika H₀ ditolak yakni terdapat minimal satu

2 2

i

σ ≠σ .

2.14 Uji Korelasi Pearson

Koefisien korelasi merupakan suatu nilai yang mengukur keeratan hubungan antara dua variabel. Koefisien korelasi yang dihitung untuk data populasi dinotasikan dengan ρ sedangkan koefisien korelasi yang dihitung untuk data sampel dinotasikan dengan r. Nilai koefisien korelasi dapat dihitung dengan menggunakan Pearson Product Moment pada persamaan (2.28) sebagai berikut:

1 disebut dengan korelasi linier positif sempurna. Apabila nilai r = −1 maka dinamakan korelasi linier negatif sempurna, sedangkan apabila nilai r =0 menunjukkan bahwa tidak terdapat korelasi diantara kedua variabel tersebut.

Pengujian koefisien korelasi dilakukan dengan menggunakan hipotesis nol yaitu kedua variabel tidak memiliki hubungan linier (ρ =0) dan hipotesis alternatif (H1) adalah ρ >0, ρ <0 atau ρ ≠0. Konversi nilai koefisien korelasi

menjadi distribusi t adalah

2

dengan derajat bebas n−2, n merupakan banyaknya pasangan data dari variabel-variabel yang diduga berkorelasi dan r merupakan nilai koefisien korelasi yang diperoleh berdasarkan persamaan (2.28). Nilai statistik uji t yang telah diperoleh berdasarkan persamaan (2.29) selanjutnya dibandingkan dengan nilai t tabel. Apabila nilai t hitung kurang dari t tabel maka H0 diterima dan dapat disimpulkan

bahwa tidak terdapat korelasi linier diantara kedua variabel, demikian sebaliknya. (Rasmussen, 2006)

2.15 Open Source Software R (OSS-R)

R merupakan salah satu software yang sering digunakan dalam statistika dan termasuk dalam kategori Open Source Software (OSS) untuk memanipulasi data, simulasi, kalkulasi, dan peragaan graphic. Bahasa R berbasis bahasa S yang (2.28)

dibangun di Bell Laboratories di tahun 80-an sehingga syntax R memiliki perbedaan yang tidak terlalu banyak atau hampir identik jika dibandingkan dengan syntax pada software S-plus (Sawitzki, 2009). R mempunyai beberapa kelebihan dan fitur-fitur yang canggih dan berguna, diantaranya :

a. Efektif dalam pengolahan data dan fasilitas penyimpanan. Ukuran file yang disimpan jauh lebih kecil dibanding software lainnya.

b. Lengkap dalam perhitungan array.

c. Lengkap dan terdiri dari koleksi tools statistik yang terintegrasi untuk analisis data, diantaranya, mulai statistik deskriptif, fungsi probabilitas, berbagai macam uji statistik, hingga time series.

d. Tampilan grafik yang menarik dan fleksibel ataupun costumized.

e. Dapat dikembangkan sesuai keperluan dan kebutuhan dan sifatnya yang terbuka, setiap orang dapat menambahkan fitur-fitur tambahan dalam bentuk paket ke dalam software R.

Software R sangat cocok digunakan untuk riset, baik statistik, ekonomi, komputasi numerik, dan pemrograman komputer (Didi, 2014). Beberapa perintah internal yang digunakan dalam OSS-R adalah sebagai berikut:

1. function( ), merupakan perintah untuk menunjukkan kumpulan dari beberapa fungsi yang digunakan dalam program. Fungsi dipanggil dengan format nama fungsi( daftar argumen ).

2. length( ), merupakan perintah yang digunakan untuk menghitung banyaknya data. Misalkan terdapat perintah length(vector), maka akan diperoleh hasil yaitu panjang dari vector tersebut.

3. plot( ), digunakan untuk membuat plot data. Beberapa penggunaan perintah ini diantaranya:

a. plot(X,Y) berarti bahwa akan dibuat plot data berupa titik dengan sumbu datar X dan sumbu tegak Y.

b. plot(X,Y,type=”l”) memberikan hasil plot bertipe garis.

c. plot(X,Y,type=”b”) memberikan hasil plot bertipe garis dan titik.

5. matrix(a,b,c), merupakan perintah yang digunakan untuk membentuk suatu matrik berukuran b c× dengan elemen a.

6. print( ), digunakan untuk menampilkan hasil atau output dari program. 7. cat(“…”), merupakan perintah untuk menuliskan kemudian menampilkan

argumen dalam bentuk karakter.

8. for( ), merupakan perintah yang digunakan untuk mengulang satu blok pernyataan berulang kali hingga memenuhi kondisi yang telah ditentukan. Format penulisan perintah ini adalah for( kondisi ) { pernyataan }.

9. repeat( ), hampir mirip dengan for( ), apabila kondisi sudah terpenuhi maka proses pengulangan akan dihentikan. Struktur penulisan statement repeat dalam R yaitu repeat{ command if( kondisi ) break}

10. if-else, merupakan perintah yang digunakan untuk seleksi kondisi. Apabila suatu kondisi bernilai benar, maka pernyataan pertama akan dijalankan, sedangkan apabila kondisi bernilai salah maka pernyataan kedua yang akan dijalankan. Struktur penulisan perintah ini adalah sebagai berikut: if( kondisi ) { pernyataan pertama }

else { pernyataan kedua }

11. solve( A ), digunakan untuk menghitung invers dari suatu matrik A. 12. sum( ), digunakan untuk menghitung jumlah dari keseluruhan data.

13. rbind( ), digunakan untuk menggabungkan suatu matrik atau vektor berdasarkan baris.

14. cbind( ), digunakan untuk menggabungkan suatu matrik atau vektor berdasarkan kolom.

15. diag( a ), merupakan perintah yang digunakan untuk membentuk suatu vektor a menjadi suatu matrik diagonal dengan elemen diagonal utamanya adalah elemen dari a dan elemen yang lain bernilai nol.

16. sort( ), merupakan perintah yang digunakna untuk mengurutkan sekumpulan data.

19. order( ), merupakan perintah untuk menunjukkan vektor posisi data apabila data tersebut diurutkan.

20. var( ), merupakan perintah untuk menghitung nilai varians dari suatu vektor atau matrik variansi-kovariansi dari suatu matrik.

2.16 Tekanan Darah

BAB III

METODOLOGI PENELITIAN

Pada bab ini akan dibahas mengenai langkah-langkah untuk menjawab rumusan masalah yang telah dirumuskan pada BAB I sebelumnya dengan landasan beberapa tinjauan pustaka pada BAB II.

3.1 Mengestimasi Model Regresi Semiparametrik Birespon

Multiprediktor Berdasarkan Estimator Penalized Spline

Langkah-langkah mengestimasi model regresi semiparametrik birespon multiprediktor berdasarkan pendekatan penalized spline adalah sebagai berikut :

1. Mengasumsikan data berpasangan

(

y_i( )r ,x t_vi, _wi

)

dengan i=1, 2,..., n

menyatakan indeks untuk subyek yang diamati, v=1, 2,...,p menyatakan indeks variabel prediktor untuk komponen parametrik, w=1, 2,...,q menyatakan indeks variabel prediktor untuk komponen nonparametrik, dan r =1, 2 menyatakan indeks variabel respon yang memenuhi persamaan model regresi semiparametrik birespon multiprediktor sebagai berikut :

( )

1

( ) 0

1

( ) ,

p q

r

i vi rw wi

v w

r

r rv i

y θ θ x f t ε

= =

= +

∑

+

∑

+

dengan ε( )_ir merupakan error random dengan mean 0 dan variansi Σ_i,

1, 2,...,

i= n.

2. Menggunakan pendekatan berdasarkan estimator spline pada frw(twi) yang merupakan kurva regresi untuk respon ke-r berderajat j dengan titik knot ξ , dan k merupakan banyaknya titik knot sebagai berikut :

(

3. Menguraikan persamaan regresi semiparametrik birespon multiprediktor, kemudian menyatakan dalam suatu matrik sehingga menjadi persamaan (3.3) sebagai berikut :

y= θ + Φ + εX Z

 merupakan parameter

pada komponen parametrik dan

(

)

merupakan parameter pada komponen nonparametrik. 4. Menyatakan X dalam suatu matrik

(1)

5. Menyatakan Z dalam suatu matrik

(1)

6. Menyatakan persamaan (3.3) sehingga menjadi persamaan (3.4) sebagai berikut :

y− θ = ΦX Z

  

dengan mengasumsikan parameter θ

 diketahui nilainya dan memisalkan

Φ

7. Menyatakan estimator penalized spline yang meminimukan fungsi Penalized Least Square (PLS) untuk variabel respon *

8. Mengestimasi model dengan meminimumkan kriteria Penalized Weighted Least Square (PWLS) sebagai berikut :

(

) (

)

dengan Wadalah matrik pembobot yang merupakan invers dari matrik variansi kovariansi error untuk respon 1 dan respon 2. Pengestimasian Φ



dengan mendefferensiasi L terhadapΦ



9. Mengestimasi nilai dugaan θ

 melalui pendefferensiasikan fungsi K

dengan menggunakan metode WLS yang meminimumkan fungsi berikut :

(

)

mengestimasi θ

 dengan mendefferensiasi K terhadapθ_

ˆ ₀

10.Mendapatkan matrik hat untuk komponen parametrik

(

A_parametrik

)

dan untuk komponen nonparametrik

(

A_{nonparametrik}

)

.

11.Menyatakan matrik hat A_semipar =A_parametrik +A_{nonparametrik}untuk dapat menghitung nilai Generalized Cross Validation (GCV).

3.2 Membuat Algoritma dan Program Untuk Mengestimasi Regresi

Semiparametrik Birespon Multiprediktor Berdasarkan Estimator

Penalized Spline yang Diterapkan Pada Data Riil atau Data Bangkitan

3.2.1 Algoritma dan Program untuk Mengestimasi Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline

penyelesaiannya. Langkah-langkah membuat algoritma untuk mengestimasi model adalah sebagai berikut :

1. Menginputkan data berpasangan

(

y_i( )r ,x t_vi, _wi

)

; i=1, 2,..., n; r=1, 2; 1, 2,...,

v= p w=1, 2,...,q .

2. Menguji korelasi antara variabel respon 1 dan respon 2 dengan menggunakan uji korelasi pearson berdasarkan persamaan (2.22).

3. Mengestimasi tanpa matrik pembobot variansi kovariansi (W)dengan langkah-langkah sebagai berikut :

a. Mendefinisikan sampel kuantil dari nilai t_wi yang diurutkan dari nilai terkecil ke nilai yang terbesar untuk pemilihan titik knot.

b. Menentukan kombinasi orde nonparametrik respon 1 dan respon 2, menggerakkan kombinasi vektor knot dan banyak knot dengan menggunakan metode full search serta menggerakkan nilai lambda untuk mendapatkan nilai lambda optimal kemudian dihitung GCV minimum berdasarkan subbab (2.8)

c. Membuat matrik X untuk regresi parametrik dan matrik Zuntuk regresi nonparametrik.

d. Membuat matrik D (matrik diagonal) yang elemen-elemen diagonalnya adalah ( )r

D . Matrik ( )r

D merupakan matrik diagonal pada respon ke-r dengan elemen diagonalnya adalah D D₁, ₂,...,D_q dan D_w merupakan matrik diagonal pada prediktor pada komponen nonparametrik ke-w yang elemen-elemen diagonalnya elemen-elemen

diagonalnya elemen-elemen diagonalnya

11, 22,..., dw 1,dw 1, 11, 22,..., k kw w;

a a a _{+ +} b b b dengan ₁₁, ₂₂,..., _{1, 1} 0

w w d d

a a a _{+ +} = dan

11, 22,..., k kw w 1

b b b = .

f. Melakukan estimasi model tanpa pembobot W _{dengan menggunakan}

parameter smoothing optimum yang telah diperoleh pada langkah b sesuai dengan subbab 2.9.

g. Memperoleh nilai ε

 untuk respon 1 dan respon 2 dari hasil estimasi.

4. Melakukan uji heteroskedastisitas terhadap matrik variansi kovariansi residual yang telah diperoleh dengan menggunakan uji glesjer pada subbab 2.13.

5. Mendefinisikan matrik pembobot W _{berdasarkan hasil pengujian} heteroskedastisitas sesuai hasil pada langkah 4.

6. Mengestimasi dengan menggunakan matrik pembobot variansi kovariansi (W)dengan langkah-langkah sebagai berikut :

a. Menentukan kombinasi orde nonparametrik respon 1 dan respon 2, menggerakkan kombinasi vektor knot dan banyak knot dengan menggunakan metode full search serta menggerakkan nilai lambda untuk mendapatkan nilai lambda optimal kemudian dihitung GCV minimum berdasarkan subbab (2.8)

b. Membuat matrik X untuk regresi parametrik dan matrik Zuntuk regresi nonparametrik.

c. Membuat matrik D (matrik diagonal) yang elemen-elemen diagonalnya adalah D( )r . Matrik D( )r merupakan matrik diagonal pada respon ke-r dengan elemen diagonalnya adalah D D₁, ₂,...,D_q dan D_w merupakan matrik diagonal pada prediktor pada komponen nonparametrik ke-w yang elemen-elemen diagonalnya elemen-elemen

diagonalnya elemen-elemen diagonalnya

11, 22,..., dw 1,dw 1, 11, 22,..., k kw w;

a a a _{+ +} b b b dengan ₁₁, ₂₂,..., _{1, 1} 0

w w d d

a a a _{+ +} = dan

11, 22,..., k kw w 1

b b b = .

d. Menentukan matrik penghalus A dengan menggunakan parameter smoothing optimum yang telah diperoleh pada langkah a.

e. Melakukan estimasi model yang telah didefinisikan pada langkah a. f. Menghitung estimasi y

g. Membuat plot data observasi dan hasil estimasi variabel respon terhadap variabel prediktor.

h. Menghitung nilai Mean Square Error (MSE) dengan menggunakan persamaan (3.6) sebagai berikut:

( )

1

(

) (

)

2

T

MSE= n − _ y−y y−y _  _{ } _{ } 

i. Menghitung nilai R-square dengan menggunakan persamaan (3.7) sebagai berikut:

2

1 JKG R

JKT = −

dengan Jumlah Kuadrat Galat (JKG) =

( ) ( )

y−yˆ T y−yˆ

   

Jumlah Kuadrat Total (JKT) =

(

y− y

) (

T y−y

)

    .

Langkah-langkah dalam merancang agoritma program untuk mengestimasi model regresi semiparametrik birespon multiprediktor berdasarkan pendekatan penalized spline dapat digambarkan dalam diagram alir sebagai berikut:

Gambar 3.1 Diagram Alir Algoritma dan Program

Memperoleh parameter smoothing optimum dengan menggunakan metode full-search berdasarkan kriteria GCV minimum

Input data

(

y_i( )r ,x t_vi, _wi

)

yang memenuhi persamaan (3.1)

Melakukan estimasi tanpa melibatkan pembobot Wdengan menggunakan parameter smoothing optimal yang telah diperoleh

Memperoleh nilai ( )

ˆr

ε



Melakukan uji heteroskedastisitas pada nilai ε



Mendefinisikan pembobot W berdasarkan uji heteroskedastisitas pada nilai ε



Uji korelasi antara y( )1

 dan

( )2

y



Menentukan parameter smoothing dengan melibatkan pembobot W

berdasarkan kriteria GCV minimum

Menghitung nilai parameter dan estimasi y



Membuat plot data observasi dan hasil estimasi y



3.2.2 Penerapan Model Regresi Semiparametrik Birespon Multiprediktor Berdasarkan Estimator Penalized Spline pada Data Riil

a. Data dan Sumber Data

Data yang digunakan dalam skripsi ini adalah data sekunder yang berasal dari rekam medis pasien yang menjalani rawat inap di Rumah Sakit Umum (RSU) Haji Surabaya pada Tahun 2014-2015 sebanyak 65 data. Data tersebut dibagi menjadi 2, 50 data digunakan untuk pemoelan insampel (Lampiran 1) dan 15 data digunakan untuk pemodelan outsample (Lampiran 2).

b. Variabel Penelitian

Variabel-variabel penelitian yang digunakan pada penelitian ini disajikan pada Tabel 3.1 sebagai berikut :

Tabel 3.1 Variabel-variabel Penelitian

No. Variabel Keterangan Variabel Satuan

1 yi(1) Tekanan darah sistolik mmHg

2 yi(2) Tekanan darah diastolik mmHg

3 x1i LDL mg/dL

4 t_1i Berat Badan Kg

5 t2i Usia Tahun

6 t_3i HDL mg/dL

(4.1)

BAB IV

HASIL DAN PEMBAHASAN

4.1 Estimasi Model Regresi Semiparametrik Birespon Multiprediktor

Berdasarkan Penalized Spline

Estimasi penalized spline dalam regresi semiparametrik birespon multiprediktor disajikan dengan menggunakan optimasi Weighted Least Square (WLS). Data berpasangan yang meliputi dua variabel respon

(

(1) (2)

)

,

i i

y y yang diasumsikan memiliki korelasi antar respon dengan p _{variabel prediktor}

1i, 2i,..., pi

x x x yang diketahui pola hubungannya serta q _{variabel prediktor}

1i, 2i,..., qi

t t t yang tidak diketahui bentuk pola hubungannya. Hubungan antara variabel ( )r

i

y , x_pi, dan t_wi mengikuti model regresi semiparametrik birespon multiprediktor sebagai berikut :

( ) ( ) ( menyatakan indeks variabel prediktor untuk komponen parametrik, w=1, 2,...,q menyatakan indeks variabel prediktor untuk komponen nonparametrik, dan

1, 2

r= menyatakan indeks variabel respon. ( )r i

y adalah variabel respon ke-r

observasi ke-i, x_vi merupakan variabel prediktor untuk komponen parametrik ke-v observasi ke-i, t_wi merupakan variabel prediktor untuk komponen nonparametrik ke-w observasi ke-i , dan ε( )r _{sebagai error random.} ε( )r _di asumsikan saling independen yang memiliki mean nol dan variansinya 2

r σ , sedangkan ε(1)

dan ε(2)

(4.5) (4.2)

(4.4) (4.3) Model regresi semiparametrik birespon multiprediktor pada persaman (4.1) dapat dijelaskan sebagai berikut :

( ) ( ) ( ) ( )

Apabila fungsi nonparametrik ( f_rw(t_wi)) didekati dengan fungsi spline dengan orde d_rw dan k_w titik knot maka fungsi tersebut dapat ditulis sebagai berikut :

dengan α_rwj adalah koefisien polinomial bernilai riil, β_rwh adalah koefisien truncated bernilai riil, dan ₁, ₂,...,

w

w w wk

ξ ξ ξ adalah titik-titik knot yang memperlihatkan perubahan perilaku dari fungsi pada sub-sub interval yang berbeda tergantung pada data. Model regresi semiparametrik birespon multiprediktor setelah dilakukan pendekatan fungsi spline dengan orde d_rw dan k_w titik knot maka persamaan (4.1) dapat ditulis menjadi persamaan sebagai berikut :

( ) ( ) ( ) ( ) ( )

(4.6) respon 1 dapat dijelaskan dengan persamaan berikut :

11

(4.12)

(4.13) Persamaan diatas dapat pula ditulis dalam bentuk matriks sebagai berikut :

(1) _{(1) (1) (1) ( )}

Masing-masing elemen pada persamaan (4.12) dapat dijelaskan sebagai berikut :

1 2

 merupakan vektor parameter komponen

parametrik respon ke−r;

adalah penjumlahan dari sekumpulan intersep komponen nonparametrik respon ke r

vektor parameter komponen nonparametrik respon ke−r;

( ) ( ) ( ) ( )

Sehingga matriks pada persamaan (4.12) dapat ditulis secara sederhana sebagai : y= θ + Φ + εX Z

(4.15)

 merupakan parameter pada komponen nonparametrik berukuran 2

Penduga Parameter Komponen Nonparametrik

Pendugaan parameter pada model regresi semiparametrik birespon tidak dapat dilakukan keseluruhan secara simultas sehingga dengan mengasumsikan θ



diketahui pada persamaan (4.13), maka model regresi semiparametrik birespon dapat dinyatakan sebagai :

y− θ = ΦX Z

Hasil estimasi fungsi regresi g t( ) dapat dinyatakan sebagai :

* _ˆ

 didapatkan dengan meminimumkan fungsi Penalized Weighted Least Square (PWLS) sebagai berikut :

( )

1

(

_*

) (

_*

)

Matrik W _{adalah matrik pembobot yang merupakan invers dari matrik}

(4.17) diketahui matriks D adalah suatu matrik diagonal yang didefinisikan sebagai berikut :

merupakan matrik nol. Pengestimasian Φ

 dilakukan dengan mendefferensiasi L terhadap Φ_ untuk mendapatkan Φˆ

(4.18)

Untuk menjamin bahwa penduga parameter Φˆ

 telah minimum maka dilakukan pendeferensiasian kedua pada L terhadap Φ

 sebagai berikut :

Berdasarkan persamaan (4.12) dapat diketahui elemen dari matrik Z dan T

Z WZ merupakan bentuk kuadratik, serta λ merupakan suatu nilai yang positif maka diperoleh :

(

)

dan terbukti bahwa penduga parameter _Φˆ

(4.19)

 dapat dinyatakan sebagai berikut :

(

)

1 _*

ˆ ( ) T T

g t =Z Z WZ+ λn D − Z Wy

 

Berdasarkan persamaan (4.15) diperoleh g tˆ ( )

 pada persamaan (4.19) yang merupakan fungsi regresi nonparametrik birespon. Estimator penalized spline untuk fungsi regresi birespon g tˆ ( )

 diberikan sebagai :

*

Sehingga matrik hat A nonparametrik yang didapatkan dari persamaan (4.19) untuk estimasi fungsi regresi adalah

(

_T

)

1 _T

n −

=Z Z Z+ λD

A W Z W

Penduga Parameter Komponen Parametrik

Berdasarkan persamaan (4.13), nilai dugaan θ

 adalah θˆ yang diperoleh melalui pendefferensiasian fungsi K terhadap θ

(4.22)

Untuk menjamin bahwa penduga parameter θˆ

 telah minimum maka dilakukan pendeferensiasian kedua pada K terhadap θ

 sebagai berikut :

Berdasarkan persamaan (4.12) dapat diketahui elemen dari matrik X dan matrik hat A yang telah didefinisikan sebelumnya, serta 2XT

(

I−A

) (

T I−A X

)

merupakan bentuk kuadratik maka diperoleh :

(

) (

)

dan terbukti bahwa penduga parameter θˆ

…(4.23)

(4.24)

(4.25)

(4.27) (4.26) Penduga parameter θˆ

 dan Φˆ yang teah didapatkan pada persamaan (4.18) dan persamaan (4.22) disubtitusikan dalam persamaan (4.13), sehingga diperoleh :

(

) (

)

persamaan (4.23) dapat dinyatakan sebagai berikut :

(

)

(

)

Persamaan (4.24) dapat ditulis sebagai berikut :

(

)

ˆ _{par nonpar}

par nonpar yang sesuai untuk variabel respon disetiap pengamatan. Nilai Generalized Cross Validation (GCV) diperoleh berdasakan subbab 2.7 untuk estimasi model regresi semiparametrik birespon berdasarkan estimator penalized spine sebagai berikut :