4. FUNGSI DUA atau TIGA PEUBAH

(1)

Fungsi Dua atau Tiga Peubah Limit dan kekontinuan Derivatif Parsial Nilai Ekstrem Integral Lipat

4.1. Fungsi Dua atau Tiga Peubah

Definisi

Suatu fungsi dua peubah f, adalah suatu aturan yang

mengawankan setiap pasangan terurut bilangan real (x,y) ke

tepat satu bilangan real z, ditulis z=f(x,y).

Koleksi pasangan terurut (x,y) disebut Domain fungsi f, sedangkan

koleksi bilangan real z yang dikawankan dengan anggota Domain

disebut Range f.

Grafik z=f(x,y) adalah suatu luasan (surface).

Contoh :

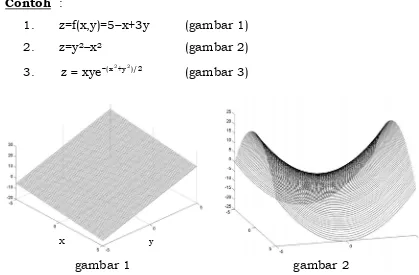
1. z=f(x,y)=5−x+3y (gambar 1)

2. z=y2−_x2 _(gambar₂₎

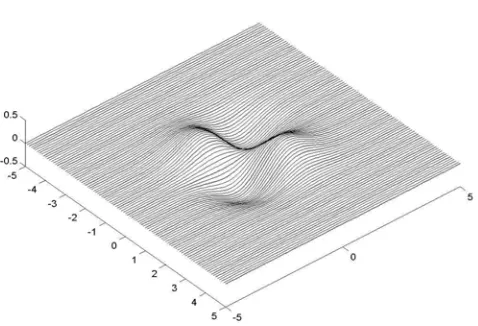
3. _z = _xye−(x2+y2)/2 _{(gambar 3)}

X y

(2)

Gambar 3

catatan : serupa dengan fungsi dua peubah, fungsi tiga peubah

ditulis w=f(x,y,z), hanya saja tidak ada grafiknya.

4.2. Limit dan kekontinuan

Bilangan real c disebut limit fungsi f(x,y) untuk (x,y) menuju

(x0,y0), ditulis

(x,ylim) (x0,y0)f

(

x,y

)

c

=

→

jika dan hanya jika :

(

x x

) (

y y

)

δ f

(

x,y

)

c ε 0

), 0 δ )( 0 ε

(∀ > ∃ > < − ₀ 2 + − ₀ 2 < ⇒ − < .

(x,y) (lim→x0,y0)f

(

x,y

)

ada jika hanya jika nilai limit tersebut sama untuk

(x,y) menuju (x0,y0) melalui sebarang kurva mulus di dalam domain f.

Pernyataan ini serupa dengan limit kiri dan limit kanan pada

pembicaraan fungsi satu peubah.

Contoh : ₍ _{) (} ₎ ₂ ₂

0 , 0 y ,

x _x _y

xy lim

+

→ tidak ada, sebab :

( ) ( )_x _y 0

xy

lim ₂ ₂

0 , 0 y ,

x → + = untuk (x,y)→(0,0) melalui kurva x=0, tetapi

( ) ( )_x _y 12

xy

lim ₂ ₂

0 , 0 y ,

(3)

Kekontinuan

Fungsi f dikatakan kontinu di titik (x0,y0), jika hanya jika

( ) ( )

(

) (

0 0

)

y , x y ,

x lim0 0 f x,y f x ,y

=

→

Seperti fungsi satu peubah, pada prinsipnya dapat dinyatakan :

• komposisi fungsi-fungsi kontinu menghasilkan fungsi kontinu

• jumlahan, pengurangan atau perkalian fungsi-fungsi kontinu

menghasilkan fungsi kontinu

• pembagian fungsi-fungsi kontinu juga menghasilkan fungsi

kontinu, kecuali di tempat fungsi penyebut bernilai nol.

Contoh :

(

)

xy 1

y x y , x f

2 3

−

= kontinu untuk setiap (x,y) kecuali pada

hiperbola xy=1.

4.3. Derivatif Parsial

Jika

(

) (

)

h

y , x f y , h x f lim

0 h

− +

→ ada, maka nilai limit tersebut

dinamakan Derivatif Parsial fungsi f terhadap x, disimbolkan

(

)

x y , x f

∂ ∂

atau fx(x,y). Jadi,

(

)

(

) (

)

h

y , x f y , h x f lim : y , x f

0 h x

− +

=

→ .

Sedangkan

(

)

(

) (

)

h

y , x f h y , x f lim : y , x f

0 h y

− + =

→

Aturan menentukan derivatif parsial suatu fungsi terhadap suatu

peubah, serupa dengan aturan derivatif fungsi satu peubah dengan

(4)

Contoh : f(x,y)=x4_sin(xy3₎

fx(x,y)=4x3sin(xy3)+x4y3cos(xy3)

fy(x,y)=3x5y2cos(xy3)

Interpretasi Geometri

z bidang y=b

kurva z=f(x,b)

Luasan z=f(x,y)

P

y

Q(a,b,0)

x

Tangen Garis, gradien=fx(a,b)

Tangen Bidang (Plane tangent)

z=f(x,y)

P

Tangen Bidang terhadap luasan z=f(x,y) di titik P(a,b,f(a,b))

memenuhi persamaan :

(5)

Derivatif Parsial Tingkat Tinggi Tingkat 2 xx 2 2 f x f x x f _≡ ∂ ∂ ∂ ∂ ≡ ∂ ∂ ₂ _yy 2 f y f y y f _≡ ∂ ∂ ∂ ∂ ≡ ∂ ∂ yx 2 f y f x y x f _≡ ∂ ∂ ∂ ∂ ≡ ∂ ∂ ∂ xy 2 f x f y x y f _≡ ∂ ∂ ∂ ∂ ≡ ∂ ∂ ∂ Tingkat 3 xxx 2 2 3 3 f x f x x f ≡ ∂ ∂ ∂ ∂ ≡ ∂ ∂ yyx 2 2 2 3 f y f x y x f _≡ ∂ ∂ ∂ ∂ ≡ ∂ ∂ ∂ xyy 2 2 3 f x y f y x y f _≡ ∂ ∂ ∂ ∂ ∂ ≡ ∂ ∂ ∂ zyx 2 3 f z y f x z y x f _≡ ∂ ∂ ∂ ∂ ∂ ≡ ∂ ∂ ∂ ∂

dan seterusnya.

Sifat

a. Diketahui f suatu fungsi dua peubah, yaitu f(x,y). Jika semua

derivatif parsial tingkat-1 dan 2 kontinu pada suatu

himpunan terbuka D, maka

fxy(x,y)= fyx(x,y) , ∀(x,y)∈D

b. Diketahui f suatu fungsi tiga peubah, yaitu f(x,y,z). Jika

semua derivatif parsial tingkat-1 dan 2 fungsi f kontinu pada

suatu himpunan terbuka D, maka

fxy=fyx, fxz=fzx dan fyz=fzy , ∀(x,y,z)∈D

Derivatif Parsial Fungsi Bersusun

Diketahui z=f(u,v) dengan u=u(x,y) dan v=v(x,y). Jika f terdiferensial

terhadap u dan v, u dan v masing-masing terdiferensial terhadap x

dan y, maka

(6)

contoh

Diketahui z=euv_{, dengan u=2x+y dan v=x/y tentukan}

y z dan x z

∂ ∂ ∂

∂

Derivatif Parsial Fungsi Implisit

Diketahui z peubah takbebas, sedangkan x dan y

masing-masing peubah bebas. x, y dan z dihubungkan oleh suatu fungsi

F dengan rumus F(x,y,z)=c, c konstan. Jika Fx,Fy dan Fz ada,

dengan Fz ≠ 0 serta F terdeferensial pada daerah D, maka

z / F

x / F x

z

∂ ∂

∂ ∂ − = ∂ ∂

dan

z / F

y / F y

z

∂ ∂

∂ ∂ − = ∂ ∂

contoh

Jika z=f(x,y) dan 2xyz +(x+y)e2z−x−y3 =0,tentukan

y z dan x z

∂ ∂ ∂

∂

4.4. Nilai Ekstrem

Diketahui f : D → R, D⊆R2 _{, dan (x}₀_,y₀₎∈_D

1. Fungsi f dikatakan mencapai nilai maksimum relatif di (x0,y0)

jika ∃δ > 0,∀

(

x,y

)

∈D∩

{

(x,y) 0 < (x−x₀)2 +(y −y₀)2 < δ

}

berlaku )f(x,y)≤f(x₀,y₀ . Jika ∀(x,y)∈D⇒f(x,y)≤f(x₀,y₀) maka dikatakan f mencapai nilai maksimum mutlak.

2. Fungsi f dikatakan mencapai nilai minimum relatif di (x0,y0)

jika δ 0,

(

x,y

)

D

{

(x,y) 0 (x x ) (y y )2 δ

}

0

2

0 + − <

− < ∩

∈ ∀

> ∃

berlaku )f(x,y)≥f(x₀,y₀ . Jika ∀(x,y)∈D⇒f(x,y)≥f(x₀,y₀) maka dikatakan f mencapai nilai minimum mutlak.

3. Jika f mencapai maksimum relatif atau minimum relatif di

(7)

Maksimum mutlak

Maksimum relatif

z=f(x,y)

Minimum Mutlak Minimum relatif

(x0,y0) disebut titik kritis fungsi f jika :

1. fx(x0,y0)=0 dan fy(x0,y0)=0, atau

2. fx(x0,y0) atau fy(x0,y0) tidak ada

Teorema

Diketahui f mempunyai derivatif parsial tingkat 2 kontinu, (x0,y0)

titik kritis fungsi f dan

(

0 0

)

xx

(

0 0

) (

yy 0 0

)

2

xy x ,y f x ,y f x ,y

f −

= ∆

a. Jika ∆<0 dan fxx(x0,y0)<0, maka f mencapai maksimum relatif

di (x0,y0).

b. Jika ∆<0 dan fxx(x0,y0)>0, maka f mencapai minimum relatif

di (x0,y0).

c. Jika ∆=0, tidak dapat diambil kesimpulan.

d. Jika ∆>0, maka titik (x0,y0) adalah titik pelana (saddle point) f

Contoh : f(x,y)=4xy-x4_-y4

Titik Kritis (x0,y0) fxx(x0,y0) fyy(x0,y0) fyy(x0,y0) ∆ Kesimpulan

(8)

4.5. Integral Lipat

Integral Lipat Dua

Diketahui fungsi f(x,y) terdefinisi pada daerah tertutup R di

bidang xy. Diambil suatu partisi pada R, yaitu A1, A2,...,An.

Jadi A R dan A_k A_l untuk k l

n 1 k

k = =∅ ≠

=

I

U

. Diambil pula

∆Ak=Luas Ak ,

(

x∗_k,y∗_k

)

∈A_kdan

{

_k

}

n k

1 A

maks

P = ∆

≤

≤ .

Integral Lipat Dua fungsi f pada daerah R, didefinisikan :

(

)

(

)

k

n 1 k k k 0 P R A y , x f lim : dA y , x

f =

∑

∆

∫∫

₌ ∗ ∗

→

Sifat

1. cf

(

x,y

)

dA c f

(

x,y

)

dA , c konstan

R R

= =

∫∫

2.

∫∫

[

(

) (

±

)

]

=

∫∫

(

)

±

∫∫

(

)

R R R dA y , x g dA y , x f dA y , x g y , x f

3.

∫∫

(

)

=

∫∫

(

)

+

∫∫

(

)

2 1 R R R dA y , x f dA y , x f dA y , x

f , dengan

R1∪R2=R dan R1∩R2=∅.

Teorema

Diketahui fungsi f kontinu pada suatu daerah tertutup R.

a. Jika R={(x,y)a≤x≤b, c≤y≤d}, maka

(

)

∫ ∫

(

)

∫ ∫

(

)

∫∫

= = b

a d c d c b a R dx dy y , x f dy dx y , x f dA y , x f

b. Jika R={(x,y)g1(y)≤x≤g2(y), c≤y≤d }, maka

(

)

(

)

( ) ( )

∫ ∫

∫∫

= d

c y g y g R 2 1 dy dx y , x f dA y , x f

c. Jika R={(x,y)a≤x≤b, h1(x)≤y≤h2(x)}, maka

(

)

(

)

( ) ( )

∫ ∫

∫∫

= b

(9)

Interpretasi geometri dari

∫∫

(

)

R

dA y , x

f adalah Volume benda tegak

dengan alas R pada bidang xy dan atap adalah proyeksi R pada

luasan f(x,y).

Proyeksi R pada f(x,y) z=f(x,y)

V=

∫∫

(

)

R

dA y , x f

R

Selain dapat digunakan untuk menghitung Volume, Integral lipat

dua juga dapat digunakan untuk menghitung luas daerah R sendiri.

Diperhatikan : =

∫∫

(

)

R

dA y , x f

V .

Di lain pihak : V=luas alas×Tinggi=Luas R × f(x,y)

Jika diambil f(x,y)=1, maka diperoleh Luas =

∫∫

R

dA

R .

Contoh

1. Hitung

∫∫

(

)

R

dA y , x

f , jika f(x,y)=1+8xy dan

R={(x,y)0≤x≤3, 1≤y≤2}. (jwb : 57)

2. Hitung Luas daerah yang dibatasi oleh parabola y=x2_{/2 dan}

garis y=2x. (jwb : 16/3)

3. Hitung Volume tetrahedron yang dibatasi luasan-luasan x=0,

y=0 dan z=4-4x-2y. (jwb : 4/3)

4. Hitung volume benda yang merupakan bagian bersama dari

silinder-silinder x2_+y2_{=4 dan x}2_+z2_=4.

(Jwb :

∫ ∫

= −

=

−

= 2

0 x

x 4

0 y

2

dx dy x 4 8

(10)

Massa Lamina

Jika suatu lamina dengan bentuk suatu daerah R pada bidang

xy dan mempunyai densitas δ(x,y), maka massa lamina tersebut

(

)

∫∫

=

R

dA y , x

δ

M .

Kejadian khusus jika bahan lamina homogen, yaitu δ(x,y)=konstan.

Pusat Massa Lamina

Pusat massa lamina R dengan densitas δ(x,y) adalah

(

x,y

)

dengan

(

)

(

)

(

)

(

)

∫∫

= = =

=

R R x R

R y

dA y , x δ

dA y , x δ y

M M y dan dA

y , x δ

dA y , x δ x

M M x

Mx disebut Momen pertama terhadap sumbu x

My disebut Momen pertama terhadap sumbu y.

Contoh :

Tentukan M, Mx, My dan

(

x,y

)

lamina segitiga dengan titik-titik

sudut (0,0), (1,0) dan (0,1) jika fungsi densitas δ(x,y)=xy. (Jwb.

M=1/24, Mx=My=1/60 dan

(

x,y

)

=(2/5,2/5)).

Momen Inersia Lamina

Momen inersia (momen kedua) lamina R dengan fungsi densitas

δ(x,y) terhadap sumbu x, sumbu y dan sumbu z, masing-masing :

(

)

∫∫

=

R 2

x y δx,y dA

I ,

(

)

∫∫

=

R 2

y x δ x,y dA

I ,

(

)

(

)

∫∫

+ =

R

2 2

z x y δx,y dA

(11)

Integral Lipat Tiga

Diketahui fungsi f(x,y,z) terdefinisi pada daerah pejal G di ruang

xyz. Diambil suatu partisi pada G, yaitu V1, V2,...,Vn.

Jadi V G dan V_k V_l untuk k l

n 1 k

k = =∅ ≠

=

I

U

. Diambil pula

∆Vk=Volume Vk ,

(

x∗_k,y∗_k,z∗_k

)

∈V_kdan

{

_k

}

n k

1 V

maks

P = ∆

≤

≤ .

Integral Lipat Tiga fungsi f terhadap G, didefinisikan :

(

)

(

)

k

n 1 k

k k k 0

P G

V z , y , x f lim : dV z , y , x

f =

∑

∆

∫∫∫

=

∗ ∗ ∗ →

Sifat

1. cf

(

x,y,z

)

dV c f

(

x,y,z

)

dV , c konstan

G G

= =

∫∫∫

2.

∫∫∫

(

) (

±

)

=

∫∫∫

(

)

±

∫∫∫

(

)

G G

G

dV z , y , x g dV

z , y , x f dV

] z , y , x g z , y , x f [

3.

∫∫∫

(

)

=

∫∫∫

(

)

+

∫∫∫

(

)

2

1 G

G G

dV z , y , x f dV

z , y , x f dV

z , y , x

f , dengan

G1∪G2=G dan G1∩G2=∅.

Demikian juga untuk terapan integral lipat tiga : Hitung Volume,

Massa, Pusat massa serta Momen-momen Inersia, serupa dengan

integral lipat dua.

Contoh :

Tentukan volume benda G dengan batas-batas silinder parabolik

z=4-x2_{dan bidang-bidang datar x=0, y=0,y=6, z=0.}

Jwb :

32

dx dy dz dxdydz V

2 0 x

6 0 y

x 4

0 z G

2

= = =

∫ ∫ ∫

∫∫∫

= = −

=

z z=4-x2

G

y

(12)

Kadang-kadang di dalam perhitungan integral lipat dua atau tiga

akan lebih sederhana jika dilakukan suatu transformasi.

Transformasi Integral Lipat Dua

Diketahui dua sistem koordinat pada ruang R2_{: x0y dan u0v}

dengan hubungan :

u=u(x,y) atau x=x(u,v)

v=v(x,y) y=y(u,v) maka dv du v , u y , x : dy dx dA       ∂ = = , dengan v y v x u y u x v , u y , x ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ =       ∂ Sifat       ∂ =       ∂ y , x v , u 1 v , u y , x

Dengan demikian transformasi integral lipat dua dapat dituliskan :

(

)

∫∫

[

(

) (

)

]

∫∫

_∗       ∂ = R R dudv v , u y , x v , u y , v , u x f dA y , x f . Contoh:

Ditinjau sistem koordinat kartesius dan sistem koordinat polar:

x = r cos θ dan y = r sin θ. Diperoleh

r θ cos r θ sin r θ sin θ cos θ y θ x r y r x θ , r y ,

x ₌ ₌

∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ =       ∂

Sehingga :

∫∫

(

)

∫∫

( )

(13)

Misalkan dihitung

∫∫

+ R 2 2 dy dx y

x dengan R daerah pada

bidang xy dengan batas-batas : x2_+y2_{=4 dan x}2_+y2_{=9, maka :}

3 π 38 θ drd r θ d dr θ , r y , x r dy dx y x π 2 0 θ 3 2 r 2 R 2 R 2

2 _ ₌ ₌

     ∂ = +

∫∫

∫ ∫

∫∫

= = ∗ .

Transformasi Integral Lipat Tiga

Diketahui dua sistem koordinat pada ruang R3_{: xyz dan uvw}

dengan hubungan :

u=u(x,y,z) atau x=x(u,v,w)

v=v(x,y,z) y=y(u,v,w)

w=w(x,y,z) z=z(u,v,w)

maka dw dv du w , v , u z , y , x dz dy dx dV       ∂ = = dengan w z w y w x v z v y v x u z u y u x w , v , u z , y , x ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ =       ∂ Contoh

1. Pada sistem koordinat bola

x = r sin ϕ cos θ

y = r sin ϕ sin θ

z = r cos ϕ

maka :

dxdydz=r2_sinϕ_drdϕ_dθ

z

•

r

ϕ

θ y

x

2. Pada sistem koordinat tabung

x = r cos θ

y = r sin θ

z = z

maka :

dxdydz = r dzdrdθ

z

• (r,θ,z)

θ y

r

R x