MAKALAH MAKALAH
INTEGRAL LIPAT DUA PADA DAERAH PERSEGI PANJANG DAN DAERAH INTEGRAL LIPAT DUA PADA DAERAH PERSEGI PANJANG DAN DAERAH
SEBARANG SEBARANG
Disusun Guna Memenuhi Tugas Terstruktur Mata Kuliah K
Disusun Guna Memenuhi Tugas Terstruktur Mata Kuliah K alkulus Lanjut 2alkulus Lanjut 2 Rombel 4
Rombel 4
Pembimbing : Bu Emy Pujiastuti Pembimbing : Bu Emy Pujiastuti
Disusun oleh : Disusun oleh :
1.
1. Ahmad Ahmad Badawi Badawi (4101411100)(4101411100) 2.
2. Eka Eka Nurjanah Nurjanah (4101411115)(4101411115) 3.
3. Lusi Lusi Nofitasari Nofitasari (4101411183)(4101411183) 4.
4. Rani Rani Christiant Christiant y y (4101411184)(4101411184)
UNIVERSITAS NEGERI SEMARANG UNIVERSITAS NEGERI SEMARANG
2013 2013
BAB I BAB I PENDAHULUAN PENDAHULUAN 1.1 1.1 DeskripsiDeskripsi
Makalah ini akan membahas tentang konsep-konsep integral lipat dua pada Makalah ini akan membahas tentang konsep-konsep integral lipat dua pada daerah persegi panjang dan daerah sebarang.
daerah persegi panjang dan daerah sebarang. 1.2
1.2 PrasyaratPrasyarat
Materi prasyarat yang diperlukan adalah sebagai berikut: Materi prasyarat yang diperlukan adalah sebagai berikut:
1.
1. Geometri Dasar.Geometri Dasar. 2.
2. Kalkulus 1 dan kalkulus 2, dan Kalkulus 1 dan kalkulus 2, dan kalkulus Lanjut 1.kalkulus Lanjut 1. 1.3
1.3 Rumusan MasalahRumusan Masalah 1.
1. Bagaimana konsep integral Riemann?Bagaimana konsep integral Riemann? 2.
2. Bagaimana definisi integral lipat dua?Bagaimana definisi integral lipat dua? 3.
3. Bagaimana arti geometri integral lipat dua?Bagaimana arti geometri integral lipat dua? 4.
4. Bagaimana konstruksi integral lipat dua pada derah persegi panjang danBagaimana konstruksi integral lipat dua pada derah persegi panjang dan daerah sebarang?
daerah sebarang? 5.
5. Bagaimana cara menghitung integral lipat dua pada daerah persegiBagaimana cara menghitung integral lipat dua pada daerah persegi panjang dan daerah sebarang?
panjang dan daerah sebarang? 1.4
1.4 KompetensKompetensi dan i dan IndikatorIndikator Kompetensi Dasar
Kompetensi Dasar : Memahami : Memahami dan dan menghitung menghitung integral integral lipat lipat dua dua padapada daerah persegi panjang dan daerah sebarang.
daerah persegi panjang dan daerah sebarang. Indikator
Indikator:: 1.
1. Mengetahui dan memahami konsep integral Riemann.Mengetahui dan memahami konsep integral Riemann. 2.
2. Mengetahui definisi integral lipat dua.Mengetahui definisi integral lipat dua. 3.
3. Memahami arti geometri integral lipat dua.Memahami arti geometri integral lipat dua. 4.
4. Mengetahui konstruksi integral lipat dua pada derah persegi panjang danMengetahui konstruksi integral lipat dua pada derah persegi panjang dan daerah sebarang.
daerah sebarang. 5.
5. Dapat menghitung integral lipat dua pada daerah persegi panjang danDapat menghitung integral lipat dua pada daerah persegi panjang dan daerah sebarang.
daerah sebarang. 1.5
1.5 Tujuan Tujuan PembelajaPembelajaranran
Mahasiswa mampu memahami dan dapat menyelesaikan perhitungan integral Mahasiswa mampu memahami dan dapat menyelesaikan perhitungan integral lipat dua pada daerah persegi panjang dan daerah sebarang.
BAB II BAB II PEMBAHASAN PEMBAHASAN PENGANTAR PENGANTAR
Integral lipat dua dari limit fungsi dua peubah real, yang dikenal sebagai Integral lipat dua dari limit fungsi dua peubah real, yang dikenal sebagai integral lipat dua (integral ganda/multiple integral) dikonstruksi dengan cara integral lipat dua (integral ganda/multiple integral) dikonstruksi dengan cara serupa dengan integral tentu fungsi satu peubah real. Sebelum kita mempelajari serupa dengan integral tentu fungsi satu peubah real. Sebelum kita mempelajari konsep integral lipat dua, ingat kembali konstruksi integral fungsi satu peubah real konsep integral lipat dua, ingat kembali konstruksi integral fungsi satu peubah real sebagai limit jumlah Riemann, yang lengkap sebagai berikut.
sebagai limit jumlah Riemann, yang lengkap sebagai berikut.
2.1
2.1 INTEGRAL LIPAT DUA PADA DAERAH PERSEGI PANJANGINTEGRAL LIPAT DUA PADA DAERAH PERSEGI PANJANG
2.1.1 KONSTRUKSI INTEGRAL TUNGGAL (INTEGRAL TENTU 2.1.1 KONSTRUKSI INTEGRAL TUNGGAL (INTEGRAL TENTU
FUNGSI SATU PEUBAH) FUNGSI SATU PEUBAH) Kita mempunyai fungsi
Kita mempunyai fungsi f f yang terdefinidsi pada selang tutup [a,b].yang terdefinidsi pada selang tutup [a,b]. 1.
1. Buatlah partisiBuatlah partisi
Δ
Δ
untuk selang tertutup [a,b] dengan pembagian untuk selang tertutup [a,b] dengan pembagian a = xa = xoo< x< x11< x< x22
< …< x
< …< x
i-1i-1< x< xii<…< x
<…< x
nn= b= bSelang bagian
ke-Selang bagian ke-ii dari partisi ini adalah dari partisi ini adalah [x
[xi -1,i -1,xxii]]
dan panjang partisinya didefinisikan sebagai dan panjang partisinya didefinisikan sebagai
= maks Δx
= maks Δx
ii1≤i≤n
1≤i≤n
2.
2. Pilihlah ciPilihlah ci
{xi-1, xi}, i {xi-1, xi}, i = 1,2,3,...,n.= 1,2,3,...,n. 3.3. Definisikan bentuk jumlahDefinisikan bentuk jumlah
x x c c f f n n ii ii
11 )) (( iiyang dinamakan jumlah Riemann fungsi
yang dinamakan jumlah Riemann fungsi f, f, pada [a,b]. pada [a,b]. 4.
4. Perhatikan bentuk limit jumlah RiemannPerhatikan bentuk limit jumlah Riemann
0 0 li limm
L L f f cc xx n n ii ii
11 )) (( iiJika limit ini ada, maka fungsi
Jika limit ini ada, maka fungsi f f dikatakan teritegralkan secara Riemann dikatakan teritegralkan secara Riemann pada[a,b].
5. Integral tentu dari fungsi f pada[a,b] didefinisikan sebagai limit jumlah Riemann (bila limit ini ada) dan ditulis dengan lambang
b a dx x f )( 0 lim f c x n i i
1 ) ( iKonstruksi ini dapat diperumum untuk fungsi dua peubah real dengan mengganti peranan selang tertutup, partisi untuk selang tertutup menjadi jaring untuk persegi panjang, elemen panjang menjadi elemen luas. Proses konstruksi integral lipat duadengan jumlah ganda adalah sebagai berikut.
2.1.2. KONSTRUKSI INTEGRAL LIPAT DUA Kita mempunyai fungsi dua peubah real
z = f (x,y)
yang terdefinisi pada daerah persegi panjang tertutup
P = [a,b] x [c,d] ={(x,y)│a ≤ x ≤ b,c ≤ y ≤ d}
1. Buatlah jaring
pada persegi panjang P dengan cara membagi [a,b] atas m dan [c,d] atas n bagian sehingga diperoleh mn persegi panjang seperti diperlihatkan pada gambar di bawahyn y j yn-1 y j-1 q j y1 c y0 d
Δy
j x1 x0 x2 xi-1 pi xi xm-n xm a bΔx
i ΔAij Y X O PUkuran jaring
didefiniskan sebagai panjang diagonal terbesar dari komponen jaringnya, ditulis dengan lambang
. Luas komponen jaring ke–
ij adalah
Aij=
xi
yidi mana
xi= xi- xi-1dan
yi= yi–
yi-12. Pilihlah titik [pi,q j] pada komponen jaring ke-ij, i = 1,2,...,m dan j =
1,2,...,n.lihat gambar
3. Definisikan bentuk jumlah
i i j i n j m i y x q p f
) , ( 1 1 atau i j ij n j m i A q p f
) , ( 1 1yang dinamakan jumlah Riemann dari fumgsi f pada persegi panjang P. 4. Pehatikan bentuk limit jumlah Riemann
0 lim
L i j i i n j m i y x q p f
) , ( 1 1Jika limit ini ada, maka fungsi z = f (x,y) dikatakan terintegralkan secara Riemann pada daerah persegi panjang P.
5. Integral lipat dua dari fungsi z = f (x,y) pada persegi panjang teretutup P didefinisikan sebagai limit jumlah Riemann ini (bila limitnya ada, dan ditulis dengan lambang
f x y dxdy
p ) , ( 0 lim i j i i n j m i y x q p f
) , ( 1 1 atau
f x y dA
p ) , ( 0 lim i j ij n j m i A q p f
) , ( 1 12.1.3 ARTI GEOMETRI INTEGRAL LIPAT DUA
Jika fungsi z = f
(x,y) kontinu dan f(x,y) ≥ 0 pada daerah persegi panjang P,
maka integral lipat dua
f x y dA p ) , (Menyatakan isi benda padat di ruang yang terletak di bawah permukaan z = f( x,y) dan di atas persegi panjang P. Perhatikan benda padatnya pada gambar di bawah.
Dalam kasus f (x,y) =1, maka integral lipat dua pada daerah P menyatakan luas persegi panjangnya sendiri, yaitu (b-a)(d-c).
2.1.4 DAERAH INTEGRASI
Daerah integrasi pada integral lipat dua berupa daerah pada bidang x-y. Daerah integrasi yang paling sederhana berbentuk daerah persegi panjang dan yang lebih rumit dapat berbentuk daerah segitiga, daerah lingkaran, dan daerah yang dibatasi kurva-kurva. Dalam bahasan ini kita berlatih menyatakan daerah integrasi yang diberikan dalam bentuk himpunan.
Misalkan daerah integrasi
*|+
seperti pada gambar di samping.P p i q j Z Y X Z = f(x ,y) x 1 1 -1
S
Cara lain untuk menuliskanS adalah
*|+
perbedaan kedua cara tersebut terletak pada urutan penempaan batas -batas x dan y. Lihat gambar berikut.Yang perlu diperhatikan bahwa kedua cara tersebut menyatakan daerah integrasi yang sama.2.1.5 CARA MENGHITUNG INTEGRAL LIPAT DUA PADA DAERAH PERSEGI PANJANG
Perhatikan gambar pertama yang menunjukkan sebuah benda padat di ruang yang terletak di atas daerah persegi panjang P di bawah permukaan
x y fz
, yang kontinu pada P dan f
x, y
0 pada P. Bidang irisan yang sejajar XOZ dengan benda padat yang melalui y
c,d . Luas bidang irisan sejajar ini adalah fungsi dari y yang dinamakan L(y) Fungsi L ini kontinu padac d a b Y X a Y Z
Z=f(x,y)
O a b XP
d c a b X Z x 1 1 -1S
[a,b] karena fungsi z
f
x, y kontinu pada P. Selanjutnya irisan sejajar untuk isi benda padat adalahIsi benda padat
p dx y x f , , Akibatnya,
p d c d c d c dy dx y x f dy y L dA y x f , ,Integral di ruas paling kanan di namakan integral berulang yang seringkali di tuliskan tanpa menggunakan kurung. Jadi hasilnya:
p d c b a d c b a dy dx y x f dxdy y x f dA y x f ( , ) ( , ) ( , )Dengan cara serupa, kita dapat mengambil bidang irisan yang sejajar YOZ dengan benda padat . Situasinya akan di perlihatkan pada gambar di bawah ini:
Gambar pertama memperlihatkan sebuah benda padat di ruang yang terletak di atas daerah persegi panjang P dan di bawah permukaan z
f
x, yyang kontinu pada P dan f ( x, y)
0 pada P. Bidang irisan yang sejajar YOZ dengan benda padat yang melalui x
a,b di perlihatkan pada gambar sebelah kanannya. Luas bidang irisan sejajar ini adalah fungsi dari X yang di namakanZ Y c d a b c d X Y O a b c d X Z Y
Z=f(x,y)
P
L(x). Fungsi L ini kontinu pada [c,d] karena fungsi z
f
x, y kontinu pada P. Selanjutnya , metode irisan sejajar untuk isi benda padat memberikan:Isi Benda Padat =
p b a dx x L dA y x f ( , ) ( ) di mana
d c dy y x f x L( ) ( , ) Akibatnya,Integral di ruas kanan juga merupakan integral berulang yang sering kali di tulis tanpa kurung.Jadi hasilnya
p b a d c b a d c dx dy y x f dx dy y x f dA y x f ( , ) ( , ) , ( , )Kita perumum hasil di atas untuk fungsi f yang kontinu pada P tetapi tidak perlu memenuhi syarat f(x,y)
0
. Jadi,kita mempunyai rumus-rumus:Teorema cara menghitung integral lipat dua dengan integral berulang.
Jika fungsi z =f(x,y) kontinu pada daerah persegi panjang tertutup p=[a,b] x [c,d] maka: 1.
p d c b a d c b a dy dx y x f dxdy y x f dA y x f ( , ) ( , ) ( , ) 2.
p b a d c b a d c dx dy y x f dydx y x f dA y x f ( , ) ( , ) ( , ) Contoh: Hitunglah
,-,-
p b a b a d c dx dy y x f dx x L dA y x f , ( ) ( , ) .Ada dua cara untuk mengerjakannya sesuai dengan cara yang telah disebutkan di atas Car a Per tama Daerah integrasi
*|+
Grafik
= − 6
X Y P 1Cara K edua Daerah integrasi
*|+
Grafik
P X Y 1Dalam berbagai situasi, integral lipat dua pada daerah persegi panjang tidak selalu dapat dihitung dengan dua cara. Pilihlah urutan pengintegralannya agar primitif dari integral yang pertama mudah dihitung.
2.1.6 SIFAT INTEGRAL LIPAT DUA
Sifat integral lipat dua hampir mewarisi semua sifat integral tunggal. Berikut sifat integral lipat dua:
a. Sifat linear
Jika fungsi f dan g terintegral pada P
, dan α dan β
adalah konstanta, maka,-
Bukti :,-
‖‖
.(
)(
)/
‖‖
(
)
‖‖
(
)
‖‖
(
)
‖‖
(
)
b. Sifat urutanJika fungsi f dan g terintegral pada P dan f(x,y) ≥ g (x,y) pada P, maka
Bukti:
‖‖
(
)
‖‖
(
)
(
)
(
)
(
)
(
)
(
)(
)
c. Sifat penjumlahan (aditif)
Jika fungsi f terintegral pada P yang dapat ditulis sebagai P=P1+P2, dengan P1dan P2 tidak saling tumpang tindih, maka
Bukti:
Tulis
jaring pada persegi panjang Pl dan
jaring pada persegi panjang P2.Jelas
‖
‖
(
)
‖
‖
(
)
‖‖
(
)
Contoh Soal Latihan 1. Hitunglah
,- ,-
( Koko Martono, Integral Lipat Dua (1991): halaman 9) 2. Hitunglah
,-,-
(Koko Martono, Integral Lipat Dua (1991): halaman 10)
Penyelesaian: 1. Hitunglah
,- ,-
Integral lipat dua ini dapat diselesaikan dengan dua cara. ( Daerah pengintegralan dapat dilihat pada gambar di bawah ini).
a. Cara pertama
Jika daerah integrasi P dipartisi terhadap sumbu y maka diperoleh: Daerah integrasi
*|+
( )
. 4 x -1 2 y Pb. Cara kedua
Jika daerah P dipartisi terhadap sumbu x maka diperoleh: Daerah integrasi
*|+
( )
. 2. Hitunglah
,-,-
Jika P dipartisi terhadap sumbu x maka diperoleh: Daerah integrasi
*| +
Integral di atas dapat dituliskan menjadi
4 y -1 x 2 P 2 0 y 1 x P 1maka integral pertama terhadap x tidak dapat dihitung nilai eksaknya karena primitif dari integrlanya tidak dapat ditentukan. Oleh karena itu kita harus mengubah urutan integralnya dalam
kemudian selesaikan, sehingga diperoleh:
./
.
/
√
.2.2 INTEGRAL LIPAT DUA PADA DAERAH SEBARANG 2.2.1 PENGANTAR
Kita akan mempelajari konstruksi integral lipat dua untuk fungsi z = f(x, y) yang terdefinisi pada daerah D yang berbentuk :
D = {
(x, y) │a ≤ x ≤ b, Φ(x) ≤ y ≤ ψ(x)
} atau D = {(x, y)│c ≤ y ≤ d, Φ(y) ≤ x ≤ ψ(y)
}di mana fungsi
y = Φ(x), y = ψ(x)
kontinu pada selang tertutup [a, b] dan fungsi x2.2.2 KONSTRUKSI INTEGRAL LIPAT DUA PADA DAERAH SEBARANG
Untuk memahami arti :
∬
buatlah persegi panjang P yang cukup untuk menutup daerah D sehingga sisi persegi panjangnya menyinggung daerah D seperti diperlihatkan gambar di bawah
ini:
D
x = b
x = a
P
(x)
(x)
y =
y =
D
P
y = c
y = d
(y)
(y)
x =
x =
Definisikan fungsi F pada daerah persegi panjang tertutup P dengan persamaan
F(x, y) =
{
Karena F merupakan perluasan dari fungsi f yang terdefinisi pada daerah D. Jika fungsi F terintegralkan pada P , maka kita dapat menuliskan
∬
‖‖
∑ ∑
D
2.2.3DEFINISI INTEGRAL LIPAT DUA PADA DAERAH SEBARANG Karena fungsi F bernilai nol pada P - D, maka integral lipat dua dari fungsi f pada D dapat didefinisikan sebagai integral lipat dua dari fungsi F pada daerah persegi panjang P , yang artinya telah kita pelajari pada pasal sebelumnya
Definisi
Misalkan fungsi z = f(x, y) terdefinisi pada daerah D dan fungsi z = F(x, y) yang terdefinisi pada persegi panjang tertutup P yang tepat memuat D dengan persamaan
F(x, y) =
{
Jika fungsi F terintegralkan pada P , maka integral lipat dua dari fungsi f pada D didefinisikan sama dengan integral lipat dua pada P , yaitu
∬ ∬
Catatan:
1. Dengan cara mendefinisikan integral lipat dua dari fungsi z = f(x, y) pada daerah D seperti di atas, semua rumus integral lipat dua yang telah dipelajari berlaku juga untuk integral lipat dua pada daerah D.
2. Integral lipat dua pada daerah sebarang lainnya dapat dinyatakan sebagai sejumlah berhingga integral lipat dua dari bentuk yang terakhir.
2.2.4 ARTI GEOMETRI INTEGRAL LIPAT DUA PADA DAERAH SEBARANG
Jika fungsi z = f(x, y) kontinu dan
f(x, y) ≥
0 pada daerah D, maka integral lipat dua∬
menyatakan isi benda padat di ruang yang terletak bawah permukaan z = f(x, y) dan di atas daerah D. Perhatikan gambar di bawah ini.
D
Y
X
z = f (x, y) = 1 Z
Dalam hal f (x, y) = 1, maka integral lipat dua pada daerah D secara numeric menyatakan luas`daerah D sendiri. Perhatikan gambar di atas. Ini berarti bahwa luas daerah sebarang pada bidang datar dapat ditampilkan dalam bentuk integral lipat dua. Z D Y Benda padat X O z = f (x, y)
2.2.5 DAERAH INTEGRASI
Berbeda dengan daerah integrasi yang berupa persegi panjang, misalkan untuk daerah integrasi yang berupa daerah segitiga, kita harus lebih hati-hati dalam mengubah urutan batas-batas x dan y. Perhatikan daerah integrasi berikut.
Daerah integrasi S ini dapat dinyatakan dalam himpunan dalam dua cara berbeda. Cara pertama dengan batas-batas x berupa konstanta dengan ketentuan ini diperoleh
}
. Tampak bahwa batas-batas y bergantung pada peubah x. Cara kedua adalah dengan mengambil batas-batas y yang konstan, dan diperoleh*|+
. Pada cara kedua ini tampak bahwa batas-batas x bergantung pada peubah y.Selain Koordinat Cartesius (yang memakai variabel x dan y) kita mengenal pula Koordinat Kutub (yang memakai variabel
). Kaiatan antara kedua sistem koordinat tersebut adalah
. Dalam hal ini r menyatakan jarak titik (x,y) dari titik asal, sedangkan
merupakan besar sudut antara sumbu x positif dengan vektor posisi (x,y) dalam arah yang berlawanan dengan arah perputaran jarum jam.2.2.6 CARA MENGHITUNG INTEGRAL LIPAT DUA PADA DAERAH SEBARANG DENGAN INTEGRAL BERULANG
Pengantar :
Intagral lipat dua pada daerah tertutup sebarang D dapat dihitung dengan cara yang sama seperti integral lipat dua pada daerah persegi panjang tertutup P . Disini cara perhitungannya dibagi dalam dua kasus.
x y Cara I 2 1
S
x 2 Cara IIS
yCara M enghitung :
a. Kasus pertama :
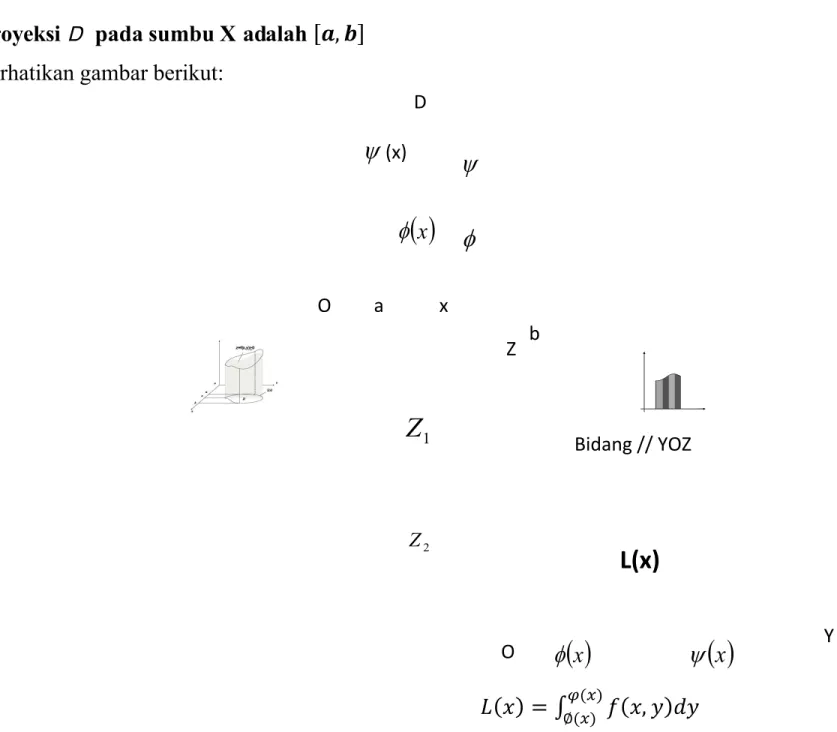
Proyeksi D pada sumbu X adalah
,-Pada kasus ini daerah D ditulis sebagai*+
Maka integral lipat duanya dapat ditulis sebagai
0
1
Integral di ruas paling paling kanan berbentuk integral berulang yang seringkali ditulis tanpa menggunakan kurung, yaitu
b. Kasus Kedua:
Proyeksi D pada sumbu Y adalah
,-Pada kasus ini daerah D ditulis sebagai*+
Maka integral lipat duanya dapat ditulis sebagai
0
1
Integral di ruas paling paling kanan berbentuk integral berulang yang seringkali ditulis tanpa menggunakan kurung, yaitu
2.2.7 TINJUAN GEOMETRI
Integral lipat dua pada daerah sebarang D untuk fungsi
kontinu dan
pada daerah D ,menyatakan isi benda padat yang terletak di atas daerah D dan dibawah permukaan f.Seperti integral lipat dua pada persegi panjang P , dari arti geometri integral lipat dua pada daerah sebarang sebagai isi benda padat kita dapat mengontruksi cara
2
Z
1
Z
menghitung isi bendanya dengan metode irisan sejajar kemudian memperumum hasilnya untuk mendapatkan rumus diatas. Tinjauan untuk setiap kasus adalah sebagai berikut.
1. Kasus pertama:
Proyeksi D pada sumbu X adalah
,-Perhatikan gambar berikut:∫
Gambar pertama memperlihatkan daerah D yang proyeksinya pada sumbu X adalah selang tertutup
,-
.Benda padat di ruang isinya dinyatakan sebagai integral lipat dua pada daerah D diperlihatkan pada gambar kedua .Bidang irisan sejajar antara benda padat dengan bidang sejajar YOZ dan melalui titik ,-
Dapat dilihat pada gambar ketiga.Y Z O
x
xL(x)
Bidang // YOZ b D
x x a
(x)
O
y
C y d Y
y D XJika luas bidang irisan sejajar ini L(x) dan L kontinu pada
,-
,maka metode irisan sejajar untuk isi benda padat memberikan
dimana
Jadi
b a b a x x D dx dy y x f dx x L d y x f , , 2. Kasus Kedua :Proyeksi D pada sumbu Y adalah (c,d) Perhatikan gambar dibawah ini :
Gambar pertama memperlihatkan daerah D yang proyeksinya pada sumbu Y adalah selang tertutup [c,d]. benda padat diruang yang isinya dinyatakan sebagai integral lipat dua pada daerah D diperlihatkan pada gambar kedua. Bidang irisan
Y Z
O
x
xL(x)
sejajar antara benda padat dengan bidang yang sejajar XOZ dan melalui titik
(0,y,0), y Є (c,d) dapat dilihat
pada gambar ketiga.Jika luas bidang irisan sejajar ini L(y) dan L kontinu pada (c,d), maka metode irisan sejajar untuk isi benda padat memberikan
Isi benda padat
D d c
dy
y
x
L
d
y
x
f
,
,
Dimana
y ydx
y
x
f
y
L
, Jadi
dy dx y x f dy y x L d y x f b a y y D d c
, , ,Perhatikan bahwa luas daerah D sendiri dapat dinyatakan sebagai integral lipat dua dengan cara mengambil f(x,y) = 1, sehingga kita mempunyai rumus berikut. Akibat : 1. Luas Daerah
x
y
a
x
b
x
y
x
D
,
,
Adalah
D b a y ydydx
d
2. Luas Daerah
x
y
c
y
d
y
x
y
D
,
,
Adalah
D d c x xdxdy
d
2.2.8 ILUSTRASIKita ingin menghitung
D
yd
x2 di mana D adalah daerah yang dibatasi oleh
Perhatikan gambar di halaman berikut yang memperlihatkan daerah D. kedua lengkungan pembatas D berpotongan di titik (0,0) dan (2,4). Periksa!
Kita dapat menghitung integral lipat dua ini dengan dua cara.
a. Cara pertama:
Proyeksi daerah D pada sumbu X adalah selang [0,2]. Pada kasus ini daerah D dapat ditulis sebagai
x y x x y x
D
, 0
2, 2
2 Jadi
2 0 2 2 0 2 2 2 2 2 2 2 2 1 x x x x D dx y x ydydx x yd x 35 23 3 5 2 64 7 64 5 64 14 1 5 2 2 1 2 2 0 2 0 7 5 6 4
x x dx x x b. Cara kedua:Proyeksi D pada sumbu Y adalah (0,4).
Invers dari y = 2x adalah x y 2 1
Invers dari y
x2 adalah x yPada kasus ini daerah D dapat ditulis sebagai
x y y y x yD 2 1 , 4 0 , X Y O 4 2 x y2 2 x y X Y O 4 2
Jadi
4 0 2 1 4 0 2 1 2 3 2 2 3 1 y y y y D dy y x ydxdy x yd x 35 23 3 70 1 256 30 256 21 256 120 1 24 2 24 1 3 1 4 0 4 0 5 3 4 2
y y y dy y y yContoh Soal: 1. Diketahui
Dimana D adalah daerah yang terletak dikuadran pertama yang dibatasi oleh grafik fungsi
√
dan garis y = 4.a. Gambarkan daerah pengintegralan D!
b. Tuliskan integral lipat dua I sebagai integral berulang dengan urutan
!c. Tuliskan integral lipat dua I sebagai integral berulang dengan urutan
! d. Hitunglah I!( Koko Martono, Integral Lipat Dua (1991): halaman 21) 2. Diketahui
a. Gambarkan daerah pengintegralannya! b. Ubahlah urutan pengintegralannya!
c. Hitunglah I!
( Koko Martono, Integral Lipat Dua (1991): halaman 24) 3. Hitunglah
(
)
Penyelesaian:
1. a. Daerah pengintegralan D diperlihatkan pada gambar di bawah.
b. Dengan urutan dydx kita mengambil proyeksi daerah D terhadap sumbu X. Daerah D dapat dituliskan dalam bentuk:
x
y
x
x
y
x
D
1
(
,
)
|
0
1
,
2
4
,
|
1
2
,
24
2
x
y
x
x
y
D
Sehingga integral berulangnya adalah
2 1 4 3 1 0 4 3 3 3 3 2 2 2 1dx
ydy
x
dx
ydy
x
dA
x
dA
x
dA
x
x x x D D Dc. Dengan urutandxdy, kita mengambil proyeksi daerah D terhadap sumbu Y. Untuk ini kita memerlukan invers fungsi pembatas daerah D.
Invers fungsi y
4 x adalah x
1 y2,y
0 invers fungsi4 4 y x y4 y x2 2 0 1
0 ,
2
x xy adalah x
y. Daerah D dapat ditulis dalam bentuk
x y y y x yD 2 16 1 , 4 0 | ) , (
sehingga integral berulangnya adalah
4 0 16 1 3 3 2 dy dx x ydA x y y D
d. Dengan menggunakan integral berulang pada jawaban di atas, integral
lipat duanya adalah
4 0 16 1 4 4 0 16 1 3 3 2 2 4 1 dy y x dy dx x ydA x I y y y y D 5 3 15 10 4 16 4 10 1 16 1 4 1 4 1 4 0 10 9 4 4 0 9 9 3
y y dy y y2. Diketahui
2 0 4 2 4 3 2 dx dy y x x I xa. Dari bentuk integral berulang yang diketahui, proyeksi daerah D terhadap sumbu X adalah selang [0,2], di atas dibatasi oleh garis y=4 dan di bawah dibatasi oleh parabol y
x2. Dalam hal ini D dapat ditulis sebagai D
x, y |0
x
2, x2
y
4 dan daerahnya diperlihatkan pada gambar di bawah.4 y x y4 y x2 2 0 1
b. Proyeksi D pada sumbu Y adalah selang [0,4]. Invers fungsi y
2 x,x
0adalah fungsi x
y,y
0, sehingga daerah D dapat ditulis dalam bentuk
x y y x y
D
, |0
4,0
.Jadi integral berulangnya dalam urutan dxdy adalah
4 0 0 4 2 3 dy dx y x x I yc. Dengan menggunakan integral berulang pada jawaban di atas diperoleh: 4 2 x y
4
y 0 2D
2 x y
4
y 0 2D
√
√
.
/
√
.
/
(√ )
(√ )
(√ )
. 3. Hitunglah(
)
Apabila kita menghitung integral ini secara langsung seperti pada contoh sebelumnya, kita harus menghitung
∫
. Integral ini sangat sulit. Langkah selanjutnya adalah dengan menukar urutan variabelnya.Daerah integrasinya adalah
}
dapat diubah menjadi*| +
. Gambar daerah integrasinya ( yang terakhir) adalah:Jelas, 2
y
4 x
(
)
(
)
(
)
.BAB III PENUTUP 3.1 RANGKUMAN
1. Integral lipat dua dari fungsi z = f (x,y) pada persegi panjang teretutup P didefinisikan sebagai limit jumlah Riemann ini (bila limitnya ada, dan ditulis dengan lambang
f x y dxdy
p ) , ( 0 lim i j i i n j m i y x q p f
) , ( 1 1 atau
f x y dA
p ) , ( 0 lim i j ij n j m i A q p f
) , ( 1 12. Teorema cara menghitung integral lipat dua dengan integral berulang. Jika fungsi z =f(x,y) kontinu pada daerah persegi panjang tertutup p={a,b} x {c,d} maka:
p d c b a d c b a dy dx y x f dxdy y x f dA y x f ( , ) ( , ) ( , ) . 1
p b a d c b a d c dx dy y x f dydx y x f dA y x f ( , ) ( , ) ( , ) . 23. Jika z = f (x,y) kontinu pada daerah persegi panjang tertutup P =
,-
,-
, maka
4. Sifat integral lipat dua hampir mewarisi semua sifat integral tunggal. Berikut sifat integral lipat dua:
a. Sifat linear
Jika fungsi f dan g terintegral pada P
, dan α dan β
adalah konstanta, maka,-
b. Sifat urutan
Jika fungsi f dan g terintegral pada P dan f(x,y) ≥ g (x,y) pada P, maka
c. Sifat penjumlahan (aditif)
Jika fungsi f terintegral pada P yang dapat ditulis sebagai P=P1+P2, dengan P1dan P2 tidak saling tumpang tindih, maka
5. Misalkan fungsi z = f(x, y) terdefinisi pada daerah D dan fungsi z = F(x, y) yang terdefinisi pada persegi panjang tertutup P yang tepat memuat D dengan persamaan
F(x, y) =
{
Jika fungsi F terintegralkan pada P , maka integral lipat dua dari fungsi f pada D didefinisikan sama dengan integral lipat dua pada P , yaitu
6. Cara menghitung integral suatu daerah:
a. Menentukan batas-batas daerah integrasi. b. Menggambar daerah pengintegralannya.
c. Menuliskan integrla lipat dua sebagai integral berulang, baik dengan urutan
ataupun
.d. Menghitung integral tersebut.
3.2 SARAN
Untuk mampu memahami dan menguasai materi integral lipat dua pada daerah persegi panjang dan daerah sebarang, mahasiswa perlu memperhatikan hal-hal sebagai berikut:
1. Mengetahui dan memahami konsep integral Riemann. 2. Mengetahui definisi integral lipat dua.
3. Memahami arti geometri integral lipat dua.

![Gambar pertama memperlihatkan daerah D yang proyeksinya pada sumbu Y adalah selang tertutup [c,d]](https://thumb-ap.123doks.com/thumbv2/123dok/2007463.3018821/24.1167.190.1063.235.1289/gambar-pertama-memperlihatkan-daerah-proyeksinya-adalah-selang-tertutup.webp)