NON-EXHAUSTIVE SEARCH DENGAN TAIL-SCAN PADA ESTIMASI ARAH KEDATANGAN SINYAL BERBASIS REKONSTRUKSI SPARSE

NON-EXHAUSTIVE SEARCH

DENGAN

TAIL-SCAN

PADA ESTIMASI ARAH KEDATANGAN SINYAL

BERBASIS REKONSTRUKSI

SPARSE

LAPORAN KEMAJUAN 3

Oleh

KOREDIANTO USMAN

NIM: 33213002

(Program Studi Teknik Elektro dan Informatika)

NON-EXHAUSTIVE SEARCH

DENGAN

TAIL-SCAN

PADA

ESTIMASI ARAH KEDATANGAN SINYAL BERBASIS

REKONSTRUKSI

SPARSE

Oleh

Koredianto Usman NIM: 33213002

(Program Studi Teknik Elektro dan Informatika) Institut Teknologi Bandung

Menyetujui Tim Pembimbing

Tanggal : 10 Desember 2015

Ketua,

(Prof. Andriyan Bayu Suksmono, Ph.D)

Anggota,

ABSTRAK

Estimasi arah kedatangan sinyal adalah teknik estimasi sudut kedatangan objek yang dideteksi dengan peralatan radar atau sonar. Teknik klasik untuk estimasi arah kedatangan antara lain adalah MVDR, MUSIC, dan ESPRIT. Peran dari

Compressive Sensing (CS) adalah pengurangan jumlah sampel akuisisi pada sisi

penerima. Pengurangan ini memberi dampak pada kecilnya data rate, sehingga

dimungkinkan membangun sistem radar terdistribusi yang saling mengirimkan data untuk memantau daerah yang luas. Teknik terkini dalam estimasi arah kedatangan sinyal dengan compressive sensing adalah dengan metoda sparsitas sudut. Teknik ini

mengasumsikan sinyal datang berasal dari beberapa sumber berbeda yang berjumlah terbatas. Teknik yang telah dikembangkan peneliti untuk skema ini adalah dengan menggunakan sensing matrix A yang tersusun atas steering vector yang berasal dari

semua sudut yang dipindai (-900 _{sampai 90}0_{). Teknik pindai pada semua sudut ini}

disebut sebagaiexhaustive search. Teknikexhaustive search ini memiliki permasalahan

pada besarnya matrik sensing A, sehingga proses rekonstruksi CS menjadi berat.

Kemungkinan pemindaian pada rentang sudut yang lebih kecil(non-exhaustive search),

yaitu pada sudut-sudut yang diduga mengandung sumber sinyal diusulkan pada penelitian ini. Pengujian yang dilakukan pada penelitian ini menunjukkan bahwa teknik ini memiliki tingkat keberhasilan yang baik. Masih terdapat masalah tambahan yang harus diselesaikan pada tekniknon-exhaustive search yaitu rekonstruksi CS tidak

konvergen jika rentang sudut pindai terlalu sempit. Penambahan pemindaian di luar area pemindaian utama (tail-scan) untuk mengatasi masalah ini juga dilakukan pada

laporan ini. Di samping penelitian pada teknik tail-scan, pada Kemajuan Tahap 3 ini

juga dilakukan teknik alternatif penyelesaian permasalahan rekonstruksi CS dengan algoritma baru yang disebut dengan metode titik berat. Teknik metode titik berat ini juga dibahas dalam laporan ini.

DAFTAR ISI

ABSTRAK . . . ii

DAFTAR ISI . . . iii

DAFTAR GAMBAR . . . v

DAFTAR TABEL . . . vi

BAB I Pendahuluan . . . 1

I.1 Latar Belakang . . . 1

I.2 State of The Art . . . 3

I.3 Premis dan Hipotesis . . . 4

I.4 Perbandingan Kemajuan 3 dengan Kemajuan sebelumnya . . . . 5

I.5 Publikasi terkait . . . 7

I.6 Kontribusi dan Kebaruan . . . 7

BAB II Landasan Teori . . . 8

II.1 Model matematis sistem . . . 8

II.2 Compressive Sensing . . . 9

II.3 Compressive sensing pada estimasi DoA . . . 11

II.4 CS solver dengan CVX Programming . . . 14

BAB III Metode yang diusulkan . . . 15

III.1 Teknik Non-Exhaustive Search . . . 15

III.2 Teknik Tail-scan . . . 17

III.3 Metode Titik Berat . . . 20

BAB IV Hasil kemajuan . . . 28

IV.1 Hal yang telah dilakukan pada semester berjalan . . . 28

IV.1.1 Hasil simulasi tekniknon-exhaustive search dengantail scan 28 IV.2 Perbandingan akurasi regular dan random tail-scan tanpa interpolasi . . . 29

IV.3 Perbandingan akurasi regular dan random tail-scan dengan interpolasi . . . 30

IV.4 Perbandingan kegagalan konvergensi pada tail-scan . . . 30

IV.5 Perbandingan waktu komputasi pada skema tail-scan . . . 31

BAB V Penutup . . . 32

DAFTAR PUSTAKA . . . 33

BAB Lampiran A : Faktorisasi QR . . . 36

1 Faktorisasi QR untuk Over determined system . . . 38

BAB Penyelesaian Persamaan Underdetermined dengan faktorisai QR . . . 40

2 QR Faktorisasi dengan Transformasi Householder . . . 42

2.1 Prinsip: Membuat elemen nol pada vektor . . . 42

2.2 Pemaktoran Matrik ke komponen Q dan R . . . 46

2.3 Contoh Ilustrasi . . . 48

2.4 QR dekomposisi dengan Column Pivoting . . . 50

DAFTAR GAMBAR

I.1 Perbandingan pekerjaan penelitian yang dilakukan pada Seminar Kemajuan I, II, dan III. . . 6 I.2 Publikasi yang telah dilakukan dan yang direncanakan . . . 7

II.1 Antennas arrangement in ULA with distance d between element . . . 8

II.2 Ilustrasi skema sparsitas sudut. Sensing matrixAdisusun daristeering vector sudut-sudut yang dipindai . . . 13

III.1 Ilustrasi exhaustive search. Algoritma memindai pada semua arah

untuk memperoleh arah sumber sinyal . . . 15 III.2 Blok diagram skema non-exhaustive search dengan fungsi pemindaian

kasar . . . 16 III.3 Ilustrasi non-exhaustive search. (a) Skema dalam diagram arah/sudut

dalam koordinat polar (b). dalam koordinat kartesian . . . 17 III.4 Ilustrasi tracking object dengan teknik non-exhaustive search serta

update scanning window pada setiap waktu. (a),(b), dan (c) pergerakan objek beserta update scanning window yang bersesuaian. (d). ilustrasi pergeseran scanning window pada setiap waktu; W1, W2, W3 adalah scanning window berturut-turut pada t1, t2 dan t3 . . . . 18 III.5 Ilustrasi detail tentang proses update scanning window dengan

menggunakan median dari posisi objek. (a) hasil scanning kasar dengan algoritma klasik pada semua sudut,(b) penerapan scanning window pada sudut yang dianggap memiliki objek, (c) objek bergerak sehingga puncak scanning bergeser menuju batas window. (d). update scanning window, sehingga puncak scanning berada di tengah scanning window . . . 19 III.6 Hasil simulasi: perbandingan skema exhaustive search terhadap . . . . 20 III.7 Non-exhaustive search dengan tail-scan . . . 20

III.8 Non exhaustive search dengan tail scan. (a) uniform tail scan, (b) random tail scan . . . 21 III.9 Solusi persamaan Ax=yterletak pada garis (A). Solusi dari Norm-L1

(B) . . . 21 III.10 (a). Iterasi awal dengan k0 yang cukup besar sehingga kurva Ax=y

dan _kx_k1 =k0 berpotongan di P1 dan P2. Titik tengah M1 dipilih

sebagai iterasi berikutnya. (b). Norm di M1 dipilih sebagai nilai k

berikutnya. Proses ini diulangi sehingga diperoleh titik yang konvergen. 22 III.11 (a). Kasus dimensi 3, _kx_k1=k0 membentuk oktahedron. Solusi dari

Ax=y dengan matrik A 1x3 adalah suatu bidang. Jika k0 cukup

besar, _kx_k1=k0 akan memotong Ax=y. (b). Bidang perpotongan

dengan titik sudut P1 sampai P5. Titik M1 dipilih sebagai kombinasi

DAFTAR GAMBAR

III.12 Faktorisasi QR Householder dengan pivot kolom (a). Pivot kolom dengan urutan L2-norm dari yang terbesar ke yang terkecil (b). Pivot kolom dengan urutan L2-norm dari yang terkecil ke yang terbesar . . 25 III.13 Perpotongan antara oktahedron norm L1 dengan solusi dari fungsi

objektif yang berupa garis. Titik potong bidang dan garis dinotasikan denganP1 danP2. TitikM1 yang merupakan kombinasi konveks dari

P1 dan P2 diilustrasikan pada gambar kanan . . . 26

DAFTAR TABEL

I.1 Perbandingan Referensi State of The Art . . . 4 I.2 Premis dan Hipotesis yang dirumuskan dalam penelitian . . . 5

BAB I Pendahuluan

I.1 Latar Belakang

Teknik compressive sensing untuk estimasi arah kedatangan sinyal memperoleh

perhatian yang besar pada dekade saat ini. Meski pun CS mulai dianggap sebagai bidang ilmu yang cukup matang pada pertengahan tahun 2000an (Donoho (2006), Candes dan Wakin (2008), Baraniuk (2007)), teknik yang mendasarinya telah berkembang lebih dahulu, seperti matching pursuit (Mallat dan Zhang (1993)), basis

pursuit Chen dkk. (2001), algoritmagreedy (Tropp (2004)) maupunwavelet. Penerapan

teknik CS telah dilakukan pada berbagai bidang, antara lain: kompresi data (Candes dan Wakin (2008), Wahidah dan Suksmono (2010)),channel coding(Candes dan Wakin

(2008)), MRI imaging (Swastika dan Haneishi (2012)), wireless channel estimation

(Hayasi dkk. (2013)).

Saat ini, teknik CS telah pula diterapkan pada bidang radar. Secara umum radar memiliki tiga fungsi, yaitu: estimasi arah kedatangan, estimasi jarak, dan estimasi kecepatan. Pada bidang estimasi arah kedatangan sinyal, teknikCompressive Sening

ditujukan untuk mengurangi jumlah sampel yang harus diakuisisi oleh penerima. Jumlah sampel yang sedikit akan memberikan keuntungan pada kebutuhanbandwidth

telekomunikasi yang rendah. Dengan demikian, skema distributed radar system dapat

diimplementasikan lebih mudah untuk menjangkau wilayah yang luas.

Secara perkembangan, teknik estimasi arah kedatangan sinyal sendiri telah berkembang sejak era analog, sampai dengan era digital. Pada era digital, teknik estimasi arah kedatangan sinyal dipelopori antara lain oleh algoritma Capon atau MVDR (Dmochowski dkk. (2007)). Dengan memanfaatkan kovariansi matrik sinyal penerima, serta steering vector pada arayh yang dipindai, algoritma ini berhasil

memperoleh estimasi arah kedatangan sinyal dengan spektrum puncak yang cukup tajam. Schmidt melakukan terobosan pada bidang estimasi DoA ini dengan mengusulkan algoritma MUSIC (Multiple Signal Classification, Schmidt (1986)).

Algoritma ini membuka dimensi baru dengan penggunaan teknik sub-space yang

berasal dari dekomposisi nilai eigen dari matrik kovariansi. Roy dkk. (1986) juga

menggunakan teknik sub-space untuk melakukan estimasi arah kedatangan sinyal.

of Signal Parameters via Rotational Invariant Techniques). Veen dan Buckley (1988)

mengajukan skema yang sederhana dibandingkan dengan MUSIC dan ESPRIT, yaitu skema delay and sum (DAS). Skema ini memiliki prinsip estimasi arah kedatangan

dengan mendelay fasa dengan suatu mekanisme pada setiap elemen antena. Pada nilai fasa tertentu, diperoleh sinyal terima terkuat. Sudut yang berkorespondensi dengan delay tersebut diambil sebagai estimasi arah kedatangan sinyal.

Teknik klasik pada umumnya bersandar pada teorema sampling klasik Shannon-Nyquist dalam mengakuisisi data. Akuisisi data dilakukan dengan kecepatan sampling sekurang-kurangnya dua kali frekuensi tertinggi sinyal informasi. Akibat dari adanya skema akuisisi ini, data yang diolah oleh algoritma klasik adalah sangat besar. Teknik distributed radar system yang bersandar pada komunikasi antar unit

(seperti wireless sensor network) akan memiliki masalah jika harus mentransmisikan

data besar setiap saat. Oleh karena itu teknik CS untuk DoA sangat diperlukan pada kondisi tersebut.

Secara umum, terdapat tiga kategori besar dalam pemanfaatancompressive sensing

untuk estimasi arah kedatangan sinyal: skema sparsitas waktu, skema sparsitas ruang, dan skema sparsitas sudut. Sparsitas waktu mengambil asumsi bahwa sinyal yang diterima sensor bersifatsparse secara sampel per sampel. Mengambil asumsi ini, maka

pengurangan sampel dilakukan dalam ranah waktu. Penelitian yang memanfaatkan skema ini antara lain adalah Wang dkk. (2009). Di sisi lain, skema sparsitas ruang mengambil asumsi bahwa sinyal yang diterima suatu sensor adalah sama dengan sinyal yang diterima oleh sensor yang lain dengan perbedaan pada fasa. Dengan asumsi ini, maka jumlah sensor dapat dikurangi sampai menjadi sebanyak sinyal yang diterima. Pengurangan jumlah sensor berarti juga mengurangi jumlah sampel yang diterima. Penelitian yang memanfaatkan skema ini antara lain adalah Gurbuz dan McClellan (2008), dan Jouny (2011). Skema sparsitas sudut mengambil asumsi bahwa sinyal yang datang hanya pada sudut-sudut tertentu. Dengan asumsi ini, maka algoritma estimasi arah kedatangan dilakukan dengan mencari spektral tak nol pada matrik sinyal penerima yang disusun terdiri dari semua sudut arah kedatangan yang dipindai. Penelitian yang menggunakan skema ini antara lain adalah Gorodnitsky dan Rao (1997) dan Stoica dkk. (2011).

Skema sparsitas sudut memiliki keuntungan utama dari pada skema sparsitas waktu dan sparsitas sensor yaitu pada jumlah sampel yang sedikit. Penelitian Gorodnitsky dan Rao (1997) mengusulkan penggunaan satu sampel untuk estimasi arah kedatangan. Untuk keperluan rekonstruksi, Gorodnitsky dan Rao menggunakan algoritma Focal Underdetermined System Solver (FOCUSS). Dalam lingkungan dengan derau yang

yang ditawarkan mengalami masalah pada lingkungan dengan derau tinggi (Usman dkk. (2014)). Teknik multi sampel yang dilakukan oleh Stoica dkk. (2011) memperbaiki performa yang lebih baik, namun proses komputasi yang lebih tinggi. Proses komputasi yang lebih tinggi ini disebabkan antara lain oleh jumlah sampel yang lebih banyak dan basis perhitungan pada bilangan kompleks. Permasalahan yang juga perlu diatasi pada skema sparsitas sudut adalah pemindaian yang dilakukan pada semua arah menyebabkan sensing matrix A memiliki dimensi yang sangat besar. Hal ini

menyebabkan proses rekonstruksi CS berjalan lambat. Penelitian yang dilakukan ini adalah untuk menjawab permasalahan tersebut.

I.2

State of The Art

Pada bagian ini, dipilih tiga referensi yang dijadikan sebagaistate of the art. Pemilihan

tiga referensi ini dikarenakan karena ketiga referensi ini adalah referensi langsung yang terkait pada upaya penyelesaian masalah yang diusulkan. Ketiga referensi ini adalah Gorodnitsky dan Rao (1997), Stoica dkk. (2011), dan Dai dkk. (2013). Detail dari ketiga referensi tersebut adalah sebagai berikut :

1. Gorodnitsky dan Rao (1997): Sparse Signal Reconstruction form Limited data Using FOCUSS: a re-weighted minimum norm algorithm, Publikasi : IEEE

Transaction on Signal Processing, Vol. 45, No.3 (Referensi #1)

2. Stoica, Babu, dan Li (2011): SPICE: A sparse covariance-based estimation method for array processing, Publikasi : IEEE Transaction of Signal Processing,

Vol.59, No.2 (Referensi #2)

3. Dai, Xu, dan Zhao (2013): Direction-of-Arrival Estimation Via Real-Valued Sparse Representation, Publikasi : IEEE Antennas and Wireless Propagation

Letters (Referensi #3)

Referensi #1 menjadi referensi utama dari skema sparsitas sudut. Sejauh yang penulis teliti, Referensi #1 dapat dianggap sebagai karya seminal dari teknik sparsitas sudut. Hal yang menarik dikaji adalah bahwa teknik ini dapat bekerja dengan menggunakan satu sampel sinyal saja. Referensi #2 membahas tentang teknik rekonstruksi dengan metode covariance-based. Teknik ini memperbaiki hasil dari

Referensi #1 dalam hal ketahanan dalam lingkungan derau tinggi. Teknik ini mengakomodasi penggunaan multi sampel. Referensi #3 membahas tentang teknik penyederhaan perhitungan rekonstruksi compressive sensing dengan cara mengubah

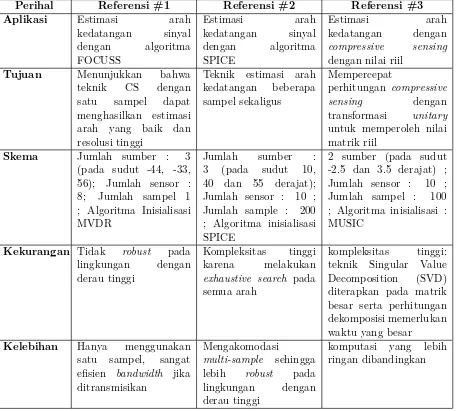
referensi ini penelitian ini dilakukan dan dikembangkan. Tabel I.1 memperlihatkan perbandingan tekniks dari ketiga referensi ini.

Tabel I.1. Perbandingan Referensi State of The Art

Perihal Referensi #1 Referensi #2 Referensi #3

Aplikasi Estimasi arah

kedatangan sinyal dengan algoritma FOCUSS

Estimasi arah kedatangan sinyal dengan algoritma SPICE

Estimasi arah

kedatangan dengan

compressive sensing

dengan nilai riil

Tujuan Menunjukkan bahwa

teknik CS dengan satu sampel dapat menghasilkan estimasi arah yang baik dan resolusi tinggi

Teknik estimasi arah kedatangan beberapa sampel sekaligus

Mempercepat

perhitungan compressive sensing dengan transformasi unitary

untuk memperoleh nilai matrik riil

Skema Jumlah sumber : 3

(pada sudut -44, -33, 56); Jumlah sensor : 8; Jumlah sampel 1 ; Algoritma Inisialisasi MVDR

Jumlah sumber : 3 (pada sudut 10, 40 dan 55 derajat); Jumlah sensor : 10 ; Jumlah sample : 200 ; Algoritma inisialisasi SPICE

2 sumber (pada sudut -2.5 dan 3.5 derajat) ; Jumlah sensor : 10 ; Jumlah sampel : 100 ; Algoritma inisialisasi : MUSIC

Kekurangan Tidak robust pada lingkungan dengan derau tinggi

Kompleksitas tinggi karena melakukan

exhaustive search pada semua arah

kompleksitas tinggi: teknik Singular Value Decomposition (SVD) diterapkan pada matrik besar serta perhitungan dekomposisi memerlukan waktu yang besar

Kelebihan Hanya menggunakan satu sampel, sangat efisien bandwidth jika ditransmisikan

Mengakomodasi

multi-sample sehingga lebih robust pada lingkungan dengan derau tinggi

komputasi yang lebih ringan dibandingkan

I.3 Premis dan Hipotesis

Pada Kemajuan II dilakukan simulasi lanjutan yaitu perbaikan skema yang ada dengan teknik non-exhaustive search. Dari percobaan-percobaan yang dilakukan, maka diperoleh premis-premis lanjutan, yaitu: 3). Skema sparsitas sudut dapat bekerja dengan sudut pindai yang lebih sempit (non-exhaustive search).

Pada Kemajuan III ini, dilakukan percobaan yang lebih intensif pada tekniktail-scan

serta pengembangan teknik rekonstruksi CS dengan dengan teknik titik berat (weight point) untuk memperoleh solusi yang dijamin kekonvergenannya. Premis-premis yang

diajukan untuk tahap ini adalah: 4). teknik tail-scan memiliki kinerja yang lebih baik dari pada tanpatail-scan, 5). Tail-scan uniform secara statistik memiliki kinerja yang

lebih baik dari padatail-scan random, 6). Rekonstruksi CS dengan menggunakan titik

berat dari bidang perpotongan normL1dan fungsi objektif memberikan solusi CS yang

dijamin kekonvergenannya.

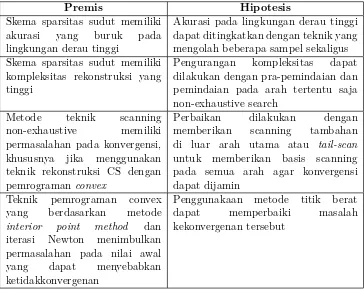
Tabel I.2. Premis dan Hipotesis yang dirumuskan dalam penelitian

Premis Hipotesis

Skema sparsitas sudut memiliki akurasi yang buruk pada lingkungan derau tinggi

Akurasi pada lingkungan derau tinggi dapat ditingkatkan dengan teknik yang mengolah beberapa sampel sekaligus Skema sparsitas sudut memiliki

kompleksitas rekonstruksi yang tinggi

Pengurangan kompleksitas dapat dilakukan dengan pra-pemindaian dan pemindaian pada arah tertentu saja non-exhaustive search

Metode teknik scanning non-exhaustive memiliki permasalahan pada konvergensi, khususnya jika menggunakan teknik rekonstruksi CS dengan pemrogramanconvex

Perbaikan dilakukan dengan memberikan scanning tambahan di luar arah utama atau tail-scan

untuk memberikan basis scanning pada semua arah agar konvergensi dapat dijamin

Teknik pemrograman convex yang berdasarkan metode

interior point method dan iterasi Newton menimbulkan permasalahan pada nilai awal yang dapat menyebabkan ketidakkonvergenan

Penggunakaan metode titik berat dapat memperbaiki masalah kekonvergenan tersebut

I.4 Perbandingan Kemajuan 3 dengan Kemajuan sebelumnya

algoritma tersebut. Pada Kemajuan I ini, belum dilakukan upaya untuk mempercepat perhitungan dengan mengurangi lebar sudut pindai. Pengurangan lebar sudut pindai dilakukan pada Kemajuan II. Proses yang dilakukan adalah memindai pada semua sudut untuk memperoleh arah kedatangan sinyal, setelah itu, pada proses berikutnya (prosesupdate), pemindaian dilakukan pada arah tertentu saja (non-exhaustive search)

pada arah yang diidentifikasi terdapat objek. Pada Kemajuan III permasalahan ketidakkonvergenan diatasi dengan dua cara yaitu dengan teknik tail-scan (uniform

dan random) dan dengan teknik rekonstruksi CS baru yang dikembangkan sendiri

menggunakan metode titik berat dari bidang perpotongan normL1 dan fungsi objektif

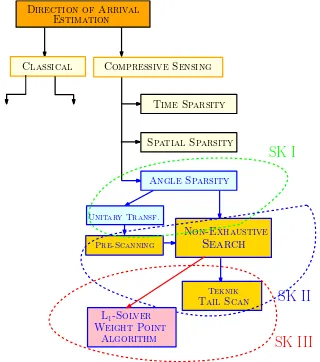
rekonstruksi. Penggunaan metoda titik berat ini dilakukan sebagai alternatif dari metoda iterasi Newton dengan kelebihan pada jaminan konvergensi. Gambar I.1 memperlihatkan skema penelitian yang dilakukan pada setiap kemajuan ini.

Direction of Arrival Estimation

Classical

Time Sparsity

Angle Sparsity Compressive Sensing

Spatial Sparsity

Unitary Transf.

Non-Exhaustive Search

Pre-Scanning

Teknik

Tail Scan

SK I

SK II

L₁-Solver Weight Point

Algorithm

SK III

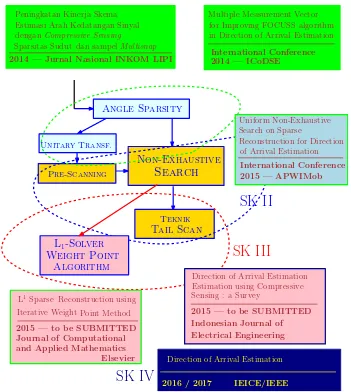
I.5 Publikasi terkait

Gambar I.2 memperlihatkan publikasi yang telah dan yang direncanakan pada setiap kemajuan.

Angle Sparsity

Unitary Transf.

Non-Exhaustive Search

Pre-Scanning

Teknik

Tail Scan

SK II

L₁-Solver Weight Point

Algorithm

SK III

Peningkatan Kinerja Skema Estimasi Arah Kedatangan Sinyal denganCompressive Sensing

Sparsitas Sudut dan sampelMultisnap

2014 — Jurnal Nasional INKOM LIPI

Multiple Measurement Vector for Improving FOCUSS algorithm in Direction of Arrival Estimation

2014 — ICoDSE

International Conference

Uniform Non-Exhaustive Search on Sparse

Reconstruction for Direction of Arrival Estimation

International Conference 2015 — APWIMob

Journal of Computational 2015 — to be SUBMITTED

L1_{Sparse Reconstruction using}

Iterative Weight Point Method

and Applied Mathematics Elsevier

Direction of Arrival Estimation Estimation using Compressive Sensing : a Survey

2015 — to be SUBMITTED Indonesian Journal of Electrical Engineering

SK IV

Direction of Arrival Estimation

IEICE/IEEE 2016 / 2017

Gambar I.2. Publikasi yang telah dilakukan dan yang direncanakan

I.6 Kontribusi dan Kebaruan

Kontribusi dan kebaruan yang diperoleh pada tahapan-tahapan penelitian yang telah dilakukan adalah:

• Teknik Non-Exhaustive Search

• Teknik Tail-Scan (uniform dan random)

BAB II Landasan Teori

II.1 Model matematis sistem

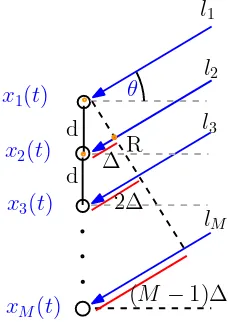
Untuk keperluan simulasi, maka model matematis dari sistem yang ditinjau perlu dijabarkan terlebih dahulu. Tinjau susunan antena (antenna array) yang terdiri dari

M buah elemen antena. Elemen antena ini disusun sehingga terletak pada satu garis,

dengan jarak antar antena konstan. Susunan ini disebut sebagaiuniform linear array / ULA. Misalkan bahwa sumber sinyal datang pada jarak yang jauh dengan sudut

kedatangan sebesar θ relatif terhadap garis normal susunan antena (Gbr. II.1). Jika jarak sistem antena ke sumber jauh lebih besar dari pada dimensi susunan antena, maka berkas yang sampai ke masing-masing antena dapat dianggap sejajar.

d

d θ

l1

l2

l3

lM ∆

2∆

(M −1)∆

R x1(t)

x2(t)

x3(t)

xM(t)

Gambar II.1. Antennas arrangement in ULA with distanced between element

Dengan menggunakan antena paling atas sebagai referensi, serta jarak antar elemen antena adalahd, maka perbedaan jarak tempuh pada masing-masing antena (∆) dapat

ditulis sebagai

∆ =d_·sin(θ). (II.1)

Perbedaan jarak ini berkorespondensi dengan delay fasa sebesar :

φ=2π

x=a_·s+n (II.3)

Pada pers.II.3,sadalah sinyal pada masukan antena (dengan dimensipkaliN snaps; p adalah jumlah objek),x menotasikan sinyal pada keluaran antena (dengan dimensi

M kali N snaps), n dalah white gaussian noise, dan a adalah array steering vector

atau array manifold. Steering vectora dapat dinyatakan sebagai :

a=h1 e−jψ _e−j(M−1)ψiT _(II.4)

Sebagai penerima, steering vector menyatakan bobot pada antena yang

berkorespondensi dengan arah penerimaan maksimum dari sinyal datang (main beam).

II.2

Compressive Sensing

Compressive Sampling/Sensing (CS), adalah pendekatan baru yang menyatukan

antara proses sampling dan kompresi. Dengan kekhususan bahwa sinyal yang disampling bersifat sparse (mayoritas sinyal adalah nol dan sedikit sisanya tak nol).

Dengan asumsi ini, maka teknik CS dapat digunakan untuk mensampling sinyal dengan rate yang jauh lebih kecil dari pada sampling rate klasik Nyquist. Pada

sampling rate yang rendah ini, CS tetap masih mampu untuk merekonstruksi sinyal semula. Kemampuan ini membuka peluang CS dapat menggantikan peralatan yang ada saat ini dengan peralatan yang bekerja berdasarkan prinsip CS yang efisien. Secara prinsip, pensamplingan dengan CS dilakukan dengan mengumpulkan secara random dari sampel lengkap.

Pada teknik sampling klasik Nyquist, proses sampling dan rekonstruksi secara prinsip adalah sederhana dibandingkan dengan sampling dan rekonstruksi pada CS. Proses sampling pada teknik sampling klasik dilakukan dengan melakukan pencuplikan pada sinyal analog dengan jarak antar sampel yang sama/konstan. Pada bagian rekonstruksi, sinyal hasil sampling difilter dengan filter Nyquist untuk memperoleh kembali sinyal semula.

diharapkan (secara statistik) sama atau mendekati sinyal asal.

Beberapa peralatan telah dikembangkan dengan prinsip CS ini. Antara lain adalah kamera-satu-piksel (Baraniuk (2007)), sparse MRI (Swastika dan Haneishi (2012)), spectra-denoising (Mingxia dkk. (2013)) dan sebagainya.

Formulasi matematika dari compressive sensing. Ada banyak cara untuk

menjelaskan prinsip kerja dari compressive sensing. Tapi yang akan dibahas di sini adalah dengan menggunakan prinsip ketidakpastian (uncertainty principle atau UP). Prinsip ini menyatakan bahwa suatu sinyal tidak mungkin secara bersamaan dapat dilokalisasi dengan baik pada ranah waktu dan frekuensi. Dengan kata lain, jika suatu sinyal terlokalisasi pada ranah waktu, maka sinyal tersebut tidak terlokalisasi pada ranah frekuensi. Sebaliknya jika suatu sinyal terlokalisasi pada ranah frekuensi, maka ia tidak terlokalisasi pada ranah waktu.

Jika suatu sinyal f tidak terlokalisasi pada suatu ranah, maka akan selalu dapat

dicari suatu transformasi Ψ pada f untuk menghasilkan suatu sinyal textbfF yang

bersifat sparse. Dengan kata lain:

F = Ψf (II.5)

Pada sinyal sparse F tersebut, CS dapat dilakukan dengan mengalikan di awal

(pre-multiplying) dengan suatu pencuplik Φ yang merupakan suatu matrik CS.

g= ΦF = ΦΨf (II.6)

Jika sinyal asal,f dan hasil transformasinya,F memiliki panjang N, maka sinyal f,

dapat direkonstruksi kembali dari sinyalg dengan panjangM (M<<N), dengan syarat M lebih besar dari suatu nilai yang diberikan oleh persamaan

M _≥C_·µ2(Φ,Ψ)_·K_·log(N) (II.7)

dimana K menyatakan tingkat sparsitas dari sinyal f, C adalah suatu konstanta (sekitar 2), dan µ(Φ, P si) menyatakan fungsi pengukur tingkat koherensi dari Φ dan Ψ. Tingkat koherensi ini diberikan oleh

µ(Φ,Ψ) = max

φ_∋Φ,ψ_∋Ψ|hφ, ψi| (II.8)

Perkalian antara fungsi sparsitas Ψ dan fungsi sampling Φ dalam bentuk matrik tersebut dapat dinyatakan sebagai matrik sensing A :

Dengan demikian

g= ΨΦf=Af (II.10)

Proses rekonstruksi secara matematis dilakukan menyelesaikan II.10 dalam f.

Namun, oleh karenaf memilikiN nilai yang tidak diketahui, sedangkan II.10 memiliki M buah persamaan (M << N), maka penyelesaian II.10 membelikan banyak alternatif solusi bagi f. Kondisi ini disebut sebagai ill-posed problem.

Agar solusi menjadi unik dan sama atau mendekati dari sinyal semula, maka

dilakukan optimasi dari solusi yang diperoleh. Optimasi yang umum dilakukan adalah dengan menggunakan optimisasinormorde-n. Orde yang lazim dipakai dengan asumsi

sinyalf bersifatsparse adalah norm- orde 1.

Proses rekonstruksi CS ini secara umum dapat dituliskan sebagai

min_|f_|1 s.t. A_·f =g (II.11)

Minimisasi _|f_|1 berarti mencari solusif yang paling sparse.

Pada lingkungan yang memiliki derau atau noise, maka sinyal terima akan

memasukkan faktor derau ini, sehingga permasalahan CS seperti pada II.10 menjadi :

g=Af+n (II.12)

Proses rekonstruksi CS dengan demikian dimodifikasi menjadi:

min_|f_|1 s.t. A_·f₋g_≤ǫ (II.13)

Dengan ǫ adalah suatu bilangan kecil.

II.3

Compressive sensing

pada estimasi DoA

Pada bidang radar yang ditinjau, khususnya pada algoritma estimasi arah kedatangan sinyal (Direction of Arrival Estimation- DoA), terdapat beberapa skema CS yang telah

dilakukan pada penelitian terdahulu. Penerapan CS pada estimasi DoA secara umum terbagi ke dalam tiga skema : sparsitas waktu (Gurbuz dan McClellan (2008), Kim dkk. (2012)), sparsitas ruang (Wang dkk. (2009), Wang dkk. (2010)), and sparsitas sudut (Gorodnitsky dan Rao (1997), Stoica dkk. (2011), Usman dkk. (2014)).

Sparsitas waktu mengambil asumsi bahwa sinyal yang dikirim adalah sinusoidal, oleh karena itu, sinyal terima bersifat sparse dalam waktu (atau frekuensi). Sinyal terima

setial blok sinyal terima ini dikalikan-sebelum (pre-multiplied) dengan sensing matrix

A (berukuran M kali k, dengan k << N) untuk memperoleh sinyal keluaran y yang berdimensi M kali k, jauh lebih kecil dari pada ukuran sinyal masukkan semula x.

Untuk proses estimasi arah kedatangan, sinyal yang telah dikompres ini kemudian dikembalikan ke sinyal semula sebelum algoritma DoA diterapkan.

Sparsitas ruang memiliki prinsip kerja yang mirip dengan sparsitas waktu. Jika sparsitas waktu mengasumsikan bahwa sinyal tersebut sparse dalam waktu, maka sparsitas ruang mengasumsikan bahwa masing-masing antena pada susunan antena penerima sebenarnya menerima sinyal yang sama dengan perbedaan hanya pada waktu kedatangan (delay). Dengan demikian, sinyal terima diasumsikan bersifatsparse pada

arah antena, atau ruang. Sinyal yang dikumpulkan oleh M buah antena, seperti halnya pada sparsitas waktu, memiliki dimensi M kali N. Proses sensing dilakukan dengan dengan mengalikan sinyal terima dengan sensing matrix A yang berdimensi k kali N. Seperti halnya sparsitas waktu, sinyal semula perlu direkonstruksi ulang dengan sebelum estimasi arah kedatangan dapat dilakukan. Dibandingkan dengan sparsitas waktu, skema sparsitas ruang memiliki kekurangan yaitu tingkat kompresi yang rendah, sedangkan kelebihannya adalah ketahanan sinyal terhadap derau lebih baik, serta lebih mudah direalisasikan dalam bentuk perangkat keras, karena matrik sensing A telah secara langsung memberikan arah panduan pada pembuatan perangkat kerasnya. Skema sistem penerima dengan sparsitas ruang dapat dilihat pada Wang dkk. (2009) dan Wang dkk. (2010).

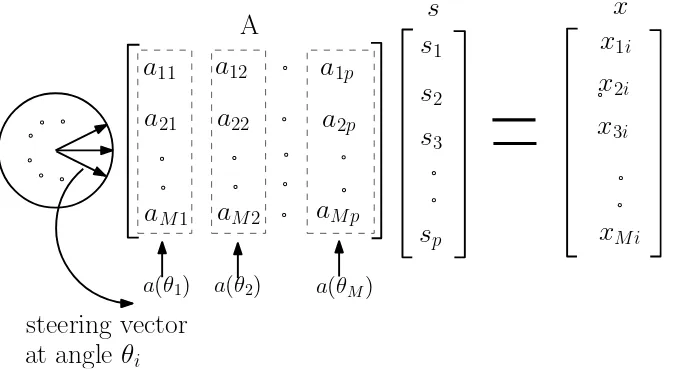
Sparsitas sudut memiliki pendekatan yang berbeda dibandingkan dengan sparsitas waktu dan sparsitas ruang sebelumnya. Skema sparsitas sudut tidak melakukan kompresi pada arah waktu dan ruang. Skema ini mengasumsikan bahwa sinyal yang diterima berasal dari sejumlah sumber sinyal yang terbatas. Beberapa sumber sinyal ini datang pada sudut-sudut yang berbeda. Berdasarkan pada anggapan ini, maka konstruksi permasalahan CS dilakukan dengan menggunakan sensing matrik A yang tersusun atassteering vector dari sinyal datang. Deskripsi matematis yang lebih rinci

diberikan pada sub-bab berikutnya. CS formulasi dilakukan dengan menggabungkan sensing matrix A, sparse vektor s, dan snapshot dari sinyal terima x. Rekonstruksi

CS tersebut dituliskan sebagai

A_·s=x (II.14)

Jika terdapat derau AWGN, maka Rekonstruksi CS tersebut dimodifikasi menjadi (analogi dengan Persamaan II.12):

A_·s=x+n. (II.15)

signifikan dibandingkan dengan skema sparsitas waktu dan sparsitas ruang, karena skema ini memerlukan sangat sedikit sinyal terima, serta proses estimasi DoA dilakukan bersamaan dengan rekonstruksi CS. Dengan kata lain, penyelesaian CS pada sparse

matrik s sekaligus juga adalah penyelesaian masalah estimasi arah kedatangan. Estimasi arah kedatangan sinyal diperoleh berdasarkan posisi element tak nol dari dari matrik solusi sparse s (Gorodnitsky dan Rao (1997)).

Gambar II.2 mengilustrasikan proses penyusunan konstruksi CS teknik sparsitas sudut.

a

11

a

21

a

M1

a

12

a

22

a

M2

a

1p

a

2p

a

M p

A

s

1

s

2

s

3

s

p

x

1i

x

2i

x

3i

x

M i

s

x

a(θ1) a(θ2) a(θM)

steering vector

at angle

θ

i

Gambar II.2. Ilustrasi skema sparsitas sudut. Sensing matrix A disusun dari steering vector sudut-sudut yang dipindai

Meski pun memiliki keuntungan ini, skema sparsitas sudut memiliki kelemahan, yaitu kurang tahan terhadap derau lingkungan. Hal ini diverifikasi oleh Usman dkk. (2014). Pada penelitian tersebut, Usman dkk. (2014) mengusulkan peningkatan performa sinyal dengan menggunakan teknik multi-snaps CS. Skema multi-snaps CS ini dilakukan dengan memperluas vektor sinyal terimaxmenjadi beberapa snap-shots. Solusi sparse s dengan demikian akan mengikuti perluasan ini. Dengan kata lain, vektor s terdiri dari beberapa kolom, yang masing-masing kolom berkorespondensi dengan hasil estimasi arah kedatangan pada setiap snap-shots. Estimasi DoA dilakukan dengan merata-ratakan nilai estimasi pada setiap snap-shots. Dengan demikian estimasi yang diperoleh menjadi lebih robust dibandingkan dengan hanya menggunakan satu snap-shot.

Upaya untuk melakukan perbaikan skema sparsitas sudut dilakukan pula oleh Stoica dkk. (2011) secara terpisah. Skema yang diusulkan oleh Stoica dkk. (2011) diistilahkan dengan independently covariance-based estimation technique (SPICE). Skema Stoica

Permasalahan lainnya dari sparsitas sudut adalah besarnya sensing matrix A.

Sebagaimana yang telah dibahas sebelumnya, sensing matrix A disusun berdasarkan

steering vector dari arah kedatangan yang dipindai. Pemindaian yang dilakukan pada

semua arah kedatangan sinyal (dari₋900_{sampai 90}0_{) disebut denganexhaustive search.}

Bab selanjutnya membahas dengan terperinci tentangexhaustive search tersebut serta

skema peningkatan yang diusulkan.

II.4 CS solver dengan CVX Programming

Ada beberapa CS solver yang dapat digunakan untuk menyelesaikan permasalahan estimasi sudut dengan rekonstruksi sparse. Dua solver yang umum dipakai adalah CVX-programming dan l1-magic. CVX-programming dikembangkan oleh

Boyd (2014), sedangkan l1-magic dikembangkan oleh oleh Candes dan Romberg

(2005). CVX-programming bersifat umum dengan kemampuan melakukan optimasi pada berbagai permasalahan pemrograman linier (Linear Programming - LP). CVX-programming juga dapat mengoptimasi pilihan solusi dengan konstrain norm. Dengan demikian, CVX-programming bersifat sangat fleksibel. Engine solver yang

digunakan pada CVX-programming antara lain adalah SDPT3 and SeDumi. Terdapat pula solver lain yang berlisensi yang dapat digunakan pada cvx seperti Gurobi dan MOSEK (Boyd (2014)). Untuk menyelesaikan persamaan CS seperti yang terdapat pada persamaan ??, pada CVX-programming, dapat kita tuliskan seperti contoh

berikut:

begin cvx

variable s(n) complex; minimize(norm(s,1)); subject to

BAB III Metode yang diusulkan

III.1 Teknik Non-Exhaustive Search

Sebelum dibahas tentang teknik non-exhaustive search, terlebih dahulu akan dibahas tentang metodeExhaustive search. Exhaustive search adalah upaya untuk menemukan

arah kedatangan sinyal dengan melakukan pemindaian pada semua arah kedatangan sinyal yang mungkin. Peneliti sebelumnya melakukan pemindaian secara exhaustive

ini. Pada makalahnya, Gorodnitsky dan Rao (1997) melakukan pemindaian pada semua sudut antara₋900 _{sampai 90}0_{. Stoica dkk. (2011) melakukan pemindaian dari} −900 sampai 900 dengan resolusi 0.10, dengan demikian terdapat 1800 arah pindai yang berkorespondensi dengan matriks sensing A yang berdimensi M kali 1800. Hal yang sama dilakukan oleh Usman dkk. (2014).

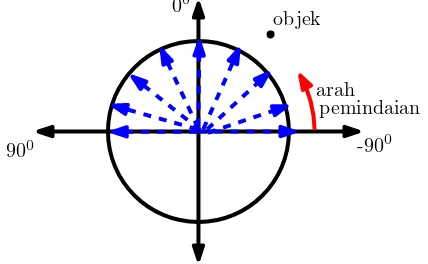
Gambar III.1 menunjukkan ilustrasi pemindaian dengan teknik exhaustive search.

objek

arah pemindaian

-900

900

00

Gambar III.1. Ilustrasiexhaustive search. Algoritma memindai pada semua arah untuk

memperoleh arah sumber sinyal

Permasalahan yang dihadapi oleh teknik exhaustive search, seperti yang telah

dikemukakan sebelumnya, adalah besarnya sensing matrix A. Sensing matriks yang besar memerlukan proses komputasi rekonstruksi CS yang besar, sumber daya yang tinggi, serta waktu yang lama. Penyelesaian permasalahan ini diusulkan pada sub-bab berikutnya yang membahas tentang pemindaiannon-exhaustive search.

Kemajuan yang dicapai pada penelitian ini berkisar pada eksplorasi teknik

non-exhaustive search. Teknik ini adalah perbaikan dari teknik exhaustive search

rentang yang lebih sempit ini dimungkinkan jika telah ada gambaran tentang arah sumber sinyal.

Untuk keperluan memperoleh gambaran tentang arah sumber sinyal tersebut, maka diperlukan suatu pemindaian kasar, misalnya dengan menggunakan estimasi DoA klasik (DAS, MVDR, MUSIC, atau ESPRIT). Setelah gambaran kasar arah kedatangan sinyal ini diperoleh, maka proses DoA selanjutnya dilanjutkan dengan teknik CS dengan rentang sudut sempit, yang diperbarui setiap saat, sesuai dengan arah gerakan objek. Skema pemindaian kasar sebelum teknik CS disebut dengan istilah pra-pemindaian.

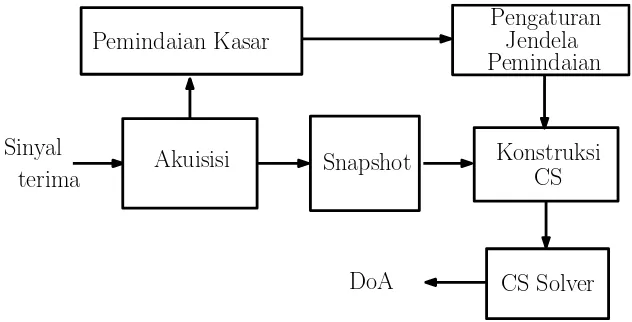
Skema non-exhaustive search dengan pra-pemindaian selengkapnya diberikan pada Gambar III.2.

Akuisisi Pemindaian Kasar

Pengaturan

CS

CS Solver

Snapshot Konstruksi

DoA Sinyal

terima

Jendela Pemindaian

Gambar III.2. Blok diagram skema non-exhaustive search dengan fungsi pemindaian

kasar

Pada Gambar III.2 tersebut, sinyal mula-mula diakuisisi oleh sistem antena penerima. Pada awal operasi, sinyal dimasukkan ke blok pemindaian kasar. Proses pada blok pemindaian kasar ini bertujuan untuk memperoleh gambaran umum tentang posisi sinyal. Blok pemindaian kasar ini dapat menggunakan salah satu algoritma klasik, seperti DAS, MVDR, MUSIC, dan ESPRIT. Pada proses kemajuan ini II ini, digunakan teknik MVDR. Teknik ini sederhana serta memiliki resolusi yang tinggi. Skema MUSIC dan ESPRIT memerlukan komputasi yang lebih tinggi, sedangkan DAS memiliki resolusi yang rendah.

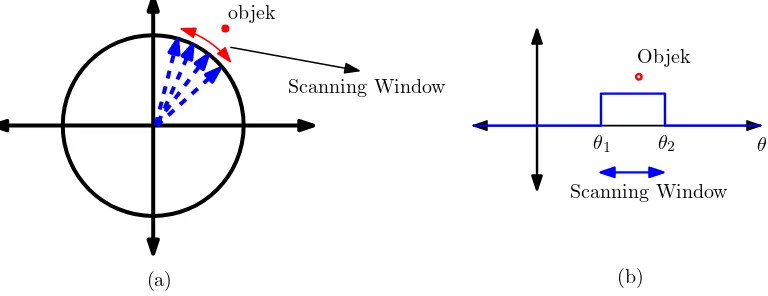
Gambar III.3 menunjukkan ilustrasi skema non-exhaustive search. Pada gambar tersebut, rentang sudut pemindaian dinyatakan sebagai jendela pindai (scanning window).

Tracking objek pada skema CS-DoA. Keuntungan utama pada skema yang

objek

Scanning Window

θ1 θ2

Scanning Window

θ

Objek

(a) (b)

Gambar III.3. Ilustrasi non-exhaustive search. (a) Skema dalam diagram arah/sudut dalam koordinat polar (b). dalam koordinat kartesian

pada interval tertentu, dan pengambilan sampel sinyal yang sedikit setiap kali pengambilan. Jendela pemindaian (scanning window) dapat digeser-geser pada setiap iterasi menyesuaikan dengan dengan posisi objek.

Untuk melakukan update scanning window ini, maka diperlukan suatu skema update. Pada penelitian ini, skema update dilakukan dengan terlebih dahulu menetapkan lebar scanning window (konstan). Pada setiap scanning, titik tengah dari scanning window diupdate sehingga berimpit atau mendekati lokasi dari posisi objek (Gbr III.5).

Proses update dengan menjadikan lokasi objek sebagai median dari jendela pindai

dapat dinyatakan dengan :

θPmax =med([θmin, θmax]) (III.1)

Pada Pers.III.1, θPmax menyatakan sudut estimasi objek, θmin dan θmax berturut-turut menyatakan batas kiri dan batas kanan dari jendela pindai.

III.2 Teknik

Tail-scan

Skema non-exhaustive search dilakukan dengan pembatasan wilayah sudut pindai

hanya pada arah-arah tertentu saja. Namun pembatasan ini ternyata memberikan masalah baru pada proses rekonstruksi CS, yaitu CS Solver yang dalam hal ini adalah cvx-programming, tidak berhasil memperoleh solusi yang konvergen. Fenomena ini tidak diperkirakan sebelumnya, karena dengan asumsi bahwa titik optimal dari CS solver terletak pada lokasi sudut keberadaan sinyal, sedangkan sudut ini sendiri berada pada cakupan sudut yang dipindai. Namun ternyata, cvx-programming tidak berhasil memperoleh solusi yang konvergen.

(b) objek

(a)

objek

(c) objek

W1

W2 W3

θ

t

1

t

2

t

3

(d)

objek objek objek

P

Gambar III.4. Ilustrasi tracking object dengan teknik non-exhaustive search serta update scanning window pada setiap waktu. (a),(b), dan (c) pergerakan objek beserta update scanning window yang bersesuaian. (d). ilustrasi pergeseran scanning window pada setiap waktu; W1, W2, W3 adalah scanning window berturut-turut pada t1, t2 dan t3

Pada gambar III.6 tersebut, terdapat tiga macam skema yang digunakan. Skema tersebut adalah skemaexhaustive search(lebar jendela pindai adalah₋900sampai 900),

skema non-exhaustive search dengan lebar jendela₋300_{sampai dengan 90}0_{, dan skema}

terakhir adalah non-exhaustive search dengan lebar jendela 00 _{sampai dengan 90}0_.

Sebagai pembanding, posisi aktual dari objek diberikan. Objek tersebut bergerak dari sudut 300 _{sampai dengan 90}0 _{dengan kecepatan 1,4}0 _{per detik. Sumbu datar adalah}

waktu (dalam detik), dan sumbu tegak adalah sudut (dalam derajat). Pada gambar III.6 tersebut skema exhaustive search dan skema non-exhaustive search dengan sudut pindai lebar (₋300 _{sampai dengan 90}0_{) berhasil mengikuti pergerakan objek dengan}

baik. Namun untuk lebar jendela pindai yang terlalu kecil (00 _{sampai dengan 90}0_),

cvx-programming gagal memberikan hasil konvergen. Hasil yang diperoleh, iterasi cvx-programming terjebak pada solusi semu di 50 _{dan 65}0_.

Untuk mengatasi permasalahan ini, maka area pemindaian diperluas mencakup pada arah selain dari arah utama. Arah tambahan ini disebut dengantail scanning. Gambar

III.7 memperlihatkan ilustrasitail-scanning.

Sifat dari tail scan adalah :

P

θ θx1

P

θ θx1

P

θ θx₂

P

θ θx₂

(a)

(b)

(c)

(d)

Gambar III.5. Ilustrasi detail tentang proses update scanning window dengan menggunakan median dari posisi objek. (a) hasil scanning kasar dengan algoritma klasik pada semua sudut,(b) penerapan scanning window pada sudut yang dianggap memiliki objek, (c) objek bergerak sehingga puncak scanning bergeser menuju batas window. (d). update scanning window, sehingga puncak scanning berada di tengah scanning window

(main-scan)

2. mengarah pada sudut yang tidak terdapat objek

3. berfungsi mencegah algoritma cvx-programming tidak konvergen atau terjebak pada solusi semu

Pada penelitian ini, diusulkan dua macam tipe tail scan yaitu uniform tail scan dan

0 10 20 30 40 50 60 70

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

an

g

le

(

degr

ee)

time(second)

w 0 to 90

w -30 to 90

w -90 to 90

Actual

Gambar III.6. Hasil simulasi: perbandingan skema exhaustive search terhadap

objek

-900

900

00

Tail scan

Gambar III.7. Non-exhaustive search dengan tail-scan

III.3 Metode Titik Berat

Metode titik berat dikembangkan pada tahap Kemajuan III ini sebagai jawaban atas permasalahan konvergensi yang dialami oleh metode convex programming yang

dikembangkan oleh Boyd (Boyd dan Vandenberghe (2004); Boyd (2014)). Metode titik berat didasarkan pada fakta geometri bahwa rekonstruksi CS dapat diselesaikan dengan membesarkan atau mengecilkan norm L1 sehingga norm tersebut bersinggungan

dengan fungsi objektif rekonstruksi. Sebagai ilustrasi, kita tinjau kasus dua dan tiga dimensi berikut. Pada kasus dua dimensi, misalkan vektor asal adalahx=x1x2

T

dan

A=A11A12 T

, sehinggay=A_·x=y1. Permasalahan rekonstruksi adalah : diberikan

A dan y, kita perlu mencari x sedekat mungkin dengan nilai asal. Kriteria sedekat

mungkin dengan nilai asal dapat diukur misalnya dengan nilai kesalahan absolut rata-rata. Karena permasalahan ini bersifat underdetermined, kita dapat memiliki

objek

-900

900

00

Tail scan

objek

-900

900

00

Tail scan

(a) (b)

Gambar III.8. Non exhaustive search dengan tail scan. (a) uniform tail scan, (b) random tail scan

A_·x=y untukx sehingga _kx_|1 minimum.

Oleh karenaAadalah matrik dengan ukuran 1x2, maka solusiA_·x=yadalah garis

yang berada pada diagram kartesianx1-x2 seperti yang ditunjukkan pada Gbr III.9.

x

1

x

2

A

·

x

=

y

x

1

x

2

A

·

x

=

y

x

s

(A) (B)

Gambar III.9. Solusi persamaan Ax=y terletak pada garis (A). Solusi dari Norm-L1 (B)

Norm orde p (p-norm) dari vektor x = x1 x2 ··· xN T

diberikan oleh persamaan:

kx_kp=qp

xp₁+xp₂+_···+xp_N (III.2)

Sebagai contoh, 0-norm (L0), 1-norm (L1), dan 2-norm (L2) berturut-turut adalah

m, _|x1|+|x2|+···+|xN|, and 2 q

x2₁+x2₂+_···+x2_N. Dengan, m adalah jumlah elemen

tak nol dari x.

Misalkan vektor x adalahx=2 3T. Misalkan pula x=0.6 0.4. Oleh karena itu y =Ax menghasilkan y =1.2. Dengan demikian permasalah rekkonstruksi adalah : diberikan y=1.2 dan x=0.6 0.4, perlu dicari x, sedemikian sehingga

kx_k1 minimum.

Oleh karenaxtidak diketahui, maka misalkanx=x1 x2

. Oleh karena ituAx=y

menghasilkan 0.6x1+ 0.4x2 = 1.2. Ada tak hingga banyak solusi dari

x1 x2

yang memenuhi 0.6x1+0.4x2= 1.2. Oleh karena kita ingin mencari pasangan

x1 x2

nilai awal yang cukup besar sehingga _kx_k1=k0 dan 0.6x1+ 0.4x2= 1.2 berpotongan

diP1 dan P2 (Gbr.III.10).

Potongan garis_kx_k1=k0 yang dibatasi olehP1 danP2 adalah konveks. Oleh karena

itu, setiap titikM yang merupakan kombinasi konveks dari P1 dan P2

M =t_·P1+ (1−t)·P2, (III.3)

(0_≤t_≤1), akan terletak di dalam interval P1 dan P2 tersebut.

x1 kxk1=k0 x2

P1

P2

M1

x1 x2

P1

P2

M1 P3M2

kxk₁=k0

kxk₁=k1

(a) (b)

Gambar III.10. (a). Iterasi awal dengank0 yang cukup besar sehingga kurva Ax=y

dan _kx_k1=k0 berpotongan di P1 dan P2. Titik tengah M1 dipilih

sebagai iterasi berikutnya. (b). Norm di M1 dipilih sebagai nilai

k berikutnya. Proses ini diulangi sehingga diperoleh titik yang konvergen.

Dari Gbr III.10 juga terlihat bahwa setiap titik M yang berasal dari kombinasi konveks dari P1 dan P2 juga memiliki norm L1 yang lebih kecil dibandingkan dengan

nilai awal.

Selanjutnya kita akan turunkan kasus yang lebih rumit pada dimensi 3 yang kemudian kita generalisasi untuk kasus dimensi n.

Misalkan sinyal sparse x adalahx=0 2 0T

. Maka sensing matriksA memiliki dua kemungkinan yaitu matriks 1x3 atau matriks 2x3. Pada kondisi matriks 1x3, sinyal kompresi yadalah vektor 1x1 dan untuk kondisi matrik A 2x3, maka vektory adalah

berdimensi 2x1.

Permasalahan rekonstruksi CS adalah sama dengan kasus dua dimensi: diberikan vektor y dan matrikA, tentukan x dengan _kx_k1 minimum. Solusi dari Ax=y pada

kasus matriks A 1x3 adalah suatu bidang, sedangkan untuk matriks A 2x3 adalah

suatu garis. Kita tinjau kasus matriks A 1x3 terlebih dahulu. Pada iterasi awal,

kita ambil k0 cukup besar sehingga bidang Ax=y berpotongan dengan oktahedron kx_k1=k0 (Gbr.III.11).

Bentuk dari bidang perpotongan dari _kx_k1=k0 dan Ax=y dapat berupa politop

solution ofAx=y

kxk1=k0

P1

P2 P3

P4

P5

(a)

(b)

M1

Gambar III.11. (a). Kasus dimensi 3, _kx_k1=k0 membentuk oktahedron. Solusi dari

Ax=y dengan matrik A 1x3 adalah suatu bidang. Jika k0 cukup

besar, _kx_k1=k0 akan memotong Ax=y. (b). Bidang perpotongan

dengan titik sudut P1 sampai P5. Titik M1 dipilih sebagai kombinasi

konveks dari titik-titikP1 sampai P5.

politof, sehingga kita dapat mencari titik beratM1 yang memiliki norm L1 yang lebih

kecil dari nilai sebelumnya.

Menemukan tiap sisi dari politop dapat dilakukan dengan menyelesaikan persamaan

kx_k1 = k0 dan Ax = y. Akan tetapi, karena sistem persamaan ini bersifat

underdetermined, maka mencari titik sudut politop menjadi sulit.

Di sini diusulkan suaatu teknik langsung untuk menyelesaikan permasalahan ini dengan menggunakan faktorisasi QR dari Householder (detail teori diberikan di Lampiran A). Penyelesaian dengan teknik ini disebut juga dengan istilah QR-factorization dengan pivot kolom Golub dan Loan (1996)). Pada teknik ini, proses permutasi kolom dari matrikA dilakukan sehingga suatu kriteria terpenuhi. Kriteria

yang umum dipakai adalah pengurutan kolom dari kolom dengan norm L2 terbesar sampai dengan yang terkecil. Kolom dengan nilai norm tidak signifikan diabaikan. Dengan demikian, solusi dari metode ini menghasilkan nilai yang banyak memiliki nol. Transformasi Householder dengan pivot kolom dijelaskan pada Golub dan Loan (1996), dengan algoritma adalah sebagai berikut. Householder QR dengan pivot kolom.

GivenA_∋Rmxn.

l1 for j=1:n

l2 c(j) =A(1 :m, j)T_{A(1 :m, j)}

l3 end

l4 r= 0; τ =max_{c(1),_···, c(n)_}

l5 cari k terkecil dengan 1_≤k_≤n sehingga c(k) =τ

l6 while τ_≥0

l7 r=r+ 1

l9 [v, β] =house(A(r;m, r))

l10 A(r:m, r:n) = (Im₋r+1−βvvT)A(r:m, r:n)

l11 A(r+ 1 :m, r) =v(2 :m₋r+ 1)

l12 fori=r+l:n

l13 c(i) =c(i)₋A(r, i)2

l14 end

l15 if r_≤n

l16 τ= max_{c(r+ 1), ..., c(n)_}

l17 Find smallest k with r+ 1_≤k_≤n so c(k) =τ

l18 else

l19 τ= 0

l20 end

l21 end

Proses pivot kolom terjadi pada baris l8 pada algoritma di atas. Pivot dilakukan

berdasarkan nilai tertinggi (barisl4 dan l5). Namun kriteria ini dapat diganti dengan

nilai terendah dariL2-norm dengan mengganti max menjadi min pada baris l4. Proses

faktorisasi QR Householder adalah pada barisl9. Setiap matriks A dapat difaktorkan

atas matrik orthonormalQ dan matrik segitiga atas R sedemikian rupa sehingga

A=QR. (III.4)

.

Proses transformasi Householder itu sendiri adalah:

Householder transformation.

Givenx_∋Rn.

l1 n=length(x) l2 σ=x(2 :n)Tx(2 :n)

l3 v=





1

x(2 :n)





l4 if σ= 0

l5 β= 0

l6 else

l7 µ=qx(1)2_+σ

l8 if x(1)_≤0

l9 v(1) =x(l)₋µ

l10 else

l11 v(1) =₋σ/(x(1) +µ)

l13 β= 2v(1)2/(σ+v(1)2) l14 v=v/v(1)

l15 end

Dengan menerapkan faktorisasi QR Householder serta pivot kolom akan menyelesaikan sistem persamaan linier dengan pada solusi di titik sudut dari bidang datar perpotongan norm orde 1 dan fungsi objektif. Akan tetapi, jika terdapat N titik sudut, teknik ini akan mendeteksiN₋1 titik sudut. Titik sudut denganL2-norm terkecil tidak dapat terpilih oleh algoritma ini.

Untuk mengatasi permasalahan ini, ditambahkan langkah khusus setelah faktorisasi QR Householder dengan pivot kolom. Pivot kolom pada langkah tambahan ini dilakukan dengan urutan nilai normL2yang terkecil, yang berkebalikan dengan kolom

pivoting sebelumnya yang didasarkan pada nilai terbesar. Langkah ini disebut dengan

backward column pivoting. Kombinasi dari kedua langkah pivot kolom ini menghasilkan

solusi lengkap dari semua titik sudut perpotongan (Gbr.III.12).

P5

P4

P3 P2

P1

O

P5

P4

P3 P2

P1

O

(a) _(b)

Gambar III.12. Faktorisasi QR Householder dengan pivot kolom (a). Pivot kolom dengan urutanL2-norm dari yang terbesar ke yang terkecil (b). Pivot kolom dengan urutanL2-norm dari yang terkecil ke yang terbesar

Sama dengan kasus dua variabel sebelumnya, setiap titik M yang berasal dari kombinasi konveks dari titik-titik sudut pada bidang solusi memberikan nilai k baru yang lebih kecil dari nilai sebelumnya.

M =α1·P1+α2·P2+···+αN·PN (III.5)

dengan

α1+α2+···+αN = 1 (III.6)

dan 0_≤αi≤1 untuk semua i.

Untuk kesederhanaan, pada metode yang diusulkan ini, dipilih setiap nilai αi yang

sama. Dengan demikian,

α1=α2=···=αN =

1

Secara geometri, pemilihan nilai αi yang sama maka akan dihasilkan titik M yang

merupakan titik berat dari politop. Pada umumnya, metode titik berat ini tidak menjamin konvergensi pada arah yang tercepat, namun ia menjamin konvergensi pada solusi optimal.

Setelah kita tinjau matrik A dengan dimensi 1x3, maka sekarang akan ditinjau

kondisi ketika matrik A berdimensi. Solusi dari permasalahan rekonstruksi Ax=y

adalah berupa irisan dari dua buah bidang yang menghasilkan suatu garis. Setiap bidang dinyatakan pada setiap baris dari persamaan linier.

Seperti halnya kondisi terdahulu, untuk nilai awal, dipilih k cukup besar sehingga oktagon _kx_k1 = k0 berpotongan dengan garis solusi fungsi objektif (Gbr.III.13).

Misalkan titik potong tersebut adalahP1 dan P2. Kondisi ini dengan demikian sama

dengan kondisi pada dua variabel. Oleh karena itu, setiap titik M1 yang berasal dari

kombinasi konveks dari P1 dan P2 akan memberikan nilai k yang lebih kecil. Nilai k

ini selanjutnya digunakan untuk iterasi berikutnya.

Solution of Ax=y

kxk₁=k0

P1

P2 P2

P1

M1

Gambar III.13. Perpotongan antara oktahedron norm L1 dengan solusi dari fungsi

objektif yang berupa garis. Titik potong bidang dan garis dinotasikan denganP1 danP2. TitikM1 yang merupakan kombinasi konveks dari

P1 dan P2 diilustrasikan pada gambar kanan

Generalisasi untuk dimensi n Setelah pembahasan pada dimensi 2 dan

dimensi 3, maka langkah-langkah yang dilakukan pada kedua dimensi tersebut dapat digeneralisasi menjadi suatu algoritma untuk dimensi n. Algoritma ini disebut dengan metode titik beratweight point. Sebelum algoritma tersebut dikemukakan, berikut ini

adalah dua teorema fundamental yang menjadi dasar dari algoritma titik berat ini.

Teorema 1Jika suatu bidang dibatasi oleh _kx_k1=k dan solusi dari persamaaan linier

Ax=y saling berpotongan, maka bentuk dari perpotongan tersebut adalah berupa suatu politop.

Bukti : - .

pada Teorema 1, maka setiap kombinasi konveks dari P1, P2, ···, PN akan

menghasilkan titik yang memiliki norm orde 1 kM yang lebih kecil dari norm orde

1 semula yang melalui Pi.

Bukti : - .

Setelah kedua teorema di atas, berikut ini adalah algoritma weight point untuk

dimensi n.

Algoritma titik berat.

1. pilih nilai awal k yang cukup besar.

2. susun persamaan _kx_k1 = k untuk setiap kombinasi dari x

3. susun set persamaan linier [A;xhi] = [y;k]

4. selesaikan set persamaan linier [A;xhi] = [y;k] dengan faktorisasi QR

Householder dengan pivot kolom pada pengurutan prioritas maksimum

5. selesaikan set persamaan linier [A;xhi] = [y;k] dengan faktorisasi QR

Householder dengan pivot kolom pada pengurutan prioritas minimum

6. kombinasikan solusi langkah 3 dan 4 untuk memperoleh semua titik sudut dari politop (P1, P2, ···, PN).

7. hitung titik berat Mi= (P1+P2+···+PN)/N

8. hitung norm L1 dari titik berat Mi dan gunakan nilai norm ini untuk iterasi

berikutnya

9. ulangi langkah 2 sampai dengan 8 sampai abs(ki+1−ki)≤epsilon, dengan < ǫ

BAB IV Hasil kemajuan

IV.1 Hal yang telah dilakukan pada semester berjalan

Pada Kemajuan III ini, hal-hal yang telah dilakukan adalah:

1. Mensimulasikan teknik non-exhaustive search dengan tail scan

2. Menurunkan algoritma rekonstruksi CS berdasarkan metode titik berat.

3. Mendraft jurnal untuk publikasi dari hasil-hasil yang diperoleh

IV.1.1 Hasil simulasi teknik

non-exhaustive search

dengan

tail scan

Simulasi komputer dilakukan untuk memverifikasi efektifitas skema non-exhaustive search dengan tail scan yang diusulkan.

Lingkungan simulasi diberikan pada Tabel IV.1

Tabel IV.1. Parameter simulasi exhaustive dan non exhaustive search

No Skema Parameter Nilai

1 Exhaustive Search Susunan Antena ULA 12 element

SNR 10 dB

Kecepatan Objek 1,40_/s

Sudut jelajah objek 300 _{sampai 60}0

Resolusi pindai 10

Jumlah objek 1 2 Non Exhaustive Search Parameter dasar sama dengan

(Jumlah antena, dll.) exhaustive search Skema pra-pemindaian MVDR

Lebar jendela pindai ₋300 _{sampai 90}0 _dan

00 _{sampai 90}0

CS Solver CVX-programming

Hasil simulasi diperlihatkan pada Gambar III.6. Pada gambar tersebut, terlihat bahwa skema non-exhaustive search dengan lebar jendela pindai yang cukup lebar (-300 _{sampai dengan 90}0_{) memiliki performa yang baik dalam melakukan tracking}

sampai 900_{. Pada rentang sudut pindai ini, rekonstruksi dengan cvx-programming}

tidak berhasil memperoleh solusi yang konvergen. Iterasi cvx-programming terjebak pada dua nilai sudut estimasi salah yaitu 50 _{dan 65}0_.

Oleh karena skema exhaustive search berhasil sedangkan teknik non-exhaustive search gagal untuk rentang sudut pindai yang sempit, maka kenyataan ini memberikan inspirasi untuk menambahkan pemindaian pada sudut-sudut tambahan di luar dari arah pindai utama. Pemindaian pada sudut-sudut tambahan ini diistilahkan dengan

tail scan.

IV.3 Perbandingan akurasi regular dan random tail-scan

dengan interpolasi

BAB V Penutup

Daftar Pustaka

Baraniuk, R. (2007): Compressive Sensing, IEEE Signal Processing Magazine, 24(4),

118–121.

Boyd, S. (2014): CVX: Matlab Software for Disciplined Convex Programming, URL

http://cvxr.com/cvx/.

Boyd, S. dan Vandenberghe, L. (2004): Convex Optimization, Cambridge University

Press.

Candes, E. dan Romberg, J. (2005): l1-Magic : Recovery of Sparse Signals via Convex Programming, URL http://users.ece.gatech.edu/ justin/l1magic/.

Candes, E. dan Wakin, M. B. (2008): Compressive Sampling, Proceedings of the International Congress of Mathematicians, Madrid, Spain,25(2), 21 – 30.

Chen, S. S., Donoho, D. L., dan Saunders, M. A. (2001): Atomic Decomposition by Basis Pursuit, SIAM Review, Society for Industrial and Applied Mathematics, 43(1), 129–159.

Dai, J., Xu, X., dan Zhao, D. (2013): Direction-of-Arrival Estimation Via Real-Valued Sparse Representation, Antennas and Wireless Propagation Letters, IEEE, 12,

376–379.

Dmochowski, J., Benesty, J., dan Affes, S. (2007): Direction of Arrival Estimation Using the Parameterized Spatial Correlation Matrix, Audio, Speech, and Language Processing, IEEE Transactions on, 15(4), 1327–1339.

Donoho, D. L. (2006): Compressed Sensing, IEEE Transactions on Information Theory, 52(4).

Golub, G. H. dan Loan, C. V. (1996): Matrix Computation, Johns Hopkins University

Press; 3rd edition (October 15, 1996).

Gurbuz, A. C. dan McClellan, J. H. (2008): A Compressive Beamforming Method,

Proceeding of the IEEE International Conference on Acoustics, Speech and Signal Processing.

Hayasi, K., Nagahara, M., dan Tanaka, T. (2013): A UserŠs Guide to Compressive Sensing for Communications Systems, In IEICE Transaction on Communication, E96-B(3), 685–712.

Jouny, I. (2011): Music DOA estimation with compressive sensing and/or compressive arrays, Antennas and Propagation (APSURSI), 2011 IEEE International Symposium on, 2016–2019.

Kim, J. M., Lee, O. K., dan Ye, J. C. (2012): Compressive MUSIC: Revisiting the Link Between Compressive Sensing and Array Signal Processing,IEEE Transctions on Information Theory, Vol. 58, No. 1, January 2012.

Mallat, S. dan Zhang, Z. (1993): Matching Pursuits With Time-Frequency Dictionaries,

IEEE Transactions on Signal Processing,41(12), 3397–3415.

Mingxia, X., Changhua, L., Xing, M., dan Weiwei, J. (2013): The Application of Compressive Sensing on Spectra De-noising,TELKOMNIKA,11(10), 6151–6157.

Telkomnika Ahmad Dahlan.

Roy, R., Paulraj, A., dan Kailath, T. (1986): Estimation of Signal Parameters via Rotational Invariance Techniques Ű ESPRIT., Proceeding of IEEE Military Communications (MILCOM) Conference - Communications, 3.

Schmidt, R. (1986): Multiple Emitter Location and Signal Parameter Estimation,

IEEE Transactions on Antennas and Propagation, 34(3), 276–280.

Stoica, P., Babu, P., dan Li, J. (2011): SPICE: A Sparse Covariance-Based Estimation Method for Array Processing, Signal Processing, IEEE Transactions on, 59(2),

629–638.

Swastika, W. dan Haneishi, H. (2012): Compressed Sensing for Thoracic MRI with Partial Random Circulant Matrices, Telkomnika, 10(1), 147–154.

Tropp, J. A. (2004): Greed is Good : Algorithmic Results for Sparse Approximation,

IEEE Transactions on Information Theory, 50(10).

Veen, B. V. dan Buckley, K. M. (1988): Beamforming: A Versatile Approach to Spatial Filtering, IEEE ASSP Magazine.

Wahidah, I. dan Suksmono, A. B. (2010): Recontruction Algorithms for Compressive Video Sensing Using Basis Pursuit, Proceeding of the 6th International Conference on Information & Communication Technology and Systems.

Wang, Y., Leus, G., dan Pandharipande, A. (2009): Direction Estimation Using Compressive Sampling Array Processing, Proceeding of IEEE SSP.

Lampiran A : Faktorisasi QR

Sebelum kita membahas tentang faktorisasi, mari terlebih dahulu kita lihat suatu contoh penguraian suatu matrikA 2x2 yang sederhana menjadi perkalian dua matrik

sederhana. Tahapan penguraiannya adalah sebagai berikut. Misalkan

A=   2 5 2 4   .

Kita dapat memandang bahwa matrik Atersusun dari dua vektor kolom yaitu

  2 2  

dan kolom kedua yaitu





5 4



. Katakanlah bahwa vektor kolom pertama adalaha1, dan

vektor kolom kedua adalah a2.

Sekarang mari kita ambil dua buah vektor referensi, yaituv1 =





1 1



 dan v2 =   1 0  .

Sekarang tugas kita yang pertama adalah menyatakan kolom vektor a1 sebagai

kombinasi linier dari referensi v1dan v2.

Tugas pertama ini gampang, karena :

a1= 



2 2



= 2· 



1 1



= 2v1= 2v1+ 0v2

Berikutnya adalah menyatakan kolom vektor a2 sebagai kombinasi linier dari

referensiv1 dan v2.

Dengan mencoba-coba, kita peroleh salah satu solusi adalah :

a2= 



5 4



= 4· 



1 1



+ 1· 



1 0



= 4v1+ 1v2

Sekarang kita susun kolom vektor a1 dan a2 untuk menghasilkan matrik A. Kita

peroleh :

A=a1 a2=2v1+ 0v2 4v1+v2

=

v1 v2 ·   2 4 0 1  =   1 1 1 0  ·   2 4 0 1 

Dengan kata lain, kita berhasil menguraikan matrik A menjadi perkalian dua

matrik D dan E seperti pada persamaan terakhir di atas. Matrik D, karena tersusun

atas vektor referensi, disebut sebagai matrik referensi atau BASIS, dan matrik E, karena tersusun sebagai informasi kombinasi dari tiap basis tadi disebut sebagai matrik BOBOT.

Faktorisasi QR bekerja dengan cara yang sama. Faktorisasi QR ini mendekomposisi suatu matrik A menjadi komponen BASISnya atau matrik Q, dan komponen bobotnya atau matrik R.

Keistimewaan dari Basis Q yang dipilih ini adalah bahwa ia bersifat ortonormal (i.e. setiap kolomnya tegak lurus dengan kolom lain, dan panjang norm orde 2 nya adalah 1). Dengan sifat seperti ini, maka inverse dari matrik Q adalah transposenya. Q−1=_QT_.

Matrik Bobot Q, di sisi lain adalah matrik yang berbentuk segitiga atas.

Ada pun proses untuk memperoleh Q dan R adalah cara Ortogonalisasi Gramm-Schmidt.

Mari kita lihat lagi contoh sebelumnya.

A=   2 5 2 4   .

Pertama kita buat dulu vektor referensi atau basis pertama yang berasal dari normalisasi kolom pertama dariA. Dengan demikian:

v1=√ 1

12_{+ 1}2·   1 1  = 1 √ 2·   1 1  

Dengan demikian, kolom pertama matrix A dapat ditulis sebagai

a1= 



2 2



= 2· √

2_·√1 2   1 1 

= 2 √

2_·v1= 2 √

2_·v1

Dengan kata lain

a1= 



2 2



= 2· √

2_·√1₂ 



1 1



= 2 √

2_·v1= 2 √

2_·v1

Selanjutnya, untuk mencari basis v2, kita reduksi dulu kolom kedua dari A dengan

basis v1, sisanya baru kita normalisasi untuk menghasilkan v2

a2= 



5 4



=<   5 4  , 1 √ 2   1 1 

>·

1 √ 2   1 1 

+r=

9 2   1 1 

Dengan de