BAB 3 PEMBAHASAN. 3.1 Prosedur Penyelesaian Masalah Program Linier Parametrik Prosedur Penyelesaian untuk perubahan kontinu parameter c

BAB 3 PEMBAHASAN

Pada bab sebelumnya telah dibahas teori-teori yang akan digunakan untuk menyelesaikan masalah program linier parametrik. Pada bab ini akan diperlihatkan suatu prosedur yang lengkap untuk menyelesaikan masalah program linier parametrik.

3.1 Prosedur Penyelesaian Masalah Program Linier Parametrik

Masalah program linier parametrik terdiri oleh 2 bagian masalah. Masalah pertama adalah perubahan kontinu parameter pada koefisien fungsi tujuan

( )

_cj dan masalah kedua adalah perubahan kontinu parameter konstan sisi kanan ( ini menunjukkan nilai kuantitas batasan ). Oleh karena itu, prosedur penyelesaian masalah program linier dibedakan menjadi 2 bagian berikut.

3.1.1 Prosedur Penyelesaian untuk perubahan kontinu parameter _cj

Untuk kasus perubahan kontinu pada parameter koefisien tujuan, permasalahan dalam bentuk skalar Minimum

( )

∑

(

)

= + = n j j j j x c z 1 θ α θ Dengan kendala _i n j j ijx b a =

∑

=1 , i=1,2,...,m _xj ≥_0,j =_1,2,...,n dan dalam bentuk matrik dinyatakan oleh Minimum z=

(

c+αθ

)

Tx

Dengan kendala Ax= b x≥0

akan diperiksa, di mana parameter θ diperkenankan mencakup semua nilai positif dan negatif.

Anggap bahwa program linier diselesaikan dengan θ =0 sehingga fungsi

tujuan

( )

∑

(

)

∑

= = = + = n j j j n j j j j x c x c z 1 1 θ α θ atau z =

(

c+αθ

)

Tx =cTx

Teknik dari analisis sensitivitas akan digunakan untuk menguji bagaimana solusi berubah ketika θ diubah dari nol. Jika basis sekarang tetap optimal, maka solusi basis optimal sekarang x_B =B−1b tidak akan berubah. Oleh karena itu hanya kondisi optimal yang perlu diperiksa. Untuk masalah pengganggu, mereka adalah

(

c +

)

−

(

cB + B

)

TB−1N ≥0 T N N α θ α θ atau

(

B N

) (

c c B N

)

T B T N T B T N 1 1 − − _{≥− −} −α α θ , di mana α dan _N B

α menyatakan gangguan-gangguan pada c dan _N c secara _B berturut-turut. Ketidaksamaan ini harus dipenuhi untuk setiap komponen dalam tes keoptimalan.

Koefisien pada sisi sebelah kanan yaitu harga reduksi metode simplex

memenuhi 1 0 ^ ≥ − = − N B c c c T_N T_B T

N karena basis sekarang diasumsikan optimal. Untuk 0

>

θ , ketidaksamaan hanya diperhatikan ketika

(

αT_N −αT_BB−1N

)

_i <0. Sebagai suatu hasil, θ dapat dinaikkan hingga nilai

(

)

(

) (

)

_    < − − − − = − − − − 0 : min ₁ 1 1 i T B T N i T B T N i T B T N i _{B N} c B N N B c c α α α α θ

sebelum basis sekarang berhenti menjadi optimal. Untuk θ >θ− basis berubah dan indeks i yang menentukan θ spesifik variabel masuk untuk metode simplex. Sama − halnya, untuk θ <0, itu mungkin untuk menurunkan θ hingga nilai

(

)

(

) (

)

_     > − − − − = − − − − max : 0 1 1 1 i T B T N i T B T N i T B T N i _{B N} B N N B c c α α α α θ

sebelum basis sekarang berhenti menjadi optimal. Lagi, indeks i yang menentukan

−

θ spesifik untuk variabel masuk.

Untuk     ∈ θ θ−

θ , harga reduksi variabel nonbasis diperlihatkan oleh formula

(

− −

)

+ N B c c BT T N 1

(

)

N B T B T N 1 − −α α

θ . Nilai tujuan parametrik ditunjukkan oleh

( ) ( )

B

T Bx z

zθ = 0 +θα di mana z

( )

0 adalah nilai tujuan untuk masalah dengan θ =0. Jika, ketika percobaan menghitung θ , di sana tidak ada indeks yang memenuhi −

(

− BT −1

)

_i <0 T

N α B N

α maka θ dapat dinaikkan tanpa batas dengan basis sekarang tetap optimal. Jika, ketika penggunaan metode simplex untuk menentukan basis baru pada

−

θ , di sana tidak ada variabel keluar, maka program linier tidak terbatas untuk θ >θ−. Sama halnya, jika tidak ada indeks yang memenuhi

(

− −1

)

>0

i T B T N α B N α maka θ

dapat diturunkan tanpa batas dengan basis sekarang tetap optimal. Jika tidak ada variabel keluar pada

−

θ , maka program linier tidak terbatas untuk

−

>θ

θ .

Prosedur di atas dapat disimpulkan sebagai berikut.

1. Ubah masalah program linier parametrik ke dalam bentuk standar. 2. Selesaikan masalah dengan θ =0 oleh metode simplex.

3. Gunakan prosedur analisis sensitivitas ( pada kasus perubahan parameter koefisien fungsi tujuan ) untuk memperkenalkan ∆c_j =α_jθ ke dalam fungsi tujuan.

4. Naikkan atau turunkan θ hingga nilai tertentu sebelum kondisi optimal dilanggar atau hingga variabel nonbasis yang memiliki koefisien pada fungsi tujuan menjadi negatif.

5. Gunakan variabel ini sebagai variabel basis yang masuk untuk iterasi metode simplex selanjutnya sehingga solusi optimal baru ditemukan. Kembali ke langkah 4.

Prosedur Penyelesaian untuk perubahan kontinu parameter _{b i}

Untuk kasus perubahan kontinu pada parameter b , bentuk masalah dalam skalar _i Minimum

( )

∑

= = n j j jx c z 1 θ Dengan kendala θ α_i i n j j ijx b a = +

∑

=1 , _i=_{1,2,...,m xj} ≥_{0, j} =_1,2,...,n

dan dalam bentuk matrix dinyatakan oleh Minimum _z=_cT_x

dengan kendala Ax= b+αθ x≥0

akan diperiksa, di mana parameter θ diperkenankan mencakup semua nilai positif dan negatif. Suatu teknik yang sama dengan prosedur penyelesaian perubahan kontinu parameter koefisien tujuan dapat dikembangkan untuk menyelesaikan masalah ini.

Anggap bahwa program linier diselesaikan dengan θ =0 sehinga konstanta

sisi kanan _{i i i} n j j ijx b b a = + =

∑

= θ α 1

atau Ax=b+αθ =b. Teknik dari analisis sensitivitas akan digunakan untuk menguji bagaimana solusi berubah ketika θ diubah dari nol. Jika basis sekarang tetap layak, maka solusi basis optimal sekarang

0 1 ^ ≥ − = − N B c c c T_N T_B T

N tidak akan berubah. Oleh karena itu, hanya kondisi layak yang perlu diperiksa.

Pada masalah pengganggu, kondisi solusi layak basis akan tetap terpenuhi sepanjang B−1

(

b+αθ

)

≥0 atau ekivalen sepanjang −1 _{≥ B−} −1αθ

b

B . Ketidaksamaan

ini harus dipenuhi untuk setiap komponen dalam tes kelayakan. Basis sekarang memenuhi B−1b≥0 karena untuk setiap komponen basis sekarang diasumsikan menjadi layak. Untuk θ >0, ketidaksamaan hanya diperhatikan ketika

(

B−1α

)

_i <0. Sebagai suatu hasil, θ dapat dinaikkan hingga nilai

( )

(

) (

)

     < − = − − − − 0 : min 1 1 1 i i i i _B B b B _α α θ

sebelum basis sekarang berhenti menjadi layak. Untuk θ >θ−, basis berubah, dan indeks i yang menetukan θ spesifik variabel masuk untuk metode simplex. Sama − halnya, untuk θ <₀, itu mungkin untuk menurunkan θ hingga nilai

( )

(

) (

)

_    > − = − − − − max : 0 1 1 1 i i i i _B B b B α α θ

sebelum basis sekarang berhenti menjadi layak. Lagi, indeks i yang menentukan

−

θ spesifik untuk variabel masuk.

Untuk     ∈ θ θ−

θ , , nilai solusi basis diperlihatkan oleh formula

α θ 1 1 − − − + =B b B

x . Nilai fungsi tujuan ditunjukkan oleh :

( )

θ = −1 + θ −1α B c b B c z T_B T_B

( )

θ 1α 0 + − = z cT_BB

di mana z

( )

0 adalah nilai tujuan untuk masalah dengan θ =0. Jika, ketika percobaan menghitung θ , di sana tidak ada indeks − _i yang memenuhi

(

−1

)

<₀

i

B α maka θ dapat dinaikkan tanpa batas dengan basis sekarang tetap layak dan optimal. Jika, ketika penggunaan metode simplex untuk menentukan basis baru pada θ , di sana tidak ada − variabel keluar, maka program linier tidak terbatas untuk θ >θ−. Sama halnya, jika tidak ada indeks yang memenuhi

(

−1

)

>0

i

B α maka θ dapat diturunkan tanpa batas dengan basis sekarang tetap layak. Jika tidak ada variabel keluar pada

−

program linier tidak terbatas untuk

−

<θ

θ . Metode dual simplex juga dapat dipakai untuk menemukan solusi basis untuk tiap-tiap titik kritis θ sehingga solusi layak dan optimal dapat diperoleh.

Kesimpulan prosedur penyelesaian masalah perubahan konstan sisi kanan adalah sebagai berikut.

1. Ubah masalah program linier parametrik ke dalam bentuk standar. 2. Selesaikan masalah dengan θ =0 oleh metode simplex.

3. Gunakan prosedur analisis sensitivitas pada kasus perubahan konstan sisi kanan untuk memperkenalkan ∆b_i =α_iθ .

4. Naikkan atau turunkan θ hingga nilai tertentu sebelum kondisi layak dilanggar atau sebelum nilai di kolom sisi kanan menjadi negatif.

5. Gunakan variabel ini sebagai variabel masuk untuk suatu iterasi metode dual simplex selanjutnya untuk menemukan solusi optimal baru. Kembali ke langkah 4.

3.2 Penyelesaian Contoh Masalah Program Linier Parametrik

3.2.1 Pada Kasus Perubahan Kontinu Parameter _cj

Pada kasus ini, masalah dibatasi dengan dua variabel keputusan pada fungsi tujuan.

Maksimum

( ) (

)

(

)

2 1 5 2 3 x x zθ = + θ + −θ Dengan kendala 1 x ≤4 2 2x ≤12 18 2 3x₁+ x₂ ≤ Dan 1 x ≥ , 0 x₂ ≥0

Langkah 1.

Masalah dalam bentuk standar menjadi :

Minimum −z

( ) ( ) (

θ =z^θ = −3−2θ

)

x₁+

(

−5+θ

)

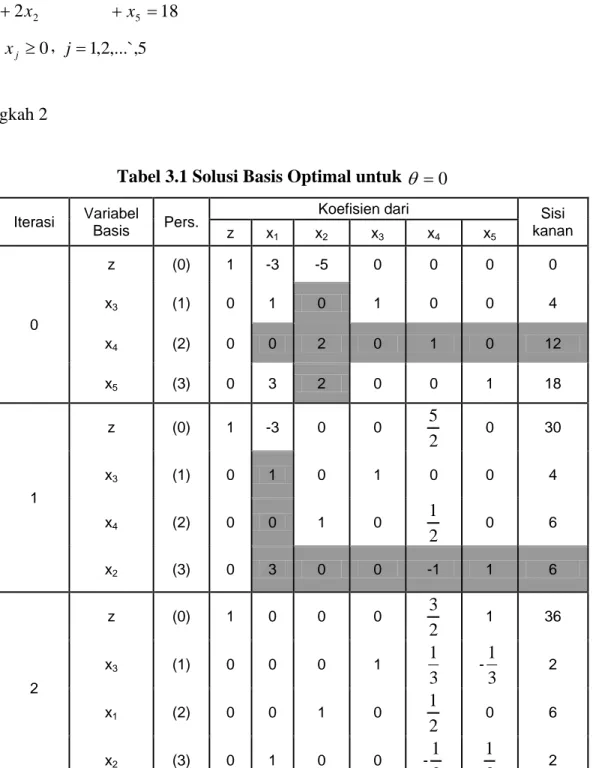
x₂ Dengan kendala 1 x + x₃ =4 2 2x + x₄ =12 2 1 2 3x + x + x₅ =18 dan _xj ≥₀, _j =_1,2,...`,5 Langkah 2

Tabel 3.1 Solusi Basis Optimal untuk θ =0

Iterasi Variabel

Basis Pers.

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 0 z (0) 1 -3 -5 0 0 0 0 x3 (1) 0 1 0 1 0 0 4 x4 (2) 0 0 2 0 1 0 12 x5 (3) 0 3 2 0 0 1 18 1 z (0) 1 -3 0 0 2 5 0 30 x3 (1) 0 1 0 1 0 0 4 x4 (2) 0 0 1 0 2 1 0 6 x2 (3) 0 3 0 0 -1 1 6 2 z (0) 1 0 0 0 2 3 1 36 x3 (1) 0 0 0 1 3 1 -3 1 2 x1 (2) 0 0 1 0 2 1 0 6 x2 (3) 0 1 0 0 -3 1 3 1 2

Langkah 3

Dengan menggunakan analisis sensitivitas pada kasus perubahan parameter koefisien fungsi tujuan akan diperkenalkan ∆_cj =α_jθ

=

c

[

_{−3 −5 0 0 0}

]

T

dan α =

[

−_{2 1 0 0 0}

]

T Solusi basis optimal sekarang

[

]

T

B x x x

x = _{3 2 1} , α_B =

[

0 1 −2

]

T dan =

N

α

[

0 0

]

T

Dengan variabel basis optimal sekarang maka nilai interval θ dapat dihitung.

[

] [

]

=_− _                 − − − − = − = − 3 2 6 7 3 1 3 1 0 0 2 1 0 3 1 3 1 1 2 1 0 0 0 1 ^ N B T B T N T N α α α dan ^ ≥₀ T N

c . Karena ada entri yang memenuhi

(

− BT −1

)

_i >0 T N α B N α dan

(

− BT −1

)

_i <0 T N α B N

α pada basis optimal sekarang maka θ dapat dinaikkan atau diturunkan nilainya untuk iterasi metode simplex selanjutnya. Untuk solusi basis optimal sekarang, batas atas θ :

(

)

(

) (

)

_    < − − − − = − − − − 0 : min ₁ 1 1 i T B T N i T B T N i T B T N i _{B N} B N N B c c α α α α θ 7 9 6 7 2 3 min =             − − = i

dan batas bawah θ :

(

)

(

) (

)

_    > − − − − = − − − − : 0 1 1 1 i T B T N i T B T N i T B T N i _{B N} B N N B c c maks α α α α θ 2 3 3 2 1 − =             − = i maks

Harga reduksi nonbasis dan nilai fungsi tujuan secara berurutan menjadi     _{− +} =    − +     = + = θα θ θ θ 3 2 1 6 7 2 3 3 2 6 7 1 2 3 ^ ^ T N T N T N c c

( ) (

θ θ

)

θα θ

[

]

36 2θ 2 6 2 2 1 0 36 0 ^ ^ + − =           − + − = + = = T _B B Bc x z z

( )

θ

( )

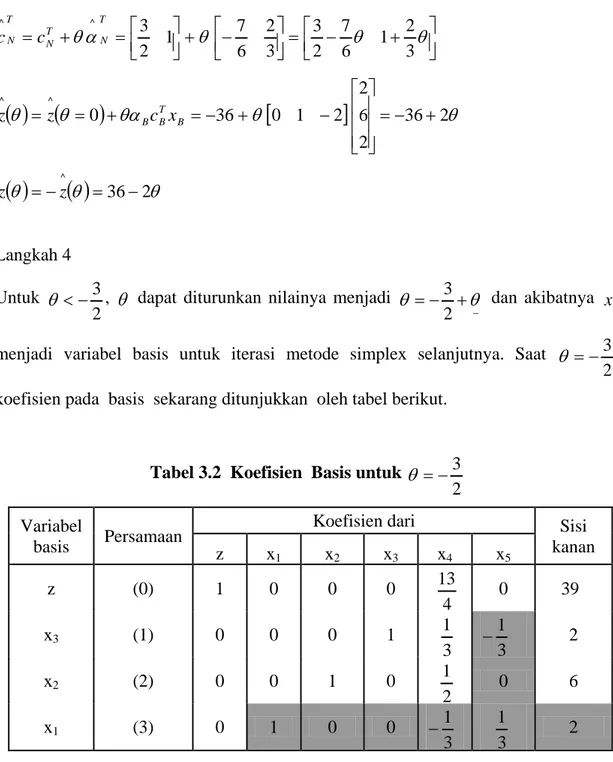
θ 36 2θ ^ − = − = z z Langkah 4 Untuk 2 3 − <

θ , θ dapat diturunkan nilainya menjadi

− + − = θ θ 2 3 _{dan akibatnya} 5 x

menjadi variabel basis untuk iterasi metode simplex selanjutnya. Saat

2 3 − =

θ ,

koefisien pada basis sekarang ditunjukkan oleh tabel berikut.

Tabel 3.2 Koefisien Basis untuk

2 3 − = θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 0 4 13 0 39 x3 (1) 0 0 0 1 3 1 3 1 − 2 x2 (2) 0 0 1 0 2 1 0 6 x1 (3) 0 1 0 0 3 1 − 3 1 2

Langkah 5

Setelah operasi pivot, solusi optimal yang baru menjadi : Tabel 3.3 Solusi Basis Optimal untuk

2 3 − < θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 0 4 13 0 39 x3 (1) 0 1 0 1 0 0 4 x2 (2) 0 0 1 0 2 1 0 6 x5 (3) 0 3 0 0 -1 1 6

Dengan variabel basis ini diperoleh nilai :

= T N ^ α

[

] [

]

=_− − _                     − − − 2 1 2 0 3 1 0 0 1 1 1 0 0 2 1 0 0 0 1 0 1 0 0 2 dan 0 ^ ≥ T N c .

Karena tidak ada entri yang memenuhi

(

α_NT −αT_BB−1N

)

_i >0 maka θ dapat diturunkan tanpa batas dengan solusi basis saat ini. Harga reduksi nonbasis dan nilai fungsi tujuan :    _{− −} − =    _{− −}       + +     = 2 5 2 3 2 1 2 2 3 4 13 0 ^ θ θ θ T N c

( )

θ θ θ

[

]

30 6θ 6 6 4 0 1 0 2 3 2 3 ^ ^ + − =                 + +       ₌₋ = z z

( )

θ

( )

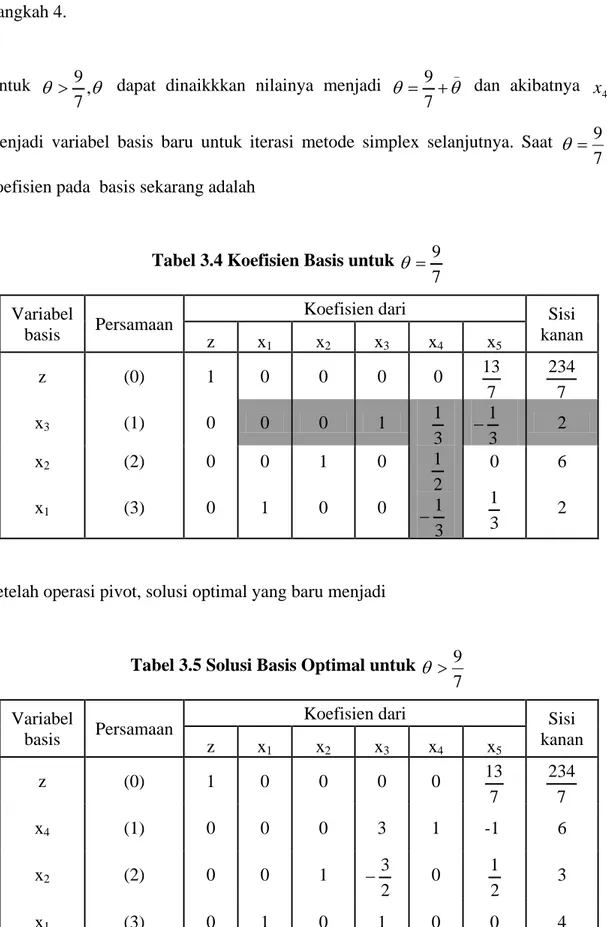
θ 30 6θ ^ − = − = z z

Langkah 4.

Untuk θ _,θ 7 9

> dapat dinaikkkan nilainya menjadi _ 7 9 _θ

θ = + dan akibatnya

4

x

menjadi variabel basis baru untuk iterasi metode simplex selanjutnya. Saat 7 9 =

θ ,

koefisien pada basis sekarang adalah

Tabel 3.4 Koefisien Basis untuk 7 9 = θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 0 0 7 13 7 234 x3 (1) 0 0 0 1 3 1 2 1 3 1 − 3 1 − 2 x2 (2) 0 0 1 0 0 6 x1 (3) 0 1 0 0 3 1 2

Setelah operasi pivot, solusi optimal yang baru menjadi

Tabel 3.5 Solusi Basis Optimal untuk 7 9 > θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 0 0 7 13 7 234 x4 (1) 0 0 0 3 1 -1 6 x2 (2) 0 0 1 2 3 − 0 2 1 3 x1 (3) 0 1 0 1 0 0 4

Dengan variabel basis ini diperoleh nilai : = T N ^ α

[

] [

]

=_ − _                     − − − − 2 1 2 7 0 0 1 0 0 1 0 0 1 2 1 0 2 3 1 1 3 2 1 0 0 0 dan 0 ^ ≥ T N c .

Karena ada entri yang memenuhi

(

α_NT −αT_BB−1N

)

_i <0 maka θ dapat dinaikkan hingga: 7 26 2 1 7 13 min =             − − = − i θ

Harga reduksi nonbasis dan nilai fungsi tujuan :

   − + − =     ₋       − +     = 2 5 2 7 9 2 1 2 7 7 9 7 13 0 ^ θ θ θ T N c

( )

θ θ θ

[

]

27 5θ 3 4 6 2 1 0 7 9 7 9 ^ ^ − − =           −       − +       = = z z

Karena masih ada 0

^

< T N

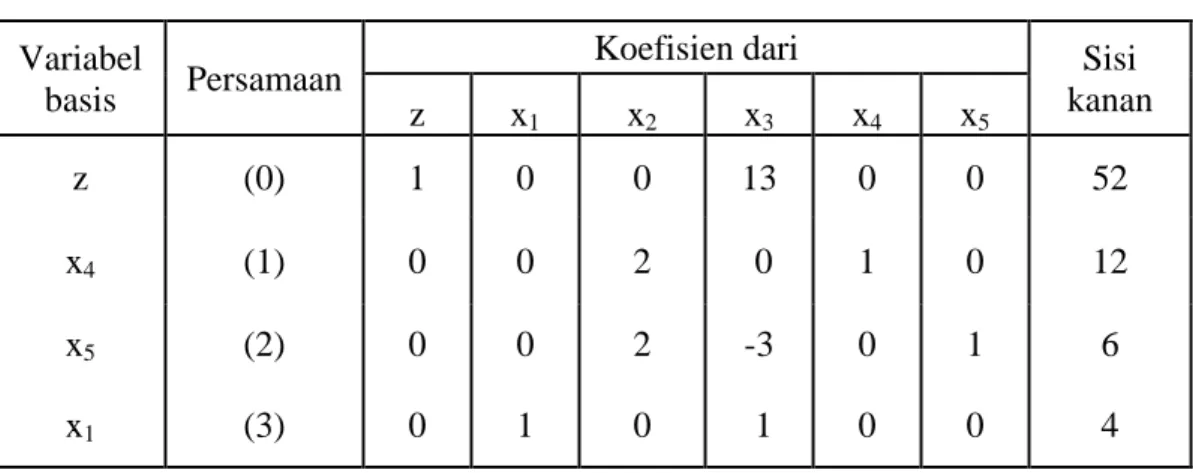
α maka θ dapat dinaikkan kembali. Untuk θ >5, maka x ₅ menjadi salah satu variabel basis berikutnya dan harga reduksi untuk θ =5 adalah

Tabel 3.6 Koefisien Basis untuk θ =5 Variabel

basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 13 0 0 52 x4 (1) 0 0 0 3 1 -1 6 x2 (2) 0 0 1 2 3 − 0 2 1 3 x1 (3) 0 1 0 1 0 0 4

( )

θ

( )

θ 27 5θ ^ + = − = z z

Setelah operasi pivot, solusi optimal yang baru adalah :

Tabel 3.7 Solusi Basis Optimal untuk θ >5 Variabel

basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 13 0 0 52 x4 (1) 0 0 2 0 1 0 12 x5 (2) 0 0 2 -3 0 1 6 x1 (3) 0 1 0 1 0 0 4

Dengan variabel basis ini diperoleh nilai :

= T N ^ α

[

] [

]

[

1 2

]

0 2 1 2 0 0 0 0 1 1 0 3 0 1 0 2 0 0 0 1 =                     − − − dan ^ ≥₀ T N c .

Karena tidak ada entri yang memenuhi

(

− −1

)

<₀

i T

B T

N α B N

α maka θ dapat dinaikkan

tanpa batas. Harga reduksi nonbasis dan nilai fungsi tujuan :

[

0 13

]

(

θ 5

)

[

1 2

] [

5 θ 3 2θ

]

^ + + − = − + = T N c

( )

θ

(

θ

) (

θ

)

[

]

12 8θ 4 6 12 2 00 0 5 5 ^ ^ − − =           − − + = = z z

( )

θ

( )

θ 12 8θ ^ + = − = z z

Tabel 3.8 Pemakaian Prosedur Program Linier Parametrik c_j

Interval Var.

basis Pers.

Koefisien dari _Sisi

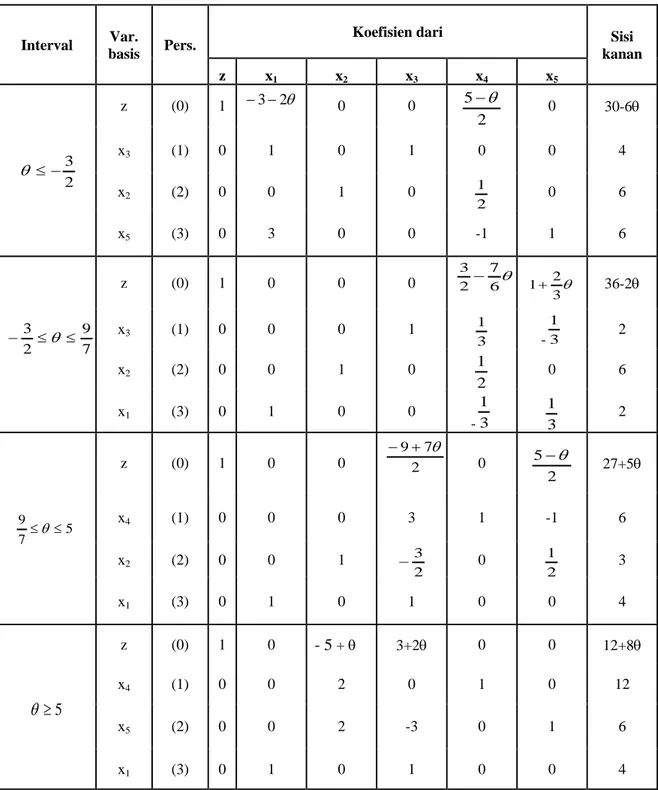
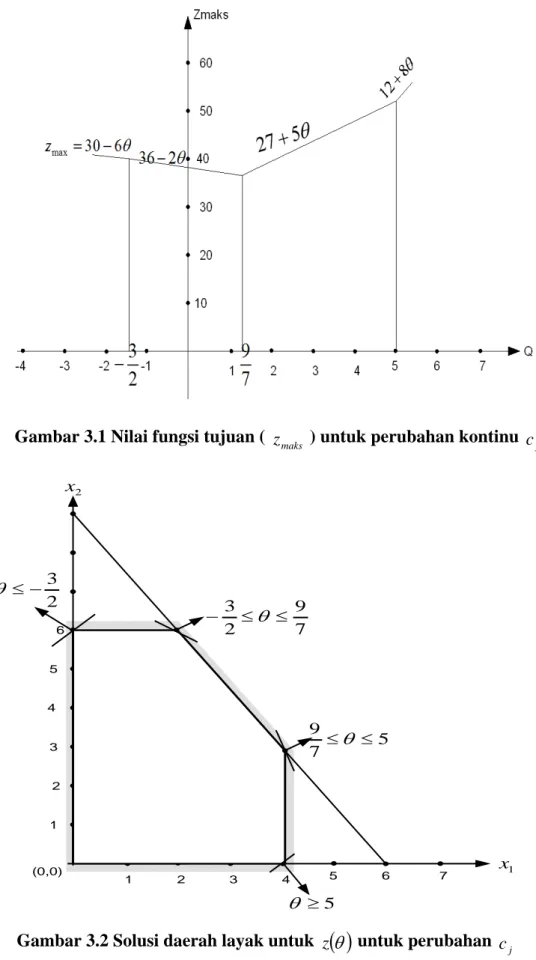
kanan z x1 x2 x3 x4 x5 2 3 − ≤ θ z (0) 1 −3−2θ 0 0 2 5−θ 0 30-6θ x3 (1) 0 1 0 1 0 0 4 x2 (2) 0 0 1 0 2 1 0 6 x5 (3) 0 3 0 0 -1 1 6 7 9 2 3 _{≤ ≤} − θ z (0) 1 0 0 0 6θ 7 2 3 − _θ 3 2 1+ 36-2θ x3 (1) 0 0 0 1 3 1 -3 1 2 x2 (2) 0 0 1 0 2 1 0 6 x1 (3) 0 1 0 0 -3 1 3 1 2 5 7 9_{≤θ ≤} z (0) 1 0 0 ₂ 7 9+ θ − 0 2 5−θ _27+5θ x4 (1) 0 0 0 3 1 -1 6 x2 (2) 0 0 1 2 3 − 0 2 1 3 x1 (3) 0 1 0 1 0 0 4 5 ≥ θ z (0) 1 0 - 5 + θ 3+2θ 0 0 12+8θ x4 (1) 0 0 2 0 1 0 12 x5 (2) 0 0 2 -3 0 1 6 x1 (3) 0 1 0 1 0 0 4

Gambar 3.1 Nilai fungsi tujuan ( z_maks ) untuk perubahan kontinu _cj

Gambar 3.2 Solusi daerah layak untuk z

( )

θ untuk perubahan _cj

1 2 3 4 5 6 7 1 2 3 4 5 6 5 7 9 _{≤θ ≤} 7 9 2 3 _{≤ ≤} − θ 2 3 − ≤ θ 1 x 5 ≥ θ 2 x (0,0)

3.2.2 Pada Kasus Perubahan Kontinu Parameter _{b i}

Pada kasus ini, masalah juga dibatasi dengan dua variabel keputusan pada fungsi tujuan. Maksimum 2 1 5 4x x z= + Dengan kendala : 2x1+ x2 ≤8+2θ θ 7 7 2 ₂ 1+ x ≤ + x θ 2 3 2 ≤ + x x₁ ≥0, x₂ ≥0 Langkah 1

Masalah dalam bentuk standar menjadi

Minimum 1 2 ^ 5 4x x z z = =− − − Dengan kendala 2x1+x2+x3 =8+2θ x1+2x2 +x4 =7+7θ x 2 + x5 =3+2θ _xj ≥_{0, j} =_1,2,...,5

Langkah 2

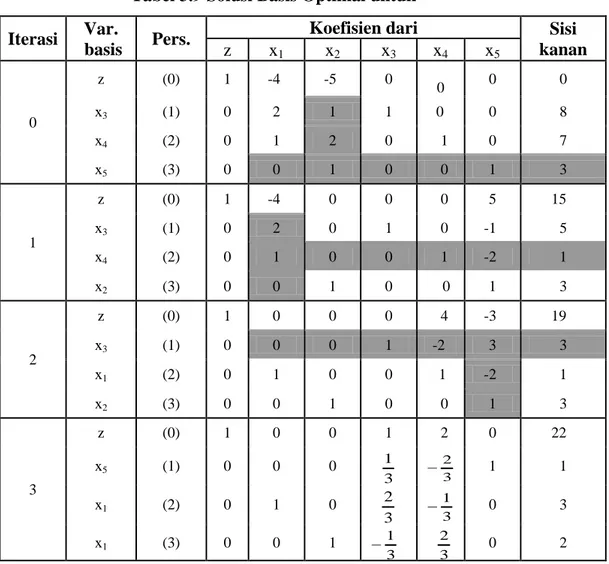
Tabel 3.9 Solusi Basis Optimal untuk θ =0 Iterasi Var.

basis Pers.

Koefisien dari Sisi

kanan z x1 x2 x3 x4 x5 0 z (0) 1 -4 -5 0 0 0 0 x3 (1) 0 2 1 1 0 0 8 x4 (2) 0 1 2 0 1 0 7 x5 (3) 0 0 1 0 0 1 3 1 z (0) 1 -4 0 0 0 5 15 x3 (1) 0 2 0 1 0 -1 5 x4 (2) 0 1 0 0 1 -2 1 x2 (3) 0 0 1 0 0 1 3 2 z (0) 1 0 0 0 4 -3 19 x3 (1) 0 0 0 1 -2 3 3 x1 (2) 0 1 0 0 1 -2 1 x2 (3) 0 0 1 0 0 1 3 3 z (0) 1 0 0 1 2 0 22 x5 (1) 0 0 0 3 1 3 2 − 1 1 x1 (2) 0 1 0 3 2 3 1 − 0 3 x1 (3) 0 0 1 3 1 − 3 2 0 2 Langkah 3

Dengan menggunakan analisis sensitivitas pada kasus perubahan konstan sisi kanan akan diperkenalkan ∆_bi =α_iθ.

[

]

T

b= 8 7 3 dan α =

[

2 7 2

]

T

Arus solusi basis optimal yaitu

[

]

T

B x x x

x = _{5 1 2} dan nilai B

x ini akan berubah menjadi ^ = +θ −1α

B x xB _B

          − − =                           − − − = − 4 1 2 2 7 2 0 3 2 3 1 0 3 1 3 2 1 3 2 3 1 1α B

Karena ada entri yang memenuhi

(

−1

)

<₀

i

B α dan

(

B−1α

)

i >0 maka θ dapat dinaikkan dan diturunkan nilainya hingga nilai tertentu. Untuk solusi basis optimal sekarang, batas atas θ adalah

( ) ( )

2 1 1 3 , 2 1 min =       − − − − = i

dan nilai batas bawah θ adalah

( )

(

) (

)

     > − = − − − − max : 0 1 1 1 i i i i _B B b B α α θ      _{− =−} = 2 1 4 2 i maks

Harga reduksi nonbasis T ≥₀ N

c . Harga sisi kanan dan nilai fungsi tujuan : α θ 1 ^ − + = x B xB _B           + − − =           − − +           = θ θ θ θ 4 2 3 2 1 4 1 2 2 3 1

( ) ( )

θ θ α θ

[

]

22 16θ 4 1 2 5 4 0 22 0 1 ^ − − =           − − − − + − = + = − B c z z T_B

( )

θ

( )

θ 22 16θ ^ + = − = z z Langkah 4 Karena ada

(

−1

)

<₀ i

B α maka θ dapat dinaikkan nilainya menjadi lebih besar dari sekarang. Untuk

2 1 =

θ , nilai sisi kanan menjadi :

( )

(

) (

)

     < − = − − − − 0 : min 1 1 1 i i i i _B B b B _α α θ

Tabel 3.10 Nilai Sisi Kanan untuk 2 1 = θ Variabel basis Persamaan

Koefisien dari _Sisi

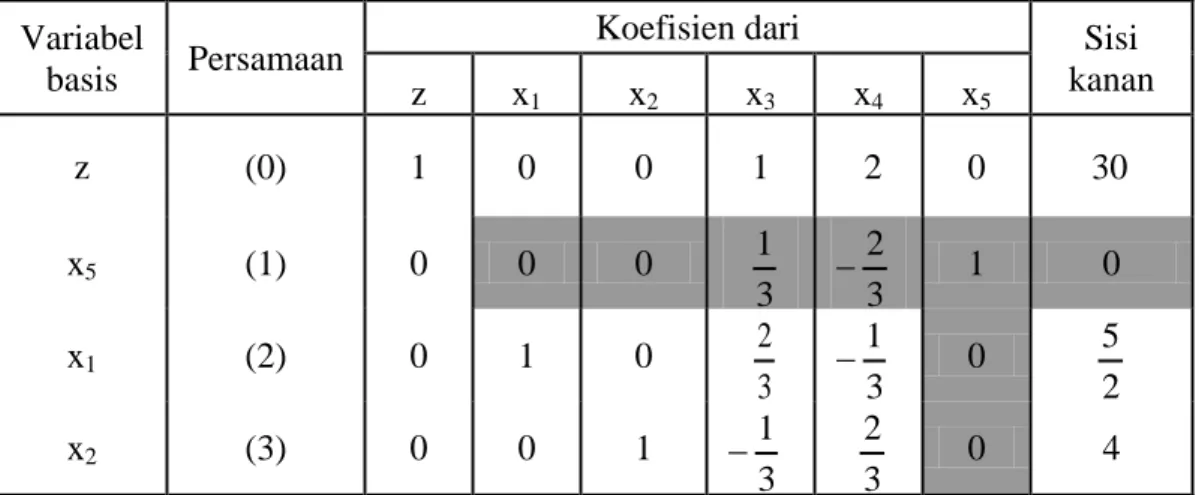
kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 1 2 0 30 x5 (1) 0 0 0 3 1 3 2 − 1 0 x1 (2) 0 1 0 3 2 3 1 − 0 2 5 x2 (3) 0 0 1 3 1 − 3 2 0 4

dan setelah operasi pivot dengan menggunakan metode dual simplex maka solusi optimal yang baru adalah

Tabel 3.11 Solusi Basis Optimal untuk 2 1 > θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z (0) 1 0 0 2 0 3 30 x4 (1) 0 0 0 2 1 − 1 2 3 − 0 x1 (2) 0 1 0 2 1 0 2 1 − 2 5 x2 (3) 0 0 1 0 0 1 4           =                           − − − = − 2 0 3 2 7 2 1 0 0 2 1 0 2 1 2 3 1 2 1 1α B dengan T ≥₀ N c

Karena tidak ada entri yang memenuhi

(

B−1α

)

_i <0 maka θ dapat dinaikkan tanpa batas dengan harga solusi basis sekarang yang tetap layak.

Harga sisi kanan dan nilai fungsi tujuan yang baru : B x ^ =                 + + − =                 − +           = θ θ θ 2 3 2 5 3 2 3 2 0 3 2 1 4 2 5 0

( )

θ θ θ α θ

[

]

25 10θ 2 0 3 5 4 0 2 1 30 2 1 1 ^ − − =           − −       − + − = +       = = − − B c z z T_B

( )

θ

( )

θ 25 16θ ^ + = − = z z Langkah 4

Untuk θ <₀, θ dapat diturunkan nilainya. Solusi basis sebelumnya akan berubah ketika θ diturunkan nilainya lebih jauh. Untuk

2 1 − =

θ , nilai sisi kanan menjadi :

Tabel 3.12 Nilai Sisi Kanan untuk

2 1 − = θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z 0 1 0 0 1 2 0 14 x5 (1) 0 0 0 3 1 3 2 − 1 2 x1 (2) 0 1 0 3 2 3 1 − 0 2 7 x2 (3) 0 0 1 3 1 − 3 2 0 0 Untuk − + − = θ θ 2 1

, setelah operasi pivot dengan menggunakan metode dual simplex maka solusi optimal yang baru adalah

Tabel 3.13 Solusi Basis Optimal untuk 2 1 − < θ Variabel basis Persamaan

Koefisien dari _Sisi

kanan z x1 x2 x3 x4 x5 z 0 1 0 3 0 4 0 14 x5 (1) 0 0 1 0 0 1 2 x1 (2) 0 1 2 0 1 0 2 7 x3 (3) 0 0 -3 1 -2 0 0           − =                     − = − 12 7 2 2 7 2 0 2 1 0 1 0 1 0 0 1α B

Karena ada entri yang memenuhi

(

−1

)

>₀

i

B α , maka θ dapat diturunkan nilainya hingga = − θ 2 1 7 2 7 , 2 2 − =             − − i

maks dan harga reduksi nonbasis cT_N ≥0.

Harga sisi kanan dan nilai fungsi tujuan yang baru :

          − − + + =                 + +           = + = − θ θ θ θ α θ 12 6 7 7 2 3 2 7 2 2 1 0 2 3 2 1 ^ B x xB _B

( )

θ θ θ α θ

[

]

28 28θ 12 7 2 0 4 0 2 1 30 2 1 1 ^ − − =           − −       + + − = +       ₌₋ = − − B c z z T_B

( )

θ

( )

θ 28 28θ ^ + = − = z z

Untuk θ <−1, persamaan kedua tidak memenuhi syarat b≥0 sehingga θ tidak dapat diturunkan lagi nilainya dan oleh karena itu, iterasi dihentikan.

Tabel 3.14 Pemakaian Prosedur Program Linier Parametrik _{b i}

Interval Vari.

Basis Pers.

Koefisien dari _Sisi

Kanan z x1 x2 x3 x4 x5 2 1 1≤ ≤− − θ z (0) 1 0 3 0 4 0 28+28θ x5 (1) 0 0 1 0 0 1 3+2θ x1 (2) 0 1 2 0 1 0 7+7θ x3 (3) 0 0 -3 1 -2 0 -6-12θ 2 1 2 1 ≤ ≤ − θ z (0) 1 0 0 1 2 0 22+16θ x5 (1) 0 0 0 3 1 3 2 − 1 1-2θ x1 (2) 0 1 0 3 2 3 1 − 0 3-θ x2 (3) 0 0 1 3 1 − 3 2 0 2+4θ 2 1 ≥ θ z (0) 1 0 0 2 0 3 25+10θ x4 (1) 0 0 0 2 1 − ₁ 2 3 − 3θ 2 3 + − x1 (2) 0 1 0 2 1 ₀ 2 1 − 2 5 x2 (3) 0 0 1 0 0 1 3+2θ

Gambar 3.3 Nilai fungsi tujuan ( zmaks ) untuk perubahan kontinu i b 1/2 1 -1/2 -1 10 20 30 40 Zmax

θ

10

25

+

θ

16

22

+

θ

28

28

max

=

+

Z

_θ

Gambar 3.4 Solusi daerah layak z

( )

θ untuk perubahan b _i

Variasi solusi optimal yang dihasilkan dengan variabel keputusan asli pada perubahan kontinu parameter _cj atau b dapat disimpulkan ke dalam kedua tabel berikut. _i

Tabel 3.15 Variasi Solusi Optimal untuk Perubahan j c θ −∞ 2 3 − 7 9 5 +∞ x1 0 2 4 4 x2 6 6 3 0 z 30-6θ 36-2θ 27+5θ 12+8θ 1 2 3 1 2 3 0 III I II 1 − = θ 1 2 3 4 1 2 3 4 II III 2 / 1 − = θ I 1 2 3 4 5 1 2 3 4 II I III θ =−1/2 0 1 2 3 4 1 2 3 4 II III 0 = θ I 1 2 3 4 5 6 7 1 2 3 4 5 6 II I III 1 = θ 1 x 1 x 1 x 1 x 1 x 2 x 2 x 2 x 2 x 2 x

Tabel 3.15 Variasi Solusi Optimal untuk Perubahan _{b i} θ -1 2 1 − 2 1 +∞ x1 7+7θ 3-θ 2 5 x2 0 2+4θ 3+2θ z 28+28θ 22+16θ 25+10θ

Kedua contoh masalah program linier parametrik ini diambil dari buku Introduction to Operations Research dan Linier and Nonlinier Programming dengan hasil optimal yang sama seperti pada Tabel 3.15 dan 3.16.

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Masalah program linier parametrik dapat diselesaikan dengan menggunakan metode simplex kecuali pada kasus khusus, perubahan kontinu parameter b , di mana untuk _i

i

b < 0 maka metode dual simplex turut digunakan untuk memperbaiki solusi optimal. Jadi dengan menggunakan metode simplex, masalah program linier parametrik dapat diselesaikan dengan mudah dan sederhana.

Pada program linier parametrik terjadi perubahan pada pada parameter _cj atau i

b secara kontinu dan berurutan sehingga akhirnya menghasilkan variasi solusi optimal sesuai batas perubahan parameter yang diizinkan terjadi seperti pada tabel 3.15 dan tabel 3.16. Hal ini nantinya akan mempermudah para pengambil keputusan untuk mengambil keputusan terbaik atau disebut sebagai keputusan optimal, keputusan yang memberikan keuntungan maksimum.

Solusi masalah program linier parametrik dapat digunakan dalam berbagai kasus di dunia nyata seperti perencanaan produksi suatu produk dengan keterbatasan bahan mentah atau waktu dan perencanaan muatan barang pada pesawat udara dengan keterbatasan volume dan berat muatan tetapi ingin memperoleh hasil yang sebesar-besarnya.

4.2 Saran

Program linier parametrik hanya mencakup perubahan kontinu pada parameter _cj atau i

b , tetapi ada juga bentuk analisis sensitivitas yang lain yaitu perubahan simultan pada struktur sistem kendala, perubahan pada koefisien _aij. Bagi para pembaca yang

berminat untuk meneliti, mungkin dapat melanjutkan penelitian ini yang berhubungan dengan perubahan kontinu parameter a_ij.