PENYELESAIAN MASALAH OPTIMISASI NONLINEAR BERKENDALA DENGAN METODE FUNGSI PENALTI INTERIOR. Skripsi

PENYELESAIAN MASALAH

OPTIMISASI NONLINEAR BERKENDALA DENGAN METODE FUNGSI PENALTI INTERIOR

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh : Daniel Teguh Kurniawan

NIM : 013114027

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

THE SOLUTION

OF NONLINEAR CONSTRAINED OPTIMIZATION PROBLEMS WITH INTERIOR PENALTY FUNCTION METHODS

THESIS

Presented as Partial Fulfillment of the Requirements to Obtain the Sarjana Sains Degree

in Mathematics

By :

Daniel Teguh Kurniawan Student Number : 013114027

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

2008

HALAMAN PERSEMBAHAN

” PERIHAL WAKTU ”

Selama-lamanya bukan berarti kekal, namun kekal adalah selama-lamanya.

Jangan biarkan waktu terbuang dengan sia-sia, karena waktu terus berlalu.

Waktu sangatlah mahal dan singkat, sekali berlalu tidak akan kembali.

MOTTO

”

Tetapi carilah dahulu Kerajaan Allah dan kebenarannya, maka

semuanya itu akan ditambahkan kepadamu

.”

(

Matius 6:33

)

Skripsi punika kawula aturaken :

Konjuk dhumateng Gusti Yesus ingkang tansah paring sih rahmat lan tentrem rahayu. Mekaten ugi Bapak lan Ibu ingkang tansah paring panggulowenthah dhumateng kula saha Mas Danang lan Mas Aris ingkang tansah paring daya panyengkuyung kagem mungkasi skripsi kula punika. Kula tansah tresna dhumateng sadaya ingkang sampun mbiyantu murih cekaping skripsi kula. Maturnuwun, Gusti berkahi.

ABSTRAK

Metode fungsi penalti interior merupakan metode yang digunakan untuk menyelesaikan masalah optimisasi nonlinear berkendala dengan mengubah masalah tersebut menjadi masalah optimisasi nonlinear tak berkendala. Dalam metode ini, pencarian penyelesaian optimalnya dimulai dari daerah layak

Bentuk umum dari fungsi penalti interior adalah φ k= φ (x, μk) = f(x) + μk m j 1= Σ B(x) dengan B(x) = ) ( 1 x j g

− , g (x) merupakan kendala dan parameter penalti . Dalam penulisan ini metode yang digunakan untuk meminimalkan

j μk >0

φ (x,μk) adalah Metode Newton. Penyelesaian optimal didapatkan jika nilai φ (x,μk) konvergen ke f(x) dengan μk ≥μk+1 danμk →0, k →∞.

ABSTRACT

Interior penalty function methods is a method which is used to solve the constrained nonlinear optimization problem by changing the problem become the unconstrained nonlinear optimization. In this method, the optimal solution searching is begun from the feasible region.

The general expression of the interior penalty function is φ k= φ (x, μk) = f(x) + μk m j 1= Σ B(x) where B(x) = ) ( 1 x j g

− , g (x) is the constraints and penalty parameters j μk >0. In this thesis, the method that is used for minimizing φ (x,μk) is a Newton methods. The optimal solution is obtained if φ (x,μk) converge to f(x) as

and 1 + μ ≥ μk k μk →0, k →∞. vii

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 12 Juni 2008

Penulis,

Daniel Teguh Kurniawan

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Daniel Teguh Kurniawan

Nomor : 013114027

Demi pengembangan ilmu pengetahuan, saya memberikan kepada perpustakaan Universitas Sanata Dharma karya ilmiah saya yamg berjudul:

“ Penyelesaian Masalah Optimasi Nonlinear Berkendala Dengan Metode Fungsi Penalti Interior ”

Dengan demikian saya memberikan kepada perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikannya secara terbatas dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya.

Dibuat di Yogyakarta Pada tanggal 12 Juni 2008 Yang menyatakan,

( Daniel Teguh Kurniawan )

KATA PENGANTAR

Segala puji dan syukur, penulis panjatkan kepada Tuhan Yesus Kristus, sang Juru Selamat. Karena kasih dan karunia-Nya maka skripsi ini dapat terselesaikan dengan baik.

Dalam penyusunan skripsi ini penulis meminta bantuan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin menyampaikan ucapan terima kasih kepada :

1. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing dan Kaprodi Matematika FST-USD yang dengan rendah hati mau meluangkan banyak waktu luang dan penuh kesabaran telah membimbing selama penyusunan skripsi ini walaupun penulis sering terlambat bahkan kabur dari jadwal bimbingan dengan waktu yang cukup lama.

2. Ir. Greg. Heliarko, S.J., S.S., B.S.T., M.Sc., M.A., selaku Dekan FST-USD. 3. Kakak-kakakku, Danang dan Aris, yang selalu mendorong untuk dapat

menyelesaikan skripsi tepat waktu tapi tidak bisa sesuai dengan yang diharapkan. .

4. Teman-teman “ Penghuni Terakhir “ : Tedy “ Bear “, Rita “ poco-poco “, Zefanya, Yuli, yang bersama-sama berjuang keluar dari “selingan hidup” ini dan yang saling memberikan semangat, motivasi supaya lulus sama-sama. 5. Keluarga Besar Rakiman di Klaten atas dukungan doanya..

6. teman pemuda remaja GKJ Gondangwinangun Klaten dan Teman-teman pemuda remaja GKJ Ketandan, terima kasih atas dukungan doanya.

7. Sahabat-sahabatku di Matematika Angkatan’01, Ariel, Ray, Andre, Indah, Deta, Maria, Erika, Ajeng, Very, Yuli, Wiwit, Vrysca, April, Alam, Dani, Tabitha, Upik. Tidak akan pernah ku lupakan semua waktu yang pernah kita lewati.

8. Mas Nadi “ sebagai pembimbing skripsi di kos”, Ridwan ” Sahabat dan saudaraku ” terima kasih atas tumpangan kostnya.

9. Teman-teman PMK “ OIKUMENE “ yang selalu berbagi suka duka dalam hidup. Maxi dan Tata “ Maranatha Family “ atas dukungan doanya.

10. Teman-teman pemuda Karang Taruna “ Mekar Sari “ di desa tempat saya tinggal, terima kasih atas dukungan doanya.

11. Teman-teman SMU 2 Klaten, Seka dan Okie terima kasih atas petuah bijaknya. 12. Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu.

Tak ada gading yang tak retak, penulis menyadari kekurangan dalam skripsi ini, untuk itu saran dan kritik sangat diharapkan dalam peningkatan kualitas skripsi ini.Akhirnya penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta, 12 Juni 2008

Penulis,

Daniel Teguh Kurniawan

DAFTAR ISI

Halaman

HALAMAN JUDUL INDONESIA ... i

HALAMAN JUDUL INGGRIS... ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

ABSTRAK ... vi

ABSTRACT ... vii

PERNYATAAN KEASLIAN KARYA ... viii

LEMBAR PERNYATAAN... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

DAFTAR GAMBAR ... xiv

DAFTAR TABEL ... xv

BAB I PENDAHULUAN ... 1

A. Latar Belakang Masalah ... 1

B. Perumusan Masalah ... 3 C. Batasan Masalah ... 3 D. Tujuan Penulisan ... 3 E. Manfaat Penulisan ... 4 F. Metode Penelitian ... 4 G. Sistematika Penulisan ... 4 xii

BAB II DASAR TEORI ... 6

A. Ruang Vektor dan Ruang Euclid ... 6

B. Barisan Konvergen dan Barisan Monoton ... 7

C. Fungsi Kontinu ... 9

D. Turunan parsial ... 10

E. Metode newton ... 10

F. Optimisasi ... 12

1. Masalah Optimasi... 12

2. Penyelesaian Masalah Optimasi... 14

BAB III METODE FUNGSI PENALTI INTERIOR... 15

A. Konsep Dasar Fungsi Penalti ... 15

B. Bentuk Umum Fungsi Penalti Interior ... 19

C. Algoritma Metode Fungsi Penalti Interior ... 20

D. Konvergensi Metode Fungsi Penalti Interior ... 54

BAB IV PENUTUP ... 57 A. Kesimpulan ... 57 B. Saran ... 58 DAFTAR PUSTAKA ... 59 LAMPIRAN ... 60 xiii

DAFTAR GAMBAR

Halaman

Gambar 2.1 Flowchart Algoritma Metode Newton... 11

Gambar 2.2 Peminimum f(x) sama dengan Pemaksimum -f(x)... 12

Gambar 3.1.1 Ilustrasi Metode Fungi Penalti Eksterior... 18

Gambar 3.1.2 Ilustrasi Metode Fungsi Penalti Interior... 18

Gambar 3.2 Flowchart Algoritma Metode Fungsi Penalti Interior... 21

DAFTAR TABEL

Halaman Tabel 3.3.1 Output penyelesaian contoh 3.3.1... 40 Tabel 3.3.2 Output penyelesaian contoh 3.3.2... 48 Tabel 3.3.3 Output penyelesaian contoh 3.3.3... 53

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Optimisasi adalah tindakan yang dilakukan untuk mendapatkan hasil terbaik dari kondisi-kondisi yang diberikan ( sebagai suatu masalah ). Optimisasi sering kita jumpai dalam kehidupan sehari-hari seperti pada bidang ekonomi maupun manajemen. Sebagai contoh perusahaan pakaian yang ingin memberikan harga yang terbaik supaya perusahaan itu mendapatkan keuntungan yang terbanyak. Dalam berbagai macam situasi praktis tindakan tersebut dapat dibawa ke dalam perumusan matematika sebagai suatu fungsi dari variabel-variabel keputusan tertentu, dengan demikian optimisasi dapat didefinisikan sebagai proses untuk menemukan nilai maksimum dan minimum dari suatu fungsi.

Bidang ilmu matematika yang secara umum mempelajari tentang optimisasi adalah Riset Operasi. Riset Operasi sendiri terbagi menjadi 3 jenis metode, yang secara khusus mempelajari tentang masalah optimisasi tersebut yaitu : Pemrograman Matematika, Proses Stokhastik dan Metode Statistika. Pemrograman Matematika digunakan untuk menemukan nilai fungsi dengan beberapa variabel dari suatu himpunan yang sudah ditentukan dengan kendala-kendalanya. Pemrograman Matematika terbagi lagi dalam beberapa bagian, diantaranya adalah Program Linear dan Program Nonlinear.

Dalam Program Nonlinear masalah optimisasi dibedakan menjadi dua, yaitu masalah optimisasi tanpa kendala dan masalah optimisasi dengan kendala.

Masalah optimisasi dengan kendala merupakan masalah mengoptimalkan fungsi sasaran dengan kendalanya, dimana fungsi sasaran dan kendala-kendalanya tersebut adalah fungsi nonlinear. Ada beberapa metode yang digunakan dalam menyelesaikan masalah optimisasi program nonlinear dengan kendala yaitu ; Metode Primal, Metode Penalti, Metode Dual dan Metode Pemotongan Kurva serta Metode Lagrange.

Pada skripsi ini akan dibahas pendekatan numeris untuk menyelesaikan masalah optimisasi Program Nonlinear dengan kendala berupa persamaan dan pertidaksamaan. Pendekatan yang digunakan adalah Metode Fungsi Penalti. Metode Fungsi Penalti merupakan salah satu Metode Numerik yang digunakan untuk mengubah masalah optimisasi dengan kendala menjadi masalah tanpa kendala dengan menambahkan fungsi penalti pada fungsi sasaran. Istilah penalti dipilih sedemikian hingga nilainya akan kecil untuk titik yang jauh dari batas kendala, dimulai dari titik layak x , yaitu sembarang titik yang memenuhi semua kendala, titik subbarisan yang dibangun akan selalu terletak di daerah layak karena batas kendala bertindak sebagai penghalang sepanjang proses minimasasi. Inilah alasan mengapa Metode Fungsi Penalti juga dikenal sebagai metode penghalang.

Pada dasarnya Metode Penalti terbagi menjadi 2 yaitu Metode Fungsi Penalti Eksterior dan Metode Fungsi Penalti Interior. Akan tetapi, skripsi ini hanya membahas Metode Fungsi Penalti Interior, dimana penalti ditambahkan pada fungsi sasaran. Metode ini menghasilkan barisan titik-titik layak yang limitnya merupakan penyelesaian optimal dari masalah asli.

B. Perumusan Masalah

Pokok masalah yang akan dibahas dalam skripsi ini sebagai berikut : 1. Apa itu Metode Fungsi Penalti Interior ?

2. Bagaimana menyelesaikan masalah optimisasi dengan kendala berupa pertidaksamaan dengan Metode Fungsi Penalti Interior ?

C. Batasan Masalah

Pada penulisan skripsi ini hanya akan dibahas tentang Metode Fungsi Penalti Interior untuk menyelesaikan masalah optimisasi Program Nonlinear dengan kendala-kendala berupa pertidaksamaan dan teknik yang digunakan dalam menyelesaikan masalah optimisasi tak berkendala menggunakan metode newton.

D. Tujuan Penulisan

Penulisan ini bertujuan untuk memberi wawasan dan pengetahuan kepada pembaca dengan pengertian dasar tentang bagaimana cara menyelesaikan masalah optimisasi Program Nonlinear dengan kendala dengan Metode Fungsi Penalti Interior.

E. Manfaat Penulisan

Manfaat dari penulisan skripsi ini yang sangat diharapkan adalah penulis dapat mengetahui dan memahami bagaimana bentuk Metode Fungsi Penalti Interior dan bagaimana cara menyelesaikan masalah optimisasi dengan kendala dengan Metode Fungsi Penalti Interior dengan kendala-kendala berupa pertidaksamaan.

F. Metode Penulisan

Metode penulisan yang digunakan dalam penulisan skripsi ini adalah metode studi literatur atau studi pustaka, yaitu dengan membaca dan mempelajari materi dari buku-buku acuan yang berkaitan dengan masalah ini. Jadi, dalam skripsi ini tidak ada penemuan-penemuan yang baru.

G. Sistematika Penulisan

BAB I : PENDAHULUAN

Dalam bab I akan dibahas tentang latar belakang, perumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan dan sistematika penulisan.

BAB II : DASAR TEORI

Dalam bab ini akan dibahas konsep ruang vektor dan ruang Euclid, fungsi kontinu dan fungsi terdiferensial, Barisan Konvergen dan Barisan Monoton, turunan parsial, syarat optimalitas untuk masalah berkendala, Metode Newton serta teori optimisasi yang nantinya akan digunakan untuk memahami metode Fungsi Penalti Interior.

BAB III : METODE FUNGSI PENALTI INTERIOR

Dalam bab III akan dibahas tentang konsep fungsi penalti, interpretasi geometris fungsi penalti, pengertian metode Fungsi Penalti Interior, bentuk umum Fungsi Penalti Interior dan algoritma metode Fungsi Penalti Interior disertai beberapa contoh masalah optimisasi nonlinear berkendala yang diselesaikan dengan metode Fungsi Penalti Interior, implementasi dengan program matlab serta konvergensi Metode Fungsi Penalti Interior.

BAB IV : PENUTUP

BAB III

METODE FUNGSI PENALTI INTERIOR

Pada bab ini akan dipaparkan tentang metode fungsi penalti interior sebagai salah satu cara untuk menyelesaikan masalah program nonlinear, yakni masalah optimisasi berkendala. Proses pencarian dalam menemukan penyelesaian optimal dengan menggunakan metode fungsi penalti interior akan dimulai dari daerah layak. Tetapi sebelum membahas lebih jauh tentang metode tersebut, akan dibahas terlebih dahulu tentang konsep dasar metode tersebut.

A. Konsep Dasar Fungsi Penalti

Salah satu cara untuk mengubah masalah optimisasi berkendala menjadi masalah optimisasi tak berkendala adalah dengan metode fungsi penalti. Dalam kehidupan sehari-hari penalti yang berarti hukuman terjadi karena adanya pelanggaran. Dengan demikian, dalam masalah optimisasi berkendala fungsi penalti terjadi karena adanya pelanggaran, yaitu dengan menghilangkan kendala pada masalah optimisasi tersebut.

Masalah optimisasi dasar dapat dinyatakan dalam bentuk

meminimalkan f (x)

dengan kendala g_j(x) ≤ 0 , j = 1, 2, Κ , m ( 3.1 )

dengan fungsi f, g_jmerupakan fungsi kontinu pada _{ℜ dan X himpunan tidak} n kosong di _{ℜ . Perhatikan bahwa jika ada sembarang kendala yang diberikan} n maka persamaan tersebut dipenuhi oleh x ∈ X . Masalah optimisasi berkendala tersebut diubah ke dalam sebuah masalah minimisasi tak berkendala dengan membangun sebuah fungsi yang berbentuk

φ _k= φ (x, μ_k) = f(x) + μ_k m j 1=

Σ B(x) ( 3.2 )

dimana B(x) adalah suatu fungsi dari kendala g_j dan μ_k adalah konstanta positif yang dinamakan parameter penalti. Suku kedua pada ruas kanan dari persamaan ( 3.2 ) disebut syarat penalti. Jika minimisasi tak berkendala dari fungsi φ diulang untuk suatu barisan dari nilai-nilai parameter penalti μ_k untuk k = 1, 2, Κ maka penyelesaiannya akan konvergen ke masalah optimisasi dasar yang dinyatakan dalam persamaan ( 3.1 ). Jadi, penalti dapat diartikan sebagai fungsi yang ditambahkan pada fungsi obyektif dengan parameter penalti. Metode penambahan fungsi penalti ini disebut sebagai Metode Fungsi Penalti.

Rumus Metode Fungsi Penalti untuk masalah berkendala dengan kendala berbentuk pertidaksamaan dapat dibagi menjadi dua kategori yaitu metode fungsi penalti interior dan metode fungsi penalti eksterior. Rumus metode fungsi penalti interior yang sering digunakan berbentuk

B(x) =

Σ

= m j 1 - ) ( 1 x j g atau B(x) =

Σ

= m j 1 ln [- g_j(x) ]

Rumus metode fungsi penalti eksterior yang sering digunakan berbentuk

B(x) = max[0, g_j(x)] atau

B(x) =

{

max

[

0,g_j(x)

]

}

2

Di dalam metode fungsi penalti interior minimal tak berkendala dari φ _k berada dalam daerah layak dan konvergen ke penyelesaian persamaan ( 3.1 ) dengan μ_k berbeda dalam aturan tertentu. Dalam metode fungsi penalti eksterior titik yang membuat nilai minimum dari masalah tak berkendala φ _k berada dalam daerah tak layak dan konvergen ke penyelesaian yang diinginkan dari luar dengan

k

μ berbeda dalam aturan khusus. Untuk masalah penalti interior dan eksterior, konvergensi dari masalah optimisasi tak berkendala φ _k diilustrasikan pada Gambar 2a dan Gambar 2b untuk masalah mencari nilai x yang

meminimalkan f(x) = α x₁

Gambar 3.1.1 Ilustrasi Metode Fungsi Penalti Eksterior

Untuk menggambarkan secara geometris metode fungsi penalti interior, dibuat terlebih dahulu grafik fungsi f(x) = α x₁ dan kendala g₁(x) = β−x₁ ≤ 0. selanjutnya masalah optimasi berkendala tersebut dibawa ke dalam masalah optimisasi tak berkendala dengan membentuk sebuah fungsi

β 1 μ α = 1 1 _x x φ _k dengan B(x) = -1 1 x −

β dan μk sebagai parameter penalti. Pencarian optimum dimulai dari daerah layak x₁ yang berada di daerah layak dan titik berikutnya yang dihasilkan selalu berada dalam daerah layak karena ada batas-batasnya. Karena pemilihan μ_k yang besar maka mengakibatkan φ masih _k jauh dari optimum. Dengan cara yang sama, jika minimasi tak berkendala dari fungsi φ diulang untuk suatu barisan nilai-nilai parameter penalti k = 1, 2, .... _k dimana μ_k >μ_k+1 maka penyelesaian akan konvergen ke masalah optimisasi dasar dan akan mendekati optimum.

B. Bentuk Umum Fungsi Penalti Interior

Dari Sub bab sebelumnya, dalam metode fungsi penalti interior sebuah fungsi baru φ yang dibentuk dengan menambahkan syarat penalti ke fungsi obyektif. Syarat penalti dipilih sedemikian hingga nilainya mengecil sehingga nilai fungsi φ akan menuju optimum. Kejadian ini bisa dilihat pada Gambar 3.1.2. Minimisasi tak berkendala dari fungsi φ (x, μ_k) dimulai dari sembarang titik layak

x

1 dan titik berikutnya yang dihasilkan selalu pada daerah layak. Hal

selama proses minimisasi. Inilah alasan mengapa metode fungsi penalti interior juga disebut sebagai metode barrier.

Fungsi φ (x, μ_k) didefinisikan sebagai

φ(x,μ_k) = f(x) - μ_k

Σ

= m j 1 ( ) 1 x j g ( 3.3 )

Terlihat bahwa nilai fungsi φ (x, μ_k) akan selalu lebih besar dari f(x) ketika g_j(x) negatif untuk semua titik layak x. Jika semua kendala g_j(x) dipenuhi dengan tanda persamaan maka nilai φ menuju tak hingga dan syarat penalti di ( 3.3 ) tidak terdefinisi jika x tak layak. Karena persamaan ini tidak diperbolehkannya adanya kendala yang dilanggar maka titik awal layak harus dicari dalam proses pencarian menuju ke titik optimum. Sebagian besar masalah optimisasi nonlinear berkendala tidaklah sulit untuk menemukan sebuah titik yang memenuhi semua kendala g_j(x) ≤ 0 karena pemilihan titik x yang bebas.

C. Algoritma Metode Fungsi Penalti Interior

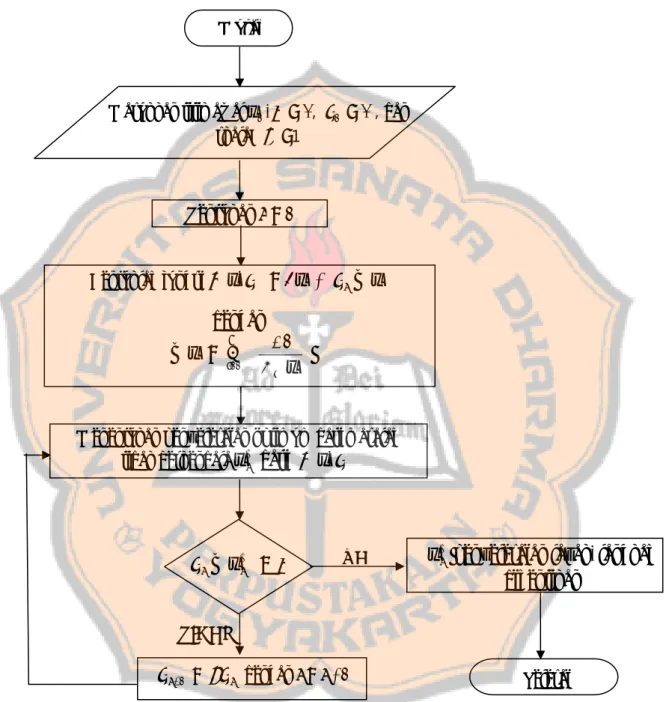
Berikut akan diberikan algoritma dari metode fungsi penalti interior untuk menyelesaikan masalah optimisasi dasar :

meminimalkan f (x)

kendala g_j(x) ≤ 0 , j = 1, 2, Κ , m

Algoritma metode fungsi penalti interior dapat diperlihatkan sebagai berikut :

Gambar 3.2 Flowchart Algoritma Metode Fungsi Penalti Interior Masukkan titik awal x₁,ε > 0, μ > 0 ₁ , dan

skalar β >1 Mulai

Tentukan k = 1

x*_k penyelesaian layak, langkah dihentikan Bentuklah fungsi φ(x,μ) = f(x) + μ_kB(x) dengan B(x) = m j 1Σ= _{( )} 1 x j g −

Menentukan penyelesaian optimum dari masalah tidak berkendala x*_k dari φ(x,μ)

Selesai k μ B(x*_k) < ε 1 + k μ = βμ_k dengan k = k +1 YA TIDAK

Secara umum langkah-langkah penyelesaian dengan metode fungsi penalti interior adalah :

Langkah 1

Menentukan nilai awal x₁, parameter penalti μ₁ > 0 dan skalar β∈(0,1) dan diberikan ε > 0 dan k = 1.

Langkah 2 Membentuk fungsi φ(x, μ_k) = f(x) + μ_kB(x) dengan B(x) =

Σ

= m j 1 - ) ( 1 x j g Langkah 3

Mencari penyelesaian optimum x*

k dari masalah optimisasi tidak berkendala φ(x, μ_k) = f(x) + μ_kB(x).

Langkah 4

Jika μ_kB(x_k) < ε langkah dihentikan, maka x_k+1 merupakan penyelesaian layak. Sebaliknya jika μ_kB(x_k) > ε, maka tetapkan μ_k+1 = β μ_k, ganti k dengan k + 1 dan ulangi Langkah 2.

Ada hal-hal yang perlu dipertimbangkan dalam menerapkan metode ini :

1 Proses iterasi dimulai dengan titik awal x₁ tetapi mungkin dalam beberapa kasus titik awal x₁ ini tidak perlu dipersiapkan

Tidaklah sulit untuk menentukan titik awal x₁ dalam masalah optimisasi nonlinear berkendala yang memenuhi semua kendala g_j(x₁)<0. Dalam

kasus khusus titik awal tidak diperlukan dalam menyelesaikan masalah optimisasi berkendala yang dapat dilihat dari fungsi kendalanya yang hanya terdapat satu variabel. Jika fungsi kendalanya terdapat beberapa variabel maka titik awal perlu dipersiapkan. Tetapi, ada beberapa keadaan sedemikian hingga titik layak tidak bisa ditemukan dengan mudah. Dalam kasus seperti ini, titik layak awal yang diminta dapat ditemukan dengan menggunakan metode fungsi penalti interior itu sendiri. Dengan memperhatikan hal-hal sebagai berikut :

Langkah i

Pilih sembarang titik x₁ dan evaluasi g_j(x) di titik x₁. Karena titik x₁ sembarang maka tidak semua titik memenuhi semua kendala pertidaksamaan. Jika ada r dari m kendala yang dilanggar, maka kendala-kendala tersebut dikelompokkan kembali sedemikian hingga r kendala yang dilanggar akan menjadi satu kelompok yang terakhir yaitu

g_j(x₁)<0, j =1,2, Κ , m-r

dan g_j(x₁)≥0, j = m-r+1, m-r +2, Κ , m ( 3.4 )

Langkah ii

Identifikasi kendala yang memiliki kesalahan terbesar di titik x₁ yaitu dengan mencari bilangan bulat k sedemikian hingga

[

( )

]

)

(x_{1 j} x₁ k maksg

Langkah iii

Selesaikan masalah optimasi yang dibuat dalam langkah 3 dengan mengambil titik x₁ sebagai titik awal. Rumuskan masalah optimisasi yang baru seperti mencari x yang meminimalkan g_k(x) dengan kendala g_j(x₁)≤0 j =1,2, Κ , m-r ( 3.6 )

dan g_j(x₁)−g_k(x₁)≤0, j = m-r+1, m-r +2, Κ , k-1, k+1, Κ , m

Langkah iv

Selesaikan masalah optimisasi pada langkah (iii) dengan mengambil titik x₁ sebagai titik awal menggunakan metode fungsi penalti interior. Metode ini dapat diakhiri ketika nilai fungsi g_k(x) ≤0 . Jadi penyelesaian akan menghasilkan x_k yang memenuhi sedikitnya satu kendala dari himpunan kendala yang dilanggar oleh x₁.

Langkah v

Jika semua kendala tidak dipenuhi oleh titik x_k, ambil titik baru x₁ = x_k dan kendala dikelompokkan kembali sedemikian hingga r pada kendala yang terakhir tidak akan dipenuhi dan ulangi langkah ii.

Langkah ini dapat diulangi sampai semua kendala terpenuhi dan didapat 0 ) (x₁ < j g , j =1,2, ... , m-r

2 Dengan mencari parameter penalti awal ( μ₁) yang sesuai

Jika minimisasi tak berkendala φ(x,μ_k) dikerjakan untuk suatu barisan turun μ_k, dengan memilih sebuah nilai μ₁ yang sangat kecil maka nilai optimum dari fungsi φ akan konvergen ke penyelesaian masalah optimisasi dasar. Namun dari segi penghitungan, untuk minimisasi fungsi φ akan lebih mudah jika μ_k besar. Hal ini dapat dilihat pada Gambar 3.1.2. Terlihat bahwa jika nilai μ_k menjadi semakin kecil, nilai fungsi φ berubah dengan lebih cepat di sekitar minimum ∗

k

φ . Pencarian minimum dari suatu fungsi lebih mudah bila grafiknya lebih mulus karena fungsinya kontinu dan dapat diturunkan. Jika μ_k besar maka minimisasi tak berkendala φ akan menjadi lebih mudah dan minimum dari φ_k, *

k

x , akan menjadi lebih jauh dari minimum x∗.

3 Nilai perkalian faktor β yang dipilih haruslah tepat

Jika nilai awal μ_k sudah dipilih maka nilai-nilai μ_k berikutnya harus dipilih sedemikian hingga μ_k+1 < μ_k. Nilai μ_k dipilih dengan μ_k+1=β μ_k dimana β < 1. Nilai β dapat diambil sebagai 0,1 atau 0,2 atau 0,5 dan seterusnya.

4 Kriteria kekonvergenan yang sesuai harus dipilih untuk menentukan nilai optimum

Karena minimisasi tak berkendala dari φ(x,μ_k) harus dikerjakan menurut suatu barisan turun nilai μ_k maka perlu menggunakan kriteria konvergensi yang sesuai untuk mengidentifikasikan titik optimum. Proses dapat dihentikan pada saat syarat berikut dipenuhi.

a. Selisih relatif antara nilai fungsi obyektif yang dihasilkan pada akhir dari sembarang dua minimisasi tak berkendala yang berurutan berada dibawah sebuah bilangan yang kecil ε₁, yaitu

1 * * 1 -k * ) ( ) ( ) ( _ε ≤ − k k f f f x x x .

b. Selisih antara titik optimum * k

x - x*_k−1 menjadi sangat kecil. Ini dapat dinyatakan dalam beberapa cara. Yang biasa digunakan adalah

2 ) (Δx _i ≤ε . Dengan xΔ = * k x - x*_k−1

(Δx)_i adalah anggota ke - i dari vektor xΔ

Max |(Δx)_i| ≤ ε₃ | xΔ | =

[

2 2

]

12 2 2 1 ( ) ( ) ) (Δx + Δx +Κ + Δx _n ≤ ε ₄

Nilai dari ε₁ sampai ε harus dipilih bergantung pada karakteristik dari ₄ masalah yang ditangani.

Berikut ini akan diberikan contoh masalah minimisasi yang tidak menggunakan titik awal.

Contoh 3.1.1

Selesaikan masalah optimisasi berkendala berikut :

Minimalkan f ( x₁ , x₂ ) = 13 (x1 + 3 )3 + x2

Kendala g₁ ( x₁ , x₂ ) = - x₁ + 1 ≤ 0

g₂ ( x₁ , x₂ ) = - x₂ ≤ 0

Penyelesaiannya :

Dalam kasus di atas titik awal tidak diperlukan karena fungsi kendalanya hanya terdapat satu variabel. Untuk mencari penyelesaian optimumnya maka dibutuhkan parameter penalti awal ( μ ) yang sesuai. ₁

Langkah 1

Misalkan ε = 0,00001

β = 0,1 μ = 1000 ₁

Langkah 2 Membentuk fungsi φ(x,μ) = f(x) + μ_kB(x) B(x) dipilih dengan B(x) =

Σ

= 2 1 j ( ) 1 x j g − = _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x Sehingga diperoleh φ(x,μ) = f(x) + μ_kB(x) = 13 (x1 + 3 ) 3_{+ x} 2- μk ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x Langkah 3

Untuk mencari penyelesaian optimum dari masalah optimisasi tak berkendala, dibutuhkan penurunan parsial φ terhadap x₁ dan x₂ :

Turunan parsial φ terhadap x₁ diperoleh :

1 x ∂ ∂φ = (x₁ + 1 )2 _- 2 1) 1 ( x k − μ = 0 atau (x₁ + 1 )2 ₌ 2 1) 1 ( x k − μ (x₁ + 1 )2 _{(1 - x} 1)2 = μk ( x₁2_{+ 2x} 1 +1 ) ( 1 - 2x1 + x12) = μ k x₁4_{- 2 x} 1 2 _{+ 1 =} k μ atau (x2 1- 1 ) 2 ₌ k μ

x2 1- 1 = μk 2 1 x₁ = (μ_k 12 +1 ) 12 (3.1.1) Turunan parsialφ terhadap x₂ diperoleh :

2 x ∂ ∂φ = 1 - ₂ 2 x k μ = 0 x2 2= μ k atau x₂= μ_k 12 _(3.1.2)

Dari persamaan (3.1.1) dan (3.1.2) diperoleh penyelesaian optimum tak berkendala dan x*₁(μ ) = (_k μ_k 2 1 +1 )12 x*₂(μ ) = k μk 2 1

Dalam masalah ini tidak diperlukan titik awal karena setelah melakukan penghitungan secara kalkulus, titik x*

k bergantung pada parameter penalti (μ1). Apabila penyelesaian optimum tersebut disubstitusikan ke fungsi φ maka

didapatkan : ) ( min μk φ = 13 (x1 + 3 )3+ x2- μk ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x = 13[(μk 2 1 +1 )12+ 1]3+ k μ 12 - k μ { [ 1 ) 1 ( 1 2 1 2 1 + + − μ_k ] – [ 12 1 k μ ] }

= 13[(μk 2 1 +1 )12+ 1]3+ k μ 12 + [ 1 ) 1 ( 12 + 12 + − − k k μ μ ] + 2 1 k k μ μ = 13[(μk 2 1 +1 )12+ 1]3+ k μ 12 + ) 1 )( ) 1 ( 1 ( ) 1 ( 2 1 2 1 k k k k μ μ μ μ + − + μ_k 12 = 1₃[( k μ 12+1 )12+ 1]3+ 2 k μ 12 - 2 1 2 1 ) 1 ( 1 1 1 + − _k k k μ μ μ = 13[(μk 2 1 +1 )12+ 1]3+ 2 k μ 12 - 2 1 2 1 2 ( 1)) 1 ( 1 1 + − _k k k μ μ μ ) ( min μk φ = 13[(μk 2 1 +1 )12+ 1]3+ 2 k μ 12 - 2 1 2 3 ₂ 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − k k k μ μ μ

Untuk mendapatkan penyelesaian dari masalah optimasi dasar dicari melalui : f _min = 0 lim → k μ φmin(μ ) k = 0 lim → k μ { 3 1 [( k μ 12+1 )12+ 1]3+ 2 k μ 12 - 2 1 2 3 ₂ 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − k k k μ μ μ } = 3 8 = 2,66667 Iterasi 1 Untuk k = 1 x*₁(μ ) = (₁ μ₁ 2 1 +1 )12

= ( 100012 + 1 ) 12 = 5,71164 dan x*₂(μ ) = 1 μk 2 1 = 100012 = 31,62278 Sehingga diperoleh : ) ( ₁ min μ φ = 13[(μ1 2 1 +1 )12+ 1]3+ 2 1 μ 12 - 2 1 2 3 ₂ 1 1 1 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ = 1₃[(₁₀₀₀ 12+1 )12+ 1]3+ 2(1000)12 - 2 1 2 3 ₂ 1000 1 1000 1 1000 1 1 ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ − = 100,777761 + 63,245554 + 210,748156 = 374,77147 dan f(μ₁) = 13

(

)

3 1+1 x + x₂ = 1_{3 ( 5,71164 + 1 )} 3 _{+ 31,62278} = 100,777761 + 31,62278 = 132,400541 1 μ B(x*₁) = μ_{k ⎥} ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x

= μ₁ 12 - 2 1 2 3 ₂ 1 1 1 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ = 31,62278 + 210,74816 = 242,37094 > ε

Penyelesaian belum optimal karena μ₁B(x*₁) > ε maka langkah diteruskan.

Langkah 4 Tetapkan μ₂=β μ₁ = (0,1)1000 = 100 Iterasi 2 Untuk k = 2 Langkah 3

Berdasarkan iterasi sebelumnya, nilai φ minimum dicari jika

x*₁(μ ) = (₂ μ₂ 12+ 1 )12 = ( 10012 + 1 )12 = 3,31662 dan x*₂(μ ) = ₂ μ₂ 12 = 10012 = 10 Sehingga diperoleh : ) ( ₂ min μ φ = {1₃[( 2 μ 12+1 )12+ 1]3+ 2

2 μ 12 - 2 1 2 3 ₂ 2 2 2 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ } = 13[(100 2 1 +1 )12+ 1]3+ 2(100)12 - 2 1 2 3 ₂ 100 1 100 1 100 1 1 ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ − = 89,9776 dan f(μ ) = ₂ 13

(

)

3 1+1 x + x₂ = 13[(100 2 1 +1 )12+ 1]3+ 10012 = 36, 8109 2 μ B(x*₂) = 10 + 43,16671 = 53,16671 > ε

Penyelesaian belum optimal karena μ₂B(x*₂) > ε maka langkah diteruskan.

Langkah 4 Tetapkan μ₃= β.μ₂ = (0,1).100 = 10 Iterasi 3 Untuk k = 3

x*₁(μ ) = (3 μ3 2 1 + 1 )12 = ( 1012+1 ) 12 = 2,04017 dan x* 2(μ ) = 3 μ3 2 1 = 1012 = 3,16228 Sehingga diperoleh : ) ( ₃ min μ φ = {13[(μ3 2 1 +1 )12+ 1]3+ 2 3 μ 12 - 2 1 2 3 ₂ 3 3 3 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ } = 13[ 2,04017 + 1 ]3+ 2 ( 3,16228 ) - 2 1 2 3 ₂ 10 1 10 1 10 1 1 ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ − = 25,3048 dan f(μ ) = ₃ 13

(

)

3 1+1 x + x₂ = 9, 36636 + 3,16228 = 12,5286 3 μ B(x*₃) = 3,16228 + 9, 61381 = 12,77609 > ε

Langkah 4

Tetapkan μ₄= β.μ₃

= (0,1).10 = 1 Iterasi 4

Untuk k = 4

Berdasarkan iterasi sebelumnya, nilai φ minimum dicari jika

x*₁(μ ) = (₄ μ₄ 12+ 1 )12 = ( 2 )12 = 1,41421 dan x*₂(μ ) = ₄ μ₄ 12 = 1 Sehingga diperoleh : ) ( ₄ min μ φ = {13[(μ4 2 1 +1 )12+ 1]3+ 2 4 μ 12 - 2 1 2 3 ₂ 4 4 4 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ } = {13[(1 2 1 +1 )12+ 1]3+ 2(1)12 - 2 1 2 3 ₂ 1 1 1 1 1 1 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ − } = 1_{3(1,41421 + 1)} 3_{+ 2 + 2,41421} = 4,69036+ 2 + 2,41421 = 9,10457 dan f(μ ) = 4 13

(

)

3 1+1 x + x₂ = 4,69036+ 1 = 5,69036

4

μ B(x*₄) = 1 + 2,41421 = 3,41421 > ε

Penyelesaian belum optimal karena μ₄B(x*₄) > ε maka langkah diteruskan.

Langkah 4

Tetapkan μ₅ = β.μ₄

= (0,1).1 = 0,1 Iterasi 5

Untuk k = 5

Berdasarkan iterasi sebelumnya, nilai φ minimum dicari jika

x*₁(μ ) = (₅ μ₅ 12+ 1 )12 = (0,112+ 1 )12 = 1,14727 dan x* 2(μ ) = μ5 2 1 = 0,112 = 0,31623 Sehingga diperoleh : ) ( ₅ min μ φ = {1_3[( 5 μ 12+1 )12+ 1]3+ 2 5 μ 12 - 2 1 2 3 ₂ 5 5 5 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ }

= {1₃[(_0,112+1 )12+ 1]3+ 2(0,1)12 - 2 1 2 3 ₂ 1 , 0 1 1 , 0 1 1 , 0 1 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − } = 3,300188 + 0,632456 + 0,06899 = 4,00163 dan f(μ ) = ₅ 13

(

)

3 1+1 x + x₂ = 3,300188 + 0,31623 = 3,61642 5 μ B(x*₅) = 0,31623 + 0,06899 = 0,38522 > ε

Penyelesaian belum optimal karena μ₅B(x*₅) > ε maka langkah diteruskan.

Langkah 4

Tetapkanμ₆= β.μ₅

= (0,1).(0,1) = 0,01 Iterasi 6

Untuk k = 6

Berdasarkan iterasi sebelumnya, nilai φ minimum dicari jika

x*₁(μ ) = (₆ μ₆ 12+ 1 )12

dan x* 2(μ ) = 6 μ6 2 1 = 0,1 Sehingga diperoleh : ) ( ₆ min μ φ = {1₃[( 6 μ 12+1 )12+ 1]3+ 2 6 μ 12 - 2 1 2 3 ₂ 6 6 6 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ } = {13[(0,01 2 1 +1 )12+ 1]3+ 2(0,01)12 - 2 1 2 3 ₂ 01 , 0 1 01 , 0 1 01 , 0 1 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − } = 2,86671 + 0,2 + 0,20488 = 3,27159 dan f(μ ) = 6 13

(

)

3 1+1 x + x₂ = 2,86671 + 0,1 = 2,96671 6 μ B(x*₆) = 0,1 + 0,20488 = 0,30488 > ε

Penyelesaian belum optimal karena μ₆B(x*₆) > ε maka langkah diteruskan. Analog dengan langkah-langkah sebelumnya, titik optimal yang merupakan penyelesaian optimal didapatkan pada iterasi yang ke-15, yakni

Langkah 4 15

μ = β.μ₁₄

Iterasi 15 Untuk k = 15

Berdasarkan iterasi sebelumnya, nilai φ minimum dicari jika

x*₁(μ₁₅) = (μ₁₅ 12+ 1 )12 = 1,00000 dan x* 2(μ15) = μ15 2 1 = 0,00000 Sehingga diperoleh : ) ( ₁₅ min μ φ = {13[(μ15 2 1 +1 )12+ 1]3+ 2 15 μ 12 - 2 1 2 3 ₂ 15 15 15 1 1 1 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − μ μ μ } = 2,66669 dan f(μ₁₅) = 13

(

)

3 1+1 x + x₂ = 2,66668 15 μ B(x*₁₅) = 0,000009

Karena μ₁₅B(x₁₅* ) = 0,000009 < ε maka langkah dihentikan. Maka diperoleh penyelesaian dari masalah di atas dengan x*

1 = 1, x * 2= 0.

Pada iterasi ke-15 penyelesaian sudah optimum karena sudah memenuhi syaratμ₁₅B(x*₁₅) = 0,000009 < ε .

Berikut akan diberikan penyelesaian dengan menggunakan program MATLAB. ( lampiran 1 )

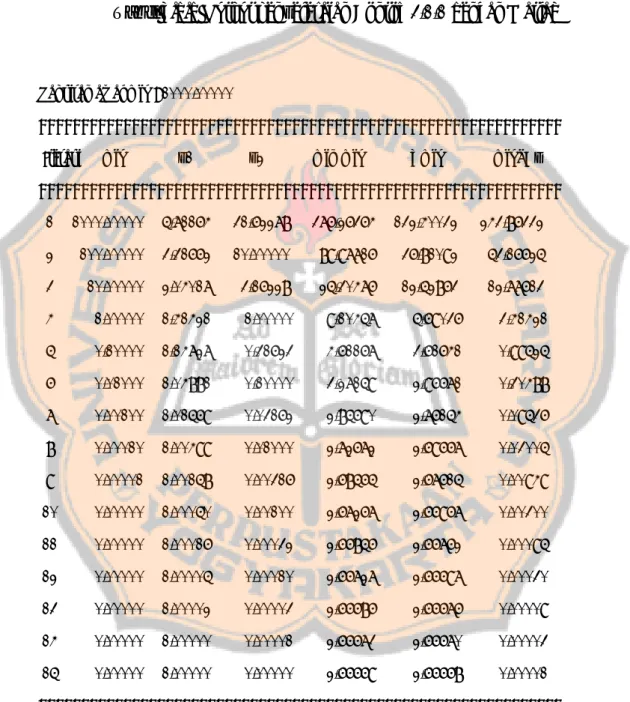
Tabel 3.1.1 Output penyelesaian Contoh 3.1.1 dengan Matlab

Taksiran awal miu : 1000.00000

============================================================== Iterasi miu x1 x2 min(miu) f(miu) miu_Bx ============================================================== 1 1000.00000 5.71164 31.62278 376.26364 132.40032 243.86332 2 100.00000 3.31662 10.00000 89.97716 36.81092 53.16625 3 10.00000 2.04017 3.16228 25.30476 12.52863 12.77613 4 1.00000 1.41421 1.00000 9.10457 5.69036 3.41421 5 0.10000 1.14727 0.31623 4.61167 3.61641 0.99525 6 0.01000 1.04881 0.10000 3.27159 2.96671 0.30488 7 0.00100 1.01569 0.03162 2.85690 2.76154 0.09536 8 0.00010 1.00499 0.01000 2.72672 2.69667 0.03005 9 0.00001 1.00158 0.00316 2.68565 2.67615 0.00949 10 0.00000 1.00050 0.00100 2.67267 2.66967 0.00300 11 0.00000 1.00016 0.00032 2.66856 2.66762 0.00095 12 0.00000 1.00005 0.00010 2.66727 2.66697 0.00030 13 0.00000 1.00002 0.00003 2.66686 2.66676 0.00009 14 0.00000 1.00000 0.00001 2.66673 2.66670 0.00003 15 0.00000 1.00000 0.00000 2.66669 2.66668 0.00001 ============================================================== Pada saat iterasi ke -15,miu_Bx<0.00001.

Jadi nilai miu yang meminimalkan min(miu) adalah : x1 = 1.00000 dan x2 = 0.00000

Berikut akan diberikan contoh masalah optimisasi nonlinear berkendala yang menggunakan titik awal.

Contoh 3.1.2

Selesaikan masalah kendala berikut :

Minimalkan f ( x₁ , x₂ ) =

(

x₁−5

) (

2 + x₂ −3

)

2 Kendala g₁ ( x₁ , x₂ ) = - x1 + x2- 3 ≤ 0 g₂ ( x₁ , x₂ ) = - x1 + 2x2- 4 ≤ 0 Penyelesaiannya : Langkah 1 Misalkan ε = 0,00001 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ = 0 0 0 x β = 0,1 μ = 1 ₁ Ditentukan k = 1 Langkah 2 Membentuk fungsi φ(x,μ) = f(x) + μ_kB(x) B(x) dipilih dengan B(x) =

Σ

= 2 1 i ( ) 1 x i g − = - _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x Sehingga diperoleh φ(x,μ) = f(x) + μ_kB(x)

=

(

x₁−5

) (

2 + x₂ −3

)

2- μ_{k ⎥} ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x Langkah 3

Untuk mencari penyelesaian optimum dari masalah tak berkendala dibutuhkan suatu titik awal sehingga diperlukan metode yang sesuai. Untuk memudahkan penghitungan dalam mencari penyelesaian optimum akan digunakan program Matlab.

Iterasi 1 Untuk k = 1

x₁(1)= 0 dan x( )₂1 = 0

Dari perhitungan dengan menggunakan Program Matlab diperoleh ) ( ₁ min μ φ = f(x) + μ B(x) ₁ =

(

) (

)

2 2 2 1 −5 + x −3 x - ( 1 ) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 34,583333 f(μ ) = ₁

(

x₁ −5

) (

2 + x₂ −3

)

2 = 34 1 μ B(x* 1) = - 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,583333 > ε

Penyelesaian belum optimal karena μ B(x₁ *

Langkah 4 Tetapkan μ =₂ β μ ₁ = (0,1).1 = 0,1 Iterasi 2 Untuk k = 2 Langkah 3

Dari perhitungan dengan menggunakan Program Matlab diperoleh ( )2 1 x = 5,180705 ( )2 2 x = 2,942802 ) ( ₂ min μ φ = f(x) + μ B(x) ₂ =

(

x₁ −5

) (

2 + x₂ −3

)

2- (0,1) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,085366 f(μ ) = ₂

(

x₁ −5

) (

2 + x₂ −3

)

2 = 0,035926 2 μ B(x* 2) = - (0,1) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,049440 > ε

Penyelesaian belum optimal karena μ B(x₂ *

Langkah 4 Tetapkan μ₃ = β μ₂ = (0,1) (0,1) = 0,01 Iterasi 3 Untuk k = 3 Langkah 3

Dari perhitungan dengan menggunakan Program Matlab diperoleh ( )3 1 x = 5,007010 ( )3 2 x = 2,987347 ) ( ₃ min μ φ = f(x) + μ₃B(x) =

(

x₁ −5

) (

2 + x₂ −3

)

2- (0,01) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,005499 f(μ₃) =

(

) (

)

2 2 2 1 −5 + x −3 x = 0,000209 3 μ B(x*₃) = - (0,01) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,005290 > ε

Langkah 4 Tetapkan μ = ₄ β μ₃ = 0,1 (0,01) = 0,001 Iterasi 4 Untuk k = 4 Langkah 3

Dari perhitungan dengan menggunakan Program Matlab diperoleh ( )4 1 x = 5,000751 ( )4 2 x = 2,998692 ) ( ₄ min μ φ = f(x) + μ B(x) ₄ =

(

) (

)

2 2 2 1 −5 + x −3 x - (0,001) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,000535 f(μ ) = ₄

(

x₁ −5

) (

2 + x₂ −3

)

2 = 0,000002 4 μ B(x* 4) = - (0,001) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,000533

Penyelesaian belum optimal karena μ B(x₄ *

Langkah 4 Tetapkan μ₅ = β μ ₄ = 0,1 (0,001) = 0,0001 Iterasi 5 Untuk k = 5 Langkah 3

Dari perhitungan dengan menggunakan Program Matlab diperoleh ( )5 1 x = 5,000076 ( )5 2 x = 2,999869 ) ( ₅ min μ φ = f(x) + μ₅B(x) =

(

x₁ −5

) (

2 + x₂ −3

)

2- (0,0001) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,000053 f(μ₅) =

(

x₁ −5

) (

2 + x₂ −3

)

2 = 0,000000 5 μ B(x*₅) = - (0,0001) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = - (0,0001) (-0,53333) = 0,000053

Langkah 4 Tetapkan μ₆ = β μ₅ = 0,1 (0,0001) = 0,00001 Iterasi 6 Untuk k = 6 Langkah 3

Dari perhitungan dengan menggunakan Program Matlab diperoleh ( )6 1 x = 5,000008 ( )6 2 x = 2,999987 ) ( ₆ min μ φ = f(x) + μ₆B(x) =

(

x₁ −5

) (

2 + x₂ −3

)

2- (0,00001) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,000005 f(μ₆) =

(

x₁ −5

) (

2 + x₂ −3

)

2 = 0,000000 6 μ B(x*₆) = - (0,00001) _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + − + − 2 4 1 3 1 2 1 2 1 x x x x = 0,000005 < ε

Dari permasalahan di atas maka diperoleh penyelesaian dengan * 1

x = 5,00000 dan *

2

x = 2,99999. Pada iterasi ke-6 penyelesaian sudah optimum karena sudah memenuhi syarat bahwa μ_kB(x*_k) < ε .

Berikut akan diberikan penyelesaian dengan menggunakan program Matlab pada contoh 3.1.2 di atas.

Tabel 3.1.2 Output penyelesaian contoh 3.1.2 dengan Matlab

Masukkan data yang dibutuhkan x1 = [0 0]

Taksiran awal mu : 1 Toleransi error = 0.00001 Max.iterasi newton = 10

=============================================================== Iterasi Nilai mu x1 x2 f z mu_Bx =============================================================== 0 1.000000 0.000000 0.000000 34.000000 34.583333 0.583333 1 0.100000 5.180705 2.942802 0.035926 0.085366 0.049440 2 0.010000 5.007010 2.987347 0.000209 0.005499 0.005290 3 0.001000 5.000751 2.998692 0.000002 0.000535 0.000533 4 0.000100 5.000076 2.999869 0.000000 0.000053 0.000053 5 0.000010 5.000008 2.999987 0.000000 0.000005 0.000005

Metode fungsi penalti interior dapat juga diterapkan ke dalam masalah optimasi berkendala linear. Berikut contohnya :

Contoh 3.1.3

Selesaikan masalah optimisasi berkendala berikut :

Minimalkan f ( x₁ , x₂ ) = x₁ + 2x₂+1 Kendala g₁ ( x₁ , x₂ ) = - x₁ + 1 ≤ 0 g₂ ( x₁ , x₂ ) = - x₂ ≤ 0 Penyelesaiannya : Langkah 1 Misalkan ε = 0,00001 β = 0,1 μ = 1000 ₁ Ditentukan k = 1 Langkah 2 Membentuk fungsi φ(x,μ) = f(x) + μ_kB(x) B(x) dipilih dengan B(x) =

Σ

= 2 1 j ( ) 1 x j g − = _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x

Sehingga diperoleh φ(x,μ) = f(x) + μ_kB(x) = x₁ +2 x₂+1 - μ_{k ⎥} ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x Langkah 3

Untuk mencari penyelesaian optimum dari masalah optimisasi tak berkendala, dibutuhkan penurunan parsial φ terhadap x₁ dan x₂ :

Turunan parsial φ terhadap x₁ diperoleh :

1 x ∂ ∂φ = 1 - ₂ 1) 1 ( x k − μ = 0 atau (x₁ + 1 )2 ₌ k μ x₁ = μk 2 1 -1 (3.3.1)

Turunan parsialφ terhadap x₂ diperoleh :

2 x ∂ ∂φ = 2 - ₂ 2 x k μ = 0 x2 2= ₂ μk atau x2= 2 1 ) 2 μ ( k (3.3.2)

Dari persamaan (3.3.1) dan (3.3.2) diperoleh penyelesaian optimum tak berkendala dan x*₁(μ ) = _k μ_k 2 1 -1 dan x* 2(μ ) = k 2 1 ) 2 μ ( k

Iterasi 1 Untuk k = 1 x*₁(μ ) = _k μ_k 2 1 -1 = 30,62278 x*₂(μ ) = _k )12 2 μ ( k = 22,36068 Sehingga diperoleh : ) ( min μk φ = x₁ + 2x₂+1 - μ_{k ⎥} ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x = (μ_k 12 +1 )12 +2 )12 2 μ ( k ₊₁ -k μ [ 2 1 2 1 ) ( 1 -2 + ) μ ( -1 2 μ k ] = 1,88103 dan f(μ ) = ₁

(

x₁+2x₂

)

+ 1 = {μ_k 12 -1}+2 )12 2 μ ( k ₊₁ = 10563,28621 1 μ B(x* 1) = - μk ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x = 74,46310

Penyelesaian belum optimal karena μ B(x₁ *

Analog dengan langkah-langkah sebelumnya, titik optimal yang merupakan penyelesaian optimal didapatkan pada iterasi yang ke-15, yakni

Langkah 4 15 μ = β.μ₁₄ = (0,1).(10−10_{) = 10}−11 Iterasi 15 Untuk k = 15

Berdasarkan iterasi sebelumnya, nilai φ minimum dicari jika

x*₁(μ₁₅) = μ₁₅ 2 1 -1 = -1,00000 dan x* 2(μ15) = 2 1 ) 2 μ ( 15 = 0,00000 Sehingga diperoleh : ) ( ₁₅ min μ φ = x₁ + 2x₂+1 - μ_{15 ⎥} ⎦ ⎤ ⎢ ⎣ ⎡ − + − ₂ 1 1 1 x x = 0,00000 dan f(μ₁₅) =

(

x₁+2x₂

)

+ 1 = 0,00000 15 μ B(x*₁₅) = 0,00000

Maka diperoleh penyelesaian dari masalah di atas dengan x*

1 = -1, x * 2= 0.

Pada iterasi ke-15 penyelesaian sudah optimum karena sudah memenuhi syaratμ₁₅B(x*₁₅) < ε .

Berikut akan diberikan penyelesaian dengan menggunakan program MATLAB.

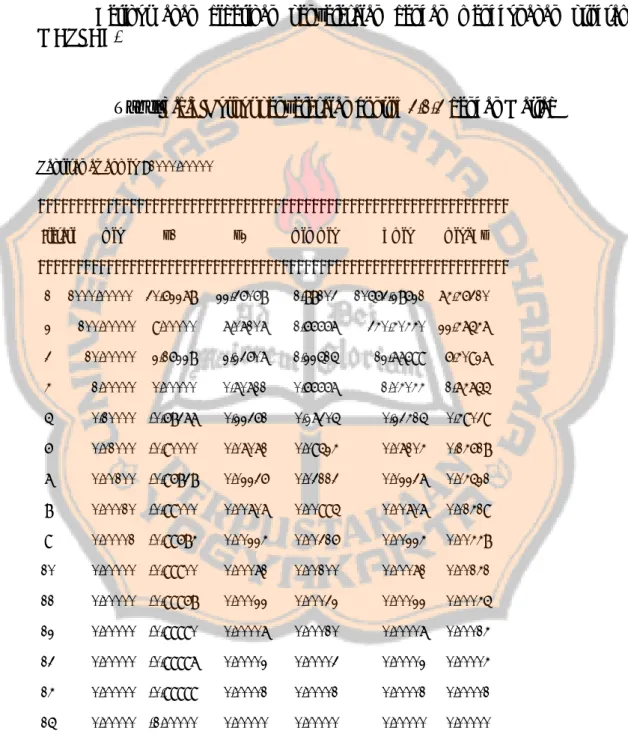
Tabel 3.1.3 Output penyelesaian contoh 3.1.3 dengan Matlab

Taksiran awal miu : 1000.00000

============================================================== Iterasi miu x1 x2 min(miu) f(miu) miu_Bx ============================================================== 1 1000.00000 30.62278 22.36068 1.88103 10563.28621 74.46310 2 100.00000 9.00000 7.07107 1.66667 340.40440 22.47547 3 10.00000 2.16228 2.23607 1.22515 12.77699 6.40927 4 1.00000 0.00000 0.70711 0.66667 1.04044 1.74755 5 0.10000 -0.68377 0.22361 0.27305 0.23415 0.49039 6 0.01000 -0.90000 0.07071 0.09524 0.07104 0.14618 7 0.00100 -0.96838 0.02236 0.03113 0.02237 0.04521 8 0.00010 -0.99000 0.00707 0.00995 0.00707 0.01419 9 0.00001 -0.99684 0.00224 0.00316 0.00224 0.00448 10 0.00000 -0.99900 0.00071 0.00100 0.00071 0.00141 11 0.00000 -0.99968 0.00022 0.00032 0.00022 0.00045 12 0.00000 -0.99990 0.00007 0.00010 0.00007 0.00014 13 0.00000 -0.99997 0.00002 0.00003 0.00002 0.00004 14 0.00000 -0.99999 0.00001 0.00001 0.00001 0.00001 15 0.00000 -1.00000 0.00000 0.00000 0.00000 0.00000 ============================================================= Pada saat iterasi ke -15,miu_Bx<0.00001.

D. Konvergensi Metode Fungsi Penalti Interior

Teorema 3.2 Teorema Konvergensi Metode Fungsi Penalti Interior Jika fungsi φ( x,μ_k) = f(x) - μ_k

Σ

= m j 1 ( ) 1 x j g (3.2.1)

suatu barisan turun terhadapμ_k, maka penyelesaian dari masalah minimisasi tak berkendala akan konvergen ke penyelesaian optimal dari masalah berkendala

Minimumkan f(x) Kendala g_j( x) ≤ 0

dengan g_j( x) ≤ 0 , j =1,2,Κ , m untuk μ_k →0

Bukti :

Jika x* _{adalah penyelesaian optimum dari masalah berkendala maka akan} dibuktikan bahwa 0 lim → k μ [min φ( x,μk) ] = φ( x * k,μk) = f (x *₎

karena f(x) kontinu dan f (x*_{) ≤ f(x) untuk setiap titik layak x maka dapat dipilih} titik layak x~ sedemikian hingga f ( x~ ) < f (x*_{) +}

2

ε _{,∀ε >0 (3.2.2)}

Perhatikan untuk titik layak x~ didapatkan

φ( x~ ,μ_k) = f( x~ ) - μ_k

Σ

= m j 1 (~) 1 x j g = f( x~ ) + μ_k

Σ

= m j 1 (~) 1 x j g − f( x~ ) + μ_k

Σ

= m j 1 (~) 1 x j g − _{≤ f (x}*_{) +} 2 ε

Pilih k yang sesuai, misalnya K sedemikian hingga K μ

_Σ

= m j 1 (~) 1 x j g − _≤ 2 ε Jadi μ ≤ _K

∑

= − m j 1 gj(~) 1 2 x ε (3.2.3)

Dari (3.2.1) didapat f (x*_{) ≤ min φ( x,} k

μ ) = φ( x*

k,μk) (3.2.4) dimana x*

k adalah penyelesaian minimum masalah tak berkendala φ( x,μk) Selanjutnya φ( x*

k,μk) ≤ φ( x *

K,μk) (3.2.5)

Karena x*

k minimum dari φ( x,μk) dan ada x lain dari x*ksebagai petunjuk suatu nilai dari φ ≥ φ( x*

k,μk). Pilih μ_k < μ dan didapatkan _K

φ( x* K,μ ) = f (xK *K) - μK

Σ

= m j 1 ( ) 1 K j g x > f (x* K) - μk

Σ

= m j 1 ( ) 1 K j g x > φ( x* k,μk) (3.2.6) dimana x*

k adalah minimum tak berkendala dari φ( x,μk) Jadi f (x*_{) ≤ φ( x}* k,μk) ≤ φ( x * K,μk) < φ( x * K,μ ) K (3.2.7) Tetapi φ( x* K,μ ) ≤ K φ(x~K,μ ) = f ( x~ ) - K μK

Σ

= m j 1 (~) 1 x j g (3.2.8)

Dari pertidaksamaan (3.2.7) dan (3.2.8) didapatkan f (x*_{)≤ φ( x}* k,μk) ≤ f ( x~ ) - μK

Σ

= m j 1 (~) 1 x j g (3.2.9) Pertidaksamaan (3.2.2) memberikan - μ_K

Σ

= m j 1 (~) 1 x j g < 2 ε (3.2.10)

Dengan menggunakan pertidaksamaan (3.2.2) dan (3.2.9) pertidaksamaan (3.2.8) menjadi f (x*_{) ≤ φ( x}* k,μk) < f (x *_{) +} 2 ε + 2 ε = f (x*_{) + ε atau} φ( x* k,μk) - f (x*) < ε (3.2.11) Diberikan suatu ε > 0 , ini memungkinkan untuk memilih suatu nilai k supaya memenuhi pertidaksamaan (3.2.10)

Untuk k→ ∞ dan μ_k → 0 didapatkan 0 lim → k μ φ( x * k,μk) = ( ) ∗ x f ∴Terbukti bahwa 0 lim → k μ [min φ( x,μk) ] = φ( x * k,μk) = f (x*)

BAB IV PENUTUP

A. Kesimpulan

Metode fungsi penalti interior merupakan metode yang digunakan untuk mengubah masalah optimisasi berkendala nonlinear menjadi masalah optimisasi tak berkendala, yakni membentuk fungsi φ μ

(

x, _k

)

dari masalah optimisasi dasar ditambah dengan fungsi kendala-kendalanya dikalikan dengan parameter penalti. Karena masalah optimisasi berkendala menjadi tak berkendala maka masalah tersebut dapat diselesaikan menggunakan metode optimisasi tak berkendala nonlinear. Salah satunya adalah metode newton.

Pencarian penyelesaian optimal yaitu dengan menemukan titik optimal yang dimulai dari daerah layak dan konvergen ke masalah optimisasi dasar berkendala nonlinear, artinya bahwa nilai dari

∗ x

(

_k

)

φ μx, mendekati nilai saat dengan . ) (x f 0 → μ_k k →∞

Syarat-syarat dalam menggunakan metode fungsi penalti interior : 1. Titik awal x₁ harus berada di dalam daerah layak

2. μ_k harus turun dengan aturan μ_k ≥μ_k+1 dan μ_k+1 =βμ_k 3. Fungsi f(x) diferensiabel

Kelebihan dari metode fungsi penalti interior ini adalah titik awalnya berada dalam daerah layak sehingga pencarian nilai optimum akan lebih mudah karena berada dalam daerah layak

∗ x

Kekurangan dari metode fungsi penalti interior ini adalah penghitungannya akan sulit jika nilai μ mengecil. Dalam kasus tertentu titik _k awal tidak diperlukan sehingga tidak sesuai dengan algoritma metode fungsi penalti interior.

B. Saran

1. Metode tidak langsung yang lain untuk menyelesaikan masalah program optimasi nonlinear berkendala yang dapat digunakan, contohnya Transformasi Variabel

2. Selain metode Newton, masih banyak metode yang digunakan dalam menyelesaikan masalah program optimasi nonlinear tak berkendala. Salah satunya dengan metode Steepest Descent.

3. Masih banyak terdapat metode optimisasi yang dapat digunakan untuk menyelesaikan sistem persamaan nonlinear baik dengan metode langsung maupun metode tak langsung.

DAFTAR PUSTAKA

Anton, Howard. (1988). Aljabar Linear Elementer (Terjemahan). Edisi kelima. Jakarta : Erlangga.

Bazaraa M, Sherali H, Shetty C. (1993). Nonlinear Programming, Theory and Algorithms. Second Edition. Singapore : John Wiley & Sons, Inc.

Purcell, Edwin J. (1988). Kalkulus dan Geometri Analitis (Terjemahan). Edisi ketiga : Jilid II. Jakarta : Erlangga.

Rao S S. (1984). Optimization Theory and Application. Second Edition. India : Wiley Eastern Limited.

Soemantri, R., dkk. (2006). Diktat Pengantar Analisis Real. Yogyakarta : FMIPA USD.

Listing Program :

miu = input('Taksiran awal miu : ');

n = input('Iterasi maksimum : '); beta = 0.1; k=1; e = 0.00001; miu = 1000; clc;

fprintf('Taksiran awal miu : %10.5f\n',miu);

fprintf('\n CONTOH METODE FUNGSI PENALTI INTERIOR \n\n');

fprintf('===================================================================== \n');

fprintf(' Iterasi miu x1 x2 min(miu) f(miu) miu_Bx \n');

fprintf('===================================================================== \n');

while k <= n

x1 = power( (power(miu,0.5)+1), 0.5 );

x2 = power(miu,0.5);

miu_Bx = power(miu,0.5) - ( 1 / ( (1/miu) - power ( ( (1 / power(miu, 3/2)) + ( 1 / power(miu, 2) ) ), 0.5 )));

min_miu_depan = ( (1/3) * power((x1 + 1), 3) ) + 2*x2;

min_miu_blkng = 1 / ( (1/miu) - power ( ( (1 / power(miu, 3/2)) + ( 1 / power(miu, 2) ) ), 0.5 ) );

min_miu = min_miu_depan - min_miu_blkng;

f_miu = ( (1/3) * power((x1 + 1), 3) ) + x2; fprintf('%3d %10.5f %8.5f %8.5f %9.5f %9.5f %9.5f\n', k,miu,x1,x2,min_miu,f_miu,miu_Bx); if miu_Bx < e break end k=k+1;

miu = beta * miu;

end

fprintf('============================================================= \n');

fprintf('Pada saat iterasi ke -%d,miu_Bx<%5.5f.\n',k,e);

fprintf('Jadi nilai miu yang meminimalkan min(miu) adalah : x1 x2 =%8.5 f\n',x1,x2);