Bab 3
Persamaan SWE Linier untuk
Dasar Sinusoidal
Pada bab ini akan dijelaskan mengenai penggunaan persamaan SWE linier untuk masalah gelombang air dengan dasar sinusoidal. Dalam menyelesaikan masalah ini langkah awal adalah melakukan pendekatan analitik dengan menggunakan metode ekspansi asimtotik multiple-scale, yang menghasilkan suatu sistem persamaan de-ngan syarat awal dan syarat batas. Hasil pada bab ini akan digunakan untuk diskretisasi numerik dan simulasi pada bab selanjutnya. Pada bab sebelumnya telah sedikit disinggung mengenai penggunaan persamaan SWE linier untuk dasar sinu-soidal. Di sini pendeskripsian masalah akan dijelaskan lebih dalam lagi.
3.1
Gelombang Air Dengan Dasar Berbentuk
Si-nusoidal
Sebelum penjelasan yang lebih jauh, terlebih dahulu akan dijelaskan mengenai salah satu sifat gelombang transmisi dan refleksi. Dalam perambatannya, gelombang air apabila diberi suatu gangguan (dalam hal ini dapat berupa perubahan kedalaman air) gelombang akan terpecah menjadi dua. Sebagian dari gelombang ini akan dire-fleksikan dan sebagian lagi ditransmisikan. Gelombang transmisi merupakan
ge-lombang yang diteruskan atau memiliki arah rambat yang sama dengan gege-lombang semula, sedangkan gelombang refleksi merupakan gelombang yang berbalik arah atau arah rambatnya berlawanan dengan arah gelombang semula.
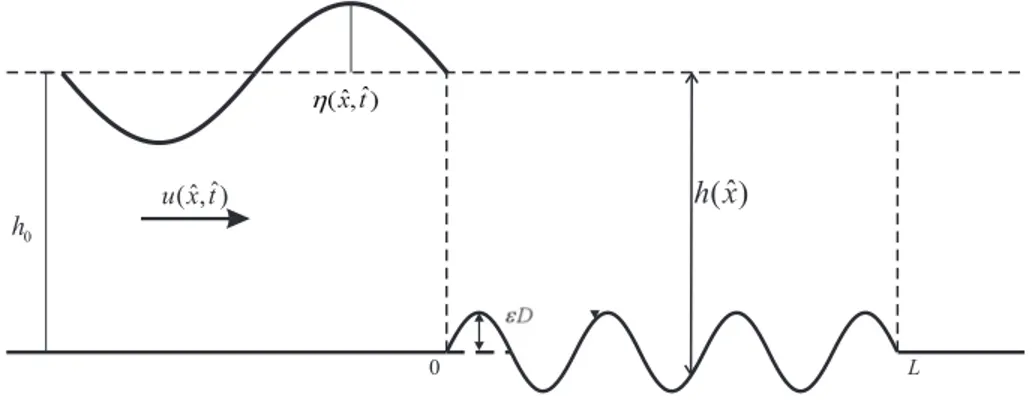
Gambar 3.1: Skema gelombang air dengan dasar berbentuk sinusoidal dengan
h(ˆx) = h0(1 +εDcosKxˆ).
Misalkan gelombang monokromatik bergerak dari kiri ke arah kanan. Dasar laut yang rata berada di bawahnya pada kedalaman h0. Apabila dasar sinusoidal berada pada 0< x < L maka saat gelombang mencapai x= 0 gelombang akan ter-pecah menjadi dua, gelombang transmisi dan gelombang refleksi. Gelombang refleksi yang bergerak ke kiri terus merambat tanpa hambatan karena dasar yang rata. Se-dangkan gelombang transmisi mengalami pemecahan gelombang yang serupa selama perambatannya menuju puncak pertama dasar sinusoidal. Setelah melewati puncak pertama dasar sinusoidal, hal serupa terjadi setiap gelombang transmisi melewati puncak dasar sinusoidal lainnya. Akan tetapi, di sini gelombang refleksi hasil pe-mecahan gelombang transmisi mengalami pepe-mecahan gelombang juga, karena saat merambat ke arah kiri gelombang refleksi ini membentur dasar sinusoidal. Proses ini terus berlangsung selama perambatan gelombang di 0< x < L.
Proses perambatan gelombang yang dijelaskan sebelumnya merupakan gambaran umum saja tentang apa yang terjadi. Sedangkan, seberapa besar gelombang dire-fleksikan dan ditransmisikan, apa yang terjadi pada gelombang-gelombang hasil pe-mecahan gelombang yang berulang-ulang, seberapa besar pengaruh ukuran dasar
sinusoidal terhadap perambatan gelombang, masih belum diketahui. Di sinilah per-samaan SWE linier diharapkan dapat mengungkapkan secara detail hal-hal tersebut dn apa yang sebenarnya terjadi.
3.2
Metode Ekspansi Asimtotik
Pada Subbab ini metode ekspansi asimtotik biasa akan digunakan untuk menyele-saikan persamaan SWE linier untuk dasar sinusoidal. Perhatikan persamaan SWE linier berikut ini: ⎧
⎨ ⎩
ηtˆ=−(h(ˆx)u)xˆ
uˆt=−gηˆx
(3.2.1)
dimana η(ˆx,ˆt) adalah simpangan gelombang dari keadaan setimbang,u(ˆx,ˆt) adalah kecepatan partikel air dalam arah horizontal, g percepatan gravitasi, h0 kedalaman air untuk dasar rata, z = −h(ˆx) adalah fungsi kedalaman dasar sinusoidal dan ˆx
sebagai variabel ruang dan ˆt sebagai variabel waktu.
Jika persamaan pertama dari (3.2.1) diturunkan terhadap ˆt sedangkan per-samaan kedua diturunkan terhadap ˆx, kemudian dilanjutkan dengan mengeliminasi
uxˆtˆmaka akan diperoleh
ηtˆˆt=g(h(ˆx)ηxˆ)xˆ (3.2.2) Sebaliknya, apabila persamaan pertama dari (3.2.1) diturunkan terhadap ˆxdan per-samaan kedua diturunkan terhadap ˆt, dilanjutkan dengan mengeliminasi ηxˆˆt maka akan diperoleh
uˆtˆt =g(h(ˆx)u)xˆxˆ (3.2.3) Perhatikan Persamaan (3.2.2), jika dasar hanya berupa dataran yang rata maka
h(ˆx) = h0 dan persamaan di atas merupakan persamaan gelombang yang memiliki solusi d’Alembert apabila diberi syarat awal. Gelombang datang dari kiri diasum-sikan sebagai gelombang monokromatikA0ei(kx−ωˆ ˆt)denganA0 sebagai amplitudo,K
bilangan gelombang, danω cepat rambat gelombang. Perhatikan bahwa gelombang monokromatik ini memenuhi (3.2.2) untuk h(ˆx) =h0 dan ωk =√gh0.
Misalkan dasar sinusoidal memenuhi fungsi kedalamanh(ˆx) = h0(1+εDcosKxˆ). Dimana εD menyatakan ketinggian puncak dasar sinusoidal dari keadaan normal (dasar rata). Maka persamaan (3.2.2) dapat dituliskan kembali menjadi
ηˆtˆt=g(h0(1 +εDcosKxˆ)ηxˆ)xˆ (3.2.4) demikian halnya dengan persamaan (3.2.3)
uˆtˆt=g(h0(1 +εDcosKxˆ)u)xˆxˆ (3.2.5) Dengan demikian menyelesaikan persamaan SWE linier untuk dasar sinusoidal sama halnya dengan menyelesaikan Persamaan (3.2.4). Sekarang, dengan meng-gunakan metode ekspansi asimtotik, misalkan solusi hampiran persamaan (3.2.4) memenuhi
η(ˆx,ˆt) = η0(ˆx,ˆt) +εη1(ˆx,tˆ) +ε2η2(ˆx,ˆt) +· · · (3.2.6) Langkah berikutnya adalah subtitusikan (3.2.6) ke dalam persamaan (3.2.4). Dari solusi hampiran berorde dua, yaitu {η0+εη1} dapat diperoleh dua buah per-samaan berdasarkan ordenya masing-masing, yaitu
O(1) : η0ˆtˆt−gh0η0ˆxˆx = 0 (3.2.7)
O(ε) : η1ˆttˆ−gh0η1ˆxxˆ = gh0D 2 ∂ˆx e
iKxˆ+e−iKˆxη
0ˆx (3.2.8) Persamaan (3.2.7) merupakan persamaan gelombang yang memiliki solusi d’ Alembert yaitu η0(ˆx,ˆt) = A 2e i(kx−ωˆ ˆt)+B 2e −i(kx−ωˆ ˆt) (3.2.9)
dengan A dan B sebagai amplitudo dan ω/k=√gh0.
Selanjutnya, turunkan (3.2.9) terhadap ˆxkemudian subtitusikan ke dalam (3.2.8). Perhatikan ruas kanan persamaan (3.2.8), apabila K = 2k, ruas kanan persamaan
(3.2.8) memiliki suku-suku yang mengandung e±i(kxˆ+ωˆt) yang merupakan solusi ho-mogen dari (3.2.8). Hal ini mengindikasikan terjadinya resonansi, sehingga nilai
η1(ˆx,ˆt) membesar. Akibatnya, pemisalan (3.2.6) sebagai solusi hampiran persamaan (3.2.4) gagal. HubunganK = 2k dikenal sebagai kondisi untuk terjadinya resonansi Bragg.
Dengan demikian, penggunaan metode ekspansi asimtotik biasa tidak cocok un-tuk masalah ini. Oleh karena itu, subbab berikutnya akan menjelaskan penggunaan metode lain, yaitu ekspansi asimtotik multiple-scale untuk menyelesaikan persamaan SWE linier untuk dasar sinusoidal.
3.3
Metode Ekspansi Asimtotik Multiple-scale
Bagian ini akan menjelaskan bagaimana menyelesaikan persamaan (3.2.2) dengan menggunakan metode ekspansi asimtotik multiple-scale. Metode ekspansi asimtotik multiple-scale menggunakan variabel cepat dan lambat dalam ruang dan waktu, yaitu
x= ˆx, x¯=εxˆ (3.3.1)
t = ˆt, ¯t =εtˆ (3.3.2)
Misalkan solusi hampiran orde dua untuk persamaan (3.2.2) adalah
η(ˆx,tˆ) =η0(x,x, t,¯ ¯t) +εη1(x,x, t,¯ ¯t) (3.3.3) maka ∂ ∂x → ∂ ∂x +ε ∂ ∂x¯ , ∂ ∂t → ∂ ∂t +ε ∂ ∂¯t (3.3.4)
Selanjutnya, dengan mensubtitusikan (3.3.3) dan (3.3.4) ke dalam persamaan (3.2.2) diperoleh dua buah persamaan diferensial untuk masing-masing orde.
Untuk orde O(1) diperoleh persamaan diferensial
∂2η0 ∂t2 −gh0
∂2η0
solusi persamaan diferensial di atas adalah η0(ˆx,ˆt) = 1 2A(¯x,¯t)e i(kx−ωt)+c.c.+1 2B(¯x,t¯)e −i(kx+ωt)+c.c. (3.3.6)
dimana A(¯x,¯t) adalah amplitudo gelombang yang bergerak ke kanan dan B(¯x,¯t) adalah amplitudo gelombang yang bergerak ke kiri.
Untuk orde O(ε) didapatkan persamaan diferensial
gh0∂ 2η 1 ∂x2 − ∂2η1 ∂t2 = 2 ∂2η0 ∂t∂t¯−2gh0 ∂2η0 ∂x∂x¯ − gh0D 2 ∂ ∂x e 2ikx+e−2ikx∂η0 ∂x (3.3.7)
dengan menggunakan solusi untuk η0 dan mensubtitusikan pada persamaan di atas diperoleh gh0∂ 2η 1 ∂x2 − ∂2η1 ∂t2 = ∂A ∂¯t(−iω)e ikx−iωt+c.c.+ ∂B ∂¯t (−iω)e −ikx−iωt+c.c. −gh0 ∂A ∂x¯(ik)e ikx−iωt+c.c.+∂B ∂x¯(−ik)e −ikx−iωt+c.c. −gh0D 4 ∂ ∂x e 2ikx+e−2ikx ∂ ∂x Ae ikx−iωt+c.c.+Be−ikx−iωt+c.c. (3.3.8) baris terakhir persamaan (3.3.8) dapat ditulis sebagai
−gh0D 4 −3k2Ae3ikx−iωt+c.c.+k2Ae−ikx−iωt+c.c. −gh0D 4 −3k2Be−3ikx−iωt+c.c.+k2Beikx−iωt+c.c.
Untuk menghindari nilai η1(x, t) yang tak terbatas maka koefisien e±i(kx−ωt) dan
e±i(kx+ωt) dari ruas kanan persamaan (3.2.8) dibuat nol. Setelah dihitung diperoleh persamaan berikut ∂A ∂¯t +c ∂A ∂x¯ = ikcD 4 B (3.3.9) ∂B ∂¯t −c ∂B ∂x¯ = ikcD 4 A (3.3.10)
dimana c=ω/k=√gh0. Kedua persamaan di atas dapat dikombinasikan menjadi
∂2A ∂¯t∂t¯−c 2 ∂2A ∂x∂¯ x¯ + kcD 4 2 A= 0 (3.3.11)
atau yang lebih dikenal sebagai persamaan Klein-Gordon.
Untuk menentukan syarat awal dan syarat batas sistem persamaan di atas per-hatikan Gambar (3.1). Misalkan gelombang monokromatik datang dari kiri dan memasuki daerah yang memiliki dasar sinusoidal. Gelombang ini terus bergerak ke kanan dan kemudian kembali ke daerah yang memiliki dasar rata h0. Pada awal pengamatan ¯t = 0, gelombang monokromatik diasumsikan baru mencapai ¯x = 0 dan belum terjadi pemantulan gelombang, sehingga pada domain 0< x < L¯ tidak ada gelombang sama sekali, jadi diperoleh syarat awal A(¯x,0) = 0 danB(¯x,0) = 0. Pada batas kiri, ¯x= 0, gelombang yang ke kanan hanya berasal dari gelombang datang sehinggaA(0,¯t) =A0 danB(0,¯t) tidak diketahui. Pada batas kanan, ¯x=L, tidak ada gelombang yang bergerak ke kiri. Hal ini berdasarkan asumsi bahwa di sebelah kanan ¯x > Ltidak ada penghalang, sehingga gelombang yang ke kanan tidak dipantulkan kembali. Jadi, syarat batasnya adalah B(L,¯t) = 0. Dari penjelasan ini, syarat awal dan syarat batas untuk sistem persamaan (3.2.9-10) dapat dituliskan sebagai berikut: ⎧ ⎨ ⎩ A(¯x,0) = 0, B(¯x,0) = 0, A(0,¯t) =A0, B(L,¯t) = 0 (3.3.12)
Berdasarkan syarat batas kanan dan kiri di atas, pada akhirnya keadaan sangat berbeda di daerah kanan dan kiri dasar sinusoidal. Oleh karena itu, daerah penga-matan dibagi menjadi tiga bagian, yaitu:
(1) Pada x < 0, amplitudo gelombang yang ke kanan, A(¯x,¯t), hanya berasal dari gelombang datang, A0ei(kx−ωˆ ˆt), sehingga amplitudo gelombang yang ke kanan tetap, yaitu sebesar A(¯x,t¯) = A0. Sedangkan B(¯x,¯t) tidak dipengaruhi oleh
A(¯x,¯t). Jadi pada domain ini persamaan yang berlaku adalah persamaan transport untuk gelombang yang bergerak ke kiri, yaitu
B¯t−cB¯x = 0
dengan syarat awal B(¯x,0) = 0 dan syarat batas A(0,¯t) =A0.
(2) Pada 0 < x < L, sudah jelas bahwa persamaan (4.1.1) berlaku pada domain ini.
(3) Pada x > L, diasumsikan bahwa tidak ada yang menghalangi gelombang yang bergerak ke kanan, makaB(¯x,¯t) = 0, karena tidak ada gelombnag yang dipan-tulkan kembali. Jadi, persamaan yang berlaku untukA(¯x,¯t) adalah persamaan transport untuk gelombang yang bergerak ke kanan, yaitu
A¯t+cAx¯ = 0 dengan syarat awal A(¯x,0) = 0.
Hasil analitik masalah nilai awal dan nilai batas (3.3.12) diberikan oleh Viska, 2007. Hasil yang diperoleh dari studi analitik ini sesuai dengan hasil simulasi nu-merik yang akan diberikan pada bab berikutnya.
Berdasarkan penjelasan pada bab ini dapat disimpulkan bahwa penggunaan metode ekspansi asimtotik multiple-scale untuk menyelesaikan persamaan (3.2.2) menghasilkan sistem persamaan diferensial (3.3.9-10). Untuk menyelesaikan sistem persamaan diferensial ini diperlukan syarat awal dan syarat batas (3.3.12). Pada bab berikutnya variabel ¯xdan ¯takan dikembalikan pada varabel fisis semula yaitu ˆx
ˆ
t. Kemudian simulasi numerik dapat dilakukan dengan menggunakan metode beda hingga.