Catatan Kuliah MEKANIKA FLUIDA
Disusun oleh: AR ROHIM 14/371863/PPA/04607
PROGRAM STUDI S2 FISIKA DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS GADJAH MADA
Daftar Isi
1 Pendahuluan 3
1.1 Fluida . . . 3
1.2 Metode Analitik dan Metode Numerik dalam Meyelesaikan Persamaan Direfensial 4 2 Persamaan Euler 6 2.1 Gambaran Euler . . . 6
2.2 Persamaan Umum Euler . . . 7
2.3 Persamaan Euler dalam Koordinat Bola . . . 10
2.4 Koorinat Silinder . . . 13
3 Gerak Fluida dan Persamaan Kontinyuitas 15
Bab 1
Pendahuluan
1.1
Fluida
Sebuah materi mempunyai tiga keadaan umum (fase), yaitu: padat, cair dan gas. Kita dapat membedakan ketiga fase ini melalui gambaran berikut. Benda padat mempertahankan bentuk dan ukuran yang tetap; bahkan jika sebuah gaya yang besar diberikan pada sebuah benda padat, benda tersebut tidak langsung berubah bentuk atau volumenya. Benda cair tidak mem-pertahankan bentuk yang tetap melainkan mengambil bentuk tempat yang ditempatinya, tetapi seperti benda padat, benda cair tidak langsung dapat ditekan dan perubahan volume yang cu-kup signifikan jika diberikan gaya yang besar. Gas tidak memliki bentuk maupun volume yang tetap-gas akan menyebar untuk memenuhi tempatnya. Sebagai contoh, ketika udara dipompa ke dalam ban mobil, udara tersebut tidak seluruhnya mengalir ke bawah ban seperti zat cair; melainan menyebar untuk memenuhi seluruh isi ban. Karena zat cair dan gas tidak memperta-hankan bentuk yang tetap, keduanya memiliki kemampuan untuk mengalir; dengan demikian keduanya sering disebut sebagai fluida(Giancoli, 1998).
Massa Jenis dan Gravitasi Khusus
Massa jenis (density) ρ sebuah benda didefinisikan sebagai massa persatuan volume:
ρ= m
V (1.1)
denganmadalah massa benda danV merupakan volumenya. Massa jenis merupakan sifat khas dari suatu zat murni. Benda-benda yang terbuat dari unsur murni, seperti emas bisa memiliki
berbagi ukuran atau massa, tetapi massa jenis akan sama untuk seluruhnya. Satuan SI untuk massa jenis adalah kg/m3.
Gravitasi khusus suatu zat didefinisikan sebagai perbandingan dari massa jenis zat tersebut terhadap massa jenis air pada 4,00C. Gravitsu khusus merupakan angka, tanpa satuan dan dimensi. Karena massa jenis air adalah 1,00 g/cm3 = 1,00x103 kg/m3, gravitasi khusus semua
zat secara numerik akan sama dengan massa jenisnya jika dinyatakan dalam g/cm3, atau 10−3
kali massa jenisnya jiam dinyatakan dalamkg/m3.
1.2
Metode Analitik dan Metode Numerik dalam
Meye-lesaikan Persamaan Direfensial
Berbicara masalah mekanika fluida maka tidak akan lepas dari persamaan diferensial. Oleh karenanya penting untuk mengetahui metode penyelesainnya karena memang fisika itu hasil pengukurannya berupa bilangan riil, jadi mau tidak mau perangkat penelitian harus bisa me-nunjuk pada bilangan tertentu baik itu berupa pendekatan maupun eksak.
Persamaan diferensial ini berperanan penting di alam, sebab kebanyakan fenomena alam dirumuskan dalam bentuk diferensial. Persamaan diferensial sering digunakan sebagai model matematika dalam bidang sains maupun dalam bidang rekayasa. Hukum-hukum dasar fisika, mekanika, listrik dan termodinamika biasanya didasarkan pada perubahan sifat fisik dan kea-daan sistem. Untuk menjelaskan keakea-daan sistem fisik secara langsung, hukum-hukum tersebut biasanya dinyatakan variabel yang merupakan fungsi ruang dan waktu, misalnya
1. Hukum II Newton yang menyatakan gaya sebagai laju perubahan momentum setiap wak-tu F = dP dt 2. Hukum Termodinamika Φpanas =−k ∂T ∂x
(dengan Φpanas=fluks panas, k = konduktivitas panas danT = suhu) dan 3. Hukum Faraday
ε=Ldi dt
(denganε= teganganL= induktansi, dani= arus). Dengan mengintegralkan persamaan diferensial, dihasilkan fungsi matematika yang menjelaskan keadaan spasial dan temporal sebuah sistem, dinyatakan dalam percepatan, energi, massa, atau tegangan.
4. Mekanika Newton : keadaan partikel kuantum diwakili oleh fungsi gelombang Ψ(r,t). Metode numerik untuk persamaan diferensial memainkan peranan sangat penting bagi re-kayasawan, karena dalam prakteknya sebagian besar persamaan diferensial tidak dapat dise-lesaikan secara analitik. Metode numerik dipakai para rekayasawan untuk memperoleh solusi persaman diferensial. Bila metode analitik memberikan solusi persamaan diferensial dalam bentuk fungsi menerus, maka metode numerik memberikan solusi persamaan diferensial dalam bentuk variabel numerik. Diantara metode numerik yang sering digunakan dalam menyelesa-ikan persamaan diferensial sial adalah Metode Euler, Metode Heun, Metode Deret Taylor dan Metode Runge-Kutta.
Bab 2
Persamaan Euler
2.1
Gambaran Euler
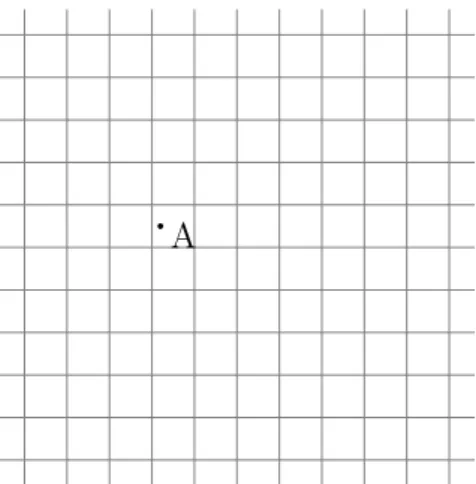
Gambaran Euler merupakan ruang yang dibagi menggunakan kisi.
.. A
Gambar 2.1: Kisi yang dilewati partikel (semakin kecil kisi, semakin banyak partikel yang melewati kotak A)
Misal terdapat N partikel melewati kotak A dengan kecepatan massing-masing partikel
vi = 1,2,3, ..., N maka keadaan fluida:
1. Kecepatan rata-rata fluida di A adalah
v = N ∑ i−=1 vi N (2.1)
2. Densitas fluida di A
ρ= N
luas kotak A (2.2)
Secara umum, keadaan partikel dapat diwakili dengan perumusan ⃗v(⃗r, t) dan ⃗ρ(⃗r, t). Bentuk persamaan diferensial yang terkait dengan⃗v dan ⃗ρdisebut sebagai persamaan Euler dalam fluida Dinamis.
2.2
Persamaan Umum Euler
Gaya total yang bekerja pada fluida yang bervolumeV yang diakibatkan oleh adalanya interaksi antar partikel dapat dinyatakan dengan
− ∮ PndS (2.3) dengan − ∮ PndS =− ∫ V ∇P dV. (2.4)
Oleh karena itu, gaya yang bekerja adalah −∇P dV dan gaya per unit volumnya adalah−∇P.
dF =−∇P dV dma=−∇P dV dm
dV a=−∇P
(2.5)
Sehingga kita dapat menuliskan persamaan kelestarian massanya dalam bentuk:
ρa=−∇P (2.6)
denganρadalah rapat massa dari fluida. Dalam kasus sederhana, jika sebuah partikel bermassa
mdan bergerak dengan kecepatanv mendapat gayaF, maka partikel tersrbut akan mempunyai percepatan a=F/m =dv/dt. Elemen kecepatannya mempunyai dua komponen, yakni
1. Elemen kecepatan pada ruang tertentu (fixed space)
dv1 = ∂v
2. Elemen kecepatan pada waktu tertentu (given time) dv2 =dx ∂v ∂x +dy ∂v ∂y +dz ∂v ∂z (2.8)
Adapun, jarak yang ditempuh partikel dalam selang waktu dt adalah
dr=dxi+dyj+dxk (2.9) dr.∇=dx ∂ ∂x +dy ∂ ∂y +dz ∂ ∂z (2.10)
Sehingga persamaan (2.8) dapat dinyatakan dalam bentuk
dv2 = (dr.∇)v, (2.11)
elemen total kecepatannya
dv=dv1+dv2 = ∂v
∂tdt+ (dr.∇)v (2.12)
dan percepatannya menjadi
a= ∂v
∂t + (v.∇)v (2.13)
Persamaan (2.13) merupakan derivatif total yang secara umum dapat dituliskan
D Dt =
∂
∂t + (v.∇) (2.14)
Deskripsi dari pergerakan fluida dipisah menjadi dua bagian, yaitu: 1. Deskripsi Euleran
terkait dengan turuan parsial ∂/∂tdan v.∇ pada ruang tertentu 2. Deskripsi Lagrangan
Berdasarkan persamaan (2.13) dan (2.14), persamaan gerak fluida adalah ρ [ ∂v ∂t + (v.∇v)v ] =−∇P ∂v ∂t + (v.∇v)v=− 1 ρ∇P Dv Dt =− 1 ρ∇P (2.15)
Persamaan (2.15) merupakan bentuk lain dari persamaan Euler.
Aplikasi penting dari persamaan gerak ini dapat dijumpai pada medan gravitasi yang terka-rakterisasi oleh percepatan (gaya per satuan massa) g. Dalam masalah ini, fluida mempunyai gayaρg, yang merupakan gaya yang bekerja pada satuan volum. Dengan demikian, persamaan gerak (2.15) dapat dituliskan dalam bentuk
∂v
∂t + (v.∇v)v=−
1
ρ∇P +g. (2.16)
Secara umum, jika fluida mendapat gaya eksternal F (dyn/cm3), maka persamaan geraknya
adalah
∂v
∂t + (v.∇v)v=−
1
ρ∇P +F (2.17)
Contoh: Bintang Statis
Diasumsikan bahwa gaya gravitasi dapat diturunkan dari potensial gravitasi g=−∇ϕ. Poten-sial ϕ dapat dihubungkan dengan kerapatan gas dalam bintang melalui persamaan Poisson,
∇2ϕ = 4πGρ (2.18)
Dari persamaan (2.16) dengan v= 0, akan didapatkan 1
ρ∇P=g =−∇ϕ (2.19)
Jika persamaan ini dikenai divergensi, ∇. ( 1 ρ∇P ) =∇.(−∇ϕ) =−∇2ϕ (2.20)
maka ∇. ( 1 ρ∇P ) =−4πGρ (2.21)
Untuk menyelesaikan persamaan (2.21) diperlukan hubungan yang melibatan P dan ρ, conn-tohnya persamaan keadaan.
2.3
Persamaan Euler dalam Koordinat Bola
Gambar 2.2: Koordinat bola dalam sistem kartesius
Vektor satuan (n,ℓ,m) dihubungkan dengan vektor satuan (i,j,k) melalui n = sinθcosϕi+ sinθsinϕj+ cosθk
ℓ = cosθcosϕi+ cosθsinϕj−sinθk m=−sinϕi+ cosϕj
(2.22)
Sedangkan vektor posisi r dan kecepatan v diberikan oleh persamaan r=rn(θ, ϕ)
Dari persamaan (2.22) akan didapatkan hubungan ∂n ∂θ =ℓ ∂n ∂ϕ = sinθm (2.24) sehingga ˙ n= ∂n ∂θ ˙ θ+∂n ∂ϕ ˙ ϕ= ˙θℓ+ ˙ϕsinθm (2.25) dan v= ˙rn+r ( ˙ θℓ+ ˙ϕsinθm ) (2.26) kecepatan v v=vrn+vθℓ+vϕm (2.27) dengan vr = ˙r vθ =rθ˙ vϕ =rsinθϕ˙ (2.28)
dan kita juga mempunyai ˙
vr = ¨r ˙
vθ = ˙rθ˙+rθ¨ ˙
ϕ= ˙rϕ˙sinθ+rϕ¨sinθ+rϕ˙cosθϕ˙
(2.29)
masih dari persamaan (2.22), kita mempunyai
∂ℓ ∂θ =−n ∂ℓ ∂ϕ = cosθm (2.30) sehingga ˙ ℓ= ∂ℓ ∂θ ˙ θ+ ∂ℓ ∂ϕ ˙ ϕ=−θ˙n+ ˙ϕcosθm (2.31)
Dari persamaan (2.22) kita juga bisa menuliskan ∂m ∂θ = 0 ∂m ∂ϕ = sinθn−cosθℓ (2.32) sehingga ˙ m= ∂m ∂θ ˙ θ+ ∂m ∂ϕ ˙ ϕ=−ϕ˙sinθn−ϕ˙cosθℓ (2.33) Menggunakan persamaan, kita dapatkan
˙
v= ( ˙vr−vθθ˙−vϕϕ˙sinθ)n+ (vrθ˙+ ˙vθ−vϕϕcos˙ θ)ℓ + (vrϕ˙sinθ+vθϕ˙cosθ+ ˙vϕ)m
(2.34)
Menggunakan persamaan (2.28) dan (2.29) ˙
v= (¨r−rθ˙2−rϕ2sin2θ)n+ (rθ¨+ 2 ˙rθ˙−rϕ2sinθcosθ)ℓ
+ (rϕ¨sinθ+ 2 ˙rϕ˙sinθ+ 2rθ˙ϕ˙cosθ)m
(2.35)
Berdasarkan persamaan (2.27) suku pertama dari persamaan (2.17) dapat ditulis dalam bentuk
∂v ∂t = ∂vr ∂t n+ ∂vθ ∂t ℓ+ ∂vϕ ∂t m (2.36)
dan tekanan dari persamaan (2.17) dapat ditulis dalam bentuk ∇= ∂P ∂rn+ 1 r ∂P ∂θℓ+ 1 rsinθ ∂P ∂ϕm (2.37)
Gaya per satuan volumenya dapat ditulis dalam bentuk
F=Frn+Fθℓ+Fϕm (2.38)
Dari berbagai persamaan di atas, maka kita dapat menyusun kembali persamaan eulernya ber-dasarkan komponen n, ℓ,m:
∂vr ∂t +vr ∂vr ∂r + vθ r ∂vr ∂θ + vϕ rsinθ ∂vr ∂ϕ − vθ2+vϕ2 r =− 1 ρ ∂P ∂r + 1 ρFr (2.39) ∂vr ∂t +v.∇vr− v2 θ +v2ϕ r =− 1 ρ ∂P ∂r + 1 ρFr (2.40)
Komponen polar, satuan vektor ℓ ∂vr ∂t +vr ∂vr ∂r + vθ r ∂vr ∂θ + vϕ rsinθ ∂vr ∂ϕ + vrvθ r − v2 ϕcotθ r =− 1 ρr ∂P ∂θ + 1 ρFθ (2.41) ∂vr ∂t +v.∇vθ+ vrvθ r − v2ϕcotθ r =− 1 ρr ∂P ∂θ + 1 ρFθ (2.42)
Komponen azimut, satuan vektor m
∂vϕ ∂t +vr ∂vϕ ∂r + vθ r ∂vϕ ∂θ + vϕ rsinθ ∂vϕ ∂ϕ + vrvϕ r + vθvϕcotθ r =− 1 ρrsinθ ∂P ∂ϕ + 1 ρFϕ (2.43) ∂vϕ ∂t +v.∇vϕ+ vθ r ∂vϕ ∂θ + vrvϕ r + vθvϕcotθ r =− 1 ρrsinθ ∂P ∂ϕ + 1 ρFϕ (2.44)
2.4
Koorinat Silinder
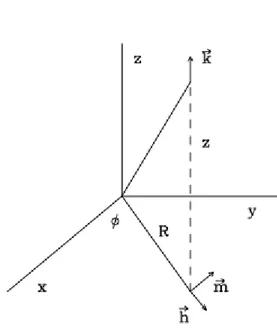
Hubungan antara vektor satuan (h,m,k) dengan sistem kartesius (i,j,k) adalah h= cosϕi−sinϕj
m=−sinϕi+ cosϕj k=k
(2.45)
Posisi r dan kecepatan v diberikan oleh persamaan r=Rh+zk v= dr dt = ˙Rh+R ˙ ϕm+ ˙zk (2.46)
Suku ∂v/∂t dalam persamaan (2.17) dapat ditulis dengan koordinat silinder dengan prosedur yang analog dengan koordinat bola. Gaya persatuan volumenya
F=FRh+Fϕm+Fzk (2.47)
Gambar 2.3: Koordinat dan vektor satuan silinder dalam sistem kartesius
Kita dapat menuliskan persamaan euler dalam 3 komponen (R, ϕ, z) sebagai berikut:
Komponen radial, satuan vektor h
∂vR ∂t +vR ∂vR ∂R + vϕ R ∂vR ∂ϕ − v2 ϕ R +vz ∂vz ∂z =− 1 ρ ∂P ∂R+ 1 ρFR (2.48)
Komponen azimuth, satuan vektor m
∂vϕ ∂t +vR ∂vϕ ∂R + vRvϕ R + vϕ R ∂vR ∂ϕ +vz ∂vz ∂z =− 1 ρ ∂P ∂ϕ + 1 ρFϕ (2.49)
Komponen vertikal, satuan vektor k
∂vz ∂t +vR ∂vz ∂R + vϕ R ∂vz ∂ϕ +vz ∂vz ∂z =− 1 ρ ∂P ∂z + 1 ρFz (2.50)
Bab 3
Gerak Fluida dan Persamaan
Kontinyuitas
Gerak fluidaditentukan oleh dua gaya yang bekerja pada partikel fluida tersebut, yakni: 1. Gaya external (misal: gravitasi) dan
2. Gaya internal oleh partikel lain dalam satu material. Gerak fluida dapat dirumuskan dengan
ai = dvi dt = 1 mi ( Fext+ N ∑ j=1 Fintj ) vi = ∫ aidt xi = ∫ vidt (3.1)
Kita membedakan dua jenis utama aliran fluida. Jika aliran fluida tersebut mulus, yaitu lapisan-lapisan yang bersebelahan meluncur satu sama lain dengan mulus, aliran tersebut di-sebut sebagai aliran lurus ataulaminer. Pada aliran jenis ini, setiap partikel fluida mengikuti lintasan yang mulus, dan lintasan-lintasan ini tidak saling bersilangan.
Di atas laju tertentu, yang bergantung dari beberapa faktor sebagaimana akan kita lihat kemudian, aliran tersebut berubah menjadi turbulen. Aliran turbulen. ditandai dengan lingkaran-lingkaran tak menentu, kecil dan menyerupai pusaran yang disebut arus eddy atau eddy. Eddy menyerap banyak energi dan walaupun gesekan internal dengan besar tertentu yang
disebut dengan viskositas ada, bahkan pada waktu aliran laminer energi tersebut jauh lebih besar ketika aliran berupa turbulen. Beberapa tetes kecil tinta atau pewarna makanan yang diteteskan ke zat car yang sedang bergerak dapat dengan cepat menunjukkan apakah aliran tersebut laminer atau turbulen.
Laju aliran didefinisikan sebagai massa ∆m dari fluida yang melewati titik tertentu per satuan waktu ∆t: laju aliran massa= ∆m/∆t. Volume fluida yang melewati titik 1 (yaitu, melalui luas A1) dalam waktu ∆t adalah A1∆l1, dengan ∆l1 adalah jarak yang dilalui dalam
waktu ∆t. Karena kecepatan fluida yang melewati fluida 1 adalahv1 = ∆l1/∆t, laju alir massa
∆m/∆t melaluiA1 adalah ∆m ∆t = ρ1∆V1 ∆t = ρ1A1∆l1 ∆t =ρ1A1v1 (3.2)
Dengan ∆V1 = A1∆l1 adalah volume dengan massa ∆m1 dan ρ1 adalah massa jenis fluida.
Dengan cara yang sama, pada titik 2 (melalui luas A2), laju alir adalah ρ2A2v2. Karena tidak
ada aliran fluida yang masuk atau keluar dari sisi-sisi, maka laju alir yang melalui A1 dan A2
harus sama. Dengan demikian, karena
∆m1 ∆t = ∆m2 ∆t maka ρ1A1v1 =ρ2v2v2 (3.3)
Persamaan ini disebut persamaan kontinyuitas. Jika fluida tersebut tidak bisa ditekan (ρ
tidak berubah terhadap tekanan), yang merupakan pendekatan yang baik untuk zat cair dalam sebagin besar kondisi (dan kadang-kadang juga untuk gas), maka ρ1 = ρ2, dan persamaan
kontinyuitasnya menjadi
A1v1 =A2v2 (3.4)
Hasil kali Avmerupakan laju aliran volume atau debit(volume fluida yang melewati suatu titik per sekon) karena ∆V /∆t =A∆l/∆t=Av, yang dalam satu SI adalah m3/s.
Bab 4
Persamaan Bernoulli
Prinsip Bernoulli menyatakan bahwa jika suatu titik dalam fluida mempunyai kecepatan fluida tinggi maka tekanannya rendah dan jika suatu titik dalam fluida mempunyai kecepatan fluida rendah maka tekanannya tinggi. Bernoulli mengembangkan persamaan yang menyatakan prin-sip ini secara kuantitatif. Untuk menurunkan persamaan Bernoulli kita anggap aliran fluida tetap dan laminer, fluida tersebut tidak bisa ditekan dan viskositas cukup kecil sehingga bisa diabaikan. Agar berlaku umum, kita anggap fluida yang mengalir dalam tabung dengan pe-nampang lintang yang tidak sama, yang ketinggiannya berubah terhadap suatu tingkat acuan tertentu. Kita akan memperhitungkan banyaknya fluida dan menghitung kerja yang dilakukan untuk memindahkannya dari posisi a ke posisi b. Pada proses ini, fluida pada titik 1 mengalir sejauh ∆l1 dan memaksa fluida pada titik 2 untuk berpindah sejauh ∆l2. Fluida di sebalah
kiri titik memberikan tekanan P1 pada bagian fluida kita dan melakukan kerja sebesar
W1 =F1∆l1 =P1A1∆l1 (4.1)
Pada titik 22, kerja yang dilakukan pada fluida tersebut adalah
W2 =−P2A2l2 (4.2)
ada tanda negatifnya karena gaya yang diberikan pada fluida berlawanan dengan gerak (dengan demikian fluida melakukan kerja pada fluida di sebalah kanan titik 2). Kerja juga dilakukan pada fluida oleh gaya gravitasi. Karena efek total proses yang ditunjukkan pada gambar adalah memindahkan massa m dari volume A1∆l1 dari titik 1 ke titik 2., kerja yang dilakukan oleh
gaya gravitasi adalah
W3 =−mg(y2−y1) (4.3)
dengan y1 dan y2 adalah ketinggian pusat tabung di atas tingkat acuan tertentu. Perhatikan
bahwa pada kasusu yang ditunjukkan pada gambar, suku ini negatif karena arah gerakan menuju ke atas melawan gaya gravitasi. Kerja total W yang dilakukan pada fluida adalah
W =W1+W2+W3
W =P1A1∆l1−P2A2∆l2 −mgy2 +mgy1
(4.4)
Menurut prinsip kerja energi, kerja total yang dilakukan pada sistem sama dengan perubahan energi kinetiknya. Dengan demikian
1 2mv 2 2− 1 2mv 1 1 =P1A1∆l1−P2A2∆l2−mgy2+mgy1 (4.5)
Massa m mempunyai volume A1∆l1 =A2∆l2. Berarti kita bisa mensubstitusikanm=ρA1l1 = ρA2l2 dan juga membagi denganA1∆l1 =A2∆l2 untuk mendapatkan:
1 2ρv 2 2 − 1 2ρv 2 1 =P1−P2−ρgy2+ρgy1 (4.6)
yang bisa kita susun ulang untuk mendapatkan
P1+ 1 2ρv 2 1+ρgy1 =P2+ 1 2ρv 2 2 +ρgy2 (4.7)
Ini merupakan persamaan Bernoulli. Karena titik 1 dan titik 2 bisa berupa dua titik mana saja sepanjang tabung aliran, persamaan Bernoulli dapat dituliskan
P +1 2ρv
2+ρgy= konstan (4.8)
Persamaan Bernoulli merupakan sebuah bentuk hukum kelestarian energi, karena kita menu-runkannya dari prinsip kerja-energi.
Daftar Pustaka
1. Maciel, W.J., 2014,Hydrodynamics and Stellar Winds, Springer 2. Giancoli, D.C., PHYSICS:Principle with applications, fifth edition
3. Kudela, H.,Equation of Fluid Motion