APLIKASI METODE KAPLAN MEIER UNTUK MENDUGA SELANG WAKTU KETAHANAN HIDUP
(Studi Kasus: Pasien Kanker Payudara di Rumah Sakit Panti Rapih Yogyakarta)
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Caecilia Bintang Girik Allo NIM : 133114013
PROGRAM STUDI MATEMATIKA, JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
TIME INTERVAL ESTIMATION
(Case Study: Breast Cancer Patients at Panti Rapih Yogyakarta Hospital)
A Thesis
Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains
Mathematics Study Program
Written by:
Caecilia Bintang Girik Allo Student Number: 133114013
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v Skripsi ini saya persembahkan kepada:
Tuhan Yesus atas segala Berkat dan Kasih-Nya sepanjang perjalanan hidup saya.
Papa dan Mama Tercinta.
Kakak-kakak saya, yaitu Kak Ardi, Kak Suhar, Kak Muli, dan Kak Rian. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, selaku dosen pembimbing skripsi yang
terbaik.
Semua orang yang akan membaca skripsi saya.
Berdoa dan Berusaha. Serahkan semua kekhawatiranmu Pada-Nya dan
vii
Metode Kaplan Meier adalah salah satu metode analisis ketahanan hidup. Metode Kaplan Meier menghasilkan penduga fungsi ketahanan hidup. Penduga ketahanan hidup dengan Metode Kaplan Meier diperoleh menggunakan Metode Kemungkinan Maksimum. Penduga variansi untuk penduga ketahanan hidup dengan Metode Kaplan Meier diperoleh menggunakan Metode Delta. Dalam pendugaan fungsi ketahanan hidup dengan Metode Kaplan Meier dibutuhkan data. Dalam praktik, data yang sering muncul pada saat pengambilan data adalah data yang tidak lengkap (data tersensor). Banyak penyebab suatu data dapat dikatakan data tersensor, seperti kondisi terakhir individu yang tidak diketahui.
Pendugaan fungsi ketahanan hidup dengan Metode Kaplan Meier langsung diaplikasikan pada pasien kanker payudara di Rumah Sakit Panti Rapih Yogyakarta tahun 2014-2016. Pendugaan akan menghasilkan selang kepercayaan waktu bertahan hidup pasien kanker payudara secara keseluruhan, pasien kanker payudara yang mengikuti kemoterapi dan yang tidak mengikuti kemoterapi pada suatu waktu. Kurva ketahanan hidup dengan Metode Kaplan Meier yang dihasilkan digunakan untuk membandingkan peluang bertahan hidup antar dua kelompok.
Dari pembahasan diperoleh empat kesimpulan. Pertama, peluang bertahan hidup pasien kanker payudara di Rumah Sakit Panti Rapih secara keseluruhan dapat dikatakan relatif kecil. Kedua, peluang bertahan hidup secara keseluruhan pasien kanker payudara yang mengikuti kemoterapi lebih besar dari pada pasien kanker payudara yang tidak mengikuti kemoterapi. Ketiga, peluang bertahan hidup pasien kanker payudara stadium 4 yang mengikuti kemoterapi lebih besar dari pada pasien kanker payudara yang tidak mengikuti kemoterapi. Keempat, kemoterapi dapat memperpanjang waktu hidup pasien kanker payudara.
viii
Kaplan Meier Method is one of the survival analysis method. Kaplan Meier Method produces an estimator for survival function. The survival estimator with Kaplan Meier Method is obtained by using Maximum Likelihood Method. Variance estimator for the survival estimator with Kaplan Meier Method is obtained by using Delta Method. Data are needed to calculate the estimation for the survival function with Kaplan Meier Method. In practice, the data that often appear in data collection are the incomplete data (censored data). There are many causes that make the survival data called censored data, such as the unknown last condition of an individual.
The survival estimation by using Kaplan Meier Method was applied to breast cancer patients at Panti Rapih Hospital Yogyakarta in 2014-2016. The estimation would produce a survival confidence interval of breast cancer patients in general, breast cancer patients who take the chemotherapy and do not take the chemotherapy. As a result, the survival curve with Kaplan Meier method is used to compare the survival probability between two groups.
There are four conclusions that can be found in this study. First, the survival probability of breast cancer patients in Panti Rapih Hospital is relatively small. Second, the survival probability for breast cancer patients who take the chemotherapy is bigger than survival probability for breast cancer patients who do not take the chemotherapy. Third, survival probability of level fourth breast cancer patients who take chemotherapy is bigger than survival probability of level fourth breast cancer patients who do not take chemotherapy. Fourth, chemotherapy can extend the lifetime for breast cancer patients.
x
Puji dan syukur penulis haturkan ke hadirat Tuhan Yang Maha Esa atas segala berkat, kasih, dan penyertaan-Nya sehingga penulis dapat menyelesaikan tugas akhir ini dengan baik. Tugas akhir yang berjudul “Aplikasi Metode Kaplan Meier untuk Menduga Selang Waktu Ketahanan Hidup (Studi Kasus: Pasien Kanker Payudara di Rumah Sakit Panti Rapih Yogyakarta)” merupakan salah satu syarat untuk memperoleh gelar sarjana Matematika pada Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta. Penulis mendapat banyak dukungan dan bantuan dalam proses menyelesaikan tugas akhir ini. Oleh karena itu, dengan tulus hati penulis ingin menyampaikan terima kasih kepada:
1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing tugas akhir yang dengan penuh kesabaran telah meluangkan waktu, tenaga, dan pikiran serta memberikan masukan, arahan, dan nasihat kepada penulis. 2. Pihak Rumah Sakit Panti Rapih Yogyakarta yang telah mengizinkan dan
membantu penulis dalam pengambilan data.
3. Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku Kepala Program Studi. 4. Ibu M. V. Any Herawati, S.Si., M.Si., selaku wakil kepala program studi
Matematika dan Dosen Pembimbing Akademik yang selalu memberikan arahan yang berkaitan dengan perkuliahan.
5. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dekan Fakultas Sains dan Teknologi.
6. Romo Prof. Dr. Frans Susilo, S.J., Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak YG. Hartono, S.Si., M.Sc., Ph.D., Ibu M. V. Any Herawati, S.Si., M.Sc., dan Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen program studi matematika yang telah membagikan ilmu dan pengalaman selama masa perkuliahan. 7. Perpustakaan Universitas Sanata Dharma dan staf sekretariat Fakultas
xii
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING iiiError! Bookmark not defined. HALAMAN PENGESAHAN ... Error! Bookmark not defined. HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... Error! Bookmark not defined. ABSTRAK ... vii
ABSTRACT ... viii
LEMBAR PERNYATAAN PERSETUJUAN ... Error! Bookmark not defined. KATA PENGANTAR ... x
1. Probabilitas dari Sebuah Kejadian ... 6
2. Probablitias Bersyarat ... 6
3. Variabel Acak ... 8
B. Distribusi Probabilitas ... 9
1. Distribusi Probabilitas Diskrit... 9
2. Distribusi Probabilitas Kontinu ... 12
3. Nilai Harapan ... 14
4. Variansi ... 18
5. Momen dan Fungsi Pembangkit Momen ... 22
6. Metode Fungsi Pembangkit Momen ... 26
C. Distribusi Probabilitas Multivariat ... 28
D. Teorema Limit Pusat ... 33
E. Pendugaan Parameter ... 36
1. Penduga Titik ... 36
2. Penduga Selang ... 37
3. Metode Pivot ... 38
xiii
BAB III METODE KAPLAN MEIER ... 45
A. Analisis Ketahanan Hidup ... 45
B. Fungsi Ketahanan Hidup ... 46
C. Fungsi Hazard ... 47
D. Distribusi Waktu Hidup Model Kontinu ... 47
E. Distribusi Waktu Hidup Model Diskrit ... 49
F. Data Tersensor ... 50
1. Penyensoran Kanan ... 51
2. Penyensoran Kiri ... 54
3. Penyensoran Interval ... 55
G. Penduga Fungsi Ketahanan Hidup dengan Metode Kaplan Meier ... 55
H. Kurva Ketahanan Hidup Kaplan Meier dengan program R ... 62
BAB IV APLIKASI METODE KAPLAN MEIER UNTUK MENDUGA SELANG WAKTU KETAHANAN HIDUP ... 65
A. Kanker ... 65
B. Proses Pengambilan Sampel ... 67
C. Ketahanan Hidup Pasien Kanker Payudara ... 71
1. Ketahanan Hidup Pasien Kanker Payudara Tahun 2014-2016 ... 72
2. Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi .. ... 74
3. Ketahanan Hidup Pasien Kanker Payudara yang Tidak Mengikuti Kemoterapi. ... 76
4. Perbandingan Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi dengan Pasien yang Tidak Mengikuti Kemoterapi ... 79
5. Ketahanan Hidup Pasien Kanker Payudara Stadium 2 ... 80
6. Ketahanan Hidup Pasien Kanker Payudara Stadium 3 ... 80
7. Ketahanan Hidup Pasien Kanker Payudara Stadium 4 ... 80
BAB V PENUTUP ... 86
A. Kesimpulan ... 86
C. Saran ... 87
1. Saran untuk Peneliti Selanjutnya ... 87
2. Saran untuk Rumah Sakit Panti Rapih ... 88 DAFTAR PUSTAKA
1 BAB I PENDAHULUAN A. Latar Belakang
Ilmu matematika dapat digunakan untuk menganalisis ketahanan hidup dari suatu obyek. Obyek dapat berupa makhluk hidup maupun benda yang mempunyai ketahanan hidup, seperti lampu dan mobil. Analisis ketahanan hidup merupakan cabang dari ilmu statistik yang dapat digunakan untuk menganalisis terjadinya suatu kejadian, misalnya kematian, munculnya suatu penyakit, atau kambuhnya suatu penyakit. Dalam tugas akhir ini kejadian yang dimaksud adalah kematian. Analisis ketahanan hidup digunakan dalam berbagai bidang ilmu seperti biologi, sosiologi, maupun bidang ilmu yang berkaitan dengan mesin, dan ekonomi. Analisis ketahanan hidup mempunyai beberapa metode, yaitu Life Tables, Kaplan Meier, Regresi Exponensial, Regresi Log-Normal, dan Regresi Proporsi Hazard.
Fungsi ketahanan hidup secara matematis dapat ditulis sebagai berikut �
dengan merupakan variabel acak waktu hidup, merupakan fungsi probabilitas, dan adalah suatu waktu.
Pada tahun 1958, Edward L. Kaplan dan Paul Meier menerbitkan sebuah makalah tentang cara menyelesaikan suatu permasalahan dengan pengamatan yang tidak lengkap. Metode ini termasuk metode nonparametrik karena pada umumnya bentuk distribusi dari populasi yang akan diteliti tidak diketahui. Metode Kaplan Meier disebut juga Metode Product - Limit. Metode Kaplan Meier sering digunakan di dalam bidang ilmu kesehatan. Metode Kaplan Meier juga menghasilkan suatu kurva yang menggambarkan ketahanan hidup dari populasi atau sampel yang dipilih.
menyebabkan data tersebut tidak bisa diperoleh. Faktor-faktor tersebut antara lain individu yang dinyatakan sembuh sebelum penelitian berakhir, individu yang tidak lagi bersedia mengikuti penelitian, individu berhenti diberi perlakuan karena suatu alasan, dan individu meninggal dunia bukan karena diberi perlakuan sebagaimana yang dimaksud dalam penelitian. Data yang dihasilkan oleh berbagai faktor tersebut disebut data tersensor. Biasanya data yang dihasilkan berupa waktu dengan satuan tahun, bulan, minggu, atau hari.
Rumus penduga ketahanan hidup �̂ dengan Metode Kaplan Meier adalah sebagai berikut
�̂ ∏
dengan:
banyaknya individu yang meninggal pada waktu ke- ,
banyaknya individu yang berada pada risiko kegagalan waktu ke- .
Kanker adalah salah satu penyakit yang menjadi penyumbang terbesar kematian di dunia. Terdapat berbagai jenis penyakit kanker diantaranya kanker payudara, kanker serviks, kanker paru-paru, kanker kulit, kanker usus, dan lain-lain. Selain kanker paru-paru, kanker payudara pun termasuk kanker yang banyak ditemui di masyarakat. Banyak faktor yang dapat menyebabkan penyakit kanker, diantaranya faktor keturunan, faktor pola hidup yang tidak sehat, faktor radiasi, dan lain-lain. Namun ada beberapa cara untuk mengatasi kanker seperti operasi, terapi radiasi, dan kemoterapi. Rumah Sakit Panti Rapih (RSPR) Yogyakarta merupakan salah satu rumah sakit swasta terbesar di Yogyakarta yang turut melayani penderita kanker. Oleh karena itu, penelitian ini bertujuan untuk menghitung probabilitas ketahanan hidup penderita kanker payudara di rumah sakit Panti Rapih.
B. Rumusan Makalah
2. Bagaimana landasan matematis untuk memperoleh Metode Kaplan Meier? 3. Bagaimana menerapkan Metode Kaplan Meier dalam bidang kesehatan,
khususnya untuk memperkirakan ketahanan hidup penderita Kanker Payudara di Rumah Sakit Panti Rapih Yogyakarta?
4. Apakah pasien kanker payudara yang mengikuti kemoterapi memiliki ketahanan yang lebih tinggi dibandingkan dengan pasien kanker payudara yang tidak mengikuti kemoterapi?
C. Batasan Masalah
Batasan masalah dalam tugas akhir ini adalah sebagai berikut: 1. Data yang digunakan merupakan data tensensor acak.
2. Teorema Ketunggalan tidak dibuktikan.
3. Teori probabilitas yang dibahas hanya yang berkaitan dengan materi pokok. 4. Interpretasi hasil perbandingan antar kelompok berdasarkan gambar.
D. Tujuan Penulisan
Tujuan dari penulisan tugas akhir ini adalah:
1. Menjelaskan penduga ketahanan hidup dengan Metode Kaplan Meier dalam perhitungan probabilitas ketahanan hidup.
2. Mengetahui penerapan penduga ketahanan hidup dengan Metode Kaplan Meier dalam kehidupan sehari-hari khususnya dalam bidang kesehatan.
E. Manfaat Penulisan
Manfaat dari penulisan tugas akhir ini adalah menghasilkan informasi tentang peluang bertahan hidup penderita Kanker Payudara di Rumah Sakit Panti Rapih Yogyakarta.
F. Metode Penulisan
G. Sistematika Penulisan
G. Penduga Fungsi Ketahanan Hidup dengan Metode Kaplan Meier H. Kurva Ketahanan Hidup Kaplan Meier dalam R
BAB IV APLIKASI PENDUGAAN KETAHANAN HIDUP DENGAN METODE KAPLAN MEIER
A. Kanker
B. Proses Pengambilan Sampel
BAB V PENUTUP A. Kesimpulan
B. Saran
6 BAB II
LANDASAN TEORI A. Probabilitas
1. Probabilitas dari Sebuah Kejadian
Oleh karena probabilitas dari suatu kejadian biasanya dibutuhkan untuk pengambilan keputusan, sangat penting untuk memahami teori probabilitas dari suatu kejadian. Banyak bidang yang berhubungan dengan probabilitas, seperti ekonomi, bisnis, kesehatan, dan lain-lain.
Definisi 2.1
Misalkan � adalah ruang sampel yang terkait dengan percobaan. Probabilitas dari kejadian dalam �, dinotasikan dengan simbol memenuhi:
Probabilitas kejadian jika diketahui kejadian telah terjadi adalah | , .
Simbol | dibaca “Probabilitas bersyarat jika diketahui kejadian terjadi”.
Contoh 2.1
Sebuah dadu setimbang dilempar sekali. Tentukan probabilitas munculnya mata dadu genap jika diketahui munculnya kejadian mata dadu prima terlebih dahulu. Jawab:
Ruang sampel percobaan � adalah { }.
{ }. { }. { }
Sehingga diperoleh:
|
Definisi 2.3
Kejadian dan kejadian dikatakan saling bebas jika salah satu dari pernyataan di bawah terpenuhi:
| ,
| ,
.
Jika tidak, berarti dua kejadian tersebut saling bergantung.
Contoh 2.2
Dua buah dadu setimbang dilemparkan secara bersamaan. Didefinisikan kejadian adalah munculnya angka dadu 2 pada dadu pertama dan kejadian adalah munculnya angka dadu 4 pada dadu kedua. Apakah kejadian dan B saling bebas?
Jawab:
Akan ditunjukkan bahwa apakah kejadian dan B saling bebas menggunakan pernyataan pada Definisi 2.3
� { } Sehingga diperoleh banyaknya elemen �, � .
dan { }
Jadi, kejadian dan kejadian saling bebas.
3. Variabel Acak Definisi 2.4
Variabel acak adalah fungsi yang memetakan setiap elemen ruang sampel ke bilangan real. Dengan kata lain variabel acak merupakan pemetaan dari himpunan ruang sampel ke himpunan bilangan real. Variabel acak ditulis dengan huruf kapital, misalnya X atau Y.
Definisi 2.5
Variabel acak dikatakan diskrit jika nilai-nilainya berhingga atau tak berhingga terbilang. Jika tidak memenuhi hal tersebut maka variabel acak dikatakan kontinu.
Contoh 2.3
Dua buah koin yang telah dilabeli angka 1 pada sisi gambar dan angka 2 pada sisi angka dilemparkan sebanyak dua kali. Variabel acak didefinisikan sebagai jumlah kedua koin yang muncul. Tentukan ruang sampelnya dan semua kemungkinan nilai variabel acak .
Jawab:
Nilai adalah 2, 3, atau 4.
B. Distribusi Probabilitas 1. Distribusi Probabilitas Diskrit Definisi 2.6
Himpunan pasangan terurut adalah fungsi probabilitas atau distribusi probabilitas dari variabel acak diskrit jika untuk setiap kemungkinan nilai :
1.
2. ∑
Contoh 2.4
Sebuah sekolah mempunyai lima pemain basket putri dan lima pemain basket putra. Sekolah harus memilih dua orang secara acak yang akan dikirim untuk mengikuti pelatihan khusus di tingkat provinsi. adalah banyaknya pemain basket putri yang terpilih. Tentukan distribusi probabilitas dari .
Jawab:
: banyaknya pemain basket putri yang terpilih. Sekolah hanya akan memilih dua orang, sehingga kemungkinan nilai adalah 0 , 1, atau 2.
�
{ } { } { } { }
3
4 >
Definisi 2.7
Fungsi distribusi kumulatif dari variabel acak yang fungsi probabilitasnya adalah
∑ , untuk .
Contoh 2.5
Tentukan fungsi distribusi kumulatif dari variabel acak pada Contoh 2.4. Jawab:
Contoh-contoh distribusi probabilitas diskrit adalah Distribusi Binomial, Distribusi Geometrik, Distribusi Hipergeometrik, dan Distribusi Poisson. Selanjutnya akan dibahas mengenai Distribusi Binomial.
Definisi 2.8
Proses percobaan Binomial memiliki sifat sebagai berikut: 1. Percobaan terdiri dari ulangan yang identik.
3. Probabilitas sukses pada sebuah ulangan adalah dan tetap sama untuk ulangan-ulangan lainnya. Probabilitas gagal dari ulangan tersebut adalah .
4. Ulangan-ulangan bersifat saling bebas.
5. Variabel acak adalah banyaknya ulangan sukses yang teramati selama ulangan.
Contoh 2.6
Sistem deteksi peringatan dini untuk pesawat terdiri dari 4 unit radar identik yang beroperasi secara independen (saling bebas) satu sama lain. Setiap unit radar memiliki peluang untuk mendeteksi adanya ganguan pada pesawat. Ketika pesawat beroperasi, variabel acak adalah banyaknya unit radar yang tidak mendeteksi gangguan. Apakah ini termasuk percobaan binomial?
Jawab:
Apabila soal di atas termasuk percobaan binomial maka percobaan harus memenuhi sifat-sifat yang ada pada Definisi 2.8. Lebih lanjut, karena variabel acak adalah banyaknya unit radar yang tidak mendeteksi gangguan maka pada kasus ini percobaan dikatakan sukses apabila radar tidak dapat mendeteksi.
Sifat 1 : Jelas bahwa percobaan terdiri dari 4 ulangan yang identik.
Sifat 2 : Setiap ulangan hanya akan menghasilkan satu dari hasil, yaitu radar tidak dapat mendeteksi atau radar dapat mendeteksi.
Sifat 3 : Setiap ulangan memiliki peluang sukses yang sama, yaitu . Sifat 4 : Ulangan-ulangan bersifat saling bebas karena setiap unit bekerja secara
independen satu sama lain.
Sifat 5 : Variabel acak adalah banyaknya sukses dalam 4 ulangan.
Definisi 2.9
Variabel acak dikatakan berdistribusi Binomial pada ulangan dengan probabilitas sukses jika dan hanya jika
Contoh 2.7
Terdapat 5000 bola lampu yang diantaranya cacat. Jika diambil sampel sebanyak 5 bola lampu untuk di tes. Tentukan probabilitas banyaknya bola lampu yang rusak paling sedikit satu.
Jawab:
: banyaknya bola lampu yang rusak. Dari soal diketahui bahwa dari bola lampu rusak, berarti terdapat 250 bola lampu yang rusak.
dan .
( ) .
2. Distribusi Probabilitas Kontinu Definisi 2.10
Fungsi adalah fungsi probabilitas (densitas) untuk variabel acak kontinu , jika
1. , untuk semua . 2. ∫ .
Contoh 2.8
Misalkan kesalahan dalam pengiriman pada suatu perusahaan pengiriman adalah variabel acak kontinu yang memiliki fungsi probabilitas densitas
{
Buktikan adalah fungsi probabilitas densitas. Jawab:
Akan dibuktikan memenuhi Definisi 2.10 1. jelas terlihat dari definisi .
2. ∫ ∫ |
Definisi 2.11
[ ] ∑( )
∑[
]
∑ ∑
∑
[ ] [ ] [ ]
Teorema 2.2
Jika adalah variabel acak kontinu dengan distribusi probabilitas dan , , , adalah fungsi dari maka
[ ] [ ] [ ] [ ].
Bukti:
[ ] ∫( )
∫[
]
∫
∫
∫
[ ] [ ] [ ]
Teorema 2.3
Kasus 2: untuk variabel acak kontinu
Karena jumlahan pertama adalah 0 dan menurut Definisi 2.9 diperoleh
Bukti:
[( ) ]
[( ) ]
[
]
[ ]
[ ]
Teorema 2.10
Jika adalah variabel acak binomial pada percobaan dan adalah probabilitas sukses, maka
Akan dibuktikan
Diketahui dari Teorema 2.7 bahwa Selanjutnya akan dicari , yaitu
∑
∑ ( )
∑
Dari bentuk di atas dapat disimpulkan bahwa mencari adalah sulit karena bukanlah faktor dari . Oleh karena itu dapat diperoleh dari [ ]
5. Momen dan Fungsi Pembangkit Momen
∫
Jika berdistribusi normal dengan parameter dan maka
dan .
Bukti:
Pembuktian nilai harapan dan variansi dari Distribusi Normal dibuktikan menggunakan fungsi pembangkit momen dari Distribusi Normal.
Dari Definisi 2.15 dan Teorema 2.11, diperoleh
∫
Metode fungsi pembangkit momen dapat digunakan untuk menentukan fungsi probabilitas.
Teorema 2.13 Teorema Ketunggalan
Misalkan dan adalah fungsi pembangkit momen dari variabel acak dan . Jika kedua fungsi pembangkit momen ada dan untuk semua nilai dari , maka dan mempunyai distribusi probabilitas sama.
Bukti:
Julie, H. (1999). Teorema Limit Pusat Lindenberg dan Terapannya. Skripsi Pada skripsi tersebut, teorema ketunggalan dibuktikan secara umum dengan menggunakan definisi fungsi karakteristik yaitu
( ) dengan adalah bilangan kompleks.
∫
∫
Maka (Skripsi halaman 54).
Berdasarkan teorema ketunggalan terdapat korespondensi satu-satu antara fungsi pembangkit momen dengan fungsi probabilitas.
Contoh 2.17
Misalkan adalah variabel yang berdistribusi normal dengan rata-rata dan variansi . Buktikan bahwa berdistribusi normal standar, yaitu berdistribusi normal dengan dan .
Jawab:
Misal dan berdistribusi normal maka [ ]
[ ]
[ ]
( )
akan sama dengan fungsi pembangkit momen dari Distribusi Normal apabila dan , sehingga menurut Teorema 2.13 berdistribusi normal standar dengan dan .
Teorema 2.14
Misalkan adalah variabel acak yang saling bebas dengan fungsi pembangkit momen . Jika , maka
Misalkan dan merupakan variabel acak diskrit. Fungsi probabilitas untuk dan ditunjukkan sebagai
, .
Definisi 2.18
Misalkan dan merupakan variabel acak dengan fungsi probabilitas bersama, maka
1. untuk semua dan 2. ∑ .
Contoh 2.18
Definisi 2.21
Misalkan dan merupakan variabel acak kontinu dengan fungsi densitas bersama yang dilambangkan dengan , maka
1. untuk semua dan 2. ∫ ∫
Contoh 2.20
Sebuah perusahaan permen mendistrbusikan dus-dus permen yang terdiri atas tiga rasa, yaitu coklat, strawberry, dan jeruk. Terdapat dua jenis permen yang diproduksi, yaitu permen karet dan permen hisap. Misalkan dipilih secara acak satu dus dan variabel acak dan menyatakan persentase dari permen karet dan permen hisap rasa jeruk dengan fungsi densitas bersama sebagai berikut:
{ ,
, lainnya.
Buktikan bahwa fungsi densitas bersamanya memenuhi Definisi 2.21. Jawab:
1. Jelas bahwa untuk semua dan .
2. Akan ditunjukkan bahwa ∫ ∫
∫ ∫ ( ) ∫ |
∫ ( )
|
.
Definisi 2.22
Diketahui variabel diskrit dan yang mempunyai fungsi probabilitas bersama
∑ ∑
Bukti terdapat pada buku Williams, David. (1991). Probability With Martingales. New York: Cambridge University Press. Halaman 185.
Maka fungsi distribusi dari konvergen ke fungsi Distribusi Normal Standar perkalian dari masing-masing fungsi pembangkit momennya (Teorema 2.14), maka
∑
[ ]
Deret Taylor dari adalah
E. Pendugaan Parameter
Dalam melakukan suatu percobaan atau penelitian pada populasi tertentu dibutuhkan sampel yang representatif. Setiap populasi memiliki karakteristik yang dinyatakan dengan sebuah bilangan yang disebut parameter. Tujuan dari percobaan atau penelitian statistik adalah untuk menduga satu atau lebih parameter yang relevan. Contoh dari parameter populasi adalah rata-rata populasi, variansi populasi, dan standar deviasi populasi. Penduga dibagi menjadi dua macam, yaitu penduga titik dan penduga selang.
Definisi 2.24
Sebuah penduga adalah aturan yang biasanya dinyatakan dalam rumus untuk menghitung nilai dari suatu dugaan berdasarkan pengukuran-pengukuran yang terkandung dalam sampel.
1. Penduga Titik
Penduga titik adalah penduga yang menghasilkan suatu nilai sebagai hasil pendugaannya. Penduga selang adalah penduga yang menghasilkan suatu selang sebagai hasil pendugaanya.
Contoh 2.22
Proporsi sampel yang dinyatakan dalam rumus
̂ ∑
merupakan salah satu penduga titik dari proporsi populasi .
Definisi 2.25
Misalkan ̂ adalah sutu penduga titik untuk sebuah parameter . Jika ( ̂) maka ̂ disebut penduga tak bias. Jika ( ̂) maka ̂ disebut penduga bias.
Definisi 2.26
Bias dari suatu penduga titik ̂ dinyatakan dalam sebuah rumus, yaitu ( ̂) ( ̂) .
Definisi 2.27
Rata-rata kuadrat galat dari suatu penduga titik ̂ adalah � ( ̂) [( ̂ ) ]. Contoh 2.23
Misalkan berdistribusi Binomial dengan parameter dan . Buktikan bahwa ̂ adalah penduga tak bias dari .
Jawab:
Menurut Definisi 2.25 berarti harus ditunjukkan bahwa ̂ .
̂ ( )
Jadi terbukti bahwa ̂ adalah penduga tak bias dari
2. Penduga Selang
Penduga selang lebih dikenal dengan selang kepercayaan. Setiap selang kepercayaan mempunyai batas atas atau batas bawah. Batas bawah dan batas atas dari selang kepercayaan disebut dengan limit bawah kepercayaan dan limit atas kepercayaan. Probabilitas bahwa selang kepercayaan akan dekat dengan disebut koefisien kepercayaan.
Jika ̂ dan ̂ adalah limit bawah kepercayaan dan limit atas kepercayaan bagi parameter , maka
( ̂ ̂ )
Selang kepercayaan juga dapat berupa selang kepercayaan satu sisi, seperti
( ̂ )
dengan selang kepercayaannya [ ̂ ] atau
( ̂ )
dengan selang kepercayaannya [ ̂ ].
3. Metode Pivot
Metode pivot merupakan metode yang sangat berguna untuk menentukan selang kepercayaan. Metode pivot bergantung pada suatu nilai yang disebut kuantitas pivot. Kuantitas pivot memiliki dua ciri, yaitu:
a. Merupakan fungsi dari pengukuran sampel dan parameter yang tidak diketahui.
b. Distribusi probabilitas dari kuantitas pivot tidak bergantung pada parameter .
Contoh 2.24
berdistribusi normal dengan tidak diketahui dan . Tentukan selang kepercayaan bagi bila diketahui kuantitas pivotnya adalah
Jawab:
Dari Contoh 2.17 diperoleh yang berarti berdistribusi normal dengan dan sehingga
√
Syarat kuantitas pivot dipenuhi, yaitu:
a. Z merupakan fungsi dari pengukuran sampel dan parameter yang tidak diketahui.
b. Distribusi probabilitas, yaitu tidak bergantung pada parameter . Selang kepercayaan bagi adalah:
Gambar 2.1. Kurva Distribusi Normal dengan
Dari Gambar 2.1 diperoleh
Dari tabel Distribusi Normal (Lampiran 4) diperoleh .
Karena kurva Distribusi Normal adalah kurva yang simetri maka . Jadi,
Substitusi Z diperoleh
Jadi, selang kepercayaan bagi adalah
4. Selang Kepercayaan untuk Sampel Besar
Saat ukuran sampel semakin besar maka semua penduga titik akan mendekati Distribusi Normal. Jika parameter target adalah maka untuk sampel yang besar
mendekati Distribusi Normal Standar. merupakan bentuk kuantitas pivot dan metode pivot dapat digunakan untuk menghasilkan selang kepercayaan bagi parameter target .
Contoh 2.25
Misalkan ̂ berdistribusi normal dengan rata-rata dan standar error ̂. Tentukan selang kepercayaan bagi yang memiliki koefisien kepercayaan sama dengan .
Jawab:
Kuantitas pivot ̂
̂ berdistribusi normal standar.
Gambar 2.2. Kurva Distribusi Normal dengan
( )
Dipilih dua nilai, yaitu dan sehingga
( )
Substitusi ke Persamaan (2.1), maka diperoleh
̂
̂
( ̂ ̂ ̂)
( ̂ ̂ ̂ ̂)
Sehingga diperoleh
̂ ̂ ̂ ̂ ̂ ̂
F. Metode Kemungkinan Maksimum
Dalam membuktikan penduga Kaplan Meier dibutuhkan Metode Kemungkinan Maksimum. Oleh karena itu perlu dipahami mengenai Metode Kemungkinan Maksimum. Misalkan terdapat sebuah kotak yang berisi tiga bola dengan kemungkinan warna dari setiap bola adalah putih atau merah, tetapi jumlah bola yang berwarna putih dan jumlah bola yang berwarna merah tidak diketahui. Pengambilan dua bola secara acak tanpa pengembalian dilakukan. Jika hasil dari pengambilan tersebut adalah dua bolah merah, maka apakah yang akan menjadi dugaan terbaik tentang jumlah bola merah di dalam kotak? Jelas bahwa jumlah bola merah yang ada di dalam kotak harus ada dua bola atau tiga bola. Kasus 1: Jika terdapat dua bola merah dan satu bola putih di dalam kotak, maka probabilitas mengambil dua bola merah secara acak adalah
( )( )
( )
Kasus 2: Jika terdapat tiga bola merah di dalam kotak, maka probabilitas mengambil dua bola merah secara acak adalah
( ) ( )
Dari dua kasus di atas dapat disimpulkan bahwa dugaan terbaik tentang jumlah bola merah di dalam kotak adalah terdapat tiga bola merah di dalam kotak karena kemungkinan mendapatkan dua bola merah lebih tinggi probabilitasnya pada kasus 2 dari pada kasus 1. Dugaan ini memaksimumkan probabilitas pengamatan sampel.
sebuah penduga disebut Metode Kemungkinan Maksimum (Maximum Likelihood).
Definisi 2.28 Fungsi Kemungkinan Likelihood dari Sampel
Misalkan sampel yang diambil dari pengamatan yang berkorespodensi dengan variabel yang distribusinya bergantung pada parameter . merupakan variabel acak diskrit maka Likelihood dari sampel adalah | | atau | | | .
Definisi 2.29 Metode Kemungkinan Maksimum (Maximum Likelihood Method)
Misalkan fungsi Likelihood bergantung pada buah parameter . Metode kemungkinan maksimum memilih penduga nilai-nilai dari parameter-parameter sedemikian sehingga memaksimalkan fungsi kemungkinan | .
Contoh 2.26
Sebuah percobaan Binomial terdiri dari ulangan menghasilkan dengan berarti ulangan ke- sukses dan berarti ulangan ke- gagal. Temukan penduga kemungkinan maksimum bagi .
Jawab:
. Agar mempermudah perhitungan maka dilakukan transformasi ln pada kedua sisi pada persamaan likelihood sehingga diperoleh:
[ ] [ ]
Metode Delta dibutuhkan untuk mencari variansi dari penduga fungsi ketahanan hidup dengan Metode Kaplan Meier. Metode Delta akan menghasilkan [ ( ̂)] dengan ̂ adalah sebuah penduga dari parameter dan adalah sebuah Penyelesaian dari kasus ini adalah mengambil pendekatan linear dari fungsi tersebut.
Mengambil variansi di kedua sisi pada persamaan , maka diperoleh
Menggunakan Teorema 2.8 dan Teorema 2.9, maka penyelesaian dari persamaan adalah
[ ( ̂)] [ ] ( ̂)
Pada kenyataannya tidak diketahui, sehingga didekati dengan ̂. Maka persamaan menjadi
45 BAB III
METODE KAPLAN MEIER
A. Analisis Ketahanan Hidup
Analisis ketahanan hidup adalah kumpulan dari prosedur statistik untuk menganalisis data dengan variabel keluaran yang diperhatikan adalah waktu sampai terjadinya suatu peristiwa atau event.Waktu dalam analisis ketahanan hidup dapat berupa tahun, bulan, minggu, atau hari. Sedangkan suatu peristiwa atau event dalam analisis ketahanan hidup dapat berupa kejadian-kejadian negatif atau positif yang terjadi pada suatu obyek. Obyek dapat berarti manusia, lampu, mobil, hewan atau apapun yang mempunyai waktu hidup. Selanjutnya obyek yang dibahas adalah manusia yang akan disebut individu. Waktu hidup atau survival time adalah waktu dari awal pengamatan hingga terjadinya suatu kejadian. Dalam analisis ketahanan hidup survival time sering disebut dengan waktu kegagalan atau failure time.
B. Fungsi Ketahanan Hidup Definisi 3.1
Fungsi ketahanan hidup atau survival function � adalah probabilitas variabel acak yang merupakan waktu hidup melebihi suatu waktu t. Secara matematis, fungsi ketahanan hidup dapat ditulis
�
Secara teori, berada diantara sampai . Fungsi ketahanan hidup memenuhi tiga sifat. Pertama, fungsi ketahanan hidup merupakan fungsi tak naik. Kedua, saat , � � , artinya awal pengamatan karena belum ada individu yang mengalami suatu peristiwa maka probabilitas ketahanan hidup pada saat itu adalah . Ketiga, saat , � , artinya jika waktu pengamatan bertambah tanpa batas maka tidak ada obyek yang bertahan hidup. Jadi, pada akhirnya kurva fungsi ketahanan hidup akan menuju nol. Pada kenyataannya, ketika digunakan data yang nyata akan diperoleh kurva ketahanan hidup berupa fungsi tangga. Oleh karena waktu pengamatan tidak mungkin menuju tak berhingga, mungkin tidak setiap individu yang diamati akan mengalami peristiwa yang sama sehingga tidak semua fungsi ketahanan hidup akan sama dengan nol pada akhir pengamatan.
Fungsi ketahanan hidup dapat diubah menjadi beberapa bentuk, sebagai berikut:
1. �
2. Jika adalah variabel acak diskrit maka fungsi ketahanan hidup adalah jumlahan dari fungsi probabilitas, yaitu
� ∑ ( )
3. Jika adalah variabel acak kontinu maka fungsi ketahanan hidup adalah integral dari fungsi densitas, yaitu
C. Fungsi Hazard
Suatu kuantitas dasar yang merupakan dasar dalam analisis ketahanan hidup adalah fungsi hazard. Fungsi hazard juga dikenal dengan hazard rate.
Definisi 3.2
� �
� � �
�
� � �
Dari persamaan diperoleh
∫ ∫ �
∫ ∫
�
∫ � |
∫ � �
Karena � maka � , sehingga diperoleh
∫ �
� ∫
Persamaan , , dan menunjukkan bahwa apabila fungsi hazard
diketahui maka fungsi densitas dan fungsi ketahanan hidup � dapat dicari, begitu pula apabila ataupun � yang diketahui maka fungsi hazard
E. Distribusi Waktu Hidup Model Diskrit
Misalkan adalah fungsi probabilitas atau distribusi probabilitas, adalah banyaknya pengamatan, dan adalah variabel acak diskrit dengan , , , adalah nilai dari . Fungsi hazard untuk variabel acak diskrit adalah
( ) ( | )
� ∏ �( ) �( )
Jadi, hubungan antara fungsi ketahanan hidup pada persamaan dan fungsi
hazard pada persamaan , yaitu
� ∏[ ( )]
F. Data Tersensor
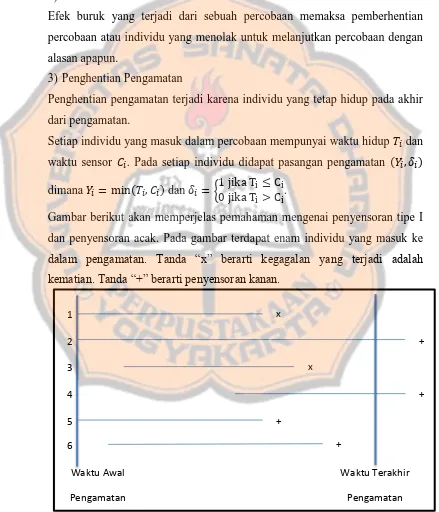
Dalam perhitungan menggunakan metode-metode analisis ketahanan hidup diperlukan data atau yang biasa disebut dengan data ketahanan hidup. Bentuk umum dari data ketahanan hidup adalah mendeskripsikan proses waktu terjadinya suatu kejadian. Bentuk utama dari struktur data ketahanan hidup adalah penyensoran. Biasanya suatu pengamatan ketahanan hidup mempunyai waktu awal mulai pengamatan dan waktu terakhir pengamatan, sehingga pengamat hanya dapat mengamati semua kejadian dan mencatat waktu kejadian selama waktu yang sudah ditentukan. Penyensoran terjadi ketika terdapat individu yang tetap bertahan hidup sampai akhir pengamatan, individu yang hilang dari pengamatan dengan berbagai alasan, atau individu mengikuti pengamatan tidak dari waktu awal. Penyensoran dibagi menjadi beberapa tipe. Tipe-tipe penyensoran dapat dilihat pada diagram dibawah ini.
1. Penyensoran Kanan
Penyensoran kanan terjadi apabila individu telah memasuki proses pengamatan tetapi hilang dari pengamatan. Waktu kejadian sesungguhnya terletak di sebelah kanan dari waktu penyensoran sepanjang sumbu waktu. Penyensoran kanan terbagi menjadi tiga tipe, yaitu penyensoran tipe I, penyensoran acak, dan penyensoran tipe II.
a. Penyensoran Tipe I
Penyensoran ini biasanya terjadi dalam aplikasi yang berkaitan dengan mesin. Setiap individu mulai diamati pada waktu dan mencacat waktu ketahanan hidup setiap individu sampai mengalami kegagalan. Tidak semua individu akan mempunyai waktu kegagalan yang cepat. Terdapat beberapa individu yang membutuhkan waktu yang lama agar individu tersebut mengalami kegagalan. Suatu percobaan biasanya memiliki batas waktu untuk mengamati setiap kejadian yang terjadi pada individu. Hingga batas waktu pengamatan berakhir biasanya ada individu yang belum mengalami kegagalan dan peneliti tidak ingin menambah waktu pengamatan. Waktu terakhir pengamatan dinotasikan dengan yang disebut juga waktu penyensoran. Jika banyaknya individu yang masuk dalam percobaan adalah , maka waktu kegagalan yang harus diamati adalah . Sebagai pengganti dari waktu yang diamati, akan diobservasi dimana
{ .
b. Penyensoran Acak
1) Hilang dari pemeriksaan (Loss to Follow Up)
Individu meninggalkan pengamatan tanpa diketahui alasannya. Waktu ketahanan hidup individu yang sebenarnya tidak diketahui, yang diketahui hanya individu bertahan hidup dari tanggal individu masuk dalam pengamatan sampai individu meninggalkan pengamatan.
2) Keluar
Efek buruk yang terjadi dari sebuah percobaan memaksa pemberhentian percobaan atau individu yang menolak untuk melanjutkan percobaan dengan alasan apapun.
3) Penghentian Pengamatan
Penghentian pengamatan terjadi karena individu yang tetap hidup pada akhir dari pengamatan.
Setiap individu yang masuk dalam percobaan mempunyai waktu hidup dan waktu sensor . Pada setiap individu didapat pasangan pengamatan dimana dan {
.
Misalnya dipilih , sehingga pada umumnya akan terdapat waktu kegagalan. Namun pada penyensoran ini, pengamatan berkahir pada saat waktu kegagalan dari kegagalan ke- terjadi. Jadi, pada percobaan hanya akan diamati pengamatan dalam sampel acak dari item. Pada penyensoran ini pengamatan mungkin saja akan membutuhkan waktu yang lama karena harus menunggu sampai kegagalan ke- terjadi. Namun pengamatan juga dapat berakhir cepat apabila kegagalan ke- terjadi sangat cepat. Misalkan adalah waktu pengamatan berakhir pada saat kegagalan ke- terjadi. Semua individu yang masih bertahan sampai waktu memiliki waktu sensor yaitu . Secara umum penyensoran ini diilustrasikan sebagai berikut:
2. Penyensoran Kiri
pengamatan telah memakai ganja tetapi anak tersebut tidak mengingat waktu pertama memakai ganja maka data dari anak tersebut tersensor kiri.
3. Penyensoran Interval
Pada penyensoran interval waktu hidup hanya terjadi pada suatu interval. Setiap waktu hidup individu, yaitu jatuh dalam interval ] yang merepresentasikan interval waktu dengan merupakan batas bawah waktu penyensoran dan merupakan batas atas waktu penyensoran. Misalkan individu ke- memperlihatkan gejala kegagalan pada waktu pemeriksaan pertama maka dan adalah waktu pemeriksaan selanjutnya. Jika individu tidak memperlihatkan gejala kegagalan sampai waktu pemeriksaan ke- tetapi menunjukkan gejala kegagalan pada waktu ke- maka adalah waktu pemeriksaan ke- dan adalah waktu pemeriksaan ke- . Jika individu tidak menunjukkan gejala kegagalan sampai waktu pemeriksaan terakhir maka adalah waktu pemeriksaan terakhir dan . Waktu ketahanan hidup pada penyensoran interval biasa ditetapkan, misalnya waktu tengah dari interval waktu.
G. Penduga Fungsi Ketahanan Hidup dengan Metode Kaplan Meier
kasus yang disensor sebelum pada kenyataannya bisa saja termasuk dalam kegagalan tanpa diketahui. Solusi untuk masalah tersebut adalah sebagai berikut: Misalkan terdapat waktu yang berbeda dengan . Untuk setiap
, ada individu yang dikatakan berada pada risiko kegagalan. Risiko berarti individu-individu tersebut tidak mengalami kegagalan dan juga belum disensor sebelum waktu ke- . Jika terdapat individu yang tersensor tepat pada waktu ke-maka individu tersebut termasuk dalam risiko pada waktu ke- . Misalkan adalah banyaknya individu yang meninggal pada waktu ke- .
Teorema 3.1
Penduga fungsi ketahanan hidup dengan Metode Kaplan Meier adalah �̂ ∏ banyaknya individu yang berisiko gagal pada waktu ke- .
Selanjutnya akan dicari penduga untuk fungsi hazard dengan mengambil turunan pertama dari [ ] terhadap ( ) sama dengan nol dan menyelesaikan persamaan tersebut untuk ( ).
Langkah 1: Tentunya akan sulit apabila persamaan di atas langsung diturunkan terhadap ( ), sehingga diperlukan cara untuk mengubah persamaan tersebut menjadi persamaan yang lebih sederhana dengan transformasi logaritma.
[ ] ∏ ( ) [ ( )]
∑ [ ( ) ( ) ( ) ]
Penduga variansi untuk penduga Kaplan Meier adalah
[�̂ ] ∑
Selanjutnya menggunakan Metode Delta persamaan diperoleh ̂[ ̂( )] [
̂( )]
̂( )[ ̂( )] [ ̂( )] ̂( )
Pembilang dan penyebut dari persamaan di atas dikalikan dengan sehingga ̂[ ̂( )] [ ̂( )] diperoleh penduga variansi dari penduga Kaplan Meier yaitu
̂[�̂ ] [�̂ ] ∑
( )
Rumus dari penduga variansi untuk penduga Kaplan Meier sering disebut dengan formula Greenwood.
� dan standar eror √ ̂[�̂ ] . Dengan demikian diperoleh kuantitas pivot ̂ √ ̂[ ̂ ] berdistribusi Normal Standar, sehingga menurut persamaan selang kepercayaan untuk � yang memiliki koefisien kepercayaan sama dengan
, yaitu pengobatan sedangkan kelompok 2 adalah kelompok yang diberi pengobatan. Pengamat ingin mengetahui apakah obat yang diberikan kepada penderita leukema dapat memperlambat kematian dengan melihat ketahanan hidup setelah 23 minggu. Berikut adalah data dari setiap pasien dengan tanda + berarti pasien tersebut tersensor.
Waktu kegagalan kelompok 1 secara berurut adalah 1, 1, 2, 2, 3, 4, 4, 5, 5, 8, 8, 8, 8, 11, 11, 12, 12, 15, 17, 22, 23. Waktu kegagalan pada kelompok 2 secara berurut adalah 6, 6, 6, 6+, 7, 9+, 10, 10+, 11+, 13, 16, 17+, 19+, 22, 23, 25+, 32+, 32+, 34+, 35+.
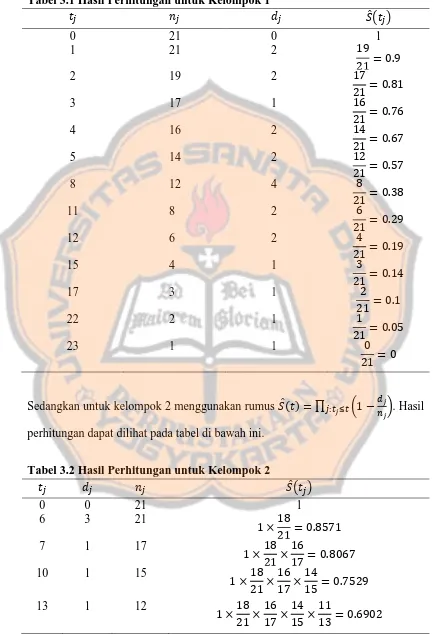
Tabel 3.1 Hasil Perhitungan untuk Kelompok 1 perhitungan dapat dilihat pada tabel di bawah ini.
Tabel 3.2 Hasil Perhitungan untuk Kelompok 2
Contoh 3.3
H. Kurva Ketahanan Hidup Kaplan Meier dengan program R
Dalam perhitungan dengan jumlah data yang banyak maka diperlukan suatu program yang dapat membantu dalam perhitungan. Program R menyediakan
packages yang dapat membantu perhitungan dalam beberapa metode ketahanan hidup. Oleh karena itu perlu diinstal packages“Survival”.
Contoh 3.4
Gambarlah kurva ketahanan hidup kelompok 1 pada Contoh 3.1 Jawab:
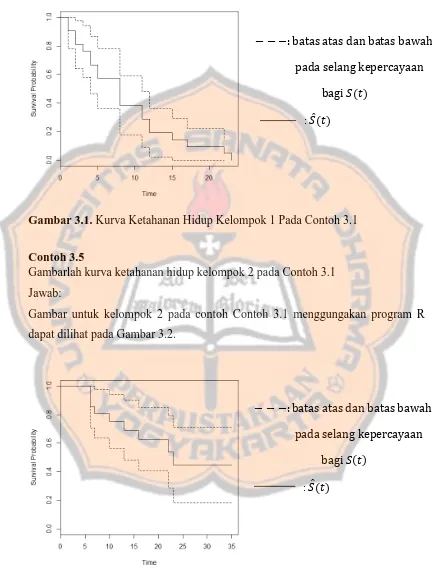
Gambar 3.1. Kurva Ketahanan Hidup Kelompok 1 Pada Contoh 3.1
Contoh 3.5
Gambarlah kurva ketahanan hidup kelompok 2 pada Contoh 3.1 Jawab:
Gambar untuk kelompok 2 pada contoh Contoh 3.1 menggungakan program R dapat dilihat pada Gambar 3.2.
Gambar 3.2. Kurva Ketahanan Hidup Kelompok 2 Pada Contoh 3.1
w
�
: �̂
w
�
Contoh 3.6
Bandingkan Gambar 3.1 dengan Gambar 3.2. Buatlah kesimpulan mengenai kedua gambar tersebut.
Gambar 3.3. Kurva Ketahanan Hidup Kelompok 1 dan Kelompok 2 Pada Contoh 3.1
65 BAB IV
APLIKASI METODE KAPLAN MEIER UNTUK MENDUGA SELANG WAKTU KETAHANAN HIDUP PENDERITA KANKER
A. Kanker
Menurut hasil survei WHO (World Health Organization), Kanker menduduki peringkat kedua penyebab kematian di dunia. Terdapat juta kematian akibat kanker pada tahun . Menurut infoDATIN (Pusat Data dan Informasi Kementerian Kesehatan Republik Indonesia) yang diterbitkan pada Oktober 2016, Kanker adalah pertumbuhan sel-sel dalam jaringan tubuh yang tidak normal. Sel-sel tersebut tidak hanya tumbuh pada satu tempat tetapi dapat menyebar ke bagian tubuh lainnya. Terdapat kurang lebih 15 tipe kanker, di antaranya kanker paru-paru, kanker payudara, kanker kulit, kanker prostat, kanker perut, Sarkoma, Leukimia, dan Limfoma.
Kanker payudara adalah tumor ganas yang terbentuk dari sel-sel payudara yang tumbuh dan berkembang tanpa terkendali sehingga dapat menyebar di antara jaringan atau organ di dekat payudara atau ke bagian tubuh lainnya. Berdasarkan estimasi Globocan, International Agency for Research on Cancer tahun 2012, insiden kanker pada perempuan di Indonesia mencapai 134 per 100.000 penduduk dengan insiden tertinggi pada perempuan adalah kanker payudara sebesar 40 per 100.000 perempuan. Estimasi Globocan angka kematian di Indonesia untuk kanker payudara adalah 16,6 kematian per 100.000 penduduk. Prevalensi kanker payudara tertinggi terdapat di D.I Yogyakarta sebesar 2,4%.
Penyebab kanker pun bermacam-macam, diantaranya faktor keturunan, faktor lingkungan, gaya hidup, dan kebiasaan. Gaya hidup sebagai perokok dan peminum menjadi penyebab kanker. Faktor keturunan berarti seorang penderita kanker mempunyai riwayat penyakit kanker pada keluarganya. Selanjutnya yang akan menjadi fokus utama pembahasan adalah kanker payudara.
dilakukan untuk mengembalikan bentuk payudara setelah kanker diangkat. Terapi radiasi adalah pengobatan menggunakan sinar dengan energi yang tinggi seperti x-ray. Terapi radiasi dilakukan untuk menghancurkan sel kanker. Kemoterapi adalah pengobatan dengan obat-obat yang dapat membunuh sel kanker. Kemoterapi dapat diberikan melalui suntikan obat atau penderita memilih untuk meminum obat secara teratur. Obat-obat berjalan melalui aliran darah menuju sel-sel kanker di dalam tubuh. Banyak efek samping yang diberikan oleh kemoterapi, tetapi antar penderita kanker belum tentu merasakan efek samping yang sama. Efek samping yang diberikan kemoterapi antara lain rambut rontok, mual, kehilangan atau meningkatnya nafsu makan.
Stadium penyakit kanker adalah suatu keadaan dari hasil diagnosa dokter terhadap penderita kanker, sejauh mana penyebaran kanker ke jaringan tubuh lainnya. Stadium hanya dikenal pada tumor ganas atau kanker dan tidak ada pada tumor jinak. Dalam penentuan stadium perlu dilakukan pemeriksaan klinis dan ditunjang dengan pemeriksaan lainnya seperti USG, rontgen, CT Scan, dan lain-lain. Banyak sekali cara untuk menetukan stadium, namun cara menetukan stadium yang paling banyak dianut saat ini adalah stadium kanker berdasarkan klasifikasi sistem TNM yang direkomendasikan oleh IUCC (International Union Against Cancer) dari WHO (World Health Organization) atau AJCC (American Joint Committe On Cancer) yang di sponsori oleh American Cancer Society dan
American College of Surgeons.
masih dapat digerakkan, N2 berarti ada metastatis ke kelenjar getah bening ketiak yang sulit digerakkan, dan N3 berarti ada metastatis ke kelenjar getah bening di atas tulang selangka atau pada kelenjar getah bening di mammary interna di dekat tulang sternum. Penilaian TNM untuk penyebaran jauh, yaitu Mx berarti mestatis jauh belum dapat dinilai, M0 berarti tidak terdapat metastatis jauh, dan M1 berarti terdapat metastatis jauh.
Selanjutnya ketiga faktor digabungkan dan diperoleh delapan stadium kanker sebagai berikut (Dipiro, Joseph T, et al. (2011). Pharmacotherapy. 8th
5. Stadium III A : T0N2M0/ T1N2M0/ T2N2M0/ T3N1M0 6. Stadium III B : T4N0M0/ T4N1M0/ T4N2M0
7. Sadium III C : Tiap T-N3M0 8. Stadium IV : Tiap T-Tiap N-M1.
B. Proses Pengambilan Sampel
Di bagian rekam medis Rumah Sakit Panti Rapih terdapat dua bagian, yaitu bagian komputer dan bagian rekam medis. Terdapat peraturan yang dibuat oleh Rumah Sakit Panti Rapih dalam melihat rekam medis dari pasien, yaitu pada hari selasa sampai sabtu peneliti hanya diperbolehkan melihat 10 rekam medis pasien per hari. Oleh karena terdapat 483 pasien kanker payudara pada tahun 2014-2016 di Rumah Sakit Panti Rapih, maka penulis membutuhkan sampel yang akan digunakan untuk menghitung ketahanan hidup pasien kanker payudara pada beberapa stadium. Semua pasien kanker payudara berjenis kelamin wanita.
2793 data. Data tersebut masih sangat acak karena data yang diberikan berdasarkan tanggal masuk dan keluar RS sehingga untuk pasien yang datang ke rumah sakit lebih dari satu kali, data dari pasien tersebut akan berulang. Sebagai contoh, misalkan individu A datang ke RS pada tanggal 20 Januari 2014 dan 8 Juni 2014, maka data individu A akan terulang lagi pada tanggal 8 Juni. Oleh karena itu, penulis mengurutkan data berdasarkan nomor pasien. Selanjutnya, penulis memilih tanggal masuk paling awal dan tanggal keluar paling lama untuk setiap pasien, sedangkan untuk status terakhir pasien penulis mengambil status terakhir pada tanggal keluar paling lama. Sebagai contoh, individu A masuk ke RS pada tanggal 20 Januari 2014 dan keluar dari RS pada tanggal 25 Januari 2014 dengan status terakhir obat jalan. Kemudian individu A masuk lagi ke RS pada tanggal 8 Juni 2014 dan keluar pada tanggal 9 Juni 2014 dengan status meninggal, maka untuk individu A penulis mengambil tanggal masuk RS yaitu 20 Januari 2014 dan tanggal keluar RS 9 Juni 2014 dengan status terakhir meninggal. Setelah mengelompokkan semua data, penulis mendapat 483 data pasien kanker payudara di Rumah Sakit Panti Rapih tahun 2014-2016. Selanjutnya, penulis meminta data pasien yang mengikuti kemoterapi dan pasien yang tidak mengikuti kemoterapi pada bagian komputer dan memasukkan data tersebut kepada data yang sudah dikelompokkan. Kemudian untuk mengetahui waktu hidup pasien, penulis mengurangi tanggal keluar pasien dengan tanggal masuk pasien, sehingga diperoleh 483 data yang terdiri dari 168 pasien kanker payudara yang mengikuti kemoterapi dan 315 pasien kanker payudara yang tidak mengikuti kemoterapi (Lampiran 6).
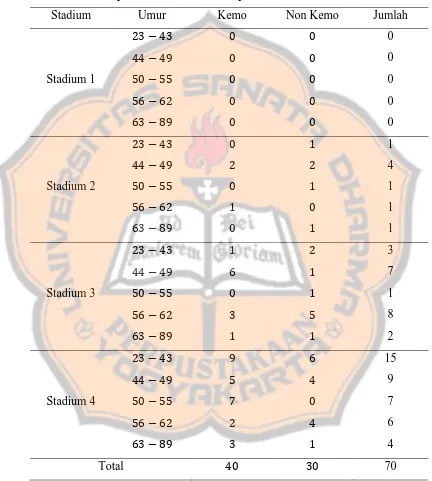
kemoterapi. Ukuran kertas kurang lebih 3.7 cm x 2.4 cm. Pada kenyataannya terdapat 118 sampel yang terambil diantaranya 54 pasien kanker payudara yang mengikuti kemoterapi dan 64 pasien kanker payudara yang tidak mengikuti kemoterapi. Oleh karena keterbatasan penulis, yaitu penulis tidak bisa membaca tulisan dokter, apabila bagi pasien yang rekam medisnya tidak ada keterangan stadium atau klasifikasi “TNM” (lihat Bab IV bagian A) dalam bentuk print dari komputer maka data stadium dari pasien tersebut tidak dimasukkan ke dalam sampel. Penulis mendapat 70 sampel pasien yang diketahui stadiumnya diantaranya 40 pasien yang mengikuti kemoterapi dan 30 pasien yang tidak mengikuti kemoterapi.
Tabel 4.1 memperlihatkan banyaknya penderita kanker dalam 5 (lima) kategori kelompok umur.
meliputi stadium IV. Tabel 4.2 memperlihatkan jumlah sampel yang telah dibagi ke dalam 5 kelompok umur dan 4 kelompok stadium.
Tabel 4.2. Pengelompokan Sampel Pasien Kanker Payudara Berdasarkan 5 Kelompok Umur dan 4 Kelompok Stadium.
mulai stadium 2. Selanjutnya, terdapat 8 pasien kanker payudara pada stadium 2, 21 pasien kanker payudara pada stadium 3, dan 41 pasien kanker payudara pada stadium 4. Hal ini berarti pasien kanker payudara paling banyak sudah mencapai stadium 4. Pada rentang umur 44-49 total pasien kanker payudara yang masuk ke dalam sampel sebanyak 20. Hal ini berarti pasien kanker payudara yang masuk ke dalam sampel paling banyak berada pada rentang umur 44-49.
C. Ketahanan Hidup Pasien Kanker Payudara
Dalam Perhitungan aplikasi pendugaan ketahanan hidup dengan Metode Kaplan Meier pada pasien kanker payudara menggunakan Teorema 3.1 (Persamaan 3.15), yaitu
�̂ ∏
dengan:
�̂ : peluang bertahan hidup pasien kanker payudara lebih dari waktu , : banyaknya pasien kanker payudara yang meninggal pada waktu ke- ,
: banyaknya pasien kanker payudara yang berada pada risiko kegagalan waktu ke- .
Dalam penentuan penduga variansi digunakan Teorema 3.2 (Persamaan 3.16), yaitu
̂[�̂ ] [�̂ ] ∑
( )
Dalam perhitungan selang kepercayaan digunakan persamaan 3.17 dengan , sehingga persamaan 3.17 menjadi
�̂ √ ̂[�̂ ] � �̂ √ ̂[�̂ ]
Selanjutnya penulis akan menghitung peluang bertahan hidup hingga selang kepercayaan bagi � pasien kanker payudara di Rumah Sakit Panti Rapih Yogyakarta.
1. Ketahanan Hidup Pasien Kanker Payudara Tahun 2014-2016
Pada bagian ini, penulis akan menghitung ketahanan hidup pasien kanker payudara secara keseluruhan pada tahun 2014-2016 tanpa membedakan pasien yang mengikuti kemoterapi atau tidak dan stadium pasien. Penulis melakukan perhitungan menggunakan program R. Data pasien kanker payudara tahun 2014-2016 dapat dilihat pada Lampiran 6. List program perhitungan juga dapat dilihat pada Lampiran 8.
Hasil perhitungan ketahanan hidup disajikan pada Tabel 4.3, sedangkan perhitungan secara keseluruhan terdapat pada Lampiran 8. Kurva ketahanan hidup pasien kanker payudara pada tahun 2014-2016 disajikan dalam Gambar 4.1.
Gambar 4.1. Kurva Ketahanan Hidup Pasien Kanker Payudara Tahun 2014-2016.
Menurut persamaan diperoleh hasil yang dapat dilihat pada Tabel 4.3. Pada Tabel 4.3 dapat dilihat bahwa �̂ dengan selang kepercayaan yang memiliki batas bawah dan batas atas . Hal ini berarti peluang bertahan hidup pasien kanker payudara untuk semua stadium dan perlakuan (kemo dan tidak kemo) melebihi hari berada pada selang [ ] yang secara kurva dapat dilihat pada Gambar 4.1. Pada Gambar 4.1 dapat dilihat bahwa kurva ketahanan hidup pasien kanker payudara secara keseluruhan turun lambat.
2. Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi Pada bagian ini, penulis akan menghitung ketahanan hidup pasien kanker payudara yang mengikuti pengobatan berupa kemoterapi di Rumah Sakit Panti Rapih tahun 2014-2016. Hasil perhitungan ketahanan hidup disajikan pada Tabel 4.4, sedangkan perhitungan secara keseluruhan terdapat pada Lampiran 9. Kurva ketahanan hidup pasien kanker payudara yang mengikuti kemoterapi pada tahun 2014-2016 disajikan dalam Gambar 4.2.
w
�
Tabel 4.4. Hasil Perhitungan Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi Tahun 2014-2016
�̂( ) Batas Bawah
Batas Atas
38 146 1 0.993 0.980 1.000
53 137 1 0.986 0.966 1.000
65 135 1 0.979 0.955 1.000
77 127 1 0.971 0.943 0.999
90 120 1 0.963 0.931 0.995
92 118 1 0.955 0.919 0.990
99 117 1 0.946 0.908 0.985
134 102 1 0.937 0.895 0.980
157 85 1 0.926 0.879 0.973
162 82 1 0.915 0.863 0.966
171 77 1 0.903 0.847 0.959
198 69 1 0.890 0.829 0.950
231 60 1 0.875 0.809 0.941
294 50 1 0.858 0.784 0.931
463 24 1 0.822 0.724 0.920
497 19 1 0.779 0.654 0.903
580 11 1 0.708 0.534 0.882
589 10 1 0.637 0.433 0.842
667 7 1 0.546 0.305 0.787
766 5 1 0.437 0.165 0.708
Gambar 4.2. Kurva Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi Tahun 2014-2016.
Menurut persamaan diperoleh hasil yang dapat dilihat pada Tabel 4.4. Pada Tabel 4.4 dapat dilihat bahwa �̂ dengan selang kepercayaan yang memiliki batas bawah dan batas atas . Hal ini berarti peluang hidup pasien kanker payudara yang mengikuti kemoterapi melebihi hari berada pada selang [ ] yang secara kurva dapat dilihat pada Gambar 4.2. Pada Gambar 4.2 dapat dilihat bahwa kurva ketahanan hidup pasien kanker payudara yang mengikuti kemoterapi turun lambat.
3. Ketahanan Hidup Pasien Kanker Payudara yang Tidak Mengikuti Kemoterapi
Pada bagian ini, penulis akan menghitung ketahanan hidup pasien kanker payudara yang tidak mengikuti pengobatan berupa kemoterapi di Rumah Sakit Panti Rapih tahun 2014-2016. Hasil perhitungan ketahanan hidup disajikan pada Tabel 4.5, sedangkan hasil perhitungan secara keseluruhan terdapat pada Lampiran 10. Kurva ketahanan hidup pasien kanker payudara yang tidak mengikuti kemoterapi pada tahun 2014-2016 disajikan dalam Gambar 4.3.
w
�
Gambar 4.3. Kurva Ketahanan Hidup Pasien Kanker Payudara yang Tidak Mengikuti Kemoterapi Tahun 2014-2016.
Pada hasil perhitungan yang terdapat pada Tabel 4.5 dijumpai NaN (Not a Number) yang berarti bagian tersebut tidak dapat dihitung. Menurut persamaan diperoleh hasil yang dapat dilihat pada Tabel 4.5. Pada Tabel 4.5 dapat dilihat bahwa �̂ . Hal ini berarti peluang hidup pasien kanker payudara melebihi hari adalah . Pada kasus ini selang kepercayaan untuk tidak dapat dicari karena akan terjadi pembagian dengan nol pada persamaan . Apabila dilihat dari kurva pada Gambar 4.3, terlihat bahwa kurva ketahanan hidup pasien kanker payudara yang tidak mengikuti kemoterapi turun cepat sampai . Saat sampai kurva ketahanan hidup stabil. Hal ini disebabkan karena tidak adanya pasien yang meninggal pada rentang waktu . Saat kurva ketahanan hidup turun tajam ke . Hal ini disebabkan karena pada saat jumlah individu yang meninggal dan individu yang masih bertahan hidup sama, yaitu . Hal ini berarti peluang bertahan hidup pasien kanker payudara yang tidak mengikuti kemoterapi lebih dari 883 hari kecil.
w
�
4. Perbandingan Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi dengan Pasien yang Tidak Mengikuti Kemoterapi
Pada bagian ini, penulis membandingkan peluang bertahan hidup pasien kanker payudara yang mengikuti kemoterapi dengan pasien kanker payudara yang tidak mengikuti kemoterapi di Rumah Sakit Panti Rapih tahun 2014-2016. Perbandingan peluang bertahan hidup dapat dilihat dari hasil pada Tabel 4.4 dan 4.5 serta kurva ketahanan hidup pada Gambar. 4.4.
Gambar 4.4. Kurva Perbandingan Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti dan Tidak Mengikuti Kemoterapi Tahun 2014-2016.
5. Ketahanan Hidup Pasien Kanker Payudara Stadium 2
Pada bagian ini, penulis akan menghitung ketahanan hidup pasien kanker payudara stadium 2 menggunakan sampel yang telah diambil. Data pasien kanker payudara dapat dilihat pada Lampiran 7. Pada saat pengambilan sampel, tidak diperoleh pasien yang meninggal dengan stadium terakhir dari pasien tersebut adalah stadium 2. Hal tersebut menyebabkan peluang bertahan hidup pasien kanker payudara stadium 2 yang mengikuti kemoterapi maupun tidak mengikuti kemoterapi tidak dapat dihitung. Perhitungan yang dimungkinkan adalah saat akan memperoleh �̂ . Hal ini tidak mempunyai arti yang bermakna karena �̂ menyatakan kondisi awal pada saat penelitian. Kondisi �̂
juga berlaku untuk pasien kanker payudara stadium 2 yang mengikuti kemoterapi dan yang tidak mengikuti kemoterapi.
6. Ketahanan Hidup Pasien Kanker Payudara Stadium 3
Data dari pasien kanker payudara stadium 3 dapat dilihat pada Lampiran 7. Pada saat pengambilan sampel, tidak diperoleh pasien yang meninggal pada stadium 3. Hal tersebut mengakibatkan hal yang sama pada stadium 2, yaitu perhitungan peluang bertahan hidup pada suatu waktu tidak dapat dilakukan kecuali pada saat . Pada saat memperoleh �̂ . �̂ menyatakan kondisi awal saat penelitian dan juga berlaku untuk pasien kanker payudara stadium 3 yang mengikuti kemoterapi dan yang tidak mengikuti kemoterapi. Oleh karena itu, hasil �̂ tidak mempunyai arti yang bermakna.
7. Ketahanan Hidup Pasien Kanker Payudara Stadium 4
a. Ketahanan Pasien Kanker Payudara Stadium 4 yang Mengikuti Kemoterapi
Tabel 4.6. Hasil Perhitungan Ketahanan Hidup Pasien Kanker Payudara yang Mengikuti Kemoterapi
Gambar 4.5. Kurva Kelangsugan Hidup Pasien Kanker Payudara Stadium 4 yang Mengikuti Kemoterapi.
w
�