Analisis fraktal garis pantai di Yogyakarta

(1)

ANALISIS FRAKTAL GARIS PANTAI DI YOGYAKARTA

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Pendidikan

Program Studi Pendidikan Matematika

Oleh :

Yosep Cahyo Ardi

NIM : 131414029

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

i

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Pendidikan

Program Studi Pendidikan Matematika

Oleh :

Yosep Cahyo Ardi

NIM : 131414029

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(3)

ii

SKRIPSI

Oleh :

Yosep Cahyo Ardi

Telah disetujui oleh :

Pembimbing

(4)

iii

SKRIPSI

Dipersiapkan dan ditulis oleh :

Yosep Cahyo Ardi

NIM : 131414029

Telah dipertahankan di depan panitia penguji

pada tanggal 15 Juni 2017

dan dinyatakan memenuhi syarat

Susunan Panitia Penguji

Nama Lengkap Tanda Tangan

Ketua : Dr. Marcellinus Andy Rudhito, S.Pd. ...

Sekretaris : Dr. Hongki Julie, M.Si. ...

Anggota I : Beni Utomo, M.Sc. ...

Anggota II : Dra. Haniek Sri Pratini, M.Pd. ...

Anggota III : Febi Sanjaya, M.Sc. ...

Yogyakarta, 15 Juni 2017

Fakultas Keguruan dan Ilmu Pendidikan

Universitas Sanata Dharma

Dekan,

(5)

iv

HALAMAN PERSEMBAHAN

Energi Mengikuti Imajinasi

(Albert Einstein)

... Janganlah kuatir akan hidupmu, akan apa yang hendak kamu makan, dan

janganlah kuatir pula akan tubuhmu, akan apa yang hendak kamu pakai.

(Lukas, 12 : 22)

Kupersembahkan untuk :

Tuhan Yesus

Bunda Maria

Ibuku Tarmi dan bapakku Haryono

(6)

v

PERNYATAAN KEASILAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak

memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam

kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Penulis

(7)

vi

ABSTRAK

Yosep Cahyo Ardi, 2017. Analisis Fraktal Garis Pantai di Yogyakarta. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan. Universitas Sanata Dharma.

Garis pantai memiliki bentuk yang tidak beraturan, karena tetidakteraturannya sulit untuk menentukan panjang garis pantai secara tepat. Garis pantai mempunyai pola-pola yang mirip dengan bangun- bangun fraktal. Garis pantai yang utuh dapat didekati dengan mengulangi pola-pola dasar sehingga mendekati bentuk garis pantai aslinya. Berdasarkan sifat kemiripan yang sesuai dengan sifat fraktal yaitu self similarity, maka penelitian ini menggunakan pendekatan fraktal. Metode yang digunakan adalah pengolahan citra satelit yang diambil dari Google Maps. Gambar garis pantai Yogyakarta terlebih dahulu dipotong-potong sesuai dengan karakteristiknya. Kemudian, dicari dimensi fraktalnya untuk tiap-tiap bagian menurut metode Dimensi Kotak dengan beberapa nilai Penghitungan dilakukan dengan bantuan

software MATLAB. Hasil dimensi fraktal inilah yang akan digunakan untuk menentukan nilai prediksi panjang garis pantai di Yogyakarta.

Hasil penelitian menunjukkan prediksi panjang garis pantai Yogyakarta adalah 134 . Panjang garis pantai berdasarkan pengukuran langsung menggunakan Google Maps adalah 127 yang artinya selisih 7 atau dengan nilai galat 5,51%. Menurut Badan Lingkungan Hidup Daerah Istimewa Yogyakarta (BLH DIY) panjang garis pantai Yogyakarta adalah 113 , yang berarti bahwa selisih 21 atau dengan nilai galat 18,58%. Prediksi dengan pendekatan fraktal ini memberikan arti bahwa panjang garis pantai Yogyakarta lebih panjang 5,51% dari pengukuran langsung dengan Google Maps, dan lebih panjang 18,58% dari data panjang garis pantai Yogyakarta berdasarkan BLH DIY.

(8)

vii

ABSTRACT

Yosep Cahyo Ardi, 2017. Fractal Analysis of Coastline in Yogyakarta. Thesis Mathematics Education Study Program, Mathematics and Sciene Education Department, Faculty of Teacher Training and Education. Sanata Dharma University.

The coastline has irregular shape, since it is difficult to determine the exact length of the coastline. The coastline has patterns that are similar to fractal builds. The intact coastline can be approached by repeating the basic patterns so as to approximate the shape of the original coastline. Based on the similarity characteristic in accordance with fractal characteristic is self similarity, this research uses fractal approach. The method used is the processing of satellite images taken from Google Maps. The image of Yogyakarta’s coastline first cut into pieces according to their characteristics. Then, looking for the fractal dimension for each section according to the Box Dimension method with multiple values . The calculation is done by using

MATLAB software. The result of this fractal dimension will be used to determine the predicted value of coastline length in Yogyakarta.

The result shows that the predicted length of Yogyakarta’s coastline is 134 . The length of the coastline based on the direct measurement using Google Maps is 127 which means the difference of 7 or with the error rate of 5,51 %. According to Yogyakarta’s Environment Agency (BLH DIY) the length of Yogyakarta’s coastline is 113 , which means that the difference is 21 with an error rate of 18,58 %. The prediction with this fractal approach gives the mean that the long of Yogyakarta’s coastline is 5,51% longer than the direct measurement with Google Maps, and 18,58% longer than the long coastline data of Yogyakarta based on BLH DIY.

(9)

viii

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma :

Nama : Yosep Cahyo Ardi

NIM : 131414029

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan

Universitas Sanata Dharma karya ilmiah yang berjudul :

Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata

Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain,

mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan

mempublikasikan di internet atau media lain untuk kepentingan akademis tanpa

meminta ijin dari saya maupun memberikan royalty kepada saya selama tetap

mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya.

Yang menyatakan

(10)

ix

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa yang

telah melimpahkan berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan

skripsi yang berjudul “Analisis Fraktal Garis Pantai di Yogyakarta” ini dengan

baik dan tepat waktu. Skripsi ini disusun untuk memenuhi salah satu syarat

memperoleh gelar Sarjana Pendidikan.

Dalam penulisan skripsi ini, penulis menemui banyak masalah yang

menghambat penulisan. Penulis menyadari skripsi ini tidak akan selesai dengan

baik tanpa dukungan dan doa dari berbagai pihak. Oleh karena itu, penulis ingin

menyampaikan ucapan terima kasih kepada :

1. Bapak Rohandi, Ph.D. selaku dekan Fakultas Keguruan dan Ilmu Pendidikan,

Universitas Sanata Dharma Yogyakarta.

2. Bapak Dr. Hongki Julie, M.Si. selaku Ketua Program Studi Pendidikan

Matematika, Universitas Sanata Dharma Yogyakarta.

3. Bapak Beni Utomo, M.Sc. selaku dosen pembimbing skripsi yang juga

sekaligus dosen pembimbing akademik yang telah bersedia meluangkan

waktu, tenaga, dan masukan selama penulisan skripsi dan selama penulis

menjalani kuliah di Program Studi Pendidikan Matematika Universitas Sanata

Dharma Yogyakarta.

4. Bapak dan ibu dosen Program Studi Pendidikan Matematika Universitas

Sanata Dharma yang telah mendidik penulis selama kuliah di Pendidikan

(11)

x

5. Seluruh staf sekretariat JPMIPA Universitas Sanata Dharma yang telah

membantu dalam hal administrasi.

6. Perpustakaan Universitas Sanata Dharma yang telah menyediakan buku-buku

yang menunjang perkuliahan selama kuliah di Program Studi Pendidikan

Matematika Universitas Sanata Dharma Yogyakarta.

7. Kedua orang tua penulis Ibu Tarmi dan Bapak Haryono yang telah

membiayai kuliah, mendukung, memberi semangat, dan berdoa untuk

kesuksesan penulis.

8. Van Deventer-maas Stichting yang telah membantu membiayai kuliah dalam

bentuk beasiswa.

9. Kakek penulis Mbah Mitro dan keluarga besar Mbah Mitro yang telah

mendukung, dan berdoa untuk penulis.

10. Saudara sepupu penulis Nidia yang telah meminjamkan laptop selama penulis

menulis skripsi.

11. Teman-teman seperjuangan Dhevin, Dora, Emi, Tri, Ipo, Dina, Gerar, dan

Ardian yang telah memberi dukungan, semangat, dan motivasi.

12. Teman-teman Pendidikan Matematika Kelas A yang telah berdinamika

berbagi pengetahuan suka, dan duka selama kuliah.

13. Teman-teman Pendidikan Matematika angkatan 2013 yang telah berdinamika

berbagi pengetahuan suka, dan duka selama kuliah.

14. Teman-teman UKM Seni Karawitan yang telah berbagi pengetahuan tentang

(12)

xi

15. Teman-teman PPL yang telah memberikan semangat dan dukungan Ines,

Shella, Ana, Clara, Agnes, Stephani, dan Br. Anton.

16. Semua pihak yang telah bermurah hati membantu penulis selama kuliah dan

selama menulis skripsi yang tidak dapat disebutkan satu persatu.

Penulis

(13)

xii

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASILAN KARYA ... v

ABSTRAK ... vi

ABSTRACT ... vii

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xii

DAFTAR TABEL ... xiv

DAFTAR GAMBAR ... xv

DAFTAR LAMPIRAN ... xx

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 5

C. Batasan Masalah... 5

D. Tujuan Penelitian ... 5

E. Manfaat Penelitian ... 6

F. Metode Penelitian... 6

G. Sistematika Penulisan ... 8

(14)

xiii

A. Ruang Metrik ... 10

B. Ruang Fraktal ... 33

C. Transformasi ... 37

D. Sistem Fungsi Iterasi ... 41

BAB III ANALISIS FRAKTAL ... 49

A. Regresi Linear ... 49

B. Dimensi Fraktal ... 52

BAB IV ANALISIS FRAKTAL GARIS PANTAI DI YOGYAKARTA... 73

A. Dimensi Fraktal Garis Pantai Yogyakarta... 74

B. Prediksi Panjang Garis Pantai Yogyakarta ... 88

BAB V PENUTUP ... 91

A. Kesimpulan ... 91

B. Saran ... 92

DAFTAR PUSTAKA ... 94

(15)

xiv

DAFTAR TABEL

Tabel 3.1 Contoh data hasil penelitian ... 51

Tabel 3.2 Nilai residual dari contoh hasil penelitian... 51

Tabel 3.3 Perolehan jumlah selimut- untuk Citra Lena ... 71

Tabel 3.4 Nilai residual masing-masing untuk Citra Lena ... 72

Tabel 4.1 Perolehan jumlah selimut- untuk garis pantai bagian I ... 75

Tabel 4.2 Perolehan jumlah selimut- untuk garis pantai bagian II ... 77

Tabel 4.3 Perolehan jumlah selimut- untuk garis pantai bagian III ... 79

Tabel 4.4 Perolehan jumlah selimut- untuk garis pantai bagian IV ... 81

Tabel 4.5 Perolehan jumlah selimut- untuk garis pantai bagian V ... 83

Tabel 4.6 Perolehan jumlah selimut- untuk garis pantai bagian VI ... 85

Tabel 4.7 Perolehan jumlah selimut- untuk garis pantai bagian VII ... 87

Tabel 4.8 Prediksi panjang garis pantai untuk tiap-tiap bagian ... 89

(16)

xv

DAFTAR GAMBAR

Gambar 1.1 (a) Segitiga Sierpinski ... 4

Gambar 1.1 (b) Kurva Koch... 4

Gambar 2.1 Contoh afinitas ... 39

Gambar 2.2 Contoh similaritas ... 40

Gambar 2.3 (a) Ilustrasi algoritma Deterministik untuk Segitiga Sierpinski... 47

Gambar 2.3 (b) Ilustrasi algoritma Random Iterasi untuk Segitiga Sierpinski ... 47

Gambar 3.1 Himpunan Cantor ... 59

Gambar 3.2 Segitiga Sierpinski ... 61

Gambar 3.3 Kurva Von Koch ... 63

Gambar 3.4 Karpet Sierpinski ... 66

Gambar 3.5 (a) Citra Asli Lena ... 69

Gambar 3.5 (b) Citra Biner Lena dengan deteksi tepi Canny ... 69

Gambar 3.6 Diagram Alir pencacahan selimut ... 69

Gambar 3.7 List program pencacahan selimut untuk Citra Lena... 70

Gambar 3.8 Garis Regresi untuk dimensi citra Lena ... 71

Gambar 3.9 Nilai residual untuk citra Lena ... 72

Gambar 4.1 (a) Garis pantai Yogyakarta via google maps ... 74

Gambar 4.1 (b) Pemotongan garis pantai menjadi 7 bagian ... 74

Gambar 4.2 (a) Garis Pantai bagian I setelah diedit dengan Photo Scape ... 75

Gambar 4.2 (b) Citra biner garis pantai bagian I dengan deteksi tepi Canny ... 75

(17)

xvi

Gambar 4.4 Nilai residual untuk garis pantai bagian I ... 76

Gambar 4.5 (a) Garis Pantai bagian II setelah diedit dengan Photo Scape ... 77

Gambar 4.5 (b) Citra Biner garis pantai bagian II dengan deteksi tepi Canny .... 77

Gambar 4.6 Garis Regresi untuk dimensi garis pantai bagian II ... 78

Gambar 4.7 Nilai residual untuk garis pantai bagian II ... 78

Gambar 4.8 (a) Garis pantai bagian III setelah diedit dengan Photo Scape ... 79

Gambar 4.8 (b) Citra biner garis pantai bagian III dengan deteksi tepi Canny ... 79

Gambar 4.9 Garis Regresi untuk dimensi garis pantai bagian III ... 80

Gambar 4.10 Nilai residual log untuk garis pantai bagian III ... 80

Gambar 4.11(a) Garis pantai bagian IV setelah diedit dengan Photo Scape ... 81

Gambar 4.11(b) Citra biner garis pantai bagian IV dengan deteksi tepi Canny ... 81

Gambar 4.12 Garis Regresi untuk dimensi garis pantai bagian IV ... 82

Gambar 4.13 Nilai residual untuk garis pantai bagian IV ... 82

Gambar 4.14(a) Garis pantai bagian V setelah diedit dengan Photo Scape ... 83

Gambar 4.14(b) Citra biner garis pantai bagian V dengan deteksi tepi Canny ... 83

Gambar 4.15 Garis Regresi untuk dimensi garis pantai bagian V ... 84

Gambar 4.16 Nilai residual untuk garis pantai bagian V ... 84

Gambar 4.17(a) Garis Pantai bagian VI setelah diedit dengan Photo Scape ... 85

Gambar 4.17(b) Citra Biner garis pantai bagian VI dengan deteksi tepi Canny ... 85

Gambar 4.18 Garis Regresi untuk dimensi garis pantai bagian VI ... 86

Gambar 4.19 Nilai residual untuk garis pantai bagian VI ... 86

Gambar 4.20(a) Garis pantai bagian VII setelah diedit dengan Photo Scape ... 87

(18)

xvii

Gambar 4.21 Garis Regresi untuk dimensi garis pantai bagian VII ... 88

(19)

xviii

DAFTAR SIMBOL

: Himpunan semua bilangan real

: Himpunan semua bilangan asli

: Jarak titik ke titik

: Untuk semua

: Elemen

: Tidak sama dengan

: Tak hingga

: Ruang dimensi atas bilangan real

: Barisan

_{: Barisan pemetaan-pemetaan kontraksi}

: Bola terbuka di dengan jari-jari , berpusat di

̅ : Bola tertutup di dengan jari-jari , berpusat di

: Himpunan bagian

: Himpunan bagian sejati

: Gabungan

: Irisan

: Himpunan kosong

� � : � � untuk suatu , Himpunan semua titik

interior �

: yang memenuhi himpunan semua titik

limit

(20)

xix : Bukan elemen

̅ : Himpunan titik closure

: � � � kompak , keluarga himpunan bagian tak kosong

yang kompak dari

� : � � jarak Hausdorff antara titik � dan di

: Skalar bernilai real

� : Dimensi Hausdorff-Besicovitch �

: Nilai pendekatan

: Implikasi kiri ke kanan

: Implikasi kanan ke kiri

: Dimensi Kotak bawah

: Dimensi Kotak atas

: Jumlah minimum selimut berukuran yang dapat menyelimuti

(21)

xx

DAFTAR LAMPIRAN

List Program Tampilan GUI (Graphical User Interface) MATLAB ... 96

(22)

1

BAB I PENDAHULUAN

A. Latar Belakang

Yogyakarta adalah salah satu tempat destinasi wisata populer di

Indonesia. Yogyakarta memiliki keindahan panorama pantai yang indah.

Secara umum pantai di Yogyakarta terbagi menjadi 3 wilayah pantai yaitu :

Kulon Progo, Bantul, dan Gunung Kidul. Berdasarkan yogyalagi.com Kulon

Progo memiliki 4 pantai, Bantul memiliki 8 pantai, sedangkan Gunung Kidul

berdasarkan noyvesto.net memiliki 70 pantai. Kulon Progo dan Bantul

tersusun oleh dataran Aluvial, sedangkan di Gunung Kidul berupa kawasan

perbukitan Batu Gamping.

Garis Pantai adalah pertemuan antara daratan dengan lautan yang

dipengaruhi oleh pasang surut air laut (UU No 4 Tahun 2011). Garis pantai

memiliki bentuk yang tak beraturan. Pembentukan garis pantai ini

dipengaruhi oleh faktor abrasi dan struktur batuan. Panjang garis pantai

dahulu dengan panjang garis pantai pada masa sekarang mungkin berbeda.

Hai ini dikerenakan faktor abrasi dan struktur batuan dari pantai tersebut.

Sulit untuk ditentukan panjang garis pantai secara tepat. Berbeda cara

pengukuran dimungkinkan akan menghasilkan hasil yang berbeda. Menurut

Dodi Sukmayadi dalam www.bakosurtanal.go.id terdapat beberapa metode

dalam menentukan dan mengukur garis pantai diantaranya : survei terestris

(dilaksanakan langsung ke lapangan), interpretasi foto udara, interpretasi citra

(23)

memiliki kelebihan dan kekurangan. Interpretasi foto udara memberikan hasil

yang akurat namum membutuhkan biaya yang mahal, foto citra satelit

membutuhkan biaya yang lebih murah namun hasilnya kurang akurat,

sedangkan dengan metode survei terestris menghasilkan hasil yang cukup

akura namun kurang efektif karena hanya dapat dilakukan untuk

daerah-daerah yang mudah dijangkau.

Matematika adalah ilmu yang dipelajari untuk membantu menyelesaikan

permasalahan yang dihadapi manusia. Secara sadar ataupun tidak sadar kita

mengetahui bahwa alam berkaitan erat dengan matematika. Matematika dapat

ditemukan di alam. Salah satu cabang matematika yang berkaitan dengan

alam adalah geometri. Geometri berasal dari dua kata bahasa Yunani yang

berarti bumi, dan ukuran, tampak bahwa Geometri muncul untuk kebutuhan

pengukuran tanah (bumi) (Burton, 2011:53). Pada mulanya geometri

digunakan oleh bangsa Mesir untuk menentukan batas-batas tanah yang

hilang karena banjir di sungai Nil. Salah satu pelopor geometri adalah

Euclides (325-265 SM) yang kini karyanya disebut sebagai Geometri Euclid.

Geometri Euclid banyak diterapkan dalam bidang teknik seperti : Arsitektur,

gambar-gambar perspektif, maupun gambar-gambar teknik lain. Geometri

Euclid juga dapat ditemui disekitar kita. Benda-benda yang menyerupai

segitiga, persegi panjang, trapesium, balok, kerucut, dan tabung dapat kita

temukan di sekitar kita.

Benda-benda alam disekitar kita mungkin secara umum menyerupai

(24)

fenomena alam yang tidak dapat dikaji dengan geometri Euclid. Geometri

Euclid terlalu umum untuk mempresentasikan benda-benda alam. Seorang

matematikawan mengatakan bahwa Clouds are not spheres, mountains are

not cones, coastlines are not circles, and bark is not smooth, nur does

lighting trevel in a straight line. More generally, I claim that many patterns

of nature are so irregular and fragmented Mandelbrot (1983:1). Secara tidak

langsung Mandelbrot mengatakan bahwa dengan Geometri Euclid saja alam

tidak dapat dikaji dengan baik. Awan tidak dapat digambarkan hanya dengan

gambar bulatan saja, gunung tidak dapat digambarkan hanya dengan sebuah

kerucut, garis pantai tidak dapat digambarkan hanya dengan lingkaran, dan

permukaan kulit kayu tidaklah halus. Secara umum Mandelbrot mengatakan

bahwa alam terdiri dari pola-pola tidak beraturan dan terpecah-pecah.

Seiring berkembangnya geometri muncullah gagasan-gagasan lain yang

bertentangan dengan geometri Euclid yang disebut sebagai Geometri

Non-Euclid. Salah satu Geometri Non-Euclid adalah Geometri Fraktal. Istilah

Fraktal pertama kali dipakai Beniot Mandelbrot pada tahun 1975. Fraktal atau

fractal dalam bahasa Inggris berasal dari bahasa latin frangere yang berarti

“rusak” kata ini untuk mendeskripsikan bentuk yang tidak beraturan

(Mandelbrot, 1983:4). Tokoh matematikawan lain yang berperan dalam

perkembangan Geometri Fraktal adalah Waclaw Sierpinski yang dikenal

dengan temuannya yaitu Segitiga Sierpinski, Helge von Koch yang dikenal

(25)

(Sumber : http://wiki.eanswers.com/id/Fraktal) (Sumber : Falconer, 2003)

Cantor dengan himpunan Cantor. Temuan-temuan itulah yang menjadi dasar

berkembangnya Fraktal.

Fraktal dikenal dengan kemampunannya dalam menyajikan alam. Alam

yang “rumit” dapat direpresentasikan dengan cukup baik oleh geometri

fraktal. Garis Pantai adalah salah satu bentuk alam yang tak teratur. Garis

Pantai memiliki lekukan-lekukan yang berbeda-beda di sepanjang garis

pantai. Namun demikian, lekukan ini mirip satu sama lain. Kemiripan adalah

sifat utama Fraktal, sebab bangun Fraktal bisa dihasilkan dengan mengulang

pola-pola sehingga membentuk suatu bangun yang mirip dengan bangun

aslinya. Ketika suatu bangun fraktal dipotong kemudian diperbesar akan

terlihat bangun itu mirip dengan bangun sebelumnya. Secara terus-menerus

dengan pemotongan di tak hingga dan diperbesar tetap mirip dengan bangun

sebelumnya sifat ini disebut self-similarity.

Berbeda dengan Geometri Euclid, Geometri Euclid mempunyai dimensi

bulat misalnya berdimensi : 0, 1, 2, atau 3. Titik mempunyai dimensi 0, garis

mempunyai dimensi 1, bidang mempunyai dimensi 2, dan benda pejal

(26)

dengan dimensi Geometri Euclid. Dimensi ini bisa tidak bulat tetapi pecahan.

Bangun fraktal bisa memiliki dimensi antara 0 dan 2, atau antara 2 dan 3.

Pegunungan, awan, pohon, dan bunga semua mempunyai dimensi antara 2

dan 3 (Oliver, 1997:32). Dimensi pecahan pada geometri fraktal ini lebih

dikenal dengan nama Dimensi Fraktal.

B. Rumusan Masalah

1. Bagaimana cara mencari dimensi fraktal garis pantai Yogyakarta?

2. Bagaimana cara menentukan nilai prediksi panjang garis pantai di

Yogyakarta?

3. Apa manfaat hasil penelitian bagi masyarakat yang tinggal di daerah

pesisir pantai Yogyakarta?

C. Batasan Masalah

Penulisan ini membahas mengenai geometri fraktal sebagai dasar

penelitian. Penelitian mengabaikan faktor susunan batuan Pantai di

Yogyakarta. Peneliti hanya fokus kepada bentuk gambar citra satelit oleh

Google Maps. Peneliti juga mempercayai keakuratan Google Maps sebab

Google Maps telah menjadi salah satu aplikasi maps terpopuler di dunia.

D. Tujuan Penelitian

Tujuan penelitian yang ingin dicapai adalah :

1. Mengetahui dimensi fraktal garis pantai Yogyakarta.

(27)

3. Mengetahui relevansi penelitian bagi masyarakat di daerah pesisir

pantai.

E. Manfaat Penelitian

a. Bagi Penulis

Penulis mendapatkan pengetahuan baru tentang Geometri Fraktal.

Disamping itu penulis juga dapat mengetahui penerapan geometri

Fraktal untuk menentukan nilai prediksi panjang garis pantai di

Yogyakarta.

b. Bagi Pembaca

Pembaca dapat mengetahui geometri lain selain geometri Euclides.

Pembaca juga dapat mengetahui cara mencari dimensi fraktal dan

dapat mengetahui penerapan ilmu pengetahuan khususnya penerapan

Geometri Fraktal untuk menemukan panjang garis pantai di

Yogyakarta. Penelitian ini juga bermanfaat bagi pembaca yang ingin

mengetahui metode lain yang dapat digunakan untuk menentukan

panjang garis pantai.

F. Metode Penelitian

a. Jenis Penelitian

Berdasarkan tujuan penelitian, penelitian ini termasuk ke dalam

Penelitian Terapan. Penelitian menggunakan teori matematika

khususnya Geometri Fraktal untuk diterapkan dalam konteks dunia

(28)

jenis data yang digunakan dalam penelitian, maka penelitian ini

termasuk dalam penelitian Kuantitatif. Data yang diperoleh berupa

data numerik yang diperoleh dari pengolahan objek yang digunakan.

b. Metode Penelitian

Metode penelitian yang dilakukan adalah studi pustaka, yaitu

dengan mempelajari buku, e-book, karya ilmiah, dan jurnal yang

berkaitan dengan topik skripsi.

c. Objek Penelitian

Objek penelitian ini berupa citra digital yaitu representasi suatu

objek yang dapat diolah dengan komputer. Objek berupa representasi

garis pantai Yogyakarta dalam bentuk citra digital berformat jpg.

d. Metode Pengumpulan Data

Metode pengumpulan data dilakukan dengan cara dokumentasi.

Data diperoleh dari pengolahan objek yang diunduh dari Google Maps.

e. Instrumen Pengumpulan Data

Instrumen yang digunakan untuk pengumpulan data adalah Google

Maps dan MATLAB. Google Maps digunakan untuk memperoleh

objek berupa citra digital representasi garis pantai Yogyakarta.

Sedangkan MATLAB, digunakan untuk memperoleh data yang akan

digunakan untuk menentukan dimensi fraktal garis pantai Yogyakarta.

f. Analisis Data

Berdasarkan tujuannya, analisis data dibedakan menjadi dua

(29)

analisis data untuk memperoleh prediksi panjang garis pantai. Untuk

memperoleh dimensi garis pantai Yogyakarta analisis data dilakukan

dengan menggunakan MATLAB. Sedangkan untuk memperoleh

prediksi panjang garis pantai Yogyakarta, digunakan suatu rumus.

g. Langkah-langkah Penelitian

Secara umum, penelitian ini dilakukan dengan langkah-langkah

sebagai berikut :

1. Menentukan topik skripsi.

2. Membaca referensi-referensi yang berkaitan dengan topik skripsi

dari buku, e-book, skripsi, maupun jurnal.

3. Mengambil gambar objek citra satelit melalui Google Maps.

4. Membagi objek menjadi beberapa bagian.

5. Mencari dimensi fraktal masing-masing bagian dengan membuat

program terlebih dahulu pada software MATLAB.

6. Mencari nilai prediksi panjang garis pantai di Yogyakarta.

7. Menyusun hasil penelitian.

G. Sistematika Penulisan

BAB I PENDAHULUAN

a. Latar Belakang

b. Rumusan Masalah

c. Pembatasan Masalah

d. Tujuan Penelitian

(30)

f. Metode Penelitian

g. Sistematika Peneltian

BAB II LANDASAN TEORI

a. Ruang Metrik

b. Ruang Fraktal

c. Transformasi

d. Sistem Fungsi Iterasi

BAB III ANALISIS FRAKTAL

a. Regresi Linear

b. Dimensi Fraktal

BAB IV ANALISIS FRAKTAL GARIS PANTAI DI YOGYAKARTA

a. Dimensi Fraktal Garis Pantai

b. Prediksi Panjang Garis Pantai Yogyakarta

BAB V PENUTUP

a. Kesimpulan

b. Saran

DAFTAR PUSTAKA

(31)

10

BAB II LANDASAN TEORI

Pada bab ini akan dibahas berbagai teori yang mendasari geometri fraktal.

Teori yang dibahas diantaranya : ruang metrik, ruang fraktal, afinitas, similaritas,

dan Sistem Fungsi Iterasi. Ruang metrik mendasari ruang fraktal, sedangkan

afinitas dan similaritas adalah sifat utama fraktal. Sistem Fungsi Iterasi adalah

suatu sistem yang membentuk bangun fraktal atau mengkonstruksi fraktal.

A. Ruang Metrik

Ruang metrik penting untuk dibahas di awal, karena teori-teori tentang

fraktal didasarkan pada ruang metrik seperti halnya barisan dan ruang fraktal.

Secara umum pada pembahasan ini didasarkan pada ruang Euclid dimensi

atau . Ketika maka yang berarti himpunan semua bilangan

real. Ketika maka akan menjadi bidang datar. Titik pada

dinotasikan dengan Jika suatu himpunan bagian dari

dengan suatu fungsi jarak yang bekerja padanya dengan beberapa aksioma

yang berlaku maka disebut sebagai ruang metrik. Berikut ini adalah syarat yang

harus dipenuhi dari suatu ruang metrik yang disajikan dalam definisi ruang

metrik.

Definisi 2.1.1 (Barnsley, 1988:11)

Misalkan adalah himpunan tak kosong. Metrik pada adalah fungsi bernilai

(32)

��

�

Metrik juga disebut sebagai fungsi jarak. Himpunan tak kosong yang

dilengkapi dengan metrik pada disebut sebagai ruang metrik, dituliskan

dengan .

Contoh 2.1.1

Misalkan fungsi didefinisikan | | buktikan

bahwa adalah metrik di .

Penyelesaian :

Untuk membuktikan bahwa merupakan metrik, maka perlu dibuktikan memenuhi aksioma-aksioma pada definisi 2.1.1.

� | |

| |

�� Nilai mutlak bilangan real adalah tak negatif. Untuk

berlaku

| |

�� | |

(33)

| |

| | | |

Dari � �� dan � adalah metrik di .

Contoh 2.1.2

Misalkan didefinisikan jarak Euclides dengan

√ dan

buktikanlah bahwa adalah metrik di .

Penyelesaian :

� √

√

�� Akar dari suatu bilangan real adalah tak negatif. Untuk

berarti bahwa atau sehingga berlaku

√

�� √

√

� √

(34)

dengan , (menurut ketaksamaan

segitiga)

√ √

Dari � �� dan � adalah metrik di .

Setelah mengetahui tentang ruang metrik, selanjutnya melihat hubungan

antar metrik. Dua metrik yang berbeda pada bisa memiliki keterkaitan satu

sama lain. Keterkaitan ini misalnya, metrik yang satu bisa dibangun oleh

metrik yang lain dengan mengalikan terhadap suatu konstanta. Dua metrik

yang demikian disebut dua metrik yang ekuivalen. Secara umum dua metrik

yang ekuivalen dicirikan oleh definisi 2.1.2 berikut ini.

Dua metrik dan pada ruang dikatakan ekuivalen jika terdapat dan

konstan dengan sedemikian sehingga .

Contoh 2.1.3

Bukti :

Akan dibuktikan bahwa metrik dan dapat dinyatakan sebagai dengan dan konstan.

(35)

| | | | | | | |

Dengan maka diperoleh

| | | | | | | | | | | | | | | |

yang artinya bahwa

dengan demikian dan adalah dua metrik yang ekuivalen.

Dua ruang metrik dan adalah ekuivalen jika terdapat fungsi

dengan fungsi bijektif sedemikian sehingga metrik ̃ pada

dengan definisi ̃ ( ) ekuivalen dengan .

Contoh 2.1.4

Misalkan , dan fungsi . Didefinisikan

sebagai metrik Euclides dan | |. Buktikanlah bahwa dan adalah dua ruang metrik yang ekuivalen.

Bukti :

Terdapat . Selanjutnya akan dibuktikan bahwa

̃ ̃ . Menurut definisi 2.1.3

berlaku bahwa

̃ ( )

| |

Berdasarkan yang diketahui | | .

(36)

| | | |

Dengan diperoleh

| | | | | |

̃ ̃

Selanjutnya, akan dibahas tentang kekontinuan suatu fungsi di dalam

ruang metrik. Fungsi yang kontinu di titik pasti mempunyai limit di tetapi

tidak sebaliknya. Berikut ini adalah definisi dari fungsi yang kontinu.

Misalkan suatu fungsi adalah pemetaan dari ruang metrik

ke ruang metrik . Fungsi dikatakan kontinu jika, untuk setiap

dan terdapat sedemikian sehingga .

Contoh 2.1.5

Misalkan diberikan dan adalah ruang metrik. Tunjukkanlah

bahwa fungsi konstan kontinu.

Bukti :

Diberikan sebarang , untuk sebarang dengan fungsi konstan

berlaku ( )

(37)

Contoh 2.1.6

Diketahui ruang metrik di dengan metrik Euclides. Diberikan fungsi

dengan definisi untuk setiap . Tunjukkanlah

bahwa kontinu.

Bukti :

Diberikan untuk sebarang . Harus dicari sedemikian

sehingga untuk setiap yang memenuhi | | berlaku | |

Dipilih maka | |

| | | | | |

dengan demikian terbukti kontinu.

Suatu barisan dalam ruang metrik dapat dibedakan menjadi dua macam

barisan, yaitu barisan konvergen dan barisan divergen. Kedua macam barisan

tersebut mempengaruhi kelengkapan dari suatu ruang metrik. Ruang metrik

dikatakan lengkap jika setiap barisan Cauchy di dalamnya konvergen ke suatu

titik di ruang metriknya. Berikut ini adalah definisi dari barisan Cauchy yang

dilanjutkan dengan definisi barisan konvergen.

Barisan dalam ruang metrik disebut barisan Cauchy jika

(38)

Suku-suku pada suatu barisan jika diperhatikan untuk nilai suku ke- yang

semakin besar, dapat dibedakan menjadi barisan divergen dan barisan

konvergen. Barisan yang menunjukkan sifat suku ke- yang semakin besar

mendekati suatu nilai tertentu disebut barisan konvergen. Sebaliknya, jika

untuk nilai suku ke- yang semakin besar dari suatu barisan tidak

menunjukkan semakin dekat dengan nilai tertentu disebut sebagai barisan

divergen. Berikut ini definisi 2.1.6 mendefinisikan secara matematis suatu

barisan konvergen.

Barisan dalam ruang metrik dikatakan konvergen ke

jika untuk sebarang terdapat bilangan bulat sehingga . Titik konvergensi adalah limit dari barisan dinotasikan

dengan . Titik yang merupakan konvergensi dari barisan

memenuhi ̅ atau bola tertutup dengan jari-jari dan berpusat di .

Kekonvergenan suatu barisan tidak lepas dengan adanya titik konvergensi.

Ketika suatu barisan diketahui konvergen, pastilah barisan tersebut mempunyai

titik konvergensi. Berikut ini adalah suatu teorema (2.1.1) yang menyatakan

bahwa titik konvergensi dari suatu barisan adalah tunggal. Selanjutnya melalui

teorema 2.1.2 ditunjukkan bahwa barisan yang konvergen merupakan barisan

Cauchy. Mengutip dari buku Metric Spaces (Shirali dan Vasudeva, 2006) pada

(39)

bagian (subbarisan). Pada definisi 2.1.7 tersebut dikatakan bahwa, jika suatu

barisan konvergen ke suatu titik maka subbarisannya juga konvergen ke titik

yang sama. Hal ini berlaku juga untuk subbarisan dari suatu barisan yang

konvergen ke suatu titik, barisannya juga akan konvergen ke titik yang sama

dengan subbarisannya. Sebagai akibat dari definisi 2.1.7 pada proposisi 2.1.1

keterkaitan antar barisan dan subbarisan ini juga berlaku untuk barisan Cauchy.

Teorema 2.1.1 (Searcoid, 2007:86)

Misalkan adalah suatu ruang metrik, barisan di yang konvergen

akan konvergen ke tepat satu titik di .

Bukti :

Diberikan barisan yang konvergen. Misalkan konvergen ke titik

dan titik yang berbeda. Ambil sebarang . Maka ada

sedemikian sehingga dan .

Dipilih sehingga untuk menurut ketaksamaan

segitiga

Jadi berarti bahwa . Terbukti bahwa barisan

konvergen ke satu titik.

Teorema 2.1.2 (Barnsley, 1988:18)

Jika barisan pada ruang metrik konvergen ke maka

barisan merupakan barisan Cauchy.

(40)

Diberikan ruang metrik dan barisan di yang konvergen ke .

Menurut definisi 2.1.6 untuk sebarang terdapat bilangan bulat positif

dan sehingga . Demikian juga untuk setiap

berlaku _� . Menurut ketaksamaan segitiga _�

� untuk setiap . Diperoleh �

sehingga barisan Cauchy.

Contoh 2.1.7

Diketahui barisan =

di ruang metrik dengan dan

adalah metrik Euclides. Buktikanlah bahwa barisan adalah barisan

Cauchy dan konvergen ke 0.

Bukti :

Diberikan sebarang , maka terdapat sehingga . Untuk

dan misalkan berlaku

� (_{) |}_|

Selanjutnya jelas bahwa

Diperoleh _� dan maka terbukti bahwa barisan

barisan Cauchy dan konvergen ke 0.

Definisi 2.1.7 (Shirali dan Vasudeva, 2006:48)

Misalkan barisan dalam ruang metrik dan barisan bilangan

(41)

dikatakan subbarisan dari . Jika { } konvergen, limitnya

merupakan limit dari . Jelas bahwa barisan di

konvergen ke jika dan hanya jika setiap subbarisannya konvergen ke .

Proposisi 2.1.1 (Shirali dan Vasudeva, 2006:48)

Jika barisan Cauchy dalam metrik memuat sub barisan yang konvergen

maka barisan itu konvergen ke limit yang sama dengan limit sub barisannya.

Bukti :

Diberikan barisan Cauchy di maka untuk setiap terdapat

bilangan bulat sehingga _� dengan . Barisan { } sub barisan dari konvergen, misal konvergen ke . Diperhatikan

bahwa _� barisan bilangan bulat positif yang naik maka ( )

untuk . Dengan ketaksamaan segitiga diperoleh

( ) ( ) ( ) untuk . Jika ,

maka ( ) . Sehingga yang artinya bahwa

konvergen ke

Pada pembahasan sebelumnya telah dibahas tentang : ruang metrik,

barisan Cauchy, dan barisan konvergen. Selanjutnya, pada definisi berikut ini

menunjukkan hubungan ketiganya yaitu tentang ruang metrik lengkap.

Ruang metrik dikatakan lengkap jika setiap barisan Cauchy di

(42)

Contoh 2.1.8

Ruang metrik dengan merupakan jarak Euclides adalah ruang metrik

lengkap.

Bukti :

√ dengan dan

. Misalkan diberikan barisan _� untuk , _�

� � didefinisikan barisan Cauchy di sehingga � �

untuk . Kemudian untuk terdapat bilangan bulat

sedemikian sehingga _� _� √( _� _� ) ( _� _� )

untuk setiap . Menggunakan prinsip kekonvergenan _� akan

konvergen ke suatu titik katakanlah _� _� _�. Berlaku untuk setiap � akan konvergen ke suatu titik .

Contoh 2.1.9

Diketahui ruang metrik dengan metrik Euclides dan . Ruang

metrik merupakan ruang metrik tidak lengkap.

Bukti :

Terdapat barisan , akan dibuktikan barisan barisan Cauchy.

Diberikan maka terdapat sehingga . Untuk setiap

berlaku , . Barisan adalah barisan Cauchy namun

(43)

Sistem bilangan real mempunyai dua tipe sifat. Sifat yang pertama adalah

aljabar dengan penjumlahan, perkalian dan yang lainnya. Sifat yang kedua

adalah topologi yang ada kaitannya dengan jarak antar bilangan dan konsep

limit (Shirali dan Vasudeva, 2006:64). Pembahasan selanjutnya yaitu tentang

topologi dalam ruang metrik khususnya himpunan terbuka dan himpunan

tertutup. Sebelum membahas tentang dua hal tersebut perlu diketahui terlebih

dahulu tentang : persekitaran, titik interior, dan titik limit.

Misalkan ruang metrik himpunan di

mana dan , disebut bola buka dengan jari-jari dan pusat .

Himpunan ̅ di mana dan ,

disebut bola tertutup dengan jari-jari dan pusat .

Contoh 2.1.10

Bola buka di garis real adalah selang terbuka . Contoh

bola tertutup ̅ di garis real adalah selang tertutup .

Diberikan ruang metrik persekitaran di adalah sebarang bola

buka di dengan pusat di .

Himpunan bagian dari ruang metrik dikatakan terbuka jika untuk

(44)

Berikut ini adalah suatu teorema 2.1.3 yang menyatakan bahwa setiap bola

buka merupakan himpunan terbuka. Terorema 2.1.4 menunjukkan keterkaitan

antar himpunan-himpunan terbuka dimana gabungan himpunan-himpunan

terbuka merupakan himpunan terbuka, demikian juga untuk irisan

himpunan-himpunan terbuka juga merupakan himpunan-himpunan terbuka.

Teorema 2.1.3 (Shirali dan Vasudeva, 2006:66)

Dalam sebarang ruang metrik , setiap bola buka adalah himpunan

terbuka.

Bukti :

Misalkan adalah bola buka tak kosong maka . Ambil

sebarang titik maka . Misalkan .

Akan dibuktikan . Untuk sebarang berlaku , berarti bahwa .

Dengan demikian dan merupakan bola buka. Sehingga

adalah himpunan terbuka di

Diberikan ruang metrik , maka

� dan adalah himpunan terbuka di .

�� Gabungan dari keluarga berhingga himpunan-himpunan terbuka adalah

himpunan terbuka.

(45)

Bukti :

� Himpunan kosong tidak memuat titik di dalamnya, syarat bahwa setiap

titik di adalah titik pusat bola buka otomatis terpenuhi yaitu himpunan

kosong juga. Selanjutnya, ruang terbuka karena setiap titik pusat bola

buka ada di .

�� Diberikan sebarang himpunan � dan : � yang merupakan

keluarga himpunan terbuka. Akan dibuktikan . Jika

maka jelas bahwa terbuka menurut � Asumsikan bahwa ,

ambil sebarang maka terdapat � sedemikian sehingga . adalah himpunan terbuka maka terdapat sehingga

. Jadi terdapat sehingga .

terbuka.

�� Diberikan himpunan _� � keluarga himpunan terbuka di

dan _� _� Akan dibuktikan terbuka. Jika maka jelas

bahwa terbuka menurut � . Asumsikan bahwa , ambil sebarang maka terdapat sedemikian sehingga . adalah

himpunan terbuka, maka terdapat sedemikian sehingga

. Dipilih maka dengan

. Dengan demikian .

(46)

Titik interior dari suatu himpunan akan dibahas pada definisi 2.1.12. Dari

definisi 2.1.12 diturunkan teorema 2.1.5 yang menunjukkan keterkaitan antara

titik interior dengan himpunan terbuka.

Misalkan � himpunan bagian dari ruang metrik . Titik disebut titik

interior � jika terdapat bola buka dengan pusat di � sedemikian sehingga � untuk suatu Himpunan semua titik interior �

dinotasikan � � � � untuk suatu .

Contoh 2.1.11

. Titik adalah titik

interior �.

Bukti :

Jelas bahwa � sebab . Menurut definisi

dengan dipilih maka | |

| | | | dengan . Akan dibuktikan

�. Ambil sebarang perhatikan bahwa

| | | | | | | |

| |

(47)

, dengan cara yang sama diperoleh dan . Kemudian

yang berarti �. Dengan demikian

�

Diberikan � himpunan bagian dari ruang metrik .

� � adalah himpunan bagian terbuka dari � yang memuat setiap

himpunan bagian terbuka dari �. �� terbuka jika dan hanya jika � � .

Bukti :

� Diberikan sebarang � . Menurut definisi terdapat bola buka

�. Berdasarkan teorema 2.1.3 adalah himpunan terbuka, setiap titik

di merupakan titik pusat dari bola buka dalam dan juga di

dalam �. Oleh karena itu setiap titik dalam adalah titik interior �

maka � . Dengan demikian adalah titik pusat bola buka dalam � . Karena � dan � berarti bahwa � terbuka. Misalkan

� dan adalah himpunan terbuka. Ambil sebarang maka

terdapat bola buka �. Jadi menurut definisi 2.1.12 � .

(48)

��

Diketahui � terbuka. Berdasarkan � diperoleh bahwa � � dan � �

yang berarti bahwa � � .

Diketahui � � , seperti halnya pada � diperoleh bahwa � terbuka

yang artinya � juga terbuka.

Suatu titik di disebut sebagai titik limit jika memenuhi definisi 2.1.13.

Jika setiap titik limit dari suatu himpunan adalah himpunan bagian dari

himpunan tersebut, maka himpunan itu dikatakan himpunan tertutup. Lebih

jelasnya himpunan tertutup didefinisikan pada definisi 2.1.14. Teorema 2.1.6

mengatakan hubungan antar himpunan terbuka dan himpunan tertutup. Melalui

teorema 2.1.6 ini dapat diketahui bahwa jika suatu himpunan adalah tertutup

maka komplemennya terbuka, demikian pula jika komplemen suatu himpunan

adalah terbuka maka himpunannya tertutup. Dengan kata lain berlaku

biimplikasi antara himpunan dan komplemen himpunannya.

Diberikan ruang metrik dan . Titik disebut titik limit jika

setiap bola buka dengan titik pusat memuat setidaknya satu titik yang

berbeda dengan di , dengan kata lain . Himpunan

(49)

Himpunan bagian dari ruang metrik dikatakan tertutup jika memuat

setiap titik limitnya dengan kata lain .

Diberikan ruang metrik dan . tertutup di jika dan hanya jika

terbuka di .

Bukti :

Andaikan tertutup di , akan dibuktikan terbuka di . Jika maka dan merupakan himpunan terbuka menurut teorema 2.1.4. Asumsikan

bahwa . Ambil sebarang maka . Karena tertutup

dan maka bukan titik limit sehingga terdapat sedemikian

sehingga . Oleh karena itu yang berarti bahwa

terbuka.

Sebaliknya, andaikan terbuka akan dibuktikan tertutup. Ambil dan

titik limit . Andaikan bahwa maka . Karena terbuka maka

terdapat sehingga yang berarti . Akibatnya

bukan titik limit , kontradiksi dengan titik limit . Sehingga haruslah

.

Seperti halnya pada himpunan terbuka. Pada terorema 2.1.7 di bawah ini

menunjukkan keterkaitan antar himpunan-himpunan tertutup dimana gabungan

himpunan-himpunan tertutup merupakan himpunan tertutup, demikian juga

(50)

Gabungan himpunan dengan himpunan titik limitnya disebut sebagai closure

(penutup). Lebih jelasnya, pada definisi 2.1.15 didefinisikan closure dari suatu

himpunan.

Diberikan ruang metrik maka � dan adalah himpunan tertutup

�� Irisan dari himpunan-himpunan tertutup adalah tertutup

�� Gabungan berhingga dari himpunan-himpunan tertutup adalah tertutup

Bukti :

� Himpunan kosong tidak memuat titik di dalamnya, syarat bahwa himpunan

tertutup memuat semua titik limitnya terpenuhi oleh himpunan kosong.

Sebarang ruang memuat semua titik, berarti bahwa memuat semua titik

limitnya.

�� Diberikan himpunan keluarga himpunan tertutup di dan .

Menurut teorema 2.1.6, tertutup jika terbuka. Dengan hukum De

Morgan

(⋂ ) ⋃

Diketahui tertutup, menurut teorema 2.1.6 adalah himpunan

terbuka. Dengan teorema 2.1.4 �� adalah himpunan terbuka

(51)

�� Diberikan keluarga berhingga himpunan-himpunan tertutup

dan misalkan _� _�. Menurut teorema 2.1.6

tertutup jika terbuka. Dengan hukum De Morgan diperoleh

(⋃ � �

) ⋂ � �

Diketahui _� untuk setiap � adalah tertutup maka menurut

teorema 2.1.6 _� untuk setiap � adalah terbuka. Dengan

menggunakan teorema 2.1.4 �� _� _� adalah himpunan terbuka.

Karena _� _� maka terbuka sehingga tertutup.

Misalkan himpunan bagian dari ruang metrik . Himpunan

disebut closure (penutup) dari dan dinotasikan dengan ̅.

Contoh 2.1.12

Diberikan ruang metrik adalah jarak Euclides di dan himpunan

� dengan � . Titik limit � adalah 2, maka �̅ � .

Sebelum mempelajari tentang ruang metrik yang kompak perlu diketahui

terlebih dahulu tentang selimut. Pada definisi 2.1.16 didefinisikan suatu selimut

terbuka dari ruang metrik.

Diberikan ruang metrik dan adalah keluarga himpunan terbuka di .

(52)

, maka disebut selimut terbuka dari . Keluarga bagian dari yang

merupakan selimut terbuka dari disebut selimut bagian.

Contoh 2.1.13

Gabungan keluarga interval-interval terbuka pada

adalah selimut terbuka di .

Ruang metrik dikatakan kompak jika setiap selimut terbuka dari

mempunyai suatu selimut bagian berhingga yaitu keluarga bagian berhingga

sedemikian sehingga _� _�.

Contoh 2.1.14

Diberikan himpunan bagian terbatas dari ruang metrik . adalah

himpunan kompak

Bukti :

Misalkan dan selimut terbuka dari dengan � maka . Untuk ada �, sedemikian sehingga

. Demikian juga untuk ada �, sedemikian sehingga .

Berlaku seterusnya hingga untuk ada � sedemikian sehingga

. Dengan demikian diperoleh keluarga bagian dari yaitu

{ }. Kerena memuat selimut bagian berhingga maka

(53)

Diberikan ruang metrik dan � himpunan bagian tak kosong dari . �

dikatakan terbatas jika terdapat sedemikian sehingga �.

Definisi 2.1.18 mendefinisikan tentang keterbatasan suatu himpunan.

Himpunan yang terbatas adalah himpunan yang memiliki nilai maksimum

untuk setiap titik-titik pada himpunannya. Nilai maksimum jarak dalam definisi

2.1.18 ditandakan dengan suatu konstantan real . Selanjutnya, melalui

teorema 2.1.8 ditunjukkan bahwa himpunan kompak dari suatu ruang metrik

adalah tertutup dan terbatas. Melalui teorema 2.1.8 ini secara tidak langsung

menunjukkan bahwa adanya keterkaitan antara kekompakan, ketertutupan, dan

keterbatasan dari suatu himpunan.

Diberikan ruang metrik dan . Jika himpunan kompak dari maka tertutup dan terbatas.

Bukti :

Diberikan himpunan bagian kompak dari ruang metrik dan ,

. Untuk suatu bilangan real positif dipilih maka

terdapat bola buka dan sedemikian sehingga

( ) ( ) . Jelas bahwa ( ). adalah

(54)

memenuhi ( _� _� ) ( _� ) . Misalkan _� _�

maka himpunan bagian terbuka dari yang memuat . Selanjutnya

dibuktikan bahwa . Jika maka untuk

suatu dalam dan . Akibatnya ( _� _� )

( � ) maka kontradiksi dengan ( � � ) ( � )

sehingga tidak ada titik di yang dapat menjadi titik limit di . Akibatnya

semua titik di titik limit , sehingga tertutup.

Selanjutnya akan dibuktikan terbatas. Jika tidak terbatas maka

terdapat dan di sedemikian sehingga untuk sebarang bilangan positif ,

. Mengingat kembali untuk titik pusat bola buka di , untuk

jelas bahwa . Karena kompak maka terdapat

sedemikian sehingga _� _� . Misalkan { ( _� ) �

}. Terdapat dan di sedemikian sehingga .

Karena maka terdapat _� dan sedemikian sehingga _� dan . Menurut ketaksamaan segitiga diperoleh _�

( � ) ( ) . Kontradiksi dengan , sehingga

terbatas.

B. Ruang Fraktal

Pembahasan sebelumnya mempelajari ruang metrik dengan

himpunan-himpunan di yang dilengkapi dengan metrik , dan dengan beberapa

(55)

gabungan dari himpunan-himpunan kompak yang membentuk suatu ruang.

Ruang tersebut dilengkapi dengan metrik yang dinamakan metrik/jarak

Hausdorff. Ruang yang terbentuk dengan gabungan himpunan-himpunan

kompak yang dilengkapi dengan metrik Hausdorff tersebut dinamakan ruang

Fraktal. Pada definisi 2.2.1 berikut ini didefinisikan yang merupakan

ruang yang titik-titiknya (elemen-elemennya) merupakan himpunan bagian tak

kosong yang kompak.

Pada definisi 2.1.1 telah didefinisikan sebagai metrik pada . Pada

ruang fraktal himpunan yang dipakai bukan lagi tetapi yang telah

disinggung sebelumnya. Konsep jarak/metrik pada berbeda dengan jarak

pada . Definisi 2.2.2, 2.2.3, dan 2.2.4 mendefinisikan tentang pengertian jarak

pada . Dari definisi-definisi jarak pada ini, diturunkanlah suatu

teorema yang menyatakan adalah suatu metrik pada . Sehingga, jika

dalam ada sebagai metrik maka di dalam ada sebagai metriknya.

Misalkan adalah ruang metrik lengkap. Kemudian didefinisikan

sebagai ruang yang titik-titiknya adalah himpunan bagian yang kompak dari

yang tak kosong.

Diberikan ruang metrik lengkap , dan didefinisikan kemudian disebut jarak dari titik ke

(56)

Diberikan ruang metrik lengkap dan � didefinisikan � � . � adalah jarak dari himpunan � ke

himpunan .

Contoh 2.2.1

Tentukan jika adalah dengan jarak Euclides, dan

Penyelesaian :

Infimum dari dicapai ketika yaitu . Jadi .

Contoh 2.2.2

Diketahui ruang metrik lengkap. Buktikan bahwa jika �

maka � �

Bukti :

� �

�

Diberikan ruang metrik lengkap . Jarak Hausdorff antara titik � dan di didefinisikan oleh

(57)

Teorema 2.2.1 (Edgar, 2008:72)

Diberikan ruang metrik . Fungsi Hausdorff adalah metrik pada .

Bukti :

metrik jika memenuhi aksioma-aksioma pada definisi 2.1.1. Maka akan

dibuktikan memenuhi aksioma-aksioma tersebut.

� � � � � � �

�� Untuk � maka terdapat sehingga � dan . Jadi jelas bahwa

. � � maka � . Karena

� � � dan � maka �

��

� Akan dibuktikan terlebih dahulu bahwa � �

Ambil sebarang � maka

�

Jadi � � dengan cara yang sama akan diperoleh

juga bahwa � �

Selanjutnya akan dibuktikan � � � � �

(58)

� �

�

Berdasar � �� dan � terbukti bahwa metrik di .

Himpunan yang dilengkapi dengan metrik atau dinotasikan

dengan ini disebut sebagai ruang fraktal.

C. Transformasi

Transformasi menjadi salah satu bagian yang penting dari Geometri

Fraktal. Secara khusus geometri fraktal dicirikan dengan transformasi Afin.

Pada bagian ini juga akan dibahas tentang similaritas. Similaritas dan Afin

menjadi sifat utama dari fraktal. Bangun fraktal seperti : Segitiga Sierpinski

dan Kurva Salju Von Koch dapat dibentuk melalui dua sifat ini. Sifat inilah

yang menyebabkan suatu bangun fraktal mempunyai kemiripan diri di setiap

skala.

a. Transformasi Afin

Transformasi Afin di diperoleh dengan menerapkan transformasi

linear dan diikuti dengan translasi. Transformasi Afin melibatkan beberapa

macam transformasi diantaranya : rotasi, translasi, dilatasi dan refleksi.

Gabungan dari transformasi tersebut membentuk transformasi baru yang

disebut dengan transformasi Afin. Sebelum membahas tentang transformsi

Afin, pada definisi 2.3.1 didefinisikan suatu transformasi dari ke �.

Definisi 2.3.2 mendefinisikan suatu translasi yang perlu untuk diketahui

(59)

Definisi 2.3.1 (Crownover, 1995:62)

Suatu transformasi dari ke � adalah suatu pemetaan yang

memenuhi untuk setiap dan skalar

Contoh 2.3.1

Sebuah contoh transformasi linear di bidang

,

Jika disajikan dalam bentuk matriks sebagai berikut :

Translasi pada adalah pemetaan dengan bentuk ,

dengan adalah ketetapan atau vektor konstan.

Berdasarkan pembahasan sebelumnya, setiap transformasi Afin

pada dapat direpresentasikan dengan matriks vektor sebagai berikut

� ,

Dalam menjadi

[ ]

Berikut ini adalah suatu gambar yang menunjukkan ilustrasi transformasi

(60)

Gambar 2.1 Contoh Afinitas

b. Similaritas

Ciri khas lain dari Geometri Fraktal selain Afin diri adalah similaritas

atau kesebangunan. Sebelum membahas tentang similaritas terlebih dahulu

perlu diketahui tentang pengertian Isometri. Similaritas lekat kaitannya

dengan isometri. Kemiripan (similaritas) penting untuk mengkonstruksi

bangun fraktal.

Transformasi disebut isometri jika memenuhi | | | |, .

Suatu transformasi disebut similar dengan rasio similaritas jika memenuhi syarat berikut

| | | |

Berikut ini adalah definisi similar untuk suatu transformasi di .

Suatu transformasi disebut similar jika transformasi afin

yang mempunyai salah satu dari bentuk

(61)

Untuk translasi , bilangan real , dan sudut dengan . disebut rotasi sudut sedangkan adalah skala. Transformasi

linear

adalah suatu rotasi. Transformasi linear

adalah suatu pencerminan.

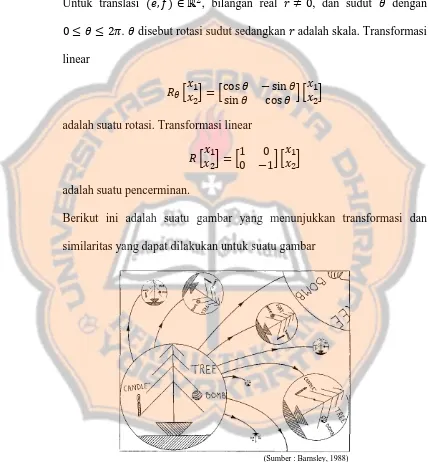
Berikut ini adalah suatu gambar yang menunjukkan transformasi dan

similaritas yang dapat dilakukan untuk suatu gambar

(Sumber : Barnsley, 1988)

(62)

D. Sistem Fungsi Iterasi

Konstruksi bangun fraktal tidak cukup dilakukan hanya dengan satu

fungsi. Pembentukan (konstruksi) bangun fraktal membutuhkan banyak

fungsi. Kumpulan fungsi-fungsi yang membentuk suatu bangun fraktal inilah

yang disebut dengan Iterated Function System (IFS) atau Sistem Fungsi

Iterasi. Sistem Fungsi Iterasi atau disingkat SFI terdiri dari himpunan

berhingga pemetaan-pemetaan kontraksi. Berikut ini pada definisi 2.4.1

didefinisikan terlebih dahulu tentang invarian (titik tetap). Suatu titik dalam

ruang metrik yang jika ditransformasikan menghasilkan titik itu sendiri

disebut titik tetap. Selanjutnya pada definisi 2.4.2 menjelaskan tentang

pemetaan kontraksi secara umum. Pemetaan kontraksi inilah yang akan

membentuk Sistem Fungsi Iterasi.

Misalkan merupakan transformasi pada ruang metrik. Titik

sedemikian sehingga ( ) disebut titik tetap.

Contoh 2.4.1

Diketahui suatu pemetaan dengan dan . Carilah

titik tetap .

Jawab :

Misalkan titik tetap dari adalah maka berlaku ( ) .

(63)

titik tetap adalah dan .

Transformasi pada ruang metrik disebut kontraktif atau

pemetaan kontraktif jika terdapat sedemikian sehingga

( ) Sebarang bilangan disebut faktor

kontraksi .

Contoh 2.4.1

Misalkan transformasi pada ruang metrik , dengan

adalah metrik Euclid. Pemetaan didefinisikan oleh ,

tunjukkanlah bahwa pemetaan kontraktif.

Bukti :

Untuk menunjukkan bahwa adalah pemetaan kontraktif maka perlu

ditunjukkan ( ) dengan .

Ambil sebarang titik pada misalkan titik dan . Metrik adalah metrik

Euclid maka

( ) ((_{) (}₎₎

(64)

dengan terbukti bahwa ( )

sehingga, adalah pemetaan kontraktif.

Berikut ini adalah suatu teorema yang menunjukkan hubungan antara

pemetaaan kontraksi dengan titik tetap.

Teorema 2.4.1 (Barnsley, 1988:76)

Misalkan pemetaan kontraksi pada ruang metrik lengkap .

Maka memiliki tepat satu titik tetap dan bahkan untuk sebarang titik

, barisan konvergen ke . Atau berlaku

Bukti :

Diberikan barisan dengan dengan dan . Berdasarkan ketidaksamaan segitiga berlaku

adalah pemetaan kontraktif, maka untuk berlaku

� ( � )

�

Diperoleh