MODEL MULTILINIER UNTUK MENSIMULASIKAN PERILAKU RESPONS HISTERETIK SAMBUNGAN BALOK-KE-KOLOM BETON BERTULANG PADA PEMBEBANAN SIKLIK

(1)

Manajemen dan Rekayasa Struktur C-135

MODEL MULTILINIER UNTUK MENSIMULASIKAN PERILAKU

RESPONS HISTERETIK SAMBUNGAN BALOK-KE-KOLOM BETON

BERTULANG PADA PEMBEBANAN SIKLIK

D.I.WAHJUDI 1,P.SUPROBO 2,H.SUGIHARDJO 3&TAVIO 4

Dep. Teknik Sipil, Fakultas Teknik Sipil & Perencanaan, ITS Surabaya.

34

Abstrak — Struktur beton bertulang, baik yang biasa maupun pracetak, pada umumnya,

menam-pilkan kinerja yang bagus dengan kekuatan dan daktilitas yang tinggi. Pada sistem rangka pemikul momen (SRPM), letak-letak sambungan balok-ke-kolom (SBK) harus didesain dan dipersiapkan dengan seksama, agar distribusi gaya-gaya dalam akibat beban bisa berlangsung dengan baik. Untuk bangunan-bangunan yang terletak di wilayah rawan gempa, sambungan-sambungan tersebut harus sanggup berperilaku respons yang baik terhadap pembebanan siklik kuat yang menirukan beban gempa. Di dalam naskah ini, akan disampaikan beberapa model analitik multilinier untuk mensimulasikan perilaku respons histeretik SBK beton bertulang terhadap pembebanan siklik. Model kemudian dibandingkan dengan beberapa hasil pengujian eksperimental yang sudah ada.

Kata kunci — beton bertulang, kinerja, SRPM, SBK, respons, pembebanan siklik.

1. PENDAHULUAN

Pada saat ini terjadi pertumbuhan yang pesat pada sektor industri konstruksi, dengan bangunan beton bertulang, baik yang biasa maupun pracetak, bermunculan di banyak tempat. Pada umumnya, ba-ngunan beton bertulang menampilkan karakteristik kinerja yang bagus, dengan kekuatan dan daktillitas yang tinggi. Untuk bangunan gedung hunian, sistem struktur yang banyak dipakai adalah sistem rangka pemikul momen (SRPM). Pada penggunaan sistem ini, masalah klasik yang timbul adalah pada pemi-lihan sistem sambungan yang baik antara balok-balok dengan kolom-kolom bangunan, agar penye-baran dan penyaluran gaya-gaya dalam akibat beban bisa berlangsung dengan baik. Sambungan-sam-bungan ini, yang dikenal dengan nama samSambungan-sam-bungan balok-ke-kolom (SBK), menurut letaknya, dibagi ke

dalam dua jenis, yaitu sambungan luar (exterior)

dan sambungan dalam (interior). Untuk keperluan

analisis, SBK bisa dimodelkan secara terpisah

seba-gai suatu subassembly, sebagai yang disampaikan

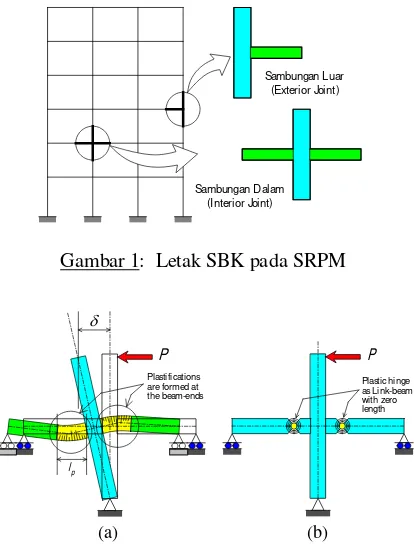
pada Gambar 1.

Penelitian-penelitian SBK biasanya berujung pada upaya-upaya pencarian perilaku hubungan an-tara beban dengan perpindahan. Untuk keperluan bangunan tahan gempa, maka hubungan beban–per-pindahan itu diarahkan pada pembebanan siklik

kuat. Pada Gambar 2 diperlihatkan subassembly

SBK yang mendapatkan gaya lateral pada ujung bebas kolom untuk memberikan pembebanan

mo-men dan gaya lintang pada sambungan. Untuk me-nirukan efek pembebanan gempa, maka

diberikan-lah beban P sebagai beban siklik (bolak-balik), dan

perpindahan yang dihasilkannya, δ, akan dicari.

Gambar 1: Letak SBK pada SRPM

(a) (b)

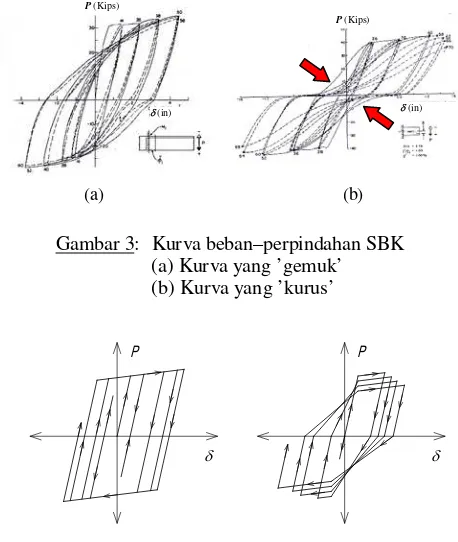
Gambar 2

(a) Terjadi plastifikasi di ujung balok : Subassembly SBK dengan beban P

(b) Daerah plastifikasi diidealisasikan sebagai sendi plastik

Sambungan Luar (Exterior Joint)

Sambungan Dalam (Interior Joint)

P

δ

Plastifications are formed at the beam-ends

l_p

P

(2)

Pembebanan yang kuat akan menyebabkan ter-jadinya plastifikasi pada struktur, yang muncul da-lam bentuk retak-retak pada beton dan perpanjangan yang tak dapat pulih pada baja-baja tulangan. Plasti-fikasi ini biasanya terbentuk secara terkonsentrasi pada daerah-daerah kritik, dan kemudian di-ideali-sasi-kan sebagai sendi-sendi plastik. Pasangan data

antara P dan δ akan menghasilkan grafik respons

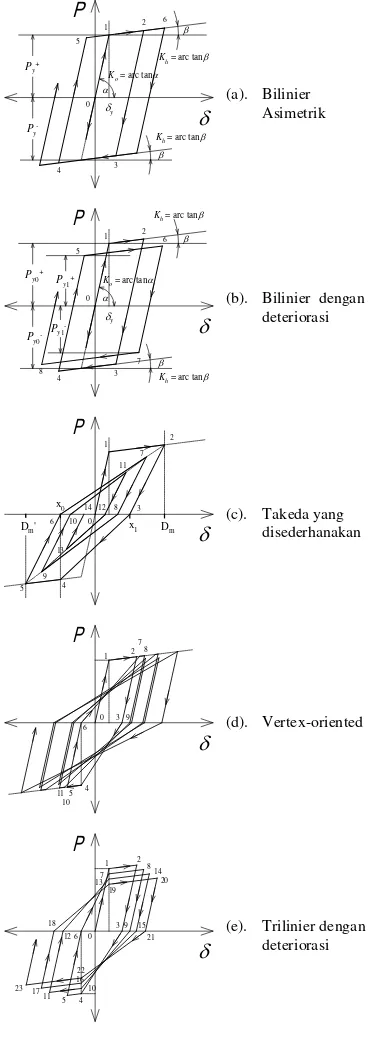
histeretik, sebagai yang diperlihatkan pada Gambar 3. Gambar 3-(a) menunjukkan grafik karakteristik beban–perpindahan dari suatu SBK beton bertulang. Lintasan gerak bolak-balik yang terjadi membentuk

‘loop’ tertutup, yang ditimbulkan akibat tercapainya

kondisi paska-leleh pada beton dan baja tulangan secara berulang. Biasanya kurva yang dihasilkannya berbentuk ‘gemuk’, untuk merefleksikan hubungan tegangan-regangan dari materialnya. Tetapi, bila pembebanan beralih dari lentur ke ragam geser dan banyak retak terbentuk pada beton sehingga terjadi

slip antara baja tulangan dengan beton di

sekeli-lingnya, maka akan dihasilkan kurva yang agak

‘kurus’ (pepat = pinched) di bagian tengahnya,

sebagai yang diperlihatkan pada Gambar 3-(b).

(a) (b)

Gambar 3: Kurva beban–perpindahan SBK (a) Kurva yang ’gemuk’ (b) Kurva yang ’kurus’

Gambar 4

Untuk kemudahan di dalam analisis, bentuk lin-tasan kurva yang lengkung biasanya disederhanakan dengan pendekatan beberapa penggal garis lurus

yang bersambung (multilinier), yang contohnya di-perlihatkan pada Gambar 4. Di dalam naskah ini akan disampaikan metoda numerik untuk mensimu-lasikan respons histeretik SBK beton bertulang ter-hadap pembebanan siklik dengan menggunakan model multilinier. Mula-mula model-model yang dipakai diuraikan, untuk kemudian dipakai meniru-kan beberapa hasil eksperimental yang sudah ada.

: Kurva beban–perpindahan dengan model multilinier.

2. MODEL MULTILINIER

Perilaku global dari SRPM beton bertulang sa-ngat dipengaruhi oleh perilaku SBK-nya. Pengalam-an dPengalam-an penelitiPengalam-an terdahulu telah mengungkapkPengalam-an, bahwa SBK beton bertulang menunjukkan perilaku yang baik, yaitu memiliki kekuatan, daktilitas dan kemampuan pemencaran energi yang cukup tinggi, yang sangat dapat dimanfaatkan sepenuhnya untuk keperluan desain seismik bangunan. Perilaku yang umum dari SBK beton bertulang terhadap beban si-klik, yang mewakili semua efek kejadian gempa,

biasanya berupa loop-loop histeretik yang diwarnai

oleh kerusakan pada kekakuan (stiffness

degradat-ion) dan kerusakan pada kekuatan (strength

dete-rioration), yang lambat-laun akan mendatangkan

kegagalan pada SBK.

Memprediksikan perilaku SBK beton bertulang sebenarnya cukup kompleks, karena dia memperhi-tungkan gabungan dari pengaruh-pengaruh seperti

nonlinieritas material (plastisitas, strain-hardening,

peretakan, dll.), nonlinieritas kontak dan slip,

non-linieritas geometri (instabilitas lokal), tegangan sisa, dan konfigurasi geometrik yang tidak sederhana. Dengan beban siklik, perilakunya semakin

bertam-bah rumit dengan pergantian arah beban (loading–

unloading–reloading) yang sambung-menyambung.

Untuk beban monotonik statik, pada saat sekarang sudah bisa dengan mudah dilakukan perhitungan untuk memprediksikan perilaku respons momen– rotasi untuk berbagai bentuk dan ukuran penampang dengan menerapkan tata langkah analisis penam-pang biasa [3, 9]. Tetapi untuk kasus beban siklik hal itu tidaklah cukup. Untuk memenuhi kebutuhan inilah model-model multilinier dikembangkan.

Ada banyak model multilinier yang sudah di-kembangkan dan dipublikasikan, namun hanya akan diambil 5 daripadanya untuk disampaikan di sini, yaitu : (a) bilinier asimetrik, (b) bilinier dengan

de-teriorasi kekuatan, (c) Takeda sederhana, (d)

vertex-oriented, dan (e) trilinier dengan deteriorasi

kekuat-an. Ilustrasinya disampaikan pada Gambar 5. Dari P (Kips)

δ (in)

P (Kips)

δ (in)

P

δ

P

(3)

kelimanya, model bilinier asimetrik adalah yang paling sederhana. Bagan perilakunya secara ringkas digambarkan seperti pada bagian kiri dari Gambar 4, dan digambarkan lagi dengan lebih jelas pada Gambar 5-(a).

Gambar 5

Pada model bilinier, perilaku respons loading

(lintasan 0-1-2), unloading (lintasan 2-3-4), dan

re-loading (lintasan 4-5-6), hanya diwakili oleh dua

garis lurus dengan kekakuan yang berbeda, yaitu K

: Kurva beban–perpindahan yang dipakai di dalam studi ini

o

(kekakuan elastik), dan Kh (kekakuan paska leleh =

strain-hardening). Selama batas-batas lelehnya

be-lum dilampaui, respons mengikuti lintasan elastik

dengan kekakuan Ko. Selanjutnya, setelah terjadi

plastifikasi, hubungan antara P dan δ mengikuti

lin-tasan leleh dengan kekakuan Kh. Dalam kasus

penampang tak simetri, untuk menampung karakte-ristik beban dan perpindahan yang berbeda pada arah momen yang sebaliknya, pada model ini juga dimungkinkan untuk memasang batas-batas leleh

yang berbeda, yaitu : Py ini sangat populer karena kesederhanaannya. Uraian yang lebih rinci mengenai model ini dapat dijumpai

pada beberapa textbook standar, misalnya buku

yang ditulis oleh Mario Paz [6].

Model yang kedua, sebagai yang diperlihatkan pada Gambar 5-(b), merupakan pengembangan mo-del yang sebelumnya. Karakteristik responsnya se-cara umum sama dengan model yang pertama, ha-nya saja pada model ini terjadi deteriorasi (kerusak-an) pada kekuatannya, sehingga batas beban yang sanggup dipikulnya pada suatu siklus akan lebih

kecil daripada siklus sebelumnya : Py(n)

Pada model yang keempat, sebagai yang terlihat

pada Gambar 5-(d), lintasan-lintasan unloading dan

reloading ditempuh dengan berorientasi pada

pun-cak-puncak (vertex) respons siklus sebelumnya

de-ngan mendapatkan koreksi dari degradasi kekakuan dan deteriorasi kekuatannya. Hal yang hampir sama . Untuk itu, suatu faktor yang

disebut strength decay parameter diperkenalkan

masuk ke dalam model ini.

Model yang ketiga, sebagai yang diperlihatkan pada Gambar 5-(c), pertama kalinya dipublikasikan

oleh Takeda dkk. pada tahun 1970. Model yang

semula bercirikan trilinier ini kemudian

disederha-nakan oleh Otani dkk. pada tahun 1981 menjadi

bilinier saja. Dengan model ini, respons menempuh

lintasan-lintasan unloading dan reloading dengan

kekakuan yang selalu berubah, yang besarnya ter-gantung pada respons yang dicapai pada siklus sebelumnya. Model ini, walaupun cukup populer, tetapi memiliki keterbatasan pemakaian, yaitu hanya bisa dipakai untuk memodelkan penampang-penampang yang simetri saja. Hal ini bisa dimak-lumi, karena pada awalnya dia dikembangkan untuk struktur kolom yang mendapatkan pembebanan lateral. Untuk uraian dan diskusi yang lebih men-dalam, Pembaca dapat merujuknya pada pustaka yang bersangkutan [8, 5].

(b). Bilinier dengan

(d). Vertex-oriented

(4)

juga terjadi model yang kelima, Gambar 5-(e). Hanya terdapat perbedaan antara keduanya, yaitu model keempat bercirikan bilinier, sedangkan model kelima berupa pendekatan trilinier. Juga, se-pertinya model yang kelima ini lebih cocok untuk mensimulasikan perilaku respons penampang yang menampilkan kemampuan disipasi energi yang lebih besar daripada model yang keempat.

3. IMPLEMENTASI NUMERIK

Berikut ini akan dilakukan analisis numerik un-tuk mendapatkan data respons histeretik dengan menggunakan model-model multilinier sebagai di-sebutkan di atas. Untuk ini akan dipakai spesimen

pengujian SBK yang sudah dilakukan oleh Ma dkk.

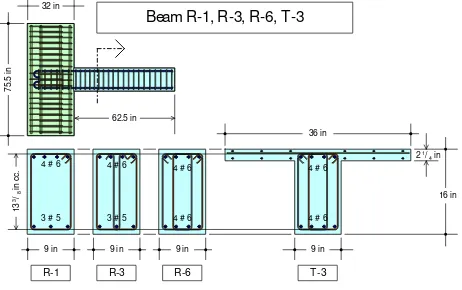
[4]. Data input yang dikehendaki meliputi geometri struktur, ukuran-ukuran penampang, tata letak pe-nulangan, sifat-sifat bahan, dan skema pembebanan siklik yang dipakai. Data ringkas dari spesimen uji disampaikan pada Gambar 6.

Gambar 6

4. DISKUSI PADA HASIL STUDI

: Spesimen SBK dari pengujian Ma yang dipakai di dalam studi ini..

Dengan mengacu Gambar 2-(b) di depan, maka plastifikasi diasumsikan terjadi pada suatu daerah yang sangat terbatas di ujung jepit balok, sedemi-kian sehingga bisa dianggap sebagai sendi plastik. Data sendi plastik dapat dipersiapkan dengan me-manfaatkan beberapa tata langkah perhitungan yang telah terpublikasikan [9, 3].

Analisis menghasilkan grafik hubungan beban-perpindahan dari SBK. Data analitik ini kemudian

di-overlay-kan pada data eksperimental untuk

ma-sing-masing spesimen. Cara ini akan memberikan

kemudahan dan kejelasan bagi Pembaca untuk membandingkan antara keduanya. Hasil analisis un-tuk spesimen R-1 disampaikan pada Gambar 7 s/d. 11, untuk menyajikan secara terpisah bagi kelima model. Terlihat pada gambar-gambar tersebut, data

analitik (lintasan warna merah) di-superimpose-kan

pada data eksperimental (lintasan warna biru).

Gambar 7: Spesimen R-1 dengan model bilinier

asimetrik (BA).

Gambar 8: Spesimen R-1 dengan model bilinier

deteriorasi (BD).

: Spesimen R-1 dengan model Takeda

yang disederhanakan (TS).

Gr afi k P - δ Spesi m en R-1 oleh M a

-3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00

Per pi ndahan Uj ung Bebas, δ (i nch)

-3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00

(5)

Dari kelima gambar tersebut terlihat, bahwa yang paling mendekati hasil eksperimental adalah

model vertex-oriented (VO) sebagai yang

disampai-kan pada Gambar 10. Sebagai dapat dilihat pada gambar, bahwa spesimen R-1 menampilkan karak-teristik respons histeretik yang kurus, sehingga mo-del-model yang gemuk, seperti model bilinier asi-metrik (BA) dan bilinier dengan deteriorasi (BD), jelas tidak akan sesuai. Kurusnya grafik yang diha-silkan oleh model Takeda yang disederhanakan (TS) mungkin sesuai dengan karakteristik respons spesimen ini (lihat Gambar 9), tetapi grafik model TS yang simetri menjadikannya tidak cocok untuk diterapkan pada spesimen ini. Sedangkan model tri-linier dengan deteriorasi (TD), walaupun agak mirip

bentuk loop-nya tapi masih agak lebih gemuk

dari-pada data eksperimentalnya.

Gambar 10: Spesimen R-1 dengan model vertex- oriented (VO).

Gambar 11

Spesimen R-3, dengan karakteristik respons his-teretik yang hampir sama dengan spesimen R-1, juga lebih cocok bila didekati dengan model VO.

Terlihat pada Gambar 12, kecocokan terdapat antara grafik eksperimental dengan analitik pada pencapai-an puncak-puncak kekuatpencapai-annya. Dengpencapai-an perkecuali-an pada sedikit siklus-siklus awal dperkecuali-an akhir

pembe-banan, kekakuan-kekakuan unloading dan

reload-ing juga menunjukkan kemiripan antara data

ekspe-rimental dengan analitik.

: Spesimen R-1 dengan model trilinier dengan deteriorasi (TD).

Gambar 12: Spesimen R-3 dengan model vertex- oriented (VO).

-3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00

: Spesimen R-6 dengan model Takeda yang disederhanakan (TS).

Berbeda dengan spesimen-spesimen sebelum-nya, SBK R-6 adalah merupakan penampang perse-gi panjang dengan tulangan yang simetrik. Dengan pemberian skema beban siklik yang simetrik, maka diharapkan responsnya akan menampilkan grafik histeretik yang simetrik pula. Untuk situasi yang se-perti ini, model Takeda yang disederhanakan (TS) akan sangat cocok sekali. Sebagai dapat dilihat pada Gambar 13, terdapat kecocokan antara grafik ekspe-rimental dengan analitik, bukan saja pada pencapai-an puncak-puncak kekuatpencapai-an, melainkpencapai-an juga pada

kekakuan-kekakuan loading–unloading–reloading,

bahkan pada gambaran strain-hardening–nya.

Gr afi k P - δ Spesi m en R-1 oleh M a

-3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00

-4.00 -3.50 -3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00 3.50

-3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00 3.50

(6)

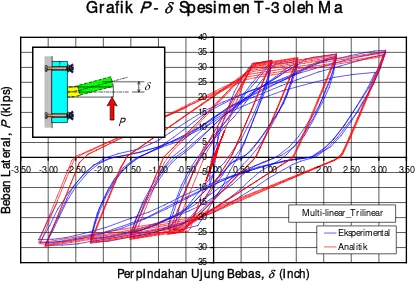
Situasi yang juga berbeda dijumpai pada spesi-men T-3. Spesispesi-men ini, yang mempunyai bentuk penampang balok T dengan tulangan simetrik pada bagian baloknya, menampilkan grafik histeretik yang agak gemuk. Untuk keadaan seperti ini, model trilinier dengan deteriorasi (TD) akan lebih cocok untuk mensimulasikan perilaku responsnya. Sebagai yang dapat dilihat pada Gambar 14, bentuk grafik dari data analitik cocok dengan yang dari data eks-perimental, baik pada kekuatan-kekuatan

puncak-nya, kekakuan-kekakuan

loading–unloading–re-loading-nya, dan juga pada gambaran peristiwa

strain-hardening yang dialaminya. Hanya saja, dari

Gambar 14 ini terlihat grafik analitik yang agak sedikit lebih gemuk dibandingkan dengan hasil eksperimentalnya.

Gambar 14

Secara umum, dari kelima model yang diteliti, hanya model-model TS, VO dan TD yang lebih bisa mewakili perilaku respons histeretik empat spesi-men yang dipilih. Keempat spesispesi-men ini merupakan kondisi umum SBK beton bertulang yang didesain

dengan azas kolom kuat – balok lemah yang umum

dipakai. Dengan ragam keruntuhan yang didominasi oleh lentur, respons akan menampilkan bentuk gra-fik yang pada umumnya gemuk. Ditambah dengan sedikit pengaruh gaya geser, telah menjadikan gra-fik agak sedikit terpipihkan pada bagian tengahnya. Untuk kondisi yang seperti ini, pemakaian model-model multilinier untuk mensimulasikan perilaku responsnya terhadap beban siklik masih menunjuk-kan kesesuaian hasil yang baik. Pemilihan model yang sederhana biasanya diutamakan sebelum

me-mutuskan pemakaian model-model yang lebih cang-gih untuk pertimbangan waktu dan biaya desain.

: Spesimen T-3 dengan model trilinier dengan deteriorasi (TD).

Karakteristik utama lainnya dari SBK beton bertulang yang juga terlihat pada pemakaian ketiga model di atas, adalah terjadinya degradasi kekakuan dan deteriorasi kekuatan. Dikombinasikan dengan

pengaruh strain-hardening, kedua fenomena di atas

akan muncul di dalam grafik respons sebagai jenjang-jenjang permukaan pada puncak-puncak kekuatan. Walaupun tidak pada laju kecepatan yang sama dengan yang ditunjukkan oleh hasil eksperi-mental, model analitik dapat merekam dan menam-pilkan kembali kedua fenomena tersebut dengan baik.

5. KESIMPULAN

Analisis numerik untuk memprediksikan perila-ku respons histeretik sambungan balok-ke-kolom beton bertulang telah dilakukan dengan mengguna-kan pendekatan model multilinier. Keterangan ring-kas tentang matematika model dan sifat-sifat karak-teristiknya telah diuraikan. Model kemudian dite-rapkan untuk mensimulasikan beberapa spesimen eksperimental yang sudah diuji dan dipublikasikan oleh para peneliti sebelumnya.

Implementasi numerik yang dilakukan telah berhasil mengungkapkan fenomena-fenomena pen-ting yang terjadi di dalam SBK yang mendapatkan pembebanan siklik untuk menirukan pengaruh be-ban gempa. Besaran-besaran seperti kekuatan (de-ngan deteriorasinya), kekakuan (de(de-ngan

degradasi-nya), dan strain-hardening telah bisa ditampilkan

kembali dengan baik melalui serangkaian loop-loop

histeretik yang berkesinambungan.

Kekurangan yang dimiliki oleh model multi-linier adalah ketidaksanggupannya untuk mengikuti lintasan-lintasan respons yang tajam melengkung, sehingga akan diperoleh hasil analitik yang lebih gemuk atau lebih kurus bila dibandingkan dengan data eksperimentalnya. Akibat yang ditimbulkannya adalah munculnya selisih pada nilai kapasitas disi-pasi energi antara data yang dihitung dengan yang sebenarnya. Hal ini tidak bisa dihindari, dan hanya bisa diperbaiki dengan penggunaan model-model yang lebih canggih dengan mengakomodasi lintas-an respons ylintas-ang berupa garis-garis lengkung.

KEPUSTAKAAN

-3.50 -3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00 3.50

(7)

[1]. ACI Committee (2008) Building Code

Re-quirements for Structural Concrete (ACI

318-08). Farmington Hills, Michigan, U.S.A., 477

h.

[2]. Badan Standarisasi Nasional (BSN) (2002)

Tata Cara Perencanaan Struktur Beton

un-tuk Bangunan Gedung (SNI 03-2847-2002).

Bandung, Indonesia, 69 h.

[3]. Imbsen & Associates, Inc. (2002) XTRACT –

Cross Section Analysis Program for

Struc-tural Engineers. Downloadable with

registra-tion from URL :

[4]. Ma, S.Y.M., Bertero, V.V. dan Popov, E.P.

(1976) Experimental and Analytical Studies

on The Hysteretic Behavior of Reinforced

Concrete Rectangular and T-Beams. UCB

Report No.: EERC 76-2, California, U.S.A., 267 h.

[5]. Otani, S. (1981) Hysteresis Models of

Rein-forced Concrete for Earthquake Response

A-nalysis. Journal of Faculty of Engineering,

University of Tokyo, Vol. XXXVI, No. 2, h 407-441.

[6]. Paz, M. (1990) Dinamika Struktur – Teori &

Perhitungan. Penerbit Erlangga, Jakarta,

In-donesia, 543 h.

[7]. SeismoSoft, Inc. (2011) SeismoStruct –

Com-puter Program for Static and Dynamic

Non-linear Analysis of Framed Structures.

Down-loadable with registration from URL :

[8]. Takeda, T., Sozen, M.A. dan Nielsen, N.N.

(1970) Reinforced Concrete Response to

Si-mulated Earthquakes. Journal of Structural

Division, ASCE, Vol. 96, No. ST12, h 2557-2573.

[9]. Wahjudi, D.I. (1994) Kajian Perilaku Momen

– Putaran Sudut Elemen Lentur pada Peme-nuhan Kebutuhan Kapasitas dan Daktilitas

Struktur Rangka Portal Beton Bertulang.

Laporan Penelitian No.: 1771/PT12.H4.FTSP /N/1992, Lemlit ITS, Surabaya, 101 h.

[10]. Wahjudi, D.I. (1999) Pengembangan Model

Analitik Perilaku Histeretik Komponen Len-tur Beton Bertulang Terhadap Pembebanan

Siklik. Laporan Penelitian No.: 429/HEP/XII/

(8)