Pengantar Analisis dan Komputasi Metode Numerik

Numerik

1.1Rasionalisasi

Matematika merupakan alat ilmu pengetahuan untuk menyelesaikan berbagai persoalan kehidupan. Dalam hal tersebut, umumnya matematika memiliki tiga cara penyelesaian, yaitu metode Analitik, Numerik dan Simulasi. Metode analitik merupakan cara penyelesaian permasalahan matematika dengan menguraiakan atau menjabarkan variabel-variabelpada model matematika tersebut. Sebagai contoh misalkan dalam menentukan berapa nilai x yang memenuhi agar f(x) = x2 _{– 5x +6 bernilai 0 (nol). Metode analitik yang}

dapat digunakan adalah degan menfaktorkan sebagai berikut:

f(x) = 0  x2 _{– 5x +6=0  (x -3) (x-2) =0}

Pernyataan (x-3)(x-2) = 0 bernilai benar jika x = 3 atau x = 2. Oleh karena itu solusi agar f(x) bernilai 0 diberikan oleh x = 2 atau x = 3. Dalam hal ini, x = 2 dan x = 3 merupakan solusi analitik dari permasalahan tersebut di atas, dan nilai yang diperoleh tersebut bersifat eksak, artinya bahwa solusi yang diperoleh merupakan penyelesaian yang sebenarnya (real) tanpa ada kesalahan (error).

Metode analitik tersebut umumnya hanya dapat menyelesaikan masalah yang sederhana, karena sangat terbatas pada model matematika yang dimiliki dan kemampuan kecepatan berfkir manusia. Sebagai contoh misalnya, berapakah nilai x yag memenuhi agar f(x) = xe-x

+cos(x) bernilai 0 (nol). Tentu saja cara analitik dalam hal ini sulit dapat ditepakan, karena model dari f(x) tidak berbentuk polynomial sementara metode faktorisasi, melengkapi kuadrat sempurna dan lainnya hanya dapat diterapkan pada model fungsi polynomial. Oleh karena itu, diperlukan cara lain, yaitu metode numerik. Metode numerik merupakan cara penyelesaian permasalahan matematika dengan menguraiakan atau menjabarkan bilangan-bilangan pada model matematika tersebut. Beberapa metode yang umumnya digunakan adalah metode Bisection, Regula Falsi, Secant, Newton Raphson dan Fixet Point.

Ripai, S.Pd., M.Si

PERSAMAAN DAN

SISTEM PERSAMAAN NON

LINIER

Numerik

1.2Solusi Persamaan Non Linier

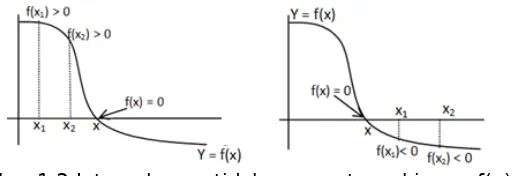
Solusi dari suatu Persamaan Non Linier (PNL) adalah nilai x sehingga suatu fungsi non linier f(x) = 0. Nilai x tersebut akan diperoleh saat kurva f(x) memotong sumbu x.

Gambar 1.1 Solusi persamaan non linier

Andaikan pada sistem koordinat tersebut, sumbu x dipandang sebagai permukaan tanah dan kurva f(x) sebagai pohon, maka solusi dari persamaan non linier tersebut dapat disebut sebagai suatu akar persamaan f(x). Hal ini disebabkan karena kenyataan bahwa nilai x sehingga f(x) = 0 terjadi posisi titik potong kurva f(x) dengan sumbu x. Jadi sesungguhnya terdapat tiga buah pengertian dari solusi persamaan non linier, yaitu:

1). nilai x sehingga f(x) = 0

2). titik potong fungsi f(x) dengan sumbu x 3). akar persamaan suatu fungsi

Terdapat banyak metode yang dapat digunakan untuk mendapatkan solusi dari persamaan non linier tersebut. Lima metode yang paling popular adalah metode Bisection, Regula Falsi, Secant, Newton Raphson dan Fixet Point. Metode Bisection dan Regula Falsi bersifat tertutup sedangkan Secant, Newton Raphson dan Fixet Point bersifat terbuka. Masing-masing metode memiliki kelebihan dan kekurangan Masing- masing-masing. Berikut diberikan penjelasan matematis dari kelima metode tersebut.

1.2.1 Metode Tertutup

Metode tertutup adalah cara penentuan akar persamaan fungsi dengan mengurung akar tersebut dalam suatu interval. Kondisi ini akan terjadi manakala nilai f(x1) f(x2) < 0 atau dengan kata

lain f(x1) berlainan tanda dengan f(x2). Berlainan tanda dalam

Numerik

akan memuat x sehingga f(x) = 0. Dua buah jenis metode tertutup akan dibahas berikut ini, yaitu metode Bisection dan Regula Falsi.

1.2.1.1 Metode Bisection

Bisection tediri dari dua kata, yakni bi = dua dan section = bagian, sehingga metode bisecton merupakan cara penyelesaian persamaan non linier dengan membuat dua buah bagian interval dari domain penyelesaian persamaan non linier tersebut. Proses pembagian interval tersebut mula-mula di awali dengan penentuan interval yang memuat solusi (akar) untuk f(x). Berikut diberikan ilustrasi grafs metode Bisection. 1. Mula-mula pilih x1 dan x2 sembarang sehingga f(x1)f(x2) < 0

Gambar 1.2 Interval yang memuat x sehingga f(x)=0 Pada tahap ini, prinsipnya adalah menentukan lokasi titik potong f(x) dengan sumbu x. Kondisi ini terjadi apabila x1

dan x2 yang dipilih memberikan nilaif(x1) dan f(x2) berlainan

tanda (positif atau negatif) sebagaimana pada gambar 1.2 di atas.Hal ini dapat ditentukan dengan jika f(x1)f(x2) < 0,

maka diantaranya ada yang negatif dan yang lainnya positif.

Ilustrasi grafs yang mengambarkan pilihan x1 dan x2 yang

salah adalah berikut ini.

Numerik

Gambar 1.3 Interval yang tidak memuat x sehingga f(x)=0

Pada gambar 1.3 di atas, terlihat kemungkinan pilihan x1

dan x2 kurang salah, hal ini disebabkan karena tidak ada x

sehingga f(x) = 0 pada interval x1< x < x2 yang dipilih. Cara

matematis untuk memeriksa hal tersebut adalah f(x1)f(x2) >

0. Artinya jika f(x1)f(x2) > 0, maka pada interval [x1 x2] tidak

memuat x sehingga f(x) = 0. Jika pada interval tersebut nilai akar f(x) dicari, maka tentunya tidak akan pernah ditemukan.

2. Hitung nilai xr = 0.5(x1 + x2)

Gambar 1.4 Model Geometris metode Bisection

Pada tahap ini sesungguhnya dilakukan upaya membagi dua interval akar menjadi dua buah bagian yang sama. Titik baginya disebut xrsehingga bagian-bagian intervalnya

menjadi x1< x < xr dan xr< x < x2.

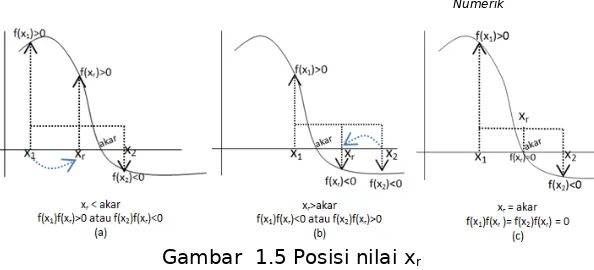
3. Periksaposisi nilai xr dengan

Posisi nilai xr ada tiga kemungkinan, yakni (1). sebelah kiri

Numerik

Gambar 1.5 Posisi nilai xr

4. Perbaharui interval akar persamaan sebelumnya

Pada tahap ini dilakukan pemilihan bagian interval yang memuat akar persamaan. Mengacu kepada gambar 1.5 di atas, maka dapat dikontruksi tolak ukur interval yang baru sebagai berikut:

a) Berdasarkan nilai f(x1).

 Jika f(x1)f(xr) > 0, maka x1 = xr (geser posisi x1 ke

xr)(gambar 1.5 a)

diperoleh interval baru [x1 x2] = [xr x2]

 Jika f(x1)f(xr) < 0, amak x2 = xr (geser posisi x2 ke

xr)(gambar 1.5 b)

diperoleh interval baru [x1 x2] = [x1 xr]

 Jika f(x1)f(xr) = 0, maka akar = xr. (gambar 1.5 c)

interval tidak perlu di buat, karena xr adalah nilai x

sehingga f(x) = 0. b) Berdasarkan nilai f(x2).

 Jika f(x2)f(xr) < 0, maka x1 = xr (geser posisi x1 ke xr)

(gambar 1.5 a)

diperoleh interval baru [x1 x2] = [xr x2]

 Jika f(x2)f(xr) > 0, amak x2 = xr (geser posisi x2 ke xr)

(gambar 1.5 b)

diperoleh interval baru [x1 x2] = [x1 xr]

 Jika f(x2)f(xr) = 0, maka akar = xr. (gambar 1.5 c)

interval tidak perlu di buat, karena xr adalah nilai x

sehingga f(x) = 0.

5. Kembali lagi diulangi membagi interval akar yang baru diperoleh dengan mengikuti langkah 2, 3 dan 4 di atas sehingga diperoleh nilai f(xr) = 0 atau f(xr) sedekat mungkin

dengan 0 (nol).

Numerik

Mencermati uraian proses metode Bisection di atas, maka dapat dirumuskan suatu algoritma program sebagai berikut:

Algortima Program Metode Bisection

Step 0. Mulai

Step 1. Tentukan interval [x1 x2]

Step 2. Hitung nilai f(x1) dan f(x2)

Step 3. Jika f(x1)f(x2) < 0, maka kerjakan step 4 sampai 11

Step 4. Masukan toleransi error (E)

Step 5. Ulangi terus step 6 sampai 11 jika |f(xr)| > e

Step 6. Hitung nilai xr = 0.5(x1 + x2)

Step 7. Hitung nilai f(xr)

Step 8. Jika |f(xr)| > e, maka kerjakan step 9

sampai 11

Step 9. Hitung nilai f(x1)

Step 10. Jika f(x1)f(xr) < 0, maka x2 = xr

Step 11. Jika f(x1)f(xr) > 0, maka x1 = xr

Step .12 Jika f(x1)f(x2) > 0, maka tidak ada akar pada [x1 x2]

Step 13. Selesai

Teladan 1.1

Tentukan nilai x dengan menggunakan metode Bisection sehingga xe-x _{+ 1 = 0 dengan toleransi kesalahan E=0.001.}

Solusi:

Dengan mengembangkan bahasa program standar pada table 1.1 di atas, maka diperoleh output numerik dari solusi masalah teladan 1.1 di atas adalah sebagai berikut:

f(x) = x*exp(-x)+1 [x1 x2] = [-1 0] f(-1) = -1.7183 f(0) = 1

Karena f(x1)f(x2)<0, maka x shg f(x)= 0 pada interval [-1 0] Toleransi Kesalahan = 0.001

Iterasi ke-1

Numerik

Karena |f(xr)| = 0.17564>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-1 -0.5]

Iterasi ke-2

xr = 0.5(x1 + x2) = 0.5(-1 + -0.5) = 0.5(-1.5) = -0.75 f(xr)= -0.58775

Karena |f(xr)| = 0.58775>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)>0, shg x1=xr Jadi interval baru adalah [-0.75 -0.5]

Iterasi ke-3

xr = 0.5(x1 + x2) = 0.5(-0.75 + -0.5) = 0.5(-1.25)

= -0.625 f(xr)= -0.16765

Karena |f(xr)| = 0.16765>0.001=e maka update [x1 x2] Karena f(x1) = -0.58775 maka f(x1)f(xr)>0, shg x1=xr Jadi interval baru adalah [-0.625 -0.5]

Iterasi ke-4

xr = 0.5(x1 + x2) = 0.5(-0.625 + -0.5) = 0.5(-1.125)

= -0.5625 f(xr)= 0.012782

Karena |f(xr)| = 0.012782>0.001=e maka update [x1 x2] Karena f(x1) = -0.16765 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-0.625 -0.5625]

Iterasi ke-5

xr = 0.5(x1 + x2)

= 0.5(-0.625 + -0.5625) = 0.5(-1.1875)

= -0.59375 f(xr)= -0.075142

Karena |f(xr)| = 0.075142>0.001=e maka update [x1 x2] Karena f(x1) = -0.16765 maka f(x1)f(xr)>0, shg x1=xr Jadi interval baru adalah [-0.59375 -0.5625]

Numerik

Iterasi ke-6

xr = 0.5(x1 + x2)

= 0.5(-0.59375 + -0.5625) = 0.5(-1.1563)

= -0.57813 f(xr)= -0.030619

Karena |f(xr)| = 0.030619>0.001=e maka update [x1 x2] Karena f(x1) = -0.075142 maka f(x1)f(xr)>0, shg x1=xr Jadi interval baru adalah [-0.57813 -0.5625]

Iterasi ke-7

xr = 0.5(x1 + x2)

= 0.5(-0.57813 + -0.5625) = 0.5(-1.1406)

= -0.57031 f(xr)= -0.00878

Karena |f(xr)| = 0.00878>0.001=e maka update [x1 x2] Karena f(x1) = -0.030619 maka f(x1)f(xr)>0, shg x1=xr Jadi interval baru adalah [-0.57031 -0.5625]

Iterasi ke-8

xr = 0.5(x1 + x2)

= 0.5(-0.57031 + -0.5625) = 0.5(-1.1328)

= -0.56641 f(xr)= 0.0020354

Karena |f(xr)| = 0.0020354>0.001=e maka update [x1 x2] Karena f(x1) = -0.00878 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-0.57031 -0.56641]

Iterasi ke-9

xr = 0.5(x1 + x2)

= 0.5(-0.57031 + -0.56641) = 0.5(-1.1367)

= -0.56836 f(xr)= 0.0033637

Karena |f(xr)| = 0.0033637>0.001=e maka update [x1 x2] Karena f(x1) = -0.00878 maka f(x1)f(xr)>0, shg x1=xr Jadi interval baru adalah [-0.56836 -0.56641]

Numerik

= 0.5(-0.56836 + -0.56641) = 0.5(-1.1348)

= -0.56738 f(xr)= -0.00066198

Karena |f(xr)| = 0.00066198<0.001=e maka proses berhenti Jadi akar persamaan adalah x = 0.56738 dengan f(xr) = -0.00066198

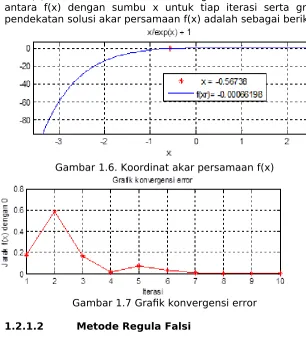
Dari hasil perhitungan di atas, untuk mendapatkan nilai x sehingga f(x) dekat dengan 0.001 dibutuhkan 10 iterasi (proses pengulangan perhitungan) dengan nilai x = -0.56738 dan f(x) = -0.00066198. Garfk konvergensi error atau seleisih antara f(x) dengan sumbu x untuk tiap iterasi serta grafk pendekatan solusi akar persamaan f(x) adalah sebagai berikut:

Gambar 1.6. Koordinat akar persamaan f(x)

Gambar 1.7 Grafk konvergensi error

1.2.1.2 Metode Regula Falsi

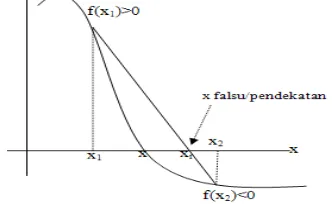
Metode Regula Falsi merupakan cara menentukan akar persamaan suatu fungsi, dengan melakukan pengulangan akar falsu yang dibentuk dari perpotongan garis yang melalui titik

Numerik

(x1,f(x1)) dan (x2, f(x2)) dengan sumbu x. Ilustrasi grafs sebagai

berikut:

Gambar 1.8 Posisi akar falsu dengan

Persamaan garis yang melalui titik (x1,f(x1)) dan (x2,f(x2))

adalah

x−x1

x2−x1=

y−f(x1)

f(x2)−f(x1)

⇒x=(x2−x1)(y−f(x1))

f(x2)−f(x1)

+x1

Jika x = xr, maka diperoleh nilai y = 0. Kenyataan ini

memberikan persamaan regula falsi sebagai berikut:

xr=x1−

f(x1)(x2−x1)

f(x2)−f(x1)

Selanjutnya tahapan-tahapan pengerjaan penentuan akar persamaan f(x) dengan metode Regula Falsi sama dengan tahapan-tahapn sebagaimana metode Bisection.

Gambar 1.9 Proses update interval metode Regula Falsi

Oleh karena itu, algoritma program metode Regula Falsi dapat diberikan sebagai berikut:

Berdasarkan teori di atas, maka algoritma program metode regula falsi dapat dirumuskan sebagai berikut:

Numerik

Step 0. Mulai

Step 1. Tentukan interval [x1 x2]

Step 2. Hitung nilai f(x1) dan f(x2)

Step 3. Jika f(x1)f(x2) < 0, maka kerjakan step 4 sampai 11

Step 4. Masukan toleransi error (E)

Step 5. Ulangi terus step 6 sampai 11 jika |f(xr)| > e

Step 6. Hitung nilai xr

=x1−x2f

(x1)−x1f(x1) f(x2)−f(x1)

Step 7. Hitung nilai f(xr)

Step 8. Jika |f(xr)| > e, maka kerjakan step 9

sampai 11

Step 9. Hitung nilai f(x1)

Step 10. Jika f(x1)f(xr) < 0, maka x2 = xr

Step 11. Jika f(x1)f(xr) > 0, maka x1 = xr

Step .12 Jika f(x1)f(x2) > 0, maka tidak ada kar pada [x1 x2]

Step 13. Selesai

Teladan 1.2

Tentukan nilai x dengan menggunakan metode Regula Falsi sehingga xe-x _{+ 1 = 0 dengan toleransi kesalahan E=0.001.} Solusi:

Penyelesaian dengan program computer setelah mengkonversi algoritma program di atas menjadi algoritma komputasi, maka diperoleh output sebagai berikut:

f(x) = x*exp(-x)+1 [x1 x2] = [-1 0] f(-1) = -1.7183 f(0) = 1

Karena f(x1)f(x2)<0, maka x shg f(x)= 0 pada interval [-1 0] Toleransi Kesalahan = 0.001

Iterasi ke-1

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1)) = -1-(0 - -1)f(-1)/(f(0)-f(-1)) = -1-(1)(-1.7183)/(1 - -1.7183) = -1-(-1.7183)/(2.7183)

= -1-(-0.63212) = -0.36788 f(xr)= 0.46854

Karena |f(xr)| = 0.46854>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr

Numerik

Jadi interval baru adalah [-1 -0.36788]

Iterasi ke-2

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))

= -1-(-0.36788 - -1)f(-1)/(f(-0.36788)-f(-1)) = -1-(0.63212)(-1.7183)/(0.46854 - -1.7183) = -1-(-1.0862)/(2.1868)

= -1-(-0.49669) = -0.50331 f(xr)= 0.16742

Karena |f(xr)| = 0.16742>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-1 -0.50331]

Iterasi ke-3

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))

= -1-(-0.50331 - -1)f(-1)/(f(-0.50331)-f(-1)) = -1-(0.49669)(-1.7183)/(0.16742 - -1.7183) = -1-(-0.85345)/(1.8857)

= -1-(-0.45259) = -0.54741 f(xr)= 0.053649

Karena |f(xr)| = 0.053649>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-1 -0.54741]

Iterasi ke-4

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))

= -1-(-0.54741 - -1)f(-1)/(f(-0.54741)-f(-1)) = -1-(0.45259)(-1.7183)/(0.053649 - -1.7183) = -1-(-0.77767)/(1.7719)

= -1-(-0.43888) = -0.56112 f(xr)= 0.016575

Karena |f(xr)| = 0.016575>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-1 -0.56112]

Iterasi ke-5

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))

Numerik

= -1-(-0.43469) = -0.56531 f(xr)= 0.0050629

Karena |f(xr)| = 0.0050629>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-1 -0.56531]

Iterasi ke-6

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))

= -1-(-0.56531 - -1)f(-1)/(f(-0.56531)-f(-1)) = -1-(0.43469)(-1.7183)/(0.0050629 - -1.7183) = -1-(-0.74692)/(1.7233)

= -1-(-0.43341) = -0.56659 f(xr)= 0.001541

Karena |f(xr)| = 0.001541>0.001=e maka update [x1 x2] Karena f(x1) = -1.7183 maka f(x1)f(xr)<0, shg x2=xr Jadi interval baru adalah [-1 -0.56659]

Iterasi ke-7

xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))

= -1-(-0.56659 - -1)f(-1)/(f(-0.56659)-f(-1)) = -1-(0.43341)(-1.7183)/(0.001541 - -1.7183) = -1-(-0.74473)/(1.7198)

= -1-(-0.43303) = -0.56697 f(xr)= 0.00046855

Karena |f(xr)| = 0.00046855<0.001=e maka proses berhenti

Jadi akar persamaan adalah x = -0.56697 dengan f(xr) = 0.00046855

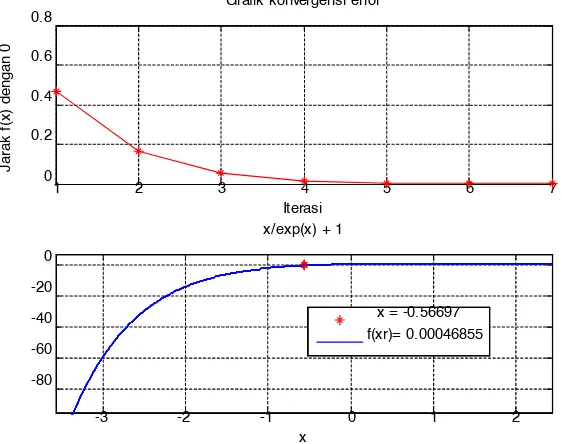
Hasil komputasi di atas, menujukkan bahwa solusi pendekatan untuk x sehingga f(x) = 0 adalah x = -0.56697. Nilai tersebut diperoleh setelah melakukan perhitungan hingga iterasi ke-7. Konvergensi iterasi ini lebih cepat jika dibandingkan dengan metode Bisection. Grafk laju konvergensi dan akar persamaan fungsi diberikan sebagai berikut:

Numerik

Gambar 1.10. Grafk konvergensi dan akar persamaan dengan metode Regula Falsi

1.2.2 Metode Terbuka

Metode terbuka adalah cara penentuan nilai x sehingga f(x) = 0 dengan tidak harus mengurung akar persamaan. Dalam hal ini, interval pencarian atau nilai awal yang diberikan tidak perlu muat akar persamaan. Tiga jenis metode yang tergolong metode terbika diantaranya adalah Metode Secant, Newton Raphson dan Fixet Point.

1.2.2.1 Metode Secant

Metode secant merupakan cara untuk mendapatkan nilai x sehingga f(x) = 0 yang bersifat terbuka, yakni penentuan nilai x1 dan x2 tidak perlu harus mengurung akar persamaan

sebagaimana pada metode Bisection dan Regula Falsi. Proses penentuak akar persamaan dengan metode Sevant adalah sebagai berikut:

1. Mula-mula pilih x1 dan x2 sembarang

2. Melalui titik (x1, f(x1)) dan (x2, f(x2)) tarik garis hingga

memotong sumbu x. Titik potongnya disebut sebagai x3.

Numerik

3. Melalui titik (x2, f(x2)) dan (x3, f(x3)) tarik garis hingga

memotong sumbu x. Titik potongnya disebut sebagai x4.

Gambar 1.10 b.

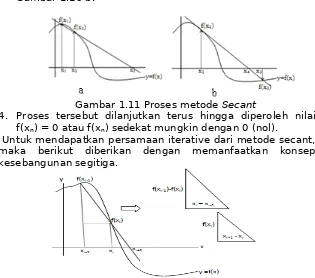
Gambar 1.11 Proses metode Secant

4. Proses tersebut dilanjutkan terus hingga diperoleh nilai f(xn) = 0 atau f(xn) sedekat mungkin dengan 0 (nol).

Untuk mendapatkan persamaan iterative dari metode secant, maka berikut diberikan dengan memanfaatkan konsep kesebangunan segitiga.

Gambar 1.12 Tafsiran geometris metode Secant

Dari dua buah segitiga yang dikontruksi, maka dapat dibuat nilai perbandingan sebagai berikut:

xi+1−xi

xi−xi−1= f(xi)

f(xi−1)−f(xi)⇒xi+1=xi+

(xi−xi−1)f(xi)

f(xi−1)−f(xi)

⇒xi+1=xi−

(xi−xi−1)f(xi)

f(xi)−f(xi−1)

Jadi persamaan iterative dari metode secant adalah

xi+1=xi−(

xi−xi−1)f(xi)

f(xi)−f(xi−1) .

Algoritma Program Metode Secant Step 0. Mulai

Step 1. Defnisikan fungsi f(x) Step 2 Pilih x1 dan x2 sembarang

Step 3. Tetapkan toleransi kesalahan E

Numerik

Step 4. Ulangi terus step 5 dan 6 jika |f(xi+1)| > e

Step 5. Hitung nilai xi+1=xi−

(xi−xi−1)f(xi) f(xi)−f(xi−1)

Step 6. Hitung nilai f(xi+1)

Step 7. Selesai

Teladan 1.3

Tentukan nilai x dengan menggunakan metode Secant sehingga xe-x _{+ 1 = 0 dengan toleransi kesalahan E = 0.001.} Solusi:

Penyelesaian dengan program komputer setelah mengkonversi algoritma program metode Secant di atas menjadi algoritma komputasi, maka diperoleh output sebagai berikut:

f(x) = x*exp(-x)+1 [x1 x2] = [-1 0]

Toleransi error = 0.001 Iterasi ke-1

x3 = x2-(x2-x1)f(x2)/(f(x2-x1) = 0-(0 - -1)(1)/(1 - -1.7183) = 0-(1)(1)/(2.7183)

= 0-(0.36788) = -0.36788

|f(x3)| = |0.46854| = 0.46854 > 0.001 = e, maka Lanjut Iterasi ke-2

x4 = x3-(x3-x2)f(x3)/(f(x3-x2)

= -0.36788-(-0.36788 - 0)(0.46854)/(0.46854 - 1) = -0.36788-(-0.36788)(0.46854)/(-0.53146) = -0.36788-(0.32432)

= -0.6922

|f(x4)| = |-0.38309| = 0.38309 > 0.001 = e, maka Lanjut

Iterasi ke-3

x5 = x4-(x4-x3)f(x4)/(f(x4-x3)

= -0.6922-(-0.6922 - -0.36788)(-0.38309)/(-0.38309 - 0.46854)

= -0.6922-(-0.32432)(-0.38309)/(-0.85163) = -0.6922-(-0.14589)

= -0.54631

Numerik

Iterasi ke-4

x6 = x5-(x5-x4)f(x5)/(f(x5-x4)

= 0.54631(0.54631 0.6922)(0.056595)/(0.056595 -0.38309)

= -0.54631-(0.14589)(0.056595)/(0.43969) = -0.54631-(0.018778)

= -0.56509

|f(x6)| = |0.0056689| = 0.0056689 > 0.001 = e, maka Lanjut

Iterasi ke-5

x7 = x6-(x6-x5)f(x6)/(f(x6-x5)

= -0.56509-(-0.56509 - -0.54631)(0.0056689)/(0.0056689 - 0.056595)

= -0.56509-(-0.018778)(0.0056689)/(-0.050926) = -0.56509-(0.0020903)

= -0.56718

|f(x7)| = |-9.7691e-005| = 9.7691e-005 < 0.001 = e, maka Stop

Jadi akar persamaan adalah x = 0.56718 dengan f(x) = -9.7691e-005

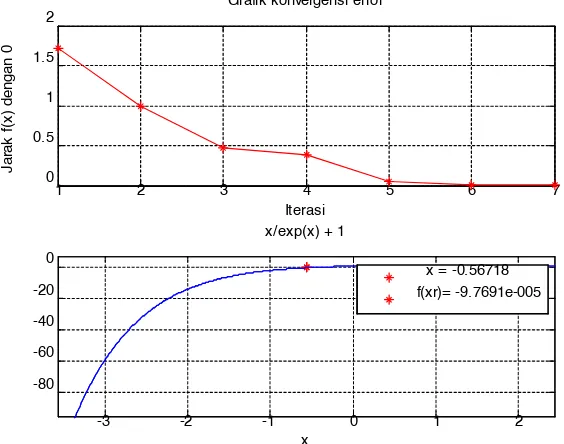
Hasil komputasi di atas diperoleh bahwa, nilai x sehingga f(x) m = 0 atau mendekati 0 (nol) adalah x = -0.56718 dengan f(x) = -0.000097691. Nilai tersebut diperoleh setelah melakukan komputasi hingga iterasi ke-5. Jika dibandingkan dengan tingkat laju konvergensi dengan metode Bisectioan dan Regula Falsi, maka metode Secan lebih cepat laju konvergensinya untuk mendapatkan akar persamaan f(x) = xe-x _{+ 1. Garik laju}

konvergensi tersebut dan posisi titik akar persamaan terlihat pada gambar 1.12 di bawah.

Numerik

Gambar 1.13 Garik konvergensi dan akar persamaan dengan metode Secant

1.2.2.2 Metode Newton Raphson

Metode Newton Raphson merupakan metode terbuka yang hanya membutuhkan sebuah nilai tebakan awal (x0) untuk

mendapatkan solusi dari persamaan non linier. Tahapan-tahapan metode Newton Raphson adalah sebagai berikut: 1. Tentukan sebuah nilai awal sembarang, missal sebut

sebagai xo.

2. Melalui titik (x0, f(x0)), tarik suatu garis singgung kurva

hingga memotong sumbux. Titik potong garis singgung tersebut dengan sumbu x disebut sebagai x1.

3. Selanjutnya melalui titik (x1, f(x1)) tarik garis singgung

kedua hingga memotong sumbu x. Titik potong garis singgung kedua dengan sumbu x dinamakan x2. Berikut

ilustrasi grafs tahapan metode Newton Raphson tersebut. 4. Proses pembuatan garis singgung dan penentuan titik

Numerik

Gambar 1.14 Tafsiran geometris metode Newton Raphson

Berdasarkan model geometris tersebut, dapat diturunkan persamaan iterative untuk metode newton raphson sebagai berikut:

Dari persamaanumum garis melalui titik (a,b) dengan gradient m, maka diperoleh persamaan sebagai berikut:

y−b=m(x−a)⇒x=y_m−b+a=y−_f'f(xi) (xi) +

xi

Untuk kasus pada metode Newton Raphson sebagaimana pada gambar 1.13 di atas, maka jika x= xi+1, maka y = 0 sehingga

diperoleh xi+1=xi−

f(xi)

f'

(xi) . Persamaan

xi+1=xi−

f(xi)

f'

(xi) disebut sebagai formula Newton Raphson.Dari persamaan tersebut, jika jika f’(xi) = 0 atau mendekati nol, maka xi+1 tidak terdefnisi

atau tidak konvergen. Oleh karena itu, dalam pemilihan nilai awal x0 hendaklah dapat memberikan nilai f’(x0) menjauh dari

nilai 0 (nol). Dari uraian di atas, maka algoritma program metode Newton Raphson adalah sebagai berikut:

Algoritma Program Metode Newton Raphson Step 0. Mulai

Step 1. Defnisikan fungsi f(x) Step 2. Tentukan f’(x)

Step 3 Pilih x0

Step 4. Tetapkan toleransi kesalahan E

Step 5. Ulangi terus step 6 dan 7 jika |f(xi+1)| > e

Step 6. Hitung nilai xi+1=xi−

f(xi)

f' (xi) Step 7. Hitung nilai f(xi+1)

Step 8. Selesai

Numerik

Teladan 1.4

Tentukan nilai x dengan menggunakan metode Newton Raphson sehingga xe-x _{+ 1 = 0 dengan toleransi kesalahan E} = 0.001.

Solusi:

Penyelesaian dengan program komputer setelah mengkonversi algoritma program metode Newton Raphson di atas menjadi algoritma komputasi, maka diperoleh output sebagai berikut:

f(x) = x*exp(-x)+1

Turunan Pertama dari f(x)

1 x --- - --- exp(x) exp(x) x0 = -1

Toleransi error = 0.001

x(1) = x0 - f(x0)/df(x0) = -1 - f(-1)/df(-1)

= -1 - (-1.7183)/(5.4366) = -1- (-0.31606)

= -0.68394 f(x1) = -0.35534

Karena |f(x3|>0.001 = e maka iterasi berlanjut

x(2) = x1 - f(x1)/df(x1)

= -0.68394 - f(-0.68394)/df(-0.68394) = -0.68394 - (-0.35534)/(3.337) = -0.68394- (-0.10649)

= -0.57745 f(x2) = -0.028734

Karena |f(x4|>0.001 = e maka iterasi berlanjut

x(3) = x2 - f(x2)/df(x2)

= -0.57745 - f(-0.57745)/df(-0.57745) = -0.57745 - (-0.028734)/(2.8102) = -0.57745- (-0.010225)

= -0.56723 f(x3) = -0.00023889

Karena |f(x5|<0.001 = e maka iterasi berakhir

Numerik

komputasi hingga tiga iterasi. Hal ini menunjukkan bahwa untuk penyelesaian akar dari f(x) = xe-x _{+ 1 mengunakan}

metode Newton Raphson laju konvergensinya lebih cepat jika dibandingkan dengan metode Bisecton, Regula Falsi dan Secan. Garik konvergensi pencapaian nilai f(x) = 0 dan lokasi x sehingga f(x) = 0 sebagaimana yang ditunjukkan pada gambar 1.14 di bawah ini.

1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

0 0.5 1 1.5

Iterasi

|

e

r

r

o

r

|

Grafik konvergensi

-3 -2 -1 0 1 2

-80 -60 -40 -20 0

x x/exp(x) + 1

x = -0.56723

f(x) = -0.00023889

Gambar 1.15. Konvergensi dan lokasi akar persamaan

1.2.2.3 Metode Fixet Point

Metode fxet point atau titik tetap disebut juga sebagai metode iterasi sederhana merupakan cara menentukan nilai x sehingga f(x) = 0 (akar fungsi) dengan cara menentukan nilai x sehingga garis y = x berpotongan dengan suatu fungsi y = g(x) diman fungsi y = g(x) tersebut dibentuk persamaan solusi x dari fungsi f(x).

Numerik

Gambar 1.16. Tafsiran geometris metode Fixet Point

Pada gambar 16.a di atas, mencari nilai x sehingga f(x) = 0 sama artinya dengan mencari nilai x sehingga x = g(x). Proses pencarian terlihat pada ilustrasi gambar 15.b dengan tahapan-tahapan sebagai berikut:

1. Mula-mula pilih nilai tebakan awal, misal sebut sebagai x0

2. Kemudian ditentukan nilai g(x0) dimana nilai ini sama

dengan x1, karena g(x0) berada sejajar dengan y = x1.

3. Selanjutnya dari x1 ditentukan nilai g(x1) dimana nilai

tersebut sama dengan x2. Hal ini disebabkan karena titik

g(x1) sejajar dengan y= x2.

4. Proses menentukan xn = g(xn-1) ini dilakukan hingga nilai

f(xn) = 0 atau dekat dengan 0 (nol).

Proses tersebut akan konvergen ke suatu solusi akar persamaan apabila nilai x0 yang dipilih memberikan |g’(x0)| <

1. Berdasarkan tahapan-tahapan tersebut, maka suatu algoritma program metode Fixet Point sebagai berikut:

Algoritma Program Fixet Point

Step 0. Mulai

Step 1. Defnisikan fungsi f(x) Step 2. Dapat fungsi g(x) dari f(x) Step 3. Tentukan nilai awal (x0)

Step 4. Tentukan toleransi kesalahan (e)

Step 5. Ulangi terus step 6 dan 7 jika |f(xi+1)|>e

Numerik

Step 7. Hitung nilai f(xi+1)

Step 8.Selesai Teladan 1.5

Tentukan nilai x dengan menggunakan metode Fixet Point sehingga xe-x _{+ 1 = 0 dengan toleransi kesalahan E = 0.001.} Solusi:

Penerapan metode fixet Point di awali dengan mendapatkan fungsi g(x) dari f(x) sebagai berikut:

f(x) = 0  xe-x _{+ 1 = 0  x = -e}x _{ g(x) = -e}x_.

Selanjunya proses iterasi yang diterapkan hingga diperoleh akar persamaan diberikan sebagai berikut:

f(x) = x*exp(-x)+1 g(x) = -exp(x) x0 = -1

Toleransi error= 0.001

Iterasi ke-1

x1 = g(x0)= -0.36788

f(x1) = f(-0.36788) = 0.46854

Karena |f(x1)| > 0.001 = e maka proses lanjut Iterasi ke-2

x2 = g(x1)= -0.6922

f(x2) = f(-0.6922) = -0.38309

Karena |f(x2)| > 0.001 = e maka proses lanjut

Iterasi ke-3

x3 = g(x2)= -0.50047

f(x3) = f(-0.50047) = 0.17447

Karena |f(x3)| > 0.001 = e maka proses lanjut

Iterasi ke-4

x4 = g(x3)= -0.60624

f(x4) = f(-0.60624) = -0.11157

Karena |f(x4)| > 0.001 = e maka proses lanjut

Iterasi ke-5

x5 = g(x4)= -0.5454

f(x5) = f(-0.5454) = 0.059034

Karena |f(x5)| > 0.001 = e maka proses lanjut

Numerik

Iterasi ke-6

x6 = g(x5)= -0.57961

f(x6) = f(-0.57961) = -0.034809

Karena |f(x6)| > 0.001 = e maka proses lanjut

Iterasi ke-7

x7 = g(x6)= -0.56012

f(x7) = f(-0.56012) = 0.019308

Karena |f(x7)| > 0.001 = e maka proses lanjut

Iterasi ke-8

x8 = g(x7)= -0.57114

f(x8) = f(-0.57114) = -0.011089

Karena |f(x8)| > 0.001 = e maka proses lanjut

Iterasi ke-9

x9 = g(x8)= -0.56488

f(x9) = f(-0.56488) = 0.0062442

Karena |f(x9)| > 0.001 = e maka proses lanjut

Iterasi ke-10

x10 = g(x9)= -0.56843

f(x10) = f(-0.56843) = -0.0035557

Karena |f(x10)| > 0.001 = e maka proses lanjut

Iterasi ke-11

x11 = g(x10)= -0.56641

f(x11) = f(-0.56641) = 0.002012

Karena |f(x11)| > 0.001 = e maka proses lanjut

Iterasi ke-12

x12 = g(x11)= -0.56756

f(x12) = f(-0.56756) = -0.0011426

Karena |f(x12)| > 0.001 = e maka proses lanjut

Iterasi ke-13

x13 = g(x12)= -0.56691

f(x13) = f(-0.56691) = 0.00064752

Karena |f(x13)| < 0.001 = e maka proses berhentit

Numerik

dengan nilai f(x) = 0.00064752. Nilai tersebut diperoleh setelah menyelesaikan proses iterasi sebanyak 13 kali pengulangan. Hal ini menunjukkan konvergensi metode ini lebih lamban jika dibandingkan dengan metode Bisection, Regula Falsi, Secant dan Newton Raphson untuk mendapatkan x sehingga xe-x _{+ 1 = 0. Kan tetapi jika diperhatikan dari sisi}

model perhitungan, maka tentunya metode Fixet Point tersebut memiliki cara yang lebih sederhana. Grafk konvergensi error tiap iterasi dan lokasi akar persamaan diperlihatkan dalam grafk 1. 16 di bawah ini.

0 2 4 6 8 10 12 14

Grafik k onvergens i

-3 -2 -1 0 1 2

1.3 SOLUSI SISTEM PERSAMAAN NON LINIER

Pada uraian sebelumnya, telah di bahas bagaimana menyelesaikan persaman non linier. Pada bagian ini akan di bahas bagaimana menyelesaikan Sistem Persamaan Non Linier (SPNL). Bentuk umum dari suatu sistem persamaan non linier adalah

diperoleh fungsi dari sistem non linier sebagai berikut:

Numerik

Menurut metode Fixet Point pada bahasan sebelumnya, maka akan terdapat solusi analitik untuk [x1, x2, x3, …, xn] sehingga persamaan non linier berikut.

3x – cos (yz) = 0.5

Sedangkan solusi analitik untuk x, y dan z dari SPNL di atas adalah

sehingga diperoleh fungsi analitik untuk solusi x, y, z pada R3

Numerik

G(x, y ,z)=

{

0.5+cosyz

3 1

9

√

1.06+sinz+x2 3−10π

60 −e

−xy 20

−0.1

1.3.1 Metode Jacobian

Metode Jacobian merupakan cara iteratif menyelesaian sistem persamaan non linier dimana untuk mendapatkan nilai pada iterasi berikutnya digunakan perolehan nilai pada iterasi sebelumnya. Persamaan umum model iterasi meode Jacobian adalah

[

x

1i+1

x

2i+1

⋮

x

ni+1

]

=

G

(

x

1i

, x

2i

,

⋯

, x

in

)

Teladan 1.7

Tentukan nilai x, y, z yang memenuhi Sistem Non Linier pada teladan 1.6 di atas hingga E = 0.00001 dengan mengambil nilai awal x0 = 0.1, y0 = 0.1 dan z0 = -0.1

Solusi:

F

(

x , y, z

)=

{

3

x

−

cos

(

yz

)−

0.5

x

2

−

81

(

y

+

0.1

)

2

+

sin

z

+

1.06

e

−xy

₊

₂₀

_z

₊

10

π

−

3

3

Dengan fungsi analitik solusi untuk x, y dan adalah

G(x, y ,z)=

{

0.5+cosyz

3 1

9

√

1.06+sinz+x2−0.1 3−10π

60 −e

−xy 20

Sehingga persamaan iterative untuk solusi sistem persamaan non linier pada teladan 1.6 di atas adalah

Numerik

maka diperoleh proses iterasi dengan metode Jacobian adalah: Iterasi ke-1

Periksa apakah nilai dari F(x,y,x) <0.001

F

(

x

1

, y

1

, z

1

)=

[

0. 5+cos(0 .009441149603713(-0. 523363310908805))

Numerik

s(i+1,:)=[subs(subs(subs(G,s(i,1)),s(i,2)),s(i,3))]'; h(i,:)=[subs(subs(subs(F,s(i+1,1)),s(i+1,2)),s(i+1,3))]';

end

s =

x y z 0.100000000000000 0.100000000000000

-0.100000000000000

0.499983333472222 0.009441149603713 -0.523101267285757

0.499995934919313 0.000025567746767 -0.523363310908805

0.499999999970157 0.000012336720363 -0.523598136413912

0.499999999993046 0.000000034167906 -0.523598467181241

0.500000000000000 0.000000016487040 -0.523598774744101

0.500000000000000 0.000000000045664 -0.523598775186123

Numerik

0.500000000000000 0.000000000022034 -0.523598775597157

0.500000000000000 0.000000000000061 -0.523598775597748

0.500000000000000 0.000000000000029 -0.523598775598299

0.500000000000000 0 -0.523598775598299

0.500000000000000 0 -0.523598775598299

0.500000000000000 0 -0.523598775598299

0.500000000000000 0 -0.523598775598299

0.500000000000000 0 -0.523598775598299

0.500000000000000 0 -0.523598775598299

h =

f1(x,y,z) f2(x,y,z)

f3(x,y,z)

-0.000037804341275 -0.159752332905067 0.005240872460956

-0.000012195152531 -0.000214383250450 0.004696510102141

-0.000000000068666 -0.000199313677479 0.000006615346582

-0.000000000020862 -0.000000286430100 0.000006151257203

0 -0.000000266350320 0.000000008840434

0 -0.000000000382802 0.000000008220688

0 -0.000000000355966 0.000000000011815

0 -0.000000000000512 0.000000000010989

0 -0.000000000000477 0.000000000000002

0 0.000000000000000 0.000000000000002

Numerik

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

Hasil komputasi sampai iterasi ke-10 menunjukkan bahwa nilai pendekatan untuk x = 0.5, y = 0 dan z = -0.523598775598299 dengan perolehan nilai F(x,y,z)=[0 0 0.000000000000002]. Nilai ini sudah dipandang mendekati 0 (nol).

Teladan 1.8.

Tentukan nilai x dan y dari system persamaan non linier berikut:

x2_{+ y}2 _{= 4}

e-x _{+ y = 1}

Solusi:

Dari SPNL yang diketahui, maka fungsi dari R2 _{ R}2 _{untuk SPNL}

tersebut adalah

F

(

x , y

)=

{

x

2

₊

_y

2

₋

₄

e

y

₊

_y

₋

₁

dengan solusi analitiknya

adalah

G

(

x, y

)=

{

√

4

−

y

2

1

−

e

x

Untuk menentukan nilai awal, maka sangat baik dengan mengambar grafk sehingga diketahui persekitaran dari nilai x dan y.

Numerik

x

y

y + exp(x ) - 1 = 0

X= -1.8421 Y = 0.83271 Lev el= -0.0087978

-6 -4 -2 0 2 4 6

-6 -4 -2 0 2 4 6

Gambar 1.18 Grafk koordinat nilai awal untuk x dan y

Salah satu solusi dari SPNL tersebut adalah berada pada sekitar nilai x = -1.8 dan y = 0.8 dengan nilai F1.8,0.8) = (-0.12, -0.034). Nilai tersebut masih belum dekat dengan 0 (nol) sehingga perlu dilakukan upaya mendapatkan nilai pendekatan dengan proses iterasi Jacobian sebagai berikut:

Iterasi 1.

[

x

1

y

1

]

=

G

(

x

₀

, y

₀

)=

[

√

4

−

y

0

2

1

−

e

x0

]

=

[

1.833030277982336

-5.049647464412947

]

F

(

x

₁

, y

₁

)=

[

1.83303027798233

2

+

-5.04964746441294

2

−

4

e

1 .83303027798233

+

-5.04964746441294

−

1

]

=

[

24.858939514852100

0.203158254125826

]

Pada iterasi 1 di atas, terlihat nilai F(x1,y1) menjauhi 0 (nol). Hal

ini memberikan harapan kecil untuk dapat konvergen. Pemeriksaan secara secap dengan pemograman komputer berikut dilakukan

syms x y

Numerik

h=[subs(subs(F,s(1)),s(2))]';

for i=1:5

s(i+1,:)=[subs(subs(G,s(i,1)),s(i,2))]'; h(i+1,:)=[subs(subs(F,s(i+1,1)),s(i+1,2))]';

end

s =

-1.8000 0.8000 -1.8330 -5.0496 -0.0000 + 4.6367i -5.2528

-0.0000 + 4.8572i 1.0756 + 0.9971i -2.0290 - 0.5286i 0.8557 + 0.9895i -2.0999 - 0.4033i -5.5681 + 3.8361i

h =

-0.1200 -0.0347 24.8589 -5.8897 2.0930 + 0.0000i -6.3284 + 0.9971i -27.4293 - 2.1451i 0.2199 - 0.0076i -0.4096 - 3.8387i -0.0307 - 0.9232i

16.5348 +41.0263i -6.4555 - 3.7881i

Dari output komputasi tersebut, diketahui bahwa nilai perolehan x dan y yang disimpan dalam variable s tidak konvergen menuju suatu solusi tunggal. Hal tersebut terlihat dari nilai yang tidak tetap. Lebih lanjut pemeriksaan nilai terhadap Fungsi dari System Non Linier F(x,y) terlihat bahwa nilai yang diperoleh tiap iterasi tidak menuju 0 (nol). Bahkan memuat bilangan imajiner. Kenyataan ini menunjukkan bahwa persamaan solusi analitik dari G(x,y) yang dirumuskan tidak tepat. Oleh karena itu alternative yang harus dilakukan adalah dengan mengubah formula solusi analitik untuk G(x,y). Formula tersebut dapat diperoleh sebagai berikut:

x2_{+ y}2 _{= 4  y =±}

√

4

−

x

2 _{ -}

√

4

−

x

2

ex _{+ y = 1  ln(e}x_{) = ln(1-y)  x = ln(1-y)}

sehingga diperoleh fungsi solusi dari SPNL adalah

G(x, y)=

{

ln(1−y) −

√

4−x2

Iterasi ke-1

Numerik

[

x1

y1

]

=G(x0, y0)=

[

ln(1−y0)

−

_√

4−x02

]

=

[

ln(1−0.8) −

_√

4−(−1.8)2

]

=

[

-1.609437912434101 -0.871779788708135

]

F

(

x

₁

, y

₁

)=

[

-1.609437912434101

2

₊

_{-0.871779788708135}

2

₋

₄

e

-1.609437912434101

+

-0.871779788708135

−

1

]

=

[

-0.649709606019764

-1.671779788708135

]

Nilai F(x,y) masih belum dekat dengan 0 (nol) sehingga perlu iterasi berikutnya.

Iterasi ke-2

[

x2

y2

]

=G(x1, y1)=

[

ln(1−y1)

−

_√

4−x12

]

=

[

ln(1−(-0.871779788708135)) −

_√

4−(-1.609437912434101)2

]

=

[

0.626889736898843

-1.187311924483101

]

F

(

x

₂

, y

₂

)=

[

0.626889736898843

2

+

-1.187311924483101

2

−

4

e

0.626889736898843

₊

_{-1.187311924483101}

₋

₁

]

=

[

-2.197299651751135

-0.315532135774966

]

Karena nilai F(x2,y2) masih belum dekat dengan 0 (nol) maka

perlu dilakukan iterasi lanjutan. Simulasi dengan computer hingga iterasi ke-15 diperoleh hasil sebagai berikut:

syms x y

F=[x^2+y^2-4;exp(x)+y-1]; G=[log(1-y);-sqrt(4-x^2)]; s=[-1.8 0.8];

h=[subs(subs(F,s(1)),s(2))]';

for i=1:15

s(i+1,:)=[subs(subs(G,s(i,1)),s(i,2))]'; h(i+1,:)=[subs(subs(F,s(i+1,1)),s(i+1,2))]';

end

s =

Numerik

0.626889736898843 -1.187311924483101 0.782673358174212 -1.899212799496386 1.064439251694108 -1.840495154681017 1.043978387215673 -1.693212650393591 0.990734774838803 -1.705904196321283 0.995436124953814 -1.737367147705144 1.006996563446307 -1.734677757145959 1.006013607047925 -1.727992454036571 1.003565973861763 -1.728564902580873 1.003775794270123 -1.729987091312213 1.004296880728624 -1.729865357430278 1.004252288358007 -1.729562885632886 1.004141481224280 -1.729588778099496 1.004150967118135 -1.729653111373697

h =

-0.120000000000000 -0.034701111778413 -0.649709606019764 -1.671779788708135 -2.197299651751135 -0.315532135774966 0.219586843366598 -0.711900875013285 0.520453334951413 0.058717644815369 -0.043140047573674 0.147282504287426 -0.108335478898543 -0.012691545927692 0.009337684788171 -0.031462951383860 0.023148999929606 0.002689390559184 -0.001978701227093 0.006685303109388 -0.004918713672468 -0.000572448544302 0.000421181269507 -0.001422188731341 0.001046379478628 0.000121733881935 -0.000089565968951 0.000302471797392 -0.000222544357003 -0.000025892466610 0.000019050448994 -0.000064333274201

Dari hasil komputasi ini, terlihat bahwa nilai x dan y yang disimpan dalam variable s pada ietrasi ke-15 sudah terlihat tetap dengan terdapat sedikit perbedaan. Hasil evaluasi nilai pada SPNL dengan mensubtitusikan nilai x dan pada F(x,y) diperleh nilai F(x15, y15) = (0.000019050448994,

-0.000064333274201). NIlai ini sudah dipandang cukup dekat dengan 0 (nol) dimana nilai |F(x,y)| < 0.0001 = 0.01%. Jadi solusi pendekatan yang dapat diambil untuk SPNL teladan 1.16 di atas adalah x = 1.004150967118135 dan y =-1.729653111373697.

Numerik

Mencermati grafk dari SPNL tersebut, solusi lainnya dari SPNL tersebut dapat dilihat pada persekitaran nilai x0 = 1 dan y0 =

-1.8. Hasil komputasi hingga iterasi ke-15 adalah sebagai berikut:

s =

1.000000000000000 -1.800000000000000 1.029619417181158 -1.732050807568877 1.005052538742381 -1.714608951266595 0.998647910329542 -1.729123880572903 1.003980634823037 -1.732830733567027 1.005337970731189 -1.729746479950265 1.004208740397612 -1.728957941826838 1.003919830037943 -1.729614062647804 1.004160230209852 -1.729781770876485 1.004221668593822 -1.729642226607832 1.004170548084132 -1.729606556511231 1.004157480316746 -1.729636236426727 1.004168353588598 -1.729643823081482 1.004171132949492 -1.729637510477604 1.004168820335984 -1.729635896872788 1.004168229193282 -1.729637239499959

h =

0.240000000000000 -0.081718171540955 0.060116144236467 0.067949192431123 -0.049985538603963 0.017441856302282 -0.012832956826945 -0.014514929306308 0.010679466294107 -0.003706852994124 0.002727320294238 0.003084253616761 -0.002269241102947 0.000788538123427 -0.000580169147546 -0.000656120820967 0.000482742791690 -0.000167708228681 0.000123391738258 0.000139544268653 -0.000102670033775 0.000035670096600 -0.000026244363510 -0.000029679915496 0.000021837072759 -0.000007586654754 0.000005581900230 0.000006312603877 -0.000004644514103 0.000001613604817 -0.000001187213790 -0.000001342627171

Numerik

dengan nilai F(x,y) = ( 0.000001187213790 , -0.000001342627171). Nilai ini sudah dianggap dekat dengan 0 (nol) dimana |F(x,y)| < 0.00001 = 0.001%

x

y

y + exp(x) - 1 = 0

X= 1.0346 Y= -1.7916 Lev el= 0.28016

-6 -4 -2 0 2 4 6

-6 -4 -2 0 2 4 6

Gambar 1.19 Nilai pendekatan awal titik x dan y

1.3.2 Metode Gauss Seidel

Metode Gauss Seidel merupakan cara penyelesaian Sistem Persamaan Non Linier dengan menentukan nilai xin+1

berdasarkan nilai xin yang paling baru. Persamaan umum unutk

metode Gauss Seidel diberikan sebagai berikut:

x

1i+1

=

g

1

(

x

i1

, x

2i

,x

3i

⋯

,x

ni

)

x

2i+1

=

g

2

(

x

1i+!

,x

2i

, x

3i

⋯

,x

ni

)

x

3i+1

=

g

3

(

x

1i+!

, x

2i+!

, x

3i

⋯

,x

ni

)

⋮ =

⋮

x

ni+1

=

g

n

(

x

1i+!

, x

2i+!

, x

3i+1

⋯

, x

n−1 i+!

_{, x}

n i

)

Teladan 1.8

Selesaikan SPNL pada teladan 1.6 dan 1.7 di atas mengunakan metode Gaus Seidel.

Solusi:

Bentuk fungsi analitik dari SPNL teladan 9 adalah

Numerik

F

(

x , y, z

)=

{

3

x

−

cos

(

yz

)−

0.5

x

2

−

81

(

y

+

0.1

)

2

+

sin

z

+

1.06

e

−xy

+

20

z

+

10

π

₃

−

3

Sedangkan solusi analitik untuk x, y dan z dari SPNL di atas adalah

x

=

0.5

+

₃

cos

yz

y

=

1

₉

_√

1.06

+

sin

z

+

x

2

−

0.1

z

=

₆₀

3

−

10

π

−

e

−xy

20

sehingga diperoleh fungsi analitik untuk solusi x, y, z pada R3

 R3 _adalah

x

_i+1

=

0.5

+

cos

₃

y

i

z

i

y

i

=

1

₉

√

1.06

+

sin

z

i

+

x

i2+1

−

0.1

z

_i

=

₆₀

3

−

10

π

−

e

−xi+1yi+1

20

Dengan x0 = 0.1, y0=0.1 dan z0 = -0.1, maka diproleh proses

iterasi dengan metode newton raphson adala sebagai berikut:

Iterasi ke-1

xi+1=

0.5+cos((0.1)(−0.1))

3 =0.499983333472222

y

i

=

1

₉

√

1.06

+

sin

(−

0.1

)+

0.499983333472222

2

−

0.1

=

0.022229793558577

z

i

=

₆₀

3

−

10

π

−

e

−(0 .49998333347222) (0 .022229793558577)

20

=

-0.523046126191366

Numerik

F(x1,y1,z1) = (0.000017595631174 ,

-0.399687898596404,0).

Karena maksimum dari |F(x1,y1,z1)|>e, maka iterasi berlanjut

Iterasi ke-2

x

i+1

=

0.5

+

cos

(

0.022229793558577-

(

-0.523046126191366

))

3

=

0.499977468261831

y

_i

=

1

₉

_√

1.06

+

sin

(

-0 .523046126191366

)+

0. 499977468261831

2

−

0.1

=

0.00002815366193

z

i

=

3

₆₀

−

10

π

−

e

−(0.499977468261831) ( 0 .000028153661935)

20

=

-0.523598071793421

Evaluasi nilai x, y dan z pada SPNL diperoleh sebagai berikut:

F(x1,y1,z1) = (0.000067595105857 ,

-0.000478075243740,0).

Karena maksimum dari |F(x1,y1,z1)|>e, maka iterasi berlanjut

Hasil yang lebih dekat dengan 0 (nol) untuk F(x,y,x) diperoleh

dengan melakukan komputasi hingga iterasi ke-10 sebagai

berikut

syms x y z

F=[3*x-cos(y*z)-0.5;...

x^2-81*((y+0.1)^2)+sin(z)+1.06;...

exp(-x*y)+20*z+(10*pi-3)/3]; X=(1/6)+cos(y*z)/3;

Y=(1/9)*sqrt(1.06+sin(z)+x^2)-0.1; Z=(3-10*pi)/60-exp(-x*y)/20;

s=[0.1 0.1 -0.1];

Numerik

h=[subs(subs(subs(F,s(1)),s(2)),s(3))]';

for i=1:10

s(i+1,1)=subs(subs(X,s(i,2)),s(i,3)); s(i+1,2)=subs(subs(Y,s(i+1,1)),s(i,3)); s(i+1,3)=subs(subs(Z,s(i+1,1)),s(i+1,2));

h(i+1,:)=[subs(subs(subs(F,s(i+1,1)),s(i+1,2)),s(i+1, 3))]';

end

s =

0.100000000000000 0.100000000000000 -0.100000000000000

0.499983333472222 0.022229793558577 -0.523046126191366

0.499977468261831 0.000028153661935 -0.523598071793421

0.499999999963783 0.000000037622018 -0.523598774657748

0.500000000000000 0.000000000050280 -0.523598775597042

0.500000000000000 0.000000000000067 -0.523598775598297

0.500000000000000 0.000000000000000 -0.523598775598299

0.500000000000000 0

-0.523598775598299

0.500000000000000 0

-0.523598775598299

0.500000000000000 0

-0.523598775598299

0.500000000000000 0

-0.523598775598299

h =

-1.199950000416665 -2.269833416646828 8.462025345715146

0.000017595631174 -0.399687898596404 0 -0.000067595105857 -0.000478075243740 0 -0.000000000108651 -0.000000608698486 0 0 -0.000000000813452 0

Numerik

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

0 0.000000000000000 0.000000000000002

Hasil komputasi tersebut menunjukkan pendekatan nilai x, y dan z sehingga F(x,y,z) = 0 adalah x = 0.5, y = 0 dan z = 0.523598775598299 dengan perolehan nilai F(x,y,z)= (0 , 0, 0.000000000000002). Nilai ini dianggap sudah sangan dekat dengan 0 (nol). Jika dibandingkan dengan metode Jacobian terlihat bahwa hingga iterasi yang sama (iterasi 10), nilai pendekatan untuk Gauss seidel lebih baik d2engan metode Jacobian. Disisi lain untuk mendapatkan nilai error < 0.001, dengan metode Gauss Seidel diperoleh pada iterasi ke-2 dengan nilai F(x,y,z) = ( -0.000067595105857,-0.000478075243740, 0) sedangkan pada metode Jacobian nilai pendekatan untuk error < 0.01 diperoleh pada iterasi ke-3 dengan nilai x = 0.499999999970157, y = 0.000012336720363 dan z = -0.523598136413912. Nilai F(x,y,z) = ( -0.000000000068666,-0.000199313677479 , 0.000006615346582).

1.3.3 Metode Newton Raphson

Pada pembahasan penyelesaian persmaan non linier mengunkan Metode Newton Raphson diperoleh persamaan

umum xi+1=xi−

f(xi)

f'

(xi) . Karena pada Sistem Non Linier dapat dikontruksi ke dalam bentuk fungsi Rn _{ R}n _sehingga

penyelesaian untuk Sistem Non Linier dapat ditentukan dengan mencari nilai (x1, x2, x3, …, xn) sehingga F(x1, x2, x3, …, xn) = 0,

maka penyelesaian iterative suatu Sistem Non Linier dapat didekati dengan formula Newton Raphson sebagai berikut:

Karena F(x1, x2, .. xn) merupakan fungsi dari suatu system,

maka nilai yang logis untuk F’(x1, x2, …, xn) dapat ditentukan

denganmatriks Jacobian sebagai berikut:

Numerik menyelesaikan system nn linier adalah

[

x1

Diketahui bahwa fungsi dari system non linier tersebut adalah

F

(

x , y, z

)=

{

Turunan pertama menurut dari F(x, y, z) adalah

F'

Numerik Dengan mengambil nilai x0= 0.1, y0 = 0.1 dan z0 = -0.1, maka proses iterasi yang diperoleh sebagai berikut:

Iterasi ke-1

F(x1, y1,z1)=(-0.000339446456206, -0.344387927635970

0.031882377923996)

Nilai ini masih belum mendekati 0 (nol) karena maksimum dari |F(x1,y1,z1| > 0.001 = standar minimal error sehingga proses

Js=subs(subs(subs(J,s(i,1)),s(i,2)),s(i,3)); Fs=subs(subs(subs(F,s(i,1)),s(i,2)),s(i,3)); s(i+1,:)=[s(i,:)'-inv(Js)*Fs]';

Numerik

h(i+1,:)=[subs(subs(subs(F,s(i+1,1)),s(i+1,2)),s(i+1, 3))]';

end

s =

0.100000000000000 0.100000000000000 -0.100000000000000

0.499869672926428 0.019466848537418 -0.521520471935831

0.500014240164219 0.001588591370294 -0.523556964347638

0.500000113467834 0.000012444783322 -0.523598450072889

0.500000000007076 0.000000000775786 -0.523598775578007

0.500000000000000 0.000000000000000 -0.523598775598299

0.500000000000000 0.000000000000000 -0.523598775598299

0.500000000000000 0.000000000000000 -0.523598775598299

0.500000000000000 0.000000000000000 -0.523598775598299

0.500000000000000 0.000000000000000 -0.523598775598299

0.500000000000000 0.000000000000000 -0.523598775598299

h =

-1.199950000416665 -2.269833416646828 8.462025345715146

-0.000339446456206 -0.344387927635970 0.031882377923996

0.000043066370115 -0.025889143215373 0.000042222093535

0.000000340424732 -0.000201222653344 0.000000288134476

0.000000000021227 -0.000000012543080 0.000000000017945

0 0 -0.000000000000002

Numerik

0 0 -0.000000000000002

0 0.000000000000000 0.000000000000002

0 0 -0.000000000000002

0 0.000000000000000 0.000000000000002

Dari komputasi tersebut, konvergensi penyelesaian pendekatan untuk SPNL diperoleh pada ietrasi ke-5 dengan nilai x = 0.5, y = 0 dan z = -0.523598775598299. Hal ini terlihat dari nilai x, y dan z yang tetap untuk iterasi berikutnya. Hasil evaluasi nilai fungsi SPNL diperoleh f(x,y,z) =(0, 0, 0.000000000000002). Nilai ini sudah dipandang sangat dekat dengan 0 (nol) karena nilai maksimum untuk |F(x,y,z)|<0.001 = toleransi kesalahan minimum yang ditetapkan sebelumnya .

1.4 RANGKUMAN

1. Solusi Persamaan Non Liniermerupakan upaya untuk mendapatkan

a. nilai x sehingga suatu fungsi f(x) = 0 b. titik potong fungsi f(x) dengan sumbu x c. akar persamaan suatu fungsi

2. Metode untuk mendapatkan solusi dari persamaan non linier adalah metode tertutup dan terbuka.

3. Metode tertutup merupakan cara menentukan solusi persamaan non linier dengan menutup atau mengurung penyelesaian dalam suatu selang interval kontinu. Metode ini meliputi metode Bisection dan Regula Falsi.

4. Metode terbuka merupakan cara menentukan solusi persamaan non linier dengan tidak mengurung penyelesaian dalam suatu selang interval kontinu. Metode ini meliputi metode Secant, Newton Raphson dan Fixet Point.

5. Formula iterative metode Bisection adalah xr = 0.5 (x1 + x2)

dengan f(x1)f(x2) < 0. Update x1 = xr jika f(x1)f(xr)>0 dan x2

= xr jika f(x1)f(xr)< 0 atau x1 = xr jika f(x2)f(xr)<0 dan x2 = xr

jika f(x2)f(xr)>0.

6. Formula iterative metode Regula Falsi adalah

xr=x1−

x2f(x1)−x1f(x1)

f(x2)−f(x1) _{dengan f(x1)f(x2) < 0. Update x1 =}

Numerik

xr jika f(x1)f(xr)>0 dan x2 = xr jika f(x1)f(xr)< 0 atau x1 = xr

jika f(x2)f(xr)<0 dan x2 = xr jika f(x2)f(xr)>0.

7. Formula iterative metode Secant adalah

xi+1=xi−

dengan syarat konvergensi |g’(x0)|<1.

10. Suatu system yang memuat persamaan non linier disebut system persamaan non linier dan dapat diselesaikan dengan metode Jacobian, Gaus Seidel dan Newton Raphson. 11. Formula iterative metode Jacobian untuk menyelesaikan

SPNL adalah

[

x

1

Numerik

matematika islam yang memberikan dasar dalam peradaban matematika dunia saat ini dengan mengembangkan konsep bilangan Hindu Arab 0 1 2 3 4 5 6 7 8 9. Bilangan tersebut adalah bilangan yang dioperasikan oleh komputer dan yang kita gunakan dalam perhitungan matematika. Sebab itulah, setiap program yang menyatakan urutan langkah dalam penyelesaian dengan computer disebut algoritma. Berikut diberikan kontruksi algoritma komplet metode penyelesaian akar persamaan yang dapat memberikan hasil komputasi proses penyelesaian secara matematis dalam penentuan akar persamaan.

Algoritma Komputasi Metode BIsection 1. clc;

2. clear all;

3. disp('---'); 4. disp('Program : Metode Bisection '); 5. disp('Programer : Ripai, S.Pd., M.Si '); 6. disp('---'); 7. syms x;

8. F=input('f(x) = '); 9. X=input('[x1 x2] = '); 10. f=subs(F,X);

11. disp(['f(',num2str(X(1)),') = ',num2str(f(1))]) 12. disp(['f(',num2str(X(2)),') = ',num2str(f(2))]) 13.if f(1)*f(2)<0

14. disp(['Karena f(x1)f(x2)<0, maka x shg f(x)= 0 pada interval [',...

15. num2str(X(1)),' ',num2str(X(2)),']']) 16. e=input('Toleransi Kesalahan = '); 17. fr=1;c=0;

18. while abs(fr)>e 19. c=c+1; 20. disp(' ')

21. disp(['Iterasi ke-',num2str(c)]) 22. xr=0.5*(X(1)+X(2));

23. fr=subs(F,xr);

24. disp(' xr = 0.5(x1 + x2)')

25. disp([' = 0.5(',num2str(X(1)),' + ',num2str(X(2)),')']) 26. disp([' = 0.5(',num2str(X(1)+X(2)),')'])

27. disp([' = ',num2str(xr)]) 28. disp(['f(xr)= ',num2str(fr)]) 29. E(c)=abs(fr);

Numerik

30. if abs(fr)>e

31. disp(['Karena |f(xr)| = ',num2str(abs(fr)),'>',num2str(e),...

32. '=e maka update [x1 x2]']) 33. f1=subs(F,X(1));

34. if fr*f1<0 35. X(2)=xr;

36. disp(['Karena f(x1) = ',num2str(f1),' maka

f(x1)f(xr)<0, shg x2=xr'])

37. disp(['Jadi interval baru adalah [',num2str(X(1)),...

38. ' ',num2str(X(2)),']']) 39. else

40. X(1)=xr;

41. disp(['Karena f(x1) = ',num2str(f1),' maka

f(x1)f(xr)>0, shg x1=xr'])

42. disp(['Jadi interval baru adalah [',num2str(X(1)),...

43. ' ',num2str(X(2)),']']) 44. end

45. else

46. disp(['Karena |f(xr)| = ',num2str(abs(fr)),'<',num2str(e),...

47. '=e maka proses berhenti']) 48. end

49. end

50. disp(' ')

51. disp(['Jadi akar persamaan adalah x = ',num2str(xr),...

52. ' dengan f(xr) = ',num2str(fr)]) 53. subplot(2,1,1)

54. plot(E,'-*r') 55. grid on

56. xlabel('Iterasi')

57. ylabel('Jarak f(x) dengan 0 ') 58. title('Grafk konvergensi error') 59. subplot(2,1,2)

60. plot(xr,fr,'*r') 61. hold on

62. ezplot(F,[xr-3 xr+3]) 63. grid on

64. legend([' x = ',num2str(xr)],['f(xr)= ',num2str(fr)]) 65.else

66. disp(['Karena f(x1)f(x2)>0, maka tidak ada x shg f(x)=0 pada interval [',...

Numerik

68.end

Algoritma Komputasi Metode Regula Falsi

1. clc; 2. clear all;

3. disp('---'); 4. disp('Program : Metode Regula Falsi '); 5. disp('Programer : Ripai, S.Pd., M.Si '); 6. disp('---'); 7. syms x;

8. F=input('f(x) = '); 9. X=input('[x1 x2] = '); 10. f=subs(F,X);

11. disp(['f(',num2str(X(1)),') = ',num2str(f(1))]) 12. disp(['f(',num2str(X(2)),') = ',num2str(f(2))]) 13.if f(1)*f(2)<0

14. disp(['Karena f(x1)f(x2)<0, maka x shg f(x)= 0 pada interval [',...

15. num2str(X(1)),' ',num2str(X(2)),']']) 16. e=input('Toleransi Kesalahan = '); 17. fr=1;c=0;

18.while abs(fr)>e 19. c=c+1;

20. disp(' ')

21. disp(['Iterasi ke-',num2str(c)]) 22. f=subs(F,X);

23. xr=X(1)-(X(2)*f(1)-X(1)*f(1))/(f(2)-f(1)); 24. fr=subs(F,xr);

25. disp(['xr = x1 - (x2-x1)f(x1)/(fx(2)-f(x1))']) 26. disp([' = ',num2str(X(1)),'-(',num2str(X(2)),' -

',num2str(X(1)),...

27.')f(',num2str(X(1)),')/(f(',num2str(X(2)),

')-f(',num2str(X(1)),'))'])

28. disp([' = ',num2str(X(1)),'-(',num2str(X(2)-X(1)),...

29.')(',num2str(f(1)),')/(',num2str(f(2)),' - ',num2str(f(1)),')']) 30. disp([' = ',num2str(X(1)),'-('

,num2str((X(2)-X(1))*f(1)),')/(',num2str(f(2)-f(1)),')'])

31. disp([' = ',num2str(X(1)),'-(' ,num2str((X(2)-X(1))*f(1)/(f(2)-f(1))),')'])

32. disp([' = ',num2str(xr)])

Numerik

33. disp(['f(xr)= ',num2str(fr)]) 34. E(c)=abs(fr);

35.if abs(fr)>e

36. disp(['Karena |f(xr)| = ',num2str(abs(fr)),'>',num2str(e),...

37.'=e maka update [x1 x2]'])

38. f1=subs(F,X(1)); 39.if fr*f(1)<0 40. X(2)=xr;

41. disp(['Karena f(x1) = ',num2str(f1),' maka f(x1)f(xr)<0, shg

x2=xr'])

42. disp(['Jadi interval baru adalah [',num2str(X(1)),...

43.' ',num2str(X(2)),']']) 44.else

45. X(1)=xr;

46. disp(['Karena f(x1) = ',num2str(f1),' maka f(x1)f(xr)>0, shg

x1=xr'])

47. disp(['Jadi interval baru adalah [',num2str(X(1)),...

48.' ',num2str(X(2)),']']) 49.end

50.else

51. disp(['Karena |f(xr)| = ',num2str(abs(fr)),'<',num2str(e),...

52.'=e maka proses berhenti'])

53.end

54.end

55. disp(' ')

56. disp(['Jadi akar persamaan adalah x = ',num2str(xr),...

57.' dengan f(xr) = ',num2str(fr)])

58. subplot(2,1,1) 59. plot(E,'-*r') 60. grid on

61. xlabel('Iterasi')

62. ylabel('Jarak f(x) dengan 0 ') 63. title('Grafk konvergensi error') 64. subplot(2,1,2)

65. plot(xr,fr,'*r') 66. hold on

67. ezplot(F,[xr-3 xr+3]) 68. grid on

69. legend([' x = ',num2str(xr)],['f(xr)= ',num2str(fr)]) 70.else

71. disp(['Karena f(x1)f(x2)>0, maka tidak ada x shg f(x)=0 pada interval [',...

Numerik

73.end

Algoritma komputasi Metode Secant

1. disp([' = ',num2str(X(c)),'-(',num2str(X(c)-X(c-1)),')(',...

2. num2str(subs(f,X(c))),')/(' ,num2str(subs(f,X(c))-subs(f,X(c-1))),')'])

3. disp([' = ',num2str(X(c)),'-(' ,num2str((X(c)-X(c-1))*subs(f,...

4. X(c))/(subs(f,X(c))-subs(f,X(c-1)))),')']) 5. disp([' = ',num2str(X(c+1))])

6. Fx=subs(f,X); 7. if abs(Fx(end))>e

8. disp(['|f(x',num2str(c+1),')| = |',num2str(Fx(end)),'| = ',...

9. num2str(abs(Fx(end))),' > ',num2str(e),' = e, maka Lanjut']) 10.else

11. disp(['|f(x',num2str(c+1),')| = |',num2str(Fx(end)),'| = ',...

12. num2str(abs(Fx(end))),' < ',num2str(e),' = e, maka Stop']) 13.end

14. c=c+1; 15.end

16. disp(' ')

17. disp(['Jadi akar persamaan adalah x = ',num2str(X(end)),...

18.' dengan f(x) = ',num2str(Fx(end))])

19. subplot(2,1,1) 20. plot(abs(Fx),'-*r') 21. grid on

22. xlabel('Iterasi')

23. ylabel('Jarak f(x) dengan 0 ') 24. title('Grafk konvergensi error') 25. subplot(2,1,2)

26. plot(X(end),Fx(end),'*r') 27. hold on

28. ezplot(f,[X(end)-3 X(end)+3]) 29. grid on

30. legend([' x = ', clc; 31. clear all;

32. disp('---'); 33. disp('Program : Metode secant '); 34. disp('Programer : Ripai, S.Pd., M.Si'); 35. disp('---'); 36. syms x

Numerik

37. f=input('f(x) = '); 38. X=input('[x1 x2] = ');

39. e=input('Toleransi error = '); 40. Fx=subs(f,X);c=2;

41.while abs(Fx(end))>e

42. disp(' ')

43. disp(['Iterasi ke-',num2str(c-1)]);

44. X(c+1)=X(c)-(X(c)-X(c-1))*subs(f,X(c))/(subs(f,X(c))-subs(f,X(c-1)));

45. disp(['x',num2str(c+1),' = x',num2str(c),'-(x',num2str(c), '-x',...

46. num2str(c-1),')f(x',num2str(c),')/(f(x',num2str(c), '-x',num2str(c-1),')'])

47. disp([' = ',num2str(X(c)),'-(',num2str(X(c)),' - ',num2str(X(c-1)),...

48.')(',num2str(subs(f,X(c))),')/(',num2str(subs(f,X(c))),' - ',...

49. num2str(subs(f,X(c-1))),')'])

50. num2str(X(end))],['f(xr)= ',num2str(Fx(end))]) Algoritma Komputasi Metode Newton Raphson 1. clc;

2. clear all;

3. disp('---') 4. disp('Program : Metode Newton Raphson ') 5. disp('Programer : Ripai, S.Pd., M.Si ') 6. disp('---') 7. syms x

8. f=input('f(x) = '); 9. df=diff(f,x);

10. disp('Turunan Pertama dari f(x)') 11. pretty(df)

12. X=input('x0 = '); 13.if abs(subs(df,X))>=1

14. e=input('Toleransi error = '); 15. c=1;

16.while abs(subs(f,X(c)))>e

17. disp(' ')

18. disp(['x(',num2str(c),') = x(',num2str(c-1),') - f(x',...

19. num2str(c-1),')/df(x',num2str(c-1),')'])

20. disp([' = ',num2str(X(c)),' - f(',num2str(X(c)),...

21.')/df(',num2str(X(c)),')'])