1 |2. Model Matematis Sistem Dinamik
MODUL AJAR
2. MODEL
MATEMATIS
SISTEM
DINAMIK
MK. SISTEM PENGENDALIAN
OTOMATIS
4 SKS – TEKNIK FISIKA ITS
2 |2. Model Matematis Sistem Dinamik
pditt.belajar.kemdikbud.go.id
2. MODEL MATEMATIKA SISTEM DINAMIK
Gambaran Umum
Kerangka Bahasan
Bagian terpenting dalam menganalisis dan merancang sistem pengendalian adalah mengetahui model plant yang akan dikendalikan. Model plant bisa dalam bentuk mekanik, listrik, elektrik, fluida, thermal, dll. Pada bagian BAB 2 ini, dijelaskan bagaimana membangun model matematik dari model-model plant tersebut diatas. Serta disajikan bagaimana menentukan variabel masukan-keluaran, serta memilih parameter yang akan menggambarkan karakteristik sistem. Dibahas bagaimana menggambarkan dinamika sistem dalam bentuk fungsi alih. Fungsi matematik yang merupakan perbandingan antara keluaran sistem dan masukan sistem. Fungsi alih inilah yang pada bab-bab selanjutnya akan digunakan untuk menjelaskan dasar pemilihan strategi pengendalian, analisis respon sistem, dan perlakuan perbaikan kinerja sistem pengendalian. Pada Bab ini juga akan disajikan beberapa contoh program MATLAB beserta SIMULINK untuk meningkatkan daya imajinasi Anda, dan Anda bisa belajar pada BAB ini secara interaktif
1. Model Sistem Mekanik,
2. Model Sistem Listrik,
3. Model Sistem Elektronik,
4. Model Sistem Fluida,
5. Model Sistem Thermal,
6. Linierisasi Model Non-linier,
7. Fungsi Alih,
8. Model Matematika Sistem Non-linier.
Tujuan Pembelajaran
1. Mampu menurunkan model matematik berbagai sistem dinamika, mulai dari
fenomena sistem sampai pada pemodelan sistem secara matematik,
2. Mampu menjelaskan variabel-variabel dan parameter-parameter yang
mempengaruhi dinamika sistem,
3. Mampu menggunakan program MATLAB dan SIMULINK untuk menggambarkan
karakteristik sistem dinamik,
4. Mampu membedakan sistem linier dan sistem non-linier yang sering dijumpai dalam
system pengendalian otomatis
5.
Mampu meningkatkan ketrampilan otak, terkait dengan potensi otak untuk
menganalisis dan berlogika.
4 |2. Model Matematis Sistem Dinamik
Pengantar
Pemodelan sistem fisis dengan menggunakan persamaan matematika, sangat diperlukan dalam perancangan sistem pengendalian. Sistem yang ditinjau biasanya sistem mekanika, elektrika, fluida, termodinamika. Dalam pemodelan sistem, sebagai representasi sifat internal digunakan model matematika. Model matematika ini diturunkan berdasarkan hokum-hukum yang berlaku pada sistem mekanika, elektrika, fluida dan thermodinamika dalam bentuk persamaan differensial. Hukum dasar yang digunakan dalam pemodelan adalah hukum kekekalan energi dan massa. Beberapa klasifikasi dari model sistem, dinyatakan sebagai model sistem mekanik, sistem listrik, sistem elektromekanik, sistem termal, sistem fluida. Bentuk persamaan differensial ini memerlukan linierisasi bila menyangkut sistem komplek yang cenderung dinyatakan dalam bentuk persamaan non linier. Bila dinyatakan dalam bentuk linier maka, transformasi Laplace dapat dimanfaatkan untuk menyederhanakan penyelesaian. Linierisasi dilakukan dengan cara pengabaian faktor – faktor yang berkaitan, dan asumsi-asumsi yang diambil. Dengan menggunakan alat matematik, dapat dilakukan penyelesaian yang menggambarkan cara kerja sistem tersebut.
Berikut merupakan penggambaran perlunya model matematik suatu sistem, dimana pada sistem dinamika, dengan adanya eksitasi terhadap sistem maka akan berdampak pada respon yang dihasilkan.
Gambar 2.1 Blok diagram eksitasi pada suatu sistem
Salah satu bentuk model matematis sebuah sistem dinyatakan dalam bentuk persamaan differensial (PD). Beberapa bentuk dari PD yaitu :
1. PD Biasa (Odinary Differential Equation = ODE) 2. PD Parsial (Partial Differential Equation = PDE) 3. PD Perubah Waktu (time variable)
4. PD Koeffisien konstan (Time invariant) 5. PD Linier 6. PD Non Linier
Siste
m
K
o
n
I
n
G
a
R
e
5 |2. Model Matematis Sistem Dinamik
v
i R C Gambar PD-1 Rangkaian RLC i(t) Lv
cv
r2.1 Persamaan Differensial Linier Koefisien Konstan
Langkah pertama dalam analisis sistem adalah mendapatkan model matematik dari sistem, yaitu mendapatkan suatu persamaan matematik yang dapat menggambarkan perilaku sistem. Salah satu bentuk model matematik suatu sistem adalah persamaan diferensial (PD) input-output.
Banyak sistem fisik yang responnya dapat dinyatakan dengan persamaan diferensial, misalnya rangkaian listrik yang tersusun atas resistor, kapasitor dan induktor, sistem mekanik yang terdiri atas pegas, dumper dan lain-lain. Berikut ini dipaparkan sistem yang dinyatakan dalam bentuk persamaan diferensial linier koefisien konstan.
Secara umum, suatu sistem LTI (Linear Time Invariant) waktu kontinyu, dapat dinyatakan dalam bentuk persamaan diferensial linier koefisien konstan sebagai berikut :
1 0 0)
(
)
(
)
(
N i M i i i i i i i N Ndt
t
x
d
b
dt
t
y
d
a
dt
t
y
d
(2.1)
dengan i =1,2,3, . . . ,N-1 , bj , j=1,…M adalah bilangan nyata dan N >M. Dalam bentuk operator D
persamaan diatas dapat ditulis :
)
(
)
(
0 1 0t
x
D
b
t
y
D
a
D
M i i i N i i i N
(2.2)
Untuk menyelesaikan persamaan diferensial tersebut diperlukan N kondisi awal :
) ( ),..., ( ' ), (t0 y t0 y( 1) t0 y N
dengan t0 adalah waktu dimana input x(t) mulai diberikan pada sistem dan y’(t) adalah turunan dari
y(t) . Bilangan bulat N merupakan derajat atau dimensi sistem.
Untuk mendapatkan PD input-output dari suatu sistem, langkah pertama yang harus dilakukan adalah menentukan variabel input dan output. Setelah itu dicari persamaan dari sistem sedemikian hingga yang muncul sebagai variabel hanya input dan output.
Contoh 3.18
Tinjau sistem yang ditunjukkan pada Gambar 2.1. Untuk sistem tersebut misalkan input dan outputnya masing-masing adalah
v
i danv
c.6 |2. Model Matematis Sistem Dinamik
Gambar 2. 1 Rangkaian RLCVariabel output tersebut bersesuaian dengan apa yang ingin diketahui dari sistem. Jika yang ingin diketahui adalah arus yang mengalir, maka variabel output yang dipilih adalah i(t). Bila yang ingin
diketahui adalah tegangan di R maka dipilih
v
r sebagai output. Persamaan yang berlaku untuk rangkaian Gambar 2.1 adalah : idt C dt di L iR vi 1
(2.3)
1 idt C vc(2.4)
sehingga c i v dt di L iR v (2.5)
Persamaan (2.3) bukan persamaan PD input-output, karena di dalamnya masih terdapat variabel lain yaitu
i
(t
)
. Karena itu, variabeli
(t
)
harus dieliminir.Dari Persamaan (2.4) diperoleh :
dt
dv
C
i
c(2.6)
sehingga Persamaan (2.3) dapat ditulis kembali sebagai berikut
c c c i
v
dt
v
d
LC
dt
dv
RC
v
2 2 atau c c c iv
dt
dv
RC
dt
v
d
LC
v
2 2(2.7)
Persamaan (2.7) merupakan PD input-output.
7 |2. Model Matematis Sistem Dinamik
Pada teori pengendalian konvensional, yang menjadi penting adalah sinyal masukan, sinyal keluaran dan sinyal kesalahan. Dalam menganalisa sinyal keluaran, maupun kesalahan melalui fungsi alih. Kelemahan dalam teori ini adalah hanya dapat diterapkan pada sistem linier dengan parameter konstan dengan satu masukan dan satu keluaran. Teori ini tidak dapat diterapkan pada sistem dengan parameter yang berubah (time varying), sistem non linier maupun sistem dengan multi masukan dan multi keluaran. Hal ini tidak bisa kita lakukan untuk merancang sistem pengendalian adaptif dan optimal, karena kedua metode tersebut sebagian besar diaplikasikan pada sistem dengan parameter berubah dan sistem non linier.
Suatu pendekatan baru dalam teori pengendalian modern, dimana teori ini berkembang sejak diketemukannya perangkat komputer. Pendekatan baru ini didasarkan pada konsep keadaan (state). Sebelum kita membahas persamaan ruang keadaan, terlebih dahulu dibahas beberapa istilah yang akan digunakan dalam bab ini. Hal – hal yang penting untuk dipahami adalah mengenai Keadaan (state), Variabel keadaan, Vektor keadaan .
Keadaan (state), keadaan suatu sitem dinamik adalah himpunan terkecil dari variabel-variabel (disebut
variabel keadaan) sedemikian rupa sehingga dengan mengetahui varibel-variabel ini pada t=to,
bersama-sama dengan masukan untuk tto, dapat menentukan secara lengkap perilaku sistem untuk
setiap waktu tto. Jadi, keadaan suatu sistem dinamik pada saat t secara unik ditentukan oleh keadaan
tersebut pada t=to dan masukan untuk tto, tidak tergantung pada keadaan dan masukan sebelum to.
Perhatikan bahwa dalam membahas sistem linier parameter konstan, biasanya dipilih waktu acuan to
sama dengan nol.
Variabel keadaan, variabel keadaan suatu sistem dinamik adalah himpunan terkecil dari
variabel-varibel yang menentukan keadaan sistem dinamik. Jika paling tidak diperlukan n variabel x1(t),x2(t),…,xn(t) untuk melukiskan secara lengkap perilaku suatu sistem dinamik (sedemikian rupa
sehingga setelah diberikan masukan untuk tto dan syarat awal pada t=to maka keadaan sistem yang
akan datang telah ditentukan secara lengkap), maka n variabel x1(t),x2(t),…,xn(t) tersebut merupakan
suatu himpunan variabel keadaan. Variabel keadaan tidak perlu merupakan besaran yang secara fisis dapat diukur atau diamati. Meskipun demikian sebaiknya dipilih variabel keadaan yang merupakan besaran dapat diukur secara mudah, karena hukum pengendalian optimal memerlukan umpan balik semua variabel keadaan dengan pembobotan yang sesuai.
Vektor keadaan, jika diperlukan n variabel keadaan untuk menggambarkan secara lengkap perilaku
suatu sistem yang diberikan, maka n variabel keadaan ini dapat dianggap sebagai n komponen suatu vektor x(t). Vektor semacam ini disebut vektor keadaan. Jadi vektor keadaan adalah suatu vektor yang
8 |2. Model Matematis Sistem Dinamik
menentukan secara unik keadaan sistem x(t) untuk setiap tto, setelah ditetapkan masukan u(t) untuk
tto.
Ruang keadaan, ruang n dimensi yang sumbu koordinatnya terdiri dari sumbu x1, sumbu x2,…, sumbu
xn disebut ruang keadaan. Setiap keadaan dapat dinyatakan dengan suatu titik pada ruang keadaan.
Contoh Soal 2-1:
Perhatikan sistem rangkaian RLC yang ditunjukan pada Gambar 2.1 di atas. Perilaku dinamika sistem dapat dilihat secara lengkap untuk tto jika harga-harga awal dari arus i(to),tegangan kapasitor vc(to),
dan tegangan masukan v(t) untuk tto diketahui. Jadi keadaan rangkaian tersebut untuk tto secara
dinyatakan sebagai i(t), vc(t) dan tegangan masukan v(t) untuk v(t) untuk tto. Maka dari itu, i(t) dan
vc(t) merupakan suatu himpunan variabel keadaan dari sistem tersebut. Pemilihan variabel keadaan
tunak suatu sistem adalah tidak unik, sebagai contoh, pada sistem ini bisa dipilih sebagai himpunan variabel keadaan adalah x1(t )= vc(t)+Ri(t) dan x2(t) = vc(t).
Jawab :
Misalkan dipilih i(t) dan vc(t) sebagai variabel keadaan, maka persamaan yang menggambarkan
dinamika sistem elektrik RLC adalah,
i
dt
dv
C
v
v
Ri
dt
di
L
c c
dalam notasi matrik-vektor, dituliskan sebagai berikut,
L
v
v
i
C
L
L
R
v
i
c c
0
1
0
1
1
ini merupakan penyajian persamaan ruang keadaan dari sistem rangkaian RLC.
Soal Latihan 2-1:
Perhatikan rangkaian listrik RLC seperti Gambar 5.2 di bawah. Bila ditentukan sebagai variabel keadaan adalah arus yang melalui induktor dan tegangan pada kapasitor C1 dan C2. Tentukan persamaan ruang keadaan sistem.
9 |2. Model Matematis Sistem Dinamik
Gambar 2. 2 Rangkaian RLC dengan loop lebih dari satu.Analisis sistem komplek, sistem modern yang komplek mungkin mempunyai beberapa masukan dan
beberapa keluaran, dan ini mungkin saling terkait secara komplek pula. Untuk menganalisis sistem seperti ini, perlu penyederhanaan model matematik. Untuk perhitungan yang berulang-ulang sangat membantu jika menggunakan komputer. Berdasarkan pandangan ini maka pendekatan yang paling sesuai pada analisis sistem adalah pendekatan ruang keadaan.
Teori pengendalian konvensional adalah berdasarkan pada hubungan masukan dengan keluaran sistem atau fungsi alih, sedangkan teori pengendalian modern berdasarkan pada diskripsi persamaan sistem dalam bentuk n persamaan diferensial orde pertama, yang dapat digunakan menjadi persamaan diferensial matrik-vektor orde pertama. Penggunaan notasi matrik-vektor akan sangat menyederhanakan penyajian model matematika dari persamaan sistem.
Penggunaan metode ruang keadaan untuk analisis suatu sistem, sangat sesuai jika menggunakan komputer digital, karena pendekatannya adalah wawasan waktu. Sehingga terhindar dari kebosanan dan kesulitan pada saat terjadi perhitungan berulang dan lebih mudah untuk menyelesaikan sistem-sistem yang berorde tinggi, ini adalah salah satu keunggulan penggunaan metode ruang keadaan.
Hal lain penting untuk diperhatikan, bahwa variabel keadaan tidak perlu menyatakan besaran-besaran fisis dari sistem. Variabel yang tidak menyatakan besaran-besaran fisis, yang tidak dapat diukur atau diamati, dapat dipilih sebagai variabel keadaan. Kebebasan dalam memilih varibel keadaan ini merupakan keunggulan lain dari metode ruang keadaan.
Persamaan Ruang Keadaan Orde-n, dengan fungsi penggerak u.
Suatu sistem persamaan diferensial orde-n dinyatakan sebagai berikut,
u y a y a y a y n n n n 1 ) 1 ( 1 ) ( ... … (2.8)
dengan perolehan data sebelumnya : (0), (0),... (0)
) 1 (n
y y
y bersama dengan masukan u(t) untuk t0,
menentukan secara lengkap perilaku yang akan datang dari sistem, maka dapat dipilih
) ( ),... ( ), ( ) 1 ( t y t y t y n
sebagai himpunan n variabel keadaan. Secara matematis, pemilihan varibel keadaan semacam itu adalah cukup mudah. Akan tetapi secara praktis, karena ketidak telitian bentuk turunan orde tinggi yang disebabkan oleh pengaruh noise inhern pada setiap kondisi praktis, maka pemilihan variabel keadaan semacam itu tidak diinginkan. Selanjutnya didefinisikan,
) 1 ( 2 1
...
n ny
x
y
x
y
x
10 |2. Model Matematis Sistem Dinamik
selanjutnya persamaan 9.1 dapat dituliskan kembali sebagai berikut,
u
x
a
x
a
x
x
x
x
x
x
x
n n n n n
1 1 1 3 2 2 1...
.
...
atau dalam bentuk persamaan ruang keadaan (matrik-vektor),
Bu
Ax
x
…(2.9) dimana,
1
0
:
0
0
,
..
1
0
0
0
:
:
:
0
..
1
0
0
0
..
0
1
0
,
.
:
1 2 1 2 1B
A
x
a
a
a
a
x
x
x
n n n n
persamaan keluaran menjadi,
n nx
x
x
x
y
1 2 10
...
0
1
atau,Cx
y
…(2.10) dimana, C=[1 0 …0]Persamaan (2.9) adalah persamaan diferensial orde pertama yang disebut dengan persamaan keadaan, sedangkan persamaan (2.10) disebut persamaan keluaran.
Contoh Soal 2-2:
Sistem didefinisikan oleh persamaan diferensial sebagai berikut :
u y y y y6116 6 …(2.11)
dimana y adalah keluaran dan u adalah masukan sistem. Tentukan penyajian ruang keadaan dari sistem yang dinyatakan pada persamaan (2.11) tersebut di atas.
11 |2. Model Matematis Sistem Dinamik
Dipilih variabel keadaan sebagai berikut,y
x
y
x
y
x
3 2 1 Selanjutnya diperoleh,u
x
x
x
x
x
x
x
x
6
6
11
6
1 2 3 3 3 2 2 1
Persamaan terakhir dari dari tiga persamaan ini diperoleh dengan menyelesaikan persamaan diferensial asal (persamaan 5.4) untuk suku turunan yang tertinggi dan kemudian mensubtitusikan persamaan yang kedua ke persamaan yang ketiga. Dengan menggunakan notasi matrik-vektor, tiga persamaan diferensial orde pertama ini dapat digabungkan menjadi satu sebagai berikut,
u
x
x
x
x
x
x
6
0
0
6
11
6
1
0
0
0
1
0
3 2 1 3 2 1
…(2.12)persamaan keluaran dinyatakan oleh,
3 2 10
0
1
x
x
x
y
…(2.13)persamaan (5.5)dan (5.6) dapat ditulis dalam bentuk standar sebagai berikut,
Cx
B
Ax
x
y
u
…(2.14) dimana,
1
0
0
6
0
0
,
6
11
6
1
0
0
0
1
0
B
C
A
Gambar 2.3 menunjukkan penyajian diagram blok dari persamaan keadaan dan persamaan keluaran (2.12) di atas. Perhatikan bahwa fungsi alih dari blok-blok umpan balik tersebut identik dengan koefisien negatif dari persamaan diferensial asal persamaan (2.12),
12 |2. Model Matematis Sistem Dinamik
Gambar 2. 3 Penyajian diagram blok sistem contoh soalSoal Latihan 2.2:
Sistem didefinisikan oleh persamaan diferensial sebagai berikut :
u y y y y 4 6 8 10 2
dimana y adalah keluaran dan u adalah masukan sistem. Tentukan penyajian ruang keadaan dari sistem tersebut diatas.
2.3 Model Sistem Mekanik
Sistem mekanik terdiri dari komponen yang mempunyai sifat seperti pegas, disipasi energi (damper – peredam), beban dengan massa tertentu, inersia, dan torsi. Sebagai contoh pada mobil, yang mempunyai respon dinamik seperti kecepatan, lintasan, putaran pada roda. Sistem suspensi dan badan mobil mempunyai respon dinamik berupa perubahan posisi saat mobil tersebut mengenai lonjakan pada jalan. Bentuk ini menggambarkan pemodelan sistem mekanik yang bisa dinyatakan dengan persamaan differensial orde-n. Besaran dari sistem mekanik dalam SI – Satuan Internasional seperti pada Tabel 2.1.
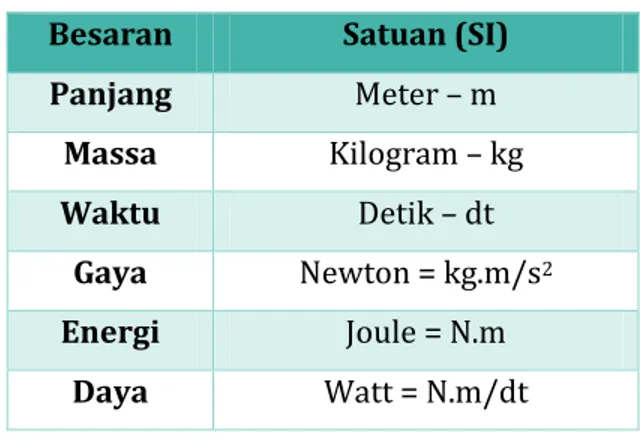
Tabel 2.1 Satuan SI untuk besaran Mekanika
Besaran Satuan (SI) Panjang Meter – m Massa Kilogram – kg Waktu Detik – dt Gaya Newton = kg.m/s2 Energi Joule = N.m Daya Watt = N.m/dt
Tiga elemen dasar yang membentuk sistem mekanik yaitu : elemen inersia, pegas dan peredam. Elemen inersia menyangkut massa dan momen inersia. Pada inersia massa dan momen inersia merupakan perubahan gaya / torsi yang diperlukan untuk membuat perubahan satu satuan percepatan / percepatan sudut. Elemen pegas adalah elemen mekanik yang dapat berubah akibat adanya gaya luar, dimana perubahan bentuk ini berbanding langsung dengan gaya / torsi yang digunakan. Sedangkan elemen peredam merupakan elemen mekanik yang menghilangkan energi dalam bentuk panas dan tidak menyimpannya.
13 |2. Model Matematis Sistem Dinamik
Gambar 2. 4 Sistem translasi mekanik.Misalnya sebagai contoh sistem translasi mekanik, terdiri dari sebuah pegas dengan tetapan K, sebuah damper dengan koeffisien B, diberi beban secara parallel dengan massa M seperti pada Gambar 2.8 di atas. Dengan menggunakan hukun Newton II, gaya yang bekerja pada sistem dapat dinyatakan dengan persamaan differensial sebagai berikut,
)
(
2 2t
f
Kx
dt
dx
B
dt
x
d
M
…(2.30)
Perhatikan persamaan (2.1), suku di sebelah kiri mengandung variable x(t). x(t) yaitu variable displacemen dari sistem mekanis. Variabel ini merupakan variable keluaran sistem. Dan suku di sebelah kanan merupakan f(t) sebagai variable masukan sistem.
Sebuah blok diagram hubungan Antara masukan dengan keluaran dari system mekanis, dapat ditunjukkan pada gamber berikut ini.
Pada persamaan (2.1), apabila diambil
x
1
x
dandt dx
x2 , maka diperoleh dua
persamaan yang dikatakan sebagai bentuk persamaan keadaan 1 (x1) dan persamaan
keadeaan 2 (x2) sebagai berikut,
2 1
x
dt
dx
…(2.31)
2 1
21
f
(
t
)
Bx
Kx
M
dt
dx
…(2.32)Sist
em
me
f
(
x(t)
14 |2. Model Matematis Sistem Dinamik
Persamaan (2.31) dan (2.32) merupakan bentuk persamaan ruang keadaan (state space), dengan variable keadaan x1 dan x2. x1 adalah displacement dan x2 adalah laju displacemen. Kedua variable
keadaan ini bias menjadi keluaran sebuah sistem mekanis.
Contoh Soal 2-7 :
Jika benda dengan massa M=1 Kg mula-mula diam, kemudian pada saat t = 0 dikenai gaya sebesar 25 Newton dan masing-masing tetapan diketahui K=12 N/m , B = 5 N/m/det. Maka benda dengan massa M akan bergerak berpindah posisi dengan kecepatan yang bervariasi.
Program MATLAB
Dengan menggunakan MATLAB tanggapan sistem untuk contoh soal 2.1 dapat diperoleh. Fungsi sistem dituliskan dalam M-file mechsys.m sebagai berikut,
function xdot = mechsys(t,x); % returns the state
derivatives
F = 25; % Step input
M =1; B = 5; K = 25;
xdot = [x(2) ; 1/M*( F - B*x(2) - K*x(1) ) ];
Sedangkan simulasi tanggapan sistem dalam interval waktu 0 s/d 3 detik, dituliskan dalam M-file ch2ex01.m dengan menggunakan ode23 sebagai berikut,
t0= 0; tfinal = 3; % time interval
x0 = [0, 0]; % initial conditions
tol = 0.001; % accuracy
trace = 0; % if nonzero, each step is printed
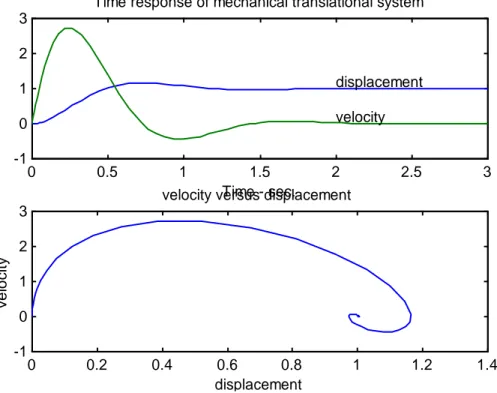
[t,x] = ode23('mechsys',t0,tfinal,x0,tol,trace); subplot(211),plot(t,x)
title('Time response of mechanical translational sistem') xlabel('Time - sec.')
text(2,1.2,'displacement') text(2,.2,'velocity') d= x(:,1); v = x(:,2); subplot(212), plot(d, v)
title('velocity versus displacement ') xlabel('displacement')
ylabel('velocity')
meta ch2ex01 % create meta file containg graph
15 |2. Model Matematis Sistem Dinamik
Gambar 2. 5 Tanggapan sistem mekanik pegas-damper pada contoh soal 2.1.
Soal Latihan 2-6 :
Tinjau sistem damper – massa - pegas yang dipasang pada kereta seperti pada Gambar 2.10 di bawah. Damper adalah alat yang memberikan gesekan liat atau redaman (damping), terdiri dari sebuah torak dan selinder yang berisi minyak. Pada saat t<0, kereta diam, dan selanjutnya pada saat t = 0, kereta digerakkan dengan kecepatan tetap u. Perpindahan (relatif terhadap tanah) y(t) dari massa adalah keluaran dari sistem. Diberikan tetapan K untuk pegas dan B untuk damper.
Carilah :
(a). Model matematika yang menggambarkan dinamika sistem.
(b). Gambarkan dengan menggunakan program MATLAB tanggapan sistem, seperti pada contoh diatas.
Gambar 2. 6 Sistem damper-massa-pegas diatas kereta.
0 0.5 1 1.5 2 2.5 3 -1 0 1 2 3
Time response of mechanical translational system
Time - sec. displacement velocity 0 0.2 0.4 0.6 0.8 1 1.2 1.4 -1 0 1 2 3
velocity versus displacement
displacement
ve
lo
ci
16 |2. Model Matematis Sistem Dinamik
2.4 Model Sistem Listrik.
Sistem elektrik terdiri dari komponen tahanan, induktor dan kapasitor yang bisa dihubungkan secara serial mapun pararel maupun kombinasi keduanya. Pada bagian ini dibahas sistem rangkaian listrik yang melibatkan tahanan, kapasitor dan induktor. Rangkaian elektrik termasuk pula transistor dan amplifier. Sebuah televisi menghasilkan respon dinamik berupa berkas pada layar, atau perubahan tuning frekuensi akan merubah apa yang tampak di layar. Pada umumnya suatu sistem elektrik yang terdiri dari komponen tahanan R, Induktor – L dan kapasitor – C, dalam menurunkan model matematisnya digunakan hukum dasar adalah hukum arus dan tegangan Kirchhoff. Model matematika dari sistem dapat diperoleh dengan menggunakan kedua hukum tersebut.
Contoh Soal 2.8 :
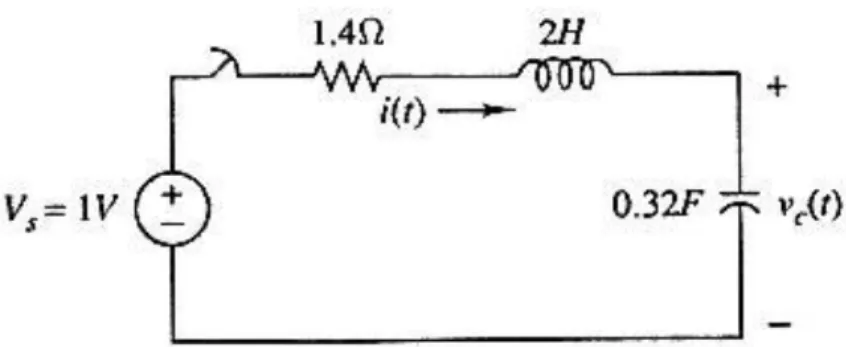
Rangkaian R-L-C yang disusun secara seri seperti pada gambar 2.11 di bawah, rangkaian tersebut terdiri dari suatu induktansi L (henry), tahanan R (ohm) dan kapasitor C (farad). Rangkaian diberi masukan berupa tegangan Vs= 1 volts (t=0). Mula-mula arus di induktor nol, dan tegangan di capasitor 0.5 volts.
Tentukan tanggapan sistem : arus yang mengalir i(t) dan tegangan capasitor vc(t). diketahui R=1,4,
L=2H dan C=0,32F.
Gambar 2. 7 Rangkaian RLC domain waktu.
Berdasarkan hukum Kirchhoff persamaan sistem adalah,
s c V v dt di L Ri dan
dt
dv
C
i
c …(2.33)ambil
x
1
v
c danx
2
i
, maka diperoleh,…(2.34)
Program MATLAB
Dua fungsi sistem dituliskan dalam M-file electsys.m sebagai berikut,
1 2
2 2 11
1
Rx
x
V
L
x
x
C
x
s
17 |2. Model Matematis Sistem Dinamik
function xdot = electsys(t,x); % returns the
state derivatives
V = 1; % Step input
R =1.4; L = 2; C = 0.32;
xdot = [x(2)/C ; 1/L*( V - x(1) - R*x(2) ) ];
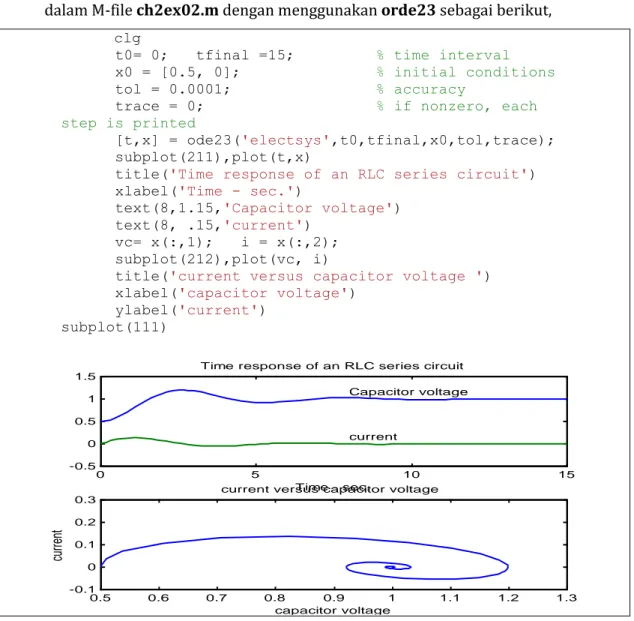
Sedangkan simulasi tanggapan sistem dalam interval waktu 0 s/d 3 detik, dituliskan dalam M-file ch2ex02.m dengan menggunakan orde23 sebagai berikut,
clg
t0= 0; tfinal =15; % time interval
x0 = [0.5, 0]; % initial conditions
tol = 0.0001; % accuracy
trace = 0; % if nonzero, each step is printed
[t,x] = ode23('electsys',t0,tfinal,x0,tol,trace); subplot(211),plot(t,x)
title('Time response of an RLC series circuit') xlabel('Time - sec.')
text(8,1.15,'Capacitor voltage') text(8, .15,'current')
vc= x(:,1); i = x(:,2); subplot(212),plot(vc, i)
title('current versus capacitor voltage ') xlabel('capacitor voltage')
ylabel('current') subplot(111)
Gambar 2. 8 Tanggapan arus dan tegangan kapasitor pada rangkaian seri RLC.
Soal Latihan 2-7 :
Tinjau rangkaian RLC yang tersusun seperti gambar dibawah. Mula-mula arus di induktor nol, dan tegangan di kapasitor 0.5 volts. Tentukan tanggapan sistem : arus yang mengalir i(t) dan tegangan vcr(t).
Diketahui R=1, L=2H dan C=0,32F. Ddiberikan masukan berupa tegangan Vs= 1 volts (t=0).
Carilah :
(a). Model matematika yang menggambarkan sistem rangkaian RLC.
(b). Gambarkan dengan menggunakan program MATLAB tanggapan sistem, seperti pada contoh diatas. 0 5 10 15 -0.5 0 0.5 1 1.5
Time response of an RLC series circuit
Time - sec. Capacitor voltage current 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 -0.1 0 0.1 0.2 0.3
current versus capacitor voltage
capacitor voltage
cu
rre
18 |2. Model Matematis Sistem Dinamik
Gambar 2. 9 Rangkaian Listrik RLC.2.5 Model Sistem Elektromekanik.
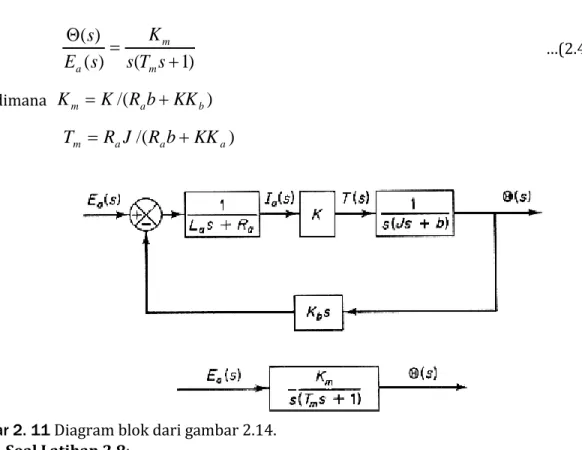
Sistem elektromekanika merupakan sistem gabungan antara alektrik dengan mekanik. Sistem elektromekanika yang akan dibahas adalah servomotor arus searah (servomotor dc) dan servomotor dua fasa. Servomotor dc atau disebut motor-dc dengan daya rendah, biasanya digunakan untuk komputer dan instrumentasi seperti misalnya disk drive, tape drive, dll. Sedangkan yang berdaya menengah digunakan untuk sistem lengan robot, mesin pemintal yang dikendalikan secara numerik. Tinjau motor arus searah, dengan arus jangkar magnetik dibuat konstan dan kecepatan dikendalikan dengan tegangan medan, motor dc tersebut dinamakan motor dc dikendalikan medan. Perhatikan diagram skematik motor dc sebagai berikut,
Gambar 2. 10 Sistem pengendali motor DC jangkar-magnet[2].
Pada sistem servomotor ini,
Ra = tahanan kumparan jangkar (ohm)
La = induktansi kumparan jangkar (henry)
ia = arus kumparan jangkar (ampere)
if = arus medan (ampere)
ea = tegangan yang dikenakan pada jangkar (volt)
eb = ggl - gaya gerak listrik balik (volt)
θ = perpindahan sudut dari poros motor (radian) T = torsi yang diberikan oleh motor (N.m)
J = momen inersia ekivalen dari motor dan beban pada poros motor (kg.m2)
b = koefisien gesekan viskos ekivalen dari motor dan beban pada poros motor (N.m/rad.dt)
19 |2. Model Matematis Sistem Dinamik
Torsi T yang dihasilkan motor adalah berbanding lurus dengan hasil kali dari arus kumparan ia dan fluks celah udara berbanding lurus dengan arus medan,
f f
i
K
…(2.35)Kf adalah konstanta, sehingga T dapat dituliskan sebagai berikut,
a f fi K i K T 1 …(2.36) dengan K1 konstan.
Perhatikan bahwa untuk medan arus konstan, fluks juga konstan dan torsi mempunyai arah sesuai arus kumparan magnet, sehingga
a
Ki
T
…(2.37)dengan K adalah konstanta torsi motor. Dari persamaan tersebut, terlihat bahwa apabila tanda arus ia dibalik maka tanda dari torsi T akan terbalik pula. Hal ini akan menyebabkan
berbaliknya arah putaran motor.
Bila kumparan magnet berputar, maka tegangan akan sebanding dengan hasil kali fluks dan kecepatan sudut yang diinduksikan pada kumparan magnet. Untuk fluks yang konstan, tegangan induksi eb berbanding lurus dengan kecepatan sudut d/dt, atau
dt d K eb b
…(2.38)dimana eb adalah emf balik dan Kb konstanta emf balik.
Kecepatan jangkar magnet servomotor dc dikendalikan oleh tegangan kumparan magnet ea. Persamaan diferensial rangkaian kumparan magnet adalah,
a b a a a a
R
i
e
e
dt
di
L
…(2.39)Arus jangkar magnet menghasilakan torsi yang bekerja terhadap inersia dan gesekan, sehingga a
Ki
T
dt
d
b
dt
d
J
2
2 …(2.40)dengan transformasi Laplace ketiga persamaan terakhir (2.38), (2.39) dan (2.40) dapat dirubah sebagai berikut,
20 |2. Model Matematis Sistem Dinamik
K
b
(
s
)
E
b(
s
)
…(2.41))
(
)
(
)
(
)
(
L
as
R
aI
as
E
bs
E
as
…(2.42) ) ( ) ( ) ( ) (Js2 bs s T s KIa s …(2.43)Dengan menyusun persamaan (2.41), (2.42) san (2.43) diperoleh fungsi alih,
a a a a b
as
L
Js
L
b
K
J
s
R
b
KK
K
s
E
s
)
(
)
(
)
(
2 …(2.44)atau dapat disederhanakan, dengan mengabaikan La, karena biasanya sangat kecil,
sehingga diperoleh fungsi alih sistem sebagai berikut,
)
1
(
)
(
)
(
s
T
s
K
s
E
s
m m a …(2.45) dimanaK
m
K
/(
R
ab
KK
b)
)
/(
a a a mR
J
R
b
KK
T
Gambar 2. 11 Diagram blok dari gambar 2.14.
Soal Latihan 2.8:
Sebuah sistem elektromekanik seperti yang ditunjukan pada gambar di bawah, yaitu sebuah servomotor dc dengan pengendali jangkar magnet, menggerakkan beban yang terdiri dari momen inersia JL. Torsi yang dikembangkan motor adalah T. Perpindahan sudut dari rotor motor dan elemen
beban adalah m dan , secara berurutan. Rasio roda gigi adalah n = /m. Dapatkan fungsi alih dari
21 |2. Model Matematis Sistem Dinamik
Gambar 2. 12 Sistem servomotor DC yang dikendalikan jangkar-magnet[2].
Sistem elektromekanik yang telah diuraikan di atas merupakan salah satu contoh dari sistem campuran. Tidak hanya servomotor, tetapi loudspeaker yang berada pada sistem stereo, aktuator solenoid juga termasuk sistem elektromekanik. Pada loudspeaker, arus listrik dari amplifier ditransformasikan untuk menggerakkan kerucut speaker dan fluktuasi udara yang menyebabkan suara dikuatkan.
2.6 Model Sistem Fluida.
Dalam analisis sistem aliran zat cair, perlu dibedakan antara aliran laminar dan turbulen, sesuai dengan besar bilangan Reynoldnya. Bila bilangan Reynold lebih besar dari 4000 maka termasuk aliran turbulen. Aliran dikatakan laminar bila bilangan Reynold lebih kecil dari 2000. Sistem aliran turbulen biasanya dinyatakan dengan persamaan differensial taklinier, sedangkan aliran laminar dinyatakan dengan persamaan differensial linier. Di industri, dimana cairan mengalir dalam pipa biasanya tidak laminar, dan ini perlu dianalisa terlebih dahulu mengenai tipe aliran yang terjadi pada sistem perpipaan di industri.
Anggap sistem fluida adalah aliran laminar, sehinga kita dapat memandang persamaannya adalah linier atau dilinierkan, persamaan differensial sistem dapat diperoleh dengan mengetahui terlebih dahulu konsep mengenai tahanan aliran, kapasitansi, dimana didefiniskan sebagai :
Tahanan suatu aliran - R, perubahan beda tinggi muka yang diperlukan untuk menimbulkan satu satuan perubahan laju aliran.
R =
dt
m
aliran
laju
perubahan
m
muka
tinggi
beda
perubahan
/
,
,
3Kapasitasnsi - C, perubahan jumlah cairan yang tersimpan , yang diperlukan untuk menimbulkan satu satuan potensial (tinggi tekan).
C =
m
tekan
tinggi
perubahan
m
tersimpan
yang
cairan
perubahan
,
,
3Karena aliran masuk dikurangi aliran keluar dalam tangki selama selang waktu dt kecil sama dengan jumlah tambahan air dalam tangki, kita dapatkan persamaan,
dt
q
q
Cdh
(
i
o)
danR
h
q
o
…(2.46)22 |2. Model Matematis Sistem Dinamik
i Rq h dt dh RC …(2.47)dengan transformasi Laplace diperoleh,
1
)
(
)
(
RCs
R
s
Q
s
H
i danR
s
H
s
Q
o)
(
)
(
…(2.48)dimana R adalah resistansi termal tetap. Maka fungsi alih bisa dituliskan antara aliran fluida keluar dan fluida masuk sebagai berikut,
1
1
)
(
)
(
RCs
s
Q
s
Q
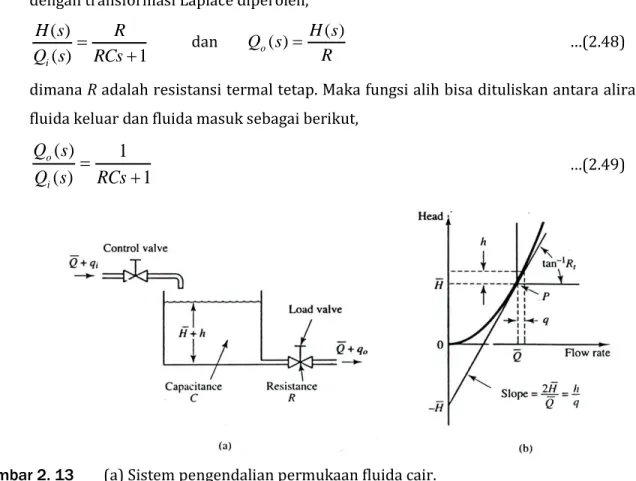
i o …(2.49)Gambar 2. 13 (a) Sistem pengendalian permukaan fluida cair.
(b) Kurva laju aliran versus permukaan fluida cair[2].
Contoh Soal 2.8:
Bila sistem yang digambarkan pada Gambar 2.14 diatas, saat kondisi steady pada laju aliran 4 x 10-4
m3/dtk dan ketinggian fluida dalam tangki kondisi steady adalah 1 m. Pada saat t = 0, valve masukan
dibuka sehingga menyebabkan laju perubahan fluida menjadi 4,5 x 10-4 m3/dtk. Tentukan resistansi R
pada valve keluaran, bila kapasitansi tangki C=0,02 m2. Tentukan respon dari ketinggian fluida pada
sistem tersebut.
Laju aliran yang melalui valve keluaran dapat diasumsikan sebagai fungsi yang dinyatakan :
H K Q
Dengan Q = 4 x 10-4 m3/dtk dan H = 1 meter, maka K = 4 x 10-4.
Saat laju aliran berubah menjadi 4,5 x 10-4 m3/dtk, kondisi tinggi fluida tangki saat steady
menjadi :
H
4 410
.
4
10
.
5
,
4
, H = 1,266 meterIni berarti terjadi perubahan tinggi fluida : 1,266 – 1 = 0,266 m. Resistansi rata rata dari valve keluaran adalah :
23 |2. Model Matematis Sistem Dinamik
4
,
5
4
.
10
40
,
552
.
10
4/
21
266
,
1
m
dtk
dQ
dH
R
Dari persamaan 2.18,1
)
(
)
(
RCs
s
Q
s
H
i , dengan masukan laju fluida tetap,)
1
)
02
,
0
10
.
532
,
0
((
266
,
0
)
(
4
s
x
s
s
H
Dengan program MATLAB
num = [0.266]; den = [106.4 1]; step (num, den); subplot (111);
Keluaran dari program seperti tampak pada gambar di bawah ini.
Gambar 2. 14 Grafik respon dinamika sistem untuk contoh soal 2.8.
Model Simulink : Pengendalian level pada tangki.
Mari kita memperhatikan sebuah model sistem pengendalian fluida dalam sebuah tangki. Tujuan dari pengendalian ini adalah untuk menjaga ketinggian permukaan fluida dalam tangki seperti yang diinginkan. Silahkan Anda membuka Program MATLAB>Demo>Simulink, selanjutnya akan tertampil layar sebagai berikut,
24 |2. Model Matematis Sistem Dinamik
Gambar 2. 15 Layar program Simulink-MATLAB.Pilih model ‘Tank Fill and Empty with Animation’, dan klik pada tulisan ‘Open this
model’ yang berada pada pojok atas sebelah kanan layar, akan tampil layar simulink
dalam bentuk blok diagram berikut,
Gambar 2. 16 Gambar blok diagram simulasi pengendalian level pada tangki.
Bisa juga Anda menampilkan simulasi proses dalam bentuk GUI. Dengan tampilan dalam bentuk GUI ini, Anda bisa merubah-rubah besar bilangan ; 2 variabel proses ‘Flow Rate-Out’ dan ‘Flow Rate-In’, Parameter sistem ‘Tank Base Area’ dan 2 parameter setting ‘Maximum Height Limit’ dan ‘Minimum Height Limit’. Sebagai contoh Anda merancang sistem dengan harga bilangan sebagai berikut,
25 |2. Model Matematis Sistem Dinamik
Langkah selanjutnya untuk menjalankan simulasi proses ini, silahkan anda klik pada kotak ‘START SIM’, selanjutnya Anda akan melihat simulasi dari hasil rancangan yang telah Anda tentukan. Fluida akan mengalir dari valve atas masuk ke tangki, dan keluar melalui valve bagian bawah dengan kesetimbangan yang telah diatur. Grafik hasil simulasi dapat diperhatikan pada layar berikut ini,
Gambar 2. 18 Grafik simulasi pengendalian level pada tangki.
Soal Latihan 2.8 :
Dengan menggunakan gambar yang sama seperti diatas, diketahui bahwa
meter
3
H
,Q
0
,
02
m
3/
det
, dan daerah potongan melintang dari tangki sama dengan 5 m2, dapatkan konstanta waktu dari sistem tersebut pada titik operasi (H
,Q
).Anggap arus fluida melalui katup adalah turbulen.
2.7 Model Sistem Termal.
Sistem termal adalah sistem yang melibatkan perpindahan panas dari bahan yang satu ke yang lain. Sistem termal dapat dianalisis dalam bentuk tahanan dan kapasitansi, meskipun kapasitansi termal dan tahanan termal tidak dapat digambarkan secara tepat sebagai parameter yang utuh, karena sebenarnya terdistribusi diseluruh bahan yang bersangkutan. Untuk menyederhanakan pembahasan, sistem termal dapat digambarkan dengan model parameter yang utuh, bahwa bahan yang dikarakterisasi sebagai kapasitansi panas mempunyai tahanan yang dapat diabaikan terhadap arus panas. Ada tiga cara panas dialirkan, yaitu konduksi, konveksi dan radiasi.
Tahanan termal R dan kapasitansi termal C untuk perpindahan panas antara dua benda dapat didefinisikan sebagai :
26 |2. Model Matematis Sistem Dinamik
R=W
panas
aliran
laju
perubahan
C
temperatur
beda
perubahan
o,
,
C =C
temperatur
perubahan
J
tersimpan
yang
kalor
perubahan
o,
,
Contoh Soal 2.9 :Tinjau sistem termal seperti gambar di bawah. Anggap bahwa tangki diisolasi untuk mencegah kehilangan panas ke udara sekitar. Anggap pula bahwa tidak terdapat panas masuk dan zat cair dalam tangki pada suhu yang seragam. Sehingga suhu tunggal dapat digunakan untuk menggambarkan suhu cairan dalam tangki dan aliran keluar tangki.
Gambar 2. 19 Skema sistem pemanas fluida dengan pemanas steam
Blok diagram dari sistem Gambar 2.23 di atas seperti terlihat pada Gambar 2.224.
Gambar 2. 20 Blok diagram Gambar 2.13
Diasumsikan bahwa suhu aliran zat cair yang masuk dijaga tetap, dan laju panas masuk sistem (kalor dari pemanas) tiba-tiba dirubah dari
H
menjadiH
+hi. Dengan hi menyatakan perubahan kecil lajupanas masuk. Laju aliran panas keluar kemudian dirubah secara perlahan dari
H
menjadiH
+ho. Suhu H
(
(
27 |2. Model Matematis Sistem Dinamik
aliran zat cair yang keluar juga akan berubah dari omenjadi o+ . dalam hal ini ho, C dan R
berturut-turut diperoleh,
Gc
h
R
Mc
C
G
h
o c o1
,
,
…(2.50)persamaan differensial sistem,
i
Rh dt
d
RC
…(2.51)Dengan melakukan transformasi laplace untuk persamaan (2.51), dan ditulis dalam bentuk fungsi alih,
1
)
(
)
(
RCs
R
s
H
s
i …(2.52) dimana
(s
)
ℒ[(t)] dan Hi(s)= ℒ[hi]2.8 Linierisasi Model Non-linier.
Sebagian besar sistem fisis adalah non-linier yang kemudian dilinierisasi pada range variabel tertentu. Proses linierisasi persamaan nonlinier sangat penting, berkaitan dengan metode-metode yang akan digunakan dalam perancangan sistem pengendalian. Linierisasi sering dilakukan, dengan menggunakan ekspansi deret Taylor disekitar titik operasi dan mempertahankan hanya bagian yang linier saja.
Contoh Soal 2.4 :
Sebuah pendulum dengan berat W=mg Kg digantungkan pada engsel dengan panjang lengan L meter (berat lengan diabaikan). Persamaan sistem secara nyata adalah persaman non-linier. Pada saat pendulum mengayun terjadi redaman oleh gesekan, faktor redaman B Kg/m/det. Pendulum mengayun dengan sudut ayun , perhatikan Gambar 2.19 berikut,
Gambar 2.19 Sistem pendulum diayun.
Sudut ayun , makin besar akibat adanya gaya tangensial , sehingga hukum Newton II: W
28 |2. Model Matematis Sistem Dinamik
BL
W
F
T
.
sin
…(2.23)dari hukum Newton untuk dinamika rotasi,
mL
F
T
…(2.24)Kombinasi dari kedua persamaan tersebut diatas diperoleh persamaan linier,
0
sin
BL
W
mL
…(2.25)ambil
x
1
danx
2
(kecepatan angular) maka,)
(
1 2 2 1x
Sin
mL
W
x
m
B
x
x
x
…(2.26)Program MATLAB
Dua fungsi sistem dituliskan dalam M-file pendulum.m sebagai berikut,
function xdot = pendulum(t,x); % returns the state
derivatives
W =2; L = .6; B = 0.02; g = 9.81; m =W/g; xdot = [x(2) ; -B/m*x(2)-W/(m*L)*sin(x(1)) ];
Sedangkan simulasi tanggapan sistem dalam interval waktu 0 s/d 5 detik, dituliskan dalam M-file ch2ex03.m dengan menggunakan ode23 sebagai berikut,
clg
t0= 0; tfinal =5; % time interval
x0 = [1, 0]; % initial conditions
tol = 0.0001; % accuracy
trace = 0; % if nonzero, each step is printed
[t,x] = ode23('pendulum',t0,tfinal,x0,tol,trace); subplot(211),plot(t,x)
title('Time response of pendulum on rigid rod') xlabel('Time - sec.')
text(3.2,3.1,'Velocity') text(3.2,1.2,'Angle-Rad.') th= x(:,1); w = x(:,2); subplot(212),plot(th, w)
title('Phase plane plot of pendulum') xlabel('Position - Rad.')
ylabel('Angular velocity') subplot(111)
29 |2. Model Matematis Sistem Dinamik
Gambar 2.20 Respon ayunan pendulum dalam sudut ayun dan kecepatan angular.
Linierisasi Sistem Non-Linier
Sistem nonlinier sering kali dilinierkan dengan anggapan kondisi sinyal sangat kecil. Persamaan differensial nonlinier yang menggambarkan gerakan ayunan pendulum seperti telah dijelaskan didepan, dapat dilinierisasi jika sudut simpangan mula-mula sangat kecil. Sudut simpangan
o
, sehingga persamaan pendulum dapat dituliskan kembali sebagai berikut,0
)
(
)
(
)
(
BL
WSin
mL
…(2.27)Dengan anggapan kecil Sin 0, Cos1, maka suku sinus dapat dihilangkan, sehingga dapat diperoleh persamaan linier sebagai berikut,
0
BL
W
mL …(2.28)Persamaan ini akan menghasilkan tanggapan yang sama dengan persamaan linier yang tealah dibahas berikutnya.
2.9 Fungsi Transfer / Fungsi Alih
0 1 2 3 4 5 -4 -2 0 2 4
Time response of pendulum on rigid rod
Time - sec. Velocity Angle-Rad. -1 -0.5 0 0.5 1 -4 -2 0 2 4
Phase plane plot of pendulum
Position - Rad. A n g u la r ve lo ci ty
30 |2. Model Matematis Sistem Dinamik
Transformasi-Laplace memainkan peranan yang sangat penting dalam analisis dan representasi sistem LTI waktu kontinyu. Salah satu sifat transformasi-Laplace yang sangat penting dan telah dibahas pada pokok bahasan Sifat-Sifat Transformasi-Laplace adalah sifat konvolusi. Sifat ini memberikan kemudahan dalam perhitungan untuk mendapatkan respon sistem. Pada pokok bahasan ini akan dieksploitasi sifat ini lebih jauh.
2.9.1 Fungsi Transfer dari Respon Impuls.
Output suatu sistem yang memiliki respon impuls
h
(t
)
dan inputx
(t
)
diberikan oleh :
d
t
h
x
t
y
(
)
(
)
(
)
(2.15)
Dengan melakukan transformasi Laplace pada kedua sisi Persamaan (2.15) dan menggunakan sifat konvolusi, diperoleh
d
t
h
x
t
y
(
)
L
(
)
(
)
L
Y(s)H(s)X(s)
(2.16)
Fungsi transfer didefinisikan sebagai perbandingan output/input sistem dalam doman-s , yaitu
)
(
)
(
)
(
s
X
s
Y
s
H
(2.17)
Dari Persamaan (2.15) dan (2.16), dapat disimpulkan bahwa
H
(
s
)
L
h
(
t
)
.Akar-akar dari pembilang dan penyebut fungsi transfer H(s) masing-masing disebut zero dan pole
dari fungsi transfer. Untuk
s
j
, H(s) tidak lain merupakan respon frekuensi dari sistem. Gambar(2.4) menunjukkan diagram blok hubungan input-output dan fungsi transfer suatu sistem .
H(s) )
(s
X Y(s)
Gambar FTs-1
Hubungan Input-Output dan Fungsi Transfer
Gambar 2. 21 Hubungan input-output dan fungsi transfer
Contoh Soal 2.4
Dapatkan fungsi transfer untuk sistem yang memiliki respon impuls
)
(
2
5
)
(
t
e
2e
10u
t
h
t t
Penyelesaian :31 |2. Model Matematis Sistem Dinamik
(
)
)
(
s
h
t
H
L
L
5
e
2t
2
e
10t
u
(
t
)
)
10
)(
2
(
54
7
10
2
2
5
)
(
s
s
s
s
s
s
H
Fungsi transfer memiliki peran yang sangat penting dalam analisis sistem. Beberapa sifat sistem LTI dapat dikaitkan dengan fungsi transfer dalam bidang-s , khususnya dengan lokasi pole dan daerah konvergensi. Sebagai contoh, untuk sistem LTI kausal, respon impulsnya nol untuk
t
0
, jadi responimpulsnya merupakan sisi kanan. Sehingga ROC- Radius of Convergence dari fungsi transfer untuk sistem kausal mencakup seluruh bidang-s di sebelah kanan pole paling kanan. Sebaliknya untuk sistem antikausal, maka ROC-nya berada di sebelah kiri pole yang paling kiri. Relasi kausalitas dan ROC ini tidak berlaku sebaliknya. Jadi jika ROC berada di sisi kanan pole yang paling kanan , tidak berarti sistemnya kausal, yang pasti bahwa respon impulsnya sisi kanan.
ROC dari H(s) juga dapat dikaitkan dengan stabilitas sistem. Sebagaimana telah dibahas bahwa
transformasi Fourier dari respon impuls sistem LTI yang stabil adalah konvergen. Jadi untuk sistem LTI yang stabil, ROC dari
H
(s
)
harus mencakup sumbuj
(yaituRe(
s
)
0
).Untuk suatu sistem LTI dengan fungsi transfer rasional yang kausal dan stabil, maka semua pole-nya harus berada di sebelah kiri setengah bidang-s. Hal ini konsekuensi dari kausalitas, yaitu ROC di sebelah kanan pole yang paling kanan, dan dari stabilitas, ROC harus mencakup sumbu
j
.Contoh Soal 2.3
Suatu sistem memiliki fungsi transfer
)
4
)(
2
(
2
)
(
s
s
s
s
H
Karena ROC-nya tidak dispesifikasikan, maka ada beberapa ROC yang berbeda untuk sistem tersebut, dan konsekuensinya respon impulsnya juga berbeda. Jika informasi tentang stabilitas dan kausalitas sistem diberikan, maka ROC yang sesuai dapat ditentukan.
32 |2. Model Matematis Sistem Dinamik
Bidang s Im Re (a) (b) X X 4 2 -2 Bidang s Im Re X X 4 2 -2 Bidang s Im Re X X 4 2 -2 (c) Gambar FTs-2 ROC untuk Contoh 1(a). kausal, tidak stabil (b). nonkausal, stabil (c). nonkausal, tidak stabil
Gambar 2. 22 ROC untuk contoh 2.3, (a) Kasual, tidak stabil, (b) Nonkasual, stabil, (c) nonkasual, tidak stabil
Misalkan, jika sistemnya diketahui kausal, maka ROC-nya ditunjukkan pada Gambar (2.5a). Jika sistemnya diketahui stabil, maka ROC-nya ditunjukkan pada Gambar (2.5 b). Sedangkan Gambar (2.5c) adalah ROC untuk sistem yang tidak stabil
Contoh Soal 2.4
Fungsi transfer sistem kausal orde-2 dengan pole kompleks konjugate diberikan oleh :
2 2 2
2
)
(
n n ns
s
s
H
dimana
0
1
, dan polenya terletak dis
n
j
n1
2 .Lokasi pole untuk
0
1
ditunjukkan pada Gambar (2.6). Karena sistemnya kausal, maka ROC-nyaberada di sebelah kanan pole yang paling besar, yaitu
s
n dan dari syarat stabilitas, ROC dari) (s
33 |2. Model Matematis Sistem Dinamik
Bidang s
Re
Gambar FTs-3
Lokasi pole dan ROC untuk sistem kausal orde-2 Im X X n
Gambar 2. 23 Lokasi pole dan ROC system kausal orde-2
2.9.2 Fungsi Transfer dari PD Input – Output
Untuk sistem dinyatakan dalam bentuk persamaan PD input-output dimana semua kondisi mula=0 :
M k k k k N k k k kdt
t
x
d
b
dt
t
y
d
a
0 0)
(
)
(
(2.18)
maka fungsi transfernya dapat diperoleh dengan mengambil
transformasi-Laplace pada kedua sisi
M k k k k N k k k kdt
t
x
d
b
dt
t
y
d
a
0 0)
(
)
(
L
L
(2.19)
Dengan menggunakan sifat linieritas , Persamaan (2.19) dapat ditulis
M k k k k N k k k kdt
t
x
d
b
dt
t
y
d
a
0 0)
(
)
(
L
L
(2.20)
dan dari sifat diferensial terhadap waktu, diperoleh
M k k k N k k ks
Y
s
b
s
X
s
a
0 0)
(
)
(
(2.21)
atau ekivalen dengan

![Gambar 2. 10 Sistem pengendali motor DC jangkar-magnet [2] . Pada sistem servomotor ini,](https://thumb-ap.123doks.com/thumbv2/123dok/4406558.2954307/18.918.379.622.54.187/gambar-sistem-pengendali-motor-jangkar-magnet-sistem-servomotor.webp)
![Gambar 2. 12 Sistem servomotor DC yang dikendalikan jangkar-magnet [2] .](https://thumb-ap.123doks.com/thumbv2/123dok/4406558.2954307/21.918.273.735.60.208/gambar-sistem-servomotor-dc-yang-dikendalikan-jangkar-magnet.webp)