GENERALISASI METODE TALI BUSUR UNTUK
MENYELESAIKAN PERSAMAAN
TAK LINEAR
SUNARSIH
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2011
ABSTRACT
SUNARSIH. Generalization of the Secant Method for Solving Nonlinear Equations.
Supervised by SISWANDI and BERLIAN SETIAWATY.
This manuscript discusses a method for determining nonlinear equations roots
from function having
(
k
1)
thderivative which are continuous on an open interval
containing the roots. The method used in this manuscript is a generalization of the
Secant method. This generalization is by substituting the linear interpolation equation
in the iteration equation by Secant method for the
(
k
1)
thderivative polynomial
interpolation equations. Convergence analyzing of the approximation roots sequence
resulting in a degree of convergence which is greater than that of the Secant method
and relatively similar to that of the Newton-Raphson method.
ABSTRAK
SUNARSIH. Generalisasi Metode Tali Busur untuk Menyelesaikan Persamaan Tak
Linear. Dibimbing oleh SISWANDI dan BERLIAN SETIAWATY.
Karya ilmiah ini membahas metode penentuan akar persamaan tak linear dari
fungsi yang memiliki turunan ke-𝑘 + 1 kontinu pada interval terbuka yang
mengandung akar. Metode yang digunakan dalam karya ilmiah ini merupakan
generalisasi dari metode Tali Busur. Generalisasi ini dilakukan dengan mengganti
persamaan interpolasi linear pada persamaan iterasi metode Tali Busur dengan
turunan interpolasi polinomial ke-𝑘 + 1. Analisis kekonvergenan barisan hampiran
akar menghasilkan derajat kekonvergenannya lebih besar daripada menggunakan
metode Tali Busur, dan relatif sama jika menggunakan metode Newton-Raphson.
Generalisasi Metode Tali Busur untuk Menyelesaikan
Persamaan Tak Linear
SUNARSIH
G54061230
Skripsi
Sebagai salah satu syarat untuk memeroleh gelar
Sarjana Sains
Pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2011
Judul
: Generalisasi Metode Tali Busur untuk Menyelesaikan Persamaan Tak
Linear
Nama
: Sunarsih
NIM
: G54061230
Mengetahui
Pembimbing I
Pembimbing II
Drs. Siswandi, M.Si.
Dr. Berlian Setiawaty, MS.
NIP. 19640629 199103 1 001
NIP. 19650505 198903 2 004
Mengetahui
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS.
NIP.19650505 198903 2 004
KATA PENGANTAR
Puji dan syukur penulis panjatkan atas kehadirat Allah SWT yang telah
melimpahkan rahmat, karunia dan hidayah-Nya kepada saya sebagai penulis sehingga
penulis dapat menyelesaikan skripsi yang berjudul “Generalisasi Metode Tali Busur
untuk Menyelesaikan Persamaan Tak Linear” tepat pada waktunya. Skripsi ini
disusun sebagai salah satu syarat kelulusan untuk memeroleh gelar Sarjana Sains
pada program sarjana di Departemen Matematika, Fakultas Matematika dan Ilmu
Pengetahuan Alam Institut Pertanian Bogor.
Pada kesempatan ini, penulis juga ingin mengucapkan terimakasih pada berbagai
pihak yang telah membantu,
1. Keluargaku tercinta: Bapak dan ibu (terima kasih atas semua doa, dukungan dan
kasih sayangnya), Kang Wito, Muji dan Riani (terima kasih atas doa dan
dukungannya).
2. Bapak Dr. Siswandi, M.Si. dan Ibu Dr. Berlian Setiawaty, Ms. Selaku
Pembimbing I dan Pembimbing II (terima kasih atas semua ilmu, kesabaran,
motivasi dan bantuannya selama penulisan skripsi ini).
3. Ibu Dra. Nur Aliatiningtyas, MS. Selaku dosen penguji, (terima kasih atas
semua ilmu, saran, dan motivasinya).
4. Semua dosen Departemen Matematika (terima kasih atas semua ilmu yang
diberikan).
5. Semua staf dan karyawan di Departemen Matematika(terimakasih atas segala
bantuannya).
6. Teman-temanku (Inang, Ken dedes, Kimel, Ndut, Rhe, Tha, Yus).
7. Teman-teman angkatan 43: Emta, Putri, Rias, Erni, Fitria, Dandi, Copi, Slamet,
Lina, Ady, Vera, Abi, NS, Leo, Nobo, Cupit, Adam, Aji, Tami, Sendi, Albrian,
Ratna, Fardan, Resti, Apri, Margi, Fajar, Wira, David, Arif, Arum, Aini, Ace,
Zul, Diah, sabar, Dwi, Faizal, Nurmalina, Suci, Faizul, Syahrul, Nanu, Destya,
Ecka, Kabil, Nia, Razon, Peli, Irsyad, Hendra, Andrew, Nidya, Subro, Agung,
Gandi, Elly, SN, dan Bertrand(terima kasih atas kebersamaan kalian).
8. Kakak-kakak kelasku angkatan 41 dan 42 (terima kasih atas doa dan
dukungannya).
9. Adik-adik kelasku angkatan 44 dan 45 (terima kasih atas doa dan
dukungannya).
Akhir kata, semoga skripsi ini memberikan manfaat untuk kita semua. Penulis
juga menyadari bahwa skripsi ini masih jauh dari sempurna sehingga kritik dan saran
yang membangun sangat penulis harapkan. Semoga Allah SWT senantiasa
melimpahkan rahmat dan karunia-Nya untuk kita semua. Amin.
Bogor, November 2011
RIWAYAT HIDUP
Penulis lahir di Pekanbaru pada tanggal 10 November 1987 sebagai anak kedua
dari empat bersaudara, anak dari pasangan Sonimin dan Siyam. Tahun 2000 penulis
lulus dari SD N 036 Siak, Pekanbaru. Tahun 2003 penulis lulus MTs-Hidayatullah
Sialang baru, Pekanbaru. Tahun 2006 penulis lulus SMA N 1 Lubuk Dalam,
Pekanbaru dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur
ujian Beasiswa Utusan Daerah (BUD), Tingkat Persiapan Bersama. Pada tahun 2007,
penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan
Alam.
Selama mengikuti perkuliahan penulis pernah aktif di IKPMR (Ikatan Keluarga
Pelajar dan Mahasiswa Riau) Bogor di bagian divisi kerohanian islam 2008/2009.
Penulis juga aktif sebagai panitia pada beberapa acara lain Pesta Sains Nasional 2009,
Dies Natalis IKPMR 2008, 2009 dan 2010, Masa Perkenalan Departemen 2008, dan
Try Out Kalkulus dan Pengantar Matematika 2008, 2009 dan 2010.
vii
DAFTAR ISI
Halaman
DAFTAR ISI ……….... vii
DAFTAR GAMBAR ………...… viii
DAFTAR TABEL ……….………. ix DAFTAR LAMPIRAN ………...……… x I PENDAHULUAN 1.1 Latar Belakang ……….……….……….. 1 1.2 Tujuan ………..………...… 1 II LANDASAN TEORI 2.1 Akar persamaan Tak Linear ………...…… 1
2.2 Interpolasi ……….…….. 3
2.3 Barisan dan kekonvergenan ……….…………..…………. 8
2.4 Sifat Akar Persamaan Polinomial ………...………… 9
III PEMBAHASAN 3.1 Rumusan Masalah 3.1.1 Metode Newton-Raphson ………... 11
3.1.2 Metode Tali Busur ……….. 12
3.1.3 Generalisasi Metode Tali Busur ………. 13
3.2 Analisis Kekonvergenan 3.2.1 Kekonvergenan Metode Newton-Raphson ………...…. 16
3.2.2 Kekonvergenan Metode Tali Busur ………... 17
3.2.3 Kekonvergenan Generalisasi Metode Tali Busur ………….………. 19
3.3 Contoh Numerik 3.3.1 Contoh dengan Metode Newton-Raphson ………. 19
3.3.2 Contoh dengan Metode Tali Busur ……….... 20
3.3.3 Contoh dengan Generalisasi Metode Tali Busur ………..……. 21
IV SIMPULAN ………..………...…………..…….. 23
V DAFTAR PUSTAKA ………..……….. 24
LAMPIRAN ……….………. 25
viii
viii
DAFTAR GAMBAR
Halaman Gambar 1 Grafik Iterasi Metode Newton-Raphson ……….……….……… 11 Gambar 2 Grafik Iterasi Metode Tali Busur ……….……… 12
ix
DAFTAR TABEL
Halaman
Tabel 1 Selisih Terbagi ...………...………...……… 15
Tabel 2 Ilustrasi Metode Newton-Raphson ………..……… 19
Tabel 3 Perubahan nilai awal terhadap banyaknya iterasi pada MNR ………. 20
Tabel 4 Ilustrasi Metode Tali Busur ………..………...………. 20
Tabel 5 Perubahan nilai awal terhadap banyaknya iterasi pada MTB ……….…………. 21
Tabel 6 Ilustrasi Generalisasi Metode Tali Busur ………..………...…… 21
Tabel 7 Perubahan nilai awal terhadap banyaknya iterasi pada GMTB ………..…………. 22
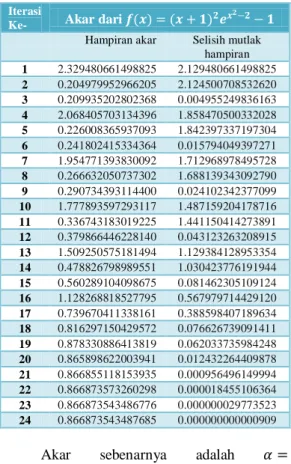
Tabel 8Hasil perolehan akar dari fungsi 𝑓 𝑥 = 𝑥 + 1 2𝑒𝑥2−2− 1 dengan metode Newton-Raphson, metode Tali Busur dan generalisasi Metode Tali Busur ………..………... 23
x
x
DAFTAR LAMPIRAN
Halaman
Lampiran 1 Pembuktian Teorema 12 ……… 26
Lampiran 2 Program dengan Metode Newton-Rapshon ………...……… 37
Lampiran 3 Program dengan Metode Tali Busur ………..… 38
Lampiran 4 Program dengan Generalisasi Metode Tali Busur ………. 39
Lampiran 5 Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.2 …….………...…. 40
Lampiran 6Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.3 …….………...…. 41
Lampiran 7Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.4 …….………...…. 42
Lampiran 8Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.5 …….………...…. 43
Lampiran 9Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.6 ………….………...…. 44
Lampiran 10Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.7………...…. 45
Lampiran 11Program Metode Newton-Raphson dengan Nilai Awal 𝑥0= 0.8 ………..…....…. 46
Lampiran 12Program Metode Tali Busurdengan Nilai Awal 𝑥0= 0.2 dan 𝑥1= 0.3.…….…....…. 47
Lampiran 13Program Metode Tali Busurdengan Nilai Awal 𝑥0= 0.3 dan 𝑥1= 0.4.………...…. 48
Lampiran 14Program Metode Tali Busurdengan Nilai Awal 𝑥0= 0.4 dan 𝑥1= 0.5.………...…. 49
Lampiran 15Program Metode Tali Busurdengan Nilai Awal 𝑥0= 0.5 dan 𝑥1= 0.6.………….…. 50
Lampiran 16Program Metode Tali Busurdengan Nilai Awal 𝑥0= 0.6 dan 𝑥1= 0.7….………..…. 51
Lampiran 17Program Metode Tali Busurdengan Nilai Awal 𝑥0= 0.7 dan 𝑥1= 0.8 …....……..…. 52
Lampiran 18Program Generalisasi Metode Tali Busurdengan Nilai Awal 𝑥0= 0.2 dan 𝑥1= 0.3.. ..53
Lampiran 19Program Generalisasi Metode Tali Busurdengan Nilai Awal 𝑥0= 0.3 dan 𝑥1= 0.4 ... 54
Lampiran 20Program Generalisasi Metode Tali Busurdengan Nilai Awal 𝑥0= 0.4 dan 𝑥1= 0.5 ... 55 Lampiran 21Program Generalisasi Metode Tali Busurdengan Nilai Awal 𝑥0= 0.5 dan 𝑥1= 0.6… 56 Lampiran 22Program Generalisasi Metode Tali Busurdengan Nilai Awal 𝑥0= 0.6 dan 𝑥1= 0.7… 57 Lampiran 23Program Generalisasi Metode Tali Busurdengan Nilai Awal 𝑥0= 0.7 dan 𝑥1= 0.8… 58
xi
I PENDAHULUAN
1.1 Latar Belakang
Salah satu masalah yang paling umum ditemui dalam bidang matematika, teknik dan beberapa bidang ilmu lain adalah mencari akar-akar persamaan. Terutama akar-akar dari persamaan tak linear yang tidak dapat diselesaikan dengan metode analitik. Persamaan tersebut lebih efektif diselesaikan dengan metode iteratif (Sahid 2005). Metode iteratif yang banyak digunakan di berbagai buku adalah metode Tali Busur dan metode Newton-Raphson. Ada juga metode lain yaitu generalisasi metode Tali Busur. Secara umum semua metode pencarian akar tersebut dapat dikelompokkan menjadi dua golongan besar, yaitu metode tertutup dan metode terbuka.
Metode tertutup atau metode pengurung (bracketing method) adalah metode pencarian akar yang akar-akarnya berada dalam interval 𝑎, 𝑏 , dalam interval ini dipastikan berisi minimal satu buah akar. Karena iterasinya selalu konvergen (menuju) ke akar, sehingga metode ini selalu menemukan akar. Contoh metode ini adalah metode Bagi Dua dan metode Regular Falsi (Munir 2003).
Metode terbuka adalah metode pencarian akar yang tidak memerlukan interval yang mengapit akar, yang diperlukan adalah nilai awal dan persamaan iterasi untuk menghitung hampiran akar yang baru. Pada metode ini hampiran akar yang diperoleh mungkin saja mendekati akar sebenarnya (konvergen) atau mungkin juga menjauhinya (divergen). Contoh metode ini adalah metode Titik Tetap, metode
Newton-Raphson, metode Tali Busur dan generalisasi metode Tali Busur (Munir 2003).
Untuk selanjutnya pembahasan pada karya ilmiah ini dibatasi untuk metode terbuka, yaitu metode Newton-Raphson, metode Tali Busur dan generalisasi metode Tali Busur. Metode Newton-Raphson merupakan metode pencarian akar yang paling cepat konvergen di antara metode-metode pencarian akar yang lain, namun metode ini memerlukan dua iterasi fungsi, yaitu nilai fungsi dan turunannya. Sedangkan metode Tali Busur adalah metode pencarian akar yang memiliki kekonvergenan yang relatif lambat, tetapi untuk setiap iterasi hanya memerlukan perhitungan fungsinya saja (Sahid 2005).
Pada karya ilmiah ini akan dibahas generalisasi dari metode Tali Busur, di mana metode ini merupakan metode pencarian akar yang hanya memerlukan iterasi fungsi saja dan kekonvergenannya relatif cepat.
1.2 Tujuan
Tujuan penulisan karya ilmiah ini adalah:
1. Menentukan akar persamaan dengan generalisasi metode Tali Busur dan menganalisis kekonvergenan barisan hampiran akar yang diperoleh (Sidi 2007). 2. Membandingkan kecepatan dalam
memperoleh akar dengan menggunakan generalisasi metode Tali Busur dengan metode Newton-Raphson dan metode Tali Busur pada aplikasi numeriknya.
II LANDASAN TEORI
2.1 Akar Persamaan Tak LinearMisalkan 𝑓 adalah suatu fungsi kontinu. Setiap bilangan 𝛼 pada domain 𝑓 yang memenuhi 𝑓 𝛼 = 0 disebut akar persamaan 𝑓 𝑥 = 0, atau disebut juga pembuat nol fungsi 𝑓. Secara singkat, 𝛼 sering disebut akar 𝑓(𝑥).
Definisi 1 (Derajat Akar)
Misalkan 𝑓 dan merupakan fungsi kontinu dengan (𝑥) ≠ 0, sedemikian sehingga 𝑓 𝑥 dapat dinyatakan sebagai
𝑓 𝑥 = 𝑥 − 𝛼 𝑚 𝑥 ,
maka 𝛼 disebut akar berderajat 𝑚. Dari persamaan di atas terlihat bahwa jika 𝛼 pembuat nol fungsi 𝑓 berderajat 𝑚, maka
𝑓 𝛼 = 0, 𝑓′ 𝛼 = 0, ⋯ , 𝑓(𝑚 −1) 𝛼 = 0, 𝑓(𝑚 )(𝛼) ≠ 0.
Jika 𝑚 = 1, maka 𝛼 disebut akar sederhana. Jika 𝑚 > 1, maka 𝛼 disebut akar ganda. Jika 𝑚 = 2, maka 𝛼 disebut akar dobel, dan seterusnya.
2
2
Definisi 2 (Galat Hampiran)Misalkan 𝑥 adalah suatu nilai hampiran yang diperoleh melalui suatu metode numerik, untuk nilai eksak (nilai sebenarnya) 𝑥 yang tidak diketahui. Nilai
𝜖𝑥 = 𝑥 − 𝑥
disebut selisih atau galat, 𝜖𝑥 disebut galat mutlak.
(Atkinson & Han 2003)
Definisi 3 (Derajat Kekonvergenan)
Misalkan 𝑥0, 𝑥1, 𝑥2, ⋯ merupakan barisan yang konvergen ke 𝛼 dan misalkan 𝜖𝑛= 𝑥𝑛− 𝛼 menyatakan persamaan galat hampiran ke-𝑛, yang didefinisikan pada Definisi 2, dengan 𝑛 = 0, 1, 2, ⋯. Jika terdapat sebuah bilangan 𝑠𝑘 dan konstanta 𝑄 ≠ 0 yang mengakibatkan
lim 𝑛 →∞
𝜖𝑛+1 𝜖𝑛 𝑠𝑘
= 𝑄,
maka 𝑠𝑘 disebut derajat kekonvergenan barisan tersebut dan 𝑄 disebut konstanta galat asimptotik. Untuk 𝑠𝑘 = 1 disebut kekonvergenan linear. Untuk 𝑠𝑘= 2 disebut kekonvergenan kuadratik, dan seterusnya.
(Atkinson & Han 2003)
Definisi 4 (Metode Iteratif)
Metode iteratif adalah suatu metode yang digunakan untuk mencari solusi suatu persamaan tak linear yang dimulai dengan memilih nilai awal dan kemudian berusaha memperbaiki hampiran ke-𝑛 yang menuju tak hingga, tetapi setiap langkahnya tetap konvergen atau menuju ke suatu akar tertentu.
(Atkinson & Han 2003)
Definisi 5 (Metode Terbuka)
Metode terbuka adalah metode pencarian akar yang tidak memerlukan interval yang mengapit akar, yang diperlukan adalah nilai awal dan persamaan iterasi untuk menghitung hampiran akar yang baru. Pada metode ini hampiran akar yang diperoleh mungkin mendekati akar (konvergen), atau mungkin juga menjauhinya (divergen).
(Munir 2003) Contoh metode ini adalah metode Titik Tetap, metode Newton-Raphson, metode Tali Busur, dan generalisasi metode Tali Busur.
Metode Newton-Raphson
Metode Newton-Raphson adalah metode pencarian akar yang hampiran akarnya diperoleh dengan mencari titik potong garis singgung kurva di titik 𝑥𝑛, 𝑓 𝑥𝑛 dengan sumbu-𝑥, dengan nilai awal 𝑥0 diberikan. Persamaan iterasi untuk mendapatkan hampiran ke-𝑛 + 1 adalah 𝑥𝑛+1 = 𝑥𝑛− 𝑓(𝑥𝑛) 𝑓′ 𝑥 𝑛 ; 𝑛 = 0, 1,2, ⋯. (1) (Atkinson & Han 2003)
Metode Tali Busur
Metode Tali Busur (secant method) adalah metode pencarian akar yang merupakan modifikasi dari metode Newton-Raphson. Pada metode Newton-Raphson hampiran akar yang dicari diperoleh dengan mencari titik potong garis singgung kurva di titik 𝑥𝑛, 𝑓 𝑥𝑛 dengan sumbu-𝑥. Kemudian dimodifikasi pada metode Tali Busur di mana hampiran akarnya diperoleh dengan menggunakan tali busur yang melalui titik 𝑥𝑛−1, 𝑓 𝑥𝑛−1 dan 𝑥𝑛, 𝑓 𝑥𝑛 sebagai hampiran 𝑓(𝑥) dan mencari titik potongnya dengan sumbu-x. Persamaan iterasi pada metode Newton-Raphson yang menggunakan turunan 𝑓(𝑥) dimodifikasi sehingga tidak harus menggunakan fungsi turunannya tersebut. Persamaan iterasi untuk mendapatkan hampiran ke-𝑛 + 1 adalah
𝑥𝑛+1= 𝑥𝑛− 𝑓 𝑥𝑛 𝑓 𝑥𝑛,𝑥𝑛−1
; 𝑛 = 1,2, ⋯. (Atkinson & Han 2003)
Definisi 6 (Deret Taylor)
Misalkan fungsi 𝑓 memunyai turunan ke 𝑛 + 1 yang kontinu pada interval [𝑎, 𝑏]. Misalkan juga untuk setiap 𝑥0∈ [𝑎, 𝑏]. Deret
𝑓(𝑘 ) 𝑥 0 𝑘! (𝑥 − 𝑥0) 𝑘 𝑛 𝑘=0
disebut deret Taylor fungsi 𝑓 di sekitar 𝑥0, dan dapat dituliskan 𝑓 𝑥 = 𝑓 (𝑘) 𝑥 0 𝑘! (𝑥 − 𝑥0) 𝑘 𝑛 𝑘=0 . Dengan memisalkan 𝑥 = 𝑥0+ , diperoleh
𝑓 𝑥0+ = 𝑓(𝑘 ) 𝑥 0 𝑘! 𝑘 𝑛 𝑘 =0 .
3
Definisi 7𝐶𝑘+1(𝐼) adalah himpunan semua fungsi yang memiliki turunan ke-𝑘 + 1 kontinu pada 𝐼, di mana 𝐼 adalah interval terbuka.
(Burden & Faires 1993)
Teorema 1 (Teorema Rolle)
Misalkan 𝑓 adalah fungsi yang kontinu pada [𝑎, 𝑏] dan fungsi 𝑓 terturunkan pada (𝑎, 𝑏). Jika 𝑓 𝑎 = 𝑓 𝑏 = 0, maka terdapat sebuah bilangan 𝑐 ∈ (𝑎, 𝑏), sehingga 𝑓′ 𝑐 = 0.
(Burden & Faires 1993)
Bukti:
Terdapat tiga kasus, yaitu
Kasus 1: 𝑓 𝑥 = 𝑘, dengan 𝑘 konstan. Dari sini diperoleh 𝑓′ 𝑥 = 0, sehingga bilangan 𝑐 dapat diambil sembarang bilangan dalam interval (𝑎, 𝑏).
Kasus 2: 𝑓(𝑥) > 𝑓(𝑎), untuk suatu 𝑥 pada (𝑎, 𝑏).
Karena 𝑓 fungsi kontinu pada 𝑎, 𝑏 , maka menurut Teorema Nilai Ekstrim 𝑓 memunyai nilai maksimum pada suatu titik dalam interval [𝑎, 𝑏]. Karena 𝑓(𝑎) = 𝑓(𝑏), 𝑓 harus mencapai maksimum pada 𝑐 ∈ 𝑎, 𝑏 , maka 𝑓 memunyai maksimum lokal pada 𝑐 dan karena 𝑓 terturunkan pada 𝑐, maka 𝑓′ 𝑐 = 0.
Kasus 3: 𝑓 𝑥 < 𝑓(𝑎) untuk suatu 𝑥 dalam interval terbuka (𝑎, 𝑏).
Karena 𝑓 fungsi kontinu pada 𝑎, 𝑏 , maka menurut Teorema Nilai Ekstrim 𝑓 memunyai nilai minimum pada suatu titik dalam interval [𝑎, 𝑏]. Karena 𝑓(𝑎) = 𝑓(𝑏), 𝑓 harus mencapai minimum pada 𝑐 ∈ 𝑎, 𝑏 , maka 𝑓 memunyai minimum lokal pada 𝑐 dan karena 𝑓 terturunkan pada 𝑐, maka 𝑓′ 𝑐 = 0.
Dengan demikian Teorema 1 terbukti.
2.2 Interpolasi
Definisi 8 (Interpolasi)
Interpolasi adalah proses pencarian dan perhitungan nilai suatu fungsi yang grafiknya melewati sekumpulan titik yang diberikan. Titik-titik tersebut mungkin merupakan hasil eksperimen dalam sebuah percobaan atau diperoleh dari sebuah fungsi yang diketahui. Fungsi interpolasi biasanya dipilih dari sekelompok fungsi tertentu, salah satu fungsi
yang paling banyak dipakai adalah fungsi polinomial.
(Atkinson & Han 2003)
Definisi 9 (Interpolasi Polinomial Linear)
Interpolasi polinomial linear adalah interpolasi dua buah titik dengan sebuah garis lurus, misal diberikan dua buah titik 𝑥1, 𝑦1 dan 𝑥2, 𝑦2 , maka polinomial yang menginterpolasi kedua titik itu adalah persamaan garis lurus yang berbentuk
𝑝1 𝑥 =𝑦1 +
𝑦2− 𝑦1 𝑥2− 𝑥1
𝑥 − 𝑥1 . (Cheney & Kincaid 1994)
Definisi 10 (Selisih Terbagi)
Selisih terbagi (divided difference) atau kadang disebut daftar selisih adalah metode untuk mendapatkan suatu penyajian secara eksplisit suatu interpolasi polinomial Newton dari data yang tertabulasi dan ditulis sebagai
𝑓 𝑥0, 𝑥1, ⋯ , 𝑥𝑘 .
Selisih terbagi dari fungsi 𝑦 = 𝑓(𝑥) untuk 𝑘 = 1,2,3, … , 𝑚 didefinisikan sebagai berikut
1. Selisih terbagi ke-nol terhadap 𝑥𝑘 adalah 𝑓 𝑥𝑘 = 𝑓 𝑥𝑘 .
2. Selisih terbagi pertama terhadap 𝑥𝑘 dan 𝑥𝑘+1 adalah
𝑓 𝑥𝑘, 𝑥𝑘+1 =
𝑓 𝑥𝑘+1 − 𝑓 𝑥𝑘 𝑥𝑘+1− 𝑥𝑘
. 3. Selisih terbagi kedua terhadap 𝑥𝑘, 𝑥𝑘 +1 dan
𝑥𝑘+2 adalah 𝑓 𝑥𝑘, 𝑥𝑘 +1, 𝑥𝑘+2 = 𝑓 𝑥𝑘+2, 𝑥𝑘+1 − 𝑓 𝑥𝑘+1, 𝑥𝑘 𝑥𝑘 +2− 𝑥𝑘 . 4. ⋯.
5. Selisih terbagi didefinisikan secara rekursif sebagai berikut 𝑓 𝑥𝑘, 𝑥𝑘+1, … , 𝑥𝑘+𝑛−1, 𝑥𝑘+𝑛 = 𝑓 𝑥𝑘+𝑛, 𝑥𝑘+𝑛−1, ⋯ , 𝑥𝑘+1 − 𝑓 𝑥𝑘+𝑛−1, ⋯ , 𝑥𝑘+1, 𝑥𝑘 𝑥𝑘+𝑛− 𝑥𝑘 ; 𝑥𝑘≠ 𝑥𝑘+𝑛.
(Cheney & Kincaid 1994)
Teorema 2 (Sifat Simetris Selisih Terbagi)
Misalkan 𝑠1, 𝑠2, ⋯ , 𝑠𝑘 +1 menyatakan permutasi dari indeks 1,2, … , 𝑘 + 1 suatu simpul pada selisih terbagi, maka untuk sebarang indeks selisih terbagi berlaku
𝑓 𝑥𝑠1, 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘+1 = 𝑓 𝑥𝑠𝑘+1, ⋯ , 𝑥𝑠2, 𝑥𝑠1 . (Atkinson & Han 2003)
Bukti: (dengan induksi pada 𝑘 + 1) 1. Basis induksi
4
4
Untuk 𝑘 = 1, maka berlaku𝑓 𝑥1, 𝑥2 = 𝑓 𝑥2 − 𝑓 𝑥1 𝑥2− 𝑥1 =𝑓 𝑥2 − 𝑓 𝑥1 𝑥2− 𝑥1 =− 𝑓 𝑥2 − 𝑓 𝑥1 − 𝑥2− 𝑥1 =𝑓 𝑥1 − 𝑓 𝑥2 𝑥1− 𝑥2 =𝑓 𝑥1 − 𝑓 𝑥2 𝑥1− 𝑥2 = 𝑓 𝑥2, 𝑥1 . 2. Hipotesis induksi
Anggap benar, untuk 𝑠1, 𝑠2, ⋯ , 𝑠𝑘 sebarang permutasi dari indeks 1,2, … , 𝑘
𝑓 𝑥𝑠1, 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘 = 𝑓 𝑥𝑠𝑘, ⋯ 𝑥𝑠2, 𝑥𝑠1 . 3. Langkah induksi
Akan dibuktikan: untuk 𝑠1, 𝑠2, ⋯ , 𝑠𝑘 +1 sebarang permutasi dari indeks 1,2, … , 𝑘 + 1 berlaku 𝑓 𝑥𝑠1, 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘+1 = 𝑓 𝑥𝑠𝑘+1, ⋯ 𝑥𝑠2, 𝑥𝑠1 . Bukti: 𝑓 𝑥𝑠1, 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘+1 = 𝑓 𝑥𝑠𝑘+1, 𝑥𝑠𝑘, ⋯ , 𝑥𝑠2 − 𝑓 𝑥𝑠𝑘, ⋯ , 𝑥𝑠1 𝑥𝑠𝑘+1− 𝑥𝑠1 =𝑓 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘+1 − 𝑓 𝑥𝑠1, ⋯ , 𝑥𝑠𝑘−1, 𝑥𝑠𝑘 𝑥𝑠𝑘+1− 𝑥𝑠1 =− 𝑓 𝑥𝑠1, ⋯ , 𝑥𝑠𝑘 −1, 𝑥𝑠𝑘 − 𝑓 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘 +1 −(𝑥𝑠1− 𝑥𝑠𝑘 +1) =𝑓 𝑥𝑠1, ⋯ , 𝑥𝑠𝑘−1, 𝑥𝑠𝑘 − 𝑓 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘+1 𝑥𝑠1− 𝑥𝑠𝑘+1 = 𝑓 𝑥𝑠𝑘+1, 𝑥𝑠𝑘, ⋯ , 𝑥𝑠1 . Berdasarkan prinsip induksi matematik, maka Teorema 2 terbukti.
Teorema 3 (Hubungan Selisih Terbagi dengan Turunan untuk Simpul Sama)
Jika didefinisikan 𝑓 𝑥1, 𝑥1 = lim𝑥2→𝑥1𝑓 𝑥1, 𝑥2
dan limitnya ada, maka berlaku 𝑓 𝑥1, 𝑥1 = 𝑓′ 𝑥
1 .
(Atkinson & Han 2003)
Bukti: Karena diketahui 𝑓 𝑥1, 𝑥1 = lim 𝑥2→𝑥1𝑓 𝑥1, 𝑥2 = lim 𝑥2→𝑥1 𝑓 𝑥2 − 𝑓 𝑥1 𝑥2− 𝑥1 (karena Definisi 10) = 𝑓′ 𝑥
1 . (menurut Definisi turunan) Dengan demikian Teorema 3 terbukti.
Teorema 4 (Interpolasi Polinomial Newton)
Misalkan fungsi 𝑓 terdefinisi pada interval terbuka 𝐼, dan misalkan 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛 −𝑘 adalah 𝑘 + 1 bilangan yang berlainan pada interval terbuka 𝐼, maka terdapat sebuah polinomial tunggal 𝑝𝑛 ,𝑘 𝑥 berderajat paling tinggi 𝑘 yang memenuhi
𝑓 𝑥𝑖 = 𝑝𝑛,𝑘 𝑥𝑖 ;
untuk 𝑖 = 𝑛, 𝑛 − 1, … , 𝑛 − 𝑘. Interpolasi polinomial Newton ini adalah 𝑝𝑛,𝑘 𝑥 = 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑖 𝑥 − 𝑥𝑛−𝑗 𝑖−1 𝑗 =0 . (2) 𝑘 𝑖=1 (Sahid 2005) Bukti:
Interpolasi polinomial Newton dapat diperoleh secara rekursif. Oleh karena itu, untuk menghitung suatu nilai dengan menggunakan interpolasi polinomial berderajat 𝑘 perlu menghitung nilai-nilai polinomial berderajat 1,2, … , 𝑘. Misalkan interpolasi polinomialnya dituliskan sebagai
𝑝𝑛 ,𝑘 𝑥 = 𝑎1+ 𝑎2 𝑥 − 𝑥𝑛 + 𝑎3 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 + ⋯ + 𝑎𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 … 𝑥 − 𝑥𝑛−𝑘 +2 +𝑎𝑘+1 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 … 𝑥 − 𝑥𝑛−𝑘+1 ,
dan akan ditentukan nilai-nilai koefisien 𝑎1, 𝑎2, 𝑎3, ⋯ , 𝑎𝑘. Di sini berlaku 𝑝𝑛,𝑘 𝑥𝑖 = 𝑓 𝑥𝑖 untuk 𝑖 = 𝑛, 𝑛 − 1, … , 𝑛 − 𝑘.
Jika 𝑥 = 𝑥𝑛 disubstitusikan pada persamaan interpolasi polinomial, maka semua suku pada sisi kanan persamaan kecuali suku pertama bernilai nol, sehingga diperoleh
𝑝𝑛,0 𝑥𝑛 = 𝑎1= 𝑓 𝑥𝑛 .
Jika 𝑥 = 𝑥𝑛−1 disubstitusikan ke dalam persamaan interpolasi polinomial, maka semua suku pada sisi kanan kecuali dua suku pertama bernilai nol, sehingga diperoleh
5
atau 𝑎2= 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 =𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛 −1− 𝑥𝑛 = 𝑓 𝑥𝑛,𝑥𝑛−1 .Jika 𝑥 = 𝑥𝑛−2 disubstitusikan ke dalam persamaan interpolasi polinomial, maka semua suku pada sisi kanan kecuali tiga suku pertama bernilai nol, sehingga diperoleh
𝑓 𝑥𝑛 −2 = 𝑝𝑛,2 𝑥𝑛−2 = 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛 −2− 𝑥𝑛 + 𝑎3 𝑥𝑛−2− 𝑥𝑛 𝑥𝑛−2−𝑥𝑛−1 atau 𝑎3= 𝑓 𝑥𝑛−2 − 𝑓 𝑥𝑛 − 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 −1 = 𝑓 𝑥𝑛−2 − 𝑓 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 − 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛−1 . Untuk memermudah perhitungan bentuk 𝑎3 dapat diubah menjadi
𝑎3= 𝑓 𝑥𝑛−2 − 𝑓 𝑥𝑛 −1 𝑥𝑛−2− 𝑥𝑛−1 − 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 = 𝑓 𝑥𝑛−1, 𝑥𝑛−2 −𝑓 𝑥𝑛, 𝑥𝑛−1 𝑥𝑛−2− 𝑥𝑛 (menurut Definisi 10) = 𝑓 𝑥𝑛−2, 𝑥𝑛−1 −𝑓 𝑥𝑛−1, 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 (karena Teorema 2) = 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛 −2 (menurut Definisi 10) ⋮ dan seterusnya.
Jika 𝑥 = 𝑥𝑛−𝑘 disubstitusikan ke dalam persamaan interpolasi polinomial, maka diperoleh 𝑓 𝑥𝑛 −𝑘 = 𝑝𝑛,𝑘 𝑥𝑛−𝑘 =𝑓 𝑥𝑛 + 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛 + 𝑓 𝑥𝑥𝑛−2 − 𝑓 𝑥𝑛−1 𝑛−2− 𝑥𝑛−1 − 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛−2− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛−1 + ⋯ + 𝑎𝑘 𝑥𝑛−𝑘− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛−1 … 𝑥𝑛−𝑘− 𝑥𝑛−𝑘+2 + 𝑎𝑘+1 𝑥𝑛−𝑘− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛−1 … 𝑥𝑛−𝑘− 𝑥𝑛−𝑘+1 , dengan 𝑎𝑘 +1= 𝑓 𝑥𝑛−𝑘 − 𝑓 𝑥𝑛 − 𝑓 𝑥𝑛−1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛 − 𝑎3 𝑥𝑛−𝑘− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛−1 − ⋯ − 𝑎𝑘 𝑥𝑛−𝑘− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛−1 … 𝑥𝑛−𝑘− 𝑥𝑛−𝑘+2 𝑥𝑛−𝑘− 𝑥𝑛 𝑥𝑛−𝑘− 𝑥𝑛−1 … 𝑥𝑛−𝑘− 𝑥𝑛−𝑘+1 . Jika diuraikan akan diperoleh bentuk
𝑎𝑘+1=𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, … , 𝑥𝑛−𝑘 .
Dari uraian di atas terlihat adanya suatu pola pada pembilang 𝑎1, 𝑎2, 𝑎3 dan seterusnya sampai 𝑎𝑘 +1. Pembilang-pembilang tersebut merupakan selisih terbagi fungsi 𝑓. Berdasarkan Definisi 10, intrpolasi polinomial Newton ini dapat dituliskan menjadi
𝑝𝑛,𝑘 𝑥 =𝑓 𝑥𝑛 +𝑓 𝑥𝑛,𝑥𝑛−1 𝑥 − 𝑥𝑛 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛 −2 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 + ⋯ + 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, … , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛 −1 … 𝑥 − 𝑥𝑛 −𝑘+1 , atau secara rekursif dapat dituliskan sebagai berikut
𝑝𝑛,0 𝑥 =𝑓 𝑥𝑛
𝑝𝑛,1 𝑥 =𝑓 𝑥𝑛 +𝑓 𝑥𝑛,𝑥𝑛−1 𝑥 − 𝑥𝑛
𝑝𝑛,2 𝑥 =𝑓 𝑥𝑛 +𝑓 𝑥𝑛,𝑥𝑛−1 𝑥 − 𝑥𝑛 +𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛 −1 ⋮
6
6
𝑝𝑛,𝑘 𝑥 =𝑓 𝑥𝑛 +𝑓 𝑥𝑛,𝑥𝑛−1 𝑥 − 𝑥𝑛 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛 −2 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 + ⋯+ 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, … , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛 −1 … 𝑥 − 𝑥𝑛 −𝑘+1 . Sehingga dapat dituliskan
𝑝𝑛 ,𝑘 𝑥 = 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑖 𝑥 − 𝑥𝑛−𝑗 . (2) 𝑖−1
𝑗 =0 𝑘
𝑖=1 Dengan demikian Teorema 4 terbukti.
Akibat (Hampiran Newton)
Misalkan 𝑝𝑛 ,𝑘 adalah interpolasi polinomial Newton yang diberikan oleh Teorema 4 dan digunakan untuk menginterpolasikan fungsi 𝑓, yaitu
𝑓 𝑥𝑖 = 𝑝𝑛 ,𝑘 𝑥𝑖 ; 𝑖 = 𝑛, 𝑛 − 1, ⋯ , 𝑛 − 𝑘. Karena 𝑓 𝑥 ≠ 𝑝𝑛,𝑘 𝑥 , maka ada galat di antara keduanya, misalkan 𝐸𝑛,𝑘 𝑥 yang akan memenuhi persamaan berikut
𝑓 𝑥 = 𝑝𝑛 ,𝑘 𝑥 + 𝐸𝑛,𝑘 𝑥 . 3 (Sahid 2005)
Lema 1 (Polinomial Bersifat Tunggal)
Misal diberikan himpunan titik-titik yang memunyai absis berlainan yaitu
𝑥𝑛, 𝑓(𝑥𝑛) , 𝑥𝑛−1, 𝑓(𝑥𝑛−1) , ⋯ , 𝑥𝑛−𝑘, 𝑓(𝑥𝑛−𝑘) , maka terdapat tepat sebuah polinomial berderajat paling tinggi 𝑘 yang melalui 𝑘 + 1 titik tersebut.
(Cheney & Kincaid 1994)
Bukti:
Misalkan 𝑝𝑛,𝑘 𝑥 adalah polinomial berderajat ≤ 𝑘 dan memenuhi
𝑝𝑛 ,𝑘 𝑥𝑖 = 𝑓 𝑥𝑖 ; untuk 𝑖 = 𝑛, 𝑛 − 1, ⋯ , 𝑛 − 𝑘.
Untuk menunjukkan bahwa 𝑝𝑛,𝑘 𝑥 tunggal, misalkan terdapat polinomial lain, 𝑇𝑛 ,𝑘(𝑥) berderajat paling tinggi 𝑘 dan memenuhi
𝑇𝑛,𝑘 𝑥𝑖 = 𝑓 𝑥𝑖 ; untuk 𝑖 = 𝑛, 𝑛 − 1, ⋯ , 𝑛 − 𝑘. Sekarang definisikan
𝐿𝑛 ,𝑘 𝑥 = 𝑝𝑛 ,𝑘 𝑥 − 𝑇𝑛,𝑘 𝑥 . Karena 𝑝𝑛,𝑘 dan 𝑇𝑛 ,𝑘 keduanya berderajat
≤ 𝑘, maka 𝐿𝑛,𝑘 berderajat ≤ 𝑘. Selanjutnya berlaku
𝐿𝑛 ,𝑘 𝑥𝑖 = 𝑝𝑛,𝑘 𝑥𝑖 − 𝑇𝑛 ,𝑘 𝑥𝑖 = 𝑓 𝑥𝑖 − 𝑓 𝑥𝑖 = 0 ; untuk 𝑖 = 𝑛, 𝑛 − 1, ⋯ , 𝑛 − 𝑘.
Ini menunjukkan bahwa 𝐿𝑛 ,𝑘(𝑥) memunyai
𝑘 + 1 akar berlainan, yakni
𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, padahal 𝐿𝑛,𝑘 berderajat ≤ 𝑘. Hal ini tidak mungkin, karena berdasarkan sifat akar polinomial,
polinomial berderajat ≤ 𝑘 hanya memunyai paling banyak 𝑘 akar, kecuali 𝐿𝑛 ,𝑘 𝑥 = 0, yakni 𝐿𝑛 ,𝑘 berupa polinomial nol. Dari sini diperoleh
0 = 𝑝𝑛 ,𝑘 𝑥 − 𝑇𝑛,𝑘 𝑥 𝑝𝑛𝑘 𝑥 = 𝑇𝑛,𝑘 𝑥 , atau 𝑝𝑛,𝑘 bersifat tunggal. Dengan demikian Lema 1 terbukti.
Lema 2 (Galat Interpolasi pada Selisih Terbagi)
Jika 𝑝𝑛,𝑘 adalah polinomial berderajat ≤ 𝑘 yang menginterpolasikan fungsi 𝑓 pada titik 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘, maka untuk 𝑥 yang merupakan titik lain pada interval terbuka 𝐼, berlaku
𝑓 𝑥 −𝑝𝑛,𝑘 𝑥 =
𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑥 𝑥 − 𝑥𝑛−𝑖 . (4) 𝑘
𝑖=0
(Cheney & Kincaid 1994)
Bukti:
Misalkan 𝑡 titik selain 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘 pada interval 𝐼, di mana 𝑓 𝑡 terdefinisi. Misal didefinisikan 𝑞𝑛 ,𝑘 merupakan
polinomial berderajat ≤ 𝑘 + 1 yang menginterpolasikan fungsi 𝑓 pada titik 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑡, sehingga polinomial 𝑞𝑛,𝑘 dapat dibentuk dari persamaan (2), yaitu 𝑞𝑛,𝑘 𝑥 = 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑖 𝑥 − 𝑥𝑛−𝑗 𝑖−1 𝑗 =0 𝑘 𝑖=1 +𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑡 𝑥 − 𝑥𝑛−𝑗 𝑘−1 𝑗 =0 𝑥 − 𝑥𝑛−𝑘 = 𝑝𝑛 ,𝑘 𝑥 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑡 𝑥 − 𝑥𝑛−𝑖 𝑘 𝑖=0 . (5)
Karena 𝑞𝑛,𝑘 merupakan polinomial berderajat ≤ 𝑘 + 1 yang menginterpolasikan fungsi 𝑓 pada titik 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘, 𝑡, maka menurut Teorema 4 berlaku
7
dan 𝑓 𝑡 = 𝑞𝑛,𝑘 𝑡 . Oleh karena itu, daripersamaan (5) diperoleh 𝑓 𝑡 =
𝑝𝑛,𝑘 𝑡 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑡 𝑡 − 𝑥𝑛−𝑖 . 𝑘
𝑖=1 Untuk 𝑡 = 𝑥, maka Lema 2 terbukti.
Lema 3 (Galat Interpolasi)
Jika 𝑝 adalah polinomial berderajat ≤ 𝑘 yang menginterpolasikan fungsi 𝑓 pada 𝑘 + 1 titik berlainan, misal 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘 dan 𝑓(𝑘+1) kontinu, maka ∀𝑥 ∈ 𝑎, 𝑏 , terdapat bilangan
𝜉=𝜉 𝑥 ∈ 𝑎, 𝑏, yang mengakibatkan 𝑓 𝑥 −𝑝𝑛,𝑘 𝑥 = 𝑓(𝑘+1) 𝜉 𝑘 + 1 ! 𝑥 − 𝑥𝑛−𝑖 𝑘 𝑖=0 . 7 (Cheney & Kincaid 1994)
Bukti: Definisikan untuk 𝑡 ≠ 𝑥𝑛−𝑖, 𝑖 = 0,1, ⋯ , 𝑘 𝑤 𝑡 = 𝑡 − 𝑥𝑛−𝑖 𝑘 𝑖=0 ; 𝑐(𝑥) =𝑓 𝑥 − 𝑝𝑛,𝑘 𝑥 𝑤 𝑥 ; 𝜙 𝑡 = 𝑓 𝑡 − 𝑝𝑛,𝑘 𝑡 − 𝑐𝑤 𝑡 , 𝑐 terdefinisi karena 𝑤 𝑡 ≠ 0 karena 𝑡 ≠ 𝑥𝑛−𝑖 .
Fungsi 𝜙 memunyai 𝑘 + 2 pembuat nol, yaitu 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘, dan 𝑡, karena 𝜙 𝑥𝑛 = 𝜙 𝑥𝑛−1 = ⋯ = 𝜙 𝑥𝑛−𝑘 = 𝜙 𝑡 = 0. Fungsi 𝜙 terdiri dari fungsi-fungsi yang kontinu pada [𝑎, 𝑏] dan memunyai turunan ke-𝑘 + 1.
Karena ada 𝑘 + 2 pembuat nol, maka terdapat 𝑘 + 1 interval yang nilai 𝜙 di titik-titik ujungnya sama dengan nol, maka menurut Teorema 1 pada setiap interval terdapat 𝑐𝑖, 𝑖 = 1,2, … , 𝑘 + 1 sehingga 𝜙′ 𝑐
𝑖 = 0.
Dengan alasan yang sama, maka 𝜙′′ memunyai 𝑘 pembuat nol, 𝜙′′′
memunyai 𝑘 − 1 pembuat nol, dan seterusnya. Akhirnya, dapat dikatakan 𝜙(𝑘+1) 𝑡 memunyai paling sedikit 1 pembuat nol. Misalkan 𝑡 =𝜉 merupakan pembuat nol 𝜙(𝑘+1) 𝑡 , maka diperoleh
𝜙 𝑘+1 𝜉 = 0
= 𝑓 𝑘+1 𝜉 − 𝑝𝑛 ,𝑘 𝑘+1 𝜉 − 𝑐𝑤 𝑘+1 𝜉 . 6 Pada persamaan di atas, 𝑝𝑛 ,𝑘(𝑘+1) 𝜉 = 0 karena 𝑝𝑛,𝑘 merupakan polinomial berderajat ≤ 𝑘. Berdasarkan sifat akar
polinomial, polinomial berderajat ≤ 𝑘, jika diturunkan sebanyak 𝑘 + 1 maka hasilnya nol.
Perhatikan juga bahwa 𝑤 𝜉 = 𝜉− 𝑥𝑛−𝑖 𝑘 𝑖=0 =𝜉𝑘 +1+ (𝜉 berderajat < 𝑘 + 1) 𝑤′ 𝜉 = 𝑘 + 1 𝜉(𝑘 )+ (𝜉 berderajat < 𝑘) 𝑤(2) 𝜉 = 𝑘 + 1 𝑘 𝜉(𝑘−1)+ (𝜉 berderajat < 𝑘 − 1) ⋮ 𝑤 𝑘 +1 𝜉 = 𝑘 + 1 𝑘 𝑘 − 1 ⋯ 2 (1) = 𝑘 + 1 !.
Akhirnya dari persamaan (6) diperoleh
𝑓 𝑘+1 𝜉 − 𝑐 𝑘 + 1 ! = 0 𝑓 𝑘+1 𝜉 − 𝑘 + 1 ! 𝑤 𝑥 𝑓 𝑥 − 𝑝𝑛,𝑘 𝑥 = 0 𝑘 + 1 ! 𝑤 𝑥 𝑓 𝑥 − 𝑝𝑛,𝑘 𝑥 = 𝑓 𝑘+1 𝜉 𝑓 𝑥 − 𝑝𝑛,𝑘 𝑥 = 𝑓 𝑘+1 𝜉 𝑘 + 1 ! 𝑥 − 𝑥𝑛−𝑖 𝑘 𝑖=0 . (7)
Dengan demikian Lema 3 terbukti.
Lema 4 (Hubungan Selisih Terbagi dan Turunan)
Jika 𝑓(𝑘 +1) kontinu pada 𝑎, 𝑏 dan 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘, 𝑡 adalah 𝑘 + 2 titik pada 𝑎, 𝑏 , maka ada 𝜉 pada (𝑎, 𝑏), yang mengakibatkan
𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑥 = 1 (𝑘 + 1)!𝑓
(𝑘 +1) 𝜉 . (Cheney & Kincaid 1994)
Bukti:
Misalkan 𝑝𝑛,𝑘 adalah polinomial berderajat ≤ 𝑘 yang menginterpolasikan fungsi 𝑓 pada titik 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘.
Dari Lema 2 diketahui untuk 𝑥 yang merupakan titik lain pada interval terbuka (𝑎, 𝑏), berlaku
𝑓 𝑥 −𝑝𝑛,𝑘 𝑥 =
𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑥 𝑥 − 𝑥𝑛−𝑖 . 𝑘
𝑖=0
Dari Lema 3 diketahui ∀𝑥 ∈ (𝑎, 𝑏), terdapat bilangan 𝜉 di mana 𝜉 𝑥 ∈ (𝑎, 𝑏), yang mengakibatkan 𝑓 𝑥 −𝑝𝑛,𝑘 𝑥 =𝑓 (𝑘+1) 𝜉 𝑘 + 1 ! 𝑥 − 𝑥𝑛−𝑖 𝑘 𝑖=0 . Dari persamaan di atas diperoleh
8
8
𝑓 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘, 𝑥 𝑥 − 𝑥𝑛 −𝑖 𝑘 𝑖=0 = 𝑓 𝑘+1 𝜉 𝑘 + 1 ! 𝑥 − 𝑥𝑛−𝑖 𝑘 𝑖=0 ; 𝑓 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘, 𝑥 = 𝑓(𝑘+1) 𝜉 𝑘 + 1 !. Dengan demikian Lema 4 terbukti.2.3 Barisan dan Kekonvergenan Definisi 11 (Barisan Konvergen)
Misalkan 𝑥𝑛 𝑛=0∞ adalah barisan bilangan real. Barisan 𝑥𝑛 𝑛=0∞ konvergen ke 𝛼, jika barisan tersebut memunyai limit 𝛼.
(Goldberg 1976)
Definisi 12 (Barisan Terbatas)
Misalkan 𝑋 = 𝑥𝑛 𝑛=0∞ adalah barisan bilangan real. Barisan 𝑥𝑛 𝑛=0∞ terbatas di atas, jika wilayah 𝑋 terbatas di atas dan terbatas di bawah, jika wilayah 𝑋 terbatas di bawah. Jika wilayah 𝑋 terbatas, maka barisan 𝑥𝑛 𝑛=0∞ barisan terbatas. Barisan 𝑥𝑛 𝑛=0∞ terbatas jika dan hanya jika terdapat 𝑀 > 0, sehingga
𝑥𝑛 ≤ 𝑀, ∀𝑛 ∈ 𝑁.
(Goldberg 1976)
Teorema 5 (Hubungan Barisan Konvergen dengan Barisan Terbatas)
Jika barisan bilangan real 𝑥𝑛 𝑛=0∞ konvergen, maka 𝑥𝑛 𝑛=0∞ terbatas.
(Goldberg 1976)
Bukti:
Misalkan 𝑥𝑛 𝑛=0∞ adalah barisan konvergen dan lim𝑛→∞𝑥𝑛= 𝛼.
Untuk 𝜀 = 1, terdapat 𝑛0∈ 𝑁, sehingga 𝑥𝑛− 𝛼 < 1, ∀𝑛 ≥ 𝑛0.
𝑥𝑛 − 𝛼 < 𝑥𝑛− 𝛼 (sifat nilai mutlak) 𝑥𝑛 < 𝛼 + 1, ∀𝑛 ≥ 𝑛0. Misalkan 𝑀 = max 𝑥1 , 𝑥2 , ⋯ , 𝑥𝑛0 , 𝛼 + 1 , maka 𝑥𝑛 < 𝑀, ∀𝑛 ∈ 𝑁. Jadi 𝑥𝑛 𝑛=0∞ terbatas.
Dengan demikian Teorema 5 terbukti.
Definisi 13 (Barisan Monoton)
Misalkan 𝑠𝑘 𝑘=1∞ adalah barisan bilangan real, barisan 𝑠𝑘 𝑘=1∞ tak turun, jika 𝑠𝑘≤ 𝑠𝑘 +1, ∀𝑘 ∈ 𝑁 dan tak naik, jika 𝑠𝑘≥ 𝑠𝑘 +1, ∀𝑘 ∈ 𝑁. Barisan 𝑠𝑘 𝑘=1∞ barisan monoton, jika barisan 𝑠𝑘 𝑘=1∞ tak turun atau tak naik.
(Goldberg 1976)
Teorema 6 (Hubungan Barisan Tak Naik dan Terbatas dengan Kekonvergenan)
Misalkan 𝜖𝑛 𝑛=0∞ adalah barisan bilangan real. Jika 𝜖𝑛 𝑛=0∞ barisan tak naik dan terbatas di bawah, maka barisan 𝜖𝑛 𝑛=0∞ konvergen.
(Goldberg 1976)
Bukti:
Misalkan 𝜖𝑛 𝑛=0∞ adalah barisan tak naik dan terbatas di bawah.
Misalkan 𝐴 = 𝜖0, 𝜖1, … terbatas di bawah dan 𝑎 = inf 𝐴.
Akan dibuktikan bahwa 𝜖𝑛 → 𝑎, bila 𝑛 → ∞, yaitu ∀𝜀 > 0, ∃𝑛0∈ 𝑁, sehingga
𝜖𝑛− 𝑎 < 𝜀, ∀𝑛 ≥ 𝑛0. Misalkan diberikan 𝜀 > 0, maka 𝑎 + 𝜀
bukan batas bawah dari 𝐴. Jadi terdapat 𝑛0∈ 𝑁, sehingga
𝜖𝑛0 < 𝑎 + 𝜀
Karena 𝜖𝑛 𝑛=0∞ adalah barisan tak naik, maka dari persamaan di atas diperoleh
𝜖𝑛 ≤ 𝜖𝑛0< 𝑎 + 𝜀, ∀𝑛 ≥ 𝑛0 (8) Karena 𝑎 adalah batas bawah terbesar dari
𝐴, maka
𝑎 ≤ 𝜖𝑛, ∀𝑛 ∈ 𝑁 (9) Dari persamaan (8) dan (9) diperoleh
𝑎 < 𝜖𝑛 ≤ 𝑎 + 𝜀, ∀𝑛 ≥ 𝑛0 ; 𝜖𝑛− 𝑎 < 𝜀, ∀𝑛 ≥ 𝑛0.
Jadi, lim𝑛→∞𝜖𝑛 = 𝑎 atau 𝜖𝑛 𝑛=0∞ konvergen ke 𝑎.
Dengan demikian Teorema 6 terbukti.
Teorema 7 (Hubungan Barisan Tak Turun dan Terbatas dengan Kekonvergenan)
Misalkan 𝑠𝑘 𝑘=1∞ adalah barisan bilangan real. Jika 𝑠𝑘 𝑘=1∞ barisan tak turun dan terbatas di atas, maka barisan 𝑠𝑘 𝑘=1∞ konvergen.
(Goldberg 1976)
Bukti:
Misalkan 𝑠𝑘 𝑘=1∞ adalah barisan tak turun dan terbatas di atas.
Misalkan 𝐴 = 𝑠1, 𝑠2, … terbatas di atas dan 𝑎 = sup 𝐴.
Akan dibuktikan bahwa 𝑠𝑘 → 𝑎, bila 𝑘 → ∞, yaitu ∀𝜀 > 0, ∃𝑘0∈ 𝑁, sehingga
𝑠𝑘− 𝑎 < 𝜀, ∀𝑘 ≥ 𝑘0.
Misalkan diberikan 𝜀 > 0, maka 𝑎 − 𝜀 bukan batas atas dari 𝐴. Jadi terdapat 𝑘0∈ 𝑁, sehingga
9
Karena 𝑠𝑘 𝑘=1∞ adalah barisan tak turun,maka dari persamaan di atas diperoleh 𝑠𝑘 ≥ 𝑠𝑘0 > 𝑎 − 𝜀, ∀𝑘 ≥ 𝑘0 (10) Karena 𝑎 adalah batas atas terkecil dari 𝐴,
maka
𝑠𝑘≤ 𝑎, ∀𝑘 ∈ 𝑁 (11) Dari persamaan (10) dan (11) diperoleh
𝑎 − 𝜀 < 𝑠𝑘≤ 𝑎, ∀𝑘 ≥ 𝑘0 ; 𝑠𝑘− 𝑎 < 𝜀, ∀𝑘 ≥ 𝑘0.
Jadi, lim𝑘→∞𝑠𝑘 = 𝑎 atau 𝑠𝑘 𝑘=1∞ konvergen ke 𝑎.
Dengan demikian Teorema 7 terbukti.
Teorema 8 (Hubungan Kekontinuan dan Kekonvergenan Barisan)
Misalkan 𝑥𝑛 𝑛=0∞ adalah barisan bilangan real. Jika fungsi 𝑓 kontinu di 𝛼 dan 𝑥𝑛 𝑛=0∞ adalah barisan yang konvergen ke 𝛼, maka 𝑓 𝑥𝑛 𝑛=0∞ konvergen ke 𝑓 𝛼 .
(Goldberg 1976)
Bukti:
Diberikan 𝜀 > 0 sebarang.
Karena fungsi 𝑓 kontinu, maka ∃𝛿 > 0 sehingga
0 < 𝑥 − 𝛼 < 𝛿 ⟹ 𝑓 𝑥 − 𝑓 𝛼 < 𝜀. Karena lim𝑛→∞𝑥𝑛= 𝛼, maka
𝑥𝑛− 𝛼 < 𝜂, ∀𝑛 ≥ 𝑛0. Dari dua pernyataan di atas, diperoleh
𝑥𝑛− 𝛼 < 𝜂 ⟹ 𝑓 𝑥𝑛 − 𝑓 𝛼 < 𝜀. Dengan demikian Teorema 8 terbukti.
Definisi 14 (Barisan Bagian)
Misalkan 𝑋 = 𝑥𝑛 adalah barisan bilangan real, dan 𝑟1< 𝑟2 < ⋯ < 𝑟𝑛 < ⋯ adalah barisan bilangan asli, maka barisan pada bilangan real yang diberikan oleh
𝑥𝑟1, 𝑥𝑟2, ⋯ , 𝑥𝑟𝑛, ⋯ disebut barisan bagian dari 𝑋.
(Goldberg 1976)
Teorema 9 (Hubungan Kekonvergenan Barisan dan Barisan Bagian)
Jika barisan 𝑥𝑛 𝑛=0∞ konvergen ke 𝛼, maka setiap barisan bagian dari 𝑥𝑛 𝑛=0∞ juga konvergen ke 𝛼.
(Goldberg 1976)
Bukti:
Misalkan 𝑥𝑛𝑖 𝑛=0 ∞
adalah barisan bagian dari 𝑥𝑛 𝑛=0∞ .
Diberikan 𝜀 > 0 sebarang.
Karena 𝑥𝑛 ⟶ 𝛼, maka terdapat 𝑛0∈ 𝑁, sehingga
𝑥𝑛− 𝛼 < 𝜀, ∀𝑛 ≥ 𝑛0. Pilih indeks 𝑘 terkecil sehingga 𝑛𝑘 ≥ 𝑛0,
maka dari persamaan di atas diperoleh 𝑥𝑛𝑖− 𝛼 < 𝜀, ∀𝑖 ≥ 𝑘. Jadi, barisan 𝑥𝑛𝑖 𝑛 =0
∞
konvergen ke 𝛼. Dengan demikian Teorema 9 terbukti.
Teorema 10 (Hubungan Perkalian Barisan yang Konvergen dan Terbatas)
Misalkan 𝑥𝑛 𝑛=0∞ dan 𝑦𝑛 𝑛=0∞ adalah barisan bilangan real. Jika barisan lim𝑛→∞𝑥𝑛 = 0, dan barisan 𝑦𝑛 𝑛=0∞ terbatas, maka
lim
𝑛→∞𝑥𝑛𝑦𝑛 = 0.
(Goldberg 1976)
Bukti:
Diberikan 𝜀 > 0 sebarang.
Karena 𝑦𝑛 𝑛=0∞ terbatas, maka terdapat 𝑀 > 0 sehingga
𝑦𝑛 ≤ 𝑀, ∀𝑛 ∈ 𝑁.
Karena 𝑥𝑛 𝑛=0∞ konvergen, maka terdapat ∃𝑛0∈ 𝑁 sehingga 𝑥𝑛− 0 ≤ 𝜀 𝑀, ∀𝑛 ≥ 𝑛0. Akibatnya 𝑥𝑛𝑦𝑛− 0 = 𝑥𝑛𝑦𝑛 = 𝑥𝑛 𝑦𝑛 ≤ 𝜀 𝑀𝑀 = 𝜀, ∀𝑛 ≥ 𝑛0. Dari sini terbukti bahwa lim𝑛→∞𝑥𝑛𝑦𝑛 = 0. Dengan demikian Teorema 10 terbukti.
Definisi 15 (𝑶 . dan 𝒐 . )
Simbol 𝑂 . dan 𝑜 . merupakan cara yang digunakan untuk membandingkan besarnya dua buah barisan, misalkan 𝑋 = 𝑥𝑛 dan 𝑌 = 𝑦𝑛 merupakan barisan bilangan real.
Notasi 𝑋 = 𝑂 𝑌 atau 𝑥𝑛 = 𝑂 𝑦𝑛 , dengan 𝑛 → ∞, menyatakan bahwa 𝑥𝑛
𝑦𝑛 terbatas, atau ∃𝑀 > 0 sehingga 𝑥𝑛 ≤ 𝑀 𝑦𝑛 . Notasi 𝑋 = 𝑜 𝑌 atau 𝑥𝑛 = 𝑜 𝑦𝑛 , dengan
𝑛 → ∞, menyatakan bahwa lim𝑛→∞ 𝑥𝑛
𝑦𝑛 = 0.
Hal ini berarti 𝑥𝑛 → 0 lebih cepat dari 𝑦𝑛 → 0.
(Bartle 1964)
2.4 Sifat-Sifat Akar Polinomial Lema 5 (Sifat Akar Polinomial)
Didefinisikan persamaan polinomial sebagai berikut
10
10
𝑔𝑘,𝑎 𝑠 = 𝑠𝑘+1− 𝑎 𝑠𝑖 𝑘 𝑖=0 = 0,maka persamaan tersebut memunyai sebuah akar real misal 𝑠𝑘 dan
max 1, 𝑎 < 𝑠𝑘< 𝑎 + 1.
(Traub 1964)
Bukti: (Lihat Traub 1964)
Lema 6 (Akar Polinomial Bersifat Naik)
Didefinisikan persamaan polinomial sebagai berikut
𝑔𝑘,𝑎 𝑠 = 𝑠𝑘+1− 𝑎 𝑠𝑖 𝑘
𝑖=0 = 0.
Persamaan tersebut memunyai sebuah akar real misal 𝑠𝑘, maka
𝑠𝑘−1< 𝑠𝑘, ∀𝑘.
(Traub 1964)
Bukti: (Lihat Traub 1964)
Lema 7 (Kekonvergenan Akar Polinomial)
Misalkan 𝑠𝑘 akar positif dari persamaan
𝑔𝑘,𝑎 𝑠 = 𝑠𝑘 +1− 𝑎 𝑠𝑖 𝑘
𝑖=0 dan 𝑘𝑎 > 1, maka berlaku
𝑘 𝑘 + 1 𝑎 + 1 < 𝑠𝑘 < 𝑎 + 1 dan lim 𝑘 →∞𝑠𝑘= 𝑎 + 1. (Traub 1964)
Bukti: (Lihat Traub 1964)
Lema 8 (Batas Akar Polinomial)
Misalkan 𝑠𝑘 akar positif dari persamaan polinomial berikut 𝑔𝑘,𝑎 𝑠 = 𝑠𝑘 +1− 𝑎 𝑠𝑖 𝑘 𝑖=0 ; dan diberikan 𝑣 = 𝑎 + 1 𝑘 𝑘 +1, maka berlaku 𝑎 + 1 − 𝑒𝑎 𝑎 + 1 𝑘< 𝑠𝑘 < 𝑎 + 1 − 𝑎 𝑎 + 1 𝑘 di mana 𝑒 basis logaritma natural.
(Traub 1964)
Bukti: (Lihat Traub 1964) Teorema 11
Misalkan persamaan galat didefinisikan sebagai berikut
𝜖𝑛+1= 𝐿 𝜖𝑛−𝑖𝑠 𝑘
𝑖=0
di mana 𝑠 bilangan positif dan 𝜖𝑛 → 0, bila 𝑛 → ∞. Misalkan juga 𝑠𝑘 adalah akar positif dari persamaan 𝑔𝑘,𝑎 𝑠 = 𝑠𝑘 +1− 𝑎 𝑠𝑖 𝑘 𝑖=0 = 0 dan 𝐿 ≠ 0, maka lim 𝑛→∞ 𝜖𝑛+1 𝜖𝑛 𝑠𝑘 = 𝐿 𝑠𝑘−1 /𝑘 . (Traub 1964)
Bukti: (Lihat Traub 1964)
III PEMBAHASAN
3.1 Rumusan MasalahDalam tulisan ini akan dicari akar dari persamaan
𝑓(𝑥) = 0, (12) yaitu nilai 𝑥 = 𝛼 yang menyebabkan 𝑓 𝛼 = 0, dengan 𝛼 merupakan akar dari persamaan tersebut. Fungsi 𝑓 dari persamaan (12) yang akan ditentukan akarnya merupakan fungsi tak linear dan memenuhi syarat 𝑓 ∈ 𝐶 𝑘+1 𝐼 dan 𝑓′ 𝛼 ≠ 0 (Sidi 2007).
Untuk menentukan akar persamaan (12) dapat digunakan metode analitik atau metode iteratif. Metode analitik adalah metode penyelesaian persamaan dengan menggunakan rumus-rumus yang sudah lazim digunakan,
seperti rumus “abc” untuk mencari akar persamaan kuadrat. Tidak semua fungsi dapat ditentukan akar persamaannya secara analitik. Oleh karena itu, diperlukan metode iteratif di dalam memberikan hampiran penyelesaian.
Pada metode iteratif pencarian akar dilakukan dengan prosedur-prosedur tertentu. Secara umum prosedurnya sebagai berikut.
Prosedur Metode Iteratif
i. Memilih nilai awal, batas toleransi 𝑇, dan maksimum iterasi 𝑁.
Biasanya setiap metode tidak selalu sama banyaknya nilai awal yang harus dipilih, misalnya metode Newton-Raphson
11
memerlukan satu nilai awal 𝑥0, dan metodeTali Busur memerlukan dua nilai awal, 𝑥0 dan 𝑥1. Semakin dekat nilai awal yang dipilih dengan akar sebenarnya, maka iterasi akan semakin cepat konvergen (Atkinson & Han 2003). Untuk memilih batas toleransi agar hampiran akar yang diperoleh sangat dekat dengan akar sebenarnya, maka batas toleransi yang dipilih harus sangat kecil.
ii. Melakukan proses iterasi.
Proses iterasi dilakukan untuk menghasilkan barisan akar, barisan akar yang dimaksud adalah hampiran-hampiran akar yang konvergen ke akar sebenarnya. Selanjutnya proses iterasi dihentikan jika
𝑥𝑛+1− 𝑥𝑛 < 𝑇.
iii. Analisis kekonvergenan.
Barisan akar yang diperoleh kemudian dianalisis kekonvergenannya, untuk mengetahui derajat kekonvergenannya. Derajat kekonvergenan menunjukkan kecepatan dalam menemukan akar. Jika derajat kekonvergenan semakin besar, maka kecepatan dalam menemukan akar akan semakin baik (Burden & Faires 1993). Adapun metode-metode iteratif yang akan dibahas antara lain: metode Newton-Raphson, metode Tali Busur, dan generalisasi metode Tali Busur.
3.1.1 Metode Newton-Raphson
Salah satu metode pencarian akar yang paling populer dalam menentukan akar-akar persamaan tak linear adalah metode Newton-Raphson. Metode ini paling disukai karena kekonvergenannya paling cepat di antara metode lainnya (Cheney & Kincaid 1994).
Metode Newton-Raphson merupakan metode pencarian akar yang hampiran akarnya diperoleh dengan mencari titik potong garis singgung kurva di titik 𝑥𝑛, 𝑓 𝑥𝑛 dengan sumbu-𝑥. Biasanya nilai awal 𝑥0 selalu diberikan. Jika tidak diberikan nilai awal bisa dipilih dengan syarat, nilai 𝑓′ 𝑥
0 ≠ 0. Hal ini disebabkan karena metode Newton-Raphson menggunakan fungsi turunan untuk setiap iterasinya dan tidak melakukan pengapitan akar.
Hampiran selanjutnya 𝑥𝑛+1 diperoleh dengan mencari titik potong garis singgung kurva di titik 𝑥𝑛, 𝑓 𝑥𝑛 dengan sumbu-𝑥. Ilustrasi penjelasan tersebut sebagai berikut.
Hampiran akar pertama 𝑥1 diperoleh dari titik potong garis singgung di titik 𝑥0, 𝑓 𝑥0 dengan sumbu-𝑥. Hampiran akar kedua 𝑥2 diperoleh dari titik potong garis singgung di titik 𝑥1, 𝑓 𝑥1 dengan sumbu-𝑥. Demikian seterusnya, sampai diperoleh hampiran akar yang paling dekat dengan akar sebenarnya. Ilustrasi penjelasan ini dapat dilihat pada gambar berikut.
Gambar 1 Grafik Iterasi Metode Newton- Raphson.
Selanjutnya akan dibahas prosedur pencarian akar dengan metode Newton-Raphson. Berdasarkan prosedur pencarian akar dengan metode iteratif, diperlukan nilai awal dan persamaan iterasi. Dalam memilih nilai awal pada metode ini sudah dijelaskan yaitu dengan syarat untuk setiap nilai awal 𝑥0, maka nilai 𝑓′ 𝑥
0 ≠ 0.
Misalkan 𝑥0 adalah nilai awal yang diberikan. Gradien garis singgung kurva 𝑦 = 𝑓(𝑥) di titik 𝑥0, 𝑓 𝑥0 adalah 𝑓′ 𝑥0 , maka persamaan garis singgungnya adalah
𝑦 − 𝑓 𝑥0 = 𝑓′ 𝑥0 𝑥 − 𝑥0 .
Hampiran akar pertama 𝑥1 diperoleh dari persamaan garis singgung pada saat 𝑦 = 0. Artinya titik 𝑥1, 0 memenuhi persamaan garis singgung, yakni 0 − 𝑓 𝑥0 = 𝑓′ 𝑥0 𝑥1− 𝑥0 −𝑓 𝑥0 𝑓′ 𝑥 0 = 𝑥1− 𝑥0 𝑥1= 𝑥0− 𝑓 𝑥0 𝑓′ 𝑥 0 .
Secara umum dengan cara yang sama, akhirnya diperoleh persamaan iterasi pada metode Newton-Raphson. Persamaan iterasi yang digunakan pada metode Newton-Raphson adalah 𝑥𝑛+1= 𝑥𝑛− 𝑓(𝑥𝑛) 𝑓′ 𝑥 𝑛 ; 𝑛 = 0, 1,2, ⋯.
12
12
Berikut ini algoritme yang akandigunakan untuk menentukan program dengan metode Newton-Raphson.
Algoritme 1: Metode Newton-Raphson
Input: 𝑓(𝑥), nilai awal 𝑥0, batas toleransi 𝑇, dan maksimum iterasi 𝑁.
Output: 𝛼 sehingga 𝑓 𝛼 = 0. Langkah-langkah:
i. Set penghitung iterasi 𝑖 = 1, ii. WHILE 𝑖 ≤ 𝑁 DO a. Menghitung 𝑥 = 𝑥0− 𝑓 𝑥0 𝑓′ 𝑥 0 . b. IF 𝑥 − 𝑥0 < 𝑇, THEN set 𝛼 = 𝑥; go to STOP.
c. Tambah penghitung iterasi 𝑖 = 𝑖 + 1 d. Set 𝑥0= 𝑥 dan 𝑓 𝑥0 = 𝑓 𝑥 . iii. STOP.
3.1.2 Metode Tali Busur
Metode Tali Busur adalah metode pencarian akar yang merupakan modifikasi dari metode Newton-Raphson. Pada metode Newton-Raphson hampiran akar diperoleh dengan mencari titik potong garis singgung kurva di titik 𝑥𝑛, 𝑓 𝑥𝑛 dengan sumbu-𝑥. Pada metode Tali Busur hampiran akarnya diperoleh dengan menggunakan tali busur yang melalui titik 𝑥𝑛−1, 𝑓 𝑥𝑛−1 dan 𝑥𝑛, 𝑓 𝑥𝑛 sebagai hampiran 𝑓(𝑥) dan mencari titik potongnya dengan sumbu-x (Atkinson & Han 2003).
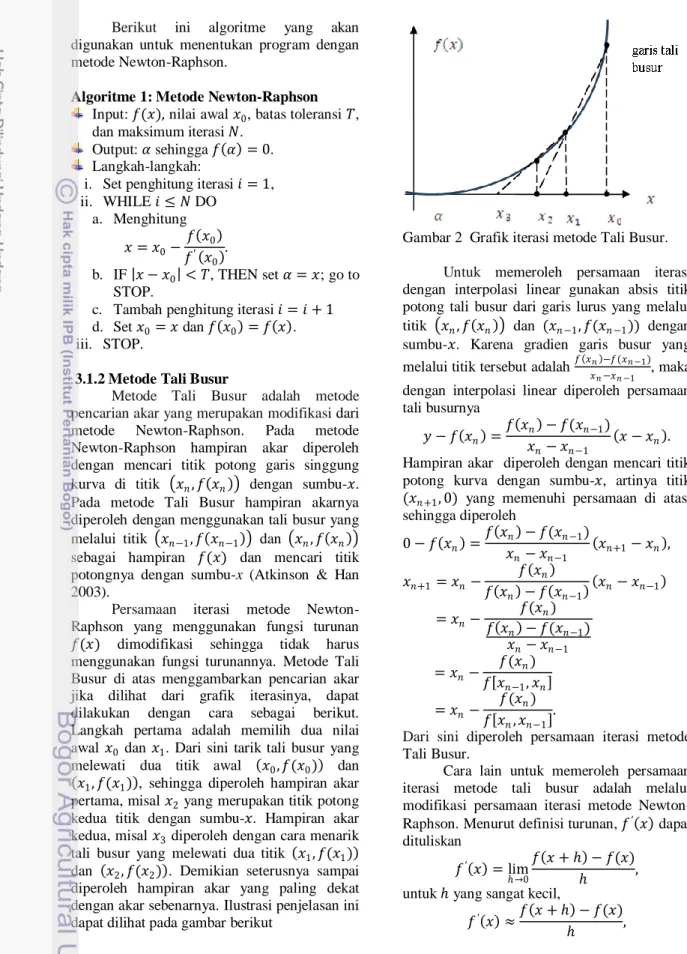
Persamaan iterasi metode Newton-Raphson yang menggunakan fungsi turunan 𝑓(𝑥) dimodifikasi sehingga tidak harus menggunakan fungsi turunannya. Metode Tali Busur di atas menggambarkan pencarian akar jika dilihat dari grafik iterasinya, dapat dilakukan dengan cara sebagai berikut. Langkah pertama adalah memilih dua nilai awal 𝑥0 dan 𝑥1. Dari sini tarik tali busur yang melewati dua titik awal 𝑥0, 𝑓(𝑥0) dan 𝑥1, 𝑓(𝑥1) , sehingga diperoleh hampiran akar pertama, misal 𝑥2 yang merupakan titik potong kedua titik dengan sumbu-𝑥. Hampiran akar kedua, misal 𝑥3 diperoleh dengan cara menarik tali busur yang melewati dua titik 𝑥1, 𝑓(𝑥1) dan 𝑥2, 𝑓(𝑥2) . Demikian seterusnya sampai diperoleh hampiran akar yang paling dekat dengan akar sebenarnya. Ilustrasi penjelasan ini dapat dilihat pada gambar berikut
Gambar 2 Grafik iterasi metode Tali Busur. Untuk memeroleh persamaan iterasi dengan interpolasi linear gunakan absis titik potong tali busur dari garis lurus yang melalui titik 𝑥𝑛, 𝑓 𝑥𝑛 dan (𝑥𝑛 −1, 𝑓(𝑥𝑛 −1)) dengan sumbu-𝑥. Karena gradien garis busur yang melalui titik tersebut adalah 𝑓 𝑥𝑛 −𝑓(𝑥𝑛 −1)
𝑥𝑛−𝑥𝑛 −1 , maka dengan interpolasi linear diperoleh persamaan tali busurnya
𝑦 − 𝑓 𝑥𝑛 =
𝑓 𝑥𝑛 − 𝑓(𝑥𝑛−1) 𝑥𝑛− 𝑥𝑛−1
𝑥 − 𝑥𝑛 . Hampiran akar diperoleh dengan mencari titik potong kurva dengan sumbu-𝑥, artinya titik (𝑥𝑛 +1, 0) yang memenuhi persamaan di atas, sehingga diperoleh 0 − 𝑓 𝑥𝑛 = 𝑓 𝑥𝑛 − 𝑓(𝑥𝑛 −1) 𝑥𝑛− 𝑥𝑛−1 𝑥𝑛+1− 𝑥𝑛 , 𝑥𝑛+1 = 𝑥𝑛− 𝑓 𝑥𝑛 𝑓 𝑥𝑛 − 𝑓 𝑥𝑛−1 𝑥𝑛− 𝑥𝑛−1 = 𝑥𝑛− 𝑓(𝑥𝑛) 𝑓 𝑥𝑛 − 𝑓(𝑥𝑛−1) 𝑥𝑛− 𝑥𝑛−1 = 𝑥𝑛− 𝑓(𝑥𝑛) 𝑓 𝑥𝑛−1, 𝑥𝑛 = 𝑥𝑛− 𝑓(𝑥𝑛) 𝑓 𝑥𝑛, 𝑥𝑛−1 . Dari sini diperoleh persamaan iterasi metode Tali Busur.
Cara lain untuk memeroleh persamaan iterasi metode tali busur adalah melalui modifikasi persamaan iterasi metode Newton-Raphson. Menurut definisi turunan, 𝑓′ 𝑥 dapat dituliskan
𝑓′ 𝑥 = lim →0
𝑓 𝑥 + − 𝑓(𝑥)
,
untuk yang sangat kecil,
𝑓′ 𝑥 ≈𝑓 𝑥 + − 𝑓(𝑥)
13
misalkan 𝑥 = 𝑥𝑛 dan = 𝑥𝑛−1− 𝑥𝑛, diperoleh𝑓′ 𝑥 𝑛 ≈ 𝑓 𝑥𝑛 −1 − 𝑓(𝑥𝑛) 𝑥𝑛−1− 𝑥𝑛 =𝑓 𝑥𝑛 −1 − 𝑓 𝑥𝑛 𝑥𝑛−1− 𝑥𝑛 = 𝑓 𝑥𝑛, 𝑥𝑛−1 .
Dari sini diperoleh persamaan iterasi metode Tali Busur. Persamaan iterasi metode Tali Busur adalah
𝑥𝑛 +1= 𝑥𝑛−
𝑓(𝑥𝑛) 𝑓[𝑥𝑛, 𝑥𝑛 −1 ]
. 13 Persamaan di atas diperoleh melalui dua cara, yaitu melalui interpolasi linear dan modifikasi metode Newton-Raphson.
Berdasarkan prosedur pencarian akar dengan metode iteratif, untuk menentukan akar dengan metode ini diperlukan nilai awal dan persamaan iterasi. Metode Tali Busur memerlukan dua nilai awal 𝑥0 dan 𝑥1. Persamaan iterasi yang digunakan adalah persamaan (13).
Berikut ini algoritme yang akan digunakan untuk menentukan program dengan metode Tali Busur.
Algoritme 2: Metode Tali Busur
Input: 𝑓(𝑥), nilai awal 𝑥0 dan 𝑥1, batas toleransi 𝑇, dan maksimum iterasi 𝑁. Output: 𝛼 sehingga 𝑓 𝛼 = 0. Langkah-langkah: i. Set 𝑖 = 2, 𝑞0= 𝑓 𝑥0 , 𝑞1= 𝑓 𝑥1 , ii. WHILE 𝑖 ≤ 𝑁 DO a. Menghitung 𝑥 = 𝑥1− 𝑞1 𝑞1− 𝑞0 𝑥1− 𝑥0 . b. IF 𝑥 − 𝑥1 < 𝑇, THEN set 𝛼 = 𝑥; go to STOP.
c. Tambah penghitung iterasi 𝑖 = 𝑖 + 1 d. Set 𝑥0= 𝑥1, 𝑥1= 𝑥, 𝑞0= 𝑞1, dan
𝑞1= 𝑞, iii. STOP.
3.1.3 Generalisasi Metode Tali Busur
Pada subbab 3.1.1 dan 3.1.2 telah dibahas metode Newton-Raphson dan metode Tali Busur. Metode Newton-Raphson memunyai kekonvergenen yang relatif cepat untuk menentukan akar, namun memerlukan iterasi turunan fungsi (Sahid 2005). Dengan
memodifikasi persamaan iterasi metode Newton-Raphson diperoleh metode Tali Busur yang tidak harus menggunakan turunan 𝑓(𝑥), namun metode Tali Busur ini memunyai kekonvergenan yang relatif lebih lambat dibandingkan metode Newton-Raphson (Sahid 2005). Oleh karena itu, diperlukan metode lain untuk menentukan akar yang memunyai kekonvergenan mendekati metode Newton-Raphson tetapi tidak harus menggunakan turunan 𝑓(𝑥) seperti metode Tali Busur (Sidi 2007). Persamaan iterasi metode Tali Busur diperoleh dengan menggunakan interpolasi polinomial Newton untuk 𝑘 = 1.
Pada bagian ini akan dibahas generalisasi metode Tali Busur, yaitu metode pencarian akar dengan menggunakan interpolasi polinomial Newton derajat 𝑘 dengan 𝑘 > 1. Generalisasi metode Tali Busur ini tidak memerlukan turunan 𝑓(𝑥), tetapi memerlukan nilai awal sebanyak 𝑘 dengan 𝑘 ≥ 2, dan sama-sama tidak harus menggunakan turunan 𝑓(𝑥) per iterasi.
Selanjutnya akan dibahas penurunan persamaan iterasi metode ini. Persamaan iterasi generalisasi metode Tali Busur adalah
𝑥𝑛+1= 𝑥𝑛− 𝑓(𝑥𝑛) 𝑝𝑛 ,𝑘′ (𝑥
𝑛)
; 𝑛 = 𝑘, 𝑘 + 1, ⋯ . (14) Persamaan di atas diperoleh melalui modifikasi metode Tali Busur yaitu dengan mengganti selisih terbagi pertama 𝑓 𝑥𝑛, 𝑥𝑛−1 dengan selisih terbagi ke-𝑘 dari turunan interpolasi polinomial Newton 𝑝𝑛 ,𝑘 dengan 𝑘 ≥ 2.
Lema 9 (Turunan Polinomial)
Misalkan 𝑝𝑛 ,𝑘 merupakan polinomial yang menginterpolasikan fungsi 𝑓 pada 𝑘 + 1 titik, yaitu 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, maka turunan polinomial tersebut adalah
𝑝𝑛,𝑘′ 𝑥 𝑛 = 𝑓 𝑥𝑛, 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑖 𝑥𝑛− 𝑥𝑛−𝑗 . 𝑖−1 𝑗 =1 𝑘 𝑖=2
Pada karya ilmiah ini hanya dibatasi sampai 𝑘 = 2 yaitu
𝑝𝑛,𝑘′ 𝑥 𝑛 =
𝑓 𝑥𝑛, 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2 𝑥𝑛− 𝑥𝑛−1 .
Bukti:
14
14
Dari Teorema 4 diketahui persamaan interpolasi polinomial Newton yang menginterpolasikanfungsi 𝑓 pada titik 𝑥𝑛, 𝑥𝑛 −1, ⋯ , 𝑥𝑛−𝑘 adalah
𝑝𝑛,𝑘 𝑥 = 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑖 𝑥 − 𝑥𝑛 −𝑗 . 𝑖−1
𝑗 =0 𝑘
𝑖=1
Untuk menurunkan 𝑝𝑛 ,𝑘(𝑥), akan dijabarkan terlebih dulu, yaitu
𝑝𝑛,𝑘 𝑥 = 𝑓 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛 −1 𝑥 − 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛 −1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, 𝑥𝑛−3 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 𝑥 − 𝑥𝑛−2 + ⋯
+ 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 ⋯ 𝑥 − 𝑥𝑛−𝑘+2 𝑥 − 𝑥𝑛−𝑘 +1 . Jika penjabaran persamaan tersebut diturunkan akan diperoleh
𝑝𝑛 ,𝑘′ 𝑥 = 0 + 𝑓 𝑥 𝑛, 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2 𝑥 − 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛 −2 𝑥 − 𝑥𝑛 −1 +𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, 𝑥𝑛 −3 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, 𝑥𝑛−3 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−2 +𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, 𝑥𝑛 −3 𝑥 − 𝑥𝑛 −1 𝑥 − 𝑥𝑛−2 + ⋯ +𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 ⋯ 𝑥 − 𝑥𝑛−𝑘+2 +𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−1 ⋯ 𝑥 − 𝑥𝑛−𝑘+3 𝑥 − 𝑥𝑛−𝑘+1 + ⋯ +𝑓 𝑥𝑛, 𝑥𝑛 −1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛 𝑥 − 𝑥𝑛−2 ⋯ 𝑥 − 𝑥𝑛−𝑘+2 𝑥 − 𝑥𝑛−𝑘+1 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛 −2, ⋯ , 𝑥𝑛−𝑘 𝑥 − 𝑥𝑛−1 ⋯ 𝑥 − 𝑥𝑛−𝑘 +2 𝑥 − 𝑥𝑛−𝑘+1 .
Misalkan 𝑥 = 𝑥𝑛, sehingga diperoleh persamaan 𝑝𝑛,𝑘′ 𝑥 𝑛 = 𝑓 𝑥𝑛, 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2 𝑥𝑛− 𝑥𝑛 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2 𝑥𝑛− 𝑥𝑛−1 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, 𝑥𝑛−3 𝑥𝑛− 𝑥𝑛 𝑥𝑛− 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, 𝑥𝑛−3 𝑥𝑛− 𝑥𝑛 𝑥𝑛− 𝑥𝑛−2 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, 𝑥𝑛−3 𝑥𝑛− 𝑥𝑛−1 𝑥𝑛− 𝑥𝑛−2 + ⋯ + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥𝑛− 𝑥𝑛 𝑥𝑛− 𝑥𝑛−1 ⋯ 𝑥𝑛− 𝑥𝑛−𝑘+2 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥𝑛− 𝑥𝑛 𝑥𝑛− 𝑥𝑛−1 ⋯ 𝑥𝑛− 𝑥𝑛−𝑘+3 𝑥𝑛− 𝑥𝑛−𝑘+1 +⋯ +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥𝑛− 𝑥𝑛 𝑥𝑛− 𝑥𝑛−2 ⋯ 𝑥𝑛− 𝑥𝑛−𝑘+2 𝑥𝑛− 𝑥𝑛−𝑘+1 +𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥𝑛− 𝑥𝑛−1 ⋯ 𝑥𝑛− 𝑥𝑛−𝑘+2 𝑥𝑛− 𝑥𝑛−𝑘+1 = 𝑓 𝑥𝑛, 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2 𝑥𝑛− 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, 𝑥𝑛−3 𝑥𝑛− 𝑥𝑛−1 𝑥𝑛− 𝑥𝑛−2 + ⋯ + 𝑓 𝑥𝑛, 𝑥𝑛−1, 𝑥𝑛−2, ⋯ , 𝑥𝑛−𝑘 𝑥𝑛− 𝑥𝑛−1 ⋯ 𝑥𝑛− 𝑥𝑛−𝑘+2 𝑥𝑛− 𝑥𝑛−𝑘+1 , atau 𝑝𝑛,𝑘′ 𝑥 𝑛 = 𝑓 𝑥𝑛, 𝑥𝑛−1 + 𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛 −𝑖 𝑥𝑛− 𝑥𝑛−𝑗 . 𝑖−1 𝑗 =1 𝑘 𝑖=2
Untuk 𝑘 = 1 diperoleh 𝑝𝑛 ,𝑘′ 𝑥𝑛 = 𝑓 𝑥𝑛, 𝑥𝑛−1 yaitu merupakan selisih terbagi pertama yang digunakan dalam metode Tali Busur. Sedangkan untuk 𝑘 ≥ 2 metode yang digunakan adalah generalisasi metode Tali Busur.
Selanjutnya akan dibahas sifat-sifat selisih terbagi. Adapun sifat-sifatnya antara lain:
i. Dapat ditentukan secara rekursif. (berdasarkan Definisi 10) ii. Simetris.
Misalkan 𝑠1, 𝑠2, ⋯ , 𝑠𝑘+1 menyatakan permutasi dari indeks 1,2, … , 𝑘 + 1 suatu simpul pada selisih terbagi, maka untuk sebarang indeks selisih terbagi berlaku 𝑓 𝑥𝑠1, 𝑥𝑠2, ⋯ , 𝑥𝑠𝑘+1 = 𝑓 𝑥𝑠𝑘+1, ⋯ , 𝑥𝑠2, 𝑥𝑠1 . (bukti disajikan pada Teorema 2)
iii. Dapat dinyatakan dalam turunan.
Jika 𝑓𝑘 kontinu pada 𝐼 dan 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘 adalah 𝑘 + 1 titik pada 𝐼, maka ada 𝜉 pada 𝐼, yang mengakibatkan
𝑓 𝑥𝑛, 𝑥𝑛−1, ⋯ , 𝑥𝑛−𝑘, 𝑥 =
1 (𝑘 + 1)!𝑓
(𝑘+1) 𝜉 .
(bukti disajikan pada Lema 4)
Selanjutnya akan dibahas penyajian selisih terbagi. Selisih terbagi yang diperoleh pada proses iterasi ke-nol, disimpan dalam tabel selisih terbagi, dapat yang kemudian akan digunakan untuk menentukan selisih terbagi pertama. Selisih terbagi pertama disimpan dalam tabel selisih terbagi yang kemudian digunakan untuk menentukan selisih terbagi kedua, dan seterusnya sampai diperoleh selisih terbagi ke-𝑘 yang diperlukan.
Dengan menggunakan Definisi 10, maka dapat dibuat tabel selisih terbagi. Untuk 𝑘 = 0 dapat dilihat pada tabel berikut.