BAB 2
LANDASAN TEORI
2.1. Pengertian Citra Digital
Citra digital merupakan sebuah fungsi intensitas cahaya f(x,y), dimana harga x dan y merupakan koordinat spasial dan harga fungsi f tersebut pada setiap titik (x,y) merupakan tingkat kecemerlangan atau intensitas cahaya citra pada titik tersebut.
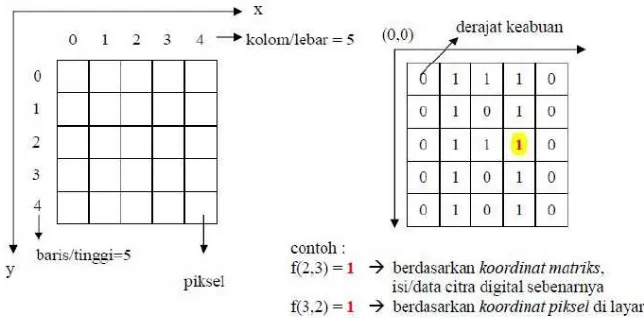
Citra digital adalah suatu matriks dimana indeks baris dan kolomnya menyatakan suatu titik pada citra tersebut dan elemen matriksnya yang disebut sebagai elemen gambar atau piksel menyatakan tingkat keabuan pada titik tersebut. Indeks baris dan kolom (x,y) dari sebuah piksel dinyatakan dalam bilangan bulat (integer). Sebuah piksel merupakan sampel dari pemandangan yang mengandung intensitas citra yang dinyatakan dalam bilangan bulat. Untuk menunjukkan lokasi suatu piksel, koordinat (0,0) digunakan untuk posisi kiri atas dalam bidang citra, dan koordinat (m-1,n-1) digunakan untuk posisi kanan bawah dalam citra berukuran m x n piksel dimana m adalah kolom dan n adalah baris.
Untuk menunjukkan tingkat pencahayaan suatu piksel, seringkali digunakan bilangan bulat yang besarnya delapan bit dengan lebar selang nilai 0-255 dimana 0
untuk warna hitam, 255 untuk warna putih, dan tingkat abu-abu berada di antara nilai 0 dan 255 [10]. Penjelasan posisi letak piksel dapat dilihat pada gambar 2.1.
Gambar 2.1 Posisi Letak Piksel
2.2. Pengolahan Citra Digital
Image processing atau sering disebut pengolahan citra digital merupakan suatu proses
filter gambar asli menjadi gambar lain sesuai dengan keinginan kita. Misalnya, kita mendapatkan suatu gambar yang terlalu gelap. Dengan image processing, kita dapat memprosesnya agar mendapatkan gambar yang jelas [7]. Secara garis besar, gambar blok diagramnya dapat dilihat pada gambar 2.2.
Gambar 2.2 Blok Diagram Pengolahan Citra
2.3. Jenis-jenis Citra Digital
Ada banyak cara untuk menyimpan citra digital di dalam memori. Cara penyimpanan
menentukan jenis citra digital yang terbentuk. Beberapa jenis citra digital yang sering digunakan adalah citra biner, citra grayscale, dan citra warna.
Gambar
Asli Gambar
Hasil Proses
2.3.1. Citra biner
Citra biner disebut juga citra monokrom. Banyak warna citra biner ada 2, yaitu hitam dan putih. Dibutuhkan 1 bit memori untuk menyimpan kedua warna ini. Setiap piksel pada citra bernilai 0 untuk hitam dan 1 untuk putih.
2.3.2. Citra grayscale
Citra warna grayscale menggunakan warna tingkatan warna abu-abu. Warna abu-abu merupaka satu-satunya warna pada ruang RGB dengan komponen merah, hijau, dan biru memepunyai intensitas yang sama. Banyaknya warna pada citra ini tergantung pada jumlah bit yang akan disediakan di memori untuk menampung kebutuhan warna ini. Citra dengan skala keabuan empat bit maka jumlah kemungkinan warnanya adalah 24 = 16 warna dengan kemungkinan warna 0 (min) sampai 15 (max).
2.3.3. Citra warna
Setiap piksel yang terdapat pada citra warna mewakili warna yang merupakan kombinasi dari tiga warna dasar (RGB = Red Green Blue). Setiap warna dasar menggunakan penyimpanan 8 bit = 1 byte, yang berarti setiap warna memiliki gradasi sebanyak 255 warna. Berarti setiap piksel memiliki kombinasi warna sebanyak 28x 28x 28 = 16 juta warna lebih. Itulah sebabnya format ini dinamakan true color karena memiliki jumlah warna yang cukup besar.
Penyimpanan citra true color di dalam memori berbeda dengan citra
grayscale. Setiap piksel dari citra grayscale 256 gradasi warna diwakili oleh 1 byte. Sedangkan 1 piksel citra true color diwakili oleh 3 byte, dimana masing-masing byte
merepresentasikan warna merah (Red), hijau (Green), dan biru (Blue) [9].
2.4. Noise
2.4.1. Pengertian noise
dapat disebabkan oleh gangguan fisik (optik) pada alat penangkap citra misalnya kotoran debu yang menempel pada lensa foto maupun akibat proses pengolahan yang tidak sesuai [7].
2.4.2. Exponential noise
Exponential Noise merupakan jenis noise yang dihasilkan oleh laser yang koheren ketika citra diperoleh. Oleh karena itu, noise ini sering disebut sebagai bercak laser (Myler and Weeks, 1993) [4]. PDF-nya berupa:
𝑝𝑝(𝑧𝑧) =�𝑎𝑎𝑎𝑎−𝑎𝑎𝑧𝑧,𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑢 0 ≤ 𝑧𝑧
0,𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑢𝑧𝑧< 0 ………….…..(2.1)
𝑎𝑎 > 0. Rata-ratanya berupa:
𝜇𝜇= 1𝑎𝑎 ………..……..(2.2)
varians berupa:
𝜎𝜎2 = 1
𝑎𝑎2 ………....(2.3) Pembangkit exponential noise dilakukan dengan menggunakan rumus:
𝑑𝑑 = −1𝑎𝑎ln(1− 𝑟𝑟𝑎𝑎𝑢𝑢𝑑𝑑) ……….………..(2.4)
Keterangan :
z = nilai keabuan
rand = bilangan random
Citra dengan exponential noise dapat dilihat pada gambar 2.3. Grafik
exponential noise dapat dilihat pada gambar 2.4. Contoh noise eksponensial negatif dapat dilihat pada gambar 2.5.
Gambar 2.4 Grafik Exponential Noise
Gambar 2.5 Contoh Noise Eksponensial Negatif
2.5. Restorasi Citra
Gambar 2.6 Contoh Noise Filtering
2.5.1. Geometric mean filter
Sebuah citra diperbaiki dengan menggunakan geometric mean filter yang diberikan oleh persamaan:
fˆ(𝑥𝑥,𝑦𝑦)=�∏(𝑠𝑠,𝑢𝑢)𝜖𝜖𝑆𝑆𝑥𝑥𝑦𝑦𝑔𝑔(𝑠𝑠,𝑢𝑢)�
1
𝑚𝑚𝑢𝑢 ………..(2.5)
𝑥𝑥,𝑦𝑦= koordinat pixel pada citra
𝑚𝑚𝑢𝑢 = dimensi citra (pixel) s,t = nilai intensitas pixel
Π = perkalian nilai 𝑝𝑝𝑝𝑝𝑥𝑥𝑎𝑎𝑝𝑝 yang terkena filter
Setiap piksel yang diperbaiki oleh hasil kali masing-masing piksel dalam
subimage window, kemudian dipangkatkan dengan 1/𝑚𝑚𝑢𝑢.
Misalkan 𝑆𝑆𝑥𝑥𝑦𝑦 adalah subimage dari sebuah citra dan 𝑆𝑆𝑥𝑥𝑦𝑦 berukuran 3𝑥𝑥3 yang
mempunyai nilai-nilai intensitas seperti pada gambar 2.7.
5 5 4
7 2 6 1 4 1
fˆ(𝑥𝑥,𝑦𝑦)= (5𝑥𝑥5𝑥𝑥4𝑥𝑥7𝑥𝑥2𝑥𝑥6𝑥𝑥1𝑥𝑥4𝑥𝑥1)31𝑥𝑥3= (33600) 1
9 = 3,18 = 3
Sehingga bagian dari citra berubah menjadi seperti pada gambar 2.8.
5 5 4
7 3 6 1 4 1
Gambar 2.8 Piksel Citra Hasil [9]
2.5.2. Alpha-trimmed mean filter
Filter ini mengganti nilai sebuah piksel dengan nilai rata-rata dari dalam subimage di bawah jendela ketetanggaan ukuran mxn setelah dikurangi nilai terkecil dan nilai terbesar, seperti persamaan berikut:
fˆ(𝑥𝑥,𝑦𝑦)= 𝑚𝑚𝑢𝑢−𝑑𝑑1 ∑(𝑠𝑠,𝑢𝑢)𝜖𝜖𝑆𝑆𝑥𝑥,𝑦𝑦𝑔𝑔𝑟𝑟(𝑠𝑠,𝑢𝑢) ………..(2.6)
𝑥𝑥,𝑦𝑦 = koordinat pixel pada citra
𝑚𝑚𝑢𝑢 = dimensi citra (pixel)
𝑑𝑑 = nilai inputan 0 - 8 s,t = nilai intensitas pixel
∑ = penjumlahan nilai 𝑝𝑝𝑝𝑝𝑥𝑥𝑎𝑎𝑝𝑝 yang terkena filter
Dimana 0≤ 𝑑𝑑 ≤ (𝑚𝑚𝑢𝑢 −1). Jika 𝑑𝑑 = 0, filter ini bekerja seperti arithmetic
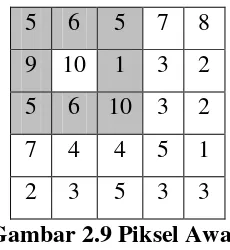
Citra piksel awal seperti pada gambar 2.9, dengan hasil filter untuk d = 2
Piksel citra tersebut kemudian akan dilakukan reduksi terhadap noise dengan nilai inputan d = 2. Maka perhitungannya adalah :
Gambar 2.10 Hasil Filter dengan d = 2
2.6. Pengukuran Kinerja Restorasi Citra
2.6.1. Mean squared error (MSE)
Perbaikan citra pada dasarnya merupakan proses yang bersifat subjektif sehingga parameter keberhasilannya bersifat subjektif pula. Untuk itu diperlukan adanya alat ukur kuantitatif yang bisa digunakan untuk mengukur kinerja prosedur perbaikan citra [9]. Semakin kecil nilai MSE maka citra hasil reduksi semakin mendekati citra aslinya. Persamaannya:
Keterangan :
M dan N = ukuran panjang dan lebar citra.
𝑓𝑓𝑎𝑎(𝑝𝑝,𝑗𝑗) = intensitas citra di titik (𝑝𝑝,𝑗𝑗) sebelum terkena noise.
𝑓𝑓𝑏𝑏(𝑝𝑝,𝑗𝑗) = intensitas citra di titik (𝑝𝑝,𝑗𝑗) setelah noise dihilangkan.
2.6.2. Peak signal-to-noise ratio (PSNR)
Kualitas citra hasil reduksi juga dapat diukur secara kuantitatif dengan mengguanakan besaran Peak Signal-to-Noise Ratio (PSNR) dengan satuan desiBel (dB). Semakin besar nilai PSNR maka citra hasil reduksi semakin mendekati citra aslinya, dengan kata lain semakin bagus kualitas citra hasil reduksi tersebut, dan berlaku sebaliknya.
Persamaannya:
𝑃𝑃𝑆𝑆𝑀𝑀𝑃𝑃 = 20 𝑥𝑥𝑝𝑝𝑙𝑙𝑔𝑔10 � 255
√𝑀𝑀𝑆𝑆𝑀𝑀� ………..(2.8)
2.7. Relevansi Penelitian
Berikut penelitian tentang pengolahan citra yang membahas metode geometric mean filter ataupun alpha-trimmed mean filter:
1. Wiliyana dari Universitas Sumatera Utara mengangkat judul skripsinya
“Perbandingan Algoritma Arithmetic dengan Geometric Mean Filter untuk
Reduksi Noise pada Citra”. Tugas akhir ini memberikan kesimpulan perbandingan antara Algoritma Arithmetic dengan Geometric Mean Filter
dalam melakukan reduksi noise pada citra. Berdasarkan penelitian ini, didapat kesimpulan bahwa Algoritma Geometric Mean Filter lebih baik dalam melakukan reduksi terhadap salt and paper noise dengan diberikan probabilitas yang sama seperti pada pengujian Algoritma Arithmetic Mean Filter. Hal ini dapat terlihat dengan adanya nilai MSE yang terdapat pada Algoritma Geometric Mean Filter lebih kecil dibandingkan dengan Algoritma
Arithmetic Mean Filter [12].
gaussian noise. Metode yang dilakukan penelitian antara lain mean filter,
wiener filter, alpa-trimmed mean filter, K-means filter, bilateral filter dan
trilateralfilter. Penelitian dilakukan dengan menggunakan parameter MSE dan PSNR. Berdasarkan hasil penelitian, didapat kesimpulan metode jenis
nonlinear filter paling bagus untuk melakukan reduksi noise [11].
3. Srinivas, R. & Panda, S. melakukan penelitian dengan judul “Performance Analysis of Various Filters for Image Noise Removal in Different Noise
Environment”. Penelitian ini bertujuan untuk membandingkan metode yang bagus dan efisien untuk mereduksi tiga tipe noise yaitu salt and pepper noise,
gaussian noise dan speckle noise dengan probabilitas 10%-60%. Dengan metode-metode yang akan dibandingkan yaitu average filter (AF), adaptive median filter (AMF), standard median filter (SMF) dan alpha-trimmed mean filter (ATMF). Penelitian dilakukan dengan menggunakan parameter MSE dan PSNR. Berdasarkan penelitian ini didapat kesimpulan bahwa standard median filter (SMF) bagus untuk mereduksi salt and pepper noise dengan probabilitas 50%-60%, average filter (AF) bagus untuk mereduksi salt and
pepper noise dengan probabilitas ≥ 60%, gaussian noise, dan speckle noise, adaptive median filter (AMF) bagus untuk mereduksi gaussian noise, dan
speckle noise dengan probabilitas 10%-20%, dan alpha-trimmed mean filter
tidak termasuk jenis metode yang baik dan efisien untuk mereduksi ketiga