PEMODELAN REGRESI SPASIAL
DENGAN PENDEKATAN RESIDUAL BOOTSTRAP
(STUDI KASUS : PEMODELAN FERTILITAS DI PROVINSI LAMPUNG) Ari Rusmasari1, Sutikno2, Setiawan3
1 Mahasiswa Pasca Sarjana, Jurusan Statistika, Institut Teknologi Sepuluh Nopember Surabaya
2,3 Jurusan Statistika, Institut Teknologi Sepuluh Nopember Surabaya
1[email protected], 2sutikno@ statistika.its.ac.id, 3[email protected]
Abstract
Estimation and testing parameters on the size of a small sample data is one of the problems that often occurs in modeling of spatial data. One of statistical techniques that could be used to overcome this problem is the bootstrap resampling method. In this research, the spatial bootstrap test is mainly used for identification model through Moran’s I test and Lagrange Multiplier test.
Generally, there are two regression models for explaining the spatial dependency of data, namely spatial autoregressive model (SAR) and spatial error model (SEM). The residual Bootstrap approach is applied to both spatial models. Results show that the SAR model suitable for modeling fertility in Lampung Province. Economic growth, percentage of women who are not family planning acceptors, mean of age at first marriage, percentage of women working in agriculture, and the percentage of women working in the industrial sector have a significant effect on the percentage of women with high fertility in Lampung Province. In addition, algorithms, programs, and Graphical User Interface (GUI) have been developed to determine bootstrap Moran’s I and bootstrap LM hypothesis testing also SAR and SEM modeling with residual bootstrap approach.
Keywords : Fertility, Spatial Bootstrap Test, SAR, SEM, Residual Bootstrap
Abstrak
Pembahasan ilmu kewilayahan berkaitan dengan analisis statistik dari suatu sampel data cross section dalam perkembangannya muncul berbagai permasalahan. Salah satu permasalahan adalah pendugaan dan pengujian parameter pada ukuran data sampel kecil.
Pendekatan untuk mengatasi masalah tersebut adalah metode resampling bootstrap yang merupakan pendekatan nonparametrik. Dalam penelitian ini, untuk identifikasi awal model digunakan metode spatial bootstrap test yang terdiri atas uji Moran’s I dan uji Lagrange Multiplier (LM) dengan bootstrap. Untuk pemodelannya digunakan metode Spatial Autoregressive Model (SAR) dan Spatial Error Model (SEM) dengan pendekatan residual bootstrap. Hasil penelitian menyimpulkan bahwa model SAR sesuai untuk memodelkan fertilitas di Provinsi Lampung. Pertumbuhan ekonomi, persentase wanita tidak KB, rata-rata umur perkawinan pertama, persentase wanita bekerja di sektor pertanian, dan persentase wanita bekerja di sektor industri berpengaruh signifikan terhadap persentase wanita dengan fertilitas tinggi di Provinsi Lampung. Di samping itu dalam penelitian ini telah disusun algoritma dan program, serta GUI pengujian bootstrap Moran’s I dan bootstrap LM, serta pemodelan SAR dan SEM dengan pendekatan residual bootstrap.
Kata kunci : Fertilitas, Spatial Bootstrap Test, SAR, SEM, Residual Bootstrap
1. Pendahuluan
Dalam dua dekade terakhir telah berkembang metode statistika yang berkaitan dengan ilmu kewilayahan, yaitu analisis data spasial. Dalam banyak kasus, pengamatan di suatu lokasi bergantung pada pengamatan di lokasi lain yang berdekatan (neighbouring).
Seiring dengan perkembangan pemodelan spasial muncul berbagai permasalahan, salah satu diantaranya adalah ukuran sampel yang kecil. Ketika sampel yang digunakan cukup kecil, maka keakuratan sifat estimator dengan menggunakan metode MLE maupun OLS menjadi kurang sesuai. Salah satu metode yang seringkali digunakan untuk menangani permasalahan tersebut yaitu metode resampling, salah satunya adalah metode Bootstrap. Pada estimasi parameter, apabila error pada sampel kecil tersebut tidak berdistribusi normal, metode Bootstrap ini dapat menjadi suatu solusi dalam memecahkan permasalahan tersebut [8].
Pada tahap identifikasi model dikembangkan suatu metode spatial bootstrap test berdasarkan OLS residual [7]. Metode ini merupakan suatu metode pendekatan alternatif yang efektif ketika asumsi kenormalan tidak terpenuhi. Monchuk, Hayes, Miranowski, dan Lambert menggunakan metode resampling Bootstrap pada Spatial Error Model untuk kasus pertumbuhan pendapatan di Amerika Serikat [9].
Tingkat fertilitas merupakan salah satu faktor demografi yang paling menentukan di dalam penurunan tingkat pertumbuhan penduduk di Indonesia.
Berdasarkan RPJM 2004- 2009, salah satu sasarannya yaitu tingkat fertilitas total di Indonesia menjadi 2,2 per wanita. Hal ini
sebagai salah satu langkah revitalisasi dengan adanya kekhawatiran baby booming yang kedua [2]. Pada tahun 2009, rata-rata anak lahir hidup di Provinsi Lampung sebesar 2,4. Angka ini juga belum memenuhi target pemerintah dalam mengurangi pertumbuhan penduduk.Penelitian ini diharapkan mampu untuk mengidentifikasi kondisi wanita dengan tingkat fertilitas tinggi di Provinsi Lampung dengan berbagai karakteristik yang berpengaruh.
Selain itu, juga ingin diidentifikasi apakah ada hubungan dependensi spasial antar wilayah berkaitan dengan tingkat fertilitas wanita yang relatif tinggi tersebut. Provinsi Lampung yang terdiri dari 14 kabupaten/kota tidak memungkinkan untuk dilakukan suatu pemodelan regresi spasial mengingat keterbatasan dengan jumlah sampel yang sedikit.
2. Metode 2.1 Model Regresi Spasial
Bentuk umum general spatial model yang dikembangkan oleh Anselin (1988) adalah sebagai berikut :
~ N( , σ ) λ
ρ ,
2I ε 0
ε u W u
u Xβ y W y
2
1
(1)
dengan ymerupakan vektor variabel respon dengan ukuran n x 1, adalah koefisien dari variabel respon spasial lag, λ adalah koefisien dalam spasial error, dan u merupakan vektor error. Sementara itu, W1 dan W2 merupakan matrik penimbang dengan ukuran n x n dimana
W1 = W2 = W. Parameter regresi dilambangkan dengan βyang merupakan vektor berukuran (p+1) x 1. Matriks Xmerupakan matriks dari variabel prediktor yang berukuran n x (p+1).
Berdasarkan persamaan 1. di atas dapat diturunkan model dalam bentuk lebih spesifik, yaitu : (1) jika ρ0dan
λ
0
maka bentuk menjadi yXβε yang merupakan bentuk model regresi OLS, (2) jika ρ0danλ
0
maka yρW1yXβε yang merupakan model spatial autoregressive (SAR), (3) jika ρ0danλ
0
maka yXβu dimanaε u W
uλ 2 yang merupakan bentuk model spatial error (SEM), (4) jika ρ0dan
λ
0
, maka membentuk yρWy XβudimanauλWuε yang biasa disebut Spatial Autoregressive Moving Average (SARMA) [1].2.2 Matriks Penimbang Spasial
Dalam penelitian ini, akan digunakan metode Queen Contiguity (persinggungan sisi dan sudut) dimana nilai penimbang wij akan bernilai 1 untuk wilayah yang bersisian dan bernilai 0 untuk wilayah yang lain [5]. Sebagai ilustrasi, Gambar 2.1 menyajikan contoh lima region yang menunjukan kedekatan dan persinggungan antar lokasi.
Gambar 1. Ilustrasi contiguity (Persinggungan).
Berdasarkan Gambar 1. matriks penimbang yang terbentuk dengan menggunakan metode Queen Contiguity diperoleh susunan matriks berukuran 5×5 dimana baris dan kolom menyatakan region yang ada pada peta. Karena matriks penimbang spasial merupakan matriks simetris, dan dengan kaidah bahwa diagonal utama selalu nol, seringkali dilakukan transformasi untuk mendapatkan jumlah baris sama dengan satu
2.3 Bootstrap Spatial 2.3.1 Moran’s I
Lin, Long, dan Wu Mei menerapkan Bootstrap Moran’s I untuk pengujian dependensi spasial [7], algoritmanya sebagai berikut.
a. Resampling Bootstrap pada residualnya yaitu εˆ sehingga diperoleh εˆ*1,εˆ*2,..., εˆ*B, dengan B merupakan banyaknya replikasi Bootstrap.
b. Pada masing-masing sampel bootstrap dihitung nilai Moran’s I sehingga diperoleh
*b *b
* b
* b
'ε ε
ε W ε '
ˆ ˆ
ˆ I ˆ
MO
* b
dimana b=1,2,...,B (2) c. Menghitung standar error (IMO*)
(4)
(3) (5)
(2) (1)
0 1 1 0 0
1 0 1 0 0
1 1 0 1 0
0 0 1 0 1
0 0 0 1 0
Q
2 0 1 2 0 1 0
2 0 1 2 0 1 0
3 1 3 0 1 3 0 1
0 2 0 0 1 2 1
0 0 0 1 0
queen
W
1/21
2
1 I I )
I (
MO MO
MO
se B
B
b
*
*
* b
,
B
b
* b
*
B 1 MO
MO 1 I
I (3)
d. Menghitung penduga selang untuk
*
I
MO . Pendekatan selang kepercayaan menggunakan persentil. Setelah diperoleh* MOb
I
di setiap replikasi B, kemudian diurutkan sehingga* B
*
*
2 MO 1 MO
MO
I ... I
I
. Maka batas bawah dan batas atas selang kepercayaan adalah [I ,I ] [I .( /2),I .(1 /2)]MO MO
MO MO
*
*
*
*
B B
up
low (4) e. Dengan menggunakan IMOi diperoleh dari resampling Bootstrap, maka Bootstrap p-value
(right tail test) dari uji statistik Moran’s I adalah
B
} I I
banyaknya{
) I
P( MO MO0
MO
b
*
(5)
dimana IMO0merupakan nilai uji statistik Moran’s I dengan menggunakan set data asli.
DenganH0 :IMO IMO0, Bootstrap p-value lebih besar dari tingkat signifikansi, maka terima Ho. Karena range dari uji statistik Moran’s I bisa positif dan negatif, maka penghitungan p-value dapat menggunakan uji sisi kiri (left tail) atau sisi kanan (right tail).
2.3.2 Uji Lagrange Multiplier 1. Algoritma bootstrap LM lag
a. Lakukan Bootstrap resampling pada residualnya yaitu mengambil n sampel dengan pengembalian dari εˆ sehingga diperoleh εˆ*1,εˆ*2,..., εˆ*B.
b. Hitung nilai yb*, dimana y*b Xβ
ˆ
εˆ
b*, sehingga diperoleh y*1,y*2,...,y*Bdimana b=1,2,...,B. B merupakan banyaknya replikasi Bootstrap.c. Menghitung nilai LM lag pada masing-masing sampelBootstrap dengan menggunakan
*
εˆ
b,y*b, dan matriks penimbang spasial yang tetap.*b 2
2
* b
b NJ
σˆ ) ( ˆ lag LM
* b
* b'Wy ε
B 1,2,..., b
σˆ ) T(
ˆ) ( ˆ)' ) (
σˆ N(
J 1
) trace(
T
N ˆ ) ˆ σˆ (
ˆ , ˆ
2
* 2 b
* b
* b
2
* b
X' X) X(X' I M
β WX β M WX
W W' WW
ε ε '
ε β X y
1
* b
* b
* b
* b
(6)
2. Algoritma bootstrap LM Error
a.
Melakukan Bootstrap resampling pada residualnya.b.
Menghitung nilai LM error pada masing-masing sampel Bootstrap dengan menggunakanεˆ
*b, b=1,2,...,B dan matriks penimbang spasial yang tetap.T
2
2
* b b
σˆ ) (
ˆ ˆ error LM
** b
* b'Wε ε
(7)
Dengan hipotesisH0:LMLM0 kemudian menentukan bootstrap p-value untuk nilai LM
lag dan LM errornya.
2.3.3 Model Bootstrap Regresi Spasial
Penelitian tentang pemodelan spasial bootstrap juga dilakukan oleh Monchuk, Hayes, Miranowski, dan Lambert [9]. Namun, hanya diterapkan pada Spatial Error Model (SEM).
Algoritmanya adalah sebagai berikut.
a.
Dengan menggunakan regresi Spatial Error Model, estimasi parameter βdan λ dengan metode maksimum likelihood dari data awalnya.b.
Hitung residualnyaε
ˆ
[
I ˆ
W]
y[
I ˆ
W]
Xβˆ
(8)c.
Melakukan Bootstrap resampling pada residualnya sebanyak B replikasi yaitu mengambil n sampel dengan pengembalian dari εˆ sehingga diperoleh εˆ*1,εˆ*2,..., εˆ*B.d.
Hitung nilai y*b, dimana b = 1,2,...,B sehingga diperoleh y*1,y*2,...,yB*
* b
*
b Xβ I W ε
y
ˆ
[
ˆ ]
1ˆ
(9)e.
Dengan menggunakan vektor y*b dan fixed X, estimasi dengan menggunakan metodemaksimum likelihood untuk masing-masing sampel bootstrapnya sehingga didapatkan estimator
ˆβ
b* danλˆ
b*dimana b=1,2,...,B. B merupakan jumlah replikasi pada resampling data.
B
1 b
B
1 b
* b
* * b
*
λˆ
B λˆ 1 βˆ , B
βˆ 1
,*
βˆ
b merupakan estimasi setiap parameterβˆ
pada masing-masing replikasi Bootstrap.βˆ
* merupakan rata-rata dariβˆ
b*. Untuk ˆ
b*adalah estimasi parameter ˆ pada masing- masing replikasi Bootstrap, sedangkan ˆ* = rata-rata dari ˆ
b*.f. Menentukan standar error dari
βˆ
dan ˆ dan penduga interval untukβˆ
danλˆ
menggunakan pendekatan persentil.
Algoritma Spatial Autoregressive Model (SAR) sebagai berikut :
a. Dengan menggunakan regresi Spatial Autoregressive Model, estimasi parameter βˆ dan
ρˆ
dengan menggunakan metode maksimum likelihood.b. Menentukan residualnya.
β X Wy
εˆyρˆ ˆ (10)
c. Melakukan resampling residual sebanyak B replikasi, diperoleh
εˆ
*b. d. Mendapatkan nilai y* pada masing-masing replikasisehingga diperoleh* B
* 2
*
1,y ,...,y
y .
* b
*
b I W Xβ I W ε
y
[
ρˆ ]
1ˆ
[
ρˆ ]
1ˆ
(11) e. Dengan menggunakan vektor y* dan X, estimasi replikasi untuk mendapatkan estimator
ˆ
*β
b danρˆ
b*. Kemudian menghitung bootstrap estimator dari βˆ* danρˆ
*.f.
Menentukan bias, standar error, selang kepercayaan, dan p-value.Dalam penelitian ini, akan dicobakan untuk beberapa nilai replikasi B (50,100, 200, 500, 1000, dan 10000) sampai mendapatkan suatu nilai dengan bias dan standar error yang terkecil.
2.4 Fertilitas
Fertilitas atau kelahiran menurut konsep BPS berkaitan dengan jumlah anak kandung lahir hidup. Anak kandung lahir hidup adalah anak kandung yang pada waktu dilahirkan menunjukkan tanda-tanda kehidupan, walaupun mungkin hanya beberapa saat saja, seperti jantung berdenyut, bernafas, dan menangis. Menurut Iswarati (2010), faktor-faktor yang mempengaruhi tinggi rendahnya fertilitas terdiri atas faktor demografi dan nondemografi.
Faktor demografi diantaranya adalah umur, status perkawinan, umur kawin pertama.
Sedangkan faktor nondemografi antara lain keadaan ekonomi penduduk, tingkat pendidikan, dan urbanisasi [3].
2.5 Variabel Penelitian
Data dalam penelitian adalah data sekunder yang berasal dari Survei Sosial Ekonomi Nasional (Susenas) di Provinsi Lampung Tahun 2010. Selain itu, juga digunakan peta Provinsi Lampung yang merupakan hasil dari Pemetaan SP2010.Variabel respon yang digunakan dalam penelitian ini adalah persentase wanita berumur 10 tahun ke atas dengan status pernah kawin dengan anak kandung lahir hidup > 2. Sedangkan variabel prediktor (Xi) yang digunakan adalah pertumbuhan ekonomi (X1), persentase wanita tidak KB (X2), rata-rata umur perkawinan pertama (X3), persentase wanita bekerja di sektor pertanian (X4), dan persentase wanita bekerja di sektor industri (X5). Software statistik yang digunakan yaitu Minitab dan Matlab.
3. Hasil dan Pembahasan 3.1 Penyusunan Program
Program aplikasi yang telah disusun meliputi matlab code untuk pengujian Bootstrap Moran’s I, Bootstrap Lagrange Multiplier, dan estimasi parameter pada pemodelan bootstrap Spatial Autoregressive Model (SAR) maupun bootstrap Spatial Error Model (SEM). Program yang dibuat dengan menambahkan beberapa syntax pada function spasial ekonometrika yang telah dibuat sebelumnya oleh LeSage (1999). Syntax yang ditambahkan yaitu resampling bootstrap, penghitungan standar error, selang kepercayaan, dan uji hipotesis hasil dari resampling bootstrap baik pada uji spasial dependensi maupun pada estimasi parameter.
3.2 Penyusunan GUI
GUI bertujuan untuk mempermudah pengguna dalam menggunakan program yang telah dibuat sebelumnya, yaitu program untuk mendapatkan statistik uji maupun pemodelan regresi spasial. Bentuk tampilan GUI yang akan digunakan dalam menjalankan program dapat dilihat pada Gambar 4.1.
Gambar 2. Aplikasi Graphic User Interface (GUI).
3.3 Deskripsi Fertilitas di Provinsi Lampung
Pada Gambar 2. menjelaskan persebaran wanita dengan fertilitas tinggi di Provinsi Lampung 2010. Persentase wanita dengan Anak Lahir Hidup (ALH) lebih dari 2 yang nilainya
relatif rendah adalah Kabupaten Lampung Tengah, sedangkan untuk nilai persentase wanita dengan fertilitas yang relatif tinggi adalah Kabupaten Tanggamus dan Kabupaten Way Kanan.
Gambar 3. Persebaran persentase wanita dengan ALH > 2 di Provinsi Lampung, 2010.
3.4 Pemodelan Dengan Regresi Spasial Pengujian Spasial Dependensi
Hasil identifikasi awal adanya dependensi antar wilayah melalui perhitungan error menunjukkan adanya spasial dependensi, namun dengan tingkat signifikansi yang relatif tinggi (p-value=0,333) ( Tabel 1). Dari hasil pengujian Lagrange Multiplier menunjukkan bahwa terdapat dependensi dalam lag, sehingga perlu dilakukan pemodelan Spatial Autoregressive (SAR).
Tabel 1. Nilai Statistik Uji dan Nilai p-value pada Identifikasi Model Regresi Spasial dengan Set Data Awal
Statistik Uji Nilai p-value
Moran’s I 0,020 0,333
LM Lag 2,837 0,092
LM Error 0,011 0,917
Pemodelan Spatial Autoregressive (SAR)
Estimasi parameter model SAR fertilitas tinggi di Provinsi Lampung disajikan pada Tabel 2. berikut.
Tabel 2. Nilai Koefisien Regresi, Standar Error, Nilai Statistik Uji-t, Nilai p-value Pengujian Parameter dan Nilai R2 Model SAR Variabel Koefisien Std. Error t-stat p-value R2
rho 0,3680 0,1897 1,9403 0,0935 0,9242
Konstanta 74,5248 11,2145 6,6454 0,0003
X1 -2,0513 0,6699 -3,0618 0,0183
X2 0,4807 0,0884 5,4391 0,0010
X3 -1,7433 0,3915 -4,4530 0,0030
X4 X5
-0,1618 -0,8865
0,0363 0,1769
-4,4623 -5,0110
0,0029 0,0015
Dengan menggunakan α = 0,10, maka seluruh variabel prediktor berpengaruh secara signifikan pada persentase wanita dengan tingkat fertilitas tinggi di Provinsi Lampung.
Besarnya koefisien determinasi (R2) pada model ini adalah 92,42 %. Hal ini berarti bahwa model yang dibentuk dapat menjelaskan 92,42 % keragaman dari variabel persentase wanita dengan fertilitas tinggi.
3.5 Model Regresi Spasial dengan Pendekatan Residual Bootstrap (Bootstrap Spatial Model)
Pengujian Spasial Dependensi dengan Pendekatan Residual Bootstrap
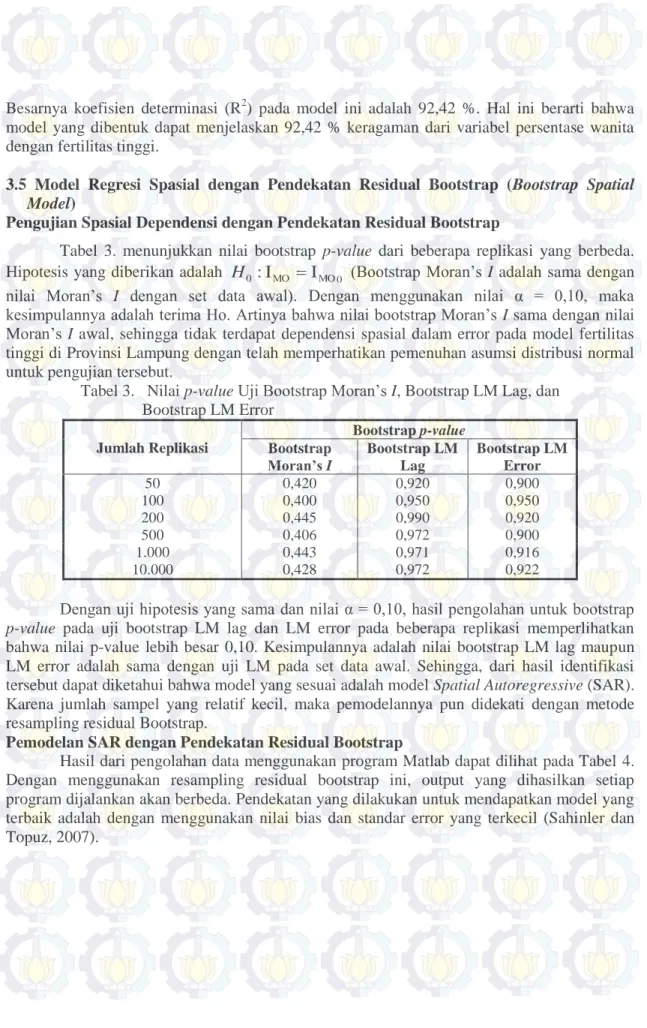
Tabel 3. menunjukkan nilai bootstrap p-value dari beberapa replikasi yang berbeda.
Hipotesis yang diberikan adalah H0 :IMO IMO0 (Bootstrap Moran’s I adalah sama dengan nilai Moran’s I dengan set data awal). Dengan menggunakan nilai α = 0,10, maka kesimpulannya adalah terima Ho. Artinya bahwa nilai bootstrap Moran’s I sama dengan nilai Moran’s I awal, sehingga tidak terdapat dependensi spasial dalam error pada model fertilitas tinggi di Provinsi Lampung dengan telah memperhatikan pemenuhan asumsi distribusi normal untuk pengujian tersebut.
Tabel 3. Nilai p-value Uji Bootstrap Moran’s I, Bootstrap LM Lag, dan Bootstrap LM Error
Jumlah Replikasi
Bootstrap p-value Bootstrap
Moran’s I
Bootstrap LM Lag
Bootstrap LM Error 50
100
0,420 0,400
0,920 0,950
0,900 0,950
200 0,445 0,990 0,920
500 0,406 0,972 0,900
1.000 0,443 0,971 0,916
10.000 0,428 0,972 0,922
Dengan uji hipotesis yang sama dan nilai α = 0,10, hasil pengolahan untuk bootstrap p-value pada uji bootstrap LM lag dan LM error pada beberapa replikasi memperlihatkan bahwa nilai p-value lebih besar 0,10. Kesimpulannya adalah nilai bootstrap LM lag maupun LM error adalah sama dengan uji LM pada set data awal. Sehingga, dari hasil identifikasi tersebut dapat diketahui bahwa model yang sesuai adalah model Spatial Autoregressive (SAR).
Karena jumlah sampel yang relatif kecil, maka pemodelannya pun didekati dengan metode resampling residual Bootstrap.
Pemodelan SAR dengan Pendekatan Residual Bootstrap
Hasil dari pengolahan data menggunakan program Matlab dapat dilihat pada Tabel 4.
Dengan menggunakan resampling residual bootstrap ini, output yang dihasilkan setiap program dijalankan akan berbeda. Pendekatan yang dilakukan untuk mendapatkan model yang terbaik adalah dengan menggunakan nilai bias dan standar error yang terkecil (Sahinler dan Topuz, 2007).
Dengan membandingkan nilai koefisien bootstrap SAR 𝛃∗ dan ρ ∗ dengan nilai koefisien model SAR, 𝛃 dan ρ pada beberapa replikasi, dapat diambil kesimpulan bahwa pada jumlah replikasi sebesar 100 memiliki bias yang kecil dan tingkat signifikansi yang konsisten dengan model awalnya. Pada tabel 4. dapat dilihat bahwa pada replikasi sebesar 100 diperoleh hasil bahwa seluruh variabel prediktor memberikan pengaruh signifikan pada model dengan α
= 0,10. Model ini menghasilkan koefisien determinasi (R2) sebesar 96,17 persen.
Tabel 4. Nilai Koefisien Regresi, Bias, Standar Error, Nilai z,
Nilai p-value Pengujian Parameter pada Model Bootstrap SAR
B
(Replikasi) Variabel Koefisien Bias Std.
Error Nilai z p-value
50
Rho 0,3303 -0,0247 0,1748 1,8896 0,0588
Konstanta 75,1682 0,0001 10,7572 6,9877 <0,0001
X1 -1,9458 0,0951 0,6275 -3,1008 0,0019
X2 0,5053 0,0233 0,0871 5,8025 <0,0001
X3 -1,7244 0,0200 0,3876 -4,4484 <0,0001
X4 -0,1708 -0,0089 0,0289 -5,9086 <0,0001
X5 -0,8849 0,0087 0,1751 -5,0528 <0,0001
100
Rho 0,3132 -0,0508 0,1865 1,6786 0,0932
Konstanta 78,1329 3,4083 10,7946 7,2381 <0,0001
X1 -1,9619 0,0862 0,6054 -3,2408 0,0012
X2 0,5014 0,0203 0,0872 5,7489 <0,0001
X3 -1,8178 -0,0741 0,3871 -4,6964 <0,0001
X4 -0,1645 -0,0027 0,0351 -4,6898 <0,0001
X5 -0,9304 -0,0417 0,1651 5,6360 <0,0001
200
Rho 0,3043 -0,0587 0,1936 1,5722 0,1159
Konstanta 77,5521 2,7806 11,0585 7,0128 <0,0001
X1 -2,0414 0,0059 0,5855 -3,4867 0,0005
X2 0,4797 -0,0015 0,0805 5,9569 <0,0001
X3 -1,7273 0,0164 0,3649 -4,7340 <0,0001
X4 -0,1621 -0,0003 0,0327 -4,9639 <0,0001
X5 -0,8887 0,0005 0,1626 -5,4647 <0,0001
500
Rho 0,2752 -0,0856 0,2097 1,3122 0,1894
Konstanta 78,8075 3,9371 11,8183 6,6682 <0,0001
X1 -1,9450 0,1007 0,6439 -3,0209 0,0025
X2 0,4838 0,0024 0,0876 5,5238 <0,0001
X3 -1,7413 0,0026 0,3892 -4,4744 <0,0001
X4 -0,1622 -0,0003 0,0357 -4,5431 <0,0001
X5 -0,9228 -0,0325 0,1600 -5,7671 <0,0001
1.000
Rho 0,2719 -0,0920 0,1965 1,3840 0,1663
Konstanta 78,7211 3,9970 10,9991 7,1570 <0,0001
X1 -1,9217 0,1264 0,6385 -3,0095 0,0026
X2 0,4908 0,0097 0,0841 5,8347 <0,0001
X3 -1,7379 0,0058 0,3941 -4,4101 <0,0001
X4 -0,1639 -0,0020 0,0356 -4,6104 <0,0001
X5 -0,9326 -0,0439 0,1711 -5,4493 <0,0001
10.000
Rho 0,2889 -0,0791 0,2026 1,4255 0,1540
Konstanta 77,8120 3,2876 11,4653 6,7867 <0,0001
X1 -1,9578 0,0935 0,6495 -3,0142 0,0026
X2 0,4863 0,0056 0,0833 5,8396 <0,0001
X3 -1,7258 0,0175 0,3893 -4,4331 <0,0001
X4 -0,1627 -0,0008 0,0348 -4,6704 <0,0001
X5 -0,9169 -0,0304 0,1717 -5,3399 <0,0001
Persamaan model bootstrap SAR yang dihasilkan adalah
5 4
3 2
1 ,
1
X 0,9304 X
0,1645 X
1,8178 X
0,5014 X
1,9619 78,1329
3132 ,
ˆ
0
n
j i i
i ijy w y
Gambar 4. Histogram Bootstrap SAR dengan jumlah replikasi 100.
Nilai rho (koefisien spasial lag) memberikan gambaran bahwa terdapat suatu dependensi antar wilayah untuk variabel persentase wanita dengan fertilitas tinggi di Provinsi Lampung. Adanya suatu dependensi memiliki arti bahwa angka fertilitas tinggi dalam hal ini persentase wanita dengan fertilitas di atas 2 anak di suatu wilayah memiliki keterkaitan dengan angka fertilitas tinggi di wilayah yang lain. Hal ini dikarenakan adanya kemiripan kebiasaan, gaya hidup, ataupun budaya antar kabupaten/kota yang berdekatan. Gambar 3.
memperlihatkan bahwa estimasi parameter pada model Bootstrap SAR diasumsikan berdistribusi normal (limiting normal distribution) untuk seluruh koefisien model.
4. Kesimpulan
Pada pemodelan fertilitas tinggi di Provinsi Lampung dengan menggunakan Bootstrap Regresi Spasial, model yang sesuai adalah model bootstrap Spatial Autoregressive (SAR).
Dengan memperhatikan nilai bias dan standar errornya, digunakan model dari hasil 100 kali replikasi. Dari hasil pemodelan bootstrap Spatial Autoregressive (SAR), variabel prediktor yang berpengaruh terhadap fertilitas di Provinsi Lampung adalah pertumbuhan ekonomi, persentase wanita yang tidak KB, rata-rata umur perkawinan pertama, persentase wanita bekerja di sektor pertanian dan persentase wanita bekerja di sektor industri.
𝛽 0∗ 𝛽 1∗ 𝛽 2∗ 𝛽 3∗
𝛽 4∗ 𝛽 5∗ 𝜌 ∗
Daftar Pustaka
[1] Anselin, L., 1988, Spatial Econometrics: Methods and Models, Kluwer, Dordrecht.
[2] Iski, 2008, “Dulu Dua Anak Cukup, Kini Dua Anak Lebih Baik”. 29 October 2008.
MIX-Marketing Communications Magazine.
[3] Iswarati, 2010, “Fertilitas di Indonesia (Analisis Lanjut SDKI 2007)”.
[4] Kogan, L., 2010, “Small-Sample Inference and Bootstrap”. MIT, Sloan, Fall 2010.
[5] LeSage J., 1999, The Theory and Practice of Spatial Econometrics, University of Toledo.
[6] Lesmana, C., 2010, Faktor-Faktor yang Mempengaruhi Tingkat Fertilitas pada Wanita Pernah Kawin Berusia Subur di Kecamatan Tempeh Kabupaten Lumajang. Skripsi, Universitas Negeri Malang
[7] Lin, K.-P., Z. Long, dan Wu Mei, 2007, ”Bootstrap Test Statistics for Spatial Econometric Models”, Journal of Econometrics.
[8] Lynch, S.M., 2003, “Alternative Estimation Strategies”, Soc504, PrincetonUniversity.
[9] Monchuk, D.C., D.J. Hayes, J.A. Miranowski, dan D.M. Lambert, 2010, “Inference Based on Alternative Bootstrapping Methods in Spatial Models with an Application to County Income Growth in the United States”. Working Paper 10-WP 507, May 2010, Center for Agricultural and Rural Development, Iowa State University.
[10] Sahinler, S. & Topuz, D., 2007, “Bootstrap and Jackknife Resampling Algorithms for Estimation of Regressions Parameters”, Journal of Applied Quantitative Methods, Vol.2, No.2, Summer 2007.