1. Konsep Peluang. EL2002-Probabilitas dan Statistik Dosen: Andriyan

1. Konsep Peluang

EL2002-Probabilitas dan Statistik

Dosen: Andriyan

Isi

1. Ruang Cuplikan (Sample Space) 2. Kejadian (Events)

3. Operasi Terhadap Kejadian 4. Pencacahan Titik Cuplikan 5. Peluang Kejadian

6. Hukum Peluang

7. Peluang Bersyarat

8. Aturan Bayes

1.1 Ruang Cuplikan

(sample space)

Data Mentah

• Def.1.1: Data mentah adalah rekaman dalam

bentuk asal, baik berupa hasil pencacahan maupun pengukuran

• Hasil pengamatan: pencacahan atau hasil numerik dari suatu pengukuran

• Percobaan (statistik): segala macam proses yang menghasilkan data mentah

– Contoh: pencacahan trafik kendaraan, pelantunan mata uang

atau dadu, pengamatan besaran fisik dalam eksperimen di

Lab, dll

Ruang Cuplikan

• Def.1.2: Himpunan semua hasil percobaan statistik disebut sebagai ruang cuplikan dan dituliskan sebagai S.

• Setiap titik dalam ruang cuplikan disebut titik cuplikan (sample point), atau elemen/anggota ruang cuplikan.

• Contoh ruang cuplikan:

– Pelantunan uang logam (koin): S = {H, T}

– S = {x|x kota dengan penduduk diatas 1 juta jiwa}

– S={(x,y)}| x² + y² ≤ 4}

– Pelantunan dadu:

• S₁={1, 2, 3, 4, 5, 6}

• S₂ = {ganjil, genap}

1.2 Kejadian/Peristiwa

(Events)

Definisi kejadian

• Def.1.3: Suatu kejadian (peristiwa) adalah himpunan bagian dari ruang cuplikan

• Contoh:

– A={3,6} adalah kejadian dalam pelantunan dadu dimana mata dadu yang muncul dapat dibagi 3

– Untuk t yng menyatakan umur komponen elektonik,

kejadian A dimana komponen berumur kurang dari

5 tahun adalah A={t|t<5}, dengan S={t|t≥1}

Kejadian sederhana dan kejadian majemuk

• Def.1.4: Jika suatu kejadian berupa himpunan yang hanya mengandung satu titik cuplikan, maka kejadian ini disebut sebagai kejadian sederhana. Kejadian majemuk adalah

kejadian yang dapat dinyatakan sebagai gabungan dari beberapa kejadian sederhana

• Contoh:

– Untuk percobaan/pengamatan jenis kartu, dimana S={ ♥, ♠, ♣ ♦}, maka A={♥} adalah kejadian sederhana, sedangkan B = {♥, ♦}

adalah kejadian majemuk.

• NB: ♥ ≡ heart, ♠ ≡ spade, ♣ ≡ club, ♦ ≡ diamond

– Sebaliknya, jika S = {seluruh 52 buah kartu yang dilihat satu persatu}, maka A={semua kartu ♥} adalah kejadian majemuk.

Ruang null

• Def.1.5: Ruang null atau ruang kosong adalah himpunan bagian dari ruang cuplik yang tidak memiliki anggota dan dilambangkan sebagai ∅.

• Contoh null-space

– Hasil pengamatan organisme mikroskopis dng mata- telanjang

– B={x|x faktor nonprima dari 7}

– Hasil percobaan pelantunan dadu (biasa) yang memberi

mata tujuh

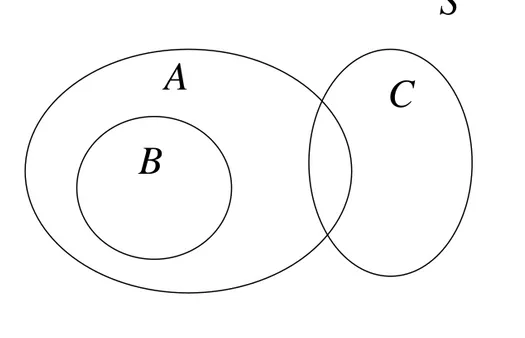
Diagram Venn

S A

B

C

A={kartu warna merah}

B={kartu J♦, Q♦, K♦}

C={kartu As}

• Penggambaran relasi antar himpunan.

S = ruang cuplikan

A, B, C: kejadian

1.3 Operasi terhadap kejadian

Irisan dua kejadian

• Def.1.6: Irisan antara kejadian A dengan kejadian B, dilambangkan sebagai A∩B, adalah kejadian yang mengandung semua elemen yang berada di A dan di B sekaligus.

S

A B

• Contoh:

– Jika A = {1, 2, 3, 4, 5} dan B={2, 4, 6, 8}, maka A∩B={2,4}

– Jika P = {a, i, u, e, o} dan Q={s,t}, maka P∩Q = ∅

• Pada contoh terakhir, P dan Q tdk

dapat terjadi bersamaan.Kejadian

spt ini disebut mutually exclusive .

Kejadian mutually exclusive

• Def.1.7: Dua buah kejadian A dan B disebut mutually exclusive jika A∩B = ∅

S

A B

Gabungan kejadian

• Def.1.8: Gabungan dua buah kejadian, A dan B, dilambangkan sebagai A∪B, adalah kejadian yang

mengandung semua elemen dari A, atau B, atau keduanya.

S

A B

• Contoh:

– Jika A = {1, 2, 3, 4, 5} dan B={2, 4, 6, 8}, maka A ∪ B={1, 2, 3, 4, 5, 6, 8}

– Jika P = {a, i, u, e, o} dan

Q={s,t}, maka P∪Q ={a, i, u, e, o, s, t}

Kejadian Komplementer

• Def.1.9: Komplemen dari kejadian A terhadap S,

dituliskan sebagai A’, himpunan semua elemen S yang tidak berada dalam A.

• Contoh:

– Jika S = {1, 2, 3, 4, 5} dan A={2, 4}, maka A’ ={1, 3, 5}

– Untuk S={ ♥, ♠, ♣ ♦} dan A={♥}, maka A’={♠, ♣, ♦}

S A

A’

Hasil-hasil penting

• A ∩ ∅ = ∅

• A ∪ ∅ = A

• A ∩ A’ = ∅

• A ∪ A’ = S

• S’ = ∅

• ∅’ = S

• (A’)’ = A

1.4 Pencacahan Titik Cuplikan

(Counting)

Isi

• Prinsip-prinsip dasar pencacahan:

– Aturan perkalian (Product rule --Theorem 1.1)

– Aturan perkalian umum (Generalized Product rule--Theorem 1.2) – Permutasi (Def. 1.10)

• Permutasi n-objek berlainan (Theorem 1.3)

• Permutasi n-objek berlainan, diambil r-objek sekaligus (Theorem 1.4)

• Permutasi sirkular (Theorem 1.5)

• Permutasi berlainan untuk n-objek dengan masing-masing ada n₁ objek jenis pertama, …, n_k objek jenis ke-k (Theorem 1.6)

• Partisi himpunan dari n-objek kedalam r-sel dengan n₁-elemen, … dst (Theorem 1.7)

• Kombinasi n-objek, diambil r-objek sekaligus – Theorem 1.8.

– Tambahan EL2009:

• Aturan penjumlahan (Sum Rule)

• Aturan penjumlahan umum (Generalized sum rule)

NB: Counting kita terjemahkan sebagai pencacahan

Aturan perkalian

• Teorema 1.1: Jika suatu operasi dapat dilakukan dengan n

₁

buah cara, dan untuk setiap operasi ini dapat dilakukan

operasi kedua sebanyak n

₂

buah cara, maka kedua operasi ini dapat dilakukan bersamaan dengan n

₁

⋅n

₂

cara

• Contoh:

– Soal: Tentukan jumlah titik cuplikan dalam pelantunan dua buah dadu!

– Jawab: Dadu pertama memberikan 6 macam keluaran. Untuk setuap hasil, dadu kedua menghasilkan 6 macam keluaran juga. Dengan demikian, sepasang dadu akan menghasilkan 6.6=36 macam

keluaran.

– Tugas Mhs:

• Berikan daftar ke-36 buah keluaran ini !

• Ulangi untuk pelantunan uang logam dengan hasil {H, T}

Aturan perkalian yang diperumum

• Teorema 1.2: Jika suatu operasi dapat dilakukan dengan n

₁

buah cara, dan untuk setiap operasi ini dapat dilakukan

operasi kedua sebanyak n

₂

buah cara, dan untuk setiap operasi ini dapat dilakukan operasi ketiga sebanyak n

₃

buah cara, … dst, maka k buah operasi ini dapat dilakukan bersamaan sebanyak n

₁

⋅n

₂

… ⋅n

_k

cara

• Contoh:

– Suatu restoran memiliki 4 jenis lauk-pauk, 3 jenis sayuran, 5 jenis kerupuk, dan 4 macam jus. Ada berapa banyak menu

yang bisa dibuat oleh restoran tersebut, jika setiap menu terdiri dari satu buah lauk, satu mangkuk, 1 bungkus kerupuk, dan 1 gelas jus?

• Jawab: akan ada 4⋅3 ⋅5 ⋅4 = 240 macam menu

Permutasi

• Def.1.10: Permutasi adalah penyusunan dari seluruh atau sebagian dari sekumpulan objek.

• Contoh:

– 4 buah huruf a, b, c, d dapat di-permutasikan sebanyak 4! = 4 ⋅ 3 ⋅ ^{2⋅1 = 24}

• Teorema 1.3: Jumlah permutasi dari n objek berlainan adalah n!

• Contoh:

– Tiga buah huruf a, b, c dapat disusun sebagai abc, acb, bac, bca,cab, dan cba

– Berdasarkan aturan perkalian, untuk n buah objek akan ada:

n(n-1) … 2 ⋅ 1 = n!

Permutasi r dari n objek

• Untuk keempat huruf tadi, permutasi per-dua huruf adalah:

ab, ac, ad, ba, ca, da, bc, bd, cb, db, cd, dc; ada sebanyak 12 buah. Dengan Teorema 1.2, ada 4 buah untuk pilihan pertama, dan ada 3 buah untuk pilihan kedua sehingga ada 4⋅3=12 permutasi.

• Pada umumnya, n objek berlainan diambil r buah sekaligus akan menghasilkan pengaturan sebanyak

n⋅(n-1)⋅ … ⋅(n – r + 1)= n!/(n-r)!

• Teorema 1.4: Jumlah r buah permutasi dari n objek berlainan adalah

_n

P

_r

= n!/(n-r)!

• Contoh:

– Banyaknya cara mengambil tiket undian untuk pemenang pertama dan kedua, dari 20 tiket adalah

20

P

₂

= 20!/(20-2)! = 20⋅19 =380

Permutasi Sirkular

• Permutasi yang muncul dalam pengaturan objek secara melingkar disebut permutasi sirkular. Dua permutasi

sirkular berbeda jika keduanya didahului atau diikuti objek yang berbeda, ketika dilihat dalam arah putar jarum jam.

• Permutasi sirkular dapat dihitung dengan mengambil satu objek tetap, kemudian melakukan permutasi objek sisanya.

Dengan demikian, permutasi n objek secara sirkular akan menghasilkan (n-1)! susunan berlainan.

• Teorema 1.5: Jumlah permutasi sirkular dari n objek

berlainan adalah (n-1)!

Permutasi beberapa jenis objek

• Tinjau permutasi tiga huruf a,b,c. Jika huruf b=c=x, maka permutasi menjadi axx, axx, xax, xax, xxa, dan xxa;

sehingga menjadi 3 buah yang berbeda.

• Teorema 1.6: Jumlah permutasi berlainan dari n buah objek yang terdiri dari n

₁

objek jenis pertama, n

₂

jenis kedua, …, n

_k

jenis ke k adalah

! ...

!

!

!

2

1

n n

k

n

n

• Contoh: ada berapa banyak cara berbeda untuk menyusun lampu warna-warni dalam seuntai tali jika ada 3 yang berwarna merah, 4 kuning, dan 2 biru?

• Jawab: ada sebanyak 9!/(3!4!2!) = 1260

Partisi himpunan

• Partisi himpunan n objek kedalam r himpunan bagian (subset) atau sel:

– Partisi berhasil jika irisan sebarang dua subset adalah ∅ dan gabungan seluruh subset menghasilkan himpunan asal.

– Contoh: Partisi S = {a, e, i, o, u} kedalam dua sel yang masing-masing mengandung 4 dan 1 buah anggota adalah: {(a, e, i, o), (u)}, {(a, i, o, u), (e)}, {(a, e, o, u), (i)}, dan {(a, e, i, u), (o)}. Sehingga ada 5 buah:

! 5 1

! 4

! 5 1

, 4

5 ⎟⎟⎠ = =

⎜⎜ ⎞

⎝

⎛

• Teorema 1.7: Banyaknya cara untuk mempartisi suatu himpunan n objek kedalam r buah sel dengan masing-masing n₁ objek untuk sel pertama, n₂ objek untuk sel kedua, …, n_r objek untuk sel ke r adalah

dimana n₁ + n₂ + … + n_r = n.

! ...

!

!

! ,

...

,

, _{2 1 2}

1 r n n nr

n n

n n

n ⎟⎟ =

⎠

⎜⎜ ⎞

⎝

⎛

Kombinasi

• Pengaturan r-objek dari sekumpulan n-buah objek tanpa memperhatikan urutan disebut kombinasi. Suatu kombinasi pada dasarnya adalah partisi

dua sel, yang pertama mengandung r-objek dan yang kedua ada (n-r) objek.

Dengan demikian banyaknya kombinasi r-objek dari n kumpulan adalah

karena sudah pasti sel kedua beranggotakan n-r

⎟⎟ ⎠

⎜⎜ ⎞

⎝

⎟⎟ ⎛

⎠

⎜⎜ ⎞

⎝

⎛

− r

ditulis n biasa

r atau n

r n ,

• Teorema 1.9: Kombinasi r dari n buah objek berlainan adalah

( )

^!

!

! r n r

n r

n

= −

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

1.5 Nilai Peluang

Inferensi dan Arti Peluang

• Ahli statistik berurusan dengan pengambilan kesimpulan

(inferensi) dalam eksperimen yang menyangkut ketidakpastian.

• Beberapa contoh:

– “

Chris John kemungkinan memenangkan pertandingan tinju malam ini.”

– “Saya punya peluang 50-50 untuk mendapatkan angka genap jika dadu ini dilantunkan”

– “Nanti malam kemungkinan besar saya tidak akan memenangkan undian.”

– “Kebanyakan mahasiswa STEI lulus dalam 8 semester”

• Dalam contoh-contoh diatas, kita mengekspresikan keluaran hasil eksperimen yang tidak pasti. Akan tetapi dengan

mengetahui informasi yang lalu atau struktur dari eksperimen, kita punya derajat keyakinan tertentu akan validitas dari

pernyataan-pernyataan diatas.

Pembobotan titik cuplikan

• Teori Matematika untuk peluang dari ruang

pencuplikan berhingga menyediakan sekumpulan bilangan yang disebut sebagai pembobot

(weights), dengan nilai antara 0 sampai 1, sebagai cara mengevaluasi kebolehjadian (likelihood)

munculnya suatu peristiwa dari eksperimen statistik.

• Setiap titik dalam ruang pencuplikan diboboti sedemikian rupa hingga jumlah keseluruhan dari pembobot menjadi 1.

– Kejadian dengan kemungkinan tinggi diberi bobot mendekati 1.

– Kejadian yang lebih mustahil diberi bobot mendekati 0.

Nilai Peluang dari Kejadian

• Peluang dari kejadian A dihitung dengan menjumlahkan seluruh bobot titik cuplikan didalam A.

• Jumlah ini disebut sebagai ukuran (measure) dari A, atau peluang A dan dituliskan sebagai P(A). Dengan demikian,

– P(∅) = 0 – P(S) = 1

• Def. 1.11: Nilai peluang dari kejadian A adalah hasil

penjumlahan pembobot dari semua titik cuplikan didalam A. Sehingga

• 0≤P(A)≤1,

• P(∅) = 0

• P(S) = 1

Contoh

• Soal: Sebuah uang logam dengan sisi H dan T dilantunkan dua kali. Berapa peluang muncul sedikitnya satu buah sisi H ?

• Jawab: Himpunan titik cuplikan dari percobaan ini adalah S={HH, HT, TH, TT}. Dengan

menganggap uang logam tak bias, setiap hasil memiliki kebolehjadian yang sama. Jika masing- masing pembobot adalah w, maka

|S|⋅w = 4w = 1. dengan demikian w = ¼.

Jika A menyatakan kejadian muncul sedikitnya satu kali H, maka A = {HH, HT, TH} dan

P(A) = |A|⋅w = 3/4

Peluang Kejadian Sederhana

• Pembobot dapat diasosiasikan dengan kejadian sederhana.

Jika eksperimen dilakukan sedemikian rupa hingga

pembobot setiap titik cuplikan didalam S bernilai sama, maka nilai peluang dari kejadian A adalah nisbah antara jumlah elemen A dengan jumlah elemen S.

• Teorema 1.9: Jika suatu eksperimen menghasilkan satu dari N buah hasil berbeda dengan kebolehjadian yang sama, dan jika n buah dari kejadian ini berasal dari

kejadian A, maka nilai peluang dari kejadian A adalah

P(A) = n/N

Contoh

• Soal: Tentukan peluang terambilnya kartu

♥ dari setumpukan lengkap kartu.

• Jawab: Banyaknya titik cuplikan didalam S adalah sejumlah kartu, yaitu 52, dimana ada 13 buah kartu ♥. Dengan demikian

P(A) = 13/52 = ¼

• Catatan: jika pembobot tidak seragam, nilai peluang harus didasarkan pada sifat eksperimen yang diketahui

sebelumnya (prior knowledge) atau bukti-bukti

eksperimental.

1.6 Beberapa Hukum Peluang

Hukum penjumlahan

• Teorema 1.10: Untuk sebarang dua kejadian A dan B akan berlaku

P(A∪B) = P(A) + P(B) – P(A∩B)

• Bukti: Tinjau diagram Venn disamping. Perdefinisi, P(A∪B) adalah jumlah pembobot titik

cuplikan dalam A∪B. Akan tetapi P(A) + P(B) adalah jumlah seluruh pembobot di A dengan seluruh

pembobot di B, sehingga kita telah menambahkan A∩B dua kali. Oleh karena itu, kita harus mengurangi P(A) + P(B) dengan P(A∩B) untuk mendapatkan P(A∪B) semestinya.

S

A B

Peluang kejadian yang saling bebas

• Corollary 1: Jika A dan B adalah kejadian yang saling bebas (mutually exclusive), maka

P(A∪B) = P(A) + P(B)

• Corrolary 1 ini adalah hasil langsung dari teorema 1.10,

karena jika A dan B saling bebas, maka P(A∩B) = P(∅) =0.

Hasil ini dapat diperumum:

• Corollary 2: Jika A

₁

, A

₂

, … dan A

_n

, adalah kejadian yang saling bebas (mutually exclusive), maka

P(A

₁

∪A

₂

∪ … ∪A

_n

) = P(A

₁

) + P(A

₂

) + …+ P(A

_n

)

• Kita ingat, jika A

₁

, A

₂

, … dan A

_n

adalah partisi dari ruang pencuplikan S, maka

P(A

₁

∪A

₂

∪ … ∪A

_n

) = P(A

₁

) + P(A

₂

) + …+ P(A

_n

)

Contoh

• Soal 1: Peluang seorang mahasiswa lulus kuliah Matematika adalah 2/3, sdangkan peluang

lulusnya untuk kuliah Biologi adalah 4/9. Jika

peluang lulus sedikitnya satu dari kedua kuliah tsb adalah 4/5, berapa peluang lulus kedua kuliah tsb?

• Jawab: Sebut M sebagai kejadian “lulus

Martematika” sedangkan B sebagai kejadian “lulus Biologi”. Berdasarkan teorema 1.10, maka

P(M∩B) = P(M) + P(B) - P(M∪B)

= 2/3 + 4/9 – 4/5 = 14/45

Peluang kejadian komplementer

• Teorema 1.11: Jika A’ adalah kejadian komple- menter dari kejadian A, maka

P(A’) = 1 – P(A)

• Bukti: Karena A∪A’ = S dan karena himpunan A tak beririsan dengan A’, maka

1 = P(S)

= P(A∪A’)

= P(A) + P(A’)

Akibatnya, P(A’) = 1 – P(A)

Contoh

• Soal: Suatu uang logam dengan muka H dan T dilantunkan enam kali berturut-turut. Berapa peluang sedikitnya satu H muncul?

• Jawab: Andaikan E adalah kejadian muncul sedikitnya satu kepala. Ruang pencuplikan S terdiri dari 2

⁶

= 64 buah titik cuplikan karena setiap lantunan memiliki dua jenis

keluaran. Kita ketahui P(E) = 1 - P(E’) dimana E’ adalah kejadian tidak munculnya sisi H, yang hanya bisa terjadi sekali—yakni seluruh lantunan menghasilkan T.

Oleh karena itu, P(E’) = 1/64 dan kita dapatkan P(E) = 1 – P(E’) = 1 - 1/64

= 63/64.

1.7 Peluang Bersyarat

Pengertian

• Nilai peluang dari munculnya kejadian B, jika diketahui adanya kejadian A disebut peluang bersyarat P(B|A).

– Dibaca: “peluang B, diberikan A”

• Tinjau kejadian B dari pelantunan dadu yang menghasilkan bilangan kuadrat sempurna (kuad. sempurna: 1, 4, 9, …). Dadu dibuat

sdemikian hingga bilangan genap muncul duakali lebih sering dibanding bilangan ganjil. Karena S={1,2,3,4,5,6} maka

P(1)=P(3)=P(5)= v, dan P(2)=P(4)=P(6) = 2v, tetapi 3v+2⋅3v = 1 =>

v=1/9. Jadi dadu ganjil berpeluang 1/9, dadu genap 2/9.

• Andaikan diketahui pelantunan menghasilkan angka diatas 3, jadi

A={4,5,6}⊆S. Untuk menghitung B, nilai peluang dari titik cuplikan di A harus ditentukan lagi shg totalnya 1, dng demikian pembobot w

untuk A adalah 2w+w+2w=5w=1, atau w=1/5;

• Relatif terhadap A, B mengandung satu elemen saja, yaitu 4, atau B|A={4}. Dengan demikian:

P(B|A) = 2/5, atau

P(B|A) = (2/9) / (5/9) = P(A∩B) / P(A)

Definisi

• Def. 1.12: Peluang bersyarat dari B, diberikan A, dituliskan sebagai P(B|A) didefinisikan sebagai

P(B|A) = P(A∩B)/P(A) jika P(A)>0

• Contoh: Suatu populasi memiliki data sbb:

Bekerja (E) Tdk bekerja

Laki-laki 460 40

Perempuan 140 260

• Tinjau dua kejadian dari seleksi acak berikut

M: terpilih Laki-laki, E: yang terpilih punya pekerjaan Dengan demikian, nilai peluang bersyarat M|E adalah

P(M|E)=460/(460+140) = 23/30

Def.1.12 juga memberikan hasil sama karena P(E∩M) = 460/900, sedangkan P(E)=600/900, shg P(M|E) = P(E∩M)/P(E) = 23/30

Teorema perkalian

• Soal: dalam satu kotak terdapat 20 buah sekering, 5 diantaranya cacat.

Jika 2 buah sekering dipilih secara acak dan diambil dari kotak secara berturutan, tanpa penggantian, berapa peluang kedua sekering yang terambil itu cacat?

• Jawab: Andaikan A kejadian terambilnya sekering cacat yang pertama dan B kejadian terambilnya sekering cacat kedua, kejadian A∩B harus ditafsirkan bahwa A terjadi, kemudian B terjadi setelah A terjadi.

Peluang terambilnya sekering pertama cacat adalah 5/20=1/4,

sedangkan terambilnya sekering kedua cacat adalah (5-1)/(20-1) = 4/19. Dengan demikian

P(A∩B) = (1/4)⋅(4/19) = 1/19.

• Teorema 1.12: Jika dalam suatu eksperimen peristiwa A dan B dapat terjadi, maka berlaku

P(A∩B) = P(A)⋅P(B|A)

P(A) P(B|A)

Generalisasi teorema perkalian

• Teorema 1.13: Jika dalam suatu percobaan kejadian A

₁

, A

₂

, A

₃

, … dapat muncul, maka berlaku

P(A

₁

∩A

₂

∩A

₃

… ) = P(A

₁

)⋅P(A

₂

|A

₁

) ⋅P(A

₃

|A

₁

∩A

₂

) …

Kejadian saling bebas

• Def.1.13 Kejadian A dan B disebut saling bebas (independent) jika, dan hanya jika,

P(A∩B) = P(A)⋅P(B)

• Soal: sepasang dadu dilantunkan dua kali. Berapa peluang mendapatkan jumlah 7 dan 11?

• Jawab: Jika A₁, A₂, B₁, dan B₂ peristiwa saling bebas bahwa jumlah 7 pada lemparan pertama, jumlah 7 pada lemparan kedua, jumlah 11 pada lemparan pertama, dan jumlah 11 pada lemparan kedua muncul.

Kita akanmencermati kejadian mutually exclusive A₁∩B₂ dan B₁∩A₂. Oleh karena itu

P[(A₁∩B₂)∪(B₁∩A₂)] = P(A₁∩B₂) + P(B₁∩A₂)

= P(A₁)⋅P(B₂) + P(B₁)⋅P(A₂)

= (1/6)⋅(/18) + ((1/18)⋅(1/6)= 1/54

Aturan Bayes

Ilustrasi

• Kembali ke contoh sebelumnya:

Bekerja (E) Tdk bekerja

Laki-laki 460 40

Perempuan 140 260

• Dengan mudah diperoleh

P(E) = (460+140)/(460+140+40+260) = 600/900=2/3

• Soal: Andaikan diketahui juga, 36 dari yang bekerja dan 12 dari yang tdk bekerja adalah anggota Rotary Club (RC), berapa peluang

seseorang yang bekerja adalah anggota RC ?

• Jawab: Misalkan A peristiwa orang yang terpilih adalah anggota RC, peluang bersyarat yang kita cari adalah:

P(E|A) = P(E∩A)/P(A)

Lanjutan …

• Tinjau diagram Venn disamping

• Peristiwa A dapat dinyatakan sebagai gabungan dua peristiwa yang mutually exclusive, yaitu E∩A dan E’∩A. Jadi

A = (E∩A) ∪ (E’∩A)

• Berdasarkan Corollary 1,Teorema 1.10, maka: P(A) = P(E∩A) + P(E’∩A)

• Sehingga bisa kita tuliskan

A E

E’

S

• Dengan demikian, untuk soal sebelumnya, kita bisa hitung:

P(E∩A) = 36/900 = 1/25 P(E’∩A) = 12/900 = 1/75

P(E|A) = (1/25)/{(1/25) + (1/75)} = 3/4

P(E|A) = P(E∩A) /{P(E∩A) + P(E’∩A)}

Aturan Bayes Umum

• Teorema 1.14 (Aturan Bayes). Andaikan {B₁, B₂, B₃, … } sekumpulan peristiwa yang membentuk partisi dari ruang cuplikan S, dimana P(B_i)≠0, untuk i=1, 2, …, n. Andaikan A sebarang peristiwa dalam S sedemikian hingga P(A)≠0. Maka, untuk k = 1, 2, … ,n berlaku

( ) ( )

( )

( ) ( )

( ) ( )

∑

∑

= =

=

∩

= ∩ _n

i

i i

k k

n

i

i k k

B A P B P

B A P B P A

B P

A B

A P B

P

1 1

|

| |

A

B

₁

B

_k

B

₃

B

₄

B

₂

B

_n

…

Sekian