Tinjau Ulang Prakalkulus Limit Kekontinu (1)

Tinjau Ulang Prakalkulus Limit, Kekontinuan Turunan dan Diferensial

Limit tak Hingga Aplikasi Turunan

Terapan Konsep dan Prinsip Menggunakan Algoritma

Setiap Solusi Masalah Dikemukakan Strateginya

Oleh

Moch Chotim

Nip. 130781008

Jurusan Matematika

FMIPA

Universitas Negeri Semarang

KATA PENGANTAR

Buku ajar ini merupakan rancangan kegiatan belajar mengajar matakuliah Kalkulus 1. Matakuliah ini diberikan pada semester 1 tahun pertama bersama program D3 dan S1 di Fakultas Matematika dan Ilmu Pengetahuan Alam dengan bobot 3 satuan kredit semester (3 SKS).

Tujuan kurikuler matakuliah Kalkulus 1 adalah: “Mahasiswa memahami konsep fungsi, kekontinuan fungsi, limit fungsi, turunan fungsi, dan aplikasinya pada masalah-masalah yang dihadapi di matematika dan kehidupan sehari-hari”.

Untuk dapat mengikuti matakuliah Kalkulus 1 mahasiswa harus sudah memahami matematika sekolah, khususnya matematika di SMA.

Agar perkuliahan dapat berhasil secara optimal, perkuliahan dilaksanakan dalam 2 kali pertemuan setiap minggu dengan masing-masing pertemuan 2 x 50 menit. Dengan cara ini mahasiswa akan lebih sering belajar, latihan, dan berdiskusi dengan dosen dibandingkan dengan jika perkuliahan diberikan 1 kali pertemuan (3 x 50 menit). Dengan cara ini diharapkan mahasiswa mencapai hasil belajar yang lebih baik.

Permasalahan matematika pada umumnya dan kalkulus pada khususnya memerlukan pendalaman teori, dan latihan soal yang banyak. Dengan demikian kegiatan belajar mahasiswa tidak cukup dilayani di kelas, dengan demikian mahasiswa harus memperkaya pengetahuan sendiri melalui tugas, baik yang ditetapkan dosen maupun yang dipilih mahasiswa sendiri. Pendekatan yang dipilih adalah pendekatan berbasis strategi dan pelaporannya menggunakan algoritma. Algoritma didefinisikan sebagai seperangkat langkah yang tersusun secara deduktif, setiap langkah dibuka dengan suatu kata pembuka yang merupakan alur berpikir. Setiap memecahkan masalah dilalui dengan suatu diskusi yang aktif dan efisien. Bahan bacaan wajib minimum dan tugas di luar kelas untuk perkuliahan ini dapat dilihat pada daftar pustaka yang dilampirkan.

Untuk memperoleh data kelulusan mahasiswa dilaksanakan 2 kali ujian, yaitu ujian tengah semester (100 menit) dan ujian akhir semester (120 menit). Selain kedua ujian itu direncanakan pula 2 kali ujian formatif masing-masing 50 menit sebelum dan sesudah ujian tengah semester. Nilai akhir mahasiswa ditetapkan berdasarkan pembobotan ujian dan tugas lain sesuai dengan peraturan yang berlaku di Universitas masing-masing.

Semarang, 18 April 2008 Penulis,

DAFTAR ISI

KATA PENGANTAR ...

SASARAN BELAJAR ...

BAB 1: TI NJAU ULANG TENTANG KONSEP-KONSEP PRAKALKULUS 1.1 Sistem Bilangan ………...

Garis bilangan ………...

Operasi padaR………...

Urutan padaR ...………...

Nilai mutlak ... 1.2 Bidang koordinat, jarak, dan lingkaran ...

Bidang koordinat ... Jarak ... Lingkaran ... 1.3 Persamaan linear ... Kemiringan garis ... Persamaan garis ……… Garis tegak dan garis datar ………... 1.4 Fungsi ………... Pengertian fungsi ... Operasi aljabar pada fungsi ... Fungsi-fungsi komposisi ... Fungsi invers ... Membuat grafik fungsi dengan metode geseran ... Fungsi Periodik: Tinjau ulang tentang fungsi Trigonometri ... Fungsi sinus dan fungsi kosinus ... Fungsi tigonometri lainnya ...

BAB 2: LIMIT DAN KEKONTINUAN FUNGSI ... 2.1 Limit fungsi ... Konsep limit secara intuitif ... Konsep limit secara formal ... Teorema-teorema limit ... Limit sepihak ... Limit fungsi trigonometri ... 2.2 Kekontinuan fungsi ... Kekontinuan fungsi di satu titik ... Kekontinuan fungsi pada suatu selang ... Kekontinuan sepihak ...

001 001 001 004 005 008 012 012 014 015 017 018 018 020 021 021 031 035 037

042 048 051

BAB 3: TURUNAN DAN DIFERENSIAL ...

3.1 Turunan ... Kemiringan garis singgung ... Pengertian turunan ... Turunan fungsi pada suatu selang ... Turunan sepihak ... Hubungan antara adanya turunan suatu fungsi dan kekontinuan fungsi di suatu titik ... Turunan fungsi trigonometri ... Teorema-teorema menentukan turunan fungsi ... Turunan fungsi invers ... Turunan fungsi invers fungsi trigonometri ... Turunan fungsi implisit ...

3.2 Diferensial ... Pengertian diferensial ... Hampiran nilai fungsi ...

BAB 4: LIMIT TAK HINGGA DAN LIMIT DI TAK HINGGA ...

4.1 Limit tak hingga ... Pengertian limit tak hingga ... 4.2 Limit di tak hinga ...

BAB 5: PENGGUNAAN TURUNAN ...

5.1 Nilai minimum dan maksimum suatu fungsi ... 5.2 Teorema Rolle dan Teorema nilai rata-rata ... 5.3 Fungsi naik dan fungsi turun ... 5.4 Kecekungan grafik suatu fungsi ... 5.5 Membuat sket grafik fungsi ...

Asimptot grafik fungsi ... Metode membuat sket grafik fungsi ... 5.6 Beberapa penggunan turunan ang lain ... Masalah maksimum dan minimum ... Masalah laju yang berkaitan ...

DAFTAR PUSTAKA

122

122 122 124 124 128

131 135 137 144

140

169 160 162

168

168 170 175

184

Konsep-konsep dan prinsip matematika yang telah diperoleh di sekolah

merupakan prasyarat untuk belajar kalkulus. Konsep dan prinsip ini perlu

diingatkan kembali sebagai penyegaran dan pendalaman.

1. Sistem Bilangan

Bilangan-bilangan real dapat di-gambarkan oleh himpunan semua titik yang terletak pada suatu garis. Pertama dipilih sebuah titik O pada garis itu yang dipakai sebagai titik pangkal. Selanjutnya dipilih ukuran satuan dan tempatkan titik-titik pada garis yang terletak satu satuan di sebelah kanan O. Titik itu ditandai dengan 1 (satu). Cara ini digunakan untuk memberi skala garis bilangan itu dan juga untuk mempertimbangkan letak setiap bilangan real. Sebagai contoh, setiap bilangan real negatif –sterletakssatuan di kiri O.

Terdapat tiga tipe bilangan real yang penting, yaitu bilangan-bilangan bulat, bi-langan-bilangan rasional, dan bilangan-bilangan tak rasional. Bilangan-bilangan-bilangan bulat adalah:

..., – 3, –2,–1, 0, 1, 2, 3,....

Bilangan-bilangan bulat dapat ditulis dalam bentuk desimal dengan di kanan koma desimal hanya terdiri nol, sebagai contoh:

2 = 2, 000...= 2,0, 12 = 12,000...= 12,0, dan

–1 = –1,000...= –1, 0. dengan tanda ” ” dibaca ”bar” berarti angka nol diulang tanpa akhir. Bilangan-bilangan rasional adalah Bilangan-bilangan-Bilangan-bilangan yang dapat dinyatakan sebagai:

b a

,

a dan b bilangan-bilangan bulat, dan b 0.

001 002

0 5 , 0 2

1 _, Ini suatu kontradiksi.

Jadi 2 merupakan bilangan tak rasional.

0 1 2 3 4 –1

–2 –3

–s r

s satuan

r satuan

3 , 0 3

1 _,

__ 27 , 2 11

25 _{, dan}

______ 538461 538461 , 1 13

20 _.

Contoh 1:

Tunjukkan bahwa

__ 63 ,

2 adalah bilangan ra-sional.

Bukti: Tulis

__ 63 ,

2 =x. Jelas 100x= 263,__63. Jadi 99x= 261

x=

99 261_.

Ini menunjukkanx=

__ 63 ,

2 merupakan sua-tu bilangan rasional.

Bilangan-bilangan real yang tak dapat dinyatakan sebagai

b a

, a dan b bilangan-bilangan bulat, dan b 0 disebut bilangan-bilangan tak rasional.

Contoh 2:

Tunjukkan bahwa 2 merupakan bilangan tak rasional.

Bukti:

Andaikan 2 merupakan bilangan rasional.

Tulis

b a

2 ,a,b B,b 0, dan (a,b) = 1. Jadia2= 2b2.

Jadia2merupakan kelipatan 2. Jadiamerupakan kelipatan 2.

Tulisa= 2muntuk suatumbilangan bulat. Jadi 4m2= 2b2 b2= 2m2.

Jadib2merupakan kelipatan 2. Jadibkelipatan 2.

Jadi (a,b) > 1.

Bilangan = 3,14159 ... yang merupakan perbandingan keliling dan diameter suatu lingkaran juga termasuk bilangan tak rasional.

Terdapat lambang-lambang baku untuk mengenali himpunan-himpunan bilangan, misalnya:

R= {x xbilangan real}, N= {x xbilangan asli}, Z= {x xbilangan bulat}, Q= {x xbilangan rasional},dan Qc= {x xbilangan tak rasional}. JelasN= {1, 2, 3, ...} dan

Z= {..., –3, –2, –1, 0, 1, 2, 3, ...}.

2. Operasi Pada

R

Operasi jumlah padaRmerupakan fungsi “+”:RxR R

(x,y) x+y

dan operasi kali padaRmerupakan fungsi “x”:RxR R

(x,y) xx y.

Operasi jumlah dan kali pada R memenuhi sifat-sifat berikut.

Jikax,y,x R, berlaku: (1) Sifat komutatif

x+y=y+xdan x.y=y.x.

(2) Sifat asosiatif

x+y+z=x+ (y+z) = (x+y) +z x.y.z =x.(y.z) = (x.y).z (3) Sifat distributif

x.(y+z) =x.y+x.z (x.y).z=x.z+y.z

(4) Unsur identitas

Terdapat unsur-unsur 0 dan 1 yang memenuhi

x+ 0 = 0 +x x Rdan x. 1 = 1 .x x R. (5) Unsur balikan

x R –x R x+ (–x) = 0 dan x R,x 0, x– 1 R x.x– 1= 1.

Kelima sifat di atas dikenal dengan sifat lapangan (field). Jadi R merupakan suatu lapangan.

Operasi selisih padaRmerupakan fungsi “–“:RxR R

(x,y) x+ (–y)

dan operasi kali padaRmerupakan fungsi “:” :RxR R

(x,y) xxy– 1.

3. Urutan pada

R

Terdapat urutan baku pada R. Jika pada garis bilangan letak b terletak di kanana, dikatakanblebih dariadan ditulis dengan

b>a.

Tentu saja sama artinya apabila dika-takanakurang daribdan ditulis

a<b. Definisi 1

Teorema 2

Contoh 3

Tentukan himpunan selesaian pertidaksa-maan: (a)x+ 2 < 5,x Rdan

(b) 9

2

3_{x ,x R.}

Penyelesaian:

(a) Jelasx+ 2 < 5

x+ 2 + (–2) < 5 +(–2) x < 3.

Jadi HS = {x R x < 3}.

(b) Jelas 9

2 3_x

9 . ).

.( ₃2

2 3 3

2 _x

6 x .

Jadi HS = {x R x 6}.

Berikut ini disajikan beberapa kesepa-katan untuk menyatakan selang-selang padaR. Apabilaa,b R, didefinisikan:

(1) (a,b) = {x R a<x<b}, (2) [a,b) = {x R a x<b}, (3) (a,b] = {x R a<x b}, (4) [a,b] = {x R a x b}, (5) [a,+ ) = {x R x a}, dan (6) (– ,a] = {x R x a}.

Contoh 4

Tentukan himpunan selesaianx2– x –2 4. Penyelesaian:

Jelasx2–x– 2 4 x2–x– 6 0 (x+ 2)(x– 3) 0. Titik-titik pembuat nol ruas kiri adalah –2 dan 3.

005 006

Dipunyaia,b R.

a<b b–a 0 dan

a<b,a=bataua>b.

Jikax,y,z,c R

maka (i)x=y, x<y, ataux>y, (ii)x<ydany<z x<z, (iii)x<y x+c<y+c,

Nilai (x+ 2), (x– 3), dan (x+ 2)(x– 3) pa-dan selang (– ,–2),( –2,3), dan (3, + ):

Jadi HS = (– ,–2] [3, + ).

Teorema 3

Bukti (a):

Dipunyai 0 a b.

Jelas a > 0, b > 0, dan a b. Jelas a + b > 0 dan a – b 0.

Jadi (a + b)(a – b) 0 a2– b2 0 a2 b2. Jadi 0 a b a2 b2.

Bukti (b):

Dipunyai 0 a b.

Jelas a > 0, b > 0, dan a b. Jelas a.b > 0 dan a – b 0.

Jadi 0

ab b a

a 1 b 1

b 1 a 1

.

Jadi

b 1 a 1 b a

0 .

Bukti lainnya diserahkan pembaca sebagai latihan.

4. Norm Baku di

R

Pada garis bilangan berikut ini jarak 2 ke 5 adalah 3, ditulis j(2,5) = 3. Demikian pula jarak 5 ke 2 juga 3, ditulis j(5,2) = 3. Sedangkan

2 – 5 = –3 < 0 dan 5 – 2 = 3.

Berdasarkan fakta ini perlu didefinisikan konsep jarak dua titik diRsebagai berikut: dipunyai a, b R, jarak a ke b didefini-sikan sebagai

J(a,b) =

0 apabila

0 apabila

b a b

a

a b a

b

.

Dengan demikian jarak x 0 ke 0 sama dengan jarak 0 ke x 0, ditulis dengan

J(x,0) =j(0,x) =

0 apabila

0 apabila

x x

x x

.

Selanjutnya, jarak x ke x ditulis j(x,x) = 0. sebagai contohj(7,7) = 0 dan j(0,0) = 0.

Definisi 4

Contoh 5 Tentukan 2,

2

3 _{, dan 1 .}

Penyelesaian: (a) Jelas 2 > 0.

Jadi 2= 2. (b) Jelas 0

2 3 _.

007 008

– – – + + + + + +

– – – – – – + + + – – –

+ + + + + +

(x+ 2)

(x– 3)

(x+ 2)(x – 3)

Gambar 2:Daerah nilai (x+ 2), (x– 3), dan (x+ 2)(x– 3).

–2

–2

–2

3

3

3

Jika x R, J(x,0) ditulis dengan x

yang dibaca “nilai mutlakx” didefini-sikan sebagai:

x =

0 apabila

0 apabila

x x

x x

. Dipunyaia,b R.

(a) 0 a b a2 b2, (b)

b a b

a 1 1

0 ,

(c) a b 0 a2 b2, dan (d)

b a b

Jadi

2 3 ₌

2 3 ) 2 3

( .

(c) Dipunyai 3,14.

Jadi 1 – 1 – 3,14 = – 2,14 < 0. Jadi 1 = –(1 – ) = – 1.

Berikut ini disajikan beberapa teorema yang penting tentang nilai mutlak.

Teorema 4

(1) a a a R. (2) ab a.b a,b R. (3) Jikac> 0 maka

c

a –c a c.

(4) a a a a R. (5) a b a b a,b R.

Bukti (1):

Ambil sembaranga R. Kasusa< 0:

Tulisa= –muntuk suatum> 0. Jelas a m ( m) m dan

m m

a .

Jadi a a. Kasusa= 0:

Jelas –a= 0. Jadi a a = 0. Kasusa> 0:

Jelas –a< 0.

Jadi a a dan a ( a) a. Jadi a a .

Jadi a a a R.

Bukti (3): Dipunyaic> 0.

( ) Ambil sembaranga R. Dipunyai a c.

Kasusa< 0:

Jelas a c –a c a –c. Jadi –c a c.

Kasusa> 0:

Jelas a c a c. Jelas –a< 0.

Jadi –a<c a> –c. Jadi –c a c.

Jadi a c –c a c. ( ) Dipunyai –c a c.

Ambil sembaranga R. Kasusa< 0:

Jelas –c a c c a c

c a

c .

Jadi a c. Kasusa= 0:

Jelas 0 c a c. Kasusa> 0:

Jelas –c a c c a c.

Jadi a c.

Jadi –c a c a c.

Bukti lainnya diserahkan pembaca sebagai latihan.

Teorema 5:

Bukti:

(a) Ambil sembaranga,b R.

Jelas a = (a b) b a b b dan

b = (b a) a b a a.

Jadi a b a b dan (a b) a b. Jadi a b a b.

(b) Ambil sembaranga,b R. Jelas a b = a ( b)

b a

= a b. Jadi a b a b a,b R.

009 010

Untuk setiapa,b Rberlaku: (a) a b a b dan

Contoh 5

Tentukan HS pertidaksamaan berikut ini:

(a) x 5 4 (c) 0

3 x

x

(b) x 1 2x 7 (d) 0

3 x

x

Penyelesaian: (a) Cara 1:

Ambil sembarangx R. Kasusx– 5 < 0:

Jelasx< 5.

Jelas x 5 4 –(x – 5) 4 –x+ 5 4 x 1. Jadi HS1= [1, 5). Kasusx– 5 0:

Jelasx 5.

Jelas x 5 4 x – 5 4 x 9. Jadi HS2= [5, 9].

Jadi HS = [1, 5) [5, 9] = [1, 9].

Cara 2:

Ambil sembarangx R.

Jelas x 5 4 – 4 x– 5 4

1 x 9.

Jadi HS = [1, 9].

(b) Ambil sembarangx R. Kasusx< – 1:

Jelas x 1 2x 7 –(x+ 1) >2x– 7 –x– 1 > 2x– 7 x < 2.

Jadi HS1= (– ,–1). Kasusx – 1:

Jelas x 1 2x 7 x+ 1 > 2x– 7 –x> – 8 x< 8. Jadi HS2= [– 1, 8).

Jadi HS = (– ,–1) [– 1, 8) = (– ,8).

(c) Ambil sembarangx R– {3}. Jelasx 3.

Jadi (x– 3)2> 0.

Jadi 0

3 x

x

x(x– 3) 0.

Selanjutnya daerah nilaix, (x– 3), dan x(x – 3) diperlihatkan pada gambar be-rikut ini.

Jadi HS = [0, 3].

(d) Ambil sembarang x R– {3}. Jelasx– 3 0.

Jadi x 3 0.

Jadi 0

3 x

x

x 3. Jadi HP = (– , 0].

4. Bidang Koordinat

Untuk menganalisis hubungan antara dua variabel, sebagai contoh:

(a) hubungan antara waktu dan jarak yang ditempuh suatu partikel yang bergerak sepanjang garis,

(b) hubungan antara tekanan dan tem-peratur suatu gas ideal,

011 012

– – – + + + + + + – – – – – – + + +

– – –

+ + + + + +

x

x– 3

x(x– 3)

0 0

0

3 3

3

diperlukan suatu sistem kordinat dalam dua dimensi. Sistem koordinat ini dibangun dengan cara sebagai berikut:

(a) pilih titik O sebagai titik pangkal, (b) melalui titik O dibangun sumbu

datar dan sumbu tegak yang selan-jutnya berturut-turut disebut dengan sumbu X dan sumbu Y,

(c) bagian positif sumbu datar adalah sumbu datar yang letaknya di kanan titik pangkal O,

(d) bagian positif sumbu tegak adalah sumbu tegak yang letaknya di atas titik pangkal,

(e) bidang yang dibangun oleh sumbu datar dan sumbu tegak disebut bidang koordinat XOY,

(f) setiap titik pada bidang XY berpa-danan dengan sepasang bilangan real (xo, yo) yang disebut koordinat titik tersebut.

Perhatikan titik P pada bidang koordinat berikut ini.

Titik-titik Q dan R berturut-turut merupa-kan projeksi titik P pada sumbu X dan sumbu Y.

Tulis j(PQ) = y_o dan j(PR) = x_o .

Jelas y_o =yodan xo =xo.

Selanjutnya xo disebut koordinat x titik P, yo disebut koordinat y titik P, dan (xo, yo) disebut koordinat titikP.

Berikut ini disajikan gambar beberapa titik di bidang koordinat.

Jarak titik-titik A, B, C, dan D ke sumbu X berturut-turut adalah:

1

1 , 3 3, 3 3, dan 1 1. Sedangkan jarak titik-titik A, B, C, dan D ke sumbu Y berturut-turut adalah:

4

4 , 1 1, 4 4, dan 2 2. Gambar berikut memperlihatkan dua titik P(x₁,y₁) dan Q(x₂,y₂).

Jarak titikPke titikQditulisj(P,Q). Jelasj(P,Q) = x₂ x₁2 y₂ y₁2

= (x₂ x₁)2 (y₂ y₁)2

Contoh 6

Tentukan jarak antara dua titik berikut: (a) A(– 3, 1) dan B(1, – 2)

(b) P(1,1) dan Q(–1,–7)

013 014

P(xo,yo)

Q R

X Y

O

Gambar 4:Bidang koordinat

X Y

A(4,1) B(–1,3)

D(2,–1)

C(–4, –3)

Gambar 5:Posisi beberapa titik pada bidang koordinat

) 1 , 1 (x y P

Gambar 6:Jarak titik P ke titik Q Y

X

) 2 , 2 (x y Q

Penyelesaian:

(a) Jelasj(A, B) = (1 3)2 ( 2 1)2

= 25 = 5.

(b) Jelasj(A, B) = ( 1 1)2 ( 7 1)2

= 68 = 2 17.

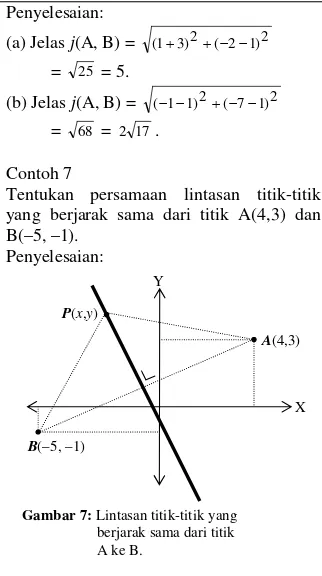
Contoh 7

Tentukan persamaan lintasan titik-titik yang berjarak sama dari titik A(4,3) dan B(–5, –1).

Penyelesaian:

Ambil sembarang titikP(x,y) pada lintasan. Jelasj(P, A) =j(P, B)

2 ) 3 ( 2 ) 4

(x y = (x 5)2 (y 1)2

8 1 4 9x

y .

Ini menunjukkan bahwa lintasannya meru-pakan suatu garis lurus.

5. Lingkaran

Lingkaran adalah lintasan titik-titik yang berjarak sama ke suatu titik tertentu. Selanjutnya, jarak yang tetap disebut

jari-jari lingkaran dan titik tertentu disebut titik pusat lingkaran.

Sekarang akan dicari persamaan lingkaran yang berpusat di titik O(0,0) dan ukuran jari-jarinyar.

Ambil sembarang titik P(x,y) pada lingkar-an.

Jelasj(O,P) =r

r y

x 0)2 ( 0)2 (

r y

x2 2

(

2 2 2

r y

x .

Tampilanx2 y2 r2 merupakan persama-an lingkarpersama-an berpusat di titik O(0,0) dpersama-an berukuran jari-jarir.

Contoh 8

(a) Tentukan persamaan lingkaran ber-jari-jari 4 dan berpusat di titik A(2,3).

Jelaskan dan sket grafik yang persamaan-nyax2+y2+ 6x – 2y + 6 = 0.

Penyelesaian:

(a) Ambil sembarang titik P(x,y) pada lingkaran.

Jelasj(P,A) = 4

015 016

4 2 ) 3 ( 2 ) 2

(x y hubungan dua peubah lebih rumit dari garis

lurus. Berdasarkan ini para ilmuwan selalu A(4,3)

B(–5, –1)

P(x,y)

X Y

Gambar 7:Lintasan titik-titik yang berjarak sama dari titik A ke B.

X Y

P(x,y)

O

16 2 ) 3 ( 2 ) 2

(x y

0 3 6 4 2

2 _{y x y}

x .

(b) Jelasx2+y2+ 6x– 2y+ 6 = 0

(x2+2.(3x).1+9)+(y2– 2.y.1+1) = 4 (x+ 3)2+ (y– 1)2= 22.

merupakan persamaan lingkaran berpu sat di titik (– 3,1) dan berukuran jari-jari 2.

Gambar lingkaran itu adalah sebagai berikut:

6. Persamaan Linear

Persamaan yang grafiknya merupa-kan garis lurus sangat penting di dalam kalkulus. Masalah mendasar seluruh objek adalah mencari persamaan garis singgung suatu kurva di suatu titik yang diketahui. Secara umum, garis merupakan gambar hubungan antara dua variabel. Biasanya

melinearkan model-model yang diperoleh dengan cara mencari suatu garis lurus yang merupakan hmpiran terbaik sebagai hu-bungan dua variabel itu yang masih dibe-narkan.

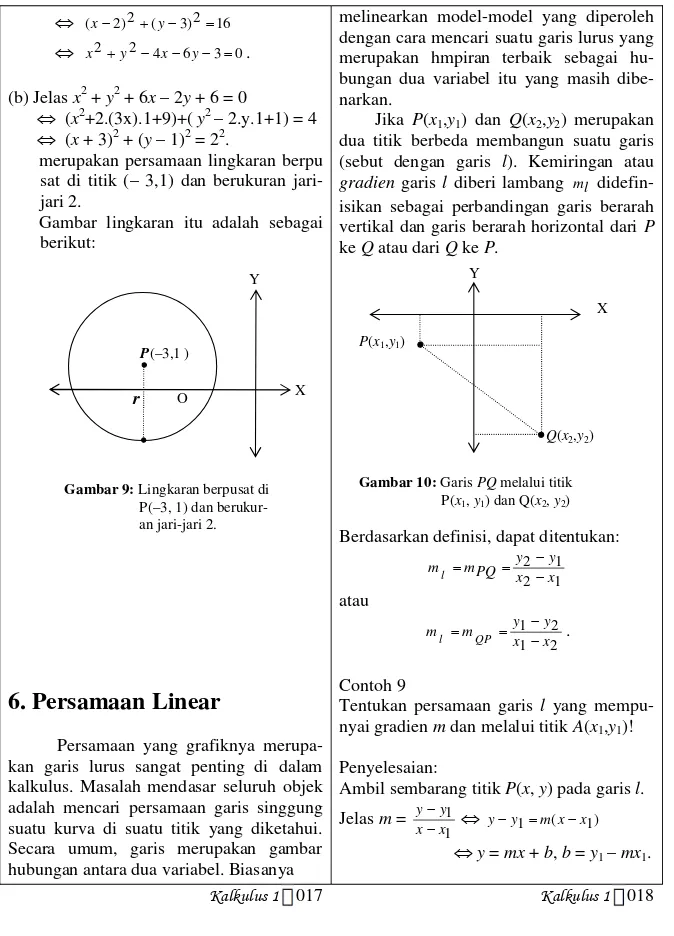
Jika P(x1,y1) dan Q(x2,y2) merupakan dua titik berbeda membangun suatu garis (sebut dengan garis l). Kemiringan atau gradien garis l diberi lambang m_l didefin-isikan sebagai perbandingan garis berarah vertikal dan garis berarah horizontal dari P keQatau dariQkeP.

Berdasarkan definisi, dapat ditentukan:

1 2

1 2

x x

y y PQ m m

l

atau

2 1

2 1

x x

y y m m

QP

l .

Contoh 9

Tentukan persamaan garis l yang mempu-nyai gradienmdan melalui titikA(x1,y1)!

Penyelesaian:

Ambil sembarang titik P(x,y) pada garisl. Jelasm=

1 1 x x

y y

) 1 ( 1 m x x y

y

y=mx+b,b=y1–mx1.

017 018

X Y

P(–3,1 )

O

r

Gambar 9:Lingkaran berpusat di P(–3, 1) dan berukur-an jari-jari 2.

P(x1,y1)

Q(x2,y2)

X Y

Contoh 10

Tentukan persamaan garis lurus yang: (a) melalui titik (3,6) dan mempunyai

kemiringanm= 3.

(b) Melalui titik-titik A(–2,3) dan B(2,– 3).

Penyelesaian:

(a) Tulisf: garis yang diminta.

Ambil sembarang titikP(x,y) padaf. Jelasm=

3 6 x y

3 =

3 6 x y

3x– 9 =y– 6 y= 3x– 3. Jadif:y= 3x– 3.

(b) Tulisg: daris yang diminta. Jelas

2 3 2 2

3 3 g

m .

Ambil sembarang titikP(x,y) padag. Jadig:

2 3 2 3

x y

3 3 2

3_{x y}

2 3x

y .

Contoh 11

Tentukan kemiringan dan koordinat titik potong garisg: 2x+ 4y– 6 = 0.

Penyelesaian: Jelas 2x+ 4y– 6 = 0

2 3 2 1_x

y .

Jadi

2 1 g

m .

Tulis

2 3 2 1 ) (x x

g .

Jelas

2 3 ) 0 (

g .

Jadi grafikgmemotong sumbu Y di (0, ) 2 3 _.

Garis vertikal mempunyi sifat bahwa setiap titik ada garis ini mempunyai koor-dinat x yang sama. Sedangkan garis hori-zontal mempunyai sifat bahwa setiap titik pada garis ini mempunyai koordinat yyang sama. Perhatikan Gambar 12 berikut ini:

Teorema 6

Buktinya sederhana, diserahkan pembaca sebagai latihan.

Contoh 12

Dipunyai garisf:y– 3x– 4 = 0. Tentukan: (a) persamaan garis g yang sejajar

dengan garis g dan melalui titik (3,0).

(b) Persamaan garis h yang tegak lurus garisfdan melalui titik (–3, 2).

Penyelesaian:

(a) Jelasy– 3x– 4 = 0 y= 3x+ 4. Jadimf= 3.

Dipunyai garisg//f. Jadimg =mf= 3.

019 020

X Y

h:y= 1 v:x= 1

Gambar 12:Garishhorizontal dan garisvvertical.

X Y

) 2 3 , 0 (

(3,0)

g Gambar 11:Grafikg: 2x+ 4y– 6 = 0

Dipunyai dua garis berbeda yang memiliki persamaan

f:y=m1x+b1dang:y=m2x+b2.

Dipunyai garisgmelalui titik (3,0). Jadig:y– 0 = 3(x– 3) y= 3x– 9.

(b) Dipunyaih f. Jadimh.mf = –1

mh = –

3 1_.

Dipunyai garishmelalui titik (–3, 2). Jadih:y– 2 = –

3

1_{(x+ 3)}

y= 1

3 x _.

7. Fungsi

Pengertian fungsi merupakan suatu hal yang mendasar dalam kalkulus. Berikut ini disajikan definisi fungsi.

Definisi 7

Selanjutnya apabila (x,y) f, ditulis y=f(x)

atau

f:x y

yang menyatakan y sebagai nilai f di x. Suatu fungsi dari A ke B digambarkan sebagai suatu grafik (Gambar 13), dan sebagai suatu pemetaan (Gambar 14).

Himpunan A disebut daerah asal (domain) fungsifdiberi lambangDf, dan

{y B (x,y) f}

disebut daerah hasil (range) fungsifdan di-beri lambingRf.

Contoh 13

Periksa pengaitan-pengaitan berikut ini merupakan fungsi atau bukan:

(a) f: R R,f(x) =x, (b) g:R R,g(x) =x3, dan

(c) h: [–5,5] [–5,5],x2+y2= 25. Penyelesaian:

(a) Ambil sembarangx R. Jelasx=f(x).

Pilihy=x. Jelasy=f(x).

Jadi x R y R y f(x). Ambil sembaranga,b R,a=b.

Jelasf(a) =a=b=f(b).

Jadi a,b R,a=b,f(a) =f(b). Jadifsuatu fungsi.

021 022

Dipunyai himpunan A dan B. Suatu fungsif dari himpunan Ake B merupa-kan pasang terurutf AxBsehingga: (1) x A y B (x,y) f dan

(2) (x,y) fdan (x,z) f y=z.

A B

f

x f(x)

Gambar 14:Fungsig:A Bsebagai suatu pemetaan.

X Y

(x,y)

x y

A B

(b) Ambil sembarangx R. Jelasx3 R.

Pilihy=x3. Jelasy=f(x).

Jadi x R y R y f(x). Ambil sembaranga, b R,a=b.

Jelasf(a) =a3=b3 =f(b). Jadi a,b R,a=b,f(a) =f(b). Jadifsuatu fungsi.

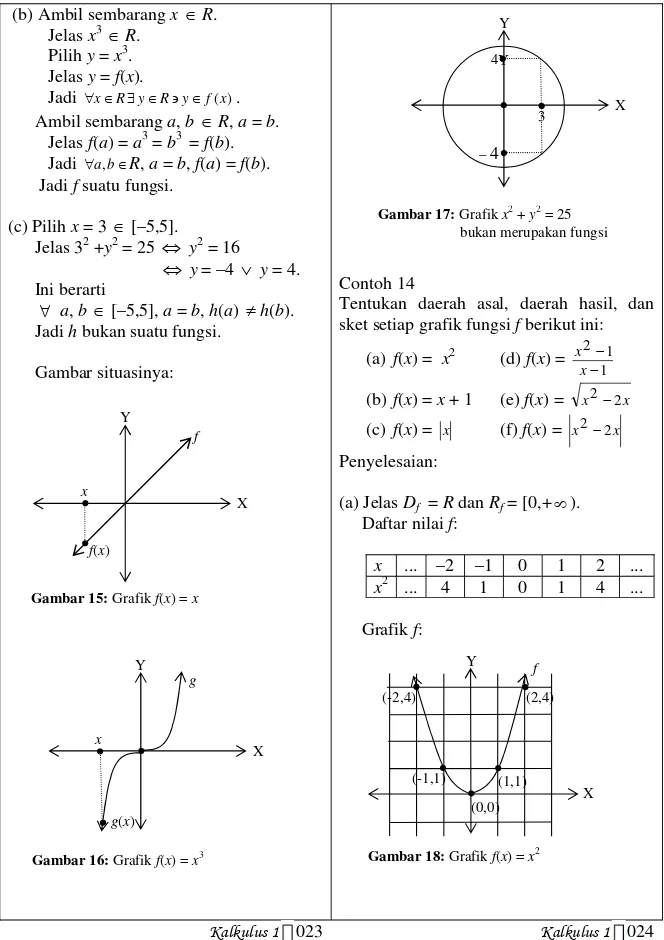
(c) Pilihx= 3 [–5,5].

Jelas 32+y2= 25 y2= 16

y= –4 y= 4. Ini berarti

a,b [–5,5],a=b,h(a) h(b). Jadihbukan suatu fungsi.

Gambar situasinya:

Contoh 14

Tentukan daerah asal, daerah hasil, dan sket setiap grafik fungsifberikut ini:

(a) f(x) = x2 (d)f(x) =

1 1 2 x x

(b) f(x) =x+ 1 (e)f(x) = x2 2x

(c) f(x) = x (f)f(x) = x2 2x

Penyelesaian:

(a) JelasDf =RdanRf= [0,+ ). Daftar nilaif:

x ... –2 –1 0 1 2 ...

x2 ... 4 1 0 1 4 ...

Grafikf:

023 024

X Y

g

x

g(x)

Gambar 16:Grafikf(x) =x3 Gambar 15:Grafikf(x) =x

X Y

f

x

f(x)

X

Y _f

(0,0) (1,1)

(2,4)

(-1,1) (-2,4)

Gambar 18:Grafikf(x) =x2

X Y

3

Gambar 17:Grafikx2+y2= 25 bukan merupakan fungsi

4

–4

(b) Dipunyaif(x) =x+ 1. JelasDf=RdanRf=R. Daftar nilaif:

x ... –1 0 1 ... x2 ... 0 1 2 ... Grafikf:

(c) JelasDf =RdanRf= [0,+ ). Daftar nilaif:

x ... –2 –1 0 1 2 ...

x2 ... 2 1 0 1 2 ...

Grafikf:

(d) Jelasf(x) =

1 1 2 x x

=x+ 1,x 1. JelasDf =R– {1} danRf=R– {2}. Daftar nilaif:

x ... –2 –1 0 1 2 ...

x2 ... –1 0 1 2 3 ...

Grafikf:

(e) Jelasx2– 2x> 0 x(x– 2) > 0 x< 0 x> 2. JadiDf= (– ,0) (2,+ ) dan

Rf= (0,+ ).

Daftar nilaif:

x ... –3 –2 2 3 ...

x2 ... 3 0 0 3 ...

Grafikf:

(f) Jelasf(x) = x2 2x

= .

) 2 , 0 ( , 2 2

) , 2 [ ] 0 , ( , 2 2

x x x

x x x

JelasRf =RdanDf = [0,+ ).

025 026

Daftar nilaif: Grafikf:

X Y

(-3,3) (-2,2)

(-1,1)

(0,0) (1,1)

(2,2) (3,3)

f

Gambar 20:Grafikf(x) = x

X Y

f f

(–2,0) (2,0)

Gambar 22:Gambarf(x) = x2 2x f

X Y

(-1,0) (0,1)

(1,2)

Gambar 19:Grafikf(x) =x+ 1

X Y

(-1,0) (0,1)

(1,2)

Gambar 21:Grafikf(x) = 1

x ... –1 0 1 2 3 ... x2 ... 3 0 1 0 3 ...

Grafikf:

Contoh 15

Jika x R, x didefinisikan sebagai bi-langan bulat terbesar yang kurang dari atau sama denganx.

Dipunyaif:R B,f(x) = x .

Periksa apakah f merupakan fungsi atau bukan.

Penyelesaian:

Ambil sembarangx R.

Pilihy= maks {b B b x}. Jelasy Bdany=f(x).

Jadi x R y B y=f(x).

Ambil sembarangx B. Pilihy=x R.

Jelasf(y) =f(x) = x =x.

Jadi x B y R y=f(x).

Jadifmerupakan suatu fungsi.

Dengan mudah dapat dihitung bahwa: f([–2, –1)) = –2,

f([–1, 0)) = –1, f([0, 1)) = 0, f([1, 2)) = 1,

f([n–1, n)) = n–1.

Berikut ini disajikan beberapa sifat fungsi.

Definisi 9

Contoh 16

Periksa fungsi-fungsi berikut merupakan fungsi injektif atau bukan.

(a)f:R R,f(x) =x3dan (b)g:R R,g(x) =x2– 1.

Penyelesaian:

(a) Ambil sembarangx1, x2 R,x1 x2. Jelas

0 ) 2 1

(x x dan 2) 0

1 2 . 1 2 1

(x x x x .

027 028

Jelasf(x1) –f(x2) (b) Ambil sembarang x [–1,+ ). Dipunyai fungsif:A B.

Fungsi f dikatakan satu-satu (injective) jika untuk setiap dua unsur beda di A mempunyai peta yang beda. Definisi ini dapat disajikan secara formal seba-gai berikut:

x1,x2 A,x1 x2,f(x1) f(x2).

X Y

f f

(0,0) (2,0)

Gambar 23:Gambarf(x) = x2 2x (3,3) (-1,3)

X Y

–1

–2

–3

1` 2` 3`

= 3

2 3

1 x

x

= (x₁ x₂)(x₁2 x₁.x₂ x₁2)

0.

Jadif(x1) –f(x2) 0.

Jadi x1,x2 R,x1 x2,f(x1) f(x2). Jadifsuatu fungsi injektif.

(b) Pilihx1= –1 danx2= 1.

Jelasg(x1) =g(–1) = 0 =g(1) =g(x2). Jadi x1,x2 R,x1 x2,g(x1) =g(x2). Jadigbukan fungsi injektif.

Definisi 10

Contoh 17

Periksa fungsi-fungsi berikut merupakan fungsi surjektif atau bukan.

(a) f:R R,f(x) = 2x– 1 dan (b)g:R [–1,+ ), g(x) =x2– 1. Penyelesaian:

(a) Ambil sembarangx R.

Jelasx= 1

2 1

2 x .

Pilihy=

2 1 x

R.

Jelasf(y) = 1 2

1

2 x =x.

Jadi x R, y R f(y) =x. Jadifmerupakan suatu fungsi surjek-tif.

Pilihy g(y) = x.

Jelasg(y) = x y2– 1 =x y2=x+ 1

1 x

y y x 1

Jelasy R.

Jadi x [–1,+ ), y R,g(y) =x. Jadigmerupakan suatu fungsi surjek-tif.

Fungsi f: I R dikatakan bijektif apabila fungsi f merupakan fungsi injektif dan sekaligus surjektif.

8. Fungsi naik dan Fungsi Turun

Banyak model fenomena alam yang mempunyai solusi sebagai suatu fungsi yang naik atau turun. Sebagai contoh model populasi suatu mahluk hidup, model peluruhan radio aktif, dan sebagainya.

Definisi 11

Definisi 12

029 030

Dipunyai fungsif:A B.

Fungsi f dikatakan pada (surjective) jika Rf =B. Definisi ini dapat disaji-kan secara formal sebagai berikut:

x B, y A f(y) =x.

Dipunyai fungnsif:A B.

Grafik fungsi f dikatakan naik jika fungsi f melestarikan urutan. Definisi ini dapat disaji-kan secara formal sebagai beri-kut:

) ( ) ( , ,

,b A a b f a f b

a .

Dipunyai fungnsi f: A B. Grafik fungsi f dikatakan turun jika fungsi f tak melestarikan urutan. Definisi ini dapat disaji-kan secara formal sebagai beri-kut:

) ( ) ( , ,

,b Aa b f a f b

Contoh 17

Periksa apakah grafik fungsi berikut naik ataukah turun:

(a)f:R R, f(x) = 2x– 1, (b)f: [0,+ ) R,f(x) =x2, dan (c)f:R R, f(x) =x2.

Penyelesaian:

(a) Ambil sembarangx1,x2 R,x1<x2. Jelasx1–x2< 0.

Jelasf(x1) –f(x2) = 2x1– 1 – 2x2+ 1 = 2(x1–x2) Jadif(x1) <f(x2).

Jadi x1,x2 R,x1<x2,f(x1) <f(x2). Jadi grafikfnaik.

(b) Ambil sembarangx1,x2 (– ,0],x1 x2. Jelasx1 0,x2 0, danx1–x2 0. Jadix1+x2 0, danx1–x2 0. Jelasf(x1) –f(x2) = x₁2 x₂2

= (x1+x2)(x1–x2) 0.

Jadi x1,x2 (– ,0],x1 x2,f(x1) f(x2). Jadi grafikfturun pada (– ,0].

(c) Pilihx1= –2 danx2= 1. Jelasx1,x2 Rdanx1<x2. Jelasf(x1) = 4 > 1 =f(x1).

Jadi x₁,x₂ R,x₁ x₂,f(x₁) f(x₂). Jadi grafikftidak naik padaR.

9. Operasi Aljabar Fungsi

Suatu cara untuk membangun suatu fungsi baru adalah dengan menjumlah,

mengurangi, mengalikan, atau membagi fungsi-fungsi yang diketahui. Berikut ini didefinisikan operasi pada fungsi:

Definisi 13

Contoh 18

Dipunyai fungsif:R R,f(x) =xdan g: [1,+ ) [0,+ ),g(x) = x 1.

(a) jika h1 = f + g, tentukan: rumus h1, daerah asal, dan daerah hasilh1.

(b) jikah2=

g f

, tentukan: rumush2, dae-rah asal, dan daedae-rah hasilh2.

Penyelesaian:

(a) Jelash1(x) =f(x) +g(x) =x+ x 1.

Jelas D_h1 [0, ) dan R_h1 [1, ). Grafikh1:

031 032

Contoh 18

Dipunyaifdangadalah fungsi-fung-si dan k suatu konstanta. Fungsi-fungsi f+g, f–g, kg, f.g, dan

g f

didefinisikan sebagai berikut:

(a) (f+g)(x) =f(x) +g(x) (b) (f–g)(x) =f(x) –g(x) (c) kg(x) =k.g(x) (d) (f.g)(x) =f(x).g(x)

(e) , ( ) 0

) (

) ( )

( g x

x g

x f x g f

untuk semuaxdi daerah definisinya.

7

Y _h

(b) Jelasg(x) = x 1 0 x (1,+ ). Jelash2(x) = (x)

g f

=

) (

) (

x g

x f

=

1 x

x

.

Jadi Dh₂ (1, ) dan Rh₂ [2, ).

Grafik h₂:

Dipunyaif:R R, f(x) =

0 , 1

0 ,

x x x

dan

g:R R, g(x) =

1 , 2

1 ,

x x

x x

. Tentukan f + g, daerah asal, dan daerah hasilnya.

Penyelesaian:

Tulisf(x) = 1

1 , 1 0 , 1

0 ,

x x x x

dan

g(x) =

1 ,

1 0

, 0 ,

2

x x

x x

x x

.

Jadi (f+g)(x) =

1 , 1

1 0

, 1

0 , 0

2

x x

x x

x

.

Dari Gambar 27, dapat dilihat bahwa:

g f

D R

dan

g f

R = [0,+ ) (–2,–1).

Grafikf+g:

033 034

1 2 3 4 5

1 2 3 4 5 6 X

X Y

g f

(2,1) (2,2) (1,1)

(1,0)

(5,2) (5,5)

(5, 2 5 )

Gambar 26:Grafikh2(x) =

g f

(x)

Gambar 27:

Gambar (f g)(x) =

1 , 2 1

1 0 , 1

0 , 0

x x

x x

x

Y g

g

f

f

f+g

f+g

f+g

10. Komposisi Fungsi-Fungsi

Kadang-kadang dua fungsi diga-bung tidak menggunakan operasi-operasi aljabar yang telah dikenal, akan tetapi dengan cara fungsi kedua didefinisikan pada daerah hasil fungsi pertama. Fungsi yang dihasilkan dengan cara ini dinama-kan fungsi komposisi.

Sebagai contoh, fungsi h(x) = x 1

dapat dibangun melalui dua fungsi, yaitu: fungsi nilai mutlak

g:R [0,+ ) dengan g(x) = x

dan fungsi linear

g:R Rdenganf(x) =x– 1.

Untuk menghitungh(a), pertama dicari a–1 dan kemudian dihitung nilai mutlaknya, yaitu a 1.

Definisi 14

Pada Gambar 28 terlihat bahwa D_{f g} ada-lah prapeta R_g D_f olehgditulis dengan

) (

1

f D g R g

dan Rf g adalah peta Rg Df oleh fdan

ditulis dengan

) (R_g D_f

f .

Gambar 28:Diagram

fungsi komposisi f g

Contoh 19

Dipunyai fungsi-fungsi f dang yang disaji-kan berturut-turut oleh

f(x) =x– 2 dang(x) =x2– 1.

Tentukan f g dan g f jika ada, selan-jutnya tentukan daerah asal dan daerah hasilnya.

Penyelesaian:

Jelas D_f R, R_f R, D_g R, dan

) , 1 [ g

R .

(a) Jelas R_g D_f [ 1, ) R=[ 1, ) . Jadi f g ada.

Jelas (f g)(x) =f[g(x)] =f(x2– 1) – 2 =x2– 3.

Jelas Df g =g– 1([–1,+ )) =Rdan g

f

R =f([–1,+ )) = [–3,+ ). (b) Jelas Rf D_g =R R=R .

Jadi g f ada.

Jelas (g f)(x) =g[f(x)] =g(x– 2) = (x– 2)2– 1.

035 036

Dipunyai fungsi-fungsi f dan g dengan Rg Df . Fungsi komposisi f g didefinisikan sebagai

(f g)(x) =f[g(x)] x Rg Df.

g f

f g

Df g R_g D_{f Rf g}

Df

Rg

Dg

Jelas D_{g f} =f– 1(R) =Rdan

f g

R =g(R) =R.

Berikut ini disajikan beberapa contoh berbagai fungsi yang dapat dikembalikan sebagi komposisi dua fungsi:

(a) Fungsih(x) = 3 2

) 7 2

(x dibangun dari

3 2

) (x x

f dan g(x) = x2 + 7 dengan rumus ( f g)(x).

(b) Fungsih(x)=4 2 x2 dibangun dari x

x

f( ) 4 dan g(x) = 2 + x2 dengan rumus ( f g)(x).

(c) Fungsih(x) = 4 2 x2 dapat pula di-bangun dari f(x) 4 xdang(x) = 2+x2 dengan rumus (f g)(x).

(d) Fungsi h(x) =

4 3

8 x

dibangun dari

fungsi

x x

f( ) 8 dan g(x) = 3 + x4 de-ngan rumus (f g)(x).

(e) Fungsi h(x) =

4 3

8

x

dapat pula

diba-ngun dari fungsi

x x

f( ) 8 dan g(x) =

4

3 x dengan rumus (f g)(x).

11. Balikan (

Invers

) Fungsi

Banyak fungsi yang sangat berman-faat dibangun dengan menggunakan fung-si yang telah dikenal. Dimulai dengan fungsi yang memetakan titik ke dirinya

sendiri yang disebut dengan fungsi iden-titas.

Definisi 15

Definisi 16

Gambar situasinya:

Perhatian 1: Tampilan f –1 merupakan in-vers fungsifdan f–1

f 1 _.

Perhatian 2: jika g adalah invers f, maka

f R g

D sebab g

didefini-sikan oleh:

g(y) =x y=f(x). Contoh 20

(a) Dipunyai fungsi

f:R R,f(x) = 2x dan

g:R R,g(x) =

2 x

.

037 038

f

f–1

A

B

Rf

Gambar 29:Diagram fungsifdanf–1 Fungsii: A BdenganA Bdisebut fungsi identitas apabila

i(x) =xuntuk setiapx A.

Dipunyai fungsif:A B. Jika terda-pat fungsig:Rf Asehingga

g[f(x)] =x x A maka fungsigdisebut inversfdan dituliskan dengan

Ambil sembarangx R. Jelasg[f(x)] =g(2x) =

2 2x _=x.

Jadig=f–1.

(b) Dipunyai fungsif:R R,f(x) = 2x– 1. Jelasffungsi bijektif.

Jadif–1ada.

Ambil sembarangx R.

Jelasx= 1

2 1 2

2 x = )

2 1 2 ( x

f .

Jadif–1(x) =f–1[f(

2 1 2x _)]

= ( )

2 1 2 )( 1

(f f x

= )

2 1 2 ( x i

=

2 1 2x _.

(c) Fungsi f : R R yang disajikan oleh f(x) = x2 tidak mempunyai invers. Hal ini disebabkan untuk setiap bilangan positif x berkorespondensi dengan 2 bilangan berbeda di Df = R. Sebagai contoh, untukx = 4 diperoleh f(–2) = 4 dan f(2) = 4. Ini berarti tak mungkin mendefinisikang(4) = 2 dan g(4) = –2. Jadi tidak ada fungsigyang memenuhi

g[f(x)] =xuntuk setiapx R.

Teorema 17

Bukti:

Bangun pengaitang:Rf Dfsehingga g(x) =y x Rfdanx=f(y).

Ambil sembaranga,b Rf,a=b. Tulisa=f(x1) danb=f(x2). Dipunyaiffungsi injektif. Jadix1=x2.

Jadi a,b Rf,a=b,g(a) =g(b). Jadigsuatu fungsi.

Ambil sembarangx Df.

Jelasg[f(x)] =g(y) untuk suatuy Rf =x.

Jadi x Df,g[f(x)] =x. Jadig=f–1.

Jelas D_g R_f

f

D 1 .

Contoh 21

Dipunyaif:R R,f(x) = 2x– 4. Jelasffungsi injektif.

Jadif–1ada.

Ambil sembarangx R. Tulis 2x– 4 =y x= 2

2 y

. Jadif–1(x) = 2

2 x _.

Jelas R_f

f

D 1 =R.

Gambar situasinya:

Hubungan grafik fungsi f dan inversnyaf –1dapat ditentukan dengan cara

039 040

Jikaf:A Bmerupakan fungsi injektif, maka

(a) fungsif–1ada, dan

(b) R_f

f

D 1 .

X Y

(4,4)

–4 2

–4 2

f g

sebagai berikut:

apabila (a,b) f maka (b,a) f –1. Ini berarti bahwa setiap titik di f –1 diperoleh dari titik dif dengan pencerminan terhadap garis y = x. Ini berarti juga bahwa grafik f danf–1simetri terhadap garisy=x.

Contoh 22 Dipunyaif:R–{–

2

1 _{} R– {}

2

3_{}, dengan}

1 2

2 3 ) (

x x x

f .

Tentukanf–1(x) apabila ada. Penyelesaian:

Ambil sembaranga,b R– {–

2

1_{},a b.}

Jelasa–b 0, 2a+ 1 0, dan 2b+ 1 0. Jelasf(a) –f(b) =

1 2

2 3 1 2

2 3

b b a

a

=

) 1 2 )( 1 2

( a b a b

0. Jadi a,b R– {–

2

1 _{},a b,f(a) f(b).}

Jadiffungsi injektif. Jadif–1ada.

Pemeriksaan:

(a) Ambil sembarangx R.

Jelasf(–x) = (–x)2– 2 =x2– 2 =f(x). Jadif(–x) =f(x) x R.

Jadifmerupakan fungsi genap.

(b) Ambil sembarangx R. Jelasg(–x) = –x= –g(x). Jadig(–x) = –g(x) x R. Jadigmerupakan fungsi ganjil.

(c) Ambil sembarangx R. Jelash(x) = x 1 =

1 , 1

1 , 1

x x

x x

.

Jelash(–x) =

1 , 1

1 , 1

x x

x x

.

Jelash(–x) h(x) dan h(–x) –h(x) Jadihbukan fungsi genap danhjuga bukan fungsi ganjil.

(d) Ambil sembarang x R. Jelasl(–x) = (–x)3+x

= –(x3–x) = –l(x). Jadil(–x) = –l(x) x R. Jadilmerupakan fungsi ganjil.

Catatan:

12. Membuat Sket Grafik Fungsi

dengan Metode Geseran

Sebelum membahas konsep perge-seran, perlu diperhatikan bagaimana meng gambar grafik fungsi-fungsi sederhana. Sebagai contoh diberikan fungsi-fungsi kuadrat berikut ini:

(a) f:R R, f(x) =x2,

(b) g:R R, g(x) = (x– 1)2, dan (c) h:R R, h(x) = (x– 1)2– 2.

Penyelesaian:

(a) Daftar nilai fungsif:

x ... –2 –1 0 1 2 ... x2 ... 4 1 0 1 4 ...

Grafikf:

041 042

X

Y f

(1,1) (2,4)

(–1,1) (–2,4)

Gambar 31:Grafikf(x) =x2

(1) Grafik fungsi genap simetri terhadap sumbu X.

(b) Daftar nilai fungsig:

x ... –1 0 1 2 3 ... x–1 ... –2 –1 0 1 2 ... (x–1)2 ... 4 1 0 1 4 ...

Grafikg:

(c) Daftar nilai fungsih:

x ... –1 0 1 2 3 ... x–1 ... –2 –1 0 1 2 ... (x–1)2– 2 ... 4 1 0 1 4 ...

Grafikh:

Pada Gambar 31, 32, dan 33 dapat dilihat bahwa grafik g diperoleh dari grafik f dengan menggeser ke kanan sejauh 1 satuan dan grafik h diperoleh dengan menggeser grafik g ke bawah sejauh 2 satuan.

Definisi 18

Contoh 23

Dipunyai grafik fungsi f. Buatlah sket grafik

y= f(x 1) 1 2.

Penyelesaian:

Tulis f₁(x) f(x 1), f₂(x) f(x 1) 1,

1 ) 1 ( ) (

3 x f x

f , dan

2 1 ) 1 ( ) (

3 x f x

f

Grafik f1 diperoleh dengan menggeser grafikfke kiri sejauh 1 satuan.

Grafik f2 diperoleh dengan menggeser grafikf1ke bawah sejauh 1 satuan. Grafik f₃ f₂ .

Sedangkan grafik f4 diperoleh dengan menggeser grafik f3 ke atas sejauh 2 satuan.

Dengan demikian sket grafiknya dapat dilihat pada gambar berikut ini.

043 044

X Y

h

(2, –1) (3,2)

(0, –1) (–1,2)

Gambar 33:Grafikh(x) = (x– 1)2– 2 (1,–2)

X

Y g

(2,1) (3,4)

(0,1) (–1,4)

Gambar 32:Grafikg(x) = (x– 1)2 (1,0)

Dipunyaifsuatu fungsi danksuatu bilangan positif.

(a) Grafik fungsi y=f(x–k) diperoleh dengan menggeser grafik fke kanan sejauhksatuan.

(b) Grafiky=f(x+k) diperoleh dengan menggeser grafikfke kiri sejauhk satuan.

(c) Grafiky=f(x) +kdiperoleh dengan menggeser grafikfke atas sejauh k satuan.

13. Fungsi Berkala

Fungsi berkala (periodik) banyak ditemukan dalam matematika terapan, seperti: model matematika ayunan mate-matika, pegas, aliran panas, dan lain sebagainya.

Pembaca dianggap telah mengenal satuan ukuran sudut dalam derajat dan telah mengenal pula bahwa ukuran sudut suatu lingkaran adalah 300o. Sistem derajat kurang cocok untuk keperluan-keperluan dalam kalkulus. Dengan demikian perlu didefinisikan ukuran sudut yang lain, yaitu ukuran sudut dalam radian.

Perhatikan suatulingkaran pada bidang koordinat XY yang berpusat di titik pangkal. Dibayangkan sebuah titik yang bergerak sepanjang lingkaran itu yang berlawanan arah dengan gerakan jarum jam dimulai dari titik (1,0).

Ukuran radian untuk sudut sama dengan ukuran panjang busur yang ditem-puh titik sepanjang gerakannya. Jelas ukur-an keliling lingkarukur-an itu adalah 2 . Jadi 2

radian = 360o.

Contoh 24

(a) Jelas 1 radian =

2 180o

57,296o 57o17`45``. (b) Jelas 1o=

180 = 0,017453

dengan 3,14159.

045 046

X

X

X

X

X Y

Y Y Y Y

f4

f3

f2

f1

f

a

a a a a a–1

a–1

a–1

a–1

a–1

Gambar 34:Grafikf4= f(x 1) 1 2

X Y

P

O (1,0)

(c) Berikut ini hubungan sudut-sudut d (dalam derajat) dan r(dalam radian).

d

0o 30o 45o 60o 90o 120o

r 0

6 4 3 2 3

2

d

135o 180o 210o 270o 315o

r 4

3

6 7

2 3

4 7

Setiap bilangan real t berpadanan dengan sebuah titik P pada lingkaran satuan dengan ketentuan sebagai berikut:

(a) Jikat> 0, dipadankan dengan gerak titik sejauhtberlawanan arah jarum jam sepanjang lingkaran.

(b) Jikat< 0, dipadankan dengan gerak titik sejauh t searah jarum jam sepanjang lingkaran satuan.

14. Fungsi Trigonometri

Titik P(x,y) adalah suatu titik pada lingkaran satuan yang berpadanan dengan sudut . Berikut ini disajikan sinus dan cosinus sudut .

Gambar situasinya adalah sebagai berikut:

Definisi 19

Contoh 25

Tentukan nilai sin dan cos apabila: =

6, = 4

3 _{, =} 3

4 _{, dan =} 2 3 _.

Penyelesaian:

(a) Perhatikan Gambar 36. Jelas OP = 1, PQ =

2

1 _{, dan OQ =}

2 3 _.

Jadi )

2 1 , 2

3 (

P .

Jadi sin

6 = 2

1 _{dan cos}

6 = 2 3 _.

(b) Perhatikan Gambar 37:

Jelas OP = 1, PQ =

2

2 _{, dan OQ =} 2

2 _.

Jelasx= –

2

2 _dany= 2

2 _.

Jadi )

2 2 , 2

2 (

P .

Jadi sin

2 2 4

3 _{dan cos}

2 2 4

3 _.

(c) Perhatikan Gambar 37:

Jelas OP = 1, PQ =

2

3 _{, dan OQ =}

2 1 _.

Jelasx= –

2

1 _{dany= –}

2 3 _.

Jadi sin

2 3 3

4 _{dan cos}

2 1 3

4 _.

047 048

Gambar 36:Titik P berpadanan Dengan sudut P(x,y)

X Y

(1,0)

(a) Sinus sudut , ditulis dengan sin , dan

sin =y.

(b) Cosinus sudut , ditulis dengan cos , dan

cos =x.

(d) Perhatikan Gambar 39. Jelas P(0, –1).

Jadi sin 1 2

3 _{dan cos}

0 2

3 _.

Berikut ini disajikan fungsi-fungsi trigonometri lainnya.

Definisi 19

Contoh 26

Buatlah sket grafik fungsi-fungsi berikut:

(a)f: [–2 ,2 ] R,f(x) = sinx, (b)g: [–2 ,2 ] R,g(x) = cosx, (c)h: [–2 ,2 ]–{

2 3 , 2 , 2 , 2

3 _{} R,}

h(x) = tanx,

(d)j: (–2 ,2 )–{– , } R, j(x) = cotx,

(e)k: [–2 ,2 ]–{

2 3 , 2 , 2 , 2

3 _{} R,}

k(x) = secx, dan

(f)j: (–2 ,2 )–{– , } R, j(x) = cscx.

Penyelesaian: (a) Grafikf:

Dapat dilihat bahwa:

Grafikfnaik pada selang-selang: [-2

,-2 3 _{], [}

2 ,

2 , dan [ 2 ,2 3 _].

Grafikfturun pada selang-selang:

049 050

Gambar 38: = 6

) 2

3 , 2 1 ( P

X Y

(0,–1) O Q

Gambar 39: = 2 3

X Y

P(0,–1)

O Gambar 40:Grafikf(x) = sinx

X Y

1

–1

2

–2

f

O X

Y

(0,–1) O

) 2 1 , 2

3 ( P

Q

Gambar 37: = 6

(a) tan =

cos

sin _{(c) sec =} cos

1

(b) cot =

sin

cos _{(d) csc =} cos

[

2 , 2

3 _{] dan [} 2 3 , 2 ].

Nilai ) 1

2 ( ) 2 3

( f

f merupakan

nilai maksimum.

Nilai ) 1

2 3 ( ) 2

( f

f merupakan

nilai minimum.

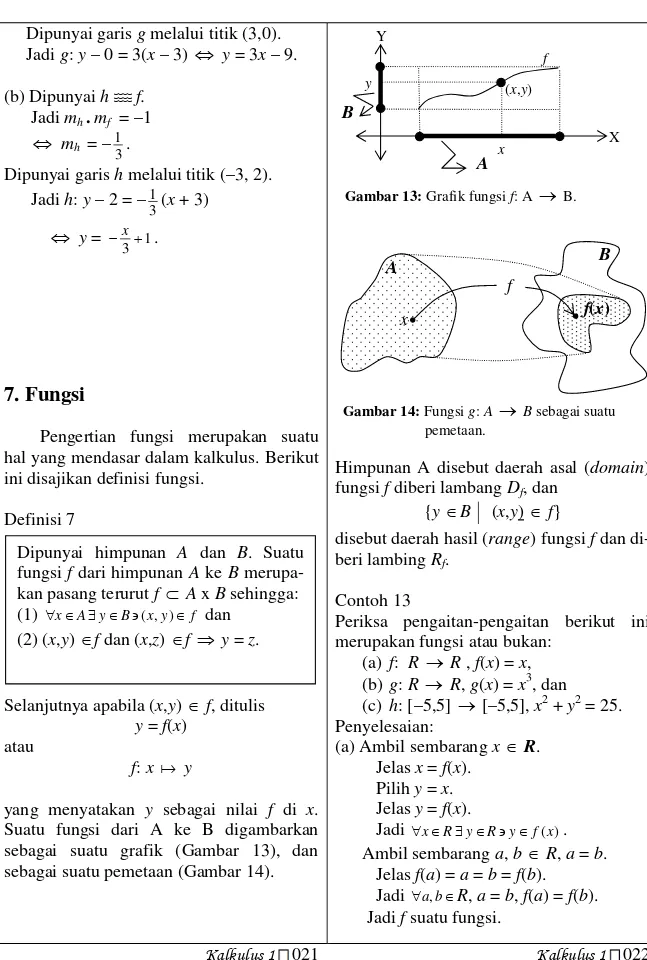
(b) Grafikg:

Dapat dilihat bahwa:

Grafikgnaik pada selang-selang: [- ,0] dan [ ,2 ]. Grafikgturun pada selang-selang:

[-2 ,- ] dan [0, ]. Nilai g( 2 ) g(0) g(2 ) 1

merupakan nilai maksimum.

Nilai f( ) f( ) 1 merupakan nilai minimum.

(c) Grafikh:

Dapat dilihat bahwa: Grafikhnaik padaDh. Asimptot tegak:

2 3

x ,

2 x ,x=

2 , dan 2 3

x .

Memotong sumbu X di:

(–2 ,0), ( ,0), (0,0), ( ,0), dan (2 ,0).

(d) Grafikj:

Dapat dilihat bahwa: Grafikjturun padaDj. Asimptot tegak:

2

x , x ,x= , dan x 2 . Memotong sumbu X di:

) 0 , 2 3

( , ,0) 2

( , ,0) 2

( , dan ,0) 2 3

( .

(f) Grafikk:

051 052

Dapat dilihat bahwa: Asimptot tegak:

Y

Gambar 41:Grafikf(x) = cosx

X 1

–1

2

–2

g

O

X Y

1

–1

2

–2

h

Gambar 42:Grafikh(x) = tanx O

Gambar 44:Grafikk(x) = secx

X Y

1

–1 2

–2

k

O

Gambar 43:Grafikj(x) = cotx

2 2

Grafikknaik pada:

) 2 3 , 2

( , , )

2 3

( , , dan

) , 2

( .

Grafikkturun pada:

) 2 ,

( , ,0) 2

( , )

2 3 ,

( , dan

) 2 , 2 3

( .

Asimptot tegak:

2 3

x ,

2 x ,x=

2 , dan 2 3 x . Grafikktak memotong sumbu X. Nilai k(-2 ) = k(0) = k(2 ) = 1 merupa-kan nilai minimum relatif. Nilai k(- ) = k( ) = –1 merupakan nilai maksimum relatif.

(f) Grafikl:

Dari Gambar 45 dapat dilihat bahwa:

Grafiklnaik pada:

) , 2 3

( , ( , ₂), , ) 2

( , dan

) 2 3 ,

( .

Grafikkturun pada:

) 2 3 , 2

( , ,0)

2

( , )

2 , 0

( , dan

) 2 , 2 3

( .

2

x , x ,x= 0, x , dan x 2 .

Grafikltak memotong sumbu X. Nilai l(

2 ) = l( 2

3 _{)= –1 merupakan nilai}

maksimum relatif. Nilail(

2 3 _{) = l(}

2 ) = 1 merupakan nilai

minimum relatif.

Contoh 27

Gambarlah grafik fungsi-fungsi berikut: (a)f: [–2 ,2 ] R,f(x) = sin 2x, (b)g: [–2 ,2 ] R,g(x) = 2sinx, dan (c)h: [–2 ,2 ] R,h(x) = sin (x–

6).

Penmyelesaian:

(a) Daftar nilai fungsif:

x 2x sin 2x

2 4 0

4 7

2

7 ₁

4 6

2

6 ₀

4 5

2

5 _–1

2 0

–3₄ 2

3 1

2 0

4 – 2

–1

0 0 0

4 2 1

2 0

4 3

2

3 _–1

2 0

Grafikfdiperlihatkan pada Gambar 46.

053 054

) 2 , 0 (

Gambar 45:Grafikl(x) = cscx Y

X 1

–1 2

–2

l

(b) Daftar nilaig:

x sinx 2 sinx

2 0 0

2

3 1 2

0 0

2

–1 –2

0 0 0

2

1 2

0 0

2

3 –1 –2

Grafikgdiperlihatkan pada Gambar 47.

(c) Daftar nilaih:

x

6 x

6 sin x

6

13 –2 0

6 10

2

3 1

6

7 – 0

6 4

2

–1

6

0 0

6 2

2

1

6

5 0

6 8

2

3 –1

6

11 2 0

Grafikgdiperlihatkan pada Gambar 48.

Berikut ini disajikan beberapa teore-ma yang sering digunakan.

Teorema 20

Bukti (1), (2), dan (3):

Perhatikan Gambar 49:

(1) Ambil sembarang titikP(x,y) pada ling-karan satuan.

TitikQadalah projeksiPpada sumbu X.

Jelas OQ =x = –x, PQ = y = –y, dan OP= 1.

055 056

Grafikf:

(1) sin2 + sin2 = 1. (2) Jika cos 0, maka

1 + tan2 = sec2 . (3) Jika sin 0, maka

1 + cot2 = csc2 . (4) sin (– ) = –sin dan

cos (– ) = cos . (5) sin (

2 ) = cos dan

cos (

2 ) = sin .

(6) sin (

2 ) = cos dan

cos (

2 ) = –sin .

(7) sin ( ) = sin dan cos ( ) = –cos . (8) sin ( ) = –sin dan

cos ( ) = –cos . (9) sin (

2

3 _{) = –cos dan}

cos (

2

3 _{) = –sin .}

(10) sin (

2

3 _{) = –cos dan}

cos (

2

3 _{) = sin .}

(11) sin (2 ) = –sin dan cos (2 ) = cos . (12) sin (2 ) = sin dan

Grafikg:

Grafikh:

057

Gambar 47:Grafikg(x) = 2 sinx Y

2

–2

2

–2

g

O X

Gambar 48:Grafikh(x) = sin (x– 6) Y

1

–1

2 –2

h

O X

Gambar 46:Grafikf(x) = sin 2x

X Y

O 1

–1 2

–2

f