BAB 2
TINJAUAN PUSTAKA
2.1 Persamaan Diferensial
Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen , suatu variabel dependen , dan satu atau lebih turunan dari terhadap (K.A. Stroud. 2003).
Secara umum persamaan diferensial linear orde koefisien konstan dituliskan sebagai:
2.1.2 Persamaan Diferensial Orde Satu
Bentuk standar dari persamaan diferensial orde satu dalam fungsi adalah
Persamaan diferensial orde satu diklasifikasikan berdasarkan cara penyelesaiannya menjadi tiga macam:
Persamaan yang dihasilkan dalam variable dan dapat diselesaikan dengan metode pemisahan variabel dan mengintegrasi pada kedua sisi persamaan yang terpisah,
Yang bergantung pada dan independen terhadap . sehingga dengan mengalikan kedua sisi persamaan dengan faktor integrasi diperoleh
Yang menghasikan persamaan eksak sehingga dapat diselesaikan dengan metode pemisahan variabel. Prosedur selanjutnya untuk persamaan dapat ditulis
Persamaan ini dapat diselesaikan dengan melakukan integrasi pada kedua sisi, dan kemudian menyelesaikannya untuk memperoleh persamaan untuk .
Contoh
solusi
∫ ∫
{ }
∫
2.1.3 Persamaan Diferensial Orde Dua
persamaan diferensial orde dua dapat ditulis dalam bentuk
Yang diperoleh dengan menuliskan
Persamaan kuadrat disebut juga persamaan karakteristik. Berdasarkan akar – akar dari persamaan kuadrat, penyelesaiannya dibedakan atas tiga tipe yaitu:
1. Akar – akar Real yang Tidak Sama
Apabila akar – akar dari persamaan kuadrat diperoleh dalam bentuk real dan berbeda dimana:
Maka solusinya diperoleh dalam bentuk
(2.3) Dimana dan adalah konstanta sembarang dan dan adalah akar – akar persamaan kuadrat.
2. Akar – akar Real yang Sama
Apabila akar – akar dari persamaan kuadrat diperoleh dalam bentuk real dan sama dimana:
Maka Solusinya diperoleh dalam bentuk
3. Akar – akar Kompleks
Apabila akar – akar dari persamaan kuadrat diperoleh dalam bentuk kompleks dimana:
Maka Solusinya diperoleh dalam bentuk
2.2 Rangkaian Listrik
Rangkaian listrik adalah suatu kumpulan elemen atau komponen listrik yang saling dihubungkan dengan cara – cara tertentu dan paling sedikit mempunyai satu lintasan tertutup. Adapun komponen listrik terdiri dari tiga macam yaitu:
1. Resistor (R) yang berfungsi sebagai penghambat arus dalam rangkaian. 2. Induktor (L) dapat menyimpan energi dalam bentuk medan magnet. 3. Kapasitor (C) menyimpan energi dalam bentuk medan listrik.
2.2.1 Rangkaian Transien
Dalam analisis transien terdapat tiga macam komponen listrik beserta sifatnya yang akan menimbulkan karakteristik baru dalam rangkaian. Resistor yang bersifat membuang energi dalam bentuk panas, induktor yang bersifat menyimpan arus bolak-balik atau alternating current (ac), dan kapasitor yang bersifat menyimpan tegangan searah atau direct current (dc), akan menimbulkan adanya sifat sementara (transien) dalam rangkaian. Dalam kondisi sementara ini, sebelum diterapkan sumber-sumber bebas dari luar, tanggapan rangkaian disebut dengan tanggapan sementara. Setelah lenyapnya tanggapan sementara, rangkaian dikatakan dalam keadaan mantap (steady state). Tanggapan yang diakibatkan oleh sumber-sumber bebas dari luar dinamakan dengan tanggapan paksa. Kombinasi dari tanggapan transien dengan tanggapan paksa merupakan tanggapan lengkap rangkaian.
2.2.2 Hukum – Hukum Rangkaian listrik
1. Hukum Arus Kirchhoff (HAK)
Gambar 2.1 Simpul Arus Sederhana
Berdasarkan hukum arus Kirchhoff pada rangkaian diperoleh persamaan =0
Atau
2. Hukum Tegangan Kirchhoff (HTK)
Hukum tegangan Kirchhoff menyatakan bahwa penjumlahan aljabar dari tegangan disekeliling suatu lintasan tertutup sama dengan nol (William H, 2005).
3. Hukum Ohm
Hukum Ohm menyatakan bahwa tegangan V yang melewati suatu penghantar berbanding lurus degan arus I dari elemen rangkaian yang ditulis sebagai
2.2.3 Elemen Resistor, Induktor, dan Kapasitor dalam Hubungan Seri dan Paralel
1. Resistor dalam Hubungan Seri dan Parallel
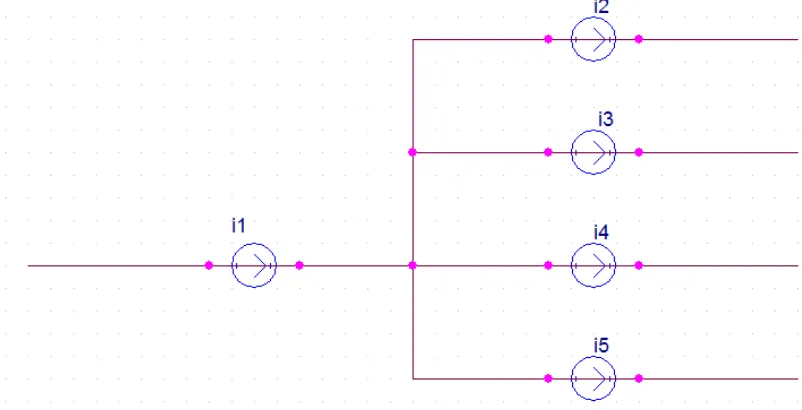
Gambar 2. 2 Kombinasi Rangkaian N Buah Resitor
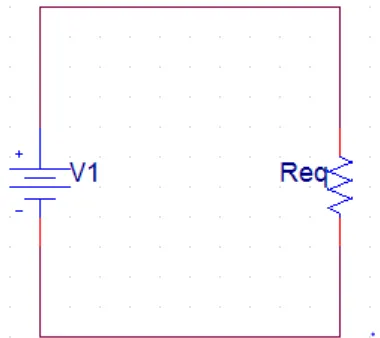
Gambar 2.3 Rangkaian Ekivalen Resistor
Dalam praktiknya kita bisa saja menggantikan suatu kombinasi resistor yang terlalu rumit dengan sebuah resistor ekivalen. Kombinasi dari N buah resistor yang terhubung seri dapat disederhanakan dengan mengantikan N buah resistor dengan sebuah resistor ekivalen (Req). Resistansi ekivalen untuk N buah resistor yang terhubung seri adalah:
Proses penyederhanaan yang serupa juga dapat diaplikasikan untuk rangkaian paralel. Sebuah rangkaian yang mengandung N buah resistor dalam hubungan paralel adalah.
Yang dapat ditulis sebagai
Untuk kasus dimana hanya terdapat dua buah resistor yang terhubung paralel. Persamaannya dapat di rumuskan sebagai:
2. Induktor dalam Hubungan Seri dan Paralel
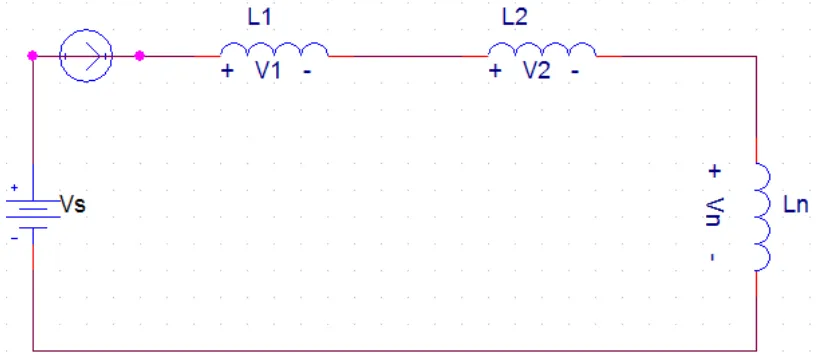
Kombinasi dari N buah induktor yang terhubung seri pada gambar dapat diganti denga sebuah rangkaian induktor ekivalen, dengan induktansi Leq untuk menggantikan kombinasi seri tersebut. Dengan menerapakan HTK (hukum tegangan Kirchhoof atau Kirchoof voltage law) pada rangkaian aslinya.
Gambar 4.5 Rangkaian Ekivalen N Buah Induktor
∑
∑
∑
untuk rangkaian ekivalen, KVL (kirchooff voltage law) menghasilkan
Untuk kasus dua induktor yang terhubung paralel
(2.8)
3. Kapasitor dalam Hubungan Seri dan Paralel
Untuk rangkaian N buah kapasitor yang terhubung paralel yaitu
(2.10)
2.2.4 Tanggapan Rangkaian RLC Seri
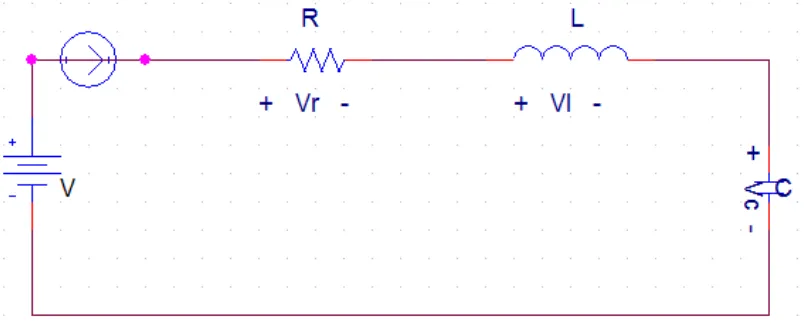
Pada rangkaian listrik, terdapat 3 respon yang dikenal, yaitu respon alami yang kurang teredam (underdamped), teredam kritis (crititically damped), dan sangat teredam (overdamped), karena yang akan dibicarakan adalah arus, maka, respon yang dimaksud adalah respon arus. Secara matematis dalam ilmu rangkaian listrik dapat dijelaskan 3 respon ini. Suatu rangkaian listrik sederhana yang terdiri dari komponen aktif R, juga komponen pasif L dan C dirangkai secara seri pada gambar dengan menerapkan hukum tegangan Kirchhoff pada gambar maka diperoleh persamaan arus, sebagai:
Gambar 2.6 Rangkaian RCL Seri
∫
Persamaan terakhir yang diperoleh dikenal sebagai persamaan karakteristik atau persamaan pelengkap (auxiliary). Karena persamaan ini adalah sebuah persamaan kuadrat, maka persamaan tersebut memiliki dua buah pemecahan yang diidentifikasikan sebagai dan
√( ) √
Dengan sebagai parameter frekuensi resonansi
√
bentuk umum tanggapan teredam berlebih
∫
Eksis. Jika limit ini tidak eksis, integral tak wajar tersebut divergen dan tidak memiliki transformasi laplace.
2.4.1 Transformasi Laplace Dari Turunan
1. Turunan Pertama
{ } ∫
Bukti:
{ } ∫
Dengan menggunakan integral parsial diperoleh
{ } ∫
∫
[ ] ∫
[ ]
∫
( )
2. Turunan Kedua
{ } ∫
Bukti:
Dengan menggunakan integral parsial dan hasil dari turunan pertama diperoleh { } ∫
Sifat – sifat transformasi Laplace invers adalah sebagai berikut
1. Transformasi invers dari suatu jumlah atau selisih dari pernyataan adalah jumlah atau selisih dari masing – masing transformasi invers itu sendiri. yang ditulis sebagai:
{ } { } { }
2. Transformasi invers dari suatu pernyataan yang dikalikan dengan suatu konstanta adalah konstanta tersebut dikalikan dengan transformasi invers dari pernyataan tersebut, dengan kata lain:
2.4.3 Transformasi Laplace dalam Ekpansi Pecahan Parsial
Di dalam penggunaannya, transformasi Laplace sering kali melibatkan bentuk
dengan banyak fraksi, di mana P(s) dan Q(s) merupakan suku polinomial. Solusinya ialah dengan cara mengetahui bagaimana fraksi – fraksi yang terlibat/dihasilkan diubah dalam bentuk fraksi pecahan (parcial fraction). Jika
dengan penyebut
Maka, terdapat tiga penyelesaiannya.
1. Akar – akar Real yang Tidak Sama
Untuk setiap faktor dari P(s) yang linear dalam bentuk
dan
diperoleh bentuk pecahan parsialnya sebagai
(2.25)
2. Akar – akar Real yang Sama
Untuk setiap faktor dari P(s) yang linear dalam bentuk
diperoleh bentuk pecahan parsialnya sebagai
Dengan , , , dan adalah konstanta yang belum diketahui nilainya.
3. Akar – akar Kompleks
Untuk setiap faktor dari P(s) dalam bentuk
Maka, pecahan parsialnya dapat ditulis dalam bentuk
2.5 Masalah Nilai Awal (Initial Value Problem)
Masalah nilai awal untuk persamaan diferensial order
( ) yaitu menentukan solusi persamaan diferensial pada interval I yang memenuhi syarat awal di subset dari real