2.1 Perkiraan Variansi Tipe SYG
Perkiraan ˆY2 tidak bias secara bersyarat untuk perkiraan tahap ˆY1 = Ps1y˙i , sebagai sampel tahap pertama s1, dimana ˙yi = π1yi
i = d1iyi. Sebagai contoh
E( ˆY2|s1) = ˆY1. Karena itu, adalah tidak bias secara tidak bersyarat untuk total
Y =P
Uyi. Variansi ˆY2 diberikan sebagai berikut:
V
ˆ
Y2
=E
j
V
ˆ
Y2|s1
k +V
j
E
ˆ
Y2|s1
k
=EjV Yˆ2|s1k+V Yˆ1
(2.1)
Perkiraan variansi bersyarat V Yˆ2|s1 pada (2.1) dengan menggunakan perkiraan variansi SYG, di tentukan ukuran sampel tahap kedua adalah fix untuk
s1 (Rao, 1979). Perkiraan variansi SYG adalah sebagai berikut:
vYˆ2|s1
=X X i<j∈s2
π2i|siπ2j|s1
π2ij|s1
˙
yi
π2i|s1
− y˙j
π2j|s1 2
(2.2)
Adalah tidak bias secara bersyarat untuk V Yˆ2|s1 dan karena itu tidak
bias secara tidak bersyarat untuk EhV Yˆ2|s1
i
Langkah kedua dalam (2.1) diperoleh :
V Yˆ1
=X X i<j∈U
(π1iπ1j−π1ij) ( ˙yi−y˙j)2 (2.3)
Dengan ukuran sampel tahap pertama adalah fix jika ukuran yi diketahui untuk semuai∈s1, kemudian perkiraan variansi SYG dariV
ˆ
Y1
adalah sebagai berikut:
vYˆ1=X X i<j∈s1
π1iπ1j−π1ij
π1ij
( ˙yi−y˙j)2 (2.4)
Tetapi y1 hanya diketahui untuk i ∈ s2 karena perkiraan (2.4) merupakan sampel tahap kedua s2 untuk memperoleh:
v2
ˆ
Y1
=X X i<j∈s2
π1iπ1j−π1ij
π1ijπ2ij|s1
( ˙yi−y˙j)2 (2.5)
Perkiraan variansi (2.5) adalah tidak bias untuk V Yˆ1. Oleh karena itu
dari (2.1) perkiraan bias pola SYG dari V Yˆ1
ditunjukkan oleh:
vSY G
ˆ
Y2=vYˆ2|s1+v2Yˆ1 (2.6)
dimanavYˆ2|s1
dan v2
ˆ
Y1
ditunjukkan oleh (2.2) dan (2.5) secara berurutan.
Untuk menggambarkan analogi tahap tunggal SYG, perkiraan pola SYG adalah V Yˆ2, tetapi rumus untuk V Yˆ2|s1terlihat tidak tepat karena
meng-gunakan ( ˙yi−y˙j)2 berdasarkan bentuk yang tepat
˙
y1 π2i|s1
− y˙j
π2j|s1 2
diberikan di persamaan (2.2).
Type-type dari perkiraan variansi HT, vHT
ˆ
Y2
adalah valid untuk kedua tahap variansi dan tidak fix pada pembuatan pola sampel yang tidak sejenis de-ngan type perkiraan variansi SYG (2.6). Bagaimanapun, perkiraan variansi SYG memberikan hasil yang valid untuk banyak pola dua tahap, dan analogi untuk ka-sus tahap umum dapat lebih stabil untuk perkiraan variansi HT dan memberikan hasil tidak negatif untuk beberapa pola yang dikenal dengan bentuk probability proportional to size (PPS). Rao (1973) memberikan bukti nyata bahwa perkiraan variansi SYG adalah lebih bagus dari perkiraan variansi HT untuk sampling tahap umum.
2.2 Pengaturan Umum
Di bagian ini, penulis mengevaluasi estimator variansi SYG (2.6) untuk sampling dua tahap untuk proses stratifikasi. Di tahap pertama, sebuah sampel yang be-sar s1 dengan ukuran n1 di buat berdasarkan desain yang ditentukan termasuk perihal batasan peluang π1i dan peluang yang berhubungan π1ij. Menggunakan informasi yang terkumpul untuk unit i ∈ s1, sampel tahap pertama s1
di strata g,P
gm1g =n1
. Di tahap kedua, sebuah sampel peluang s2g dengan ukuran m2g dibentuk dari s1g, bebas terhadap zg, dan sifat dari keuntungan, y,
telah tercatat. Angka dari strata tahap kedua G(s1) dan ukuran sampel m1g dan m2g tergantung pada s1, meskipun G(s1) mungkin dapat didefinisikan
ter-lebih dahulu, sebagai contoh, G(s1)∞G. Sebagai kesederhanaan notasi, penulis menyederhanakan persamaan yang tergantung pada s1.
Yang penting diperhatikan adalahπ2ij|s1 =π2i|s1π2j|s1 jikai∈s1g danj ∈s1g dan j ∈s1l(g 6=l), v
ˆ
Y2|s1
dapat menjadi
V Yˆ2|s1
=
G X
g=1
X
i<j∈s2g
X
△2ij|s1g
˙
yi
π2i|s1g
− y˙j
π2j|s1g
2
(2.7)
dimana
△2ij|s1g =
π2i|s1gπ2j|s1g −π2ij|s1g
π2ij|s1g
(2.8)
Persamaan (2.7) dapat digunakan untuk sampling tahap kedua tanpa strata dengan peluang yang bersifat bersyaratπ2i|s1g danπ2ij|s1g memenuhiPs1π2i|s1g diperlukan untuk menyelesaikans1yang diberikan. Di kasus khusus dari sampling random yang sederhana tanpa strata tahap kedua, diperoleh bahwa π2i|s1g =
m2g
m1g
dan π2ij|s1g =
m2g(m1g−1)
⌊m1g(m1g−1)⌋ dan persamaan (3.1) disederhanakan menjadi
vYˆ2|s1
=
G X
g=1 m21g
1−f2g
m2g
1
m2g−1
X
i<j∈s2g
X
( ˙yi−y˙j)2 (2.9)
dimana f2g = m2m1g
g
Sekarang menggunakan identitas Langrange
m X
i<j=1
X
(zi−zj)2 =m m X
i
= 1 (zi−z¯)2 (2.10)
Persamaan (2.3) disederhanakan menjadi
vYˆ2|s1= G X
g=1
1−f2g
m2g
m21g
1
m2g−1
ˆ
S22gy˙ (2.11)
dimana ˆS22gy˙ adalah rata rata kuadrat dari sampel yang ada, dari pembobotan tahap pertama ˙yi = πyi
HT (1.2), menggunakan sampling acak yang sederhana tanpa strata tahap kedua, menghasilkan nilai yang sejalan dengan persamaan (2.5), formula dari S¨arndal et.al,. Komponen v2
ˆ
Y1
di estimator variansi SYG (2.6) berdasarkan sampling random yang sederhana tanpa strata tahap kedua, menyederhanakan persamaan tersebut menjadi
v2
ˆ
Y1
=
G X
g=1
m1g(m1g−1)
m2g(m2g−1) X
i<j∈s2g
X
△1ij( ˙yi−y˙j)2
+ G X
g<l=1
Xm1gm1l
m2gm2l X
i∈s2g
X
j∈s2l
△1ij( ˙yi−y˙j)2
=v2(1)Yˆ1
+v2(2)Yˆ1
(2.12)
dimana
△1ij =
π1iπ1j−π1ij
π1ij
(2.13)
Untuk penyederhanaan lebih lanjut yang mungkin untuk menggeneralisasi-kan tahap pertama dengan peluang π1i dan p1ij.
Contoh: Jika sampel tahap pertama s1 dengan ukuran n1 dipilih dengan
sam-pling acak sederhana dari sebuah populasiU denganN, selanjutnyaπ1i = n1N, π1ij = n1(n1−1)
[N(N−1)] dan △1ij = (1−f1)
(n1−1). Estimator kedua tahap ˆY2 disederhanakan menjadi
NP
gW1gy¯2g dimana ¯y2g =m
−1 2
P
s2gyi . Menggunakan identitas
Langrange dan nilaiπ1i dan π1ij, di atas, komponen pertama di persamaan (2.6) disederhanakan menjadi
v2(1)Yˆ1
= N
2(1−f 1) n1
G X
g=1 w1g
(m1g −1)
n1−1 Sˆ
2
2gy (2.14)
Komponen yang kedua dari persamaan (2.6) disederhanakan menjadi
S¨arndal et.al, (1992) menyederhanakan komponen pertama dari estimator variansi HT(1.2) untuk kasus spesial dari sampling acak sederhana di tahap perta-ma (tanpa memberikan detailnya) untuk menghasilkan (2.16). Formula ini sejalan dengan persamaan v2
ˆ
Y1
yang dihasilkan oleh persamaan (2.15).
2.3 Penarikan Sampel Dua-Tahap
Subpenarikan sampel dapat diterapkan secara luas melebihi cakupan survei sampel. Kapan saja suatu proses yang mencakup pengujian secara kimia, fisika atau biologi dapat dilaksanakan dengan jumlah material yang kecil, yang lebih disukai dengan mengambilnya sebagai sebuah subsampel dari suatu jumlah yang besar yang mana jumlah itu sendiri adalah sebuah sampel.
Pertimbangan sederhana, yang setiap unit terdiri dariM subunit yang sama,
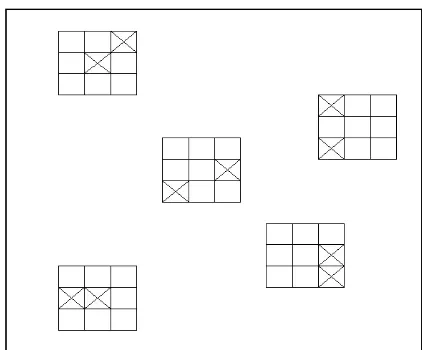
m dipilih bila setiap unit subsampel. Sebuah penyajian secara skema dari
pe-narikan sampel dua tahap, dimana M = 9 dan m = 2, ditunjukkan dalam gambar (2.1) berikut.
Gambar 2.1 Gambar secara skema dari penarikan sampel (N=81, n=5, M=9 dan m=2)
Keuntungan utama dari penarikan sampel dua tahap adalah bahwa cara ini lebih fleksibel dari penarikan sampel satu tahap. Ini mengurangi penarikan sampel satu tahap bila m = M, kecuali ini adalah pilihan terbaik dari m, kita mempun-yai kesempatan mengambil beberapa nilai yang lebih kecil yang kelihatan lebih efisien. Seperti biasa, persoalan ini mengurangi keseimbangan antara ketelitian secara statistik dan biaya. Bila subunit dalam unit yang sama sangat dekat, pertimbangan-pertimbangan ketelitian membutuhkan satu nilai m yang kecil.
Misalkan populasi U adalah populasi U adalah populasi yang distratifikasi dengan menggunakan strata H, Uh dengan Nh adalah anggota di tahap ke h−
thPHh=1Nh =N
. Di dalam tahap pertama, digunakan contoh s1h sederhana dari tahap pertama strataUh dan menyelidiki sebuah variabel skalar xuntuk i∈
s1h, h = 1,· · · , H, dimana ukuran s1h adalah n1h PH
h=1n1h =n1
. Kemudian dilakukan stratifikasi ulang sampelydengans1 =∪H
h=1s1hke dalamGtahapan ˜s1g dengan populasi m1g
PG
g=1m1g =n1
, menggunakan vaiabel tambahan untuk diselidiki di tahap pertama, sampel acak sederhana s2g dengan populasi m2g dan kemudian diambil secara acak dari strata kedua ˜s1g(g = 1,· · · , G).
Untuk gambaran diatas, π1i= n1Nh
h jikai∈s1h dengan i6=j,
π1ij =
n1h(n1h−1)
Nh(Nh−1)
jikai6=j ∈s1h
n1hn1k
NhNk
jikai∈s1h, j ∈s1k, h6=k
(2.17)
Estimator fase kedua ˆY2 dapat disederhanakan menjadi
ˆ
Y2 =
H X
h=1 Nh
n1h G X
g=1 m1g
m2g X
i∈s2gh
yi (2.18)
dimana s2gh =s1hs2g, dengan catatan bahwa beberapa s,2ghs mungkin kosong, di beberapa kasus penggunaan P
i∈s2ghyi menjadi nol di persamaan (2.2).
Beralih ke permasalahan estimasi variansi, komponenv( ˆY2|s1) diberikan oleh
(2.5) dengan ˙y1 =y1(Nh
n1h) jikai∈s1h. Untuk mengevaluasiv2
ˆ
Y1diberikan oleh
persamaan (2.6), dibutuhkan nilai△1ij. Dengan menggunakan (2.3), diperoleh
△1ij =
1−f1h
n1h−1
jika ij ∈˜s2h
= 0 jikai∈ ˜s2h, j ∈s˜2k, h6=k
(2.19)
dimana ˜s2h =∪gs2gh dan f1h = n1Nh
h.
Substiusi yang dilakukan pada batas atas △1ij di persamaan (2.6), kompo-nen pertama v(1)2 Yˆ1
disederhanakan menjadi
v2(1)Yˆ1= G X
g=1
m1g(m1g−1)
m2g(m2g−1) X
h=Ag
Nh
n1h 2
1−f1h
n1h−1 X
i<j∈s2gh
X
dimana Ag adalah himpunan dari strata h fase pertama dengan menggunakan paling sedikit dua unit di s2gh, untuk sisa strata fase pertama tidak memberikan kontribusiv(1)2 Yˆ1
, menggunakan identitas Langrange (2.4), menggunakan (2.7) mereduksi persamaan menjadi
v(1)2 Yˆ1=
dimana mgh adalah banyaknya unit s2gh dan ˆS22ghy adalah kuadrat sampel rata-rata dari nilaiyi untuki ∈S2gh.
Dapat dituliskan bahwav(2)2 Yˆ1 sebagai gambaran dari
v2(2)Yˆ1
dimana ∪2gl adalah himpunan strata h fase pertama dengan paling sedikit satu unit di kedua s2gh dan s2gl. Untuk kesederhanaan dari persamaan (2.10) adalah
tidak mungkin sederhana tanpa memenuhi m2gh ≥ 2 untuk semua (gh). Tipe variansi estimator SYG, vYˆ2
, sekarang diberikan oleh perpaduan persamaan (2.5), (2.15) dan (2.16), dan selalu menghasilkan angka yang tidak negatif.
Sekarang gunakan kasus spesial m2gh ≥ 2 untuk semua (gh). Di kasus
v(1)2 Yˆ1diberikan oleh (2.15) dengan P
Ag berubah menjadiPHh=1 Untuk lebih
jauh dapat ditulis bahwa v2(2)Yˆ1sebagai gambaran dari
v2(2)Yˆ1
Kombinasi dari (2.15) dengan (2.18), diperoleh
Kedalam bentuk I pada (2.17), dapat ditulis
I =
Estimator variansi vYˆ2 sekarang diberikan dengan menjumlahkan per-samaan (2.5), (2.12) dan (2.13). Estimator variansi HT dari Binder et.al, (2000) diturunkan dari persamaan (1.2), adalah berbeda dari hasil vYˆ2
yang dihasilkan dari persamaan (2.5) adalah sejenis dengan formula yang ditemukan Binder et.al, Perumusan Binder et.al, (2000) tersebut berkores-pondensi dengan persamaan (2.19) yang diberikan
G
dimana ¯y2gh adalah rata-rata dari y untuk s2gh. Persamaan Binder et.al, (2000)
berkorespondensi dengan persamaan (2.13) di berikan
Estimasi variansi Binder et.al, (2000) sekarang diberikan dengan menjum-lahkan (2.5), (2.12) dan (2.13). Dengan catatan bahwa bentuk n1ˆ h
n1h −1
dapat menghasilkan positif atau negatif.
2.4 Penarikan Sampel Tiga-Tahap
Misalkan yiju adalah nilai yang diperoleh untuk unit ke-u tahap ketiga pada unit ke-j tahap kedua diambil dari unit utama ke-i. Rata-rata unit yang sesuai popu-lasi per-unit ketiga adalah
¯
Yij = ΣK
uyiju
K ,Y¯¯ =
ΣM
j ΣKuyiju
M K ,Y¯¯¯ =
ΣN
i ΣMj ΣKuyiju
N M K (2.30)
Varians populasi yang dibutuhkan:
S12 = PN
i
¯¯
Yi−Y¯¯¯ 2
N −1
S22 = PN
i Σ M j
¯
Yij −Y¯¯i 2
N(M −1)
S32 = PN
i Σ M j ΣKu
¯
Yijk−Y¯¯i 2
N M(K −1)
Jika penarikan sampel acak sederhana digunakan pada ketiga tahap, rata-rata sampel Y¯¯¯ per-unit tahap ketiga adalah suatu perkiraan yang tidak bias dari
¯¯¯
Y, dengan varians
vY¯¯¯= 1−f1
n S
2 1 +
1−f2
nm S
2 2 +
1−f3
nmk S
2
3 (2.31)
dimana f1 = Nn, f2 = Mm, f3 = Kk adalah fraksi penarikan sampel pada tahap
ketiga. Selanjutnya :
¯¯¯
y−Y¯¯¯ =y¯¯¯−Y¯¯¯nm Y¯¯¯nm−Y¯¯¯n
+Y¯¯¯n−Y¯¯¯
(2.32)
dimanaY¯¯¯nmadalah rata-rata populasinmunit tahap kedua yang telah dipilih dan ¯¯¯
Kontribusi dari bentuk yang telah dikuadratkan akan menjadi:
Ey¯¯¯−Y¯¯¯nm 2
= 1−f3
nmk S
2 3
EY¯¯¯nm−Y¯¯¯n 2
= 1−f2
nm S
2 2
EY¯¯¯n−Y¯¯¯ 2
= 1−f1
n S
2 1
Bila ketiga bentuk tersebut dijumlahkan, teorema diatas diperoleh suatu perkiraan tidak bias pada V(Y¯¯¯) dari samplenya
vY¯¯¯= 1−f1
n S
2 1 +
f1(1−f2)
nm S
2 2 +
f1f2(1−f3)
nmk S
2
3 (2.33)
dimana S2
1, S22, S32 adalah perkiraan varians sampel dari S12, S22, S32. Hal ini
dapat dibuktikan dengan menunjukkan
E(S12) =S12+ 1−f2
m S
2 2 +
1−f3
mk S
2 3
E(S22) =S22+ 1−f3
k S
2 3
(2.34)
dan E(S32) = S22. Untuk mendapatkan hasil yang pertama, misalkan ¯¯yik menya-takan rata-rata m unit tahap kedua pada unit utama ke-i, dengan syarat bahwa seluruhK elemen telah dihitung pada tahap ketiga. Misalkan ¯¯¯yK adalah rata-rata dari n nilai ¯¯yik. Maka penarikan sampel dua tahap menjadi
E
"Pn ¯¯
yiK −y¯¯¯K2
n−1
#
=S12 +1−f2
m S
2
2 (2.35)
Sekarang bila ¯¯yi adalah rata-rata sampel untuk unit utama ke-i menjadi
¯¯
yi −y¯¯¯= ¯¯yiK −y¯¯¯K+
(¯¯yi−y¯¯iK)− y¯¯¯−y¯¯¯K (2.36)
Dengan diawali merata-ratakan seluruh sampel yang mana unit-unit tahap pertama dan tahap kedua tetap, dapat ditunjukkan bahwa:
1
n−1E n X
(¯¯yi−y¯¯iK)− y¯¯¯−y¯¯¯K2
= (1−f3)S
2 3
mk (2.37)
Oleh karena itu,
E
v y¯¯¯
=1−f1
n
S12+ 1−f2
m S
2 2 +
1−f3
mk S
2 3
+ f1(1−f2)
nm
S22+ 1−f3
k S
2 3
+f1f2(1−f3)
nmk S
2 3
=1−f1
n S
2 1 +
1−f2
nm S
2 2 +
1−f3
nmk S
2 3
=V(y)
(2.38)
Seperti dengan penarikan sampel dua tahap, hal ini hal ini jelas dari (2.33), bahwa jika f1 diabaikan v y¯¯¯
menjadi
v y¯¯¯= S
2 1
n =
Pn
(¯¯yi−y¯¯)2
n(n−1) (2.39)
Perkiraan ini konservatif bilaf1 tidak diabaikan. Dengan sebuah fungsi biaya dari
bentuk
C =c1n+c2nm+c3nmk (2.40)
Nilaik dan m optimum adalah
kopt =
s3
q S2
2−S 2 3 K
r
c2 c3
,mopt = q
S2 2−S
2 3 K q
S2 1−S
2 3 M
c1 c2
(2.41)