1
BAB IPENDAHULUAN A. Latar Belakang
Misalkan nomor plat mobil di negara X terdiri atas 5 angka angka diikuti dengan 2 huruf. Angka pertama tidak boleh 0. Berapa banyak nomor plat mobil yang dapat dibuat?
Cara yang paling sederhana untuk menyelesaikan persoalan di atas dengan cara mengenumerasi semua kemungkinan jawabannya. Mengenumerasi atau mencacah atau menghitung (count) satu persatu untuk setiap kemungkinan jawaban. Untuk persoalan dengan jumlah objek yang sedikit,mengenumerasi setiap objek masih dapat dilakukan, akan tetapi untuk persoalan dengan jumlah objek yang banyak, cara enumerasi mungkin tidak efisien dan efektif.
Mungkin kita sudah lelah sebelum usaha untuk mengenumerasi semua kemungkinan nomor plat mobil selesai, karena nomor plat mobil yang dibentuk sangat banyak. Disinilah peran kombinatorial dapat digunakan untuk menjawab persoalan semacam ini. Hal ini dapat dilakukan karena dalam kombinatorial terdapat kaidah dasar menghitung, dengan kaidah ini, berbagai persoalan menghitung jumlah cara pengaturan objek dapat diselesaikan.
Dalam penyelidikan banyaknya bilangan prima dalam yang tidak melebihi suatu bilangan bulat positif tertentu tentunya sangat tidak efektif jika kita mengenumerasi bilangan prima,oleh karena itu di dalam kombinatorial juga terdapat prinsip inklusi – eksklusi yang dapat digunakan untuk menyelesaikan masalah ini. Dalam kombinatorial juga terdapat permutasi yang dapat digunakan untuk melakukan jumlah cara pengaturan objek-objek.
B. Rumusan Masalah
Dari latar belakang, dapat dirumuskan masalah yaitu : 1. Apa saja kaidah dasar menghitung?
2. Bagaimana Aplikasi prinsip inklusi-eksklusi? 3. Bagaimana Aplikasi prinsip permutasi?
C. Tujuan
Dengan memahami rumusan masalah yang ada di atas, mahasiswa dapat menggunakan dan mengaplikasikan kombinatorial dalam kehidupan nyata.
2
BAB IIPEMBAHASAN
A. Kaidah Dasar Menghitung.
Di dalam kombinatorial , kita harus menghitung (counting) semua kemungkinan pengaturan objek. Dua kaidah dasar yang digunakan sebagai teknik menghitung dalam kobinatorial adalah Kaidah perkalian (rule of product) dan Kaidah penjumlahan (rule of sum). Kedua kaidah ini dapat digunakan untuk memecahkan banyak masalah persoalan menghitung (Munir,2010:227).
1. Kaidah perkalian (rule of product)
Bila percobaan 1 mempunyai p hasil percobaan yang mungkin terjadi ( atau menghasilkan p kemungkinan jawaban), percobaan 2 mempunyai q hasil percobaan yang mungkin terjadi ( atau menghasilkan q kemungkinan jawaban), maka bila percobaan 1 dan percobaan 2 dilakukan maka terdapat p × q hasil percobaan ( atau menghasilkan p × q kemungkinan jawaban ).
Misalkan,
Percobaan 1: p hasil Percobaan 2: q hasil maka,
Percobaan 1 dan percobaan 2: pq hasil
2. Kaidah penjumlahan (rule of sum)
Bila percobaan 1 mempunyai p hasil percobaan yang mungkin terjadi ( atau menghasilkan p kemungkinan jawaban), percobaan 2 mempunyai q hasil percobaan yang mungkin terjadi ( atau menghasilkan q kemungkinan jawaban), maka bila hanya satu percobaan saja yang dilakukan (percobaan 1 atau percobaan 2), terdapat p + q kemungkinan hasil percobaan ( menghasilkan p + q kemungkinan jawaban) yang mungkin terjadi.
Misalkan,
Percobaan 1: p hasil Percobaan 2: q hasil maka,
3
Contoh :1. Sekelompok mahasiswa terdiri atas 4 orang pria dan 3 orang wanita . Berapa jumlah cara memilih satu orang pria dan satu orang wakil wanita?
Penyelesaian:
wakil wanita. Jika dua orang wakil harus dipilih, masing-masing 1 pria dan 1 wanita, maka jumlah kemungkinan perwakilan yang dapat dipilih adalah 4×3=12
2. Sekelompok mahasiswa terdiri atas 4 orang pria dan 3 orang wanita . Berapa jumlah cara memilih satu orang yang mewakili kelompok tersebut (tidak peduli pria atau wanita)?
Penyelesaian :
Ada 4 kemungkinan memilih satu wakil pria, dan 3 kemungkinan memilih satu wakil wanita. Jika hanya satu orang wakil yang harus dipilih (pria atau wanita), maka jumlah kemungkinan wakil yang dapat dipilih adalah 4+3=7
Perluasan Kaidah Dasar Menghitung
Kaidah perkalian dan kaidah penjumlahan di atas dapat diperluas hingga mengandung lebih dari dua percobaan. Jika n buah percobaan masing-masing mempunyai p1,p2,…….,pn, hail percobaan yang mungkin terjadi yang dalam hal ini setiap p tidak bergantung pada pilihan sebelumnya, mak jumlah hasil percobaan yang mungkin terjadi adalah :
1. Kaidah perkalian (rule of product) p1 p2 … pn hasil
2. Kaidah penjumlahan (rule of sum) p1 + p2 + … + pn hasil
Contoh:
Sandi-lewat (password) sistem komputer panjangnya enam sampai delapan karakter. Tiap karakter boleh berupa huruf atau angka; huruf besar dan huruf kecil tidak dibedakan. Berapa banyak sandi-lewat yang dapat dibuat?
4
Penyelesaian:Banyaknya huruf alfabet adalah 26 (A-Z) dan banyak angka desimal adalah 10 (0-9), jadi seluruhnya 36 karakter.
Untuk sandi-lewat dengan panjang 6 karakter, jumlah kemungkinan sandi-lewat adalah (36)(36)(36)(36)(36)(36) = 366 = 2.176.782.336
untuk sandi-lewat dengan panjang 7 karakter, jumlah kemungkinan sandi-lewat adalah (36)(36)(36)(36)(36)(36)(36) = 367 = 78.364.164.096
dan untuk sandi-lewat dengan panjang 8 karakter, jumlah kemungkinan sandi-lewat adalah
(36)(36)(36)(36)(36)(36)(36)(36) = 368 = 2.821.109.907.456
Jumlah seluruh sandi-lewat (kaidah penjumlahan) adalah
2.176.782.336 + 78.364.164.096 + 2.821.109.907.456 = 2.901.650.833.888 buah.
B. Prinsip Inklusi – Ekslusi
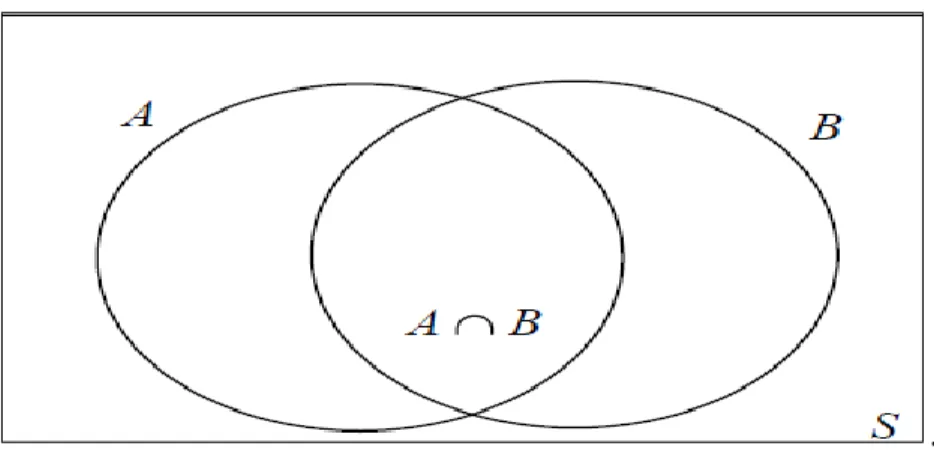
Berapa banyak anggota di dalam dua buah himpunan A dan B?. Penggabungan dua buah himpunan menghasilkan himpunan baru yang elemennya berasal dari kedua himpunan tersebut. Himpunan A dan Himpunan B mungkin saja memiliki elemen-elemen yang sama. Banyaknya elemen bersama antara A dan B adalah AB. Setiap unsur yang sama itu telah dihitung dua kali sekali pada Adan sekali B pada ,meskipun ia seharusnya dianggap sebagai satu buah elemen di dalam AB . Karena itu ,jumlah elemen hasil penggabungan seharusnya adalah jumlah elemen di masing-masing himpunan dikurangi dengan jumlah elemen di dalam irisannya, atau B A B A B A
5
ContohDalam sebuah program studi pendidikan matematika yang terdiri atas 350 mahasiswa, terdapat 175 mahasiswa yang mengambil mata kuliah persamaan diferensial dan 225 mahasiswa yang mengambil mata kuliah analisis kompleks, dan 50 mahasiswa yang mengambil mata kuliah persamaan diferensial dan analisis kompleks. Ada berapa mahasiswa di dalam perkuliahan itu jika setiap mahasiswa mengambil mata kuliah persamaan diferensial, analisis kompleks, atau kedua-duanya?
Misalkan :
A = banyaknya mahasiswa yang mengambil mata kuliah persamaan diferensial B = banyaknya mahasiswa yang mengambil mata kuliah analisis kompleks. A B = himpunan mahasiswa yang mengambil kedua mata kuliah tersebut. Banyaknya mahasiswa di dalam kelas itu yang mengambil mata kuliah persamaan diferensial, analisis kompleks, atau kedua-duanya adalah
B A B A B A 350 50 -225 175
Ini berarti, terdapat 350 mahasiswa di dalam kelas yang mengambil mata kuliah persamaan diferensial, analisis kompleks, atau kedua-duanya. Karena banyaknya siswa keseluruhan di dalam kelas tersebut adalah 350 mahasiswa, artinya tidak terdapat mahasiswa yang tidak memilih salah satu dari kedua konsentrasi itu. Perhatikan diilustrasi berikut.
6
.C. Permutasi
Masalah penyusunan kepanitiaan yang terdiri dari Ketua, Sekretaris dan Bendahara dimana urutan dipertimbangkan merupakan salah satu contoh permutasi. Jika terdapat 3 orang (misalnya Amir, Budi dan Cindy) yang akan dipilih untuk menduduki posisi tersebut, maka dengan menggunakan Kaidah Perkalian kita dapat menentukan banyaknya susunan panitia yang mungkin, yaitu: (http://ftsi.files.wordpress.com/2007/09/03_permutasi_kombinasi.pdf)
Pertama menentukan Ketua, yang dapat dilakukan dalam 3 cara.
Begitu Ketua ditentukan, Sekretaris dapat ditentukan dalam 2 cara.
Setelah Ketua dan Sekretaris ditentukan, Bendahara dapat ditentukan dalam 1 cara. Sehingga banyaknya susunan panitia yang mungkin adalah 3×2×1 = 6.
Secara formal, permutasi dapat didefinisikan sebagai berikut :
Definisi 1.
Permutasi dari n unsur yang berbeda x1,x2 , , , , xn adalah pengurutan dari n unsur tersebut.
Contoh 1:
Tentukan permutasi dari 3 huruf yang berbeda, misalnya ABC ! Penyelesaian :
Permutasi dari huruf ABC adalah ABC, ACB, BAC, BCA, CAB, CBA. Sehingga terdapat 6 permutasi dari huruf ABC.
Teorema 1
7
Terdapat n! permutasi dari n unsur yang berbeda.Bukti.
Asumsikan bahwa permutasi dari n unsur yang berbeda merupakan aktivitas yang terdiri dari n langkah yang berurutan. Langkah pertama adalah memilih unsur pertama yang bisa dilakukan dengan n cara. Langkah kedua adalah memilih unsur kedua yang bisa dilakukan dengan n - 1 cara karena unsur pertama sudah terpilih. Lanjutkan langkah tersebut sampai pada langkah ke-n yang bisa dilakukan dengan 1 cara. Berdasarkan Prinsip Perkalian, terdapat n(n - 1)(n - 2). . . .2.1 = n! permutasi dari n unsur yang berbeda.
Contoh 2
Berapa banyak permutasi dari huruf ABCDEF jika subuntai ABC harus selalu muncul bersama?
Penyelesaian :
Karena subuntai ABC harus selalu muncul bersama, maka subuntai ABC bisa dinyatakan sebagai satu unsur. Dengan demikian terdapat 4 unsur yang dipermutasikan, sehingga banyaknya permutasi adalah 4×3×2×1 = 24.
Definisi 2.
Permutasi r dari n elemen adalah jumlah kemungkinan urutan r buah elemen yang dipilih dari n buah elemen, dengan r n, yang dalam hal ini, pada setiap kemungkinan urutan tidak ada elemen yang sama.
Contoh 3
Tentukan permutasi-3 dari 5 huruf yang berbeda, misalnya ABCDE. Penyelesaian :
Permutasi-3 dari huruf ABCDE adalah 2
ABC ABD ABE ACB ACD ACE ADB ADC ADE AEB AEC AED BAC BAD BAE BCA BCD BCE BDA BDC BDE BEA BEC BED
8
CAB CAD CAE CBA CBD CBECDA CDB CDE CEA CEB CED DAB DAC DAE DBA DBC DBE DCA DCB DCE DEA DEB DEC EAB EAC EAD EBA EBC EBD ECA ECB ECD EDA EDB EDC
Sehingga banyaknya permutasi-3 dari 5 huruf ABCDE adalah 60.
Teorema 2
Banyaknya permutasi-r dari n unsur yang berbeda adalah
( ) ( )
Perlu diperhatikan bahwa jika r = n maka persamaan di atas menjadi
! 1 ! ! 0 ! ) , (n r n n n P Bukti.
Dengan induksi matematika: Basis induksi
Untuk n=0 , P(0,0) adalah jumlah cara memilih 0 buah elemen dari himpunan kosong =0!/0!=1, yang jelas benar.
Langkah induksi
Asumsikan bahwa P(n) benar ,yaitu mengasumsikan bahwa P (n,r)=n!/(n-r)! Untuk r = 0,1,. . . . Akan dibuktikan bahwa P(n+1,r)=(n+1)!/(n+1- r )! Benar. Untuk menunjukkan bahwa P(n+1) benar maka ada dua kasus yang harus dipertimbangkan :
9
Kasus 1Jika r = 0 , maka ada satu cara memilih 0 buah elemen dari himpunan (n+1) elemen dan disini P(n+1,0)=(n+1)!/(n+1-0)!=1, yang jelas benar
Kasus 2
Jika r >0. Disini kita menghitung nilai P(n+1,r) dengan (i) menghitung jumlah cara memilih elemen pertama di dalam susunan yang di ambil, dan (ii) kemudian menghitung jumlah cara mengambil r-1 elemen dengan menggunakan hipotesis induksi. Ada (n+1) cara memilih untuk elemen pertama. Karema tinggal n buah elemen yang belum di ambil untuk mengisi r – 1 posisi lainnya, maka ada P(n,r-1) cara melengkapi r-1 posisi itu. Dengan aturan perkalian maka (Munir,2010:240)
1
! ! 1 ! 1 ! 1 1 1 1 r n n r n n n ) )P(n,r-,r)=(n+ P(n+ Contoh 4Gunakan Teorema diatas untuk menentukan permutasi-3 dari 5 huruf yang berbeda, misalnya ABCDE.
Penyelesaian :
Karena r = 3 dan n = 5 maka permutasi-3 dari 5 huruf ABCDE adalah
60 3 4 5 2! 5! )! 3 5 ( ! 5 ) 3 , 5 ( P
Jadi banyaknya permutasi-3 dari 5 huruf ABCDE adalah 60. Definisi 3
10
Permutasi melingkar dari n objek adalah penyusunan objek-objek yang mengelilingi sebuahlingkaran ( atau kurva tertutup sederhana ). Jumlah susunan objek yang mengelilingi lingkarab adalah (n-1)! (Munir,2010:243)
Pembuktian jumlah susunan objek permutasi melingkar
Misalkan objek pertama ditempatkan di mana saja pada lingkaran dengan 1 cara. Sisa n-1 objek lainnya dapat diatur searah jarum jam ( misalnya) dengan P(n-1,n-1)=(n-1)! Cara.
BAB III PENUTUP
Kesimpulan :
Dari pembahasan di atas dapat disimpulkan kombinatorial mempunyai beberapa bagian diantaranya kaidah dasar menghitung, prinsip inklusi-eksklusi, dan permutasi. Dan masing-masing bagian memiliki fungsi masing-masing-masing-masing yang dapat diaplikasikan dalam menghitung jumlah cara pengaturan objek-objek.
11
DAFTAR PUSTAKAMunir, Rinaldi. 2010 . Matematika Diskrit. Bandung : Informatika
http://ftsi.files.wordpress.com/2007/09/03_permutasi_kombinasi.pdf diakses pada tanggal 8 November 2010 pukul 20.00 WITA