METODE ITERASI DUA LANGKAH BERDASARKAN ATURAN KUADRATUR BARU UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR. Meutia Raya Fitri 1 ABSTRACT

METODE ITERASI DUA LANGKAH BERDASARKAN ATURAN KUADRATUR BARU UNTUK MENYELESAIKAN

PERSAMAAN NONLINEAR Meutia Raya Fitri1∗

1 _{Mahasiswa Program Studi S1 Matematika}

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus Binawidya Pekanbaru (28293), Indonesia

∗_{meutia242@gmail.com}

ABSTRACT

This article discusses the two-step iterative method derived following the pattern in obtaining the iterative method proposed by Ujevic [Appl. Math. Comput. 174 (2006): 1416-1426.]. Analytically using fixed point iteration, it is shown that the proposed method converges to the root of nonlinear equations. Then numerical sim-ulations show that the proposed method is comparable to methods Ujevic’s method and better than Newton’s method.

Keywords: Nonlinear equations, Newton method, Ujevic’s method

ABSTRAK

Artikel ini membahas tentang metode iterasi dua langkah yang diturunkan mengikuti pola penurunan metode iterasi yang dikemukakan oleh Ujevic [Appl. Math. Com-put. 174(2006): 1416-1426.]. Secara analitik menggunakan iterasi titik tetap ditun-jukkan bahwa metode yang dikemukakan konvergen ke akar persamaan nonlinear. Kemudian melalui simulasi numerik terlihat bahwa metode iterasi yang dikemukakan adalah sebanding dengan metode Ujevic dan lebih baik dari metode Newton. Kata kunci: Persamaan nonlinear, metode Newton, metode Ujevic

1. PENDAHULUAN

Teknik mendapat metode untuk menyelesaikan persamaan nonlinear secara numerik berkembang sangat pesat. Bermula dari memodifikasi metode Newton yang bentuk iterasinya

xk+1 =xk− f(xk) f′(xk)

, k = 0,1,2,· · · , f′(xk)̸= 0,

berlanjut dengan mengkombinasikan metode Newton dengan metode lainnya. Pada artikel ini diturunkan metode iterasi baru yang penurunnnya mengikuti penurunan metode Ujevic[6] yang merupakan review dari karya Zhu et al.[5]. Pem-bahasan dimulai dengan menurunkan metode iterasi dan kekonvergenannya ke akar

persamaan nonlinear dibagian dua. Dibagian tiga diberikan simulasi numerik dengan melakukan perbandingan dengan metode Ujevic dan metode Newton.

2. METODE ITERASI DUA LANGKAH BERDASARKAN ATURAN KUADRATUR BARU UNTUK MENYELESAIKAN

PERSAMAAN NONLINEAR 2.1 Penurunan Metode Iterasi Dua Langkah

Pandang fungsi K1(x, t) yang didefinisikan dengan

K1(x, t) =      t− 2a+b 3 , t∈[a, x], t− a+ 2b 3 , t∈[x, b]. (1)

Selanjutnya bila dikalikan f′(t) pada kedua ruas persamaan (1), diperoleh

K1(x, t)f′(t) =        ( t− 2a+b 3 ) f′(t), t∈[a, x], ( t− a+ 2b 3 ) f′(t), t∈[x, b], (2) dimana x∈[a, b].

Dengan mengintegralkan K1(x, t)f′(t) persamaan (2) pada interval [a, b] dan menggunakan integral parsial [4], setelah penyederhanaan, diperoleh

∫ b a K1(x, t)f′(t)dt= ∫ x a ( t− 2a+b 3 ) f′(t)dt+ ∫ b x ( t− a+ 2b 3 ) f′(t)dt = [( t−2a+b 3 ) f(t) ]x a − ∫ x a f(t)dt + [( t− a+ 2b 3 ) f(t) ]b x − ∫ b x f(t)dt ∫ b a K1(x, t)f′(t)dt= b−a 3 ( f(a) +f(b) +f(x) ) − ∫ b a f(t)dt. (3) Jika dimisalkan x = a+b

2 , kemudian substitusikan x ke persamaan (3) maka diperoleh ∫ b a K1 ( a+b 2 , t ) f′(t)dt = b−a 3 ( f(a) +f(b) +f ( a+b 2 )) − ∫ b a f(t)dt. (4)

Dari persamaan (4) terlihat bahwa ∫_abK1

(

a+b 2 , t

)

f′(t)dt dapat dipandang se-bagai taksiran error dari ruas kanan persamaan (4).

Selanjutnya dengan menyusun ulang ruas kanan dari persamaan (4) didapat ∫ b a K1(x, t)f′(t)dt = 2 3 (( b−a 2 )( f(a) +f(b) ) − ∫ b a f(t)dt ) +1 3 ( (b−a)f ( a+b 2 ) − ∫ b a f(t)dt ) .

Dengan menggunakanerror aturan trapesium [2] dan aturan titik tengah [2], didapat

∫ b a K1(x, t)f′(t)dt= 2 3 ( (b−a)3 12 ) f′′+1 3 ( (b−a)3 24 ) f′′. Jadi ∫ b a K1(x, t)f′(t)dt ≤ 2 3 ( (b−a)3 12 ) |f′′|+1 3 ( (b−a)3 24 ) |f′′| ≤ 2 36(b−a) 3 _max|f′′_|+ 1 72(b−a) 3 _max|f′′_| ∫_abK1(x, t)f′(t)dt ≤ 5 72(b−a) 3_||f′′_|| ∞. Kemudian definisikan juga

K2(x, t) =

{

t−a, t ∈[a, x],

t−b, t∈[x, b]. (5) Jika f′(t) dikalikan ke kedua ruas persamaan (5) diperoleh

K2(x, t)f′(t) =

{

(t−a)f′(t), t∈[a, x],

(t−b)f′(t), t ∈[x, b], (6) dimana x∈[a, b].

Bila diintegralkan persamaan (5) pada [a, b] diperoleh

∫ b a K2(x, t)dt= ∫ x a (t−a)dt+ ∫ b x (t−b)dt = [ 1 2t 2₋ at ]x a + [ 1 2t 2₋ bt ]b x ∫ b a K2(x, t)dt= (b−a) ( x−a+b 2 ) . (7)

Bila diintegralkan persamaan (6) secara parsial, diperoleh

∫ b a K2(x, t)f′(t)dt= ∫ x a ( t−a ) f′(t)dt+ ∫ b x ( t−b ) f′(t)dt = [(t−a)f(t)]x_a− ∫ x a f(t)dt+ [(t−b)f(t)]b_x− ∫ b x f(t)dt ∫ b a K2(x, t)f′(t)dt= (b−a)f(x)− ∫ b a f(t)dt. (8)

Selanjutnya dihitung∫_abK2(x, t)f′(t)dt− 1 b−a ∫b aK2(x, t)dt ∫b a f′(t)dtmenggunakan persamaan (8), (7), dan Teorema Dasar Kalkulus [3], dapat disederhanakan men-jadi ∫ b a K2(x, t)f′(t)dt− 1 b−a ∫ b a K2(x, t)dt ∫ b a f′(t)dt = (b−a)f(x)− ∫ b a f(t)dt− 1 b−a ( (b−a) ( x− a+b 2 )) ∫ b a f′(t)dt = (b−a)f(x)− ∫ b a f(t)dt− 1 b−a ( (b−a) ( x− a+b 2 )) (f(b)−f(a)) ∫ b a K2(x, t)f′(t)dt− 1 b−a ∫ b a K2(x, t)dt ∫ b a f′(t)dt = (b−a)f(x)− ( x− a+b 2 ) (f(b)−f(a))− ∫ b a f(t)dt. (9) Dari persamaan (9) diperoleh

∫_abK2(x, t)f′′(t)dt− 1 b−a ∫ b a K2(x, t)dt ∫ b a f′′(t)dt = ∫ b a K2(x, t)f′′(t)dt− 1 b−a ( ∫ b a K2(x, s)ds ) ∫ b a f′′(t)dt = ∫ b a ( K2(x, t)− 1 b−a ∫ b a K2(x, s)ds ) f′′(t)dt ≤max|f′′(t)| ∫ b a ( K2(x, t)− 1 b−a ∫ b a K2(x, s)ds ) dt = ∫ b a ( K2(x, t)− 1 b−a ∫ b a K2(x, s)ds ) dt ||f′′||_∞ ≤ (b−a)2 4 ||f ′′_|| ∞. Bila dinyatakan R1(x) = ∫ b a K1(x, t)f′(t)dt, maka dari persamaan (3) diperoleh

∫ b a f(t)dt= b−a 3 ( f(a) +f(x) +f(b) ) −R1(x). (10) Bila dinyatakan R2 = ∫ b a K2(x, t)f′(t)dt− 1 b−a ∫ b a K2(x, t)dt ∫ b a f′(t)dt,

maka dari persamaan (9) diperoleh ∫ b a f(t)dt = (b−a)f(x)− ( x− a+b 2 )( f(b)−f(a) ) −R2(x). (11)

Berdasarkan persamaan (10), dengan mengabaikan nilai R1 diperoleh

∫ b a f(t)dt= b−a 3 ( f(a) +f(x) +f(b) ) , (12)

dengan mengabaikan nilai R2 dari persamaan (11), diperoleh

∫ b a f(t)dt = (b−a)f(x)− ( x− a+b 2 )( f(b)−f(a) ) , (13) dan dengan menyamakan persamaan (12) dan (13) diperoleh

b−a 3 ( f(a) +f(x) +f(b) ) = (b−a)f(x)− ( x− a+b 2 )( f(b)−f(a) ) . (14) Jika f(b) = 0, pada persamaan (14) diperoleh

b−a 3 ( f(a) +f(x) ) = (b−a)f(x) + ( x− a+b 2 ) f(a). (15) Jika b = ¯b adalah solusi dari persamaan (15) maka diperoleh

¯ b−a 3 (f(a) +f(x)) = (¯b−a)f(x) + ( x− a+ ¯b 2 ) f(a). (16) Dengan melakukan manipulasi aljabar pada persamaan (16) dan menyelesaikan un-tuk ¯b diperoleh ¯_{b=a+ 6(x−a)} f(a) 5f(a)−4f(x). Misalkan x=a−αf(a) f′(a), 0< α≤1,

dan dengan mengambil ¯b =xk+1, a=xk dan x=zk persamaan (16) diperoleh xk+1 =xk+ 6(zk−xk) f(xk) 5f(xk)−4f(zk) , (17) dengan zk =xk−α f(xk) f′(xk) , 0< α≤1.

Persamaan (17) inilah yang disebut dengan bentuk umum dari metode iterasi dua langkah untuk persamaan nonlinear.

2.2 Kekonvergenan Metode Iterasi Dua Langkah

Misalkan f ∈ C2(c, d), f(b) = 0, b ∈ (c, d), f′(x) ̸= 0, f′′(x) ̸= 0, x ∈ (c, d) didefinisikan sebagai ψ(a) = a+ 6(x−a) f(a) 5f(a)−4f(x), (18) dengan x=a−αf(a) f′(a), 0< α≤1. (19) Teorema 1 [5] Misalkanf ∈C2_{(c, d), f(b) = 0, b ∈(c, d), f}′_{(x)̸= 0, f}′′_{(x)̸= 0, x∈} (c, d) dan a0 ∈ U(b) dengan U(b) adalah lingkungan disekitar b sedemikian hingga

|ψ′(a)|<1 untuk setiapa ∈U(b). Kemudian barisanxk+1 =ψ(xk), dengan x0 =a0 dan ψ definisi dari persamaan (18).

Bukti: Berdasarkan persamaan (19) diperoleh lim a→bx= lima→b ( a−αf(a) f′(a) ) = lim a→ba−lima→bα f(a) f′(a) =b−α f(a) lima→bf′(a) lim a→bx=b.

Perhatikan turunan dari ψ′(a) di lingkungan di sekitar b. Jika persamaan (18) diturunkan terhadap a maka diperoleh

ψ′(a) = 1 + 6(x′_a−1) f(a) 5f(a)−4f(x) + 6(x−a) ( f′(a) 5f(a)−4f(x) − f(a)(5f′(a)−4f′(x)x′_a) (5f(a)−4f(x))2 ) , (20) dengan x′_a= dx da.

Kemudian persamaan (19) diturunkan terhadap a maka diperoleh dx

da = 1−α

(

f′(a)2_−f(a)f′′_(a) f′(a)2

)

. (21)

Selanjutnya dengan mengambil limit pada persamaan (21), diperoleh lim a→b dx da = lima→b ( 1−αf

′_(a)2_−f(a)f′′_(a) f′(a)2 ) lim a→b dx da = lima→b1−lima→bα ( lim a→b f′(a)2 f′(a)2 −lim_a→b f(a)f′′(a) f′(a)2 ) ,

karena lima→bf(a) = 0, maka lim a→b dx da = 1−α·1−0 lim a→b dx da = 1−α. Berdasarkan aturan L’Hospital [1]

lim a→b f(x) f(a) = lima→b f′(x) f′(a) dx da lim a→b f(x) f(a) = 1−α, dan lim a→b f(x) 3f(a)−2f(x) = lima→b 1 3−2f_f(₍x_a)) = 1 3−lima→b2 f(x) f(a) = 1 3−2 lima→b f_f(₍x_a)) = 1 3−2(1−α) lim a→b f(x) 3f(a)−2f(x) = 1 1 + 2α.

Kemudian dengan mengambil limit pada persamaan (20) untuk a →b adalah lim a→bψ ′_{(a) = 1 + lim} a→b ( 6 ( dx da −1 ) f(a) 5f(a)−4f(x) ) + lim a→b ( 6(x−a) ( f′(a) 5f(a)−4f(x) − f(a)(5f′(a)−4f′(x)dx_da (5f(a)−4f(x))2 )) = 1 + lim a→b6(x−1) lima→b f′(a) 5f(a)−4f(x) + lim a→b6(x−a) lima→b ( f′(a) 5f(a)−4f(x) − f(a)(5f′(a)−4f′(x)dx_da (5f(a)−4f(x))2 ) = 1−6 α 1 + 4α + 6α 1 + 4α −6αlima→b ( 5−4f ′_(x) f′(a) dx da ) ( 5− 4f(x) f(a) )2 = 1−6α 1 1 + 4α + 0 lim a→bψ ′_{(a) = 1−6α} 1 1 + 4α + 0.

Jika α∈ [0,1] maka |1−6α₁₊₄1_α|<1. Dengan demikian dapat disimpulkan bahwa terdapat lingkungan disekitar b sedemikian sehingga

|ψ′(a)|< β <1 untuk setiap a∈U(b), dengan menggunakan Teorema Nilai Rata-rata [3]

ψ(x)−ψ(y) =ψ′(ξ)(x−y), ξ ∈(x, y), x, y ∈U(b), atau

ψ(x)−ψ(y) = β|(x−y)| untuk 0< β <1, x, y ∈U(b).

Oleh karena itu disimpulkan bahwa ψ adalah fungsi kontraktif. Jadi terdapat titik tetap ˆb yaitu ψ(ˆb) = ˆb, sehingga ψ(ˆb) = ˆb−6αf(ˆb) f′(ˆb)· f(ˆb) 5f(ˆb)−4f(ˆx) = ˆb, dengan ˆ x= ˆb−αf(ˆb) f′(ˆb), f(ˆb) = 0, dengan demikian ˆ_b=b. 3. KOMPUTASI NUMERIK

Pada bagian ini dilakukan perbandingan numerik untuk membandingkan jumlah iterasi dan cots komputasi dari metode Newton, metode Ujevic, dan metode Iterasi Dua Langkah dalam menghampiri nilai akar suatu persamaan.

Dalam melakukan perbandingan antara metode Newton, metode Ujevic, dan metode Iterasi Dua Langkah, persamaan nonlinear yang digunakan adalah

1. f(x) = 1 x −1 2. f(x) = 1 x −sin(x) + 1 3. f(x) = exp(1−x)−1 4. f(x) = exp(x2_{+ 7x−30)−1}

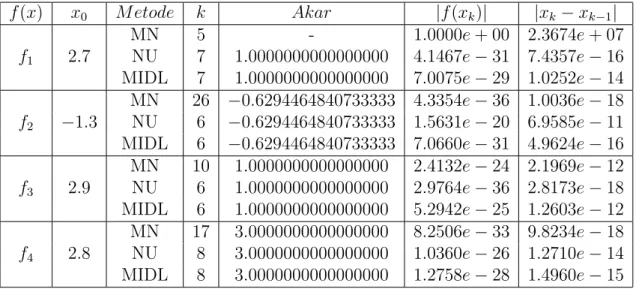
Hasil dari simulasi numerik terhadap ke empat fungsi di atas, ditunjukkan pada Tabel 1. Pada Tabel 1 dapat dilihat, k menunjukkan jumlah iterasi, x0 menunjukkan tebakan awal, metode Newton disingkat dengan MN, metode Ujevic disingkat dengan MU, dan metode iterasi dua langkah disingkat dengan MIDL, kolom pertama merupakan contoh 1 sampai 4 buah contoh yang berbeda. Pada Tabel 1 juga ditunjukkan akar dan tingkat error dari setiap metode yang dibandingkan.

Tabel 1: Perbandingan metode Newton, metode Ujevic, dan metode iterasi dua langkah

f(x) x0 M etode k Akar |f(xk)| |xk−xk−1| MN 5 - 1.0000e+ 00 2.3674e+ 07 f1 2.7 NU 7 1.0000000000000000 4.1467e−31 7.4357e−16 MIDL 7 1.0000000000000000 7.0075e−29 1.0252e−14 MN 26 −0.6294464840733333 4.3354e−36 1.0036e−18 f2 −1.3 NU 6 −0.6294464840733333 1.5631e−20 6.9585e−11 MIDL 6 −0.6294464840733333 7.0660e−31 4.9624e−16 MN 10 1.0000000000000000 2.4132e−24 2.1969e−12 f3 2.9 NU 6 1.0000000000000000 2.9764e−36 2.8173e−18 MIDL 6 1.0000000000000000 5.2942e−25 1.2603e−12 MN 17 3.0000000000000000 8.2506e−33 9.8234e−18 f4 2.8 NU 8 3.0000000000000000 1.0360e−26 1.2710e−14 MIDL 8 3.0000000000000000 1.2758e−28 1.4960e−15

Dari Tabel 1 maka dapat dilihat bahwa Metode Newton memerlukan iterasi yang lebih banyak dibandingkan dengan metode Ujevic dan metode iterasi dua langkah untuk hampir semua fungsi dari persamaan nonlinear yang diberikan. Hal ini dapat dilihat pada contoh 1 untuk tebakan awal 2.7 metode Newton tidak men-emukan akar sampai iterasi 100, sedangkan metode Ujevic dan metode iterasi dua langkah hanya memerlukan 7 iterasi. Pada fungsi kedua untuk tebakan awal −1.3 metode Newton memerlukan 26 iterasi, sedangkan metode Ujevic dan metode iterasi dua langkah hanya memerlukan 6 iterasi. Pada fungsi ketiga untuk tebakan awal 2.9 metode Newton memerlukan 10 iterasi, sedangkan metode Uje-vic dan metode iterasi dua langkah hanya memerlukan 6 iterasi. Pada contoh 4 untuk tebakan awal 2.8 metode Newton memerlukan 17 iterasi, sedangkan metode Ujevic dan metode iterasi dua langkah hanya memerlukan 8 iterasi.

Ucapan Terimakasih Penulis mengucapkan terimakasih kepada Dr. Imran M., M.Sc. dan Zulkarnain, M.Si. yang telah memberikan arahan dan bimbingan dalam penulisan skripsi yang menjadi acuan artikel ini.

DAFTAR PUSTAKA

[1] Bartle, R. G. & D. R. Shebert. 2000. Introduction to Real Analysis, 3rd _Ed. John Wiley dan Sons, New York.

[2] Burden, R. & J. D. Faires. 2003. Numerical Methods, 3th _{Ed. Brooks Cole,} Belmont.

[4] Stewart, J. 2012. Calculus, 7th Ed. Brooks Cole, Belmont.

[5] Zhu, J., Y. Yao., & P. Guo. 2014. A New Two-Step Iterative Method Based on a New Quadrature Rule For Solving Nonlinear Equations. Journal of Interdisciplinary Mathematics. 17:1–10.

[6] Ujevic, N. 2006. A Method for Solving Nonlinear Equations. Appl. Math. Com-put, 174: 1416–1426.