Sifat-sifat Operasi Perkalian Modular pada Graf Fuzzy

Sifat-sifat Operasi Perkalian Modular

pada Graf Fuzzy

Triyani

1

, Cahyo Baskoro

2

, Niken Larasati

3

, Ari Wardayani

4 Universitas Jenderal Soedirman1, 2, 3, 4

trianisr@yahoo.com.au

Abstrak— Artikel ini bertujuan menyelidiki sifat-sifat operasi perkalian modular pada graf fuzzy yang diperkenalkan oleh Dogra [1]. Sifat yang diselidiki adalah perkalian modular pada graf fuzzy lengkap, graf fuzzy efektif dan graf fuzzy komplemen. Metode yang digunakan pada penelitian ini adalah metode penelitian teoritik. Hasil penelitian menunjukkan bahwa perkalian modular dari dua graf fuzzy lengkap bukan merupakan graf fuzzy lengkap, jika ke dua graf fuzzy efektif, maka perkalian modular dari dua graf fuzzy komplemennya sama dengan perkalian modular dari dua graf fuzzy efektif tersebut dan perkalian modular dari dua graf fuzzy bersifat isomorfik.

Kata kunci: graf fuzzy, perkalian modular, graf fuzzy lengkap, graf fuzzy efektif, graf fuzzy komplemen

I. PENDAHULUAN

Graf merupakan suatu model matematika paling sederhana yang dapat merepresentasikan hubungan antar objek dengan titik mewakili objek tertentu dan sisi yang menghubungkan antara dua objek merepresentasikan hubungan antara dua objek tersebut. Ketika terdapat ketidakjelasan atau ketidakpastian dalam mendiskripsikan hubungan antara dua objek, maka sangat dibutuhkan suatu desain model graf fuzzy.

Graf fuzzy telah diprakarsai oleh Rosenfeld [2]. Graf fuzzy merupakan perluasan dari graf klasik yang dikembangkan berdasarkan konsep pada logika dan relasi fuzzy dalam teori himpunan fuzzy. Jika pada graf klasik setiap elemen-elemennya (titik dan sisi) mempunyai nilai keanggotaan satu atau nol, maka pada graf fuzzy, setiap titik dan sisinya memiliki nilai keanggotaan yang terletak pada interval tutup [0,1]. Nilai keanggotaan setiap elemen ini menyatakan derajat keanggotaan elemen tersebut dalam graf fuzzy.

Sejak diperkenalkan graf fuzzy ini, para peneliti mulai menggeneralisasi dan mengembangkan beberapa kajian dalam graf klasik ke dalam graf fuzzy baik secara teori maupun aplikasi. Secara aplikasi graf fuzzy dapat dikatakan sebagai suatu topik yang dapat diterapkan dalam ilmu dan teknologi modern khususya dalam bidang teori informasi, jaringan syaraf, analisis cluster, diagnosa medis, dan teori kontrol [3]. Dey A, dan Anita P [3], telah mengaplikasikan graf fuzzy untuk menyelesaikan masalah traffic light dan Swaminathan [4], telah menerapkan graf fuzzy ke dalam masalah pengalokasian pekerjaan.

Secara teori, Yeh dan Bang [5] juga telah memperkenalkan beberapa konsep yang berhubungan dengan graf fuzzy seperti konsep keterhubungan pada graf fuzzy. Setelah konsep-konsep dalam graf fuzzy diperkenalkan, hasil-hasil teoritis yang lebih mendalam tentang graf fuzzy banyak diberikan, diantaranya oleh Moderson dan Peng [6] memperkenalkan konsep operasi-operasi pada graf fuzzy antara lain operasi gabungan, join, hasil kali kartesian, dan komposisi pada dua graf fuzzy. Selanjutnya Dogra [1] telah mendefinisikan operasi perkalian modular pada graf fuzzy dan menyelidiki sifat operasi modular pada dua graf fuzzy sembarang serta graf fuzzy efektif. Dalam artikelnya, Dogra [1] belum mengkaji sifat-sifat operasi perkalian modular pada graf fuzzy yang berkaitan dengan graf fuzzy lengkap, graf fuzzy komplemen, dan graf fuzzy isomorfis. Oleh karena itu berdasarkan uraian tersebut, tujuan dari penulisan artikel ini adalah menyelidiki sifat operasi perkalian modular pada dua graf fuzzy lengkap, operasi perkalian modular pada komplemen dari dua graf fuzzy efektif dan menunjukan bahwa perkalian modular graf fuzzy G1 dan graf fuzzy G2 isomorfik dengan perkalian modular G2 dan G1.

II. METODE PENELITIAN

Metode penelitian yang digunakan dalam penelitian ini adalah studi literatur mengenai operasi perkalian modular pada graf fuzzy yang didefinisikan oleh Dogra [1]. Selanjutnya perkalian modular ini dikenakan pada dua graf fuzzy lengkap, dan komplemen dari graf fuzzy efektif. Hasil operasi perkalian modular ini selanjutnya dituangkan sebagai sifat-sifat operasi perkalian modular yang ditulis dalam bentuk bukti secara sistematis.

III. HASIL DAN PEMBAHASAN

Definisi yang terdapat dalam artikel ini diambil dari [1], [6].

Definisi 3.1. Graf fuzzy. Misal V adalah himpunan tak kosong dan berhingga. Suatu graf fuzzy G

dinotasikan dengan _G₍ _{, )} adalah pasangan fungsi



yang menyatakan himpunan fuzzy dari V dan µ merupakan relasi fuzzy simetris pada



sedemikian sehingga:

i.



:V[0, 1]

ii.µ V V:  [0, 1] yang memenuhi ( , )



( ), ( ) ,



i j min i j

µ v v   v  v untuk setiap , v v_{i j}V. Selanjutnya,



disebut sebagai himpunan titik fuzzy dan µ disebut sebagai himpunan sisi fuzzy. Notasi



( )

v

_i pada graf fuzzy menyatakan derajat keanggotaan dari titik

v

_i dan

µ v v

(

_i

,

_j

)

menyatakan derajat keanggotaan dari sisi (v v_i, _j). Graf fuzzy yang dibahas dalam artikel ini adalah graf fuzzy sederhana, sehingga berlaku (v vi, i)0 untuk setiap viV. Gambar 1., merupakan graf fuzzy.

1(0, 4) v v₂(0, 6) 4( )1 v 3(0, 8) v 0, 4 0, 6 0, 8 0, 2 0, 4

GAMBAR 1. GRAF FUZZY

G



(

 

,

)

Definisi 3.2. Graf dasar dari graf fuzzy. Graf dasar dari graf fuzzy G( , ) dinotasikan dengan

*,

* (

*)

G



 

dengan * merujuk pada himpunan tak kosong V dan * = E  V x V adalah graf fuzzy dengan setiap titik dan sisi di

G



(

 

,

)

mempunyai derajat keanggotaan 1.

Definisi 3.3. Perkalian modular pada dua graf fuzzy. Misalkan

G

₁



(

 

₁

,

₁

)

dan

2 ( 2, 2)

G 

 

adalah dua graf fuzzy dengan masing-masing graf dasar *

1 ( ,1 1)

G  V E , *

2 ( ,2 2)

G  V E , dan V₁  V₂ . Jika perkalian modular dari G1* dan G2* adalah G*

G

1*

⊙

G

2*



( , )V E dengan himpunan titik dan

sisinya didefinisikan sebagai

i.

V



V

₁

⊙

V

₂

  

V V

_{1 2}

{( , ) |

u v u V v V



₁

,



₂

}

ii. EE₁⊙E₂{(( ,u v_{i j})( , )) |u v_{k l} u u_{i k}E v v₁, _{j l}E₂ atau

u u

_{i k}



E v v

₁

,

_{j l}



E

₂

}

dimana 1

,

1, 2,...,|

|

i k



V

2 , 1, 2,...,| | j l V

dengan syarat ik dan jl , maka perkalian modular dari dua graf fuzzy G₁( ₁, ₁) dan

2 ( 2, 2)

G    dinotasikan dengan

1 2 ( 1 2, 1 2)

GG⊙G   ⊙ ⊙ adalah pasangan fungsi yang

i.

(



₁

⊙



₂

)( , )

u v





₁

( )

u





₂

( )

v

, dimana 1 uV dan

v V



₂ ii. 1 2 1 2 1 2 1 1 2 2 1 2

(

)

(

),

(

)(( ,

)( , ))

( )

( )

( )

( ),

i k j l i k j l i j k l i j k l i k j l

u u

v v

u u

E dan v v

E

u v

u v

u

u

v

v

u u

E dan v v

E









 



_

_

_



_

_

_

_

_





_



⊙

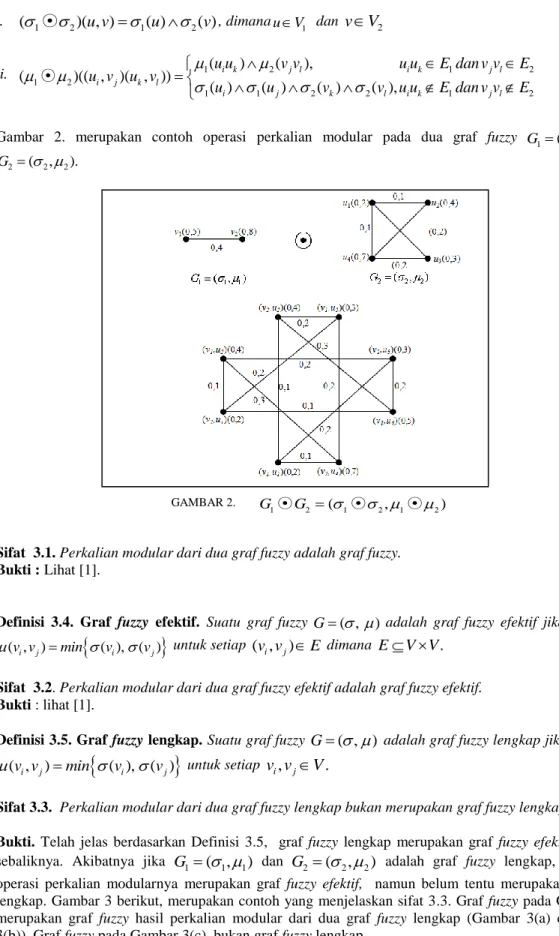
Gambar 2. merupakan contoh operasi perkalian modular pada dua graf fuzzy G₁( ₁, ₁) dan

2 ( 2, 2).

G   

GAMBAR 2.

Sifat 3.1. Perkalian modular dari dua graf fuzzy adalah graf fuzzy. Bukti : Lihat [1].

Definisi 3.4. Graf fuzzy efektif. Suatu graf fuzzy G(

 

, ) adalah graf fuzzy efektif jika memenuhi





(v v_i, _j) min ( )v_i , ( )v_j

    untuk setiap (

v v

_i

,

_j

)



E

dimana E V V.

Sifat 3.2. Perkalian modular dari dua graf fuzzy efektif adalah graf fuzzy efektif. Bukti : lihat [1].

Definisi 3.5. Graf fuzzy lengkap. Suatu graf fuzzy

G



(

 

,

)

adalah graf fuzzy lengkap jika memenuhi





(v v_i, _j) min ( )v_i , ( )v_j









untuk setiap

v v

_i

,

_j



V

.

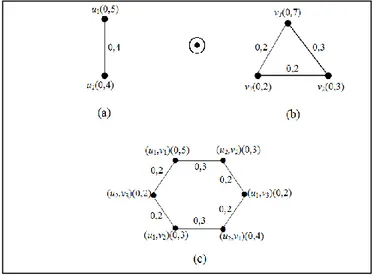
Sifat 3.3. Perkalian modular dari dua graf fuzzy lengkap bukan merupakan graf fuzzy lengkap.

Bukti. Telah jelas berdasarkan Definisi 3.5, graf fuzzy lengkap merupakan graf fuzzy efektif dan tidak sebaliknya. Akibatnya jika

G

₁



(

 

₁

,

₁

)

dan

G

₂



(

 

₂

,

₂

)

adalah graf fuzzy lengkap, maka hasil operasi perkalian modularnya merupakan graf fuzzy efektif, namun belum tentu merupakan graf fuzzy lengkap. Gambar 3 berikut, merupakan contoh yang menjelaskan sifat 3.3. Graf fuzzy pada Gambar 3(c) merupakan graf fuzzy hasil perkalian modular dari dua graf fuzzy lengkap (Gambar 3(a) dan Gambar 3(b)). Graf fuzzy pada Gambar 3(c), bukan graf fuzzy lengkap.

1 2 ( 1 2, 1 2)

GAMBAR 3. (a) Graf fuzzy lengkap

G

₁ (b) Graf fuzzy lengkap

G

₂

(c) Graf fuzzy

G

₁⊙

G

₂

Definisi 3.6. Komplemen dari graf fuzzy. Misal V adalah himpunan tak kosong. Komplemen dari graf

fuzzy G( , )  adalah graf fuzzy C ( C, C)

G    dimana



C



_dan





( , ) ( ), ( ) ( , ) C i j i j i j v v min v v v v













untuk setiap v vi, jV.

Sifat 3. 4. Misal diberikan graf fuzzy efektif

G

₁ dan graf fuzzy efektif

G

₂. Jika

1 C G dan 2 C G adalah graf fuzzy komplemen dari G₁ dan G₂ maka

G

₁C⊙

G

₂C



G

₁⊙

G

₂.

Bukti. Misalkan diberikan dua himpunan tak kosong

V

₁ dan

V

₂. Selanjutnya diberikan dua graf fuzzy efektif G₁(

 

₁, ₁) dan

G

₂



(

 

₂

,

₂

)

. Graf

G

₁C



(

 

₁C

,

₁C

)

adalah komplemen dari graf

1

(

1

,

1

)

G



 

. Graf

G

₂C



(

 

₂C

,

₂C

)

adalah komplemen dari graf G₂(

 

₂, ₂). Berdasarkan Definisi 3.6.,

1

C

G memiliki derajat keanggotaan titik ₁C

( )

₁

( )

u

u







dan sisi 1 ( ) min{ ( ),1 1( )} 1( ) C i k i k i k u u u u u u













. Hal ini berlaku pula pada

2

C

G memiliki derajat keanggotaan titik



₂C

( )

u





₂

( )

u

, dan sisi ₂C( ) min{ ₂( ), ₂( )} ₂( )

i k i k i k

u u u u u u













Sisi pada graf

G

₁C terbagi menjadi dua kasus.

Kasus 1. Jika

u u

_{i k}



E

₁, maka



₁

(

u u

_{i k}

)



min{ ( ),



₁

u

_i



₁

(

u

_k

)}

.

Hal ini berarti



₁C

(

u u

i k

)



min{ ( ),



₁

u

i



₁

(

u

k

)} min{ ( ),





₁

u

i



₁

(

u

k

)}



0

.

Dengan kata lain

u u

_{i k}



E

₁C. Kasus 2. Jika

u u

_{i k}



E

₁ , maka

1(u ui k) 0

  .

Hal ini berarti ₁C

(

)

min{ ( ),

_{1 1}

( )} 0

i k i k

u u

u

u













min{ ( ),



₁

u

i



₁

( )}

u

k Dengan kata lain

u u

_{i k}



E

₁C.

Analog untuk G₂. Graf fuzzy efektif G2, memiliki derajat keanggotaan titik



2

( )

v

dan derajat keanggotaan sisi



₂

(

v v

_{j l}

)



min{



₂( ),vj



₂( )}vl . Graf 2

C

G memiliki derajat keanggtaan titik

2 ( ) 2( )

C

v v

2 ( ) C

j l

v v



min{



₂( ),v_j



₂( )}v_l 



₂(v v_{j l}). Sisi pada graf

G

₂C juga terbagi dalam dua kasus.

Kasus 1. Jika v v_{j l}E₂, maka



₂

(

v v

_{j l}

)



min{



₂

( ),

v

_j



₂

( )}

v

_l . Hal ini berarti

2 ( ) min{ ( ),2 2( )} min{ ( ),2 2( )} C j l j l j l v v v v v v

















0

. Dengan kata lain ₂C

j l

v v



E

. Kasus 2. Jika 2 j l v v E maka 2

(

v v

j l

)

0





.

Hal ini berarti ₂C( ) min{ ₂( ), ₂( )} 0

j l j l

v v v v













min{



₂

( ),

v

j



₂

( )}

v

l Dengan kata lain

2 C j l

v v E .

Selanjutnya sesuai Definisi 3.3., hasil perkalian modular dari

1 C G dan 2 C G dinotasikan dengan 1 2 C C

G

⊙

G



(



₁C⊙

 

₂C, ₁C⊙



₂C) adalah pasangan fungsi dengan (i)

(

₁C ₂C

)( , )

₁C

( )

₁C

( )

u v

u

v



⊙















1( )u 



1( )v 1 2 (

 

)( , )u v  ⊙ . (ii) 1 2

(



C⊙



C)( , )( , )u vi j u vk l yang terbagi menjadi dua kasus, yaitu: Kasus 1. ₁C i k

u u



E

dan 2 C j l v vE .

(

₁C ₂C

)(( ,

)(

, ))

₁C

( )

₁C

(

)

₂C

( )

₂C

( )

i j k l i j k l

u v

u v

u

u

v

v



⊙























1( )ui 



1( )uj 



2( )vk 



2( )vl 1 2 (

 

)(( ,u v_{i j})( , )u v_{k l}  ⊙ . Kasus 2. ₁C i k

u u



E

dan 2 C j l v vE . 1 2 1 2 ( C C)(( , )( , )) C( ) C( ) i j k l i k j l u v u v u u v v



⊙











min{ ( ),



₁ui



₁( )} min{uk 



₂( ),vj



₂( )}vl 1(u ui k) 2(v vj l)





  .

Akibatnya dari (i) dan (ii), diperoleh bahwa

(

₁C ₂C

)( , )

(

_{1 2}

)( , )

u v

u v



⊙





 

⊙ dan _{( 1}C ₂C_{)( , )}

i j u v  ⊙

(

u v

_k

, )

_l





1

(

u u

i k

)





2

(

v v

j l

)

. Dengan demikian terbukti bahwa 1 2

C C

G

⊙

G



G

₁⊙

G

₂

.

∎ Definisi 7. Misal





1 1, 1 G    dan





2 2, 2

G    adalah dua graf fuzzy dengan himpunan titik V1, V2. Jika terdapat pemetaan bijektif

1 2 : f V V yang memenuhi : i. ₁

 

u ₂



f u( )



 u V₁ ii.



₁

 

_{u v}

_,





₂



_{f u}

_{( ), ( )}

_{f v}





_{u v V}

_,



₁ maka dikatakan





1 1, 1 G    dan





2 2, 2

G    saling isomorfis, dan dinotasikan dengan

1 2. G G Sifat 3. 5. 1 2 G ⊙G  2 1 G ⊙G

Bukti : Untuk membuktikan sifat ini, diambil sembarang (u,v) V1 x V2, akan dibuktikan ada pemetaan bijektif f: V1 x V2 →V2 x V1 yang memenuhi

i.

(



₁

⊙



₂

)( , ) (

u v





₂

⊙



₁

)( ( ), ( )),

f u

f v

ii.

(



₁

⊙



₂

)(( ,

u v

i j

)( , )) (

u v

k l





₂

⊙



₁

)( ( ,

f u v f u v

i j

) ( , )), ( ,

k l



u v

i j

), ( , )

u v

k l



V xV

_{1 2} Berdasarkan definisi 3.3, diperoleh

1 2 ( 1 2, 1 2)

G⊙G 



⊙

 

⊙



dengan

1 2 1 2 2 1 2 1 2 1

(

)( , )

( )

( )

( )

( )

(

)( , )

(

)( ( ), ( ))

u v

u

v

v

u

v u

f u

f v

































⊙

⊙

⊙

dan 1 2 1 2 2 1 2 1 2 1 1 2

(

)(( ,

)( , ))

(

)

(

)

(

)

(

)

(

)(( , )( ,

))

(

)( ( ,

) ( , )) ,

.

i j k l i k j l j l i k j i l k i j k l i k j l

u v

u v

u u

v v

v v

u u

v u

v u

f u v

f u v

untuk u u

E dan v v

E





































⊙

⊙

⊙

1 2 1 1 2 2 2 2 1 1 2 1 2 1 2 1 1 2

(

)(( ,

)( , ))

( )

( )

( )

( )

( )

( )

( )

( )

(

)

(

)

(

)(( , )( ,

))

(

)( ( ,

) ( , )),

.

i j k l i k j l j l i k j l i k j i l k i j k l k i l j

u v

u v

u

u

v

v

v

v

u

u

v v

u u

v u

v u

f u v

f u v

untuk u u

E dan v v

E





























































⊙

⊙

⊙

Berdasarkan bukti (i) dan (ii), diperoleh G₁⊙G₂G₂⊙G₁. ∎

IV. SIMPULAN DAN SARAN

A. Simpulan

Dari pembahasan yang telah diberikan dapat disimpulkan sebagai berikut :

a) Perkalian modular dari dua graf fuzzy lengkap bukan merupakan graf fuzzy lengkap. b) Jika G1 dan G2 graf fuzzy efektif, maka

1 2 1 2

C C

G ⊙G G⊙G . c) G₁⊙G₂G₂⊙G₁.

B. Saran

Perlu dikembangkan operasi perkalian modular dari n graf fuzzy. Apakah sifat-sifat operasi perkalian modular pada dua graf fuzzy juga berlaku untuk perkalian modular dari n graf fuzzy?.

DAFTAR PUSTAKA

[1] Dogra, S. 2015. Different Types of Product of Fuzzy Graphs. Progress in Nonlinear Dynamics and Chaos. Vol. 3 No. 1, pp. 41- 56.

[2] Rosenfeld, A.,. 1975,Fuzzy Graphs, “Fuzzy Sets and their Applications to Cognitive and Decesion Processes” (eds. L.A

Zadeh,K.S. Fu & M. Shimura), Academic Press, New York, Pp. 77-95.

[3] Dey A, dan Anita P. , 2013, Fuzzy Graph Coloring Technique to Classify The Accidental Zone of a Traffic Control Annals of Pure and Applied Mathematics. Vol. 3 No.2, pp. 169-178.

[4] Swaminathan S., 2012, Fuzzy Graph Applications of Job Allocation, International Journal of Engineering anf Innovative Technology, Vol. 1., Issue 2, .

[5] Yeh RT dan Bang SY, 1975, Fuzzy Relations, Fuzzy Graphs and their Application to clustering analysis, In Zadeh L A, Fu

KS & Shimura M (eds). Fuzzy Sets and their Applications to Cognitive and Decesion Processes), Academic Press, New York,

pp. 125-149.

[6] Mordeson, J.N dan Peng C,S. 1994. Operation on Fuzzy Graphs , Information Science 79, pp 159-170. i.