BAB 4
HASIL DAN PEMBAHASAN
4.1 Proses Pengolahan Data
Data yang akan diolah ditampilkan dalam bentuk tabel-tabel, diagram pencar, dan grafik menggunakan fitur yang tersedia oleh R Language.
Kemudian dilakukan pengolahan data menggunakan metode Kuadrat Terkecil Biasa dan metode Kuadrat Median Terkecil.
Dengan memperhatikan segi efisiensi maka tidak semua data akan ditampilkan oleh penulis, tidak semua proses pengolahan diuraikan, hanya hasil pengolahan, persamaan regresi, dan nilai standar error. Data dibangkitkan dengan fungsi rnorm dan rcauchy (pada R Language), data sekunder langsung tidak lagi dimodifikasi penulis(langsung digunakan). Proses penelitian dengan R Language, pada data sample yang dibangkitkan dengan fungsi rnorm dan rcauchy. Fungsi rnorm adalah menghasilkan bilangan acak dengan sebaran normal baku, sedangkan pada fungsi rcauchy, untuk memunculkan outlier. Untuk memperbesar ukuran nilai digunakan fungsi runif yang memperbesar nilai pada rnorm
4.1.1 Penyajian dan analisis data cell
Sintak yang digunakan untuk menampilkan data Cell:
>data(cell)
>data.entry(cell)
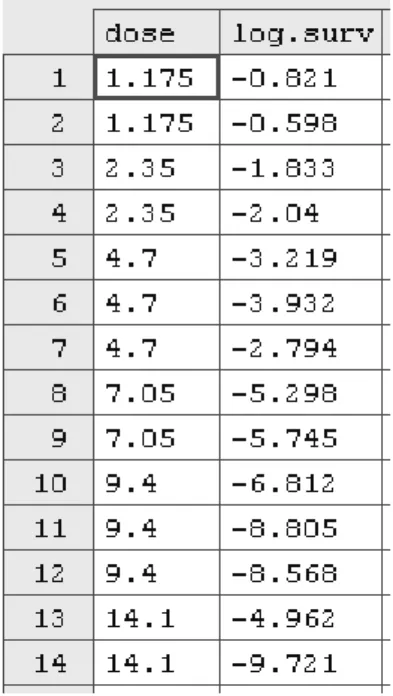
Hasil output data disajikan dalam table 4.1 :
Tabel 4.1 tabel data Cell
Untuk lebih jelas, data Cell kemudian data akan ditampilkan dalam bentuk scatter plot(diagram pencar).
> x <- cell[ , 1]
> y <- cell[ , 2]
> op<-par(mfrow=c(1,1),pty="s")
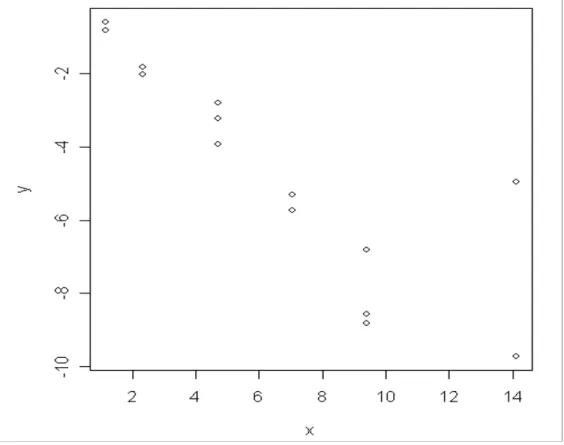
> plot(x,y)
Gambar 4.1 Diagram pencar data Cell
Dari data tersebut terlihat tidak ada hubungan antara kedua variabel. Berdasarkan besaran koefisien korelasi dan diagram pencar menunjukkan asumsi bahwa tidak terjadi multikolinieritas pada data.
4.1.1.1 Metode Kuadrat Terkecil Biasa untuk Sampel Data Cell
Dari data Cell, data diolah menggunakan metode Kuadrat Terkecil Biasa.
Statement dalam R Language adalah sebagai berikut :
> library(stats)
> data(cell)
> attach(cell)
> x<-cell[ ,1]
> y<-cell[ ,2]
> matx<-matrix(x,ncol=1)
> matx2<-cbind(1,matx)
> xt<-t(matx2)
> xtx<-xt%*%matx2
> invtxtx<-solve(xtx)
> maty<-matrix(y,ncol=1,byrow=F)
> xty<-t(matx2)%*%maty
> reg1<-invxtx%*%xty
perhitungan dengan modul lm
> reg2<-lm(y~x)
> reg2
> ypre=reg2$fit
> residual=reg2$res
> data.entry(x,y,ypre,residual)
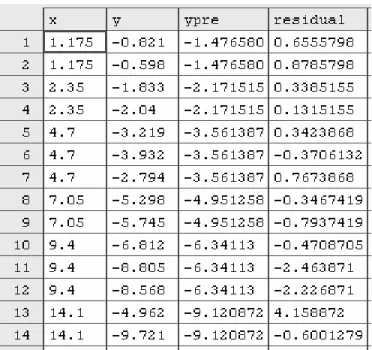
Hasil pengolahan data ditunjukkan pada tabel 4.2
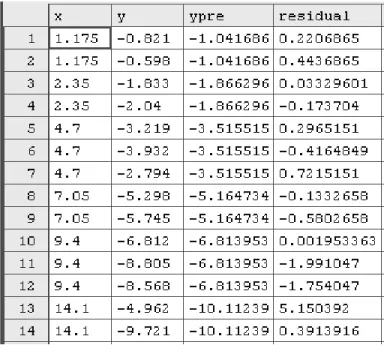
Tabel 4.2 Hasil regresi dengan Metode Kuadrat Terkecil Biasa
Keterangan :
ypre menunjukkan y estimasi (Ŷ)
residual menunjukkan selisih antara y dengan y estimasi
Dengan menggunakan metode Kuadrat Terkecil Biasa diperoleh Persamaan regresi : Ŷ : -0.7816 - 0.5914 x
Nilai standar error : 1.564879
Korelasi antara nilai residual dengan y estimasi ditunjukkan oleh pada Gambar 4.2 . Statement dalam R Language adalah :
> library(graphics)
> op<-par(mfrow=c(1,1),pty="s")
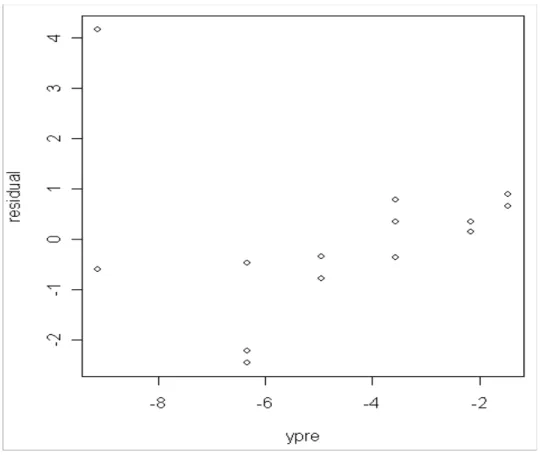
> plot(ypre,residual)
Dihasilkan dalam bentuk diagram pencar :
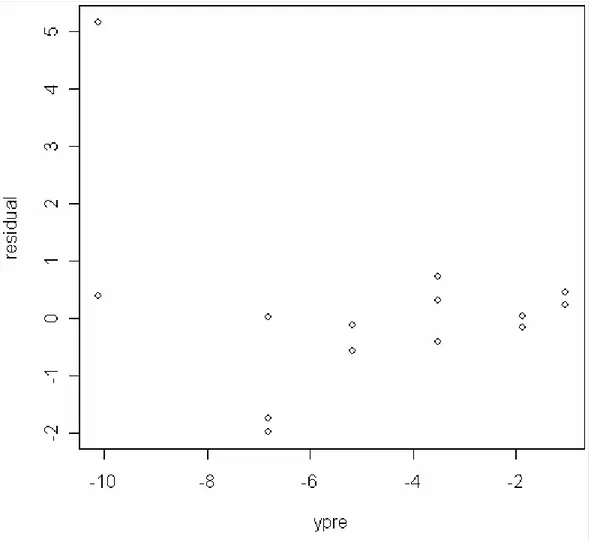
Gambar 4.2 Diagram Pencar Ŷ dengan residual
Dari gambar terlihat bahwa residual tidak dipengaruhi oleh besarnya nilai y estimasi, dan nilai x.
4.1.1.2 Distribusi Pada Data Cell
Statement R Language untuk memperoleh nilai distribusi :
> library(graphics)
> residual=reg2$res
> plot(density(residual))
Hasil ditunjukkan pada gambar 4.3
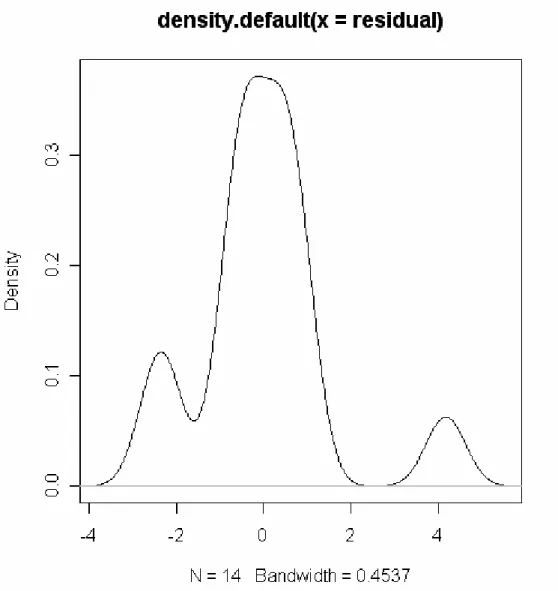
Gambar 4.3 Bentuk Distribusi Data Cell
Bentuk disribusi menunjukkan kurva normal yang mempunyai arti sebaran data berdistribusi normal..
4.1.1.3 Metode Kuadrat Median Terkecil Untuk Data Cell
Pengolahan data dilanjutkan dengan penggunaan metode yang berbeda, yaitu dengan Metode Kuadrat Median Terkecil.
Statement dalam R Language
> library(bootstrap)
> data(cell)
> x <- cell[ , 1]
> y <- cell[ , 2]
> library(lqs)
> fred <- lmsreg(y ~ x )
> ypre<-fred$fit
> residual<-fred$res
> data.entry(x,y,ypre,residual)
Hasil pengolahan ditunjukkan dengan tabel 4.3
Tabel 4.3 Hasil Regresi Dengan Metode Kuadrat Median Terkecil
Keterangan :
ypre adalah y estimasi (Ŷ)
residual adalah selisih antara y dengan y estimasi
Dengan menggunakan metode Kuadrat Median Terkecil didapat : Persamaan regresi : Ŷ = -0.2170769 -0.7017954 x
Nilai standar error : 1.374392
Diagram pencar antara y estimasi dan residual pada gambar 4.4
> library(graphics)
> op<-par(mfrow=c(1,1),pty="s")
> plot(ypre,residual)
Gambar 4.4 Diagram pencar Ŷ Dengan Residual
4.1.1.4 Distribusi Pada Data Cell
Statement R Language untuk memperoleh nilai distribusi terhadap residual:
> library(graphics)
> residual=fred$res
> plot(density(residual))
Hasil ditunjukkan pada gambar 4.5
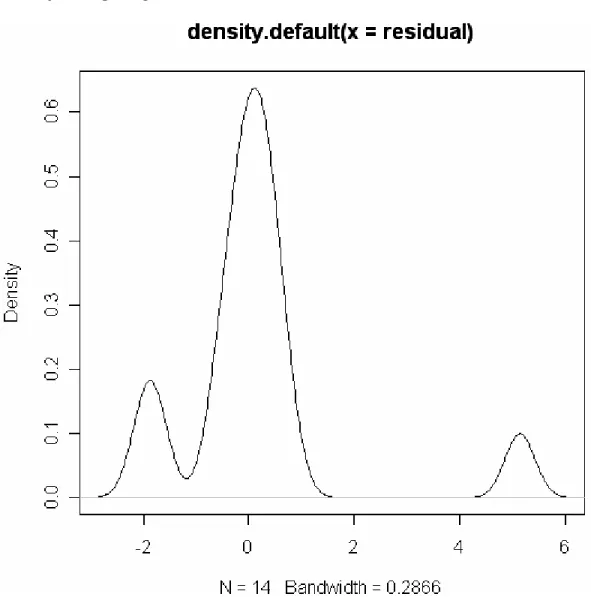
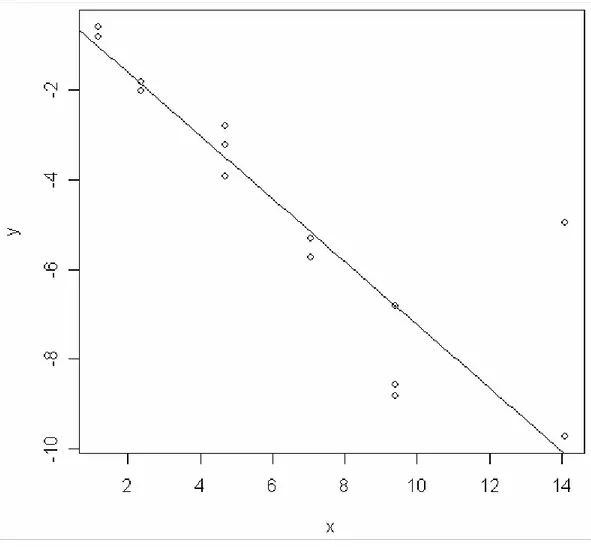
Gambar 4.5 Bentuk Distribusi Residual Dari Kuadrat Median Terkecil Persamaan regresi ditunjukkan pada gambar 4.6
> plot(x, y)
> curve(predict(fred, data.frame(x = x)), add = TRUE)
Gambar 4.6 Garis Persamaan Regresi dari Metode Kuadrat Median Terkecil Metode Kuadrat Median Terkecil melakukan pencarian median kuadrat residu sehingga didapat standar error terkecil dengan melakukan perulangan, tampak pada gambar 4.7 Statement R Language yang digunakan adalah :
> resid <- residuals(fred)
> pred <- predict(fred)
> n <- length(x)
> nboot <- 1000
> beta1.star <- double(nboot)
> beta2.star <- double(nboot)
> for (i in 1:nboot) {
+ k.star <- sample(n, replace = TRUE) + y.star <- pred + resid[k.star]
+ sally <- lmsreg(y.star ~ x)
+ curve(predict(sally, data.frame(x = x)), + add = TRUE, col = "lightseagreen") + beta1.star[i] <- coefficients(sally)[2]
+ }
> points(x, y, pch = 16)
> curve(predict(fred, data.frame(x = x)), + add = TRUE, lwd = 2)
Gambar 4.7 Grafik perulangan LMS regresi
4.1.2 Penyajian dan Analisis dari data yang dibangkitkan n=50
Data akan dibangkitkan dengan R Language. Statement yang digunakan adalah sebagai berikut:
> library(stats)
> n=50
> set.seed(12340)
> p=15*runif(n)
> set.seed(12341)
> x=p+12*runif(n)+rnorm(n)+rcauchy(n)
> set.seed(12342)
> y=x+3*rnorm(n)
> data.entry(x,y)
Hasil pembangkitan data disajikan pada tabel 4.4 Tabel 4.4 Hasil pembangkitan sampel dengan n=50
.
.
Keterangan :
y menunjukkan variabel tidak bebas, x menunjukkan variabel bebas
Diagram pencar dari x dan y adalah ditunjukkan oleh gambar 4.8
Gambar 4.8 Diagram Pencar x dan y
4.1.2.1 Metode Kuadrat Terkecil Biasa Untuk n=50
Selanjutnya dilakukan pengolahan data menggunakan metode Kuadrat Terkecil Biasa. Statement R Language yang digunakan adalah:
> library(stats)
> matx<-matrix(x,ncol=1)
> matx2<-cbind(1,matx)
> xt<-t(matx2)
> xtx<-xt%*%matx2
> invtxtx<-solve(xtx)
> maty<-matrix(y,ncol=1,byrow=F)
> xty<-t(matx2)%*%maty
> reg1<-invxtx%*%xty
perhitungan dengan modul lm
> l<-lm(y~x)
> l
> ypre=l$fit
> residu=l$res
> data.entry(x,y,ypre,residu)
Tabel 4.5 Hasil Pengolahan Dengan Metode Kuadrat Terkecil
. .
Keterangan :
ypre menunjukkan y estimasi (Ŷ)
residual menunjukkan selisih antara y dengan y estimasi
Dengan menggunakan metode Kuadrat Terkecil Biasa diperoleh Persamaan regresi : Ŷ : 0.2751 + 0.9635 x
Nilai standar error : 3.559953
Korelasi antara nilai residual dengan y estimasi ditunjukkan oleh pada Gambar 4.2 . Statement dalam R Language adalah :
> library(graphics)
> op<-par(mfrow=c(1,1),pty="s")
> plot(ypre,residu)
Dihasilkan dalam bentuk diagram pencar :
Gambar 4.9 Diagram Pencar Ŷ terhadap residu 4.1.2.2 Distribusi Pada Sampel n=50
Statement R Language untuk memperoleh nilai distribusi terhadap residual:
> library(graphics)
> residu=l$res
> plot(density(residu))
Hasil ditunjukkan pada gambar 4.10
Gambar 4.10 Distribusi Data Dari Residu
Kurva berbentuk lonceng, sehingga data berdistribusi normal.
4.1.2.3 Metode Kuadrat Median Terkecil Data Sampel
Data kemudian diolah dengan penggunaan Metode Kuadrat Median Terkecil.
Statement dalam R Language untuk metode Kuadrat Median Terkecil
> library(bootstrap)
> data(cell)
> library(lqs)
> fred <- lmsreg(y ~ x )
> ypre<-fred$fit
> residual<-fred$res
> data.entry(x,y,ypre,residual)
Hasil pengolahan ditunjukkan dengan tabel 4.6
Tabel 4.6 Hasil Estimasi Dengan Kuadrat Median Terkecil
. .
Keterangan :
prde adalah y estimasi (Ŷ)
resid adalah selisih antara y dengan y estimasi
Dengan menggunakan metode Kuadrat Median Terkecil didapat : Persamaan regresi : Ŷ = 0.3641222 + 0.9572739 x
Nilai standar error : 3.327453
>plot(x,y)
> for(i in 1:nboot){
k.star<-sample(n,replace=TRUE) y.star<-pred+resid[k.star]
sally<-lmsreg(y.star~x ,nsamp=”exact”)
curve(predict(sally,data.frame(x=x)),add=TRUE,col="lightseagreen") }
> points(x, y, pch = 16)
> curve(predict(fred, data.frame(x = x)),
+ add = TRUE, lwd = 2)
Gambar 4.11 Grafik perulangan Dalam LMS
4.1.3 Penyajian Dan Analisis Pada Data Hawkins
Data set Hawkins Bradu Kas (1984) terdiri dari 128 observasi dan 3 variabel bebas.
Data ini memiliki banyak nilai outlier.
>library(MASS)
>library(lqs)
#data set Hawkins et al.(1984)
> y<-
c(8.88,12.18,5.75,11.75,10.52,10.57,1.70,5.31,8.51,1.21,3.36,8.26,10.14,-0.58,7.10,- 0.63,5.87,-0.25,-9.45,8.93,18.88,4.01,8.48,-0.16,7.26,1.69,-4.46,3.36,7.53,3.91,6.73,- 2.91,8.80,1.80,-2.40,6.25,15.60,1.06,9.99,2.10,1.63,5.84,-2.30,1.42,2.67,-
6.93,0.75,14.31,2.93,2.06,5.97,9.78,10.20,8.90,7.55,7.11,12.60,2.80,5.88,3.38,7.10,4.43,9 .47,4.92,2.44,2.03,10.35,5.65,2.02,3.45,8.94,9.69,13.81,2.66,2.55,5.61,3.21,3.41,3.95,2.2 8,10.65,5.70,7.35,6.69,6.01,1.01,10.14,-2.33,4.05,-0.90,10.72,-2.72,-0.52,16.00,-
0.55,4.77,2.27,8.13,7.36,4.71,2.93,3.42,6.78,4.97,0.47,7.64,4.90,6.91,6.46,6.94,-
8.69,11.03,4.18,5.16,8.70,6.83,3.27,1.71,7.78,0.20,6.86,12.06,7.10,11.21,5.79,15.30,7.33, 7.76)
> x1<-
c(-15,9,-3,-19,-3,11,11,-11,-3,9,-3,-9,5,-11,-3,7,9,11,-1,-7,1,-3,-11,13,-21,-1,1,-
1,5,7,3,15,5,-5,-13,7,-7,-1,-3,-9,-3,-9,7,7,-5,7,-3,-15,-5,3,3,-11,11,-15,-5,3,5,-9,5,-11,-9,- 3,11,17,-1,-15,13,3,-17,9,1,3,13,-7,3,9,17,13,15,1,-7,-9,-17,-9,21,9,-13,1,3,23,-1,-3,11,- 7,-13,-1,-5,-9,5,19,7,-1,-23,15,-7,17,1,11,1,5,-13,-17,-5,-11,-7,-5,9,17,3,15,-17,1,3,- 5,9,5,-11,3)
> x2<-
c(2,18,16,8,-8,-16,-18,16,-6,6,-8,26,-6,8,18,-2,8,16,2,10,-2,-18,-26,0,0,-10,8,0,-18,0,16,- 2,-8,8,-2,-10,2,2,-18,-18,-16,-6,0,10,10,2,16,-8,-2,-18,6,18,18,-10,18,-16,-8,-8,-8,6,2,26,- 8,-16,0,0,2,-16,-16,10,10,16,-10,0,8,-2,18,-8,0,10,0,-8,-8,-8,0,-26,0,8,18,8,-8,-16,26,-2,8,- 10,8,-10,26,-8,0,-8,-8,8,-10,16,0,-6,0,2,10,-18,8,-18,0,6,8,8,18,10,16,-2,8,-26,8,-10,-16,- 26)
> x3<-
c(59,74,49,95,57,97,27,62,56,60,43,53,72,67,24,61,68,7,10,58,76,69,78,6,43,49,2,49,67, 68,77,1,97,1,7,94,89,28,92,94,7,11,1,1,93,38,16,96,23,68,89,88,73,80,84,80,98,19,79,21, 94,69,31,59,31,29,73,48,81,25,58,25,24,44,83,49,33,6,22,14,78,28,82,75,90,40,94,6,12,1, 61,30,2,53,23,57,14,91,95,67,9,5,58,97,18,8,23,87,58,76,9,89,70,81,82,98,25,9,86,11,59, 91,62,91,87,92,64,53)
Hasil output data disajikan dalam table 4.1 :
Tabel 4.7 tabel data Hawkins
. .
4.1.3.1 Matrix Korelasi data Hawkins
Dari data Cell kemudian akan dilihat korelasi dalam bentuk matrik korelasi, untuk melihat apakah ada hubungan antar variabel.
Matrik korelasi dalam R Language adalah :
>library(base)
> mat=matrix(c(x1,x2,x3),ncol=3)
> round(cor(mat),4)
Hasil pengolahan ditampilkan sebagai berikut:
Dari matrik korelasi terlihat bahwa hubungan kedua variabel dalam data Cell cukup besar, nilai ini dianggap cukup besar sehingga disimpulkan adanya korelasi
(multikolinieritas).
Untuk lebih jelas, data Cell kemudian data akan ditampilkan dalam bentuk scatter plot(diagram pencar).
> op<-par(mfrow=c(1,3),pty="s")
> plot(x1,x2)
> plot(x1,x3)
> plot(x2,x3)
Hubungan antara variabel x ditunjukkan pada gambar 4.12
Gambar 4.12 Diagram pencar data Hawkins
4.1.3.2 Metode Kuadrat Terkecil Biasa untuk Sampel Data Hawkins
Dari data Hawkins, data kemudian diolah menggunakan metode Kuadrat Terkecil Biasa.
Statement dalam R Language adalah sebagai berikut :
> library(stats)
> y<-
c(8.88,12.18,5.75,11.75,10.52,10.57,1.70,5.31,8.51,1.21,3.36,8.26,10.14,-0.58,7.10,- 0.63,5.87,-0.25,-9.45,8.93,18.88,4.01,8.48,-0.16,7.26,1.69,-4.46,3.36,7.53,3.91,6.73,- 2.91,8.80,1.80,-2.40,6.25,15.60,1.06,9.99,2.10,1.63,5.84,-2.30,1.42,2.67,-
6.93,0.75,14.31,2.93,2.06,5.97,9.78,10.20,8.90,7.55,7.11,12.60,2.80,5.88,3.38,7.10,4.43,9 .47,4.92,2.44,2.03,10.35,5.65,2.02,3.45,8.94,9.69,13.81,2.66,2.55,5.61,3.21,3.41,3.95,2.2 8,10.65,5.70,7.35,6.69,6.01,1.01,10.14,-2.33,4.05,-0.90,10.72,-2.72,-0.52,16.00,-
0.55,4.77,2.27,8.13,7.36,4.71,2.93,3.42,6.78,4.97,0.47,7.64,4.90,6.91,6.46,6.94,-
8.69,11.03,4.18,5.16,8.70,6.83,3.27,1.71,7.78,0.20,6.86,12.06,7.10,11.21,5.79,15.30,7.33, 7.76)
> x1<-
c(-15,9,-3,-19,-3,11,11,-11,-3,9,-3,-9,5,-11,-3,7,9,11,-1,-7,1,-3,-11,13,-21,-1,1,-
1,5,7,3,15,5,-5,-13,7,-7,-1,-3,-9,-3,-9,7,7,-5,7,-3,-15,-5,3,3,-11,11,-15,-5,3,5,-9,5,-11,-9,- 3,11,17,-1,-15,13,3,-17,9,1,3,13,-7,3,9,17,13,15,1,-7,-9,-17,-9,21,9,-13,1,3,23,-1,-3,11,- 7,-13,-1,-5,-9,5,19,7,-1,-23,15,-7,17,1,11,1,5,-13,-17,-5,-11,-7,-5,9,17,3,15,-17,1,3,- 5,9,5,-11,3)
> x2<-
c(2,18,16,8,-8,-16,-18,16,-6,6,-8,26,-6,8,18,-2,8,16,2,10,-2,-18,-26,0,0,-10,8,0,-18,0,16,- 2,-8,8,-2,-10,2,2,-18,-18,-16,-6,0,10,10,2,16,-8,-2,-18,6,18,18,-10,18,-16,-8,-8,-8,6,2,26,- 8,-16,0,0,2,-16,-16,10,10,16,-10,0,8,-2,18,-8,0,10,0,-8,-8,-8,0,-26,0,8,18,8,-8,-16,26,-2,8,- 10,8,-10,26,-8,0,-8,-8,8,-10,16,0,-6,0,2,10,-18,8,-18,0,6,8,8,18,10,16,-2,8,-26,8,-10,-16,- 26)
> x3<-
c(59,74,49,95,57,97,27,62,56,60,43,53,72,67,24,61,68,7,10,58,76,69,78,6,43,49,2,49,67, 68,77,1,97,1,7,94,89,28,92,94,7,11,1,1,93,38,16,96,23,68,89,88,73,80,84,80,98,19,79,21, 94,69,31,59,31,29,73,48,81,25,58,25,24,44,83,49,33,6,22,14,78,28,82,75,90,40,94,6,12,1,
61,30,2,53,23,57,14,91,95,67,9,5,58,97,18,8,23,87,58,76,9,89,70,81,82,98,25,9,86,11,59, 91,62,91,87,92,64,53)
> x<-c(x1,x2,x3)
> matx<-matrix(x,ncol=3)
> matx2<-cbind(1,matx)
> xt<-t(matx2)
> xtx<-xt%*%matx2
> invtxtx<-solve(xtx)
> maty<-matrix(y,ncol=1,byrow=F)
> xty<-t(matx2)%*%maty
> reg<-invxtx%*%xty
perhitungan dengan modul lm
> reg2<-lm(y~x1+x2+x3)
> reg2
> ypre=reg2$fit
> residual=reg2$res
> data.entry(x1,x2,x3,y,ypre,residual)
Hasil pengolahan data ditunjukkan pada tabel 4.8
Tabel 4.8 Hasil regresi dengan Metode Kuadrat Terkecil Biasa
. .
. .
Keterangan :
ypre menunjukkan y estimasi (Ŷ)
residual menunjukkan selisih antara y dengan y estimasi
Dengan menggunakan metode Kuadrat Terkecil Biasa diperoleh Persamaan regresi : Ŷ : 0.289096 - 0.003234 - 0.002321 + 0.094531 Nilai standar error : 3.782613
Korelasi antara nilai residual dengan y estimasi ditunjukkan oleh pada Gambar 4.13 . Statement dalam R Language adalah :
> library(graphics)
> op<-par(mfrow=c(1,1),pty="s")
> plot(ypre,residual)
Dihasilkan dalam bentuk diagram pencar :
Gambar 4.13 Diagram Pencar Ŷ dengan residual 4.1.3.3 Distribusi Pada Data Hawkins
Statement R Language untuk memperoleh nilai distribusi :
> library(graphics)
> plot(density(residual))
Hasil ditunjukkan pada gambar 4.14
Gambar 4.14 Bentuk Distribusi Data Hawkins
Bentuk disribusi menunjukkan sebaran data membentuk kurva normal artinya data berdistribusi normal atau tersebar normal.
4.1.3.4 Metode Kuadrat Median Terkecil Untuk Data Hawkins
Pengolahan data dilanjutkan dengan penggunaan metode yang berbeda, yaitu dengan Metode Kuadrat Median Terkecil. Dalam metode Kuadrat Median Terkecil, pada regresi berganda estimasi yang dilakukan menghasilkan persamaan regresi yang berbeda pada setiap pengeksekusian. Dalam hal ini penulis menggunakan metode perulangan
dengan mencari standar deviasi yang lebih kecil dari metode Kuadrat Terkecil Biasa. Jika standar deviasi lebih kecil dari standar deviasi dari Kuadrat Terkecil Biasa maka nilai persamaan regresi dan residu disimpan.
Statement dalam R Language adalah:
fred <- lmsreg(y ~ x1+x2+x3) resid <- residuals(fred)
pred <- predict(fred) n <- length(x1) nboot <- 100
for (i in 1:nboot) {
k.star <- sample(n, replace = TRUE) y.star <- pred + resid[k.star]
sally<- lmsreg(y.star ~ x1+x2+x3 ,nsamp="exact") sl<-sd(sally$res)
lr<-sd(l$res) if(sl<lr)
{reg<-sally$coef rsd<-sally$res
} }
Persamaan regresi :Ŷ = 0.482755205 -0.026795100x1+ 0.002107481x2 + 0.090871834x3 Nilai standar error : 3.690433
Nilai residu yang dihasilkan oleh Kuadrat Median Terkecil lebih baik dari Kuadrat Terkecil Biasa, akan tetapi metode Kuadrat Median Terkecil tidak stabil dan proses membutuhkan waktu lama.
Hasil persamaan regresi dan standar error dapat dilihat pada tabel 4.9 dan 4.10.
Tabel 4.9 Hasil regresi untuk semua data
Tabel 4.10 Hasil standar error untuk semua data