BAB II LANDASAN TEORI
A. Sistem Persamaan Linear dan Sistem Pertidaksamaan Linear
Persamaan linear adalah bentuk kalimat terbuka yang memuat variabel dengan derajat tertinggi adalah satu. Sedangkan sistem persamaan linear adalah beberapa buah persamaan linear yang mempunyai hubungan satu sama lainnya dalam nilai-nilai variabelnya (Priyatna, Dudung dkk. 2007).
Suatu persamaan linear dalam n peubah adalah persamaan dalam bentuk: a1X1 + a2X2 + . . . + anXn = b
dimana a1, a2, . . . , an dan b adalah bilangan real dan X1, X2, . . . , Xn adalah peubah. Dengan demikian suatu sistem persamaan linear dari m persamaan dalam n peubah adalah suatu sistem berbentuk:
a11X1 + a12X2 + . . . + a1nXn = b1 a21X1 + a22X2 + . . . + a2nXn = b2 : : : am1X1 + am2X2 + . . . + amnXn = bm
dimana aij dan bi semuanya adalah bilangan-bilangan real.
(Leon, Steven J. 2001) Pertidaksamaan adalah kalimat terbuka yang memuat salah satu dari tanda ketidaksamaan seperti: lebih dari (>), lebih dari sama dengan (≥ ), kurang dari (<), kurang dari sama dengan (≤ ). Sedangkan pertidaksamaan linear adalah suatu pertidaksamaan yang didalamnya memuat n variabel dan
masing-masing variabel itu berderajat satu. Jadi sistem pertidaksamaan linear terbentuk dari dua atau lebih pertidaksamaan dengan variabel-variabel yang sama (Wirodikromo, Sartono. 2006).
Suatu pertidaksamaan linear dalam n peubah berbentuk: a. a1X1 + a2X2 + . . . + anXn > b
b. a1X1 + a2X2 + . . . + anXn ≥ b c. a1X1 + a2X2 + . . . + anXn < b d. a1X1 + a2X2 + . . . + anXn ≤ b
dimana a1, a2, . . . , an dan b adalah bilangan real dan X1, X2, . . . , Xn adalah peubah. Dengan demikian suatu sitem pertidaksamaan linear dari m pertidaksamaan dalam n peubah adalah suatu sistem berbentuk:
a11X1 + a12X2 + . . . + a1nXn (<, >, ≤ , ≥ ) b1 a21X1 + a22X2 + . . . + a2nXn (<, >, ≤ , ≥ ) b2 : : : : am1X1 + am2X2 + . . . + amnXn (<, >, ≤ , ≥ ) bm
Dimana aij dan bi semuanya adalah bilangan-bilangan real dan tidak boleh sama dengan nol. Tanda pertidaksamaan hanya berlaku salah satu (Sriyanto, 2009).
B. Model Matematik dan Langkah-langkah Analisis
Dalam riset operasi dikenal beberapa model yang menggambarkan karakteristik dan bentuk sistem suatu permasalahan. Salah satunya adalah model matematik. Model matematik mencakup model-model yang mewakili
situasi riil sebuah sistem yang berupa fungsi matematik. Sebelum menerapkan dan mempelajari persoalan riset operasi, diperlukan langkah-langkah dalam proses pemecahan masalah riset operasi sebagai berikut:
1. Mendefinisikan masalah
Pada langkah ini terdapat tiga unsur utama yang harus diidentifikasi: a. Fungsi tujuan: penetapan tujuan untuk membantu mengarahkan upaya
memenuhi tujuan yang akan dicapai.
b. Fungsi batasan/kendala: batasan-batasan yang mempengaruhi persoalan terhadap tujuan yang akan dicapai.
c. Variabel keputusan: variabel-variabel yang mempengaruhi persoalan dalam pengambilan keputusan.
2. Mengembangkan model
Mengumpulkan data untuk menaksir besaran parameter yang berpengaruh terhadap persoalan yang dihadapi. Taksiran ini digunakan untuk membangun dan mengevaluasi model matematis dari persoalannya.
3. Memecahkan model
Dalam memformulasi persoalan ini biasanya digunakan model analitis, yaitu model matematis yang menghasilkan persamaan, sehingga dicapai pemecahan yang optimum.
4. Menguji keabsahan model
Menentukan apakah model yang dibangun telah menggambarkan keadaan nyata secara akurat. Jika belum, perbaiki atau buat model baru.
5. Implementasi hasil akhir
Menerjemahkan hasil studi atau perhitungan kedalam bahasa sehari-hari agar mudah dimengerti.
(Aminudin,2005)
C. Kendala Optimasi
Di dalam masalah optimasi, tujuanya adalah mengoptimumkan (maksimum atau minimum) sebuah fungsi. Fungsi ini dinamakan fungsi tujuan. Misalnya fungsi yang akan dimaksimumkan adalah penerimaan dalam suatu produksi pesawat televisi, atau ingin meminimumkan fungsi jika fungsinya adalah ongkos persatuan produksi kamera jenis tertentu.
Pada sebagian besar masalah optimasi fungsi tujuan bergantung pada beberapa peubah X1, X2, . . . , Xn
peubah-peubah ini dinamakan peubah kendali, sebab kita dapat mengendalikan atau mengontrolnya, artinya menentukan nilai-nilainya. Misalnya, hasil suatu proses kimiawi mungkin tergantung pada tekanan (X1) dan suhu (X2).
Teori optimasi mengembangkan berbagi metode untuk pemilihan optimal X1, X2, . . . , Xn yang memaksimumkan (meminimumkan) fungsi tujuan. Dengan kata lain mengembangkan metode untuk menentukan nilai-nilai optimal X1, X2, . . . , Xn.
Di dalam permasalahan optimasi, pemilihan nilai-nilai X1, X2, . . . , Xn tidak seluruhnya bebas melainkan dikenai suatu kendala (constrain), yaitu
syarat atau kondisi tambahan yang berasal dari sifat alamiah masalah itu sendiri dan peubah-peubahnya. Misalnya X1 adalah ongkos produksi, maka X1≥ 0, yang hanya mungkin mengambil nilai-nilai tidak negatif. Kendala juga mungkin mengambil bentuk sebuah persamaan (alih-alih pertidaksamaan).
(Kreyszig, Erwin. 1993)
D. Program Linear
Program linear merupakan suatu model umum yang dapat digunakan dalam pemecahan masalah pengalokasian sumber yang terbatas secara optimal. Simbol-simbol yang digunakan dalam masalah program linear adalah sebagai berikut:
m = macam batasan-batasan sumber atau fasilitas yang tersedia.
n = macam kegiatan-kegiatan yang menggunakan sumber atau fasilitas tersebut.
i = nomor setiap macam sumber atau fasilitas yang tersedia (i=1,2,3,..,m) j = nomor setiap macam kegiatan yang menggunakan sumber atau fasilitas
yang tersedia (j=1,2,3,..,n)
Xj = tingkat kegiatan ke-j (j=1,2,3,...,n)
aij = banyaknya sumber i yang diperlukan untuk menghasilkan setiap unit keluaran kegiatan j (i=1,2,3,..,m) dan j (j=1,2,3,..,n)
bi = banyaknya sumber i yang tersedia untuk dialokasikan ke setiap unit kegiatan (i=1,2,3...n)
Z = nilai yang dioptimalkan (maksimum atau minimum)
Cj = kenaikan nilai Z apabila ada penambahan tingkat kegiatan xj dengan satuan unit, atau merupakan sumbangan setiap satuan keluaran kegiatan j terhadap nilai Z.
Apabila disusun dalam tabel akan menjadi:
Tabel 1.1 Simbol dalam Program Linear Kegiatan
Sumber
Pemakaian sumber per unit kegiatan (keluaran) 1 2 3 ... n Kapasitas sumber 1 2 3 : m a11 a12 a13 ... a1n a21 a22 a23 ……… a2n a31 a32 a33 ……… a3n : : : : am1 am2 am3 ……… anm b1 b2 b3 : bm ΔZ
pertam-bahan tiap unit Tingkat
kegiatan
C1 C2 C3 ... Cn X1 X2 X3 ... Xn
Atas dasar tabel di atas kemudian dapat disusun suatu model matematis yang digunakan untuk mengemukakan suatu permasalahan program linear sebagai berikut: Fungsi tujuan: Maks Z = C1X1 + C2X2 + C3X3 + ... + CnXn Dengan kendala: a11X1 + a12X2 + a13X3 + ... + a1nXn ≤ b1 a21X1 + a22X2 + a23X3 + ... + a2nXn ≤ b2 a31X1 + a32X2 + a33X3 + ... + a3nXn ≤ b3 . . . . . . . . . . . . am1X1 + am2X2 + am3X3 + ... + amnXn ≤ bm dan X1≥ 0, X2≥ 0, X3≥ 0, . . . , Xn≥ 0
Terminologi umum untuk model program linear yang diuraikan di atas dapat diringkas sebagai berikut:
1. Fungsi yang akan dimaksimumkan: C1X1 + C2X2 + C3X3 + ... + CnXn disebut fungsi tujuan.
2. Fungsi-fungsi batasan dapat dikelompokan menjadi dua macam yaitu; a. Fungsi batasan fungsional, yaitu fungsi-fungsi batasan sebanyak m
(am1X1 + am2X2 + am3X3 + ... + amnXn)
b. Fungsi batasan non-negatif, yaitu fungsi-fungsi batasan yang dinyatakan dengan Xn≥ 0.
3. Variabel Xj disebut variabel-variabel keputusan.
4. aij, bi dan Cj, yaitu masukan-masukan konstan, disebut sebagai parameter model.
Kriteria yang harus dipenuhi dalam membuat formulasi model matematis program linear adalah:
1) Proportionality
Berarti bahwa naik turunnya nilai Z dan penggunaan sumber atau fasilitas yang tersedia akan berubah secara sebanding dengan perubahan tingkat kegiatan.
2) Additivity
Berarti bahwa nilai tujuan tiap kegiatan tidak saling mempengaruhi. 3) Divisibility
Menyatakan bahwa keluaran yang dihasilkan oleh setiap kegiatan dapat berupa bilangan pecahan. Demikian pula dengan nilai Z yang dihasilkan.
4) Deterministik
Menyatakan bahwa semua parameter yang terdapat dalam model program linear(aij,bi,Cj) dapat diperkirakan dengan pasti, meskipun jarang dengan tepat.
(Subagyo, Pangestu dkk,1983)
E. Metode Simplex
Metode simplex merupakan pengembangan metode aljabar yang hanya menguji sebagian dari jumlah solusi dalam bentuk tabel. Tabel simplex hanya menggambarkan masalah program linear dalam bentuk koefisiennya saja, baik koefisisen fungsi tujuan maupun koefisien setiap kendala. Langkah-langkah yang dapat dilakukan dalam penggunaan metode simplex adalah:
1) Merubah masalah program linear kedalam bentuk standar. Bentuk standar secara umum adalah sebagai berikut: Maks Z = C1X1 + C2X2 + C3X3 + ... + CnXn Dengan kendala: a11X1 + a12X2 + a13X3 + ... + a1nXn + S1 = b1 a21X1 + a22X2 + a23X3 + ... + a2nXn + S2 = b2 a31X1 + a32X2 + a33X3 + ... + a3nXn + S3 = b3 . . . . . . . . . . . . am1X1 + am2X2 + am3X3 + ... + amnXn+ Sn = bm
Bila menghadapi pertidaksamaan dapat diubah menjadi persamaan dengan menambahkan slack variabel atau mengurangkannya dengan surplus variabel. Jika fungsi tujuannya adalah minimum maka diubah menjadi maksimum dengan cara dikalikan dengan minus satu.
Misal:
Min Z = C1X1 + C2X2 + C3X3 Dengan kendala:
a11X1 + a12X2 + a13X3 ≤ b1 a21X1 + a22X2 + a23X3 ≥ b2
diubah menjadi bentuk persamaan sebagai berikut: Maks (–Z) = –C1X1 – C2X2 – C3X3
Dengan kendala:
a11X1 + a12X2 + a13X3 + S1 = b1 a21X1 + a22X2 + a23X3 – S2 = b2
2) Memeriksa apakah setiap kendala memiliki variabel basis. Jika tidak, tambahkan satu variabel basis semu yang bertindak sebagai variabel basis, misal Q yang jumlahnya sesuai dengan kebutuhan. Jika terdapat variabel basis semu, maka koefisien fungsi tujuan diberi nilai yang sangat besar yaitu – M untuk tujuan maksimum atau + M untuk tujuan minimum. Misal:
Max Z = C1X1 + C2X2 + C3X3 Dengan kendala:
a21X1 + a22X2 + a23X3 – S2 = b2 Diubah menjadi persamaan berbentuk:
Max Z = C1X1 + C2X2 + C3X3 + 0S1 – 0S2 – MQ Dengan kendala:
a11X1 + a12X2 + a13X3 + S1 = b1 a21X1 + a22X2 + a23X3 – S2 + Q = b2
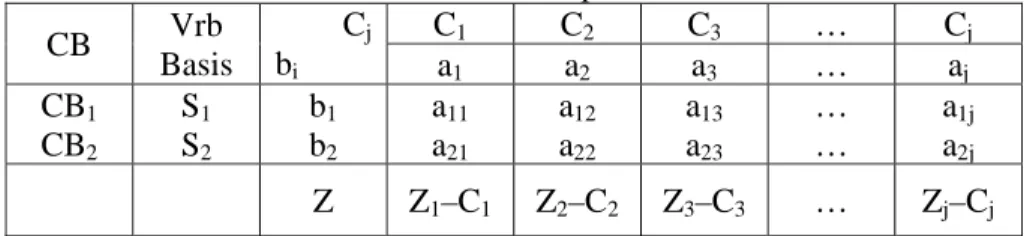
3) Memasukan semua nilai kendala ke dalam tabel simplex. Bentuk umum tabel simplex:
Tabel 1.2 Simplex CB Vrb Basis Cj bi C1 C2 C3 … Cj a1 a2 a3 … aj CB1 CB2 S1 S2 b1 b2 a11 a21 a12 a22 a13 a23 … … a1j a2j Z Z1–C1 Z2–C2 Z3–C3 … Zj–Cj Keterangan tabel:
a) CB menggambarkan koefisien fungsi tujuan untuk variabel dalam basis.
b) Kolom variabel dalam basis berisikan slack variabel yang akan digantikan oleh variabel keputusan
c) Kolom bi berisikan konstanta ruas kanan setiap kendala.
d) Baris Cj berisikan koefisien fungsi tujuan setiap variabel keputusan. e) Baris aj berisikan variable keputusan.
f) Baris Z–C berisikan angka hasil pengurangan Zj–Cj yang akan memberikan informasi apakah tabel sudah optimal atau belum.
4) Memasukan nilai koefisien fungsi tujuan pada baris Zj–Cj, dengan rumus: Zj–Cj = CB.Yj–Cj. Rumus ini hanya digunakan pada awal tabel simplex. 5) Menentukan kolom kunci, yaitu kolom yang memiliki nilai negatif
terbesar pada baris Zj–Cj pada fungsi tujuan maksimum. Sedangkan untuk fungsi tujuan minimum yang telah diubah menjadi maksimum, dipilih nilai positif terbesar. Jika terdapat dua nilai yang sama, dapat dipilih salah satu.
6) Menentukan baris kunci, yaitu nilai yang memiliki nilai indeks terkecil dan bukan negatif, dengan menggunakan rumus:
Min, , Yik ≥ 0
7) Mencari angka baru yang terdapat dalam baris kunci dengan cara membagi semua angaka yang terdapat pada baris kunci dengan angka kunci. Angka kunci adalah angka yang terdapat pada persilangan baris kunci dengan kolom kunci.
8) Mencari angka baru pada baris yang lain dengan rumus:
Angka baru = nilai pada baris lama dikurangi dengan perkalian koefisien pada kolom kunci dengan angka baru baris kunci.
9) Apabila solusi optimal belum ditemukan, kembali ke langkah kelima di atas sehingga nilai yang terdapat pada baris Zj–Cj 0≥
(Yamit, 1996: 88-122)
F. Dualitas
Tiap persoalan program linear disebut primal, mempunyai persoalan sehubungan secara tunggal yang dinamakan persoalan dual. Kedua persoalan ini berhubungan sangat erat, dimana persoalan yang satu dibentuk dari persoalan yang lain, sehingga:
1) Keduanya menggunakan koefisien (data) yang sama meskipun dengan urutan yang berbeda.
2) Keduanya mempersoalkan sumber-sumber yang sama. Xbi
3) Jawab optimal dari yang satu menghasilkan jawab optimal bagi yang lain. 4) Jika problem primal berbentuk maksimum maka problem dual berbentuk
minimum, demikian sebaliknya.
Jika terdapat rumusan program linear sebagai berikut: Maks Z = C1X1 + C2X2 + . . . + CnXn Dengan kendala a11X1 + a12X2 + . . . + a1nXn ≤ b1 a21X1 + a22X2 + . . . + a2nXn ≤ b2 : : : am1X1 + am2X2 + . . . + amnXn ≤bm Xi ≥ 0, i = 1, 2, . . . , n
Maka rumusan di atas jika disajikan dalam bentuk tabulasi, sebagai berikut: Tabel 1.3 Tabulasi Program Linear
Variabel primal X1 X2 . . . Xn Batasan Primal a11 a12 . . . a1n ≤ b1 a21 a22 . . . a2n ≤ b2 . . . . . . . . am1 am2 . . . amn ≤ bm Fungsi tujuan primal C1 C2 . . . Cn Z (max)
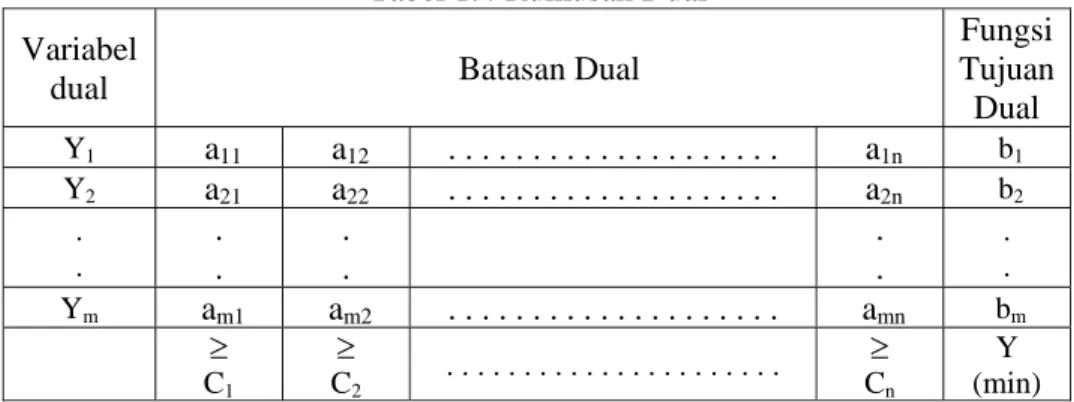
Sehingga rumusan persoalan dual dapat di tulis dalam bentuk Tabel 1.4 berikut:
Tabel 1.4 Rumusan Dual Variabel
dual Batasan Dual
Fungsi Tujuan Dual Y1 a11 a12 . . . a1n b1 Y2 a21 a22 . . . a2n b2 . . . . . . . . . . Ym am1 am2 . . . amn bm ≥ C1 ≥ C2 . . . ≥ Cn Y (min)
Persoalan dual ini dapat dirumuskan dalam bentuk program linear sebagai berikut: Min Y = b1Y1 + b2Y2 + . . . + bmYm Dengan kendala a11Y1 + a12Y2 + . . . + am1Ym ≥C1 a21Y1 + a22Y2 + . . . + am2Ym ≥ C2 : : : : : : a1mY1 + a2mY2 + . . . + amnYm ≥Cn Yj ≥ 0, j = 1, 2, . . . , m dengan singkat dapat ditulis :
I. Primal : Maks Z =
∑
= n j 1 CjXj Dengan kendala:∑
= n j 1 aijXj ≤ bi , i = 1, 2, . . . , m Xj ≥0, j = 1, 2, . . . , nII. Dual : Min Y =
∑
= m i 1 biYi Dengan kendala:∑
= m i 1 aijYj ≥ Cj, j = 1, 2, . . . , n Yi ≥ 0 , i = 1, 2, . . . , mDari rumus I dan II di atas, persoalan bentuk primal dual mempunyai karakteristik sebagai berikur:
1) Setiap variabel dari persoalan yang satu bersesuaian dengan batasan dalam persoalan yang lain.
2) Unsur-unsur diruas kanan dari batasan dalam persoalan yang satu sama dengan koefisien dari fungsi tujuan dalam persoalan yang lain.
3) Persoalan yang satu mencari harga maksimum dan persoalan yang lain mencari harga minimum fungsi tujuan.
4) Persoalan maksimum mempunyai batasan bertanda (≤ ) dan persoalan minimum mempunyai batasan bertanda (≥ ).
5) Kedua persoalan mempunyai batasan tidak negatif bagi tiap variabel. Karena persoalan dual adalah juga program linear, maka ia pasti mempunyai bentuk dual yaitu primal, sehingga dapat dikatakan bahwa bentuk dual dari persoalan dual adalah primal.
(Siagian, 2006: 131-133) Aturan untuk memudahkan formulasi dari bentuk primal kedalam bentuk dual pada persoalan program linear adalah sebagai berikut:
a) Mengubah semua kendala dalam bentuk hubungan lebih kecil atau sama dengan (≤ ) jika fungsi tujuannya adalah maksimum.
b) Mengubah semua kendala dalam bentuk hubungan lebih besar atau sama dengan (≥ ) jika fungsi tujuannya adalah minimum.
c) Apabila suatu persoalan mempunyai bentuk persamaan (sama dengan), maka kendala ini harus diganti dengan dua kendala baru yang berhubungan, yaitu:
(i) Satu kendala adalah lebih kecil sama dengan (≤ ).
(ii) Dan kendala yang lain adalah lebih besar sama dengan (≥ ).
Ini berarti salah satu ketidaksamaan harus dikalikan dengan minus satu (–1) untuk membentuk kanonikal baru.
2) Mengubah koefisien fungsi tujuan primal menjadi konstanta sisi kanan dual. Sebaliknya, konstanta sisi kanan primal menjadi koefisien fungsi tujuan dual.
3) Mengubah elemen baris kendala primal menjadi elemen kolom dalam dual. Sehingga elemen kolom primal menjadi elemen baris dual.
4) Membalik tanda pertidaksamaan.
5) Mengubah tujuan dari minimisasi (maksimisasi) dalam primal menjadi maksimisasi (minimisasi) dalam dual.