MENINGKATKAN KEMAMPUAN ANALOGI DAN GENERALISASI MATEMATIS SISWA SMP MENGGUNAKAN PEMBELAJARAN DENGAN METODE DISCOVERY.

(1)

Samsul Maarif, 2012

KATA PENGANTAR

Bismillahirohmanirrohim,

Segala puji dan syukur senantiasa dipanjatkan kepada Allah SWT atas

segala limpahan nikmat dan karunia-Nya yang diberikan. Sholawat serta salam

semoga tercurah kepada junjunan besar Nabi Muhammad SAW yang telah

membawa umat manusia dari zaman kebodohan menuju era yang terang

benderang, yang menjadi rahmat bagi seluruh alam. Berkat rahmat dan karunia

serta izin-Nya peneliti dapat menyelesaikan penulisan tesis dengan judul

“Meningkatkan Kemampuan Analogi dan Generalisasi Matematis Siswa

SMP Menggunakan Pembelajaran dengan Metode Discovery” sebagai salah

satu syarat untuk memperoleh gelar Magister Pendidikan Matematika.

Tesis ini terdiri dari lima bab. Bab I berisi uraian tentang latar belakang

masalah, rumusan masalah, tujuan penelitian, manfaat penelitian dan hipotesis

penelitian. Bab II berisi kajian pustaka, membeberkan kerangka teoritis yang

menjadi acuan dalam melakukan penelitian ini. Bab III berisi metodologi

penelitian, desain penelitian yang digunakan, pemilihan sampel dan populasi,

serta analisis data yang digunakan. Bab IV berisi penjelasan tentang hasil

penelitian dan pembahasannya, dan Bab V menjelaskan kesimpulan penelitian dan

saran untuk penelitian selanjutnya.

Dengan segala kekurangan dan keterbatasan, penulis berharap semoga

(2)

dapat memperkaya khasanah penelitian-penelitian sebelumnya, dan dapat

memberi inspirasi untuk penelitian lebih lanjut.

Bandung, Juni 2012

Penulis

(3)

PERSEMBAHAN

Dengan penuh kerendahan hati dan teriring rasa syukur ke hadirat Allah SWT,

penulis persembahkan buah karya sederhana ini sebagai bukti cinta kasih kepada:

1. Ayahanda Sholihin dan Ibunda Umi Yati, yang selalu memberikan yang

terbaik bagi anak-anaknya dengan segala yang mereka punya.

2. Adikku Faozi Saiful Ikhsan, yang selalu memberi semangat motivasi.

3. Guru dan dosen penulis, sebagai pembimbing dan penerang jalan hidup dalam

meraih kesuksesan.

(4)

UCAPAN TERIMA KASIH

Penulis menyadari dan merasakan sepenuhnya, bahwa dalam penyelesaian tesis

ini tidak terlepas dari bantuan, bimbingan, arahan, dan motivasi dari berbagai

pihak. Untuk itu penulis menyampaikan ucapan terima kasih yang

sebesar-besarnya kepada yang terhormat:

1. Bapak Prof. Dr. H. Didi Suryadi, M.Ed selaku Pembimbing I dan selaku

Direktur SPs UPI, yang dengan kritis memberikan dukungan dan motivasi

dalam menyelesaikan tesis ini di tengah-tengah kesibukannya.

2. Bapak Dr. H. Tatang Mulyana, M.Pd. selaku Pembimbing II dan selaku

pembimbing akademik penulis, di tengah-tengah kesibukannya dengan penuh

kesabaran memberikan arahan dan saran dalam penyusunan dan penyelesaian

tesis ini.

3. Bapak Prof. H. Yaya Sukjaya Kusumah, M.Sc., Ph.D selaku Ketua Program

Studi Pendidikan Matematika SPs UPI beserta stafnya atas layanan terbaiknya

selama penulis mengikuti studi di Universitas Pendidikan Indonesia.

4. Ucapan terima kasih dan penghargaan kepada Kepala Sekolah dan dewan guru

SMPN 13 Jakarta, khususnya bapak Drs. Sukirman, M.Pd dan bapak Risqi

Rahman, M.Pd yang telah membantu penulis dalam melakukan penelitian di

SMPN 13 Jakarta.

5. Teman-teman mahasiswa S2 dan S3 Pendidikan Matematika di Sekolah

Pascasarjana Universitas Pendidikan Indonesia yang telah banyak membantu

(5)

6. Sahabatku di Asrama Rumah Cahaya (Pa Ncep, Pa Dani, Pa Ucu, Pa Ros,

Ejong alias Aji, Crisna, Pa Dedy sekeluarga) sahabat yang penuh warna dan

keceriaan.

7. Semua pihak yang telah membantu dalam penyelesaian tesis ini baik secara

langsung maupun tidak langsung.

Penulis berharap semoga Allah SWT membalas amal dan budi baik mereka.

Akhirnya, semoga tesis ini dapat bermanfaat.

Bandung, Juni 2012 Penulis

(6)

MOTTO

“Semangat dalam bekerja, tekun dalam berdoa”

(samsul maarif)

“cogito ergo sum (AKU BERPIKIR KARENA ITU AKU ADA)_”

(7)

B. Rumusan dan Batasan Masalah ...14

C. Tujuan Penelitian ...15

D. Manfaat Penelitian ...16

E. Definisi Oerasional ...17

F. Hipotesis Penelitian ...19

BAB II KAJIAN PUSTAKA A. Metode Pembelajaran Matematika ...21

B. Pembelajaran dengan Metode Discovery ...22

C. Pembelajaran Metode Ekspositori ...31

D. Kemampuan Penalaran Matematis ...32

E. Penalaran Induktif ...34

F. Kemampuan Analogi Matematis ...37

G. Kemampuan Generalisasi Matematis ...39

(8)

I. Klasifikasi Kemampuan Siswa ...43

J. Teori Belajar yang Mendukung...44

J. Penelitian yang Relevan...51

BAB III METODELOGI PENELITIAN A. Desain Penelitian ...53

B. Populasi dan Sampel Penelitian ...54

C. Variabel Penelitian ...56

D. Instrumen Penelitian ...57

E. AnalisisHasil Uji Coba ...66

F. Prosedur Penelitian ...73

G. Tekhnik Analisis Data ...75

BAB IV HASIL PENGAMATAN DAN PEMBAHASAN A. Diskripsi Kegiatan ...84

B. Diskripsi Hasil Pengolahan Data ...97

C. Pembahasan ...144

D. Keterbatasan ...169

BAB V KESIMPULAN, IMPLIKASI DAN REKOMENDASI A. Kesimpulan ...171

D. Rekomendasi ...172

DAFTAR PUSTAKA 175

(9)

DAFTAR TABEL

Tabel Hal

3.1 Keterkaitan Weiner tentang keterkaitan antara Variabel Bebas,

Terikat dan Kontrol...57

3.2 Kriteria Penilaian Kemampuan Analogi Matematis ... 59

3.3 Kriteria Penilaian Kemampuan GeneralisasiMatematis ...59

3.4 Klasifikasi Koefisien Korelasi ...61

3.5 Klasifikasi Reliabilitas ...62

3.6 Klasifikasi Tingkat Kesukaran Soal ...64

3.7 Klasifikasi Nilai Daya Pembeda ...65

3.8 Hasil Uji Validitas Kemampuan Analogi Matematika Siswa ...67

3.9 Hasil Uji Reliabilitas Kemampuan Analogi Matematika Siswa ...68

3.10 Hasil Uji Daya Pembeda Kemampuan Analogi Matematika Siswa...68

3.11 Hasil Uji Tingkat Kesukaran Kemampuan Analogi Matematika Siswa ...69

3.12 Hasil Uji Validitas Kemampuan Generalisasi Matematika ...70

3.13 Hasil Reliabilitas Kemampuan Generalisasi Matematika ...70

3.14 Hasil Uji Daya Pembeda Kemampuan Generalisasi Matematika Siswa ... 71

3.15 Hasil Uji Tingkat Kesukaran Kemampuan Generalisasi Matematika siswa ...71

3.16 Hasil Uji Validitas Skala Sikap Siswa terhadap Matematika ...72

3.17 Hasil Reliabilitas Sikap Siswa terhadap Matematika Matematika ...73

3.18 Keterkaitan Klasifikasi Gain ... 77

4.1 Statistika Diskriptif Kemampuan Analogi Matematis Siswa...98

(10)

4.3 Uji Normalitas Skor Pretes Kemampuan Analogi Matematis

Siswa ... 101

4.4 Uji Normalitas Skor Pretes Kemampuan Generalisasi Matematis

Siswa ...101

4.5 Uji Homogenitas Variansi Skor Pretes Kemampuan Analogi

Matematis Siswa ...102

4.6 Uji Homogenitas Variansi Skor Pretes Kemampuan Generalisasi

4.7 Uji Kesamaan rataan Pretes Kemampuan Analogi Matematis

Siswa ...103

4.8 Uji Kesamaan rataan Pretes Kemampuan Generalisasi Matematis

Siswa ...104

4.9 Uji Normalitas Skor Postes Kemampuan Analogi Matematis

Siswa ...105

4.10 Uji Homogenitas Variansi Skor Postes Kemampuan Analogi

4.11 Uji Normalitas Skor Postes Kemampuan Generalisasi Matematis

Siswa ...106

4.12 Uji Homogenitas Variansi Skor Postes Kemampuan Generalisasi

4.13 Statistika Diskriptif Skor Gain Ternormalisasi Kemampuan

Analogi Matematis Menurut Metode Pembelajaran dan Kategori

Kemampuan Siswa ...108

4.14 Uji Normalitas Skor Gain ternormalisasi Kemampuan Analogi

Matematis ...111

4.15 Uji Homogenitas Variansi Skor Gain ternormalisasi Kemampuan

Analogi Matematis ...111

4.16 Analisis Variansi Gain Ternormalisasi Kemampuan Analogi

Matematis Menurut Metode Pembelajaran dan Kategori

(11)

4.17 Perbedaan Rataan Gain Ternormalisasi Kemampuan Analogi

Matematis Siswa Menurut Kategori Kemampuan Siswa ...115

4.18 Statistika Diskriptif Skor Gain Ternormalisasi Kemampuan

Generelisasi Matematis Menurut Metode Pembelajaran dan

Kategori Kemampuan Siswa ...117

4.19 Uji Normalitas Skor Gain ternormalisasi Kemampuan

Generelisasi Matematis ...119

4.20 Uji Homogenitas Variansi Skor Gain ternormalisasi Kemampuan

Generelisasi Matematis ...120

4.21 Analisis Variansi Gain Ternormalisasi Kemampuan Generelisasi

Matematis Menurut Metode Pembelajaran dan Kategori

Kemampuan Siswa ...121

4.22 Perbedaan Rataan Gain Ternormalisasi Kemampuan Generelisasi

Matematis Siswa Menurut Kategori Kemampuan Siswa ...124

4.23 Statistika Diskriptif Skor Skala Sikap Siswa terhadap Matematika

Menurut Metode Pembelajaran dan Kategori Kemampuan Siswa...126

4.24 Uji Normalitas Skor Skala Sikap Siswa terhadap Matematika ...127

4.25 Uji Homogenitas Variansi Skor Skala Sikap Siswa Terhadap

Matematika ...128

4.26 Analisis Variansi Skala Sikap Siswa terhadap Matematika

Menurut Metode Pembelajaran dan Kategori Kemampuan Siswa ...129

4.27 Perbedaan Rataan Skala Sikap Siswa terhadap Matematika

Menurut Kategori Kemampuan Siswa ... 131

4.28 Hasil Pengamatan Aktivitas Guru selama Pembelajaran dengan

Metode Discovery ...134

4.29 Hasil Pengamatan Aktivitas Siswa selama Pembelajaran dengan

Metode Discovery ...137

(12)

DAFTAR DIAGRAM DAN GAMBAR

Diagram/

Gambar

Hal

2.1 Contoh Soal Analogi Matematis Siswa ...36

3.1 Diagram Alur Pelaksanaan Penelitian ...82

4.1 Siswa Melakukan Pengukuran Segitiga yang Tersedia Pada LKS ...85

4.2 Aktivitas Siswa dalam Menemukan Jumlah Sudut Dalam Segitiga ...87

4.3 Hasil Aktivitas Siswa dalam Menemukan Keliling dan Luas Daerah Segitiga ...93

4.4 Hasil Aktivitas Siswa dalam Menemukan Luas Daerah Segitiga ...95

4.5 Hasil Skala Sikap Siswa terhadap Matematika ...120

4.6 Hasil Pengamatan Aktivitas Guru selama Pembelajaran dengan Metode Discovery ...136

(13)

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Dalam menjalani abad ke 21, kita bangsa Indonesia harus mempersiapkan

sumber daya manusia (SDM) yang benar-benar unggul dan dapat diandalkan

untuk menghadapi persaingan bebas di segala bidang kehidupan yang kian ketat

sebagai dampak dari globalisasi dunia. Dampak globalisasi dunia tidak hanya kita

rasakan pada sendi-sendi perekonomian, pertahanan-keamanan, politik dan sosial

budaya semata, namun juga pada sendi-sendi pendidikan pada umumnya. Bila

kualitas pendidikan dalam negeri terjamin, maka tentu pendidikan kita minimal

akan menjadi tuan di negaranya sendiri. Oleh karena itu merupakan suatu hal yang

logis bila kita harus lebih memperhatikan kualitas pendidikan.

Pendidikan merupakan ujung tombak dalam mempersiapkan SDM yang

handal, karena pendidikan diyakini akan dapat mendorong memaksimalkan

potensi siswa sebagai calon SDM yang handal untuk dapat bersikap kritis, logis

dan inovatif dalam menghadapi dan menyelesaikan setiap permasalahan yang

dihadapinya. Hal tersebut senada dengan pendapat Sumarmo (2005) yang

menyatakan bahwa pendidikan matematika sebagai proses yang aktif, dinamis,

dan generatif melalui kegiatan matematika (doing math) memberikan sumbangan

yang penting kepada siswa dalam pengembangan nalar, berfikir logis, sistematik,

ktitis dan cermat, serta bersikap obyektif dan terbuka dalam menghadapi berbagai

(14)

merupakan mata pelajaran yang terdapat dalam setiap jenjang pendidikan, baik

pendidikan di lembaga formal maupun di lembaga non formal, bahkan di lembaga

latihan kerja serta bidang lain yang berkaitan dengan tujuan peningkatan kualitas

SDM sekalipun.

Salah satu fungsi dan tujuan umum pembelajaran matematika di sekolah

sebagai lembaga formal (Depdiknas, 2004) adalah untuk mempersiapkan siswa

agar dapat mengembangkan kemampuan matematis, melatih cara berpikir dan

bernalar dalam menarik kesimpulan, serta menggunakan ide-ide matematika

dalam kehidupan sehari-hari dan mempelajari berbagai ilmu pengetahuan. Artinya

target kompetensi dasar matematik siswa harus dapat ditumbuhkembangkan

dalam proses belajar di sekolah sebagai wujud pengembangan proses berpikir

siswa.

Tetapi faktanya, hasil penelitian The Third International Mathematics and

Science Study (TIMSS) yang dilakukan terhadap siswa SMP kelas dua di

Indonesia terhadap nilai rata-rata matematika yang dicapai hanya 397 jauh di

bawah rata-rata internasional TIMSS yang mencapai 500 (TIMSS, 2008). Nilai

yang dicapai siswa-siswa Indonesia ternyata juga lebih rendah apabila

dibandingkan dengan beberapa negara lain di kawasan Asia seperti Taiwan

(dengan rata-rata nilai 598), Korea Selatan (597), Singapura (593), Jepang (570)

bahkan Malaysia (474). Sedangkan laporan PISA 2006, Indonesia menempati

rangking 52 dari 57 negara. Sementara hasil nilai matematika pada Ujian

Nasional, pada semua tingkat dan jenjang pendidikan selalu terpaku pada angka

(15)

menetapkan standar minimal nilai kelulusan bagi siswa adalah 3,01 dengan rata

rata angka kelulusan siswa SMP, SMA dan SMP sebesar 71,55%. Selama

beberapa tahun penyelenggaraan UN tingkat SMP/Mts, nilai rata-rata mata

pelajaran matematika 7,08 di tahun 2005/2006 dengan nilai terendah 0,67 dan

6,92 di tahun 2006/2007 dengan nilai terendah 0,33 (Yunengsih, dkk. 2008). Hal

tersebut menandakan bahwa pembelajaran matematika di Indonesia perlu

ditingkatkan proses pembelajaranya sehingga dapat memperoleh hasil belajar

matematika yang lebih baik.

Rendahnya kemampuan matematis siswa, bisa jadi salah satunya disebabkan

karena kemampuan siswa dalam melakukan penalaran matematis yang masih

rendah. Menurut hasil penelitian Rahman (2004) hasil tes awal menunjukkan

bahwa kemampuan generalisasi matematik siswa berada pada kualifikasi kurang.

Hal senada juga diungkapkan oleh Suryadi (2005) bahwa siswa kelas dua SMP di

kota dan kabupaten Bandung mengalami kesulitan dalam kemampuan

mengajukan argumentasi serta menemukan pola dan pengujian bentuk umumnya.

Begitu juga dengan Herdian (2010) dalam penelitiannya menemukan bahwa

kemampuan analogi dan generalisasi matematis siswa yang memiliki kemampuan

rendah berada pada kualifikasi kurang. Hal ini dapat terjadi karena proses

pembelajaran melalui metode discovery dirasakan lebih sulit bagi siswa

lemah, dan sebaliknya bagi siswa pandai. Selain itu, Yuliani (2011)

mengemukakan bahwa kemampuan analogi dan generalisasi matematis siswa

berkemampuan sedang dan rendah berada pada kualiikasi kurang yang dilakukan

(16)

Masih rendahnya kualitas kemampuan analogi dan generalisasi matematis

merupakan indikasi bahwa tujuan pembelajaran matematika belum tercapai secara

optimal. Agar tujuan tersebut dapat tercapai dengan optimal, salah satu cara yang

bisa dilakukan adalah dengan melaksanakan proses pembelajaran yang

berkualitas. Banyak faktor yang mempengaruhi kualitas pembelajaran

matematika. Salah satu faktor yang mempengaruhinya adalah ketepatan

dalam penerapan metode pembelajaran oleh guru. Selain itu, rendahnya

kemampuan matematis siwa juga disebabkan karena masih belum sepenuhnya

dipahami oleh guru tentang pembelajaran sebagai upaya membuat siswa belajar,

hal ini nampak di lapangan dominasi guru dalam pembelajaran masih menjadi

pilihan para guru sehingga siswa lebih banyak pasif dalam pembelajaran. Hal

serupa disampaikan Silver bahwa aktivitas siswa sehari-hari terdiri atas menonton

gurunya menyelesaikan soal-soal di papan tulis, kemudian meminta siswa bekerja

sendiri dalam buku teks atau LKS yang disediakan (Turmudi, 2008).

Penekanan guru untuk memenuhi target pencapaian kurikulum daripada

penguasaan materi mengakibatkan kurang maksimalnya guru mengidentifikasi

masalah-masalah yang muncul dalam sebuah pembelajaran di kelas. Guru tidak

jarang terkesan tergesa-gesa dalam mengajar sehingga berorientasi pada tujuan

bukan pada proses pembelajarannya. Hal tersebut yang menjadikan suatu

pembelajaran tidak efektif sehingga proses transfer materi kurang dipahami oleh

siswa. Keadaan seperti itulah yang dikhawatirkan menjadi sebuah pembelajaran

membosankan dan menjadikan minat siswa dalam pembelajaran matematika

(17)

Metode yang kerap guru gunakan adalah metode ekspositori dengan

menerangkan materi dan selanjutnya memberi contoh soal. Hal tersebut

disebabkan oleh beberapa kemungkinan yaitu: 1) Sekolah sudah memiliki alat

peraga tetapi belum memanfaatkannya secara optimal; 2) Sekolah sama sekali

belum memiliki alat peraga; 3) Sekolah telah memiliki alat peraga namun belum

memadai baik tempat, kualitas maupun kuantitasnya (Asyhadi, 2005).

Rendahnya kemampuan penalaran matematis siswa berdampak pada

rendahnya prestasi belajar matematikanya. Hal ini sesuai dengan temuan

Wahyudin (Herdian, 2010:1) dalam penelitiannya yang mengungkapkan bahwa

salah satu kecenderungan yang menyebabkan sejumlah siswa gagal menguasai

dengan baik pokok-pokok bahasan dalam matematika akibat siswa kurang

menggunakan nalar yang logis dalam menyelesaikan soal atau persoalan

matematika yang diberikan. Hasil penelitian Rif’at (Suzana, 2003: 2) juga

menunjukkan kelemahan kemampuan matematis siswa dilihat dari kinerja dalam

bernalar. Misalnya, kesalahan dalam penyelesaian soal matematika karena

kesalahan menggunakan logika deduktif.

Penalaran dan matematika adalah dua hal yang tidak dapat dipisahkan

karena matematika dipahami melalui penalaran, sedangkan penalaran dipahami

dan dilatihkan melalui belajar matematika. Ini diperkuat dengan hasil penelitian

yang dilakukan oleh Prowsri dan Jearakul (Priatna, 2003: 4) bahwa pada siswa

sekolah menengah Thailand terdapat keterkaitan yang signifikan antara

kemampuan penalaran dengan hasil belajar matematika mereka. Hal ini

(18)

siswa. Siswa yang memiliki kemampuan penalaran yang baik diharapkan

mempunyai prestasi belajar matematika yang baik pula.

Menurut Mundari (2000) terdapat dua analogi, yaitu analogi induktif dan

analogi deklaratif atau analogi penjelas. Analogi induktif adalah analogi yang

disusun berdasarkan persamaan prinsipil antara dua fenomena yang berbeda.

Sebagai contoh, terdapat kesamaan antara manusia dengan mahluk hidup lainnya.

Hewan sebagai makhluk hidup memerlukan sumber makanan dan asupan mineral

untuk tumbuh, berkembang biak untuk melestarikan jenisnya. Demikian juga

manusia memerlukan sumber makanan dan asupan mineral untuk kelangsungan

hidupnya, berkembang biak untuk mempertahankan keturunannya. Atas dasar

keserupaan itulah maka tidak salah apabila kita menyimpulkan bahwa

kemungkinan hewan itu mempunyai jenis kelamin jantan dan betina seperti

manusia. Adapun analogi deklaratif atau analogi penjelas merupakan suatu

metode untuk menjelaskan yang belum dikenal atau masih samar, dengan

menggunakan hal yang sudah dikenal. Sebagai contoh, ilmu pengetahuan itu

dibangun oleh fakta-fakta sebagaimana rumah itu dibangun oleh bahan bangunan

seperti batu, pasir semen dan sebagainya, walaupun tidak semua kumpulan fakta

itu ilmu sebagaimana tidak semua kumpulan batu itu rumah.

Dengan kasus-kasus analogi siswa dilatih untuk melihat sejauh mana mereka

memahami konsep dan melihat struktur mikroskopis konsep dengan menelaah

keterkaitan antar konsep dengan kasus analogi, serta membuka pikiran siswa

tentang aplikasi atau manfaat dari mempelajari konsep tersebut. sehingga siswa

(19)

sedang dipelajari dan menyadari akan kelebihan dan keterbatasannya dalam

belajar sehingga ia akan mencari solusi yang tepat untuk menyempurnakan

kelemahannya dalam belajar.

Selain analogi, generalisasi juga merupakan bagian dari penalaran induktif.

Ruseffendi (Rahman, 2004: 3) mengungkapkan bahwa membuat generalisasi

adalah membuat konklusi atau kesimpulan berdasarkan kepada pengetahuan

(pengalaman) yang dikembangkan melalui contoh-contoh kasus. Dalam

melakukan penarikan kesimpulan (generalisasi) anak dapat membuat konjektur

berdasarkan pengamatan dari fakta-fakta yang diberikan, baik itu pola tumbuh dan

pola berulang yang dinyatakan dengan bilangan atau gambar (geometri).

Konjektur ini sangat membantu anak dalam melakukan penarikan kesimpulan.

Menurut Gagne (Herdian, 2010) generalisasi dapat diartikan sebagai transfer

belajar yang berkaitan dengan kemampuan seseorang untuk menangkap struktur

pokok, pola dan prinsip-prinsip umum. Lebih lanjut, siswa akan mampu

mengadakan generalisasi, yaitu menangkap ciri-ciri atau sifat umum yang terdapat

dari sejumlah hal-hal khusus. Apabila siswa telah memiliki konsep, kaidah,

prinsip (kemahiran intelektual) dan siasat masalh-masalah tersebut. Dengan

demikian, siswa yang memiliki kemampuan generalisasi matematis maka telah

terjadi transfer belajar dalam hal membuat kesimpulan matematis yang terlihat

dari kegiatan siswa melakukan berbagai strategi terhadap penyelesaian suatu

masalah.

Menurut Pott (Herdian, 2010) untuk mengembangkan kemampuan analogi

(20)

yang mempunyai karakteristik membangun katagori, menentukan masalah dan

menciptakan lingkungan yang mendukung. Metode pembelajaran yang

mempunyai karakteristik tersebut diantaranya Discovery Learning. Hal ini

didasarkan pada proses pembelajaran penemuan yang digambarkan Veermans

(Yuliani, 2011) yaitu orientasi, menyusun hipotesis, menguji hipotesis, membuat

kesimpulan dan mengevaluasi (mengontrol).

Ruseffendi (1991: 329) mengemukakan bahwa metode discovery adalah

metode mengajar yang diatur sedemikian rupa sehingga anak memperoleh

pengetahuan yang sebelumnya belum diketahuinya itu tidak melalui

pemberitahuan, dimana sebagian atau seluruh pengetahuan ditemukan sendiri

dengan bantuan guru. Sejalan dengan Ruseffendi, Sund (Suriadi, 2006: 5)

mengungkapkan bahwa penemuan ialah proses mental sehingga siswa mampu

mengasimilasikan suatu konsep atau prinsip. Proses mental yang dimaksud antara

lain: mengamati, mencerna, mengerti, menggolong-golongkan, membuat dugaan,

menjelaskan, mengukur, membuat kesimpulan dan sebagainya. Diharapkan, jika

siswa secara aktif terlibat didalam menemukan suatu prinsip dasar sendiri, Ia akan

memahami konsep lebih baik, ingat lama dan akan mampu menggunakannya

kedalam konteks yang lain.

Blake et al. (Rochaminah, 2008: 32) membahas metode discovery yang

dipublikasikan oleh Whewell. Whewell mengajukan metode discovery dengan

tiga tahap, yaitu: (1) mengklarifikasi, (2) menarik kesimpulan secara induktif, (3)

membuktikan kebenaran (verifikasi). Dari tiga tahap tersebut terlihat bahwa dalam

(21)

suatu masalah matematika sehingga siswa dapat mengklarifikasi sebuah persoalan

untuk kemudian mengidentifikasi fakta-fakta untuk menarik sebuah kesimpulan.

Setelah siswa menarik kesimpulan siswa juga dapat membuktikan kebenaran dari

kesimpulan tersebut.

Metode discovery struktur pembelajarannya adalah induktif, yaitu

menekankan siswa untuk menemukan pola-pola, aturan, prinsip, dan struktur

matematik melalui eksplorasi terhadap contoh-contoh. Sebagaimana yang

dikemukakan Taba (Trisnadi, 2006: 21) bahwa metode discovery melibatkan suatu

urutan induktif, urutan ini dimulai tidak dengan penjelasan sebuah prinsip umum

tetapi dengan menghadapkan siswa kepada beberapa contoh dari prinsip, dimana

mereka dapat menganalisis, memanipulasi dan bereksperimen.

Metode discovery memberi kesempatan yang leluasa kepada siswa untuk

belajar melakukan aktivitas bekerja matematika, siswa diberi kesempatan

mengembangkan strategi belajarnya secara sendiri maupun berinteraksi dan

bernegosiasi dengan sesama siswa serta dengan guru. Melalui kegiatan seperti itu

dimungkinkan siswa tidak merasa tertekan, tidak cemas, rasa percaya dirinya

muncul dan termotivasi untuk belajar matematika (Yuliani, 2011). Bila hal itu

benar-benar terjadi dalam pembelajaran matematika, bukan mustahil sikap positif

siswa terhadap matematika akan tumbuh. Ini penting, karena sikap positif

terhadap matematika berkorelasi positif dengan hasil belajar matematika.

Sehingga diduga metode discovery dapat meningkatkan sikap positif terhadap

(22)

Dalam kegiatan pembelajaran matematika kondisi siswa sangat berpengaruh

berhasil atau tidaknya suatu pembelajaran karena siswa merupakan subjek dari

materi yang diberikan oleh guru. Oleh sebab itu, kondisi siswa sangat menentukan

berhasil atau tidaknya tujuan pembelajaran tersebut. Pengalaman menyenangkan

atau tidak menyenangkan akan berpengaruh pada sikap siswa terhadap pelajaran

matematika. Hal tersebut juga akan terlihat perilaku siswa ketika pembelajaran

matematika berlangsung. Sebagai contoh, pada pembelajaran terdapat siswa yang

hanya diam dan terliahat mengantuk tidak memperhatikan pembelajaran. Setelah

siswa tersebut ditanya, mereka menjawab “tidak suka matematika karena rumit”.

Slameto (Saragih, 2011) mengungkapkan bahwa sikap terbentuk melalui

pengalaman yang berulang-ulang, imitasi, sugesti, dan melalui identitas. Hal

tersebut menunjukkan jika pembelajaran matematika yang menyenangkan

dilakukan secara berulang-ulang akan menjadikan siswa menyenangi pelajaran

matematika, sehingga sikap siswa terhadap matematika.

Sikap siswa terhadap matematika tidak dipungkiri dipengaruhi oleh guru

dalam menyampaikan materi didepan kelas. Kurangnya guru dalam memfasilitasi,

membimbing, memotivasi dan mengajr dengan metode pembelajaran yang tidak

tepat. Sehubungan dengan itu, maka kedekatan emosianal antara guru sengan

siswa harus dibangun dengan baik. Selain itu, guru juga harus melakukan inovasi

dalam pembelajaran dengan menggunakan metode pembelajaran yang menarik

dan menyenangkan. Dalam kegiatan pembelajaran, guru juga harus bisa

membimbing dan memfasilitasi siswa dengan memberikan bimbingan apa yang

(23)

dalam menanggapi pertanyaan/masalah yang diajukan siswa dengan tetap

memperdayakan siswa dalam membangun konsep materi yang diajarkan.

Ruseffendi (Darhim, 2004) juga menjelaskan bahwa untuk menumbuhkan

sikap positif terhadap matematika antara lain dengan cara mengajarkan

matematika sesuai dengan lingkungan dan pengetahuan siswa. Oleh karena

itu, sikap siswa terhadap matematika tidak dapat dipisahkan dari kemampuan

awal matematika siswa. Siswa dengan kemampuan matematis yang rendah

akan cenderung bersikap negatif terhadap matematika, karena mereka sudah

memiliki ketakutan terlebih dahulu terhadap pelajaran matematika. Sebaliknya

untuk siswa dengan kemampuan matematika yang tinggi akan cenderung

bersikap positif terhadap matematika. Namun tidak menutup kemungkinan

bahwa siswa yang memiliki kemampuan matematika rendah akan menjadi

bersikap positif terhadap matematika. Pembelajaran dengan metode discovery

menempatkan guru sebagai vasilitator, membimbing dan memotivasi siswa. Di

samping itu, adanya masalah yang harus dipecahkan oleh siswa untuk ditarik

kesimpulan guru juga membri jawaban yang diperlukan oleh siswa untuk

menyimpulkan materi yang diajarkan.

Adanya interaksi antar siswa dalam pembelajaran memberikan kontribusi

untuk mengungkapkan pendapat satu sama lain sehingga antara siswa yang kurang

memahami materi akan diberi masukan oleh siswa yang memahaminya.

Terciptanya situasi pembelajaran yang aktif oleh adanya interaksi antar siswa

dapat mendorong siswa untuk menata proses berpikirnya, sehingga pada akhirnya

(24)

dapat diakomodir pada pembelajaran dengan metode discovery yang salah satu

aspeknya adanya interaksi antar siswa. Oleh sebab itu, perlunya pengelompokan

siswa untuk mempermudah adanya interaksi antar siswa berjalan lebih efektif.

Dalam penelitian ini kemampuan siswa diklasifikasikan berdasarkan

pengetahuan awal matematika, yang terdiri dari siswa kemampuan tinggi,

kemampuan sedang, dan kemampuan rendah. Setiap siswa mempunyai

kemampuan yang berbeda dalam memahami matematika. Menurut Galton

(Ruseffendi, 1991) dari sekelompok siswa yang dipilih secara acak akan

selalu dijumpai siswa yang memiliki kemampuan tinggi, sedang, dan rendah.

Hal ini disebabkan kemampuan siswa menyebar secara distribusi normal.

Proses penentuan kelompok tinggi, kelompok sedang dan kelompok

rendah ini adalah dengan cara mengurutkan skor hasil belajar matematika

sebelumnya (ulangan harian dan ujian tengah semester), serta

pengklasifikasian yang dilakukan oleh guru kelas. Hal ini sejalan dengan

temuan Begle (Darhim, 2004) melalui penelitiannya bahwa salah satu prediktor

terbaik untuk hasil belajar matematika adalah hasil belajar matematika

sebelumnya. Lebih lanjut dikatakan bahwa peran variabel kognitif lainnya

ternyata tidak sebesar variabel hasil belajar sebelumnya.

Matematika merupakan mata pelajaran yang dipelajari dari jenjang sekolah

dasar hingga perguruan tinggi. Selain itu, sifat matematika sendiri yang abstrak

diperlukan juga memahami aspek pemahaman kemampuan siswa. Pemahaman

karakteristik kemampuan siswa dapat menjadi modal awal dalam proses

(25)

terhdapa materi yang akan diajarkan guru dapat membuat persiapan proses

pembelajaran sesuai dengan proporsi kemampuan siswa. Selain itu, guru juga

dapat memprediksi perlakukan-perlakuan apa yang ingin dilakukan pada siswa

dengan kemampuan-keampuan yang dimilikinya. Hal ini senada dengan pendapat

Bagle (Darhim, 2004) yang menyatakan bahwa salah satu prediktor pembelajaran

matematika terbaik adalah hasil pembelajaran matematika sebelumnya, dan

peranan faktor kognitif lainnya tidak sebesar hasil belajar matematika

sebelumnya. Sehingga, kemampuan awal siswa sangat dapat menentukan hasil

belajar selanjutnya karena dengan hasil belajar yang diperoleh siswa sebelumnya

guru dapat memprediksi perlakuan atau tindakan apa yang harus dilakukan pada

siswa berdasarkan kemampuan atau hasil belajar matematika sebelumnya.

Selain itu, dalam kondisi pembelajaran di kelas kemampuan siswa

berbeda-beda sehingga diperlukan penyesuaian lingkungan belajar. Pemilihan metode yang

tepat diperlukan untuk mengcover semua kemampuan siswa yang terjadi dalam

kelas. Hal ini seperti yang diungkapkan oleh Russeffendi (1991), perbedaan

kemampuan siswa bukan semata-mata bawaan dari lahir, tetapi juga dipengaruhi

oleh lingkungan. Oleh karena itu, pemilihan metode yang tepat untuk

pembelajaran matematika sangat diperlukan. Metode discovery yang memberikan

kesempatan siswa untuk mengutarakan ide dan pemikiranya untuk menyimpulkan

suatu persoalan diduga cocok untuk mengakomodir pembelajaran matematika

(26)

Dari uraian di atas maka melalui penelitian ini akan diungkap

”meningkatkan kemampuan analogi dan generalisasi matematis siswa SMP

menggunakan pembelajaran dengan metode discovery”.

B. Rumusan dan Batasan Masalah

Berdasarkan uraian pada pendahuluan di atas, maka rumusan masalah yang akan dikaji dalam penelitian ini difokuskan dalam bentuk pertanyaan-pertanyaan penelitian sebagai berikut:

1. Apakah peningkatan kemampuan analogi matematis siswa yang

memperoleh pembelajaran dengan metode discovery lebih baikdaripada siswa

yang memperoleh metode pembelajaran dengan metode ekspositori?

2. Apakah terdapat perbedaan peningkatan kemampuan analogi

matematis siswa dilihat dari kategori (a) kelompok siswa berkemampuan

tinggi, (b) kelompok siswa berkemampuan sedang dan (c) kelompok siswa

berkemampuan rendah?

3. Apakah peningkatan kemampuan generalisasi matematis siswa yang

memperoleh pembelajaran dengan metode discovery lebih baik daripada

siswa yang memperoleh pembelajaran dengan metode ekspositori?

4. Apakah terdapat perbedaan peningkatan kemampuan generalisasi

(27)

5. Apakah sikap siswa terhadap matematika yang memperoleh

pembelajaran dengan metode discovery lebih baik daripada siswa yang

memperoleh pembelajaran dengan metode ekspositori?

6. Apakah terdapat perbedaan sikap siswa terhadap matematika dilihat

dari kategori (a) kelompok siswa berkemampuan tinggi, (b) kelompok siswa

berkemampuan sedang dan (c) kelompok siswa berkemampuan rendah?

C. Tujuan Penelitian

Secara umum penelitian ini bertujuan untuk memperoleh gambaran yang

objektif mengenai kemampuan analogi dan generalisasi matematis siswa SMP

melalui pembelajaran dengan metode discovery.

Secara rinci tujuan penelitian ini adalah:

1. Mendeskripsikan/menelaah peningkatan kemampuan analogi matematis siswa

yang yang memperoleh pembelajaran dengan metode discovery dengan siswa

yang memperoleh pembelajaran dengan metode ekspositori

2. Mendeskripsikan/menelaah perbedaan peningkatan kemampuan analogi

berkemampuan rendah.

3. Mendeskripsikan/menelaah kemampuan generalisasi matematis siswa yang

mengikuti pembelajaran dengan metode discovery dengan siswa yang

memperoleh pembelajaran dengan metode ekspositori.

4. Mendeskripsikan/menelaah perbedaan peningkatan kemampuan analogi

(28)

berkemampuan rendah.

5. Mendeskripsikan/menelaah sikap siswa SMP terhadap matematika setelah

memperoleh pembelajaran dengan metode discovery dengan siswa yang

memperoleh pembelajaran dengan metode ekspositori.

6. Mendeskripsikan/menelaah sikap siswa SMP terhadap matematika dilihat dari

kategori (a) kelompok siswa berkemampuan tinggi, (b) kelompok siswa

berkemampuan sedang dan (c) kelompok siswa berkemampuan rendah.

D. Manfaat Penelitian

Hasil penelitian ini dapat memberikan manfaat dan kontribusi yang berarti

bagi pihak-pihak tertentu yang berkecimpung dalam dunia pendidikan

diantaranya :

1. Bagi Guru

a. Memberikan informasi tentang implementasi metode discovery dalam

meningkatkan hasil belajar siswa;

b. Menjadi salah satu alternatif pembelajaran di sekolah.

2. Bagi Siswa

a. Melatih siswa untuk terlibat aktif dalam pembelajaran;

b. Melatih siswa dalam menemukan konsep matematika dengan cara

(29)

3. Bagi Sekolah

Penelitian ini dapat memberikan sumbangan pemikiran dan masukan

dalam menerapkan inovasi metode pembelajaran dengan metode discovery

guna meningkatkan mutu pendidikan.

4. Bagi peneliti lain

Menjadi salah satu tambahan bahan rujukan/ referensi untuk melakukan

penelitian mengenai penerapan metode discovery di sekolah.

E. Definisi Operasional

Agar tidak terjadi kesalahan dalam menangkap maksud dari penelitian ini,

perlu dijelaskan beberapa istilah yang digunakan.

1. Kemampuan analogi matematis adalah ketrampilan menghubungkan dua hal

yang berlainan berdasarkan keserupaannya, dan berdasarkan keserupaan

tersebut ditarik kesimpulan sehingga dapat digunakan sebagai penjelas atau

sebagai dasar penalaran. Adapun indikator dari kemampuan analogi matematis

adalah: menentukan kesamaan hubungan dalam suatu pola gambar atau

bangun dan menentukan kesamaan hubungan dalam suatu pola sifat dari

bangun.

2. Kemampuan generalisasi matematis adalah ketrampilan proses penarikan

kesimpulan dengan memeriksa keadaan khusus menuju kesimpulan umum

atau pola umum. Adapun indikator dari kemampuan generalisasi adalah:

perception of generality, expression of generality, symbolic expression of

(30)

3. Pembelajaran dengan metode discovery adalah bentuk pembelajaran yang

dilaksanakan dengan menemukan kembali konsep, teorema, rumus, aturan dan

sejenisnya. Dalam hal ini, guru hanya bertindak sebagai pengarah dan

pembimbing saja. adapun langkah-langkah metode pembelajaran discovery

adalah sebagai berikut:

a. guru mermberikan masalah yang harus di pecahkan dalam bentuk

pertanyaan atau pernyataan;

b. guru menentukan proses kegiatan mental yang akan dikembangkan;

c. alat-alat dan bahan yang diperlukan harus tersedia;

d. pengarahan diberikan melalui tanya jawab;

e. siswa melakukan penyelidikan atau percobaan sampai menemukan konsep

atau prinsip yang ditetapkan guru;

f. siswa mengumpulkan data;

g. Guru memberikan jawaban dengan tepat informasi yang diperlukan siswa.

4. Pembelajaran dengan metode ekspositori adalah bentuk pembelajaran yang

dilaksanakan dengan menjelaskan materi pelajaran, memberikan contoh, dan

siswa mengerjakan latihan secara individual.

5. Sikap siswa terhadap matematika adalah respon yang ditunjukkan untuk

menyukai atau tidak menyukai pelajaran matematika yang dinyatakan

dengan skor jawaban terhadap skala sikap model Likert dan Fennema-

Sherman, yang setiap pernyataan dilengkapi dengan lima pilihan jawaban,

yaitu sangat setuju (SS), setuju (S), netral (N), tidak setuju (TS), dan sangat

(31)

6. Kategori kemempuan matematika siswa adalah pengelompokkan siswa

didasarkan pada kemampuan awal matematika siswa. Proses penentuan

dengan cara mengurutkan skor hasil belajar matematika sebelumnya

(ulangan harian dan ujian tengah semester), serta pengklasifikasian yang

dilakukan oleh guru kelas. Pengelompokan siswa menjadi tiga kelompok

kategori, yaitu kelompok tinggi, sedang, dan rendah dengan

perbandingan 30%, 40% dan 30% .

F. Hipotesis Penelitian

Hipotesis merupakan jawaban sementara terhadap rumusan masalah

penelitian. Sugiyono (1999 : 51) mengungkapkan bahwa hipotesis dapat

dinyatakan sebagai jawaban teoritis terhadap rumusan masalah penelitian, bukan

jawaban yang empirik. Berdasarkan kajian permasalahan yang telah diuraikan,

maka penelitian ini mengajukan hipotesis sebagai berikut.

1. Peningkatan kemampuan analogi matematis siswa yang memperoleh

pembelajaran dengan metode discovery lebih baik daripada siswa yang

memperoleh metode pembelajaran dengan metode ekspositori;

2. Terdapat perbedaan peningkatan kemampuan analogi matematis siswa dilihat

dari kategori (a) kelompok siswa berkemampuan tinggi, (b) kelompok siswa

berkemampuan sedang dan (c) kelompok siswa berkemampuan rendah;

3. Peningkatan kemampuan generalisasi matematis siswa yang memperoleh

pembelajaran dengan metode discovery lebih baik daripada siswa yang

(32)

4. Terdapat perbedaan peningkatan kemampuan generalisasi matematis siswa

dilihat dari kategori (a) kelompok siswa berkemampuan tinggi, (b) kelompok

siswa berkemampuan sedang dan (c) kelompok siswa berkemampuan rendah;

5. Sikap siswa terhadap matematika yang memperoleh pembelajaran dengan

metode discovery lebih baik daripada siswa yang memperoleh pembelajaran

dengan metode pembelajaran ekspositori;

6. Terdapat perbedaan Sikap siswa terhadap matematika dilihat dari kategori (a)

kelompok siswa berkemampuan tinggi, (b) kelompok siswa berkemampuan

(33)

BAB III

METODE PENELITIAN

A. Desain Penelitian

Metode yang digunakan dalam penelitian ini yaitu metode eksperimen.

Penelitian eksperimen dapat diartikan sebagai suatu penelitian yang berusaha

untuk mengungkap hubungan antara dua variabel atau lebih. Penelitian

eksperimen juga dapat difungsikan untuk mencari pengaruh suatu variabel

terhadap variabel lainnya. Penelitian ini melibatkan tiga variabel, yaitu variabel

bebas, variabel terikat dan variabel kontrol. Metode pembelajaran discovery dan

metode pembelajaran ekspositori sebagai variabel bebas. Sikap siswa terhadap

matematika, kemampuan analogi matematis dan kemampuan generalisasi

matematis sebagai variabel terikat. Kemudian siswa berkemampuan pandai dan

siswa berkemampuan lemah sebagai variabel kontrol.

Metode eksperimen yang dilakukan dalam penelitian ini yaitu dengan cara

memberikan perlakuan terhadap subjek penelitian berupa penggunaan metode

pembelajaran yang berbeda. Metode discovery diberikan kepada siswa kelompok

eksperimen, sedangkan metode pembelajaran ekspositori (metode pembelajaran

ekspositori ) diberikan kepada siswa kelompok kontrol.

Desain yang digunakan dalam penelitian ini adalah factorial design,

yaitu dengan memperhatikan adanya variabel kontrol yang mempengaruhi

(34)

akan dilakukan pada siswa dari dua kelas yang dipilih dengan pertimbangan

tertentu. Desain penelitian ini berbentuk:

Kelas Eksperimen : O X O

Kelas Kontrol : O O

Dimana:

O : Pretest = posttest (tes kemampuan analogi dan generalisasi matematis

siswa)

X : Perlakuan pembelajaran dengan metode discovery

Penelitian ini menggunakan model faktorial 2x2x3, dimana 2 adalah

banyaknya faktor pembelajaran (metode pembelajaran discovery dan metode

pembelajaran ekspositori), 2 adalah banyaknya faktor kemampuan matematis

siswa (kemampuan analogi matematis dan kemampuan generalisasi matematis)

dan sikap siswa terhadap matematika, dan 3 adalah banyaknya faktor kemampuan

awal siswa (siswa tinggi, siswa sedang dan siswa rendah).

B. Populasi dan Sampel Penelitian

1. Populasi Penelitian

Populasi adalah keseluruhan subjek penelitian. Sugiyono (2008: 117)

menyatakan bahwa populasi adalah wilayah generalisasi yang terdiri atas: objek/

subjek yang mempuyai kualitas dan karakteristik tertentu yang ditetapkan peneliti

dan kemudian ditarik kesimpulannya. Populasi dalam penelitian ini adalah

siswa-siswi SMP N 13 Jakarta. Berdasarkan peringkat sekolah SMP N 13 Jakarta

(35)

siswanya heterogen dan dapat mewakili siswa dari tingkat kemampuan tinggi,

sedang dan rendah.

2. Sampel Penelitian

Sampel adalah bagian dari jumlah dan karakteristik yang dimiliki oleh

populasi (Sugiyono, 2008: 118). Pengambilan sampel pada penelitian ini

dilakukan dengan menggunakan teknik purposive sampling (sampel acak

bertujuan). Teknik purposive sampling adalah teknik pengambilan sampel secara

sengaja dengan pertimbangan tertentu (Sugiyono, 2008: 124). Sampel penelitian

ini adalah siswa-siswi SMP N 13 Jakarta kelas VII sebanyak dua kelas yaitu kelas

VII.6 dan kelas VII.8 dengan masing-masing kelas dipilih 36 orang siswa untuk

dijadikan sampel.

Alasan pemilihan sampel adalah siswa kelas VII, karena mereka dianggap

sudah bisa beradaptasi dengan pembelajaran baru (lain dari biasa) dan tidak

mengganggu program sekolah dalam mempersiapkan siswa untuk mengikuti ujian

akhir nasional (jika dipilih siswa kelas IX). Pengelompokkan siswa

didasarkan pada kemampuan matematika dengan cara mengurutkan skor hasil

belajar matematika sebelumnya (ulangan harian dan ulangan tengah semester)

serta pengklasifikasian yang dilakukan oleh guru kelas. Pembagian

kemampuan siswa terdiri dari tiga kelompok kategori, yaitu kelompok tinggi,

sedang, dan rendah denga perbandingan 30%, 40% dan 30% (Dahlan, 2004).

Hasil pengelompokan kategori kemampuan siswa pada kelas eksperimen

dan kontrol sama, yaitu 11 siswa termasuk kategori tinggi, 14 siswa

(36)

Pengelompokkan siswa kategori tinggi, sedang dan rendah pada kelas

eksperimen dan kelas kontrol selengkapnya dapat dilihat pada Lampiran D.1.

C. Variabel Penelitian

Variabel adalah objek penelitian atau apa yang akan menjadi titik perhatian

suatu penelitian. Menurut Sudjana (2005: 8) penelitian eksperimen adalah suatu

penelitian yang berusaha mencari pengaruh variabel tertentu terhadap variabel lain

dalam kondisi yang terkontrol secara ketat. Pada penelitian ini variabel yang

digunakan terdiri dari variabel bebas (X), variabel terikat (Y), dan variabel

kontrol (Z).

Pada penelitian ini variabel yang digunakan terdiri dari variabel bebas

(X), variabel terikat (Y), dan variabel kontrol (Z). Variabel bebas (X) pada

penelitian ini yaitu: (a) metode pembelajaran discovery yang diberikan

kepada kelompok eksperimen, (b) metode pembelajaran ekspositori yang

diberikan kepada kelompok kontrol. Kemudian yang menjadi variabel

terikat (Y) pada penelitian ini yaitu: (a) kemampuan analogi matematis; (b)

kemampuan generalisasi matematis; dan (c) sikap siswa terhadap matematika.

Selanjutnya yang menjadi variabel kontrol (Z) pada penelitian ini adalah (a)

siswa kemampuan tinggi; (b) siswa kemampuan sedang; dan (b) siswa

kemampuan rendah.

Berikut ini akan ditampilkan keterkaitan antara variabel bebas (metode

pembelajaran discovery dan metode pembelajaran ekspositori ), dengan variabel

(37)

siswa terhadap matematika), dan variabel kontrol (siswa kemampuan tinggi,

sedang dan rendah). dapat dilihat pada Tabel 3.1.

Tabel 3.1

Keterkaitan Weiner tentang Keterkaitan Antara Variabel Bebas, Terikat dan Kontrol

KG : Kemampuan Generalisasi Matematis Siswa;

SS : Sikap Siswa terhadap Matematika

MPD (A) : Metode Pembelajaran Discovery;

MPE (B) : Metode Pembelajaran Ekspositori

Contoh : KAAT adalah kemampuan analogi matematis siswa

kemampuan tinggi yang memperoleh pembelajaran dengan

metode discovery.

D. Instrumen Penelitian

Sebagai upaya untuk mendapatkan data dan informasi yang lengkap

mengenai hal-hal yang ingin dikaji dalam penelitian ini, maka dibuatlah

seperangkat instrumen. Penelitian ini menggunakan empat jenis instrumen, yaitu

(38)

1. `Tes

Tes yang digunakan adalah tes kemampuan analogi dan generalisasi

matematis yang terdiri dari tes awal (pretest) dan tes akhir (posttest). Tes yang

diberikan pada setiap kelas eksperimen dan kelas kontrol baik soal-soal untuk

pretest maupun posttest ekuivalen/ relatif sama. Tes awal dilakukan untuk

mengetahui kemampuan awal siswa pada kelas eksperimen maupun kelas kontrol

dan digunakan sebagai tolak ukur peningkatan prestasi belajar sebelum

mendapatkan pembelajaran dengan metode yang akan diterapkan, sedangkan tes

akhir dilakukan untuk mengetahui perolehan hasil belajar dan ada tidaknya

pengauh yang signifikan setelah mendapatkan pembelajaran dengan metode

pembelajaran yang akan diterapkan. Jadi, pemberian tes pada penelitian ini

bertujuan untuk mengetahui perbedaan pengaruh hasil belajar matematika antara

siswa yang mendapat pembelajaran dengan metode pembelajaran discovery

maupun metode pembelajaran ekspositori terhadap kemampuan analogi dan

generalisasi matematis siswa.

Untuk memberikan penilaian yang objektif, kriteria pemberian skor

untuk soal tes kemampuan analogi dan generalisasi matematis berpedoman

pada rubrik penskoran kemampuan analogi matematis dengan mengadopsi

kriteria penilaian penalaran matematis dari holistic scoring rubrics (Cai, Lane dan

Jakabcsin, 1996). Hal ini dikarenakan kemampuan analogi matematis merupakan

(39)

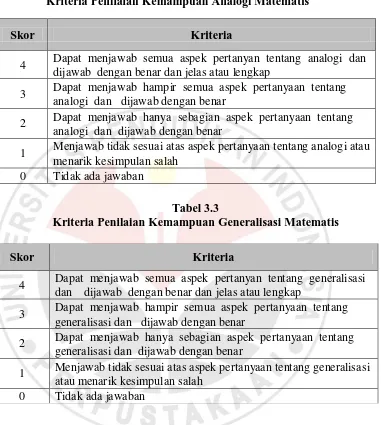
Tabel 3.2

Kriteria Penilaian Kemampuan Analogi Matematis

Skor Kriteria

4 Dapat menjawab semua aspek pertanyan tentang analogi dan dijawab dengan benar dan jelas atau lengkap

3 Dapat menjawab hampir semua aspek pertanyaan tentang analogi dan dijawab dengan benar

2 Dapat menjawab hanya sebagian aspek pertanyaan tentang analogi dan dijawab dengan benar

1 Menjawab tidak sesuai atas aspek pertanyaan tentang analogi atau menarik kesimpulan salah

0 Tidak ada jawaban

Tabel 3.3

Kriteria Penilaian Kemampuan Generalisasi Matematis

Instrumen penelitian perlu dilakukan uji coba terlebih dahulu. Uji coba

dilakukan pada siswa yang telah mendapatkan materi yang akan disampaikan. Uji

coba dilakukan untuk mengetahui tingkat validitas, reliabilitas, tingkat kesukaran,

dan daya pembeda instrumen tersebut.

a. Validitas

Suatu instrumen dikatakan valid (absah atau shahih) apabila instrumen

tersebut mampu untuk mengevaluasi/ mengukur apa yang seharusnya dievaluasi.

Skor Kriteria

4 Dapat menjawab semua aspek pertanyan tentang generalisasi dan dijawab dengan benar dan jelas atau lengkap

3 Dapat menjawab hampir semua aspek pertanyaan tentang generalisasi dan dijawab dengan benar

2 Dapat menjawab hanya sebagian aspek pertanyaan tentang generalisasi dan dijawab dengan benar

1 Menjawab tidak sesuai atas aspek pertanyaan tentang generalisasi atau menarik kesimpulan salah

(40)

Oleh karena itu untuk menentukan validitas suatu alat evaluasi hendaknya dilihat

dari berbagai aspek diantaranya validitas isi dan validitas muka.

1) Validitas Isi

Validitas isi suatu alat evaluasi artinya ketepatan alat tersebut ditinjau dari

segi materi yang dievaluasikan yaitu materi (bahan ajar) yang dipakai sebagai alat

evaluasi tersebut yang merupakan sampel representatif dari penguasaan yang

dikuasai. Arikunto (2002: 67) menyatakan bahwa validitas isi (content validity),

artinya tes yang digunakan merupakan sampel yang mewakili kemampuan yang

akan diukur.

Suatu test matematika dikatakan memiliki validitas isi yang baik apabila

dapat mengukur Kompetensi Dasar (KD), Standar Kompetensi (SK) serta

indikator yang telah ditentukan sesuai dengan kurikulum KTSP. Pertimbangan

para pakar (dosen pembibing dan mahasiswa S3 yang sedang menempuh

perkuliahan) sangat berperan dalam menyusun validitas isi suatu instrumen dalam

hal yang berkaitan dengan konsep-konsep matematika.

2) Validitas Muka

Validitas muka atau sering disebut pula validitas tampilan suatu alat evaluasi

yaitu keabsahan susunan kalimat atau kata-kata dalam soal sehingga jelas

pengertiannya atau tidak menimbulkan multi tafsir. Validitas muka adalah derajat

kesesuaian tes dengan jenjang sekolah/ pendidikan siswa. Soal tes disesuaikan

(41)

3) Validitas Butir Soal

Validitas butir soal dari suatu tes adalah ketepatan mengukur yang dimiliki

oleh sebutir soal (yang merupakan bagian tak terpisahkan dari tes sebagai suatu

totalitas), dalam mengukur apa yang seharusnya diukur lewat butir soal tersebut.

Sebuah butir soal dikatakan valid bila mempunyai dukungan yang besar terhadap

skor total. Untuk menentukan perhitungan validitas butir soal digunakan rumus

korelasi produk moment pearson (Suherman dan Sukjaya, 1990: 154), yaitu :

rxy =

Tolak ukur untuk menginterprestasikan derajat validitas digunakan kriteria

menurut Guilford (Suherman dan Sukjaya, 1990 : 147).

(42)

b. Reliabilitas

Instrumen memiliki reliabilitas yang baik apabila alat ukur itu memiliki

konsistensi yang handal pada tingkatan yang sama, walaupun dikerjakan oleh

siapun, di manapun dan kapanpun berada. Suatu alat ukur memiliki daya

keajegkan mengukur atau reliabilitas yang baik, bila alat ukur itu memiliki

konsistensi yang handal. Untuk mengukur reliabilitas soal menggunakan Rumus

alpha-cronbach yaitu:

Hasil perhitungan koefisien reliabilitas, kemudian ditafsirkan dan

diinterpretasikan mengikuti interpretasi menurut J.P. Guilford (Suherman dan

(43)

c. Tingkat kesukaran

Arikunto (2002: 207) mengungkapkan bahwa soal tes hasil belajar dapat

dinyatakan sebagai butir-butir soal yang baik, apabila butir-butir soal tersebut

tidak terlalu sukar dan tidak pula terlalu mudah. Soal yang terlalu mudah tidak

merangsang siswa untuk berusaha memecahkannya, dan soal yang terlalu sukar

akan menyebabkan siswa putus asa dan tidak bersemangat untuk mencoba lagi

karena di luar jangkauannya.

Taraf kesukaran bertujuan untuk mengetahui bobot soal yang sesuai dengan

kriteria perangkat soal yang diharuskan. Penentuan siswa kelompok atas dan

siswa kelompok bawah, dilakukan dengan cara mengurutkan terlebih dahulu skor

siswa dari yang tertinggi hingga terendah. Arikunto (2002: 212) menyatakan

bahwa untuk kelompok kecil, ambil sebanyak 50% siswa yang skornya tertinggi

dan 50% siswa yang skornya terendah. Selanjutnya masing-masing disebut

kelompok atas dan kelompok bawah.

Tingkat kesukaran pada masing-masing butir soal dihitung dengan

menggunakan rumus:

S = jumlah skor kelompok bawah

A

(44)

B

J = jumlah skor ideal kelompok bawah

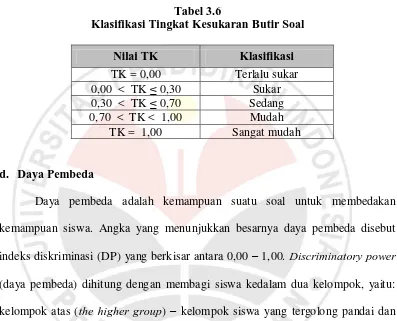
Kriteria penafsiran harga Indeks Kesukaran suatu butir soal menurut

Suherman dan Sukjaya (1990 : 213) adalah sebagai berikut :

Tabel 3.6

Daya pembeda adalah kemampuan suatu soal untuk membedakan

kemampuan siswa. Angka yang menunjukkan besarnya daya pembeda disebut

indeks diskriminasi (DP) yang berkisar antara 0,00 – 1,00. Discriminatory power

(daya pembeda) dihitung dengan membagi siswa kedalam dua kelompok, yaitu:

kelompok atas (the higher group) – kelompok siswa yang tergolong pandai dan

kelompok bawah (the lower group) – kelompok siswa yang tergolong rendah

Sukjaya (1990: 202).

Untuk menentukan daya pembeda digunakan rumus:

A

(45)

A

J = jumlah skor ideal kelompok atas

Kriteria penafsiran Daya Pembeda suatu butir soal menurut Suherman dan

Sukjaya (1990: 202) adalah sebagai berikut :

Tabel 3.7

Klasifikasi Nilai Daya Pembeda

2. Angket

Angket yang digunakan adalah angket sikap siswa terhadap matematika.

Angket ini bertujuan mengungkapkan sikap siswa terhadap matematika setelah

memperoleh pembelajaran. Angket sikap yang digunakan terdiri dari 5 komponen,

yaitu : (a) kepercayaan diri belajar matematika, (b) kecemasan matematika, (c)

kegunaan matematika, (d) motivasi dalam belajar matematika, dan (e) peranan

guru (Herdian, 2010).

Sebelum angket sikap ini digunakan, terlebih dahulu dilakukan ujicoba

pada siswa yang sudah pernah menempuh materi yang akan diajarkan. Tujuan dari

ujicoba ini adalah untuk mengetahui apakah pernyataan-pernyataan dalam skala

sikap dapat dipakai untuk membedakan sikap siswa terhadap matematika.

Kisi-kisi angket disusun berdasarkan lima komponen di atas, yang setiap

komponennya memiliki pernyataan positif dan negatif. Angket sikap ini

menggunakan bentuk skala Likert yang dilengkapi lima pilihan jawaban, yaitu

Nilai DP Klasifikasi

(46)

sangat setuju (SS), setuju (S), netral atau ragu-ragu atau tidak tahu (N), tidak

setuju (TS) dan sangat tidak setuju (STS).

3. Observasi

Observasi merupakan kegiatan melihat sesuatu secara cermat untuk

memperoleh pemahaman yang lebih baik tentang sesuatu itu. Observasi ini

digunakan untuk mengamati aktivitas siswa dan guru selama proses pembelajaran

berlangsung. Dalam pengumpulan data aktivitas siswa dan guru digunakan lembar

observasi yang dilakukan dengan cara membubuhkan tanda ceklist () pada setiap

aspek yang dilakukan siswa dan guru selama proses pembelajaran berlangsung

yang berupa skor.

4. Wawancara

Pedoman wawancara merupakan panduan yang digunakan untuk mencari

informasi tambahan terhadap proses pembelajaran yang sudah dilakukan. Siswa

yang dipilih untuk diwawancarai berasal dari kelas eksperimen. Banyaknya siswa

yang diwawancarai pada setiap kelasnya adalah 10 orang.

E. Analisis Hasil Uji Coba Instrumen

Instrumen yang diujicobakan dalam penelitian ini ada tiga jenis, (1)

instrumen tes kemampuan analogi matematika siswa, (2) instrumen tes

kemampuan generalisasi matematika siswa, dan (3) instrumen sikap siswa

terhadap matematika. Berikut akan dijabarkan hasil uji coba dan analisis

(47)

1. Analisis Hasil Uji Coba Tes Kemampuan Analogi Matematis Siswa

Instrumen tes kemampuan analogi matematika ini terdiri dari enam soal

uraian. Masing-masing soal memiliki bobot penilaian sama yaitu empat.

Instrumen ini sebelum digunakan dalam penelitian, diujicobakan terlebih dahulu

kepada siswa yang telah mendapatkan materi yang akan diajarkan dalam

penelitian ini. Uji coba instrumen ini bertujuan untuk melihat validas soal,

reliabilitas soal, daya pembeda dan tingkat kesukaran soal. Dari hasil uji validitas

terdapat satu item yang tidak valid atau tidak signifikan yaitu item nomor 3.

Berikut adalah hasil uji coba instrumen tes kemampuan analogi matematis siswa.

a. Validitas Butir Tes

Validitas butir tes kemampuan analogi matematis siswa dalam penelitian

ini dapat dilihat pada Tabel 3.8 berikut:

Tabel 3.8

Hasil Uji Validitas Kemampuan Analogi Matematis Siswa

b. Reliabilitas

Koefisien reliabilitas instrumen tes kemampuan analogi matematis siswa

dalam penelitian ini dapat dilihat pada Tabel 3.9 berikut:

Nomor Soal r xy Interpretasi Signifikansi

1 0.617 Signifikan Tinggi

3 0.135 Tidak Signifikan Rendah

(48)

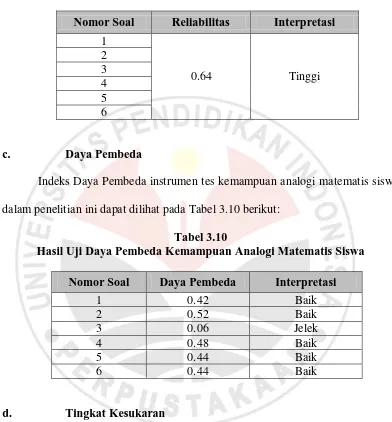
Tabel 3.9

Hasil Uji Reliabilitas Kemampuan Analogi Matematis Siswa

Nomor Soal Reliabilitas Interpretasi

1

0.64 Tinggi

2 3 4 5 6

c. Daya Pembeda

Indeks Daya Pembeda instrumen tes kemampuan analogi matematis siswa

Tabel 3.10

Hasil Uji Daya Pembeda Kemampuan Analogi Matematis Siswa

Nomor Soal Daya Pembeda Interpretasi

1 0.42 Baik

2 0.52 Baik

3 0.06 Jelek

4 0.48 Baik

5 0.44 Baik

6 0.44 Baik

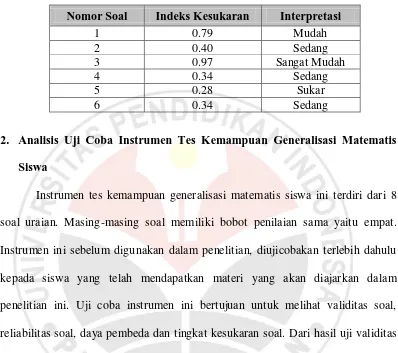
d. Tingkat Kesukaran

Indeks kesukaran instrumen tes kemampuan analogi matematis siswa

(49)

Tabel 3.11

Hasil Uji Daya Pembeda Kemampuan Analogi Matematis Siswa

Nomor Soal Indeks Kesukaran Interpretasi

1 0.79 Mudah

2 0.40 Sedang

3 0.97 Sangat Mudah

4 0.34 Sedang

5 0.28 Sukar

6 0.34 Sedang

2. Analisis Uji Coba Instrumen Tes Kemampuan Generalisasi Matematis

Siswa

Instrumen tes kemampuan generalisasi matematis siswa ini terdiri dari 8

soal uraian. Masing-masing soal memiliki bobot penilaian sama yaitu empat.

Instrumen ini sebelum digunakan dalam penelitian, diujicobakan terlebih dahulu

kepada siswa yang telah mendapatkan materi yang akan diajarkan dalam

penelitian ini. Uji coba instrumen ini bertujuan untuk melihat validitas soal,

reliabilitas soal, daya pembeda dan tingkat kesukaran soal. Dari hasil uji validitas

terdapat satu item yang tidak valid atau tidak signifikan yaitu item nomor 1b dan

4a, akan tetapiuntuk soal no 4b diperbaiki. Berikut adalah hasil uji coba instrumen

tes kemampuan generalisasi matematis siswa.

a. Validitas Butir Tes

Validitas butir tes kemampuan generalisasi matematis siswa dalam

(50)

Tabel 3.12

Hasil Uji Validitas Kemampuan Generalisasi Matematis Siswa

Untuk soal no. 4a tidak signifikan akan tetapi soal tersebut diperbaiki dan

diikutkan menjadi instrumen penelitian karena nilai r = 0,391 > rtabel = 0,297 untuk

n = 44 dalam taraf signifikansi 5%.

b. Reliabilitas

Koefisien reliabilitas instrument tes kemampuan generalisasi matematis

siswa dalam penelitian ini dapat dilihat pada Tabel 3.13 berikut:

Tabel 3.13

Hasil Reliabilitas Kemampuan Generalisasi Matematis Siswa

Nomor Soal Reliabilitas Interpretasi

1a

Nomor Soal r xy Interpretasi Signifikansi

1a 0.580 Signifikan Cukup

4a 0.391 Tidak Signifikan Rendah

(51)

c. Daya Pembeda

Indeks Daya Pembeda instrumen tes kemampuan generalisasi matematis

siswa dalam penelitian ini dapat dilihat pada Tabel 3.14 berikut:

Tabel 3.14

Hasil Uji Daya Pembeda Kemampuan Generalisasi Matematis Siswa

Nomor Soal Daya Pembeda Interpretasi

1a 0.33 Cukup

Indeks kesukaran instrumen tes kemampuan generalisasi matematis siswa

Tabel 3.15

Hasil Uji Tingkat Kesukaran Kemampuan Generalisasi Matematis Siswa

Nomor Soal Indeks Kesukaran Interpretasi

1a 0.83 Mudah

3. Analisis Hasil Uji Coba Angket Sikap Siswa terhadap Matematika

Uji coba angket diujikan kepada 44 siswa yang telah mendapatkan materi

(52)

validitas diperoleh hasil bahwa dari 25 item ada 5 item yang tidak valid, yaitu

item nomor 4, 9, 14, 18 dan 24, atau dengan kata lain 20 item lainnya valid. Uji

validitas angket sikap siswa terhadap matematika tersaji dalam Tabel 3.16 berikut:

Tabel 3.16

Hasil Uji Validitas Skala Sikap Siswa terhadap Matematika

No Soal Pearson Correlation Sig. (2-tailed) N

1 .521* 0.000 44

* Correlation is significant at the 0.05 level (2-tailed)

Setelah itu dilakukan uji reliabiltas instrument tes kemampuan

generalisasi matematis siswa dalam penelitian ini dapat dilihat pada Tabel 3.17

(53)

Tabel 3.17

Hasil Reliabilitas Angket Sikap Siswa Terhadap Matematika

Nomor Item Reliabilitas Interpretasi

1

Tahap ini diawali dengan dokumentasi teoritis berupa studi kepustakaan

terhadap pembelajaran matematika dengan metode pembelajaran discovery,

pengungkapan analogi dan generalisasi matematis siswa. Hasil kegiatan ini berupa

proposal penelitian, dengan proses bimbingan dengan dosen pembimbing

akademik.

Setelah proposal selesai dilanjutkan dengan pembuatan instrument

(54)

kemampuan analogi matematis dan soal tes kemampuan.generalisasi matematis,

serta skala sikap siswa dan lembar observasi. Uji coba dilaksanakan pada tanggal

26 maret dan 27 maret 2011 di kelas VIII.1 dan VIII.2 SMP N 13 Jakarta.

2. Tahap Pelaksanaan

Dalam tahap pelaksanaan langkah pertama adalah pemberian pretest pada

kelas eksperimen dan kelas kontrol dengan tes kemampuan analogi dan

generalisasi matematis yaitu di kelas VII.6 sebagai kelas eksperimen dan kelas

VII.8 sebagai kelas kontrol. Adapun penelitian ini dilakukan di SMP N 13 Jakarta

yang memiliki kemampuan homogen pada masing-masing kelasnya.

Selanjutnya pemberian pembelajaran dengan metode pembelajaran

discovery pada materi segitiga, persegi panjng dan persegi pada kelas eksperiman

sedangkan pada kelas kontrol dengan pembelajaran dengan metode pembelajaran

ekspositori dengan materi yang sama. Adapun jumlah pertemuan pada

masing-masing kelas yaitu tujuh kali pertemuan. Dalam kelas eksperimen siswa dibagi

beberapa kelompok masing-masing kelompok terdapat 4-5 siswa.

3. Tekhnik Pengumpulan Data

Pengumpulan data pada penelitian ini dilakukan melalui tes, skala sikap,

observasi dan wawancara. Tes yang terdiri dari dua buah tes yaitu tes kemampuan

analogi matematis dan tes kemampuan generalisasi matematis. Kedua jenis tes ini

diberikan ketika seluruh pembelajaran pada kelas eksperimen dan kelas kontrol

sudah selesai.

Skala sikap siswa diberikan untuk menentukan sikap siswa terhadap