B. OUTLINE PROPOSAL
I. PENDAHULUAN
I.1. Latar Belakang
Rangka batang kuda-kuda baja merupakan salah satu elemen dari gedung yang berfungsi untuk mendukung beban atap (air hujan, angin, genteng, reng dan plafon) termasuk juga berat sendiri kuda-kuda dan sekaligus memberi bentuk pada atap. Rangka batang terdiri dari beberapa elemen yang dihubungkan pada titik joint sehingga membentuk segitiga atau kombinasi segitiga. Dengan
mempertimbangkan berat atap, berat rangka batang kuda-kuda dan penutup atap maka kontruksi kuda-kuda akan berbeda antara satu dengan yang lain, sehingga setiap susunan rangka batang harus membentuk satu kesatuan yang kokoh dan mampu memikul beban yang bekerja tanpa mengalami perubahan.Baik itu yang terbuat dari baja maupun kayu, pada tempat-tempat tertentu harus disambung, hal ini dikarenakan keterbatasan ketersediaan material dipasaran dan juga
berhubungan dengan kemudahan pemasangan dilapangan, sambungan merupakan suatu hal yang perlu mendapatkan perhatian serius yang matang karena pada rangka baja dan kayu, elemen-elemen rangka baja yang disambung tidak bisa bersifat monolit.
Pada umumnya sambungan berfungsi untuk memindahkan gaya-gaya yang bekerja pada elemen-elemen struktur yang disambung. Sambungan di buat karena keterbatasan bahan yang tersedia di pasaran dan juga untuk memudahkan
pemasangan dilapangan serta kemudahan dalam hal pengangkutan.
Alat-alat sambung yang biasa digunakan pada konstruksi baja adalah sambungan dengan paku keling (rivet), Sambungan dengan baut (Bolt) dan sambungan dengan las (welding). Jika dibandingkan ketiga alat sambung ini, maka las merupakan alat sambung yang menghasilkan kekakuan yang paling besar, sedangkan paku keling menghasilkan sambungan yang lebih kaku jika dibandingkan dengan baut, tetapi kurang kaku jika diba ndingakan dengan las. Tetapi pada dewasa ini sambungan dengan menggunakan paku keling sudah jarang digunakan karena kesulitan dalam pemasangannya. Oleh karena itu pada tugas akhir ini perencanaan sambungan akan memakai sambungan baut dan las.
Perhitungan pada perencanaan rangka batang dan perhitungan sambungan las dan baut menggunakan metode SNI-1729-2002.
I.2. Perumusan Masalah
Rumusan masalah pada perencanaan ini yaitu ingin merencanakan sambungan pada rangka batang kuda-kuda yang aman.
I.3. Maksud dan Tujuan
Merencanakan sambungan yang aman untuk konstruksi rangka batang kuda-kuda yang ditinjau dengan sambungan las atau baut.
I.4. Ruang Lingkup Penelitian
Perencanaan rangka batang kuda-kuda yang aman, termasuk gording sebagai penerus beban atap ke kuda-kuda kemudian direncanakan sambungan baut atau las yang aman.
I.5. Manfaat Penelitian
Memberikan informasi terkait tata cara perhitungan sambungan
berdasarkan metode SNI-1729-2002, dengan menggunakan alat sambung baut dan las. Dan juga didapat sebuah alternatif perhitungan desain yang aman dengan menggunakan Spreadsheet Microsoft Excel dan SAP2000.
Sambungan merupakan sesuatu hal yang tidak dapat dihindarkan dalam perencanaan struktur baja. Hal ini dikarenakan bentuk struktur banagunan yang begitu kompleks. Adapun contoh yang dapat kita jumpai adalah sambungan elemen struktur rangka batang kuda-kuda pada bangunan. Kegagalan dalam sambungan tersebut dapat mengakibatkan perubahan fungsi struktur bangunan tersebut, dan yang paling berbahaya adalah keruntuhan pada struktur tersebut. Sehingga untuk mencegah hal tersebut maka kekakuan sambungan tersebut harus sangat baik.
2.1 Tipe - Tipe Struktur
Schodek (1995) berpendapat bahwa struktur merupakan sarana untuk menyalurkan beban akibat penggunaan dan kehadiran bangunan ditanah dan didalam tanah. Struktur berfungsi sebagai suatu kesatuan dari serangkaiaan unsur-unsur yang berbeda-beda. Unsur-unsur-unsur ini ditempatkan dan di interelasikan denga cara tertentu agar seluruh struktur mampu berfungsi dalam memikul beban baik secara vertikal maupun secara horizontal kedalam tanah.
Dewobroto (2007) berpendapat bahwa Tipe-tipe struktur terdiri dari 3 jenis, yaitu rangka batang (truss),balok (beam), dan portal bidang (frame). Rangka batang adalah susunan batang-batang lurus yang disambung pada titik joint membentuk segitiga atau kombinasi segitiga, sehingga menjadi bentuk rangka batang yang tidak dapat berubah bentuk apabila diberi beban eksternal tanpa adanya perubahan bentuk pada satu atau lebih pada batangnya. Balok (beam), elemen balok merupakan elemen struktur yang paling umum dijumpai, dan umumnya digunakan sebagai struktur pendukung lantai, baik lantai bangunan gedung maupun lantai jembatan. Portal bidang (frame), merupakan konstruksi rangka bidang vertikal yang dibebani dalam arah bidang dan gaya-gaya dominan yang bekerja adalah lentur dan aksial,disebut sebagai struktur rangka bidang.
Schodek (1995) berpendapat bahwa rangka batang adalah susunan batang-batang lurus yang disambung pada titik joint membentuk segitiga atau kombinasi segitiga, sehingga menjadi bentuk rangka batang yang tidak dapat berubah bentuk apabila diberi beban eksternal tanpa adanya perubahan bentuk pada satu atau lebih pada batangnya. Setiap elemen tersebut secara umum dianggap tergabung pada titik hubungnya dengan sambungan sendi, batang-batang disusun sedemikian rupa sehingga beban dan reaksi terjadi pada titik hubung.
Apabila beban-beban eksternal bekerja pada titik hubung rangka batang maka akan menyebabkan gaya tarik dan tekan, sedangkan jika beban-beban eksternal bekerja tepat pada batang maka akan timbul gaya tarik, gaya tekan, dan gaya lentur. Bentuk konstruksi yang stabil adalah segitiga, maka sembarang susunan segitiga juga membentuk struktur stabil dan kokoh. Bentuk kaku yang lebih besar untuk sembarang geometri dapat dibuat dengan
memperbesar/memperbanyak segitiga. Sifat dan besar gaya yang ada pada batang bergantung pada kondisi pembebanan keseluruhan rangka batang. Setiap batang harus mampu memikul gaya maksimum (kritis) yang mungkin terjadi, maka dari itu setiap batang dirancang terhadap kondisi pembebanan yang berbeda-beda.
2.3 Sifat Bahan Baja
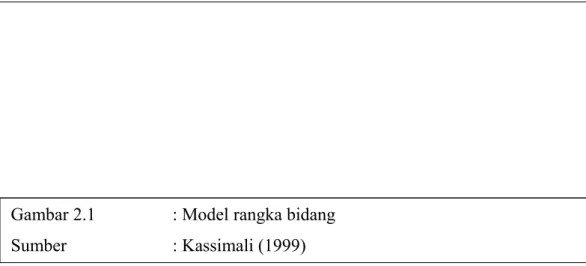
Gambar 2.1 : Model rangka bidang
Anonim (2002) menjelaskan bahwa Sifat mekanis suatu bahan adalah kemampuan bahan tersebut memberikan
perlawanan apabila diberikan beban pada bahan tersebut. Atau dapat dikatakan sifat mekanis adalah kekuatan bahan didalam memikul beban yang berasal dari luar. Sifat penting pada baja adalah kuat tarik.
Pada waktu terjadi regangan awal, dimana baja belum sampai berubah bentuknya dan bila beban yang menyebabkan regangan tadi dilepas, maka baja akan kembali ke bentuk semula. Regangan ini disebut dengan regangan elastis karena sifat bahan masih elastis. Perbandingan antara tegangan dengan regangan dalam keadaan elastis disebut dengan “Modulus
Elastisitas/Modulus Young”. Ada 3 jenis tegangan yang terjadi pada baja, yaitu:
a). Tegangan, dimana baja masih dalam keadaan elastis; b). Tegangan leleh, dimana baja mulai rusak/leleh; dan
c). Tegangan plastis, tegangan maksimum baja, dimana baja mencapai kekuatan maksimum.
Kekerasan baja adalah ketahanan baja terhadap besarnya gaya yang dapat menembus permukaan baja. Ketangguhan baja adalah hubungan antara jumlah energi yang dapat diserap oleh baja sampai baja tersebut putus.Sifat- sifat bahan struktur yang paling penting dari baja adalah sebagai berikut :
1. Modulus elastisitas (E) berkisaran antara 193000 MPa sampai 207000 MPa.Nilai untuk design lazimnya diambil 200000 MPa. 2. Modulus geser (G) dihitung berdasarkan persamaan :
G = E / 2 (1 +
µ ) ... (2.1)
Dimana :
µ = angka perbandingan poisson
Dengan mengambil µ = 0,30 dan E = 200000 MPa, akan memberikan G = 80000MPa
3. koefisien ekspansi (α), diperhitungkan sebesar :
α = 12,10 x 10−6 / ° C ... (2.2)
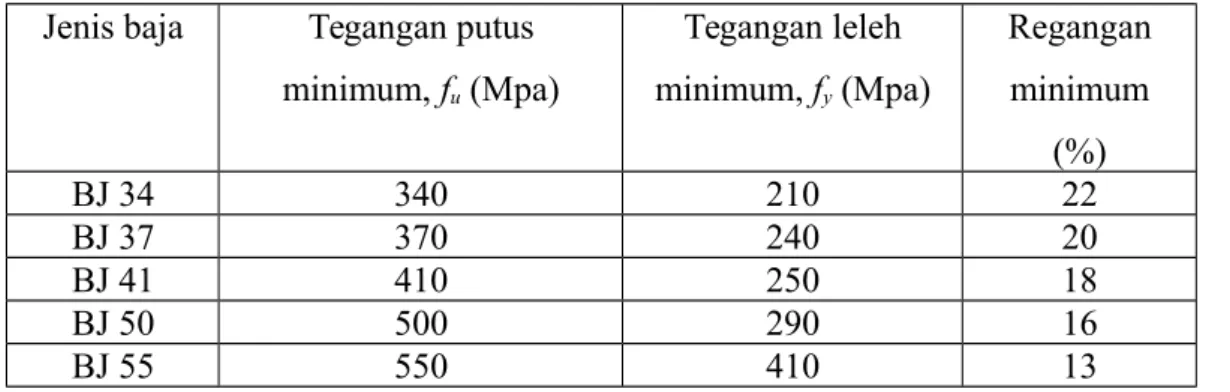
Sedangkan berdasarkan tegangan leleh dan tegangan putusnya, Anonim (2002) mengklarifikasi mutu dari material baja menjadi 5 kelas mutu sebagai berikut :
Tabel 2.1 Sifat-Sifat Mekanis Baja Struktural Jenis baja Tegangan putus
minimum, fu (Mpa) Tegangan leleh minimum, fy (Mpa) Regangan minimum (%) BJ 34 340 210 22 BJ 37 370 240 20 BJ 41 410 250 18 BJ 50 500 290 16 BJ 55 550 410 13
2.4 Pembebanan
Anonim (2002) menjelaskan bahwa dalam perencanaan suatu kontruksi kuda-kuda perlu ditinjau pembebanan yang terjadi pada kuda-kuda tersebut. Beban yang ditimbulkan pada kuda-kuda berupa beban vertikal dan beban horizontal, beban vertikal terdiri atas beban mati (dead load) dan beban hidup (live load). Sedangkan beban horizontal adalah beban yang disebabkan oleh pengaruh angin (wind load) dan beban gempa (earthquake load).
2.4.1 Beban Mati
Setiawan (2008) berpendapat bahwa beban mati adalah berat dari semua bagian dari suatu gedung yang bersifat tetap, termasuk segala unsur tambahan, mesin-mesin serta peralatan tetap yang merupakan bagian yang tidak terpisahkan dari gedung tersebut.
a). Berat Penutup Atap dan Gording
P = P1 + P2 ...(2.3) Sehingga:
P1 = Berat penutup atap x Jarak antar kuda-kuda x Jarak gording P1 = Berat gording x Jarak antar kuda-kuda
b). Berat Plafond dan Penggantung
q = Berat plafond + berat penggantung ...(2.4)
2.4.2 Beban Hidup
Setiawan (2008) berpendapat bahwa beban hidup adalah semua beban yang bekerja pada struktur yang terjadi akibat penghunian atau penggunaan gedung, termasuk didalamnya beban-beban pada lantai dan bahan-bahan yang dapat dipindah-pindah.Lebih lanjut, menurut anonim (1989) beban hidup dibagi menjadi:
a). Beban terpusat berasal dari seorang pekerja dengan peralatannya (P) sebesar 100 kg.
b). Beban terbagi rata akibat air hujan
Dimana:
α = Sudut kemiringan atap.
2.4.3 Beban Angin
Sebuah pendapat lain dikemukakan oleh Setiawan (2008) bahwa beban angin adalah semua beban yang bekerja pada gedung atau bagian gedung yang disebabkan oleh selisih dalam tekanan udara. Beban angin ditujukan dengan menganggap adanya tekanan positif dan tekanan negatif (isapan) yang bekerja tegak lurus pada bidang-bidang yang ditinjau. Besarnya tekanan positif dan tekanan negatif ini dinyatakan dalam kg/m2 ditentukan dengan mengalikan tekanan tiup yang telah ditentukan dengan koofesien-koofesien angin yang telah ditentukan dalam peraturan. Tekanan angin (W) diambil sebesar 40 kg/m2, sedangkan untuk koefisien angin tergantung pada sudut kemiringan atap dan dinding vertikalnya. Adapun besarnya nilai koefisien angin tekan dan angin hisap adalah sebagai berikut :
Ctekan = 0,02 . α – 0,...(2.6) Chisap = -0,40 ...(2.7) Dimana:
α = Sudut kemiringan atap < 65° .
2.5 Kombinasi Beban
Anonim (2012) mengemukakan bahwa struktur komponen elemen struktur harus dirancang sedemikian hingga tahanan rencana harus melebihi jumlah dari beban-beban kerja dikalikan dengan suatu faktor beban kerja dengan kombinasi-kombinasi sebagai berikut:
1,4D ...(2.8) 1,2D + 1,6L + 1,5 (La atau H) ...(2.9) 1,2D + 1,6 (La atau H) + (ɣL . L atau 0,8W) .(2.10)
1,2D + 1,3W + ɣL . L + 0,5 (La atau H) ...(2.11) 1,2D + 1,0E + ɣL . L .(2.12)
0,9D + (1,3W atau 1,0E ) ...(2.13)
Dimana:
D = beban mati tetap
L = beban hidup yang ditimbulkan oleh penggunaan gedung La = beban hidup atap
W = beban angin H = beban hujan
E = beban gempa yang ditentukan dari peraturan gempa ɣL = 0,5 bila L < 5 Kpa, dan L = 1 bila L > 5 Kpa.ɣ
2.6 Batang Tekan
Anonim (1997) menjelaskan bahwa batang tekan adalah elemen struktur baja yang memikul/menstranfer gaya aksial tekan antara dua titik pada struktur. Akan tetapi gaya aksial yang diterima adalah gaya aksial tekan sehingga pengaruh tekuk (buckling) atau lenturan tiba-tiba akibat ketidakstabilan merupakan
persoalan yang mendapat perhatian lebih pada batang tekan. Dengan ungkapan lain, kekuatan batang tekan tidak hanya dipengaruhi bahannya tetapi juga dipengaruhi bentuk geometris penampang (jari-jari girasi penampang). Keruntuhan yang mungkin terjadi pada elemen tekan yaitu tekuk, tekuk yang terjadi pada batang akan mengikuti salah satu dari tiga macam tekuk yang ada yaitu: lokal, lentur, torsi. Tekuk lokal (local buckling) adalah tekuk yang terjadi pada pelat elemen (sayap/badan) yang menekuk karena tipis, ini dapat terjadi sebelum batang menekuk lentur secara keseluruhan. Tekuk lentur (flexural buckling) adalah tekuk yang menyebabkan elemen batang lentur terhadap sumbu lemah batang. Tekuk torsi (torsional buckling) adalah tekuk yang terjadi pada elemen pelat yang menyebabkan penampang berputar/memuntir terhadap sumbu batang.
.
Gambar 2.3 :Tekuk lentur pada arah sumbu lemah, Tekuk torsi dan. Tekuk lentur-torsi.
2.6.1 Tahanan Tekan Nominal
Anonim (2002) mejelaskan bahwa suatu komponen struktur yang mengalami gaya tekan kosentris, akibat beban terfaktor Nu harus memenuhi :
Nu ≤ Øc . Nn ...(2.14)
Nn = Ag . fcr = Ag . f yω ... (2.15)
Dimana :
Nu = Kuat tekan terfaktor
Nn = Kuat tekan nominal komponen struktur = Ag . fcr fcr = Tegangan tekan yang terjadi
Øc = 0,85
Berdasarkan tegangan kritis untuk daerah elastis dapat ditentukan nilai koefisien tekuk (w) sebagai berikut :
Sehingga :
λc = λπ .
√
f yE...(2.16) Dimana:
λ = k . I
λc = Kelangsingan Struktur tekan fy = Tegangan leleh baja
E = Modulus elastisitas
Dengan besarnya koefisien tekuk (ω) ditentukan oleh λc : a). Untuk λc < 0,25 maka ω = 1
b). Untuk 0,25 ≤ λc ≤ 1,2 maka ω = 1,431,6 0,67 . λc˗ c). Untuk λc > 1,2 maka ω = 1,25 . λc2
Dalam perhitungan kuat tekan nominal juga harus diperhitungkan faktor yang ditentukan oleh dimensi badan (web), dengan nilai koefisien ketentuan tekuk sebagai berikut : y 170 f 2tf b ≤ ...(2.17)
2.6.2 Komponen Struktur Tekan Tersusun
Komponen struktur tekan dapat tersusun dari dua atau lebih profil, yang disatukan dengan menggunakan pelat kopel. Analisis kekuatannya harus dihitung terhadap sumbu bahan dan sumbu bebas bahan (Setiawan, 2008). Kelangsingan pada arah sumbu bahan (sumbu x) λx dan pada arah sumbu bebas bahan (sumbu y) harus dihitung kelangsingan ideal λiy:
λx =
k . Lx
rx ... .(2.18)
λiy =
√
λy2+m2 . λI2 ... .(2.19) λy = k . Lyry ...(2.20) λ1 = L1 rmin ...(2.21) dimana:Lx , Ly = Panjang komponen struktur tekan arah x dan arah y
K = Faktor panjang tekuk
rx , ry , rmin = Jari - jari girasi komponen struktur tekan
m = Konstanta yang besarnya ditentukan dalam peraturan L1 = Jarak antar pelat kopel pada arah komponen struktur tekan
Untuk menjaga kestabilan elemen-elemen penampang struktur tersususun, maka harga λx, λiy, dan λ1 harus memenuhi:
a). λx ≥1,2 λ1 b). λiy≥1,2 λ1 c). λ1≤50
Pelat kopel yang digunakan harus cukup kaku sehingga memenuhi persamaan: Ip a ≥ 10 . I1 L1 ... (2.22) Ip = 2 . 12 . t . h1 3 ... (2.23) Dimana:
Ip = Momen inersia pelat kopel, untuk pelat kopel dimuka dan dibelakang yang tebalnya (t) dan tingginya (h) (mm4).
t = tebal plat h = tinggi plat
I1 = Momen inersia minimum satu buah profil (mm4).
a = Jarak antar dua pusat titik berat elemen komponen struktur (mm4) Pelat kopel dihitung dengan mengganggap bahwa pada seluruh panjang komponen struktur tersusun bekerja gaya lintag sebesar:
Du = 0,02 . Nu ...(2.24) Dimana:
NU = Kuat tekan komponen struktur tersusun akibat beban-beban terfaktor. Kuat geser pelat kopel:
Vu ≤ Ø.Vn ...(2.25) Dimana:
Vu = Gaya geser perlu Ø = Faktor reduksi 0,85 Vu = Kuat geser nominal
2.6.3 Tekuk Lentur Torsi
Menurut anonim (2002), kuat tekan tekuk lentur torsi dari komponen struktur tekan yang terdiri dari siku ganda dan profil T harus memenuhi:
Nu < Øn . Nnlt ...(2.26) Dimana :
Nnlt = Ag. fclt
Tegangan Kritis Tekuk Lentur Torsi (fclt) :
fcit = fcry+fcrz)2 ¿ ¿ 1−4 . fcry . fcrz . H¿ 1-√¿
(
fcry+fcrz 2 . H)
¿ ...(2.27) Dimana : fcrz = G. J Ag . ´r 02 G = 2 . (1+V ) E J = Ʃ 13 . b . t3 ´ r 02 = Ix + IyAg + x o2+ y o2 fcry = ωiyfy H = 1 - x 0 2 +y 02 ´ r 02 Dimana: G = Modulus geserJ = Konstanta puntir ´
r 02
= Jari-jari girasi polar terhadap pusat geser
xo dan yo = Koordinat pusat geser terhadap titik berat, xo = 0, untuk profil siku ganda dan profil T
2.7 Batang Tarik
Anonim (1997) menjelaskan bahwa batang tarik adalah elemen struktur baja yang memikul/menstransfer gaya aksial tarik antara dua titik pada struktur. Batang tarik didesain untuk mencengah beberapa keruntuhan yang diakibatkan gaya yang bekerja pada batang dalam kondisi normal. Keruntuhan tersebut diantaranya, leleh diseluruh luasan penampang, fraktur di luasan efektif penampang, blok geser, retak akibat geser disepanjang sambungan. Untuk mencegah terjadinya defleksi yang besar serta untuk mencegah bergetarnya batang oleh angin atau beban getar, maka kelangsingan batang utama dan batang sekunder perlu dibatasi. Secara teoritis, kekuatan penampang batang tarik dapat dimobilisasikan secara maksimal hingga penampang mencapai keruntuhan. Akan tetapi pada kondisi sebenarnya, kekuatan batang tarik harus direduksi dengan adanya lobang pada sambungan dan tidak sentrisnya gaya tarik yang bekerja. Dengan ungkapan lain, kekuatan batang tarik ditentukan oleh seberapa luas suatu penampang secara efektif ikut serta memikul gaya aksial tarik tersebut.
2.7.1 Tahanan Nominal
Setiawan (2008) berpendapat bahwa dalam menentukan tahanan nominal suatu batang tarik, harus diperiksa terhadap dua macam kondisi keruntuhan yaitu :
Semua komponen struktur yang memikul gaya tarik aksial terfaktor sebesar Nu, maka harus memenuhi persyaratan:
NU ≤ Ø. Nn ...(2.28) Dimana:
Nu = Beban terfaktor
Ø = Faktor tahanan/reduksi Ø = 0,90 untuk kondisi leleh.
Ø = 0,75 untuk kondisi fraktur/putus.
a) Leleh dari penampang kotor di daerah yang jauh dari sambungan
Bila kondisi leleh yang menentukan, maka tahanan nominal Nn dari batang tarik memenuhi persamaan :
Nn = Ag . fy (2.29) Dimana:
Ag = Luas penampang kotor (mm2) fy = Kuat leleh material (Mpa)
b). Kondisi fraktur/putus dari luas penampang efektif pada sambungan. Bila kondisi fraktur pada sambungan yang menentukan, maka tahanan nominal (Nn) dari batang tersebut memenuhi persamaan:
Nn = Ae . fu ...(2.30) Dimana:
Ae = Luas penampang efektif/netto = U. An An = Luas netto penampang (mm2)
U = Koefisien reduksi = 1 - Lx´ x = Eksentrisitas sambungan (mm)
L = Panjang sambungan dalam arah gaya tarik fu = Tegangan tarik putus baja (Mpa)
b) Geser Blok
Sebuah elemen pelat yang menerima beban tarik yang disambungkan pada alat pengencang, tahanan dari komponen tarik tersebut ditentukan dari kondisi batas sobek atau sering disebut geser blok. Keruntuhan geser blok merupakan penjumlahan tarik leleh (tarik fraktur) pada satu irisan dengan geser fraktur (geser leleh) pada irisan lainnya yang saling tegak lurus. Tahanan nominal tarik dalam keruntuhan geser blok yaitu:
Nn = 0,6. fy.Agv+ fu.Ant ...(2.31) Dimana:
fu = Tegangan tarik putus baja (sesuai mutu baja) fu = Tegangan leleh baja (sesuai mutu baja) Ant = Luas netto akibat tarik
Agv = Luas kotor akibat geser
Geser fraktur dengan tarik leleh
Nn = 0,6. fu.Anv+ fy.Agt ...(2.32) Dimana:
Anv = Luas netto akibat geser Agt = Luas kotor akibat tarik 2.7.2 Kelangsingan Struktur Tarik
Untuk mengurangi lendutan besar, maka komponen struktur tarik harus memenuhi syarat kekakuan. Syarat ini berdasarkan pada rasio kelangsingan yaitu:
λ = Lkr < 240 ...
(2.33) Dimana:
λ = Kelangsingan komponen struktur L = Panjang komponen struktur r = Jari - jari girasi
(Setiawan, 2008) Nilai λ diambil maksimum 240 untuk batang tarik. 2.7.3 Luas Penampang Netto Minimum
Setiawan (2008) berpendapat lubang yang dibuat pada sambungan untuk menempatkan alat pengencang seperti baut atau paku keling, mengurangi luas penampang sehinnga akan mengurangi pula penampang tersebut.
Anet ≤ 0,85 . Ag ...(2.34) Luas netto penampang batang tarik tidak boleh diambil lebih besar dari pada 85% luas bruttonya
2.7.4 Efek Lubang Berselang-seling Pada Luas Netto
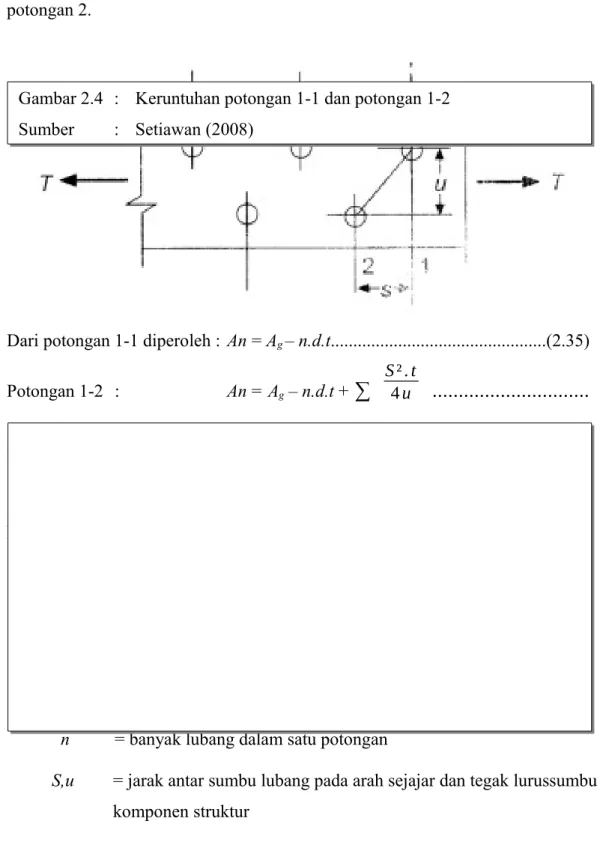
Lubang baut dapat diletakkan berselang-seling seperti dalam gambar (2.4). Dalam SNI 03-1729-2002 pasal 10.2.1 diatur mengenai cara perhitungan luas netto penampang dengan lubang yang diletakkan berselang-seling, dinyatakan
bahwa luas netto harus dihitung berdasarkan luas minimum antara potongan 1 dan potongan 2.
Dari potongan 1-1 diperoleh : An = Ag – n.d.t...(2.35)
Potongan 1-2 : An = Ag – n.d.t +
∑
S ² . t4 u
...
(2.36)
Dimana :
Ag = Luas penampang kotor Au = Luas penampang netto t = tebal penampang d = diameter lubang
n = banyak lubang dalam satu potongan
S,u = jarak antar sumbu lubang pada arah sejajar dan tegak lurussumbu komponen struktur
2.8 Sambungan
Gambar 2.4 : Keruntuhan potongan 1-1 dan potongan 1-2 Sumber : Setiawan (2008)
Anonim (2002) menjelaskan bahwa setiap struktur baja merupakan
gabungan dari beberapa komponen barang yang disatukan dengan alat pengencang/ alat sambung. Sambungan berfungsi untuk menyalurkan gaya-gaya dalam (momen, lintang/geser, aksial) antar komponen-komponen struktur yang disambung.
Sambungan yang cukup populer digunakan pada penyambungan komponen struktur konstruksi adalah sambungan baut dan sambungan las.
2.8.1 Sambungan Baut (bolt)
Setiawan (2008) berpendapat bahwa pada setiap struktur baja merupakan suatu elemen yang paling vital untuk diperhitungkan, hal ini di karanekan baut merupakan alat sambung yang paling sering digunakan. Ada dua jenis utama baut yaitu baut mutu tinggi dan mutu normal A307 terbuat dari baja kadar karbon rendah.
Dua tipe dasar baut mutu tinggi yang distandarkan oleh ASTM adalah tipe A325 dan A490. Baut ini mempunyai kepala berbentuk segi enam. Baut A325 terbuat dari baja karbon yang memiliki kuat leleh 560-630 MPa, baut A490 terbuat dari baja alloy dengan kuat leleh 790-900 MPa, tergantung pada diameternya. Diameter baut mutu tinggi berkisar antara ½ - 1½ in, yang sering digunakan dalam struktur bangunan berdiameter ¾ dan ⅞ in, dalam desain jembatan antara ⅞ hingga 1 in.
Dalam pemasangan baut mutu tinggi memerlukan gaya tarik awal yang cukup, yang diperoleh dari pengencangan awal. Gaya ini akan memberikan friksi sehingga cukup kuat untutk memikul beban yang bekerja . Gaya ini dinamakan proof load. proof load diperoleh diperoleh dengan mengalikan luas daerah tegangan tarik (As), dengan kuat leleh yang diperoleh dengan metoda 0,2% tangen atau 0,5 % regangan yang besarnya 70% untuk A325, dan 80% fu untuk A490.
As = π4
[
d b−0,9743n]
2 ... (2.37)Dimana :
db = adalah diameter nominal baut n = adalah jumlah ulir per mm Tabel 2.2 Tipe – Tipe Baut
Tipe baut Diameter Proof strees (MPa) Kuat Tarik Min (MPa)
A307 6,35 – 104 - 60
A325 12,7 – 25,4 585 825
28,6 – 38,1 510 725
A490 12,7 – 38,1 825 1035
1) Tahanan nominal baut
Suatu baut yang memiliki gaya terfaktor Ru harus memenuhi :
Ru ≥ Ø.Rn ...(2.38) Dimana:
Ru = gaya terfaktor baut Rn = tahanan nominal baut Ø = faktor reduksi 0,75
a). Tahanan geser baut
Rn = m . r1 . fub . Ab ...(2.39)
Ab = 14 . π . d n2
Dimana:
r1 = 0,50, untuk baut tanpa ulir pada bidang geser r1 = 0,40, untuk baut dengan ulir pada bidang geser fub = kuat tarik baut (MPa)
Ab = luas brutto penampang baut pada daerah tak berulir
m = jumlah bidang geser dn = diameter nominal baut
b). Tahanan Tarik Baut
Baut yang memikul gaya tarik tahanan nominalnya dihitung menurut :
Rn = 0,75 . fub . Ab ...(2.40) Dimana :
fu = kuat tarik baut (MPa)
Ab = luas brutto penampang baut pada daerah tak berulir
c). Kuat tumpu baut
Rn = 2,4 . db . tp . fu ...(2.41) Dimana :
db = diameter baut pada daerah takberulir tp = Tebal pelat
fu = Kuat tarik putus terendah dari baut atau pelat
2) Kebutuhan baut
nb = RuØ . Rn ...(2.42)
3) Tata letak baut
Jarak antar pusat lubang baut harus diambil tidak kurang dari 3 kali diameter nominal baut dan jarak antara baut tepi dengan ujung pelat harus sekurang-kurangnya 1,5 diameter nominal baut. Jarak maksimum antar pusat lubang baut tidak boleh melebihi 15 tp (dengan tp adalah tebal pelat lapis tertipis dalam sambungan) atau 200 mm, sedangkan jarak tepi maksimum harus tidak melebihi (4 tp + 100 mm) atau 200 mm.
Persyaratan jarak antar baut sebagai berikut :
3.db ≤ S ≤ 15 tp atau 200 mm ...(2.43) 1,5.db ≤ S ≤ (4.tp + 100 mm ) atau 150 mm ...(2.44) Dimana :
db = diameter baut
S = jarak antar baris baut dan jarak antar sumbu baut S1 = jarak antar sumbu baut ke tepi pelat
2.8.2 Sambungan Las
Setiawan (2008) menyebutkan bahwa pengelasan adalah suatu proses penyambungan bahan logam yang menghasilkan peleburan bahan dengan memanasinya hingga suhu yang tepat dengan atau tanpa pemberian tekanan dan dengan atau tanapa pemakaian bahan pengisi.
Beberapa jenis sambungan yang sering ditemui dalam sambungan las adalah:
1. Sambungan sebidang (butt joint), sambungan ini umumnya dipakai untuk penyambung pelat datar dengan ketebalan sama atau hampir
sama,keuntungan sambungan ini adalah tak adanya eksentrisitas. 2. Sambungan lewatan (lap joint), jenis sambungan ini paling banyak
dijumpai karena sambungan ini mudah disesuaikan keadaan dilapangan dan juga penyambungannya relatif lebih mudah .
3. Sambungan tegak (tee joint), sambungan ini banyak dipakai terutama untuk membuat penampang tersusun sepeerti bentuk I, pelat girder, stiffener.
Gambar 2.5 : Tata letak baut Sumber : Setiawan (2008)
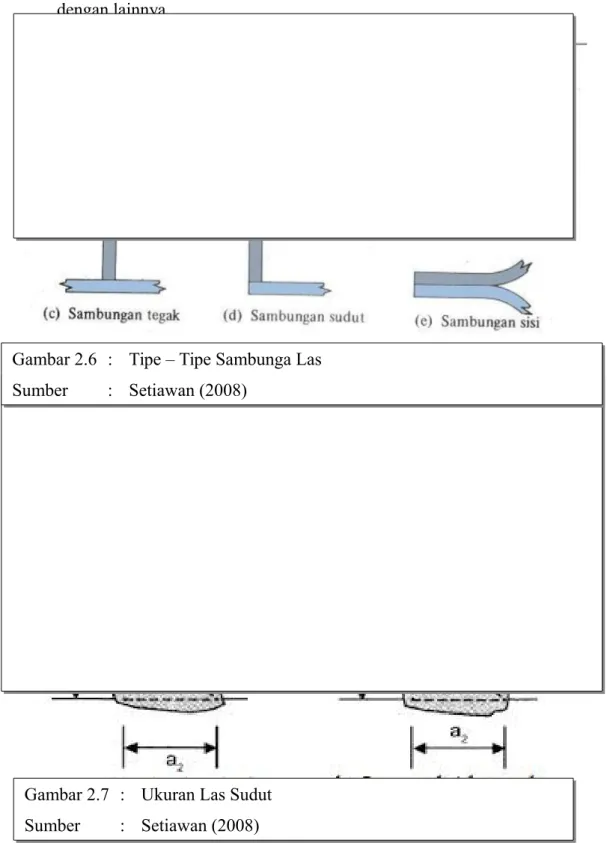
4. Sambungan sudut (corner joint), dipakai untuk penampang tersusun berbentuk kotak yang digunakan untuk kolom atau balok yang menerima gaya torsi yang besar.
5. Sambungan sisi (edge joint), sambungan ini bukan jenis struktural dan digunakan untuk menjaga agar dua atau lebih pelat tidak bergeser satu dengan lainnya.
Jenis-jenis las yang sering dijumpai antara lain adalah las tumpul (groove welds), las sudut (fillet welds), dan las baji dan pasak (slot and plug welds).Namun pada kajian perencanaan ini hanya memakai satu jenis las yaitu las sudut (fillet welds).
ccdvd
Gambar 2.6 : Tipe – Tipe Sambunga Las Sumber : Setiawan (2008)
Tabel 2.3 Ukuran Minimum Las sudut
Sumber : Setiawan (2008)
Sedangkan pembatasan ukuran maksimum las sudut :
a). Untuk komponen dengan tebal kurang dari 6,4 mm, diambil setebal komponen
b). Untuk komponen dengan tebal 6,4 mm atau lebih, diambil 1,6 mm kurang dari tebal komponen.
1. Tahanan Nominal Sambungan Las
Filossofi umum dari LRFD terhadap persyaratan keamanan suatu struktur, dalam hal ini terutama untuk las, adalah terpenuhinya persamaan :
Ø . R nw ≥ Ru ... (2.45)
Dimana :
Ø = adalah faktor tahanan
R nw = adalah tahanan nominal per satuan panjang las Ru = adalah beban terfaktor per satuan panjang las A. Las Tumpul
Kuat las tumpul penetrasi penuh ditetapkan sebagai berikut :
a. Bila sambungan dibebani dengan gaya tarik atau gaya tekan aksial tarhadap luas efektif, maka :
Tebal pelat(t, mm) Paling Tebal Ukuran Minimum Las Sudut (a, mm)
t ≤ 7 3
7 < t ≤ 10 4
10 < t ≤ 15 5
Ø . R nw = 0,90 . t . f (bahan dasar)...ₑ ʸ (2.45)
Ø . R nw = 0,90 . t . f (las)...ₑ ʸʷ (2.46)
b. Bila sambungan dibebani dengan gaya geser terhadap luas efektif, maka : Ø . R nw = 0,90 . t . (0,6 . f ) (bahan dasar)...ₑ ʸ (2.47)
Ø . R nw = 0,80 . t . (0,6 . fu ) (las)...ₑ ʷ (2.48)
B. Las Sudut
Kuat rencana per satuan panjang las sudut, ditentukan sebagai berikut : Ø . R nw = 0,75 . t . (.0,6 . fₑ uw) (las) ... (2.49)
Ø . R nw = 0,75 . t . (.0,6 . ₑ fu) (bahan dasar) ... (2.50)
2. Geser Eksentris – Metoda Elastik
Analisa didasarkan pada prinsip mekanika bahan homogen, menggabungkan antara geser langsung dengan puntir. Tegangan pada penampang homogen :
f = ʼ PA ( tegangan akibat geser langsung)... (2.51)
f ˮ = T .rI p (tegangan akibat momen puntir)... (2.52)
Dimana :
r = adalah jarak daari titik berat ke titik tegangan Ip = adaalah momen inersia polar
3. Geser Eksentris – Metoda Plastis
Metoda ini jauh lebih rumit dari pada metoda elastik, seperti halnya pada saat pembahasan geser eksentris pada sambungan baut.
Ø . R nw = Ø . t . 0,60 . fₑ uw . ( 1 + 0,50 . sin ˡ 5 θ ) ...(2.53)
Dimana : Ø = 0,75
θ = adalah sudut beban diukur dari sumbu memanjang arah las
Jika segmen las merupakan bagian dari suatu konfigurasi las yang terkena beban geser eksentris, maka persamaan 2.20 domodifikasi menjadi :
Ri = 0,60 . fuw . te . (1 + 0,50 . sin 1 . 5 θ )
[
∆ i ∆ m(
1,9−0,9. ∆i ∆ m)
]
0,3... (2.54) Dimana :Ri = adalah tahanan nominal segmen las, N/mm
θ = adalah sudut beban diukur dari sumbu memanjang las, derajat ∆ i = adalah deformasi elemen ke – i = ri .
[
∆ ur
]
min ∆ m = 5,31 . ( θ + 2) -0,32 . a , mm∆ u = 27,61 . ( θ + 6)-0,65 . a ≤ 4,318 . a , mm a = adalah panjang kaki las sudut, mm
2.9 Pemodelan Struktur Rangka Batang/Kuda-kuda
Menurut Suhendro (2005), rangka batang terbentuk dari elemen-elemen batang lurus yang dirangkai dalam bidang datar dengan sambungan antar ujung-ujung batang diasumsikan sebagai sendi sempurna. Beban luar yang bekerja harus berada di titik buhul (titik sambungan) dengan arah sembarang namun harus sebidang dengan bidang struktur tersebut. Pemodelan rangka bidang (plane truss) diperlihatkan pada gambar 2.4 dengan penentuan Number Degress of Freedom (NDOF).
2.10 Software SAP2000
Dewobroto (2007) menyatakan bahwa program SAP2000 merupakan pengembangan program SAP1 yang dibuat oleh Prof. Edward L. Wilson dari University of California at Barkeley, US sekitar tahun 1970. Untuk melayani keperluan komersial dari program SAP, pada tahun 1975 dibentuk perusahaan Computer and Structure, Inc. Dipimpin oleh Ashraf Habibullah, dimana perusahaan tersebut sampai saat ini masih tetap eksis dan berkembang.
Sebagai program komputer analisa struktur yang dikembangkan cukup lama dari lingkungan universitas sehingga source code pada awal mulanya dapat dengan mudah dipelajari, maka program SAP menjadi cikal bakal program-program analisa struktur lain di dunia. Dengan reputasi lebih dari 30 tahun, program SAP dikenal secara luas dalam komunitas rekayasa, khususnya di bidang teknik sipil dan secara spesifik lagi adalah para structural engineer.
Dasar teori statik yang digunakan program SAP2000 adalah metode matrik kekakuan, dimana suatu persamaan keseimbangan struktur dapat ditulis dalam bentuk matrik sebagai berikut.
[K] {δ}={F} ...(2.55) Dimana :
[K] = adalah matrik kekakuan
{δ} = adalah vektor perpindahan atau deformasi (translasi atau rotasi) struktur.
{F} = adalah vektor gaya/momen yang dapat berbentuk beban pada titik nodal bebas atau gaya reaksi tumpuan pada titik nodal yang di-restraint.
Untuk menganalisa struktur rangka batang yang stabil dengan program SAP2000, data properti penampang yang diperlukan hanya A (Croos-section-axial area). Sedangkan data properti penampang lain, khususnya untuk kekakuan
lentur (momen inersia penampang), kekakuan torsi aksial G dan K dapat dihilangkan (diberi nilai nol).
Jika digunakan A (Croos-section-axial area), element batang tidak perlu di release untuk menjadi element truss. Tapi ingat, konfigurasi geometri harus mengikuti syarat truss, yaitu R + M – 2J ≥ 0 (truss 2D) atau R + M – 3J ≥ 0 (truss 3D), dimana M = member; R = gaya reaksi, dan J = titik nodal.Ʃ Ʃ Ʃ
III.METODELOGI PENELITIAN
Untuk melakukan sebuah kajian yang baik maka diperlukan sebuah rancangan penelitian yang sistematiks dan terarah, sehingga diperoleh suatu hasil kajian dengan hasil yang maksimal.
3.1 Sumber dan Jenis Data
Data yang diperlukan dalam kajian ini adalah data sekunder. Data tersebut didapat dari konsultan perencana yang mengerjakan proyek pembangunan yaitu CV.Tessa Engineering Consultant.
3.2 Situasi dan Lokasi proyek
Pembangunan gedung ini telah selesai dikerjakan pada tahun 2014 yang terletak di Sigli, kabupaten Pidie, Provinsi Aceh . Lokasi pelaksana proyek ini dapat dilihatpada peta provinsi Aceh di lampiran A Gambar A. 1.2. halaman
Dalam melakukan kajian ini, untuk mencapai hasil sesuai dengan yang diharapkan ada beberapa tahapan atau prosedur yang akan dilakukan seperti : penentuan tipe struktur, perhitungan beban, analisa struktur, perencanaan sambungan dan kombinasi pembebanan.
3.3.1 Penentuan Tipe Struktur
Rangka batang dimodelkan sebagai rangka bidang (plane truss) yang terdiri dari batang tarik dan batang tekan. Panjang kuda-kuda 10 m, sebagai gambaran bentuk rangka kuda-kuda diperlihatkan pada gambar 3.1.
60 60
686
Gording Atap Aspal Iko
RB 15/20 1000 300 60 60 60 60 60 60 60 60 60 128 1 : 50 DETAIL K.1 ( Mutlipleks 9 mm Dilapisi Underlayer 3.3.2 Perhitungan Beban
Setelah penentuan tipe struktur kemudian dilanjutkan dengan perhitungan beban :
a. Desain gording atau perhitungan berat sendiri
b. Menghitung beban mati dengan menggunakan persamaan 2.3 sampai dengan persamaan 2.4.
c. Menghitung beban hidup dengan menggunakan persamaan 2.5.
d. Menghitung beban angin dengan menggunakan persamaan 2.6 sampai dengan persamaan 2.7.
3.3.3 Analisa Struktur/ input SAP2000
Setelah desain gording selesai dan perhitungan beban selesai dilanjutkan input data ke SAP2000 .
a. Kombinasi beban akan dihitung dengan persamaan 2.8 sampai dengan persamaan 2.11.
b. Gaya batang tarik/ tekan
Gambar 3.1 : Bentuk rangka kuda-kuda Sumber : Konsultan perencana
c. Reaksi tumpuan
3.3.4 Desain Elemen Rangka Batang
Setelah input data ke SAP2000 selesai dilanjutkan dengan desain elemen nya, jika desain elemen nya tidak aman maka harus dilakukan pengulangan desain elemennya.
3.3.5 Perencanaan Sambungan
Setelah perhitungan analisa struktur kemudian menentukan sambungan, Sambungan disini dikelompokkan menjadi dua bagian, yaitu sambungan baut dan las.
a). Sambungan Baut
Prosedur selanjutnya yang dilakukan adalah menghitung sambungan baut : 1. Tahanan nominal baut dengan menggunakan persamaan 2.36
- Tahanan geser baut menggunakan persamaan 2.37 - Tahanan tarik baut menggunakan persamaan 2.38 - Kuat tumpu baut menggunakan persamaan 2.39 2. Kebutuhan baut dengan menggunakan persamaan 2.40
3. Tata letak baut dengan menggunakan persamaan 2.41 samapai 2.42 b). Sambungan Las
Prosedur selanjutnya yang dilakukan adalah menghitung sambungan las : 1. Tahanan nominal sambungan las dengan menggunakan persamaan 2.43
sampai dengan persamaan 2.49
2. Geser eksentris – metoda elastik dengan menggunakan persamaan 2,.50 sampai 2.51
3. Geser eksentris – metoda plastis dengan menggunakan persamaan 2.52 sampai 2.53
3.3.6 Pengolahan Data
Pengolahan data dilakukan setelah perhitungan beban berdasarkan rumus-rumus pada tinjauan pustaka. Pengolahan data akan dilakukan dengan
menggunakan software SAP2000.
Dalam melakukan kajian ini, ada beberapa hasil yang ingin diperoleh antara laim :
1. Dapat diketahui ketahanan elemen rangka batang terhadap gaya aksial yang bekerja.
2. Dapat diketahui reaksi tumpuannya
3. Didapat kekuatan/ketahanan sambungan elemen rangka batang yang memenuhi persyaratan keamanan.
V. KESIMPULAN DAN SARAN
Dari hasil kajian diharapkan akan diperoleh beberapa kesimpulan dan saran antara lain
1. Mengetahui desain sambungan rangka batang yang aman terhadap beban-beban yang akan diterima.
VI. DAFTAR PUSTAKA
Anonim., 1997, Universitas Gunadharma: Struktur Baja 1, Jakarta : Erlangga. Dewobroto, Wiryanto., 2007, Aplikasi Rekayasa Konstruksi dengan SAP2000,
Jakarta :PT. Elex Media Komputindo.
Kassimali, A., 1989, Matrix Analysis of Structure, Brooks/cole Publishing Company, USA.
PPBI,. 1984, Standar PBBI 1984: Perencanaan Bangunan Baja Indonesia (PBBI), Cetakan Kedua, Bandung : Yayasan LPMB
Pedoman Penulisan Tugas Akhir Jurusan Teknik Sipil 2013 (Edisi Revisi). Fakultas Teknik Universitas Muhammadiyah Aceh.
Peta Lokasi Proyek, http://googleearth.com. Diakses tanggal 17 may 2016. Peta Provinsi Aceh, http://google.com. Diakses tanggal 17 may 2016.
Setiawan, Agus., 2008, Perencanaan Struktur Baja dengan Metode LFRD, Jakarta : Erlangga.
Schodek, D. L., 1995 Struktur, Terjemahan Bambang Surya Atmono, Cetakan Kedua, Bandung : PT. Eresco.
Suhendro, Bambang., 2005, Analisis Struktur Metode Matrix, Yogyakarta : Beta Offset
SNI., 1989,Standar SNI 03-1727-1989: Pedoman Perencanaan Pembebanan untuk Rumah dan Gedung, Bandung : Departemen Pekerjaan Umum. SNI., 2002, Standar SNI 03-1729-2002: Tata Cara Perencanaan Struktur Baja