1
BINOMIAL SIGN TEST FOR A SINGLE-SAMPLE (Uji Tanda Binomial untuk Satu Sampel)
Oleh: Ade Heryana, SST, MKM
Prodi Kesehatan Masyarakat, FIKES Univ. Esa Unggul
PENDAHULUAN
Uji Binomial Sign Single-sample atau uji “Tanda Binomial Satu Sampel” adalah salah satu uji statistik non-parametrik yang digunakan untuk menguji hipotesis pada populasi yang terdiri dari dua kategori data, yaitu menguji apakah proporsi sampel pada satu dari dua kategori sama dengan nilai yang ditentukan.
Karakteristik dari uji tanda-binomial satu sampel adalah:
1. Berdasarkan distribusi binomial merupakan salah satu distribusi probilitas pada data yang bersifat diskret yaitu distribusi yang nilai-nilai variabelnya terbatas. Dalam distribusi normal, setiap n observasi yang bersifat independen dilakukan secara acak pada sebuah populasi, dan setiap obervasi tersebut dikelompokkan ke dalam satu dan dua kategori yang bersifat mutually exclusive (yakni hasil dari observasi yang satu tidak dipengaruhi oleh observasi yang lain). Dalam populasi yang berdistribusi binomial, kemungkinan sebuah observasi akan masuk dalam kategori 1 sama dengan 𝜋1 dan kemungkinan sebuah observasi akan masuk dalam kategori 2 sama dengan 𝜋2. Sehingga 𝜋1+ 𝜋2 = 1 atau 𝜋2 = 1 − 𝜋1. Rata-rata () dan standar deviasi () variabel yang terdistribusi normal adalah:
𝜇 = 𝑛𝜋1 Persamaan (1)
𝜎 = √𝑛𝜋1𝜋2 Persamaan (2)
Ada tiga kemungkinan bentuk dari distribusi binomial yaitu: a. Simetris, jika 𝜋1 = 𝜋2 = 0,5
b. Menceng positif ke arah mendekati nol, jika 𝜋1 < 0,5 c. Menceng negatif ke arah mendekati satu, jika 𝜋1 > 0,5
2. Menggunakan distribusi binomial untuk menentukan kemungkinan bahwa x atau lebih (atau x atau kurang) dari n observasi memiliki sampel yang masuk dalam satu dari dua kategori.
2
3. Uji hipotesisnya dapat dinyatakan sebagai berikut: berdasarkan populasi yang direpresentasikan oleh sampel, apakah terdapat perbedaan antara frekuensi observasi pada dua kategori dengan frekuensi yang diharapkan?
4. Umumnya dipakai pada sampel dalam jumlah kecil. Bila sampel yang dipakai berjumlah besar, maka perhitungan memerlukan bantuan aplikasi pengolah data komputer.
CONTOH SOAL-11
Sebuah eksperimen dilakukan untuk menentukan apakah sebuah koin (yang memiliki sisi “kepala” dan “ekor”) tidak simetris sehingga memiliki kesalahan hitung atau tidak. Koin diputar sebanyak sepuluh kali dan menghasilkan 8 kepala dan 2 ekor. Apakah hasil eksperimen tersebut menunjukkan bahwa koin memiliki kesalahan pengukuran?
CONTOH SOAL-22
Sepuluh wanita dikumpulkan untuk mencoba apakah dua merk obat gosok salisil yang akan diluncurkan memiliki rasa panas atau tidak. Delapan wanita menunjukkan obat gosok salisil merk A panas, sedangkan dua wanita menyatakan yang panas adalah merk B. Apakah terhadap perbedaan yang signifikan terhadap jawaban sepuluh wanita tersebut?
JAWABAN
Pada prinsipnya kedua soalnya tersebut memiliki data yang sama, sehingga jawaban keduanya adalah sebagai berikut
Hipotesis
Hipotesis nol 𝐻0: 𝜋1 = 0,5
Hipotesis alternatif 𝐻1 ≠ 0,5 (two-tailed)
1 Sumber: Sheskin (2004, hal. 269) 2 Sumber: Sheskin (2004, hal. 269)
3 Perhitungan statistik
Sesuai dengan contoh-1 maka hipotesis nol dan hipotesis alternatif menggambarkan bahwa bila koin tersebut dalam keadaan baik (simetris) maka probabilitas untuk menghasilkan “kepala” adalah 0,5 atau 𝜋1 = 0,5. Begitu pula probabilitas untuk memunculkan sisi “ekor” adalah 0,5 atau 𝜋2 = 0,5.
Sementara itu sesuai contoh-2 diasumsikan bahwa bila tidak ada perbedaan dalam pemilihan kedua merk obat gosok salisil, maka probabilitas seorang wanita memilih merk A adalah 0,5 atau 𝜋1 = 0,5 dan probabilitas seorang wanita memilih merk B adalah 0,5 atau 𝜋2 = 0,5.
Dari kedua contoh di atas, pertanyaan yang harus dijawab adalah bila n = 10 dan 𝜋1 = 𝜇2 = 0,5 berapakah probabilitas bahwa 8 atau lebih observasi berada dalam 1 dari 2 kategori?
Dari kedua contoh soal di atas maka frekuensi munculnya sisi “kepala” dari koin atau wanita memilih merk A adalah 8 atau x = 8. Sedangkan frekuensi munculnya sisi “ekor” dari koin atau wanita memilih merk B adalah 2 atau n - x = 8, dimana n = 10. Maka proporsi observasi untuk kategori 1 (sisi “kepala” atau merk A) adalah 𝑝1=
8 10= 0,8. Sedangkan proporsi observasi untuk kategori 2 (sisi “ekor” atau merk B) adalah 𝑝2 = 2
10= 0,2.
Perhitungan untuk menyimpulkan hasil uji hipotesa bisa menggunakan cara probabilistik (dengan rumus dan aplikasi komputer) dan cara klasik (dengan tabel). a. Cara probalistik (dengan rumus distribusi binomial)
Formula yang dipakai untuk menghitung probabilitas bahwa x tepat berada dalam satu dari dua kategori dari n observasi adalah:
𝑃(𝑥) = (𝑛
𝑥) (𝜋1)𝑥(𝜋2)(𝑛−𝑥) Persamaan (3)
dimana: (𝑛
𝑥) = koefisien binomial atau secara umum menjelaskan jumlah kombinasi dari n terhadap x pada waktu tertentu, dan dihitung dengan persamaan berikut:
4 (𝑛 𝑥) = 𝑛! 𝑥! (𝑛 − 𝑥)! Persamaan (4) Pada contoh soal-1 dan contoh soal-2 di atas, koefisien binomialnya adalah (10
8) yaitu kombinasi 10 terhadap 8. Bila nilai koefisien ini dikalikan dengan (0,5)8 dan (0,5)2 menghasilkan probabilitas terjadinya tepat 8 sisi “kepala”/merk A dari 10 observasi yang diberi notasi 𝑃(8
10). Nilai 𝑃( 8
10) dihitung dengan persamaan (3) di atas menghasilkan:
𝑃(8/10) = (10 8) (0,5)
8(0,5)(10−2) = (45)(0,5)8(0,5)2 = 0,0439
Untuk menjawab permasalahan contoh soal-1 dan soal-2 di atas, tidak cukup hanya mendapatkan probabilitas terjadinya tepat 8 kejadian saja, namun juga perlu dihitung probalilitas kumulatif jika x = 8, 9 dan 10, sehingga dengan persamaan (3): 𝑃(9/10) = (10 9) (0,5) 9(0,5)(10−1) = (45)(0,5)9(0,5)1 = 0,0098 𝑃(10/10) = (10 10) (0,5) 10(0,5)(10−10) = (45)(0,5)10(0,5)0 = 0,0010
Sehingga probabilitas kumulatif 𝑃(8,9, 𝑎𝑡𝑎𝑢 10 10⁄ ) = 0,0439 + 0,0098 + 0,0010 = 0,547.
b. Cara tabel
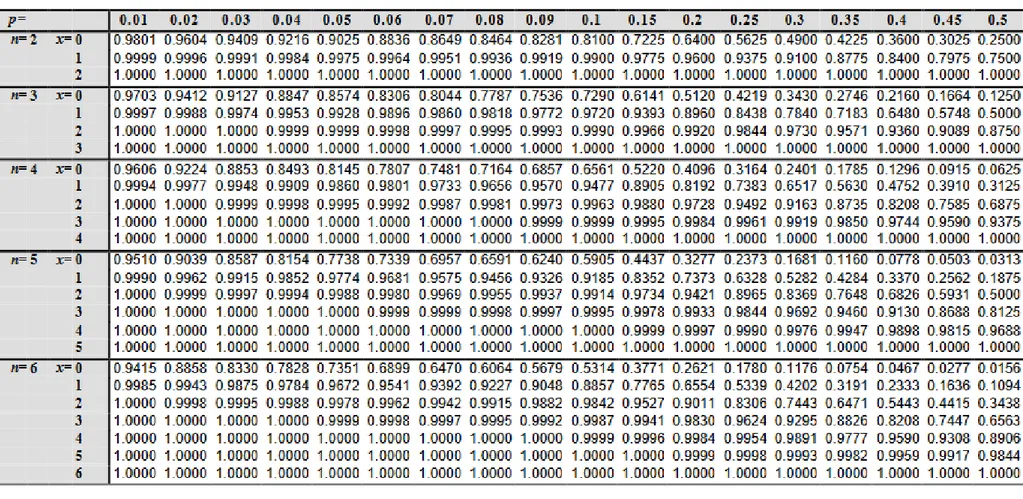
Cara lain menghitung probabilitas kumulatif x = 8,9, dan 10 adalah dengan tabel Distribusi Binomial Probabilitas Kumulatif (Lihat lampiran). Dengan n = 10, x = 8 dan = 0,5 maka probabilitas kumulatifnya adalah 0,9453. Sehingga probabilitas tepat x = 8,9, dan 10 adalah 1 – 0,9453 = 0,0547.
Interpretasi hasil perhitungan
Berdasarkan hasil perhitungan dengan rumus atau tabel didapat p value = 0,0547 atau lebih besar dari = 0,05 sehingga hipotesis ditolak atau terdapat perbedaan antara nilai observasi dengan nilai harapan atau tidak cukup bukti untuk menyatakan bahwa koin memiliki bias (contoh-1) atau wanita memilih merk A dibanding merk B (contoh soal-2).
5 REFERENSI
Viterel, V (NA). Tables of Binomial Cumulative Distribution. Diunduh tanggal 16 April 2017 dari https://mat.iitm.ac.in/home/vetri/public_html/statistics/binomial.pdf
Sheskin, David J. (2004). Handbook of Parametric and Nonparametric Statistical Procedures, edisi 3. DC: Chapman & Hall/CRC
LATIHAN SOAL
1. Sebuah studi berminat melakukan uji fluorescent antibody guna meneliti adanya reaksi serum setelah pengobatan pada penderita malaria falcifarum. Dari 25 subjek yang telah disembuhkan, 15 subjek ditemukan bereaksi positif. Jika sampel itu memenuhi semua asumsi yang mendasari uji binomial, dapatkah kita menyimpulkan dari data itu bahwa proporsi reaksi positif dalam populasi yang bersangkutan adalah lebih besar dari 0,5? Misalkan α = 0,053
2. Dari 15 mobil ambulans yang beroperasional di sebuah Rumah Sakit, 10 diantaranya rutin masuk bengkel. Berapa probabilitas bahwa ambulans yang rutin masuk bengkel lebih besar dari yang tidak rutin masuk bengkel, dengan = 5%, atau dengan kata lain apakah proporsi ambulans rutin masuk bengkel lebih besar daripada tidak masuk bengkel?
3. Dari 36 mobil ambulans yang beroperasional di sebuah Rumah Sakit, 11 diantaranya rutin masuk bengkel. Berapa probabilitas bahwa ambulans yang rutin masuk bengkel lebih besar dari yang tidak rutin masuk bengkel, dengan = 5%, atau dengan kata lain apakah proporsi ambulans rutin tidak masuk bengkel lebih besar daripada rutin masuk bengkel?
4. Dari 20 dokter yang bekerja di sebuah Rumah Sakit, 8 diantaranya tidak setuju dengan kebijakan baru. Berapa probabilitas bahwa dokter yang tidak setuju lebih besar dari yang setuju kebijakan baru, dengan = 5%, atau dengan kata lain
3 Sumber: Wayne W.Daniel, 2003, hal 67
6
apakah proporsi dokter yang tidak setuju lebih kecil daripada setuju kebijakan baru?
7
Lampiran: Tabel Distribusi Binomial Kumulatif
(Sumber: Vetrivel, Indian Institute of Technology, Madras)4
Tabel berikut menyajikan probabilitas terjadinya paling sedikit x kejadian pada n percobaan yang independen atau probabilitas sukses (p of success). Bila X adalah jumlah sukses, maka probabilitasnya adalah 𝑃(𝑋 ≤ 𝑥) = ∑𝑥 𝐶𝑟𝑛𝑝𝑟(1 − 𝑝)𝑛−𝑟
𝑟=0
11