Informasi Dokumen
- Penulis:
- Bambang Haryadi
- Pengajar:
- Diyah Nuraini, Editor
- Sekolah: Pusat Perbukuan, Departemen Pendidikan Nasional
- Mata Pelajaran: Fisika
- Topik: Fisika: Untuk SMA/MA Kelas XI
- Tipe: buku
- Tahun: 2009
- Kota: Jakarta
Ringkasan Dokumen
I. Kinematika dengan Analisis Vektor
Bab ini membahas konsep dasar kinematika yang mencakup posisi, kecepatan, dan percepatan. Kinematika adalah cabang fisika yang mempelajari gerak tanpa mempertimbangkan penyebabnya. Pemahaman tentang gerak sangat penting dalam kehidupan sehari-hari, dan buku ini bertujuan untuk memberikan fondasi yang kuat bagi siswa. Konsep-konsep ini disajikan dengan cara yang sistematis dan komprehensif, sehingga siswa dapat memahami hubungan antara posisi, kecepatan, dan percepatan dengan baik.
1.1. Posisi Titik Materi pada Suatu Bidang
Posisi suatu benda dapat dinyatakan dalam bentuk vektor. Vektor posisi adalah vektor yang menghubungkan titik acuan dengan titik materi. Buku ini menjelaskan bagaimana menggambarkan posisi dalam bidang kartesius dan memperkenalkan vektor satuan yang digunakan dalam analisis posisi.
1.2. Kecepatan
Kecepatan adalah perubahan posisi terhadap waktu. Buku ini membahas kecepatan rata-rata dan kecepatan sesaat, serta bagaimana menghitungnya menggunakan persamaan yang tepat. Pemahaman tentang kecepatan sangat penting untuk memahami gerak benda dalam fisika.
1.3. Percepatan
Percepatan adalah perubahan kecepatan per satuan waktu. Buku ini menjelaskan konsep percepatan rata-rata dan percepatan sesaat, serta bagaimana menghubungkannya dengan gerak benda. Pemahaman tentang percepatan membantu siswa mengerti dinamika gerak.
1.4. Gerak Lurus
Gerak lurus adalah gerak dengan kecepatan konstan atau percepatan konstan. Buku ini memberikan contoh dan rumus yang diperlukan untuk menganalisis gerak lurus, termasuk gerak lurus berubah beraturan. Hal ini penting untuk memahami berbagai fenomena fisika yang terjadi di sekitar kita.
1.5. Gerak Parabola
Gerak parabola adalah kombinasi antara gerak lurus beraturan dan gerak lurus berubah beraturan. Buku ini menjelaskan bagaimana menganalisis gerak peluru dan berbagai aplikasi dalam kehidupan nyata, seperti olahraga dan teknologi. Pemahaman ini penting untuk siswa yang ingin melanjutkan ke studi lanjut di bidang fisika.
1.6. Gerak Melingkar
Gerak melingkar melibatkan posisi sudut, kecepatan sudut, dan percepatan sudut. Buku ini mengajarkan siswa bagaimana menghitung dan menganalisis gerak benda yang bergerak dalam lintasan melingkar. Konsep ini sangat relevan dalam banyak aplikasi teknik dan fisika.
II. Gravitasi Planet dalam Sistem Tata Surya
Bab ini membahas hukum gravitasi Newton dan penerapannya dalam sistem tata surya. Siswa diajarkan bagaimana menghitung percepatan gravitasi dan memahami hukum-hukum Kepler. Pemahaman tentang gravitasi sangat penting untuk memahami gerakan planet dan fenomena astronomi lainnya.
2.1. Hukum Gravitasi Newton
Hukum gravitasi Newton menjelaskan bagaimana dua benda saling tarik menarik berdasarkan massa dan jarak mereka. Buku ini memberikan penjelasan yang jelas dan contoh penerapan hukum ini dalam kehidupan sehari-hari.
2.2. Percepatan Gravitasi
Percepatan gravitasi adalah percepatan yang dialami benda akibat gaya gravitasi. Buku ini menjelaskan bagaimana menghitung percepatan gravitasi di berbagai lokasi dan pentingnya konsep ini dalam fisika.
2.3. Penerapan Hukum Gravitasi Newton
Bab ini memberikan contoh penerapan hukum gravitasi dalam berbagai fenomena alam, seperti gerakan planet dan satelit. Penerapan konsep ini sangat penting dalam memahami dinamika sistem tata surya.
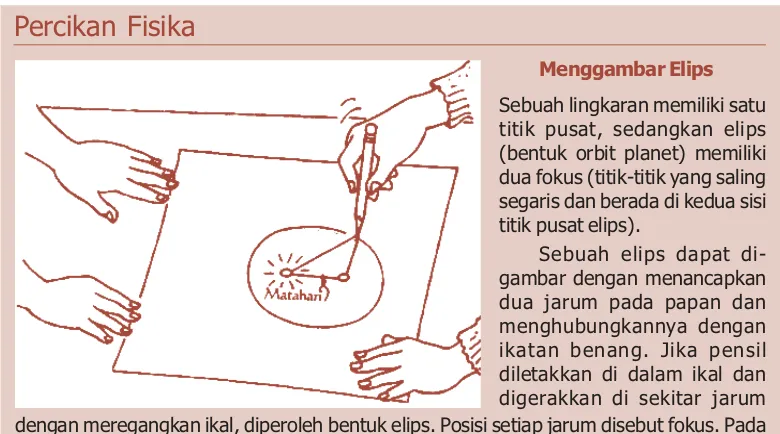
2.4. Hukum-Hukum Kepler
Hukum-hukum Kepler menjelaskan gerakan planet di sekitar matahari. Buku ini membantu siswa memahami hubungan antara waktu revolusi dan jarak planet dari matahari, yang merupakan konsep kunci dalam astronomi.
III. Pengaruh Gaya pada Elastisitas Bahan
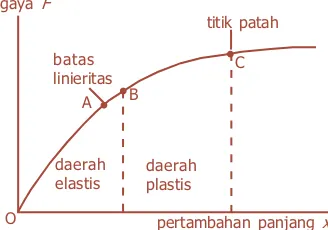
Bab ini membahas elastisitas dan bagaimana gaya mempengaruhi sifat bahan. Siswa diajarkan tentang hukum Hooke dan aplikasinya dalam berbagai konteks. Pemahaman tentang elastisitas penting untuk berbagai aplikasi teknik dan rekayasa.
3.1. Elastisitas Zat Padat
Elastisitas mengacu pada kemampuan bahan untuk kembali ke bentuk semula setelah mengalami deformasi. Buku ini menjelaskan konsep ini dengan baik dan memberikan contoh yang relevan.
3.2. Tegangan dan Regangan
Tegangan adalah gaya per satuan luas yang diterapkan pada suatu bahan, sedangkan regangan adalah perubahan bentuk akibat tegangan. Buku ini menjelaskan hubungan antara keduanya dan bagaimana hal ini mempengaruhi sifat bahan.
3.3. Hukum Hooke
Hukum Hooke menyatakan bahwa regangan suatu bahan berbanding lurus dengan tegangan yang diterapkan. Buku ini memberikan penjelasan yang mendalam tentang hukum ini dan aplikasinya dalam berbagai bahan.
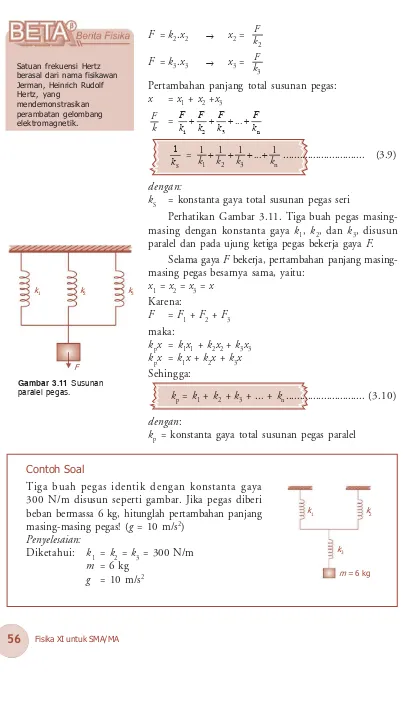
3.4. Analisis Gerakan Pegas
Bab ini membahas bagaimana pegas berperilaku di bawah berbagai kondisi. Pemahaman tentang pegas sangat penting dalam banyak aplikasi teknik dan fisika.
IV. Usaha dan Energi
Bab ini menjelaskan konsep usaha dan energi dalam fisika. Siswa diajarkan tentang hukum kekekalan energi dan aplikasinya. Pemahaman tentang usaha dan energi sangat penting untuk memahami banyak fenomena fisika.
4.1. Usaha
Usaha adalah produk gaya dan jarak yang ditempuh. Buku ini memberikan penjelasan yang jelas tentang bagaimana menghitung usaha dalam berbagai konteks.
4.2. Energi
Energi adalah kemampuan untuk melakukan usaha. Buku ini membahas berbagai bentuk energi dan bagaimana mereka saling berhubungan.
4.3. Daya
Daya adalah laju usaha yang dilakukan. Buku ini menjelaskan bagaimana menghitung daya dan pentingnya dalam berbagai aplikasi.
4.4. Hukum Kekekalan Energi Mekanik
Hukum ini menyatakan bahwa energi total dalam sistem tertutup adalah konstan. Buku ini memberikan contoh penerapan hukum ini dalam berbagai konteks fisika.
V. Momentum dan Impuls
Bab ini membahas konsep momentum dan impuls, serta hubungan antara keduanya. Siswa diajarkan tentang hukum kekekalan momentum dan aplikasinya. Pemahaman tentang momentum dan impuls sangat penting untuk analisis gerakan.
5.1. Pengertian Momentum dan Impuls
Momentum adalah produk massa dan kecepatan, sedangkan impuls adalah perubahan momentum. Buku ini menjelaskan konsep ini dengan jelas dan memberikan contoh yang relevan.
5.2. Tumbukan
Tumbukan adalah interaksi antara dua benda yang bertabrakan. Buku ini membahas berbagai jenis tumbukan dan bagaimana momentum dipertahankan selama tumbukan.
5.3. Aplikasi Hukum Kekekalan Momentum
Hukum kekekalan momentum menyatakan bahwa dalam sistem tertutup, momentum total sebelum dan sesudah tumbukan adalah sama. Buku ini memberikan contoh penerapan hukum ini dalam berbagai konteks.
VI. Dinamika Rotasi dan Kesetimbangan Benda Tegak
Bab ini membahas konsep dinamika rotasi dan kesetimbangan benda tegar. Siswa diajarkan tentang momen gaya dan aplikasinya. Pemahaman tentang dinamika rotasi penting untuk berbagai aplikasi teknik.
6.1. Momen Gaya (Torsi)
Momen gaya adalah ukuran dari seberapa besar gaya yang dapat menyebabkan benda berputar. Buku ini menjelaskan konsep ini dengan baik dan memberikan contoh aplikasinya.
6.2. Momen Inersia
Momen inersia adalah ukuran dari seberapa sulitnya mengubah keadaan gerak rotasi suatu benda. Buku ini membahas bagaimana menghitung momen inersia untuk berbagai bentuk benda.
6.3. Hubungan antara Momen Gaya dengan Percepatan Sudut
Buku ini menjelaskan hubungan antara momen gaya dan percepatan sudut, serta bagaimana keduanya saling mempengaruhi dalam gerak rotasi.
6.4. Energi dan Usaha Gerak Rotasi
Energi dalam gerak rotasi berhubungan dengan momen inersia dan kecepatan sudut. Buku ini memberikan penjelasan yang mendalam tentang konsep ini.
6.5. Momentum Sudut
Momentum sudut adalah produk momen inersia dan kecepatan sudut. Buku ini menjelaskan bagaimana menghitung momentum sudut dan aplikasinya.
6.6. Kesetimbangan Benda
Kesetimbangan benda terjadi ketika semua gaya dan momen gaya yang bekerja pada benda seimbang. Buku ini membahas kondisi kesetimbangan dan aplikasinya dalam berbagai konteks.
VII. Fluida
Bab ini membahas sifat-sifat fluida dan hukum-hukum yang mengaturnya. Siswa diajarkan tentang tekanan dan aplikasinya dalam berbagai konteks. Pemahaman tentang fluida sangat penting dalam banyak bidang ilmu.
7.1. Tekanan dan Tekanan Hidrostatik
Tekanan adalah gaya per satuan luas yang diterapkan pada suatu permukaan. Buku ini menjelaskan bagaimana menghitung tekanan dan aplikasinya dalam fluida.
7.2. Hukum Dasar Fluida Statis
Hukum ini menjelaskan hubungan antara tekanan, kedalaman, dan berat jenis fluida. Buku ini memberikan penjelasan yang jelas dan contoh penerapan hukum ini.
7.3. Tegangan Permukaan
Tegangan permukaan adalah fenomena yang terjadi pada permukaan fluida akibat gaya tarik menarik antar molekul. Buku ini menjelaskan konsep ini dan aplikasinya.
7.4. Fluida Dinamis
Buku ini membahas perilaku fluida yang bergerak dan hukum-hukum yang mengaturnya, termasuk hukum Bernoulli. Pemahaman tentang fluida dinamis penting dalam berbagai aplikasi teknik.
VIII. Teori Kinetik Gas
Bab ini membahas teori kinetik gas dan bagaimana gas berperilaku pada tingkat molekuler. Siswa diajarkan tentang hukum-hukum gas dan aplikasinya. Pemahaman tentang gas sangat penting dalam banyak bidang ilmu.
8.1. Hukum-Hukum tentang Gas
Hukum-hukum gas menjelaskan hubungan antara tekanan, volume, dan suhu gas. Buku ini memberikan penjelasan yang mendalam tentang hukum Boyle, hukum Charles, dan hukum Avogadro.
8.2. Teori Kinetik Gas
Teori ini menjelaskan perilaku gas berdasarkan gerakan molekulnya. Buku ini membantu siswa memahami konsep tekanan dan suhu dalam konteks teori kinetik.
8.3. Teori Ekipartisi Energi
Teori ini menjelaskan bagaimana energi dibagi di antara molekul gas. Buku ini memberikan penjelasan yang jelas dan contoh penerapan teori ini.
IX. Termodinamika
Bab ini membahas konsep dasar termodinamika dan hukum-hukumnya. Siswa diajarkan tentang usaha, energi, dan proses termodinamika. Pemahaman tentang termodinamika penting dalam banyak aplikasi teknik dan fisika.
9.1. Usaha dan Proses dalam Termodinamika
Usaha dalam termodinamika terkait dengan perubahan energi dalam sistem. Buku ini menjelaskan berbagai jenis proses termodinamika dan bagaimana menghitung usaha yang dilakukan.
9.2. Hukum I Termodinamika
Hukum ini menyatakan bahwa energi tidak dapat diciptakan atau dimusnahkan, hanya dapat berubah bentuk. Buku ini menjelaskan hukum ini dan aplikasinya dalam berbagai konteks.
9.3. Siklus pada Termodinamika
Siklus termodinamika adalah proses yang mengubah energi dalam sistem. Buku ini membahas berbagai siklus dan aplikasinya dalam mesin dan teknologi.
9.4. Hukum II Termodinamika
Hukum ini menjelaskan arah alami proses termodinamika dan konsep entropi. Buku ini memberikan penjelasan yang mendalam tentang hukum ini dan aplikasinya.
X. Uji Kompetensi
Bagian ini berisi soal-soal uji kompetensi untuk mengevaluasi pemahaman siswa terhadap materi yang telah dipelajari. Soal-soal ini dirancang untuk membantu siswa mengukur kemampuan mereka dalam menerapkan konsep-konsep fisika.
Referensi Dokumen
- Kamus Lengkap Fisika ( Alan Isaacs )
- Fundamental University Physics ( Alonso, Finn )
- Jendela Iptek Teknologi ( Bri d gman, Roger )
- Jendela Iptek Energi ( Challoner, Jack )
- Kamus Fisika Bergambar ( Corrine Stockley, Chris Oxlade, Jane Wortheim )