APLIKASI MATRIKS VARIAN-KOVARIAN ROBUST PADA ANALISIS FAKTOR SKRIPSI AYU ANDINI

APLIKASI MATRIKS VARIAN-KOVARIAN ROBUST PADA ANALISIS FAKTOR

SKRIPSI

AYU ANDINI 140803034

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2018

APLIKASI MATRIKS VARIANS-KOVARIANS ROBUST PADA ANALISIS FAKTOR

SKRIPSI

Ditulis Sebagai Syarat untuk Mencapai Gelar Sarjana Sains di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

AYU ANDINI 140803034

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2018

i

PERNYATAAN ORISINALITAS

APLIKASI MATRIKS VARIAN-KOVARIAN ROBUST PADA ANALISIS FAKTOR

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri,kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, September 2018

Ayu Andini 140803034

PENGESAHAN SKRIPSI

Judul : Aplikasi Matriks Varian-Kovarian Robust Pada Analisis Faktor

Kategori : Skripsi

Nama : Ayu Andini

Nomor Induk Mahasiswa : 140803034

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Disetujui di

Medan, September 2018

Komisi Pembimbing: Disetujui Oleh

Departemen Matematika FMIPA USU

Pembimbing Ketua

Dr. Elly Rosmaini, M.Si Dr. Suyanto, M.Kom NIP.196005201985032002 NIP.195908131986011002

iii

APLIKASI MATRIKS VARIAN-KOVARIAN ROBUST PADA ANALISIS FAKTOR

ABSTRAK

Salah satu metode estimasi pada analisis faktor adalah metode analisis komponen utama. Analisis Faktor dengan metode Analisis Komponen Utama menjelaskan struktur matriks varian-kovarian data melalui sejumlah kecil komponen yang tidak saling berkorelasi, dimana komponen tersebut merupakan kombinasi linier dari variabel-variabel asal sedemikian hingga mempunyai variansi yang maksimal.

Matriks varian-kovarian robust dapat diestimasikan dengan Minimum Volume Ellipsoid (MVE). Pada penelitian ini, faktor loading yang dihasilkan dari setiap variabel dengan estimasi robust dan estimasi klasik memiliki perbedaan, yaitu dengan estimasi robust faktor loading-faktor loading yang dihasilkan memiliki nilai yang tidak jauh berbeda. Seperti pada variabel X1 faktor loading-nya adalah 2,6069; -3,2191; dan -0,0762. Sedangkan dengan estimasi biasa (klasik) faktor loading-faktor loading yang dihasilkan memiliki perbedaan nilai yang cukup jauh.

Seperti pada variabel X1 faktor loading-nya adalah 1,6546; 13,4489; dan -0,5143.

Kata Kunci: Analisis faktor, analisis komponen utama, multivariat, MVE, robust

THE APPLICATION OF ROBUST VARIANCE-COVARIANCE MATRIX ON FACTOR ANALYSIS

ABSTRACT

One of the estimation methods in factor analysis is the principal component analysis method. Factor Analysis with the Principal Component Analysis method describes the structure of the variance-covariance matrix of data through a small number of components that are not correlated with each other, where the component is a linear combination of the origin variables so that they have maximum variance. The robust covariance-variant matrix can be estimated by the Minimum Ellipsoid Volume (MVE). In this study, the robust estimated factor loading and the classic estimated factor loading have different results such in variable X1 , the factor loadings are 2,6069; -3,2191; and -0,0762. However, the classic estimated factor loadings are 1,6546; 13,4489; and -0,5143.

Keyword: Factor Analysis, Multivariate, MVE, Principal Component Analysis, Robust

v

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Allah SWT, atas limpahan karunia-Nya penulis dapat menyelesaikan penyusunan skripsi dengan judulAplikasi Matriks Varian-KovarianRobust Pada Analisis Faktordengan baik,guna melengkapi syarat memperoleh gelar S1Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam diUniversitas Sumatera Utara.

Dalam kesempatan ini, penulis ingin mengucapkan terima kasih yangsebesar-besarnya kepada semua pihak yang telah membantu dan membimbingpenulis dalam penyusunan skripsi ini, ucapan terima kasih penulis sampaikankepada Bapak Alm. Drs. Pengarapen Bangun, M.Si dan IbuDr. Elly Rosmaini, M.Si selaku Dosen Pembimbing.Bapak Dr. Sutarman, M.Scdan IbuDra. Laurentina Pangaribuan, MSselaku DosenPembanding atas segala saran dan masukan yang diberikan dalam penyelesaian skripsi ini.Bapak Dr. Suyanto, M.Kom dan Bapak Drs. Rosman Siregar, M.Siselaku Ketua dan Sekretaris Departemen Matematika FMIPA USU.Bapak Dr. Kerista Sebayang, MS selaku Dekan FMIPA USU serta semuaWakil Dekan FMIPA USU.Semua Dosen Departemen Matematika FMIPA-USU dan pegawai diFMIPA-USU.Ayahanda Helmi Wahyudi, Ibunda Suriyani, M.Pd,Saudara penulis, Ari Andrian, S.T dan Dimas Anhari, serta keluarga yang memberikan doa dan dukungan bagi penulis.Seluruh teman-teman.

Penulis menyadari bahwa masih terdapat banyak kekurangan dalam penulisanskripsi ini. Maka, diperlukan kritik dan saran dari pembaca untukpenyempurnaan skripsi ini.

Medan, September 2018 Penulis

Ayu Andini

DAFTAR ISI

Halaman

PERNYATAAN ORISINALITAS i

PENGESAHAN SKRIPSI ii

ABSTRAK iii

ABSTRACT ^iv

PENGHARGAAN v

DAFTAR ISI vi

BAB 1 PENDAHULUAN

1.1 Latar Belakang 1

1.2 Rumusan Masalah 2

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 3

1.5 Manfaat Penelitian 3

1.6 Metodologi Penelitian 3

BAB 2 TINJAUAN PUSTAKA

2.1 Matriks 5

2.1.1 Definisi Matriks 5

2.1.2 Matriks Invers 5

2.1.3 Matriks Definit dan Semidefinit Positif 6

2.1.4 Matriks Ortogonal 6

2.1.5 Matriks Simetrik 7

2.1.6 Matriks Transpose A 7

2.1.7 Matriks Identitas 7

2.1.8 Determinan Matriks 7

2.2 Analisis Faktor 8

2.3 Metode Estimasi 11

2.3.1 Analisis Komponen Utama 12 2.3.2 Faktor Model Solusi Komponen Utama 14 2.4 Analisis Komponen Utama Yang Robust 14

2.5 Minimum Volume Ellipsoid (MVE) 15

2.5.1 Algoritma MVE 15

BAB 3 HASIL DAN PEMBAHASAN

3.1 Pengumpulan Data 18

3.2 Analisis Faktor Dengan Metode MVE 3.3 Analisis Faktor Klasik

19 21

3.4 Estimated Factor Loading 23

BAB 4 KESIMPULAN DAN SARAN

4.1 Kesimpulan 25

4.2 Saran 25

vii

DAFTAR PUSTAKA 26

LAMPIRAN

BAB I PENDAHULUAN

1.1 Latar Belakang

Teknik multivariat berperan dalam mengakomodasi banyak variabel untuk memahami hubungan kompleks yang tidak bisa dipahami dengan metode univariat atau bivariat. Semakin banyak variabel, semakin besar kemungkinan bahwa variabel- variabel tersebut berhubungan (berkorelasi) dan tidak mewakili konsep yang berbeda atau variabel-variabel ini mewakili konsep yang lebih umum.

Analisis faktor membantu pemilihan variabel-variabel yang lebih representatif atau membuat variabel baru sebagai pengganti variabel asli tapi masih mengandung karakteristik dari variabel asli tersebut. Ada beberapa metode estimasi pada analisis faktor, salah satunya adalah metode analisis komponen utama.

Analisis Faktor dengan metode Analisis Komponen Utama (Principal Component Analysis) menjelaskan struktur matriks varian-kovarian data melalui sejumlah kecil komponen yang tidak saling berkorelasi, dimana komponen tersebut merupakan kombinasi linier dari variabel-variabel asal sedemikian hingga mempunyai variansi yang maksimal. Seringkali Analisis Komponen Utama digunakan sebagai langkah pertama dalam analisis data, seperti dalam regresi komponen utama, analisis diskriminan, analisis cluster dan berbagai metode analisis multivariat lainnya.

Matriks varian-kovarian sangat sensitif terhadap pengamatan outlier. Pada kenyataannya, data lapangan seringkali mengandung beberapa pengamatan outlier dan biasanya tidak mudah untuk dipisahkan dari data. Oleh karena itu, penyusutan dimensi data berdasarkan Analisis Komponen Utama yang klasik menjadi tidak dapat diandalkan lagi apabila pengamatan outlier muncul dalam data (Sujatmiko et al., 2005).

Outlier adalah pengamatan yang berada jauh (ekstrim) dari pengamatan- pengamatan lainnya. Pendeteksian outlier pada pengamatan univariat telah dilakukan

2

oleh Hawkins (1980) yang melihat suatu outlier tunggal pada sampel dengan melihat pengamatan yang menyimpang dari pengamatan lain. Barnet dan Lewis (1994) melihat pengaruh pengamatan yang tidak konsisten dengan pengamatan lain pada proses multivariat, Pena dan Prieto (2001) menyajikan prosedur pendeteksian outlier didasarkan pada analisis proyeksi dari titik-titik sampel, dan Filzmoser (2005) mengidentifikasi outlier didasarkan pada jarak Mahalanobis.

Keberadaan outlier akan mengganggu dalam proses analisis data dan harus dihindari dalam banyak hal. Dalam kaitannya dengan analisis, outlier dapat menyebabkan residual yang besar dari model yang terbentuk, varians pada data tersebut menjadi lebih besar, taksiran interval memiliki rentang yang lebar.

Pengamatan outlier dapat diatasi dengan Analisis Komponen Utama yang robust. Pendekatan pertama dilakukan dengan menggantikan matriks varian-kovarian yang klasik dengan suatu estimator yang robust. Berbagai metode untuk mendapatkan estimator yang robust telah banyak ditawarkan. Namun, breakdown point (tingkat robust) yang dimiliki tidak lebih dari ¹

(𝑝+1) , dimana p merupakan dimensi data. Hal ini berarti bahwa untuk dimensi yang besar, suatu kelompok pencemar yang sangat kecil dapat menghasilkan estimasi yang masih dipengaruhi oleh pengamatan outlier. Matriks varian-kovarian robust dapat diestimasikan dengan fast Minimum Covariance Determinant (fast-MCD) atau Minimum Volume Ellipsoid (MVE). Pada penelitian ini penulis menggunakan metode MVE sebagai estimator robust pada matriks varian-kovarian. Biasnya yang rendah membuat MVE sangat berguna untuk deteksi outlier dalam data multivariat, sering kali melalui penggunaan jarak robust berbasis MVE.

Dari uraian di atas, penulis mencoba membuktikan performansi Analisis Faktor dengan metode Analisis Komponen Utama yang menggunakan estimator MVE.

1.2 Rumusan Masalah

Berdasarkan latar belakang di atas, didapati bahwa outlier akan mengganggu hasil dari analisis faktor. Gangguan ini disebabkan oleh matriks varian-kovarian yang

3

tidak konsisten di dalam analisis faktor. Maka, salah satu metode yang dapat digunakan untuk menaksir matriks varian-kovarian adalah Minimum Volume Ellipsoid (MVE).

1.3 Batasan Masalah

Adapun yang menjadi batasan masalah dalam penulisan skripsi ini yaitu metode yang digunakan pada Analisis Faktor adalah metode Analisis Komponen Utama dengan estimator Minimum Volume Ellipsoid (MVE).

1.4 Tujuan Penelitian

Tujuan utama dari penelitian ini adalah menggunakan matriks varian-kovarian robust pada analisis faktor dan memperlihatkan bahwa Minimum Volume Ellipsoid (MVE) merupakan estimator robust yang berguna untuk pendeteksian outlier pada data multivariat.

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai referensi pengaplikasian matriks varian- kovarian robust pada analisis faktor.

1.6 Metodologi Penelitian

Penelitian disusun dengan langkah-langkah sebagai berikut:

1. Studi Pendahuluan

Mengumpulkan dan mempelajari berbagai informasi berupa buku-buku ataupun jurnal-jurnal yang berhubungan dengan analisis faktor dan estimasi MVE.

2. Pengumpulan Data

4

Data yang digunakan sebagai contoh pengaplikasian adalah data Stackloss Brownlee.

3. Melakukan perhitungan analisis faktor robust dengan langkah sebagai berikut:

a. Menghitung estimator parameter model untuk analisis faktor robust.

b. Melakukan analisis faktor dengan menggunakan estimator robust.

c. Menghitung proporsi kumulatif varian yang dapat dijelaskan dari hasil yang didapat dari analisis faktor robust.

4. Membuat kesimpulan.

BAB 2

TINJAUAN PUSTAKA

Pada bab ini akan diurai tinjauan pustaka yang digunakan di dalam penulisan skripsi ini.

2.1 Matriks

2.1.1 Definisi Matriks

Sebuah matriks adalah jajaran empat persegi panjang dari bilangan-bilangan.

Bilangan-bilangan dalam jajaran tersebut disebut entri dari matriks (Anton & Rorres, 2004).

Matriks dapat dituliskan sebagai berikut:

𝑨 = [

𝑎₁₁ 𝑎₁₂ ⋯ 𝑎_1𝑝 𝑎₂₁ 𝑎₂₂ ⋯ 𝑎_2𝑝

⋮ 𝑎_𝑝1

⋮ 𝑎_𝑝2 ⋱

⋯

⋮ 𝑎_𝑝𝑝

]

2.1.2 Matriks Invers

Invers matriks A merupakan matriks kebalikan dari A. Hal tersebut dapat dinyatakan dengan 𝑨⁻¹. Adapun formulasi invers dinyatakan sebagai berikut :

𝑨⁻¹= 1

|𝑨|𝑎𝑑𝑗(𝑨) dimana,

|𝑨| : determinan A

𝑎𝑑𝑗(𝑨) : adjoint A atau transpose dari matriks kofaktor A

Invers matriks A merupakan kebalikan dari matriks A, maka hasil dari perkalian antara matriks A dengan inversnya akan menghasilkan identitas (I).

𝑨𝑨⁻¹= 𝑨⁻¹𝑨 = 𝑰

6

Dimana,

𝑨⁻¹ : invers matriks 𝑨 : matriks A

𝑰 : matriks identitas (Anton & Rorres, 2004).

2.1.3 Matriks Definit dan Semidefinit Positif

Sebuah matriks A berukuran 𝑛 × 𝑛 dikatakan bersifat definit positif jika untuk sembarang vektor 𝒙 ≠ 0 , bentuk kuadratik 𝒙^−𝟏𝑨𝒙 > 0. Sedangkan dikatakan semidefinit jika 𝒙^−𝟏𝑨𝒙 ≥ 0. Jika A adalah definit positif maka persamaan 𝒙^−𝟏𝑨𝒙 = c dengan c adalah konstanta. Jika A adalah matriks diagonal yang semua unsur diagonalnya bernilai positif, maka A adalah matriks definit positif. Akan tetapi, apabila ada sebuah unsur bernilai nol dan yang lain positif maka A akan menjadi matriks semidefinit positif. Matriks diagonal yang unsurnya ragam peubah akan bersifat demikian karena ragam tidak pernah bernilai negatif.

Matriks yang definit positif, akar-akar cirinya semua bernilai positif dan determinan dari matriks definit positif juga bernilai positif karen berupa hasil perkaliannya. Jadi determinannya tidak sama dengan nol, sehingga A bersifat non- singular.

Matriks B berukuran 𝑚 × 𝑛, maka 𝐁𝐁^𝐓 dan 𝐁^𝐓𝐁 bersifat semidefinit positif. Jika 𝑚 < 𝑛 dan 𝑟(𝐵) = 𝑚, maka 𝐁𝐁^𝐓 definit positif, tetapi 𝐁^𝐓𝐁 masih semidefinit positif.

2.1.4 Matriks Ortogonal

Suatu matriks bujur sangkar A disebut ortogonal jika 𝑨𝑨^𝑇 = 𝑨^𝑇𝑨 = 𝑰 yaitu jika 𝑨^𝑇 = 𝑨⁻¹.

7

2.1.5 Matriks Simetrik

Sebuah matriks A berukuran n x n dikatakan simetrik jika A^T = A. Misalnya, jika a_ij adalah unsur ke (i,j) dari matriks, maka untuk matriks simetrik adalah a_ij = a_ji , untuk semua i dan j.

2.1.6 Matriks Transpose A

Jika A adalah sebarang matriks 𝑚 × 𝑛, maka transpose dari A dinyatakan oleh A^T dan didefinisikan dengan matriks 𝑛 × 𝑚 yang didapatkan dengan mempertukarkan baris-baris dan kolom-kolom dari A, sehingga kolom pertama dari A^T adalah baris pertama dari A, kolom kedua dari A^T adalah baris kedua dari A, dan seterusnya (Anton & Rorres, 2004).

2.1.7 Matriks Identitas

Jika R adalah bentuk eselon baris tereduksi dari matriks 𝐴_𝑛×𝑛 , maka terdapat dua kemungkinan yaitu R memiliki satu baris bilangan nol atau R merupakan matriks identitas 𝐼_𝑛 (Anton & Rorres, 2004).

2.1.8 Determinan Matriks

Menurut Mattjik dan Sumertajaya (2011), determinan matriks 𝐴_𝑛×𝑛 adalah perkalian dari semua akar ciri A, 𝜆₁, 𝜆₂, ⋯ , 𝜆_𝑛 dapat dinotasikan |𝐴|, sehingga

|𝐴| = 𝜆_𝑛× ⋯ × 𝜆_𝑛.

Jadi |𝐴| = 0 jika dan hanya jika paling tidak ada satu akar yang nol, yaitu terjadi jika dan hanya jika A singular.

8

2.2 Analisis Faktor

Analisis faktor adalah nama umum yang diberikan kepada kelas metode statistik multivariat yang tujuan utamanya adalah menentukan struktur yang mendasari dalam matriks data. Secara umum, analisis faktor membahas masalah menganalisis struktur hubungan timbal balik (korelasi) di antara sejumlah besar variabel (misalnya, nilai tes, item tes, tanggapan kuesioner) dengan mendefinisikan satu set dimensi umum yang mendasari, yang dikenal sebagai faktor. Dengan analisis faktor, peneliti dapat mengidentifikasi dimensi terpisah dari struktur dan kemudian menentukan sejauh mana setiap variabel dijelaskan oleh masing-masing dimensi. Setelah dimensi ini dan penjelasan masing-masing variabel ditentukan, dua penggunaan utama untuk analisis faktor—peringkasan dan reduksi data—dapat dicapai (Hair, 2010).

Menurut Johnson dan Wichern (1982), analisis faktor merupakan teknik analisis multivariat yang bertujuan untuk meringkas sejumlah p variabel yang diamati menjadi sejumlah m faktor penting, dengan 𝑚 < 𝑝. Misal X adalah vektor random teramati dengan yang memiliki p komponen pada pengamatan ke-i, dengan vektor rata-rata (𝝁) dan matriks kovariansi (𝚺). Vektor X bergantung secara linier dengan variabel 𝐹₁, 𝐹₂, … , 𝐹_𝑚 yang disebut faktor bersama dan sejumlah sumber variansi dari 𝜖₁, 𝜖₂, ... , 𝜖_𝑝 yang disebut faktor spesifik. Model analisis faktor menurut Johnson dan Wichern adalah:

𝑋₁− 𝜇₁ = 𝑙₁₁𝐹₁+ 𝑙₁₂𝐹₂+ ⋯ + 𝑙_1𝑚𝐹_𝑚+ 𝜀1

𝑋₂− 𝜇₂ = 𝑙₂₁𝐹₁+ 𝑙₂₂𝐹₂ + ⋯ + 𝑙_2𝑚𝐹_𝑚+ 𝜀2

⋮

𝑋_𝑝− 𝜇_𝑝 = 𝑙_𝑝1𝐹₁+ 𝑙_𝑝2𝐹₂+ ⋯ + 𝑙_𝑝𝑚𝐹_𝑚+ 𝜀p

Dengan:

𝑋_𝑝 : Variabel ke-p

𝜇_𝑝 : Rata-rata variabel ke-p

𝑙_𝑝𝑚: Bobot variabel (factor loading) ke-p pada faktor ke-m 𝐹_𝑚 : Faktor bersama (common factor) ke-m

𝜀p : Faktor spesifik ke-p

9

Faktor spesifik berkorelasi dengan yang lain dan dengan common factor.

Common factor dapat dinyatakan sebagai kombinasi linier dari variabel yang diteliti.

Dengan persamaan:

𝐹_𝑗 = 𝑊_𝑗1𝑋₁+ 𝑊_𝑗2𝑋₂+ 𝑊_𝑗3𝑋₃+ ⋯ + 𝑊_𝑗𝑝𝑋_𝑝 Dimana:

𝐹_𝑗 : Faktor ke-j yang diestimasikan W : Bobot atau koefisien skor faktor

𝑋_𝑝 : Banyaknya variabel X pada faktor ke-p p = 1, 2, ..., n ; j = 1, 2, ... , n

Struktur kovarian untuk model faktor ortogonal adalah:

1. 𝐶𝑜𝑣 (𝑋) = 𝐿𝐿^′+ Ψ Atau

𝑉𝑎𝑟 (𝑋_𝑖) = ℓ_𝑖1² + ⋯ + ℓ_𝑖𝑚² + Ψ_𝑖 𝐶𝑜𝑣 (𝑋_𝑖, 𝑋_𝑘) = ℓ_𝑖1ℓ_𝑘1+ ⋯ + ℓ_𝑖𝑚ℓ_𝑘𝑚 2. 𝐶𝑜𝑣 (𝑋, 𝐹) = 𝐿

Atau

𝐶𝑜𝑣 (𝑋_𝑖, 𝐹_𝑗) = ℓ_𝑖𝑗

Struktur Eigen pada matriks kovarian ditentukan dengan misalkan X adalah vektor random p-komponen dimana p adalah jumlah variabel. Matriks kovarian, 𝚺, diberikan oleh E(XX’). Misalkan 𝛾′ = (𝛾₁ 𝛾₂ ⋯ 𝛾_𝑝 ) adalah sebuah vektor bobot untuk membentuk kombinasi linier dari variabel-variabel asli, dan 𝜉 = 𝛾′𝑿 adalah variabel baru, yang adalah kombinasi linier dari variabel-variabel asli. Varian dari variabel baru tersebut diberikan oleh E(𝜉𝜉′) dan sama dengan E(𝛾′𝑿𝑿′𝛾) atau 𝛾′ Σ𝛾.

Masalahnya sekarang mengurangi untuk mendapatkan vektor bobot, 𝛾′, sedemikian hingga variannya, 𝛾′ Σ𝛾 , dari variabel baru tersebut maksimal pada kelas kombinasi linier yang bisa dibentuk subjek pada kendala 𝛾^′𝛾 = 𝐼.

10

Solusi untuk maksimalisasi masalah tersebut dapat diperoleh sebagai berikut:

Misalkan

𝒁 = 𝛾^′Σ𝛾 − 𝜆(𝛾^′𝛾 − 1) 𝒁 = Σ𝛾²− 𝜆(𝛾²− 1)

𝒁 = Σ𝛾²− 𝜆𝛾²+ 𝜆

dimana 𝜆 adalah pengali Lagrange. Vektor p-komponen dari turunan parsialnya diberikan dengan

𝝏𝒁

𝝏𝛾 = 2Σ𝛾 − 2𝜆𝛾

membentuk vektor turunan parsial di atas menjadi nol pada solusi akhir. Yakni, (Σ − 𝜆𝐼)𝛾 = 0

agar sistem persamaan homogen di atas memiliki sebuah solusi nontrivial, determinan (Σ − 𝜆𝐼) harus nol. Yakni,

|Σ − 𝜆𝐼| = 0

Persamaan di atas adalah polinomial dalam 𝜆 derajat p, dan karena itu memiliki p akar. Misalkan 𝜆₁ ≥, 𝜆₂ ≥, … , 𝜆_𝑝 adalah p akar. Persamaan di atas menghasilkan nilai p untuk 𝜆, dan masing-masing nilai disebut eigenvalue atau akar dari matriks Σ.

Masing-masing nilai 𝜆 menghasilkan bobot yang diperoleh dari vektor 𝛾 p- komponen dengan menyelesaikan persamaan berikut:

(Σ − 𝜆𝐼)𝛾 = 0 𝛾^′𝛾 = 𝐼

Maka, eigenvektor pertama, 𝛾₁ , sesuai dengan eigenvalue pertama, 𝜆₁, diperoleh dengan menyelesaikan persamaan

(Σ − 𝜆₁𝐼)𝛾₁ = 0

11

𝛾′₁𝛾₁ = 1

Perkalian (Σ − 𝜆₁𝐼)𝛾₁ = 0 dengan 𝛾′₁ menghasilkan 𝛾′₁(Σ − 𝜆₁𝐼)𝛾₁ = 0

𝛾′₁Σ𝛾₁ = 𝜆𝛾′₁𝛾₁ 𝛾′₁Σ𝛾₁ = 𝜆₁

karena 𝛾′₁𝛾₁ = 1. 𝛾′₁Σ𝛾₁ adalah varian dari variabel baru, 𝜉, dan sama dengan eigenvalue, 𝜆₁. Principal component yang pertama diberikan oleh eigenvektor, 𝛾₁, sesuai dengan eigenvalue terbesar, 𝜆₁.

Misalkan 𝛾₂adalah vektor bobot p-komponen kedua yang membentuk

kombinasi linier lainnya. Kombinasi linier selanjutnya dapat ditemukan sedemikian hingga varian dari 𝛾′₂𝑿 adalah subjek maksimum pada kendala 𝛾′₁𝛾₂ = 0 dan 𝛾′₂𝛾₂ = 1. Dapat ditunjukkan bahwa principal component yang tersisa,

𝛾′₃, 𝛾′₄, … , 𝛾′_𝑝, adalah eigenvektor yang sesuai dengan eigenvalue, 𝜆₃, 𝜆₄, … , 𝜆_𝑝, pada matriks kovarian, 𝚺. Maka, masalah dalam menemukan bobot merupakan menemukan struktur eigen dari matriks kovarian. Eigenvektor memberikan vektor bobot dan eigenvalue mewakili varian dari variabel-variabel baru atau nilai principal components.

2.3 Metode Estimasi

Pada pengamatan yang diberikan 𝑥₁, 𝑥₂, … , 𝑥_𝑛 dengan variabel sejumlah p yang secara umum berkorelasi, analisis faktor akan mencari jawaban dari pertanyaan:

“Apakah model faktor, dengan faktor berjumlah sedikit, dapat merepresentasikan data dengan tepat?” Pembuatan model statistik ini dilakukan dengan memverifikasi hubungan kovarian.

Matriks kovarian sampel S adalah sebuah estimator matriks 𝚺 kovarian populasi yang belum diketahui. Jika elemen-elemen off-diagonal dari S kecil atau elemen-elemen dari matriks korelasi sampel R pada dasarnya nol, variabel-variabel

12

tersebut tidak berhubungan, dan analisis faktor tidak akan terbukti berguna. Dalam keadaan ini, faktor-faktor spesifik memainkan peran dominan, dimana tujuan utama analisis faktor adalah untuk menentukan beberapa faktor umum yang penting.

Jika 𝚺 muncul menyimpang secara signifikan dari matriks diagonal, maka model faktor dapat dibentuk, dan masalah awalnya adalah memperkirakan faktor loading ℓ_𝑖𝑗 dan varian tertentu Ψ_𝑖. Penulis menggunakan metode estimasi Komponen Utama (dan Faktor Utama) untuk menyederhanakan interpretasi faktor.

2.3.1 Analisis Komponen Utama (Principal Component Analysis)

Misalkan 𝚺 mempunyai pasangan eigenvalue-eigenvektor (𝜆_𝑖, 𝑒_𝑖) dengan 𝜆₁ ≥ 𝜆₂ ≥

⋯ ≥ 𝜆_𝑝 ≥ 0. Maka,

𝚺 = 𝜆₁𝐞_𝟏𝐞′_𝟏+ 𝜆₂𝐞_𝟐𝐞′_𝟐+ ⋯ + 𝜆_𝑝𝐞_𝐩𝐞′_𝐩

= [√𝜆₁ 𝐞_𝟏⋮ √𝜆₂ 𝐞_𝟐⋮ ⋯ ⋮ √𝜆𝑝 𝐞_𝐩] [

√𝜆¹ 𝐞′_𝟏

√𝜆₂ 𝐞′_𝟐

⋮

√𝜆𝑝 𝐞′_𝐩]

(2.1)

Ini sesuai dengan struktur kovarian yang ditentukan untuk model analisis faktor yang memiliki banyak faktor sebagai variabel (m = p) dan varian tertentu Ψ_i = 0 untuk semua i. Matriks loading mempunyai j kolom yang diberikan oleh √𝜆𝑗 𝐞_𝐣. Dapat ditulis

𝚺_{(𝐩 ×𝐩)} = 𝐋_{(𝐩 ×𝐩)}𝐋′_{(𝐩 ×𝐩)} + 𝟎_{(𝐩 ×𝐩)} = 𝐋𝐋′ (2.2) Terlepas dari faktor skala √𝜆𝑗, faktor loading pada faktor ke-j adalah koefisien untuk komponen utama ke-j dari populasi.

Meskipun representasi analisis faktor dari 𝚺 di (2.1) tepat, dia tidak terlalu berguna: dia menggunakan banyak faktor umum karena ada variabel-variabel dan tidak memungkinkan variasi dalam faktor-faktor spesifik. Penulis lebih memilih model yang menjelaskan struktur kovarian hanya dari beberapa faktor umum. Satu pendekatan, ketika eigenvalue terakhir p−m kecil, adalah dengan mengabaikan kontribusi dari 𝜆_𝑚+1𝐞_𝐦+𝟏𝐞^′_𝐦+𝟏+ ⋯ + 𝜆_𝑝𝐞_𝐩𝐞′_𝐩 terhadap 𝚺 di (2.1). Dengan mengabaikan kontribusi ini, dapat diperoleh pendekatan

13

𝚺 = [√𝜆₁ 𝐞_𝟏 ⋮ √𝜆₂ 𝐞_𝟐⋮ ⋯ ⋮ √𝜆_𝑚 𝐞_𝐦] [

√𝜆¹ 𝐞′_𝟏

√𝜆₂ 𝐞′_𝟐

⋮

√𝜆_𝑚 𝐞′_𝐦]

= 𝑳_(𝒑×𝒎)𝑳′_(𝒎×𝒑) (2.3)

Representasi pendekatan di (2.3) mengganggap bahwa faktor-faktor spesifik 𝜀 di model faktor ortogonal dengan m faktor 𝑿_(𝑝×1) = 𝝁_(𝑝×1)+ 𝑳_(𝒑×𝒎) 𝑭_(𝒎×𝟏)+ 𝜺_(𝒑×𝟏) adalah kepentingan minor dan bisa juga diabaikan dalam pemfaktoran 𝚺. Jika faktor- faktor spesifik dimasukkan di dalam model, variannya bisa diambil untuk elemen diagonal dari 𝚺 − 𝐋𝐋′ , dimana 𝐋𝐋′ didefinisikan pada (2.3).

Memungkinkan untuk faktor-faktor tertentu, diperoleh pendekatan menjadi 𝚺 = 𝑳𝑳^′+ Ψ

= [√𝜆₁ 𝐞_𝟏 ⋮√𝜆₂ 𝐞_𝟐 ⋮ ⋯ ⋮√𝜆_𝑚 𝐞_𝐦] [

√^{𝜆1 𝐞′𝟏}

√𝜆₂ 𝐞′_𝟐

⋮

√𝜆_𝑚 𝐞′_𝐦] +[

Ψ_𝟏 𝟎 ⋯ 𝟎

𝟎 Ψ_𝟐 ⋯ 𝟎

⋮ 𝟎

⋮ 𝟎

⋱ ⋮

⋯ Ψ_𝒑

] (2.4)

Dimana Ψ_𝒊= 𝝈_𝒊𝒊− ∑^𝒎_𝒋=𝟏𝓵_𝒊𝒋^𝟐 untuk i = 1, 2, ..., p.

Untuk menggunakan pendekatan ini pada data 𝑥₁, 𝑥₂, … , 𝑥_𝑛, yang pertama dilakukan adalah memusatkan pengamatan dengan mengurangi mean sampel 𝑥̅.

Pengamatan terpusat

𝑥_𝑗− 𝑥̅ = [ 𝑥_𝑗1 𝑥_𝑗2

⋮ 𝑥_𝑗𝑝

] − [ 𝑥̅₁ 𝑥̅₂

⋮ 𝑥̅_𝑝

] = [

𝑥_𝑗1− 𝑥̅₁ 𝑥_𝑗2− 𝑥̅₂

⋮ 𝑥_𝑗𝑝− 𝑥̅_𝑝]

j = 1, 2, ..., n (2.5)

mempunyai matriks kovarian sampel S yang sama dengan pengamatan asli.

Dalam kasus ini dimana unit variabel tidak sepadan, biasanya dapat berhasil dengan variabel yang sudah distandardisasi

𝑧

_𝑗

=

[

𝑥_𝑗1−𝑥̅₁

√𝑠11 𝑥_𝑗2−𝑥̅₂

√𝑠22

⋮

𝑥_𝑗𝑝−𝑥̅_𝑝

√𝑠𝑝𝑝

]

j = 1, 2, ..., n

14

yang matriks kovarian sampelnya adalah matriks korelasi sampel R dari pengamatan 𝑥₁, 𝑥₂, … , 𝑥_𝑛. Standardisasi mencegah memiliki satu variabel dengan varian besar yang terlalu mempengaruhi penentuan faktor loading.

Representasi dalam (2.4), ketika digunakan pada matriks kovarian sampel S atau matriks korelasi sampel R, dikenal sebagai solusi komponen utama (principal component solution). Nama tersebut diambil dari fakta bahwa faktor loading-nya adalah koefisien skala dari beberapa komponen utama sampel pertama.

2.3.2 Faktor Model Solusi Komponen Utama

Analisis faktor komponen utama dari matriks kovarians sampel S ditentukan dalam hal pasangan eigenvalue-eigenvektornya (𝜆̂, 𝑒₁ ̂ ), (𝜆₁ ̂, 𝑒₂ ̂ ), ..., (𝜆₂ ̂, 𝑒_𝑝 ̂), dimana 𝜆_𝑝 ̂ ≥₁ 𝜆₂

̂ ≥ ⋯ ≥ 𝜆̂. Misalkan 𝑚 < 𝑝 adalah jumlah faktor-faktor umum. Maka matriks _𝑝 faktor loading yang diperkirakan {ℓ̃} diberikan oleh _𝑖𝑗

𝑳̃ = [√𝜆̂₁𝐞̂ ⋮ √𝜆̂_{𝟏 2}𝐞̂ ⋮ ⋯ ⋮ √𝜆̂_{𝟐 𝑚}𝐞̂ ] (2.6) _𝐦 perkiraan varians tertentu disediakan oleh elemen diagonal dari matriks S−𝑳̃𝑳̃′, maka

Ψ̃ = [

Ψ̃_𝟏 𝟎 ⋯ 𝟎

𝟎 Ψ̃_𝟐 ⋯ 𝟎

⋮ 𝟎

⋮ 𝟎

⋱ ⋮

⋯ Ψ̃_𝒑]

dengan Ψ̃_𝒊 = 𝒔_𝒊𝒊− ∑^𝒎_𝒋=𝟏𝓵̃_𝒊𝒋^𝟐 (2.7)

Komunalitas diperkirakan sebagai

ℎ̃_𝑖² = ℓ̃_𝑖1² + ℓ̃_𝑖2² + ⋯ + ℓ̃_𝑖𝑚² (2.8) Analisis faktor komponen utama dari matriks korelasi sampel diperoleh dengan memulai dengan R di tempat S (Wichern, 2007).

2.4 Analisis Komponen Utama Yang Robust

Untuk mendapatkan analisis komponen utama yang robust dapat dilakukan dengan menggantikan matriks varian-kovarian yang klasik dengan suatu estimator yang

15

robust. Estimator robust yang diinginkan adalah memiliki breakdown point (tingkat robust) yang tinggi.

2.5 Minimum Volume Ellipsoid (MVE)

Estimator Minimum Volume Ellipsoid (MVE) didasarkan pada ellipsoid volume terkecil yang mencakup h dari n pengamatan. MVE adalah estimator multivariat yang kuat dan penyebaran multivariasi yang affine equivariant dengan breakdown tinggi. MVE dapat dihitung dengan algoritma resampling. Biasnya yang rendah membuat MVE sangat berguna untuk pendeteksian outlier dalam data multivariat, sering kali melalui penggunaan jarak robust berbasis MVE.

Minimum Volume Ellipsoid (MVE), pertama kali diperkenalkan oleh Rousseeuw, adalah estimator robust pertama dengan breakdown tinggi yang umum digunakan. MVE menjadi populer karena ketahanannya yang tinggi terhadap outlier, yang membuat MVE menjadi alat yang diandalkan untuk pendeteksian outlier.

2.5.1 Algoritma MVE

Misalkan diberikan data hasil n pengamatan dengan p variabel acak sebagai berikut:

Pengamatan: X1 X2 ⋯ Xp

1 X11 X12 ⋯ X1p

2 X21 X22 ⋯ X2p

3 X31 X32 ⋯ X3p

4 X41 X42 ⋯ X4p

⋮ ⋮ ⋮ ⋱ ⋮

n Xn1 Xn2 Xnp

Dari data dengan n pengamatan ini, akan terdapat subsampel sebanyak ( 𝑛

𝑝 + 1) yang memuat (𝑝 + 1) pengamatan.

16

Untuk mendapatkan ellipsoid dengan volume minimum, dilakukan langkah- langkah sebagai berikut:

1. Dipilih himpunan bagian yang memuat (𝑝 + 1) pengamatan. Selanjutnya untuk setiap himpunan bagian berukuran (𝑝 + 1) tersebut, sebutlah himpunan indeks 𝐽 = {𝑖₁, … , 𝑖_𝑝+1} ⊂ {1, … , 𝑛} .

2. Menentukan rata-rata (mean) sampel dengan rumus 𝑥̅_𝐽 = ¹

𝑝+1∑^𝑝+1_𝑗=1𝑥_𝑖𝐽 sehingga diperoleh pusat ellips 𝑇_𝐽 = (𝑥̅₁, 𝑥̅₂, 𝑥̅₃) dimana:

𝑥̅₁ =𝑥₁₁+ 𝑥₂₁+ 𝑥₃₁+ ⋯ + 𝑥_(𝑝+1)1 𝑝 + 1

𝑥̅₂ =𝑥₁₂+ 𝑥₂₂+ 𝑥₃₂+ ⋯ + 𝑥_(𝑝+1)2 𝑝 + 1

𝑥̅₃ =𝑥₁₃+ 𝑥₂₃+ 𝑥₃₃+ ⋯ + 𝑥_(𝑝+1)3 𝑝 + 1

Selanjutnya ditentukan matriks kovarian dari sampel dengan rumus 𝑆_𝐽 =1

𝑝∑(𝑥_𝑖𝐽

𝑝+1

𝑗=1

− 𝑥̅_𝐽)(𝑥_𝑖𝐽− 𝑥̅_𝐽)^𝑡 yang secara rinci bisa dinyatakan dalam bentuk matriks:

𝑆_𝐽 = 𝑆 = [

𝑆₁² 𝑆₁₂ ⋯ 𝑆_1𝑝 𝑆₂₁ 𝑆₂² ⋯ 𝑆_2𝑝

⋮ 𝑆_𝑛1

⋮ 𝑆_𝑛2

⋱ ⋮

⋯ 𝑆_𝑝²] dimana

𝑠_𝑖𝑗 = 1

𝑛 − 1∑(𝑥_𝑘𝑖

𝑛

𝑘=1

− 𝑥̅_𝑖)(𝑥_𝑘𝑗 − 𝑥̅_𝐽)

Matriks kovarian 𝑆_𝐽 ini pada umumnya nonsingular, dan memang harus nonsingular. Bila tidak, banyaknya pengamatan harus ditambah sampai pemilihan (𝑝 + 1) himpunan bagian dari sampel ini mengakibatkan 𝑆_𝐽 nonsingular.

3. Selanjutnya dihitung jarak kuadrat:

𝐷_𝐽² = [(𝑥_𝑖 − 𝑥̅_𝐽)^𝑡(𝑆_𝐽)⁻¹(𝑥_𝑖 − 𝑥̅_𝐽)]

ℎ:𝑛

17

dimana h : n menunjukkan jarak kuadrat terkecil ke-h di antara jarak kuadrat dari n pengamatan dalam 𝑋_𝑛. Dengan menggunakan jarak kuadrat tersebut, dibuat faktor skala 𝐷_𝐽²

𝑐²

⁄ dengan 𝑐 = √𝑋𝑝,𝛼2 . 𝐷_𝐽

⁄𝑐 ini merupakan jari-jari ellips ke arah sumbu XJ.

4. Sebagai penentu yang sangat penting dalam MVE adalah volume ellipsoid yang proporsional dengan nilai

𝑉_𝐽 = (𝐷_𝐽

𝑐)^𝑝det (𝑆_𝐽)^1/2

Setelah selesai langkah ke-4 dengan memperoleh nilai volume ellips untuk subsampel pertama, selanjutnya ulangi langkah 1 sampai 4 di atas untuk subsampel ke-2 berukuran sama yaitu (𝑝 + 1) sehingga diperoleh volume ellips ke-2. Proses terus diulang sampai sebanyak ( 𝑛

𝑝 + 1) subsampel. Selanjutnya, dipilih subsampel yang ellipsnya memiliki volume paling minimum. Dari ellips terpilih tersebut, berikutnya dihitung T(X) dan S(X) di mana

𝑇(𝑥) = 𝑇_𝐽 𝑑𝑎𝑛 𝑆(𝑋) =𝑐²(𝑛, 𝑝) 𝑋_𝑝,𝛼² 𝐷_𝐽² 𝑆_𝐽 dengan 𝑐²(𝑛, 𝑝) = [1 + ¹⁵

𝑛−𝑝]² yang disebut dengan correction term.

Berdasarkan T(X) dan S(X) tersebut di atas, dihitung jarak robust dengan rumus 𝑅𝐷_𝑖 = √(𝑥_𝑖− 𝑇(𝑋))𝑆(𝑋)⁻¹(𝑥_𝑖− 𝑇(𝑋))^𝑇

untuk setiap pengamatan i. Selanjutnya pencilan data ditentukan apabila 𝑅𝐷_𝑖 >

√𝑋_𝑝,𝛼² .

18

BAB 3

HASIL DAN PEMBAHASAN

3.1 Pengumpulan Data

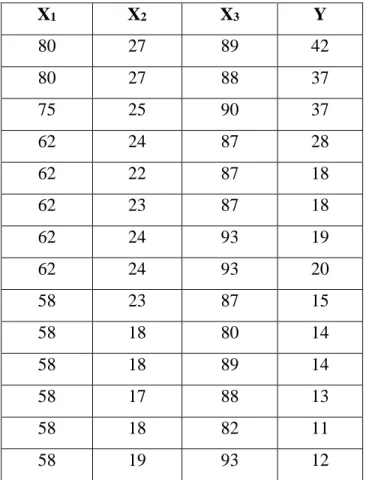
Data yang digunakan dalam penelitian ini merupakan contoh data stackloss Brownlee.

Tiga variabel berikut sesuai dengan pengukuran untuk faktor pengoksidasian amonia menjadi asam nitrat pada tanaman pada 21 hari berturut-turut.

X1 : aliran udara pada tanaman X2 : suhu air masuk pendingin X3 : konsentrasi asam

Variabel Y menunjukkan hilangnya amonia (stackloss).

Tabel 3.1 Stackloss Data

X1 X2 X3 Y

80 27 89 42

80 27 88 37

75 25 90 37

62 24 87 28

62 22 87 18

62 23 87 18

62 24 93 19

62 24 93 20

58 23 87 15

58 18 80 14

58 18 89 14

58 17 88 13

58 18 82 11

58 19 93 12

19

50 18 89 8

50 18 86 7

50 19 72 8

50 19 79 8

50 20 80 9

56 20 82 15

70 20 91 15

3.2 Analisis Faktor dengan Metode MVE

Analisis faktor yang akan dilakukan pada data tersebut pertama menggunakan metode MVE untuk subsampel pertama. Subsampel yang diambil harus memuat (p+1) pengamatan, yaitu

[

80 27 89

80 27 88

75 62

25 24

90 87 ]

Kemudian, dari subsampel yang diambil, dihitung mean sampel dengan rumus

𝑥̅_𝐽 = 1

𝑝 + 1∑ 𝑥_𝑖𝐽

𝑝+1

𝑗=1

sehingga diperoleh 𝑥̅₁ = 74,25; 𝑥̅₂ = 25,75; 𝑥̅₃ = 88,5. Matriks varian-kovarian sampel dihitung dengan rumus:

𝑆_𝐽 = 1

𝑝∑(𝑥_𝑖𝐽

𝑝+1

𝑗=1

− 𝑥̅_𝐽)(𝑥_𝑖𝐽− 𝑥̅_𝐽)^𝑡

Untuk subsampel pertama diperoleh matriks varian-kovarian robust:

20

𝑆 = [

108,375 17,625 9,75 17,625 3,375 0,75 9,750 0,750 2,5

]

Ada 5.985 subsampel dari 4 pengamatan yang diambil dari 21 pengamatan, maka perhitungan selanjutnya dilakukan dengan software SAS sehingga dihasilkan matriks varian-kovarian robust dari data sebagai berikut:

𝑆 = [

23,470588235 7,5735294118 16,102941176 7,5735294118 6,3161764706 5,3676470588 16,102941176 5,3676470588 32,389705882

]

Eigenvalue dari matriks varian-kovarian robust tersebut adalah:

𝜆̂₁ 46,597431018 𝜆̂₂ 12,155938483 𝜆̂3 3,423101087

Eigenvector dari matriks varian-kovarian robust tersebut adalah:

[

0,3819 0,6990 0,6046

−0,9233 0,3177 0,2158

−0,0412 −0,6406 0,7688 ]

Maka matriks faktor loading yang diperkirakan {ℓ̃} diberikan oleh _𝑖𝑗 𝑳̃ = [√𝜆̂₁𝐞̂ ⋮ √𝜆̂_{𝟏 2}𝐞̂ ⋮ ⋯ ⋮ √𝜆̂_{𝟐 𝑚}𝐞̂ ] _𝐦

ℓ̃ = (₁₁ 6,826)(0,3819) ℓ̃ = 2,6069 ₁₁

ℓ̃ = (₁₂ 6,826)(0,6990) ℓ̃ = 4,7715 ₁₂ ℓ̃ = (₁₃ 6,826)(0,6046)

ℓ̃ = 4,1271 ₁₃

21

ℓ̃ = (₂₁ 3,486)(−0,9233) ℓ̃ = −3,2191 ₂₁ ℓ̃ = (₂₂ 3,486)(0,3177)

ℓ̃ = 1,1076 ₂₂ ℓ̃ = (₂₃ 3,486)(0,2158)

ℓ̃ = 0,7524 23

ℓ̃ = (₃₁ 1,8501)(−0,0412) ℓ̃ = −0,07622 ₃₁ ℓ̃ = (₃₂ 1,8501)(−0,6406)

ℓ̃ = −1,1852 ₃₂ ℓ̃ = (₃₃ 1,8501)(0,7688)

ℓ̃ = 1,4224 ₃₂

3.3 Analisis Faktor Klasik

Setelah menganalisis data dengan metode MVE, data akan dianalisis dengan analisis faktor klasik menggunakan seluruh data sekaligus, yaitu

[

80 27 89

80 27 88

75 62 62 62 62 62 58 58 58 58 58 58 50 50 50 50 50 56 70

25 24 22 23 24 24 23 18 18 17 18 19 18 18 19 19 20 20 20

90 87 87 87 93 93 87 80 89 88 82 93 89 86 72 79 80 82 91]

22

Kemudian, dari data tersebut, dihitung mean dengan rumus

𝑥̅_𝐽 = 1

𝑝 + 1∑ 𝑥_𝑖𝐽

𝑝+1

𝑗=1

sehingga diperoleh 𝑥̅₁ = 60,429; 𝑥̅₂ = 21,095; 𝑥̅₃ = 86,286. Matriks varian-kovarian dihitung dengan rumus:

𝑆_𝐽 = 1

𝑝∑(𝑥_𝑖𝐽

𝑝+1

𝑗=1

− 𝑥̅_𝐽)(𝑥_𝑖𝐽− 𝑥̅_𝐽)^𝑡

Sehingga diperoleh matriks varian-kovarian dari data adalah:

𝑆 = [

840,571 226,571 245,714 226,571 99,905 66,214 245,714 66,214 287,143

]

Eigenvalue dari matriks varian-kovarian robust tersebut adalah:

𝜆̂₁ 36,0472 𝜆̂2 195,8116 𝜆̂₃ 995,7602

Eigenvector dari matriks varian-kovarian robust tersebut adalah:

[

0,2756 0,3207 0,9062

−0,9611 0,1079 0,2542

−0,0163 −0,9410 0,3380 ]

Maka matriks faktor loading yang diperkirakan {ℓ̃} diberikan oleh _𝑖𝑗 𝑳̃ = [√𝜆̂₁𝐞̂ ⋮ √𝜆̂_{𝟏 2}𝐞̂ ⋮ ⋯ ⋮ √𝜆̂_{𝟐 𝑚}𝐞̂ ] _𝐦

ℓ̃ = (₁₁ 6,0039)(0,2756) ℓ̃ = 1,6546 ₁₁ ℓ̃ = (₁₂ 6,0039)(0,3207)

23

ℓ̃ = 1,925 ₁₂ ℓ̃ = (₁₃ 6,0039)(0,9062)

ℓ̃ = 5,4407 ₁₃ ℓ̃ = (₂₁ 13,993)(−0,9611)

ℓ̃ = 13,4489 21

ℓ̃ = (₂₂ 13,993)(0,1079) ℓ̃ = 1,5098 ₂₂ ℓ̃ = (₂₃ 13,993)(0,2542)

ℓ̃ = 3,557 23

ℓ̃ = (₃₁ 31,555)(−0,0163) ℓ̃ = −0,5143 ₃₁ ℓ̃ = (₃₂ 31,555)(−0,9410)

ℓ̃ = −29,6938 ₃₂ ℓ̃ = (₃₃ 31,555)(0,3380)

ℓ̃ = 10,6658 ₃₂

3.4 Estimated Factor Loading

Hasil analisis faktor menggunakan Analisis Komponen Utama dengan metode Minimum Volume Ellipsoid (MVE) dan metode klasik pada contoh data stackloss Brownlee adalah sebagai berikut:

Variabel

Estimated factor loading

ℓ̃ = √𝜆̂_{𝑖𝑗 𝑖}𝐞̂_𝐢𝐣

Robust Klasik

𝐹1 𝐹2 𝐹3 𝐹1 𝐹2 𝐹3

X1 : aliran udara pada tanaman

2,6069 -3,2191 -0,0762 1,6546 13,4489 -0,5143

24

X2 : suhu air masuk pendingin

4,7715 1,1076 -1,1852 1,925 1,5098 -29,6938

X3 : konsentrasi

asam 4,1271 0,7524 1,4224 5,4407 3,557 10,6658

Eigenvalues 46,5974 12,1559 3,4231 36,0472 195,8116 995,7602

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Dari hasil analisis dan pembahasan maka diperoleh kesimpulan bahwa faktor loading yang dihasilkan dari setiap variabel dengan estimasi robust dan estimasi klasik memiliki perbedaan, yaitu dengan estimasi robust faktor loading-faktor loading yang dihasilkan memiliki nilai yang tidak jauh berbeda. Seperti pada variabel X1 faktor loading-nya adalah 2,6069; -3,2191; dan -0,0762. Sedangkan dengan estimasi biasa (klasik) faktor loading-faktor loading yang dihasilkan memiliki perbedaan nilai yang cukup jauh. Seperti pada variabel X1 faktor loading-nya adalah 1,6546; 13,4489; dan - 0,5143. Begitupula pada variabel X2 dan X3.

4.2 Saran

Dari penelitian ini penulis menyarankan sebagai berikut:

1. Analisis faktor robust pada penelitian ini hanya menggunakan metode MVE sehingga memungkinkan penelitian selanjutnya untuk menggunakan estimator robust yang lain.

2. Analisis faktor robust pada penelitian ini menggunakan Analisis Komponen Utama sehingga memungkinkan penelitian selanjutnya untuk menggunakan metode yang lain.

26

DAFTAR PUSTAKA

Aelst Van, Rousseeuw Peter. 2009. Minimum Volume Ellipsoid. 1:71-82.

Anton, H. & Rorres, C. 2004. Aljabar Linear Elementer. Edisi 8. (diterjemahkan oleh :Indriasari, R., dan Harmein, I). Jakarta: Erlangga.

Hair, Joseph F. 1998. Multivariate Data Analysis. New Jersey: Prentice-Hall, Inc.

Johnson, R. A and D. W. Wichern. 1982. Applied Multivariate Statistical Analysis. New Jersey: Prentice-Hall, Inc.

Mattjik, A.A & Sumertajaya, I.M. 2011. Sidik Peubah Ganda Dengan Menggunakan SAS. Bogor: IPB Press.

Parmikanti Kankan, Irianingsih I., Joebaedi K, Rusyaman. 2016. Menentukan Pusat Ellips Pada Metode MVE Menggunakan Jarak Robust. Prosiding Seminar Nasional MIPA 2016.

Sharma, Subhash. 1996. Applied Multivariate Techniques. Canada: John Wiley &

Sons, Inc.

Sujatmiko, Irwan., Linuwih, Susanti., A.W., Dwi Atmono. 2005. Analisis Komponen Utama Dengan Menggunakan Matriks Varian Kovarian Yang Robust. Jurnal Matematika Vol. 8, No. 2.

Supranto, J. 2004. Analisis Multivariat Arti dan Interpretasi. Jakarta: PT Rineka Cipta Jakarta.

27

LAMPIRAN

/* X1 X2 X3 Y Stackloss data */

aa = { 1 80 27 89 42, 1 80 27 88 37, 1 75 25 90 37, 1 62 24 87 28, 1 62 22 87 18, 1 62 23 87 18, 1 62 24 93 19, 1 62 24 93 20, 1 58 23 87 15, 1 58 18 80 14, 1 58 18 89 14, 1 58 17 88 13, 1 58 18 82 11, 1 58 19 93 12, 1 50 18 89 8, 1 50 18 86 7, 1 50 19 72 8, 1 50 19 79 8, 1 50 20 80 9, 1 56 20 82 15, 1 70 20 91 15 };

a = aa[, 2:4];

optn = j(8, 1, .);

optn[1] = 2; /* ipri */

optn[2] = 1; /* pcov: print COV */

optn[3] = 1; /* pcor: print CORR */

optn[5] = -1; /* nrep: use all subsets */

call mve(sc, xmve, dist, optn, a);

28

29

30