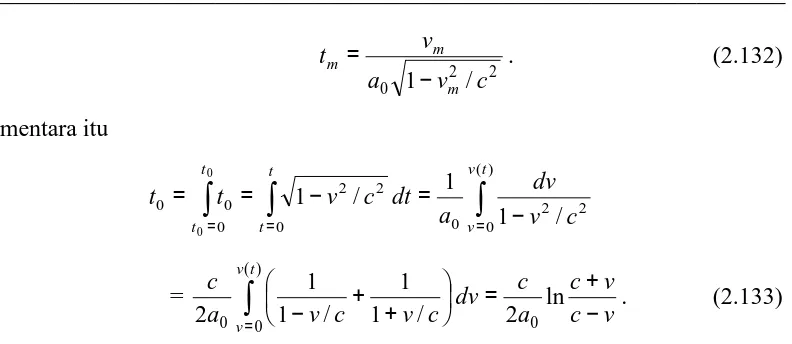TEORI RELATIVITAS DAN KOSMOLOGI

Dr. Eng. Rinto Anugraha NQZ

Jurusan Fisika FMIPA UGM

Bismillahirrahmanirrahim

Alhamdulillah, akhirnya buku Teori Relativitas dan Kosmologi ini dapat kami selesaikan. Buku ini disusun untuk digunakan sebagai bahan perkuliahan mata kuliah Teori Relativitas di Jurusan Fisika FMIPA UGM. Isi buku ini sedapat mungkin disesuaikan dengan silabus mata kuliah yang terdapat dalam Buku Panduan FMIPA UGM.

Penyajian buku ini dimulai dari Teori Relativitas Khusus, serta beberapa penerapannya, baik pada bidang Elektrodinamika, maupun dinamika partikel relativistik. Selanjutnya ditelaah Teori Relativitas Umum yang diawali dari analisis matematika tensor. Setelah merumuskan persamaan gravitasi Einstein, disajikan beberapa penerapan Teori Relativitas Umum, seperti pada lubang hitam, presesi orbit planet, pergeseran cahaya bintang, kosmologi dan lain-lain. Khusus pembahasan kosmologi disediakan dua bab, yaitu pada Bab V dan VI. Pada Bab penutup, ditelaah dinamika gerak partikel dan foton baik dalam lubang hitam maupun di jagad raya.

Meski telah disiapkan cukup lama, kami menyadari bahwa buku ini masih memiliki banyak kekurangan. Diantaranya, tidak terdapat soal-soal latihan. Barangkali pula di sana sini masih terdapat salah tulis dan ketik. Karena itu kami dengan tangan terbuka sangat mengharap masukan positif dari para pembaca, dalam rangka penyempurnaan buku ini. Akhirnya kami berharap, semoga buku ini dapat bermanfaat bagi pengembangan fisika di masa depan.

Yogyakarta, Mei 2011

BAB I TEORI RELATIVITAS KHUSUS 1 1.1 Pendekatan Energetika dan Penjabaran Kaedah

Transformasi Lorentz 2

1.2 Transformasi Lorentz untuk besaran (E,p) 9 1.3 Metode lain penurunan bentuk eksplisit besaran-besaran

fisis relativistik 15

1.4 Transformasi Lorentz Vektor-4 melalui Transformasi

Koordinat-4 18

1.5 Kaedah Transformasi untuk Vektor 18

1.6 Ruang-Waktu Minkowski dan Kaedah Transformasi Lorentz 19 1.7 Transformasi Lorentz untuk besaran-besaran elektrodinamika 25

Soal-Soal Latihan Bab I 30

BAB II PENERAPAN TEORI RELATIVITAS KHUSUS 33

2.1 Paradoks Kembar 33

2.2 Tinjauan Gerakan Partikel relativistik yang dikenai Gaya

Konstan dan Medan Gravitasi Seragam 38

2.2.1 Gerakan Partikel oleh Gaya Konstan 38

2.2.2 Gerakan Partikel dalam Medan Gravitasi Seragam 42

2.3 Efek Compton 51

Soal-Soal Latihan Bab II 58

BAB III ANALISIS TENSOR DAN TEORI RELATIVITAS UMUM 61

3.1 Analisis Ruang Riemann 61

3.2 Operasi pada Tensor 64

3.3 Ruang Datar dan Lengkung 65

3.4 Tensor Metrik 67

3.5 Turunan Kovarian 68

3.6 Tensor Riemann-Christoffel, Ricci dan Einstein 69

3.7 Persamaan Geodesik 71

3.8 Teori Relativitas Umum 72

3.9 Hukum Gravitasi Einstein 80

Soal-Soal Latihan Bab III 86

BAB IV PENERAPAN TEORI RELATIVITAS UMUM 93

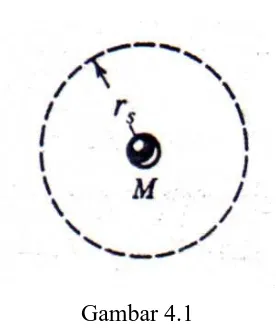
4.1 Penyelesaian Schwarzschild 93

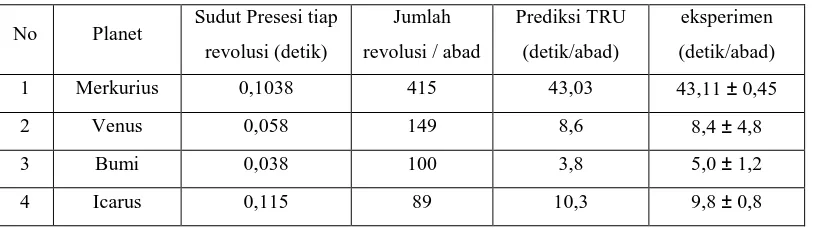
4.2 Presesi Orbit Planet 100

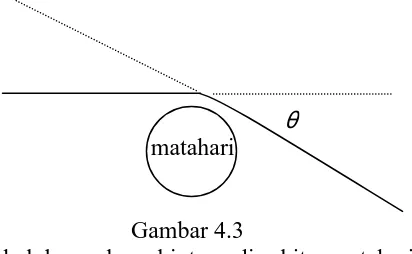
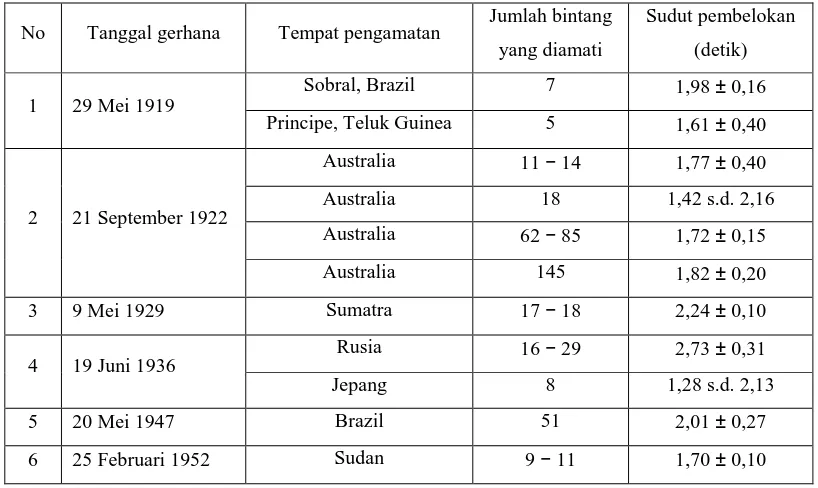
4.3 Pembelokan cahaya bintang di sekitar massa massif 105

4.4 Gelombang gravitasi 109

4.5 Lubang hitam Schwarzschild dan Kruskal-Szekeres 111

4.6 Struktur bintang 115

5.1 Pendahuluan 121

5.2 Asas Kosmologi 124

5.3 Geometri Bolahiper 125

5.4 Metrik Robertson-Walker 126

5.5 Pergeseran merah galaksi 127

5.6 Ekspansi Jagad Raya 130

5.7 Sejarah Suhu Jagad Raya menurut Big Bang 133 5.8 Radiasi Kosmik Latar Belakang Gelombang Mikro 139

Soal-Soal Latihan Bab V 145

BAB VI KOSMOLOGI : DINAMIKA JAGAD RAYA 149

6.1 Dinamika Jagad Raya 149

6.2 Rapat Energi dan Tekanan Jagad Raya 155

6.3 Masa Dominasi Materi 157

6.4 Horison Partikel dan Horison Peristiwa 166

6.5 Masa Dominasi Radiasi 167

6.6 Data Fisis Jagad Raya 171

6.7 Masa Depan Jagad Raya 173

Soal-Soal Latihan Bab VI 175

BAB VII DINAMIKA GERAK PARTIKEL DAN FOTON 177

7.1 Persamaan Gravitasi Einstein 178

7.2 Persamaan Geodesik 179

7.3 Dinamika Gerak Partikel dalam Medan Schwarzschild 179 7.4 Dinamika Gerak Foton dalam Bidang Datar Medan

Schwarzschild 183

7.5 Dinamika Gerak Foton secara Radial dalam Medan

Schwarzschild 185

7.6 Dinamika Gerak Partikel dan Foton dalam Jagad Raya

bermetrik Robertson-Walker 186

7.7 Solusi Persamaan Eisntein untuk Jagad Raya 187 7.8 Dinamika Gerak Partikel dalam Jagad Raya 188 7.9 Dinamika Gerak Foton dalam Jagad Raya 197

7.10 Dinamika Metrik de Sitter 198

7.11 Dinamika Gerak Foton dalam Metrik de Sitter 200 7.12 Dinamika Gerak Partikel dalam Metrik de Sitter 202 7.13 Metrik dan Jagad Raya de Sitter 204 7.14 Dinamika Gerak Foton dalam Jagad Raya de Sitter 205

Soal-Soal Latihan Bab VII 207

BAB I

TEORI RELATIVITAS KHUSUS

Fisika adalah ilmu yang berupaya secara ilmiah menelaah gejala alam mulai dari skala mikro (partikel elementer) hingga skala makro (jagad raya), serta mulai dari kelajuan rendah hingga kelajuan maksimum. Teori relativitas merupakan salah satu tulang punggung fisika modern. Sumbangannya terutama dalam bentuk penataan dan pelurusan konsep−konsep dasar dalam fisika, khususnya yang berkaitan dengan ruang−waktu, momentum−energi sebagai aspek kinematika semua gejala alam, yang selanjutnya mengangkat cahaya sebagai pembawa isyarat berkelajuan maksimum.

Sumbangan teori relativitas, dalam hal ini adalah teori relativitas khusus adalah mampu menampilkan persamaan Maxwell, yang merupakan persamaan dasar dalam elektrodinamika, dalam bentuk yang kovarian. Konsekuensi teori relativitas khusus adalah kelajuan gelombang elektromagnet dalan ruang vakum sama dengan c (laju cahaya di ruang hampa). Beberapa percobaan menunjukkan bahwa dalam elektromagnetik, tidak ada kerangka istimewa. Dalam kerangka inersial, kelajuan cahaya sama dengan c, atau dengan kata lain, c merupakan suatu besaran invarian. Selain itu sistem persamaan Maxwell berlaku dalam smua kerangka inersial, yang oleh karena itu konsep ruang−waktu dan momentum−energi yang mutlak harus diganti.

Ada tiga asas yang melandasi teori relativitas khusus, yaitu :

Asas ke nol (Asas perpadanan / korespondensi) : untuk setiap gerakan berkelajuan rendah (momentum rendah), konsep−konsep dan hukum−hukum relativistik yang muncul harus sesuai dengan konsep−konsep yang telah ada dalam teori Newton.

Asas kedua : Laju maksimal yang dapat dimiliki oleh isyarat tidak bergantung (invarian) dari kerangka acuan inersial yang digunakan.

Nilai kelajuan maksimal c ini merupakan salah satu tetapan alam yang sangat penting dalam fisika dan memegang peranan utama dalam penelusuran konsep ruang−waktu serta momentum−energi. Nilainya sebagaimana yang ditetapkan oleh Badan Umum Internasional mengenai Berat dan Ukuran adalah c = 299792458 m/s. Hal ini berarti satu meter adalah jarak yang ditempuh oleh cahaya dalam ruang vakum selama selang waktu 1/299792458 detik.

Terdapat dua pendekatan yang digunakan untuk menelusuri kaedah transformasi antara besaran−besaran fisis (transformasi Lorentz) dari kerangka inersial yang satu (K) menuju kerangka inersial yang lain (K~) yang bergerak dengan kecepatan konstan V terhadap K.

Pendekatan pertama yang digunakan bersifat konvensional yaitu dengan memilih ruang dan waktu sebagai variabel awal yang digunakan dalam merumuskan kaedah transformasi Lorentz. Dengan pendekatan ini, kaedah transformasi untuk besaran momentum dan energi baru ditelusuri kemudian.

Pendekatan kedua bersifat pendekatan energetika, yaitu dengan memilih momentum−energi sebagai variabel awal, yang selanjutnya transformasi untuk besaran ruang dan waktu baru ditampilkan kemudian. Menurut Muslim (1997), pendekatan ini tampil lebih ringkas dan lebih sesuai apabila diterapkan untuk proses mikroskopik pada zarah elementer, mengingat data−data pada proses hamburan dan spektroskopi biasanya melibatkan besaran momentum dan energi.

Berikut ini akan dijabarkan perumusan kaedah transformasi Lorentz melalui pendekatan energetika (momentum−energi), mengacu pada Muslim (1997).

1.1 Pendekatan Energetika dan Penjabaran Kaedah Transformasi Lorentz

Menurut asas korespondensi, perumusan hukum Newton kedua yang berbentuk

dt dp

dapat pula berlaku dalam energetika relativistik (untuk momentum dan energi relativistik), dengan modifikasi definisi bagi momentum p. Dalam hal ini, F adalah gaya luar yang melakukan kerja dW pada zarah dalam selang waktu dt, dengan akibat terjadinya perubahan momentum sebesar dp dan energi sebesar dE

sewaktu zarah tersebut melakukan pergeseran sejauh dr. Perubahan tenaga tersebut dapat dituliskan sebagai

r . p

d dt d

dE 

    

= = p. r v.dp

dt d

d  =

    

. (1.2)

Pada saat zarah dalam keadaan rehat (v = 0 ), energi zarah bernilai E₀ yang dinamakan dengan energi rehat. Selanjutnya jika zarah bergerak (v ≠ 0 ), energi

zarah tersebut akan bertambah dengan energi kinetik sebesar E_k menjadi energi total E yang dirumuskan sebagai

k

E E

E= ₀+ . (1.3)

Jika zarah tersebut bergerak lurus maka v // p sehingga

dE = v dp. (1.4)

Untuk foton dengan v = c konstan dan invarian (asas kedua teori relativitas), maka diperoleh energi foton sebesar

∫

=

∫

= +

= dE c dp pc konstan

E . (1.5)

Mengingat tidak ada foton dengan kecepatan nol, maka disimpulkan bahwa tetapan konstan tersebut sama dengan nol. Jadi diperoleh

2 2 2

c

E =p untuk v = c. (1.6)

Selanjutnya untuk zarah bermassa dengan v atau p atau E_k sembarang,

bentuk kuadrat momentum p2 dapat diuraikan ke dalam suatu deret Taylor dalam

k

E = E−E₀ yang berbentuk

... 2 2 1

0

2_{= + + +}

k k a E E

a a

p (1.7)

Untuk zarah rehat (v = 0), nilai p maupun E_k = 0, sehingga a₀ = 0. Dari

zarah berkelajuan tinggi, E tinggi sehingga nilai _k E2 ≈E_k2, mengingat untuk daerah ini E dapat diabaikan. Dari kondisi ini diperoleh ₀ a₀ =1 c/ 2, sedangkan untuk a dan seterusnya sama dengan nol. Adapun untuk kelajuan rendah, tentu ₃ saja a₁≠0. Jadi untuk sembarang daerah kelajuan / energi kinetik, berlaku kaitan dispersi untuk zarah bebas yang berbentuk

2 2 1

2

/ c E E a _k + _k

= =p.p

p untuk 0 ≤ v ≤ c. (1.8)

Apabila ungkapan di atas diambil turunannya, serta dengan mengingat bahwa dE

E E d

dE_k = ( − ₀)= (1.9) diperoleh

2p.dp = (a₁+2E_k /c2)dE (1.10) atau

p . p

d c E a dE

k 2 1

2

1 + _/

= (1.11)

yang harus = v . dp. Dari sini diperoleh kesamaan

(

2

)

1 2

1_{a E /c} k

+ =v

p . (1.12)

Pangkat dua persamaan di atas adalah

_

  

  

+ +

= 1_{2 4}2

1 4 1 2 2

c E c

E a

a k k

v

p (1.13)

yang harus bernilai sama dengan

p2 =a₁E_k +E_k2/ c2. (1.14) Dua persamaan terakhir di atas dapat dituliskan dengan mengumpulkan E_k yang berpangkat sama sebagai

₂ 1_{4 1}2 2

2 1 2

2 2 2

1

1 E a v

c v a c E c v

k

k =

    

  

− +

    

  

− . (1.15)

Dengan mengalikan persamaan di atas dengan

) / 1

( 2 2

2

c v

c

− , diperoleh

) / 1 (

4 2 2

2 2 2 1 2

1 2

c v

c v a E

c a

E_{k k}

− =

yang ternyata sama dengan p2c2. Dengan demikian

2 2 1

/ 1

2 v c

v a p

−

= . (1.17)

Untuk kelajuan rendah, berlaku rumus Newton :

p=mv (1.18)

dan

1 /

1−v2 c2 ≈ (1.19) sehingga

2

1v

a

mv=

atau

m

a₁=2 . (1.20)

Dengan mengisikan hasil ini ke dalam pers. (1.17) diperoleh vektor momentum relativistik sebagai

2 2

/ 1 v c

m

−

= v

p = γmv (1.21)

dengan

2 2

/ 1

1 c v

− =

γ

≥ 1. (1.22)

Selanjutnya dengan mengisikan nilai a₁=2m ke dalam pers. (1.12) diperoleh

γ

mv=v(m+E_k /c2) (1.23)

atau

) 1 (

2 ₋

=mc

γ

E_k . (1.24)

Mengingat energi kinetik partikel adalah energi relativistik partikel dikurangi dengan energi rehatnya, atau yang dituliskan sebagai

E_k =E−E₀ (1.25)

2 2

2 2

/

1 v c

mc mc

E

− =

=

γ

(1.26)

dan

E₀ =mc2 (1.27)

Untuk limit non−relativistik, bentuk

γ −1=(1−v2/c2)−1/2−1≈(1+v2/2c2)−1=v2/2c2 (1.28) sehingga tenaga kinetik nonrelativistik menjadi

2 2 1 2 2 2

) 2 /

(v c mv

mc

E_k = = (1.29)

yang bersesuaian dengan teori Newton.

Kuadrat energi relativistik partikel bernilai

(

2 4 2 2 2 2 2 2

)

2 2 2

2 4 2 2

/ 1

1 /

1 v c v c m c m v c m v c

c m

E − +

− = −

=

= 2 2 4 2 2

2

2 2 2

2 2 2 4 2

/ 1 )

/ 1 (

) / 1 (

c c

m c c v mv c

v c v c m

p + =

    

  

− + −

−

(1.30)

sehingga

4 2 2 2

c m c p

E= + (1.31)

Hubungan antara p, dan v E dapat dituliskan dalam bentuk

2 / 2 ₂

c E c mc

mv v v

p=γ =γ = . (1.32)

Dari persamaan (1.31), dapat dibuat ilustrasi yang menggambarkan hubungan tersebut dalam segitiga siku-siku, seperi yang terdapat pada Gambar 1.1.

E mc 2

p

Gambar 1.1

Contoh soal :

Tentukan kecepatan sebuah partikel dalam c atau laju cahaya dalam ruang hampa agar

a. rumus Newton p=mv dapat digunakan dengan kesalahan 10−6.

b. rumus 2

2 1_mv

E_k = dapat digunakan dengan kesalahan yang sama.

c. rumus p=mv hanya memberikan setengah dari nilai momentum yang sebenarnya dimiliki partikel tersebut.

d. rumus 2

2 1_mv

E_k = hanya memberikan nilai setengah dari yang sebenarnya

dimiliki oleh partikel tersebut.

e. Tenaga kinetik partikel sama dengan 10 × tenaga rehatnya. Jawaban :

a. Jika rumus momentum

2 / 1 2 2

/ 1 2 2

) 1 ( )

/ 1

( − − = − −

=mv v c mv

β

p

seperti yang terdapat pada persamaan (1.21) diuraikan menggunakan deret, diperoleh

...) 1

( 4

8 3 2 2

1 _{+ +}

+

=mv β β

p .

Dengan demikian rumus Newton yang hanya memuat suku pertama deret di

atas dapat digunakan dengan kesalahan 10−6, jika

6 2

2

1_{β ≤10}−

atau

m/s 10 24 , 4 10

41 ,

1 × 3 = × 5

≤ − c

v .

Kecepatan ini cukup tinggi (lebih dari 100 kali kecepatan bunyi di udara). b. Tenaga kinetik partikel seperti dirumuskan pada persamaan (1.24) adalah

] 1 )

1

[( 2 1/2

2 _{− −}

=mc β −

E_k

yang jika diuraikan ke dalam deret menjadi

...) 1

( 2

4 3 2 2

1 _{+ +}

= mv β

Jadi supaya rumus tenaga kinetik klasik masih dapat digunakan dengan tingkat kesalahan tersebut, maka

6 2

4 3

10−

≤

β

atau

c v≤1,15×10−3 . Nilai ini sedikit lebih kecil dari nilai pada (a). c. Untuk pertanyaan tersebut

2 / 1 2 2 2

1

) / 1

( − −

= mv v c

mv

yang berarti

c

v 3

2 1

= .

d. Untuk pertanyaan tersebut

] 1 )

/ 1

[( 2 2 1/2

2 2 1 2 2

1_{mv = mc −v c} − ₋

yang berarti

2 / 1 2 2

) 1 (

1+

β

= −

β

− .

Bentuk ini dapat dituliskan dalam bentuk

1 1

) 1 )( 2

1

( +

β

2 +

β

4 −

β

2 = −

β

6 −

β

4 +

β

2 = sehingga

0 ) 1

( 4 2

2

β

₋

β

_{− =}

β

.

Bentuk persamaan kuadrat dalam

β

2 di atas memiliki akar positif )

1 5 (

2 1

2 _{= −}

β

sehingga

8

10 36 , 2 79 ,

0 = ×

= c

v m/s.

e. Untuk

2 2

/ 1 2 2

10 ] 1 )

1

[( mc

mc

E_k = −β − − =

11 )

1

( −

β

2 −1/2 = sehingga

121 120

2 ₌

β

atau

8

10 988 ,

2 ×

=

v m/s.

1.2 Transformasi Lorentz untuk besaran (E, p)

Ditinjau transformasi Lorentz antara kerangka K dan kerangka K~ yang bergerak terhadap K dengan kecepatan V, yang secara linear menghubungkan

perangkat besaran (E,p_x,p_y,p_z) dan (E~,~p_x,p~_y,~p_z) serta sebagai bentuk

pengkhususan dipilih transformasi yang hanya ditinjau ke arah salah satu sumbu koordinat saja, dalam hal ini dipilih sumbu x. Bentuk transformasi Lorentz tersebut adalah (Muslim, 1985)

z z y

y x

x

x p p aE p p p p

bp E

E~=Γ'( + ); ~ =Γ( + ); ~ = dan ~ = . (1.33)

Jadi pada bentuk di atas, komponen momentum ke arah sumbu y dan z tidak mengalami perubahan, sehingga transformasi hanya melibatkan pasangan (E,p_x).

Untuk mencari parameter−parameter transformasi yaitu Γ,Γ',a dan b, akan ditinjau

dua kasus khusus yaitu kasus partikel bermassa rehat m yang rehat masing−masing

di K dan K~. Ilustrasi tentang kerangka K dan K~ terdapat pada Gambar 1.2. z~

z

V O~ y~

O y

x x~

Saat partikel rehat di K~, yang berarti

~p_x = ~p_y = ~p_z =0 (1.34) maka memberikan

p_y = p_z =0 (1.35)

serta

p_x +aE=0 (1.36)

atau

p_x =−aE. (1.37)

Padahal hubungan antara p, dan v E adalah

2

c Ev

p= (1.38)

sehingga diperoleh kesimpulan

₂

c v

a=− . (1.39)

Mengingat partikel tersebut rehat di K~, itu berarti partikel tersebut bergerak dengan

kecepatan v=V=Vn_x di K. Akhirnya dapat disimpulkan bahwa

₂

c V

a=− . (1.40)

Selanjutnya saat partikel rehat di K, yang berarti 0

= =

= y z

x p p

p , (1.41)

yang dari transformasi Lorentz memberikan

~p_y = ~p_z =0 (1.43)

serta

.

~ 2

2 2

Vm mc

c V aE

p_x =Γ =− Γ =−Γ (1.44)

Partikel tersebut berarti bersama−sama dengan kerangka K bergerak terhadap K~

2 2

/ 1 V c

mV p_x

− −

= (1.45)

sehingga diperoleh

2 2

/ 1

1 c V

− =

Γ . (1.46)

Kemudian dihitung nilai energi E~ di K~ menurut

) 0 (

' /

1

~ 2

2 2

2

+ Γ

= −

= mc

c V mc

E (1.47)

sehingga diperoleh

=Γ −

= Γ

2 2

/ 1

1 '

c V

. (1.48)

Untuk menentukan tetapan b, ditinjau kembali partikel yang rehat di K~, sehingga transformasi Lorentz untuk energi E~ di K~ menghasilkan

) (

'

~ 2 2

mV b mc mc

E = =Γ Γ + Γ (1.49)

atau

(

2 2

)

2

2 2 2

2

1 /

1 V c mV

mc mc mc

bmV − = − − =−

Γ

= (1.50)

yang berarti bahwa

V

b=− . (1.51)

Dengan demikian transformasi Lorentz antara kerangka K dan kerangka K~ yang bergerak dengan kecepatan V ke arah sumbu x untuk perangkat besaran

) , , ,

(E p_x p_y p_z dan (E~,p~_x,~p_y,~p_z)adalah

2 2

/ 1 ~

c V

Vp E

E x

− −

= ; (1.52)

2 2

2 / 1

/ ~

c V

c VE p p_x x

− −

= ; (1.53)

~p_y = p_y; ~p_z = p_z. (1.54)

p_x → p_// ; (1.55) p_ydan p_z → p_⊥; (1.56)

p_xV → p_//V =p⋅V (1.57)

diperoleh 2 2 / 1 ~ c V E E − ⋅ −

= p V ; (1.58)

2 2 2 // // / 1 / ~ c V c E − −

=p V

p ; (1.59)

⊥ ⊥ =p

p

~

(1.60)

Karena K bergerak terhadap K~ dengan kecepatan −V, maka transformasi balik untuk bentuk di atas adalah

2 2 / 1 ~ ~ c V E E − ⋅ +

= p V ; (1.61)

2 2 2 // // / 1 / ~ ~ c V c E − +

=p V

p ; (1.62)

p_⊥ =p~_⊥ (1.63)

Ditinjau sebuah partikel bermassa m yang bergerak di K dengan kecepatan v

dan di K~ dengan kecepatan ~v. Kaedah transformasi untuk energi E~ di kerangka K~ memberikan

_       − ⋅ − − − = − = 2 2 2 2 2 2 2 2 2 2 / 1 / 1 / 1 1 / ' 1 ~ c v m c v mc c V c v mc

E v V (1.64)

yang dengan membalik pembilang dan penyebut persamaan di atas, kemudian menyederhanakannya diperoleh ₂ 2 2 2 2 2 2 / 1 / 1 / 1 / ' 1 c c v c V c v V v⋅ − − − =

− . (1.65)

Akibat lain dari persamaan di atas adalah dengan menuliskannya sebagai

2 / 1

1 1

' 1

c

V v⋅

− Γ =

γ

γ

(1.66)

atau

) / 1

(

' 2

c

V v⋅

− Γ =

γ

γ

(1.67) Sementara itu dari pers. (1.63) untuk komponen momentum tegaklurus diperoleh

γ'm~v_⊥ =γmv_⊥ (1.68) yang menghasilkan kaedah kecepatan tegaklurus sebagai

) / 1

( ~

2

c

V v

v v

⋅ − Γ

= ⊥

⊥ . (1.69)

Sedangkan untuk komponen momentum yang sejajar, diperoleh

) (

) / (

~

'mv_// =Γ

γ

mv_// −V

γ

mc2 c2 =Γ

γ

m v_// −V

γ

(1.70)

sehingga

2 //

/ 1

~

c

V v

V v v

⋅ −

−

= . (1.71)

Dengan menggunakan kaedah penjumlahan kecepatan di atas, dapat

diturunkan transformasi koordinat (ct,r) dan (c~t,~r) menurut resep

v=d /r dt (1.72)

dan

~v=d~r/d~t . (1.73)

Untuk transformasi kecepatan tegaklurus, diperoleh

) / 1

( ~

~ 2

c dt

d t

d d

V v r r

⋅ − Γ

= ⊥

⊥ . (1.74)

Dengan berlakunya simetri gerak pada panjang yang tegaklurus V, untuk vektor koordinat yang tegaklurus diperoleh

⊥ ⊥ =r

r

~

(1.75)

dan sekaligus juga

d~r_⊥ =dr_⊥, (1.76)

d~t =dtΓ(1−v⋅V/c2)=Γ(dt−dr⋅V/c2). (1.77) Untuk syarat awal : t=~t =0 dan r=0, integrasi persamaan di atas memberikan hasil transformasi waktu koordinat :

~t =Γ(t−r⋅V/c2). (1.78) Sementara itu dari kaedah transformasi kecepatan yang sejajar, bentuknya dapat ditulis sebagai

) / 1

( ) / 1

( ~ ~

~ 2

// 2

// //

c dt

dt d

c dt

d t

d d

V v

V r V

v r r

⋅ −

− =

⋅ − Γ

= (1.79)

atau

d~r_// =Γ(dr_// −Vdt). (1.80) Dengan menerapkan syarat awal

0 ~₌

=t

t dan r~_// =r_// =0, maka pengintegralan persamaan di atas memberikan

~r_// =Γ(r_// −Vt). (1.81) Gabungan antara pers. (1.75) dan (1.81) menghasilkan

~r =r+(Γ−1)(r⋅V)V/V2−ΓVt (1.82) Contoh Soal :

Sebuah pesawat antariksa dilihat dari bumi sedang bergerak ke arah timur dengan kecepatan v_p =0,6ciˆ dan dalam waktu lima detik akan bertabrakan dengan sebuah

komet yang sedang bergerak ke arah barat dengan kecepatan v_k =−0,8ciˆ. a. Dilihat dari pesawat antariksa, berapakah kecepatan komet mendekatinya ? b. Menurut pilot pesawat antariksa tersebut, berapa waktu yang tersedia untuk

menghindari tabrakan tersebut? Jawaban :

a. Ditinjau dari pesawat antariksa yang bergerak dengan kecepatan V =v_p

i c c

c c

c c i

c V v

V v

v _k k 0,946 ˆ

/ ) 6 , 0 )( 8 , 0 ( 1

6 , 0 8 , 0 ˆ

/ 1

'

2 2

// //

// =−

− −

−

− − =

− −

= .

Jadi kecepatan komet tersebut menurut pilot pesawat adalah 0,946c mendekati pesawat tersebut.

b. Dengan menggunakan dilatasi waktu, dapat ditentukan waktu yang tersedia bagi pilot tersebut untuk menghindari tabrakan. Karena faktor dilatasi waktu adalah

25 , 1 )

6 , 0 1

( − 2 1/2 = =

Γ −

maka

detik 4 detik 25 , 1 5

' = =

Γ ∆ =

∆t t .

1.3 Metode lain penurunan bentuk eksplisit besaran−−−−besaran fisis relativistik Metrik ruang−waktu datar empat dimensi (metrik Minkowski) yang digunakan dalam teori relativitas khusus muncul dari bentuk invarian metrik

2 2 2 2 2 2 2 2 2

r

d dt c dz dy dx dt c dx dx

ds =

η

_µν µ ν =− + + + =− + (1.83)

dengan vektor koordinat−4 kontravarian dirumuskan

xµ =(x0,xm)=(x0,x1,x2,x3)=(ct,x,y,z)=(ct,r) (1.84) Pada metrik pers. (1.83), komponen tensor metrik rank−2 kovarian adalah

−

η

₀₀ =

η

₁₁ =

η

₂₂ =

η

₃₃ =1 (1.85)

dan

η_µν =0 untuk µ ≠ν . (1.86)

Sementara itu pasangan komponen tensor metrik rank−2 kontravarian adalah

1

33 22 11

00 _{= = = =}

−η η η η (1.87)

dan

ηµν =0 untuk µ ≠ν (1.88)

Kaitan antara waktu pribadi

τ

dengan elemen garis s adalah

sehingga pers. (1.83) menjadi

2 2 1₂

(

dx2 dy2 dz2

)

c

dt

dτ = − + + (1.90)

Diperkenalkan vektor kecepatan−3 v yang memiliki komponen−komponen Cartesan dt dz v dt dy v dt dx

v_x = , _y = , _z = (1.91)

Dengan substitusi komponen−komponen kecepatan−3 di atas, pers. (1.90) dapat dituliskan menjadi

[

]

       − =       + + −

= 2 2 2 2 ₂2

2 2 2 1 ) / ( ) / ( ) / ( 1 1 c dt dt dz dt dy dt dx c dt

d

τ

v (1.92)

atau

γ

τ

dt dt

c

d _ =

      − = 2 / 1 2 2

1 v , (1.93)

dengan 2 2_/ 1 1 c v − =

γ

. (1.94)

Didefinisikan vektor kecepatan−4 kontravarian Vµ yang memiliki komponen

( ) ( )

ct,r c,v

dt d d dt dt dx d dx

V

γ

γ

τ

τ

µ µ

µ _{= = = = (1.95)}

sedangkan komponen vektor kecepatan−4 kovarian V_µ dapat dicari dari Vµ dengan menggunakan tensor metrik kovarian pers. (1.85) − (1.86) :

) , ( c v V

V_µ =

η

_µν ν =

γ

− . (1.96)

Sementara untuk vektor kecepatan−4 kontravarian Pµ, komponen−komponennya adalah

( )

      =         = =

= ,v , v ,p

2 c E m c mc c m mV

Pµ µ

γ

γ

γ

(1.97)

dengan energi :

dan momentum−3 :

p=γmv. (1.99)

Hasil pers. (1.98) dan (1.99) berturut-turut sama dengan pers. (1.26) dan (1.21). Sedangkan vektor momentum−4 kovarian P_µ adalah

) , / ( E c p

P

P_µ =

η

_µν ν = − (1.100)

Adapun vektor gaya−4 kontravarian F memiliki komponenµ −komponen

   

 

= =

= ,f

cdt dE d

dt dt dP d

dP

F

γ

τ

τ

µ µ

µ _(1.101)

dengan gaya−3 f didefinisikan sebagai

dt dp

f = (1.102)

Sementara itu vektor gaya−4 kovarian F_µ dirumuskan sebagai

_

  

 

− =

= ,f

dt c

dE F

F_µ

η

_µν ν

γ

. (1.103)

Perkalian dalam (inner product) antara dua vektor kovarian dan kontravarian akan menghasilkan suatu skalar, seperti misalnya

₂ 2

2 2

2 2 2 2 2

1 )

, ( ) ,

( c

c c

c c

c V

V _=−

  

  

− −

= +

− = −

=

γ

v

γ

v

γ

γ

v

γ

v

µ

µ (1.104)

dan

P_µPµ =(−E/c,p)(E/c,p)=−

(

E/c

)

2 +p2 = −m2c2 (1.105) Dari turunan pers. (1.104) di atas diperoleh

(

_µ µ

)

_µ µ _µ µ

τ mV V F V V F

d d

+ =

=

0 = _

  

 

− +

   

 

− ,f ( ,v) ( ,v) ,f

dt c

dE c

c dt

c dE

γ

γ

γ

γ

= 

  



_{− + ⋅}

v f

dt dE

2

2γ (1.106)

sehingga diperoleh

=f⋅v

dt dE

Dengan hasil di atas, vektor gaya−4 kontravarian dan kovarian berturut−turut dapat dituliskan menjadi

F

µ

=

γ

(

f

⋅

v

/ c

,

f

)

(1.108) dan

F

_µ

=

γ

(

−

f

⋅

v

/ c

,

f

)

(1.109) Dari pers. (1.105) berlaku kaitan

E2 =p2c2 +m2c4. (1.110) Sementara dari pers. (1.107) :

dE =v⋅f dt=v⋅dp. (1.111) Bentuk di atas sama dengan pers. (1.2)

1.4 Transformasi Lorentz Vektor−−−−4 melalui Transformasi Koordinat−−−−4

Berikut ini akan dijabarkan kaedah alih bentuk Lorentz untuk komponen vektor−4, baik dalam bentuk kovarian maupun kontravarian melalui transformasi koordinat−4 (1.3 dimensi ruang dan 1 dimensi waktu) di ruang−waktu Minkowski. Mula−mula diberikan aturan transformasi koordinat untuk vektor dalam ruang sembarang berdimensi N. Selanjutnya diberikan deskripsi ruang−waktu Minkowski yang menjadi wahana teori relativitas khusus Einstein. Diberikan kaitan transformasi koordinat di dalam ruang−waktu tersebut bagi dua kerangka inersial yang salah satunya bergerak dengan kecepatan konstan V terhadap lainnya.

Dengan kaitan tersebut selanjutnya melalui kaedah transformasi untuk vektor, nilai−nilai komponen beberapa vektor−4 dihitung dan diperoleh relasi yang mengaitkan besaran−besaran pada kedua kerangka tersebut. Vektor−4 yang dipilih di sini berkaitan berkaitan dengan masalah dalam dinamika relativistik dan elektrodinamika, seperti vektor kecepatan−4, vektor momentum−4, vektor gaya−4, vektor potensial−4 dan vektor kerapatan−4.

1.5 Kaedah Transformasi untuk Vektor

N

x = (x1,x2,...,xN). (1.112) Jika dilakukan transformasi ke koordinat

N x

~ ₌ N

x x x ,~ ,...,~ ~

( 1 2 ) (1.113)

di dalam ruang tersebut, kaedah transformasi yang mengubungkan vektor

kontravarian Aν dan A~µ serta antara vektor kovarian A_ν dan A~_µ berturut−turut adalah (Lawden, 1982)

ν ν

µ

µ _A

x x A

∂ ∂ = ~

~

(1.114)

dengan inversi

µ µ ν

ν _A

x x

A _~ ~

∂ ∂

= , (1.115)

serta

ν µ ν

µ A

x x

A~ _~

∂ ∂

= (1.116)

dengan inversi

_{ν µ}

µ

µ A

x x

A ~

~

∂ ∂

= . (1.117)

Di sini telah digunakan kesepakatan penjumlahan Einstein, yaitu jika terdapat indeks berulang, maka penjumlahan harus dilakukan meliputi jangkuan indeks tersebut. Apabila penjumlahan tak ingin dilakukan, maka hal tersebut harus diungkapkan secara eksplisit.

1.6 Ruang−−−−Waktu Minkowski dan Kaedah Transformasi Lorentz

Metrik ruang waktu Minkowski dengan koordinat

) , , ,

(x0 x1 x2 x3

xµ = = (ct, x, y, z) = (ct,r) (1.118)

dapat mengambil bentuk

ds2 =g_µνdxµdxν =−c2dt2+dx2+dy2+dz2 =−c2dt2+dr2 (1.119)

dengan

Ditinjau dua kerangka inersial yakni kerangka K dengan koordinat x dan µ kerangka K~ dengan koordinat x~µ yang bergerak dengan kecepatan konstan V terhadap kerangka K ke arah

//

r = V

V V . r

2 (1.121)

Kaitan Lorentz antara koordinat−4 di dalam ruang−waktu Minkowski adalah (Zahara dkk, 1997)

// ~

r = Γ(r_// −Vt) (1.122)

⊥ ⊥ =r

r

~

(1.123)

) / (

~ 2

c t

t =Γ −r.V (1.124)

dengan

2 2

/ 1

1 c

V

− =

Γ . (1.125)

Kalau komponen ruang di atas ingin digabungkan, hasilnya

// ~ ~

r

r = +r~_⊥ = V V

V V . r r

c ct

Γ − −

Γ

+( 1)(₂ ) (1.126)

yang jika diuraikan ke dalam komponen−komponennya menjadi

i i i i j j i

i i i

n x c V n V V

V x n

x n

x ( 1)₂ 0

~ _{= +} Γ− ₋Γ _(1.127)

atau

~ ( 1)₂ x0

c V x V

V V x

i j j i i

j

i ₋Γ

    

 

 _Γ−

+

=

δ

(1.128)

Sedangkan penguraian untuk komponen waktu adalah

~ ( i xi) c V ct t

c =Γ − (1.129)

atau

~0 ( 0 i xi) c V x

Dari pers. (1.128) dan (1.130), jika dilakukan derivatif parsial koordinat K~

terhadap K, diperoleh

2 ) 1 ( ~ V V V x x j i i j j

i Γ−

+ = ∂ ∂

δ

(1.131) c V x

xi ₌₋Γ i

∂ ∂ 0 ~ (1.132) c V x x _i i Γ − = ∂ ∂~0

(1.133) Γ = ∂ ∂ 0 0 ~ x x

. (1.134)

Ditinjau suatu vektor−4 kontravarian di ruang K

) , ( ) ,

(S0 S S0 S

Sµ = m = (1.135)

dan vektor−4 kontravarian di ruang K~

) ~ , ~ ( ) ~ , ~ (

~ 0 0

S

S S

S

Sµ = m = . (1.136)

Dengan menggunakan kaedah transformasi untuk komponen vektor kontravarian, diperoleh : n n S x x S x x S x x S ∂ ∂ + ∂ ∂ = ∂ ∂

= 0 0

0 0 0

0 ~ ~ ~

~ _ν

ν = ΓS0 

      _⋅ − Γ = Γ − c S S c

Vn n 0 S V

(1.137) dan _n n m m m m S x x S x x S x x S ∂ ∂ + ∂ ∂ = ∂ ∂ = ~ ~ ~ ~ ₀ 0 ν

ν = _c S0

Vm

Γ

− + n n

m m n S V V V         _Γ−

+( 1)₂

δ

= m Vm

V

S +(Γ−1)₂S⋅V Vm c S0

Γ

− (1.138)

yang jika dinyatakan dalam notasi vektor menjadi

S~ S ( 1)₂S VV

V ⋅ − Γ + = V c S0 Γ

− . (1.139)

Mengingat bentuk

(S⋅V)V/V2 =S_//, (1.140)

~S_// =S_//+(Γ−1)S_// V

c S0

Γ

− = Γ

(

S_// −(S0/c)V

)

. (1.141)

Sementara itu kaedah untuk komponen vektor S yang tegaklurus V adalah

⊥ ⊥ =S

S

~

. (1.142)

Selanjutnya ditinjau vektor kecepatan−4 kontravarian :

) , (γ γv

µ c

V = (1.143)

sehingga

c

S0 =γ (1.144)

dan

v

S=γ . (1.145)

Dengan menggunakan hasil pers. (1.137), untuk komponen ke nol, diperoleh

   



 _⋅

+ Γ =

c c

c

γ

γ

v V

γ

~ _(1.146)

yang memberikan hasil

_

  



 _⋅

+ Γ

= 1 ₂

~

c

V v

γ

γ

. (1.147)

Persamaan di atas menghubungkan faktor dilatasi partikel yang bergerak di kedua kerangka. Sedangkan dengan menggunakan pers. (1.139) untuk komponen vektor, diperoleh

V V

V v v

v

c c V

γ γ

γ

γ~~= +(Γ−1)₂ ⋅ −Γ _(1.148)

yang jika disederhanakan menjadi

   



 _⋅

− Γ

Γ − ⋅ − Γ + =

2 2

1 ) 1 ( ~

c V

V v

V V V v v

v (1.149)

2 // //

1 ~

c

V v

V v v

⋅ −

−

= (1.150)

Sedangkan untuk v adalah _⊥

   



 _⋅

− Γ

= ⊥

⊥

2 1 ~

c

V v v

v (1.151)

Berikutnya ditinjau vektor momentum−4 kontravarian yang memiliki komponen :

) , / (E c p

Pµ = (1.152)

sehingga

S0 =E/c (1.153)

dan

S=p. (1.154)

Kaedah transformasi Lorentz untuk energi adalah

   



 _⋅

− Γ

=

c c E c

E~/ / p V (1.155)

atau

E~=Γ

(

E−p⋅V

)

. (1.156)

Bentuk (1.156) di atas sama dengan pers. (1.58). Adapun kaedah transformasi Lorentz untuk vektor momentum−3 adalah

V V

V p p

p ( 1)_{2 2}

~

c E V

Γ − ⋅ − Γ +

= . (1.157)

Untuk komponen vektor momentum−3 sejajar dan tegaklurus, kaedahnya adalah

p~_// p_// ( 1)p_{// 2} V

(

p_// (E/c2)V

)

c E

− Γ = Γ − − Γ +

= (1.158)

dan

⊥ ⊥ =p

p

~

(1.159)

(

f

v

/ c

,

f

)

F

µ

=

γ

⋅

(1.160)

sehingga

c

S0 =

γ

f⋅v (1.161)

dan

f

S=γ . (1.162)

Diperoleh

~f~ f ( 1)₂f VV f₂ vV

c V ⋅ Γ − ⋅ − Γ + =γ γ γ γ (1.163)

yang dengan menggunakan pers. (1.139), bentuk di atas dapat dituliskan menjadi

      _⋅ − Γ ⋅ Γ − ⋅ − Γ + = 2 2 2 1 ) 1 ( ~ c c V V v V v f V V f f

f . (1.164)

Kaedah f untuk komponen sejajar dan tegaklurus berturut−turut adalah

      _⋅ − ⋅ − =       _⋅ − Γ ⋅ Γ − − Γ + = 2 2 // 2 2 // // // 1 1 ) 1 ( ~ c c c c V v V v f f V v V v f f f

f . (1.165)

dan       _⋅ − Γ = ⊥ ⊥ 2 1 ~ c V v f

f . (1.166)

Selanjutnya jika ditinjau kasus khusus dengan v=V, atau partikel rehat di K~, yang berarti bahwa :

2 2

1− ⋅ =Γ−

c

V V

, (1.167)

2 // //

)

(f⋅V V= f VV=f V , (1.168)

_// 2

2 2

2 //

0 //

1 1 ~

f f

f =

    

  

−     

  

− =

c V c V

(1.169)

dan

⊥ −

⊥

⊥ =_ΓΓf =Γf

f0 ₂

~

. (1.170)

Jadi untuk kerangka rehat partikel di K~, kaedah transformasi Lorentz untuk vektor gaya−3 adalah

⊥ ⊥ = +Γ

+

=f f f f

f0 ~_//0 ~0 _//

~

. (1.171)

1.7 Transformasi Lorentz untuk besaran−−−−besaran elektrodinamika

Diketahui ρ dan v berturut−turut adalah rapat muatan dan kecepatan aliran

relatif terhadap suatu kerangka inersial K. Rapat arus j dirumuskan sebagai

v

j=ρ . (1.172)

Persamaan kontinuitas muatan dirumuskan sebagai

0

= ∇ + ∂ ∂

j .

t ρ

(1.173)

Dalam elektrodinamika dikenal skalar potensial listrik φ dan vektor

potensial listrik−3 A yang mana gabungan keduanya bersama−sama membentuk

suatu vektor potensial−4 Aµ dengan komponen

) , / ( ) ,

(A0 A c A

Aµ = m = φ (1.174)

Mengikuti sistem satuan SI, terdapat perumusan−perumusan berikut

0 1

2 ∂ +∇ = ∂

A .

t c

φ

(1.175)

j A

A

0 2

2 2 2

1 _{+∇ =−µ}

∂ ∂ −

t

c (1.176)

2 0 2

2 2 2

1

c t

c φ µ ρ

φ _{+∇ =−}

∂ ∂

Gabungan dua persamaan di atas menghasilkan

µ

µ

µ

_j

A =− ₀

∆ (1.178)

dengan vektor kerapatan−4 jµ didefinisikan sebagai

) , ( ) ,

(j0 j c j

jµ = = ρ . (1.179)

Operator skalar−4 ∆ didefinisikan sebagai

2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 z y x t c t c ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∇ + ∂ ∂ − = ∂ ∂ = ∆ µ

µ (1.180)

Operator turunan koordinat−4 kovarian dan kontravarian masing-masing dirumuskan sebagai       _∇ ∂ ∂ =       ∂ ∂ ∂ ∂ = ∂ ∂ =

∂ ₀ , 1 ,

t c x

x

xµ m

µ (1.181)       ∇ ∂ ∂ − = ∂ =

∂ 1 ,

t c ν

µν

µ _{η (1.182)}

Bentuk syarat Lorentz pers. (1.175) dapat dituliskan sebagai

0

=

∂_µAµ (1.183)

sedangkan bentuk persamaan kontinuitas muatan (pers. (1.173)) dapat dituliskan menjadi

0

=

∂_µjµ (1.184)

Kaedah transformasi Lorentz untuk komponen vektor kerapatan−4 adalah

        _⋅ − Γ = c c

c

ρ

j V

ρ

~ _(1.185)

atau _       _⋅ − Γ = ₂ ~ c V j

ρ

ρ

(1.186) serta

~j j ( 1)₂j VV

V

⋅ − Γ +

= −ΓρV, (1.187)

(

j V

)

j_// =Γ _// −

ρ

~

dan

⊥ ⊥ = j

j

~

. (1.189)

Sementara itu kaedah transformasi Lorentz untuk komponen vektor potensial−4 adalah

    

 

 _⋅

− Γ =

c c c

V A

φ

φ

~

(1.190)

atau

(

−A⋅V

)

Γ

= φ

φ~ , (1.191)

serta

A~ A ( 1)₂A VV ₂ V

c V

φ

Γ − ⋅ − Γ +

= , (1.192)

   



 ₋

Γ

= A V

A~_{// // 2}

c φ

, (1.193)

dan

⊥ ⊥ =A

A~ . (1.194)

Jika kita ingin mencari transformasi balik dari kerangka K~ ke kerangka K,

hal itu dapat dilakukan dengan mudah, yaitu dengan substitusi V=−V. Dengan substitusi ini, diperoleh kaedah transformasi Lorentz besaran-besaran berikut ini :

Vektor kecepatan−3 :

    

 

 _⋅

+ Γ

Γ + ⋅ − Γ + =

2 2

~ 1

~ ) 1 ( ~

c V

V v

V V V v v

v (1.195)

2 //

// ~

1 ~

c

V v

V v v

⋅ +

+

= (1.196)

    

 

 _⋅

+ Γ

= ⊥

⊥

2

~ 1

~

c

V v v

Energi : E=Γ

(

E~+p~⋅V

)

(1.198) Vektor momentum−3 :

V V

V p p

p _{2 2}

~ ~ ) 1 ( ~ c E V Γ + ⋅ − Γ + = (1.199) _      + Γ

= p V

p_{// // 2}

~ ~

c E

(1.200)

p_⊥ =p~_⊥ (1.201)

Vektor gaya−3 :

        _⋅ + Γ ⋅ Γ + ⋅ − Γ + = 2 2 2 ~ 1 ~ ~ ~ ) 1 ( ~ c c V V v V v f V V f f f (1.202)         _⋅ + ⋅ + = 2 2 // // ~ 1 ~ ~ ~ c c V v V v f f

f (1.203)

        _⋅ + Γ = ⊥ ⊥ 2 ~ 1 ~ c V v f

f . (1.204)

Rapat muatan _

      _⋅ + Γ = ₂ ~ ~ c V j

ρ

ρ

(1.205)

Vektor rapat arus

j j ₂j VV

~ ) 1 ( ~ V ⋅ − Γ +

= +Γρ~V (1.206)

      ₊ Γ

= j V

j_// ~_//

ρ

~ (1.207)

⊥ ⊥ = j

j ~ . (1.208)

Skalar potensial listrik : 

     _{+ ⋅} Γ

=

φ

~ A~ V

Vektor potensial−3 listrik :

A A ₂A VV ₂ V

~ ~

) 1 ( ~

c V

φ

Γ + ⋅ − Γ +

= (1.210)

    

  

+ Γ

= A V

A_{// // 2}

~ ~

c

φ

(1.211)

⊥ ⊥ =A

A ~ . (1.212)

Soal-Soal Latihan Bab I

1. Sebuah pesawat bergerak ke arah timur dengan laju 0,8 c diukur menurut menara yang diam. Pesawat tersebut melepaskan peluru dengan laju 0,6 c terhadap pesawat. Carilah masing-masing laju dan arah gerak peluru terhadap menara jika arah peluru terhadap pesawat adalah

(a) timur (b) utara (c) barat (d) timur laut.

2. Sebuah partikel bermassa m bergerak terhadap kerangka I dengan kecepatan

) ˆ 2 ˆ 2 ˆ )( 5 /

(c i − j+ k

=

v . Jika terdapat kerangka II yang bergerak terhadap

kerangka I dengan kecepatan V=(c/5)(2iˆ+ ˆj−2kˆ), carilah :

(a) momentum dan tenaga kinetik dan tenaga total partikel menurut kerangka I.

(b) kecepatan, momentum, tenaga kinetik dan tenaga total partikel menurut kerangka II.

3. Dua buah partikel bergerak sepanjang sumbu Z kerangka K masing-masing dengan kecepatan v₁ dan v₂ dengan v₁>v₂. Agar ditinjau dari K’, kedua partikel tersebut mempunyai kecepatan yang berlawanan, tunjukkan bahwa kecepatan gerak kerangka K’ ke arah sumbu Z terhadap K besarnya adalah

2 1

2 2 2 2 1 2 2

1 2

) )(

( v v

v c v c v

v c

−

− −

− −

.

4. Sebuah elektron dalam suatu akselerator tenaga tinggi bergerak dengan kelajuan 0,5 c. Carilah kerja yang harus dilakukan terhadap elektron untuk menaikkan kelajuannya menjadi

(b) 0,99 c

(c) Untuk kedua nilai kelajuan tersebut, tentukan faktor peningkatan tenaga kinetik maupun momentum elektron.

5. Sebuah inti radioaktif bergerak dengan kecepatan v =0,6ciˆ terhadap kerangka K (lab), sewaktu ia memancarkan partikel beta dengan kecepatan

j c

v_β =0,75 ˆ terhadap inti tersebut (kerangka K ). ₀

(a) Tentukan besar dan arah kecepatan partikel beta menurut kerangka K. (b) Jika partikel beta tersebut tetap dipancarkan dengan kelajuan 0,75c di

0

K , namun arahnya dilihat dari K sejajar dengan sumbu y, tentukan

arah pancaran diamati dari inti dan kelajuan partikel beta diamati di K.

6. Di kerangka K, dua partikel A dan B bergerak masing-masing dengan kecepatan v_A =v_Aiˆ dan v_B =v_Biˆ (v_B >v_A >0). Jika terdapat kerangka K~ yang bergerak terhadap K dengan kecepatan V=Viˆ (diketahui

0 v_A

B >V > >

v ) :

(a) Tentukan kecepatan A dan B menurut K~, yaitu ~v dan _A ~v . _B

(b) Jika menurut pengamat yang rehat di K~, kecepatan A dan B sama besar namun berlawanan arah, tunjukkan bahwa

B A

2 B 2 2 A 2 B

A

2 _{) ( )( )}

(

v v

v c v c v

v c V

+

− −

− +

= .

7. Di kerangka K, sebuah partikel bergerak dengan kecepatan u . Di K tersebut

8. Diketahui vektor−4 kontravarian :Xµ =

γ

(Y/c, cZ) dengan γ = )

/ 1

( −u2 c2 , u = vektor kecepatan−3 dan c laju cahaya di ruang hampa. (a) tuliskan kaedah tranformasi Lorentz untuk besaran Y danZ. (Petunjuk :

jangan lupa relasi antara γ dengan γ ’ )

(b) Jika terdapat hubungan : Y =kc dan Z=k /u c dengan k suatu invarian Lorentz, carilah invarian Lorentz yang dapat diperoleh dari vektor−4 tersebut, serta berapakah nilainya ?

9. Jelaskan bahwa gaya Lorentz yang dirasakan oleh sebuah partikel di kerangka K menjadi gaya Coulomb di kerangka diam K’. Bagaimana dengan sebaliknya, gaya Coulomb di K’ menjadi gaya Lorentz di K ?

10. Di kerangka K’, sebuah partikel bermassa rehat m bermuatan q bergerak dengan kecepatan konstan u ’. Di K’ tersebut terdapat medan listrik E ’ dan

medan imbas magnet B ’. Jika kerangka K’ bergerak terhadap kerangka K

dengan kecepatan konstan V:

(a) Tentukan energi, energi kinetik dan momentum partikel di K maupun di K’.

BAB II

PENERAPAN TEORI RELATIVITAS KHUSUS

Teori Relativitas Khusus sebagai salah salah satu pilar fisika modern memiliki beberapa kegunaan dalam menelaah secara lebih kompak dan terpadu berbagai gejala alam. Berikut ini akan disajikan beberapa penerapan teori relativitas khusus pada beberapa fenomena, diantaranya adalah persoalan paradoks kembar, gerak partikel relativistik dalam medan gaya konstan dan medan gravitasi seragam, efek hamburan Compton dan sebagainya.

2.1 Paradoks Kembar (Twin Paradox)

Paradoks kembar (atau paradoks jam) adalah satu persoalan yang cukup membingungkan dalam relativitas khusus. Kasus paradoks kembar dapat dinyatakan sebagai berikut : Misalkan kita punya dua orang kembar : John dan Mary. John diputuskan tetap tinggal di bumi, sementara Mary menjadi astronot yang akan mengadakan perjalan ruang angkasa menuju sebuah bintang. Mary mengendarai pesawat ruang angkasa dan terbang menuju bintang tersebut dengan kecepatan V (diasumsikan agar nampak efek relativitas, nilai V dalam orde c) dan sesudah sesaat tiba di bintang, Mary kembali ke bumi dan bertemu dengan John dengan kecepatan yang sama. Lihat Gambar 2.1

Bumi Bintang

Gambar 2.1

Perjalanan pulang pergi bumi-bintang

Teori relativitas khusus menyatakan bahwa jika Mary bergerak terhadap John, maka selang waktu dalam kerangka inersial Mary mengalami dilatasi sebesar

γ

yang dirumuskan

2 2

/ 1−V c

=

Jadi pada akhir perjalanan Mary, dia lebih muda daripada John. Paradoks muncul dari kenyataan bahwa (dengan mengabaikan selang waktu saat Mary bergerak dipercepat dan diperlambat), Mary berada dalam kerangka inersial, dan selanjutnya dari prinsip relativitas, Mary dapat mengklaim bahwa Johnlah yang bergerak, bukan dia. Kalau demikian selang waktu John seharusnya yang mengalami dilatasi, bukan Mary, sehingga saat Mary kembali, ia menjumpai saudara kembarnya itu lebih muda daripadanya. Manakah yang benar ?

Untuk menyederhanakan kasus ini, diasumsikan perjalanan Mary terjadi saat ia lahir (yang juga berarti saat John lahir). Pada saat itu, berarti waktu lokal T = 0 dan posisi X = 0. Selanjutnya akan dibandingkan jarak bumi−bintang menurut kedua orang tersebut. Jarak antara bumi dan bintang diukur oleh pengamat yang stasioner di bumi (John) adalah D . Jarak bumi _J − bintang yang diukur oleh Mary adalah

D_M =D_J /

γ

. (2.2) Perumusan ini disebabkan oleh adanya kontraksi Lorentz. Indeks J dan M berturut-turut menunjukkan pengukuran menurut John dan Mary. Akan diukur umur relatif John dan Mary. Caranya, pertama dengan melakukan penghitungan dalam kerangka John dan selanjutnya penghitungan dikerjakan dalam kerangka Mary. Nanti akan ditunjukkan bahwa dua penghitungan tersebut akan memperoleh hasil yang sama. Kesamaan ini menunjukkan tidak adanya perbedaan antara dua kerangka inersial yang ditinjau.

Sekarang penghitungan dilakukan dalam kerangka John. Mary menempuh perjalanan total (menuju bintang dan kembali ke bumi) sejauh 2D_J dengan kecepatan V (−V saat kembali). Perjalanan bumi−bintang bolak-baik ini memakan waktu 2D_J /V . Transformasi Lorentz untuk waktu memberikan hubungan antara waktu yang ditunjukkan oleh jam milik John (T ) dan waktu yang ditunjukkan oleh _J Mary (T ) sebagai _M

]

[ ₂

c VX T

dengan X adalah jarak antara mereka. Selama perjalanan Mary menuju ke _J bintang, berlaku persamaan

XJ =VTJ. (2.4)

Substitusi persamaan di atas ke dalam pers. (2.3), diperoleh T_M =

γ

[T_J −(V2/c2)T_J] =

γ

[1−(V2/c2)]T_J =

γ

J T

. (2.5) Dalam bentuk penulisan selang waktu,

γ

J M

T T = ∆

∆ . (2.6)

Persamaan ini menunjukkan bahwa jam Mary bergerak lebih lambat daripada jam milik John dengan faktor 1/γ . Di sini perlu diingat bahwa

γ≥ 1. (2.7)

Dengan cara yang sama dapat ditunjukkan pula bahwa hal tersebut berlaku pula untuk perjalanan Mary pulang ke bumi. Saat kembali ke bumi dengan kecepatan yang sama, jam milik Mary juga bergerak lebih lambat dari jam milik John dengan faktor yang sama : 1/γ . Maka selama perjalanan total, umur John adalah

V D

A J

J

2

= , (2.8)

sedangkan umur Mary adalah

γ 1 2

V D

A J

M = . (2.9)

Tampak bahwa umur John lebih besar daripada umur Mary, atau dengan kata lain dalam kerangka John, saat Mary kembali ke bumi, John lebih tua. Selisih umur mereka adalah

V D A

A J

M J

2 1

1 _

    

− = −

γ . (2.10)

   



 ₋

= ₂

c VX T

T_J γ _M M . (2.11)

Dan dengan penurunan selanjutnya dapat ditunjukkan kaitan untuk selang waktu masing-masing jam sebagai

γ

M J

T T =∆

∆ (2.12)

yang berarti jam milik John bergerak lebih lambat daripada jam milik Mary dengan faktor 1/

γ

. Sekilas nampak adanya paradoks atau kontradiksi dengan ungkapan sebelumnya yang menyatakan bahwa jam Mary bergerak lebih lambat daripada John. Namun demikian yang sebenarnya tidak demikian, karena hal ini disebabkan relativitas khusus menyatakan bahwa kita tidak dapat menghubungkan waktu yang ditunjukkan oleh jam pada tempat yang berbeda (yang dalam hal ini umur orang kembar yang terpisah) sampai kemudian kedua orang tersebut bertemu kembali. Ketika mereka berdua bertemu kembali, baru tampaklah siapa yang lebih tua atau lebih muda dengan cara membandingkan selang waktu yang ditunjukkan oleh jam masing-masing.

Menurut Mary, perjalanannya memakan waktu 2D_M /V , sehingga selama perjalanan, umur Mary adalah

γ

M M

D

A = 2 . (2.13)

Perlu diingat bahwa telah diasumsikan bahwa waktu untuk mempercepat dan memperlambat roket telah diabaikan. Karena jam John bergerak lebih lambat dengan faktor 1/

γ

, John berumur

γ

1 2

V D

A_J = M . (2.14)

Jika dilatasi waktu menjadi satu-satunya faktor dalam penghitungan, Mary dapat mengklaim bahwa dirinya berusia lebih tua dari John dengan selisih umur mereka adalah

V D A

A_{M J} 1 1_2 M

    

�