Pertemuan 6 Integral 2 6.1 Pendahuluan - 6 Integral 2

(1)

Pada pertemuan sebelumnya, kita telah mempelajari hubungan antara Jumlahan Riemann dan proses integrasi. Kita temukan pula bahwa untuk sebuah fungsi kontinu pada [ ], limit dari sebagai norm dari partisi | | mendekati nol adalah nilai

∫ ( ) ( ) ( )

dimana sembarang antiderivative dari . Kita terapkan hal ini untuk menghitung luas area diantara sumbu- dan grafik ( ) untuk , dan menghitung luas area diantara dua buah kurva.

Sekarang kita akan mencoba menerapkan integral untuk menemukan volume, panjang bidang kurva, pusat massa, luas permukaan perputaran, tekanan dan daya cairan. Di sini kita gunakan limit dari Jumlahan Riemann fungsi-fungsi kontinu pada interval tertutup, yakni integral tertentu yang dapat dihitung dengan menggunakan Teorema Dasar Kalkulus.

6.2 Volume Sebuah Benda

Pada bab ini kita akan mendefinisikan volume dari sebuah bangun yang beririsan dengan daerah suatu bidang.

Definisi 6.1 Volume

Volume dari sebuah bangun dari area terintegrasi beririsan, ( ) dari ke

adalah integral dari ke ,

∫ ( )

(2)

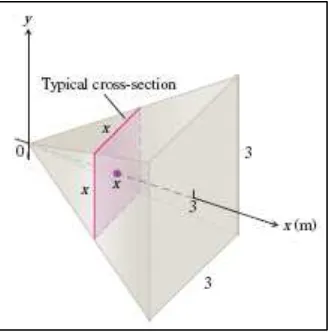
Sebuah piramida dengan tinggi 3 m memiliki alas persegi dengan panjang sisi 3 m. Bidang irisan piramida tegak lurus dengan tinggi m dari titik puncaknya adalah sebuah persegi dengan panjang sisi m. Tentukan volume dari piramida!

Jawaban

1. Kita gambarkan piramida dengan tingginya sepanjang sumbu- dan titik puncaknya berada di titik pusat dan termasuk bidang irisannya. Perhatikan gambar berikut.

Gambar 6.1 Bidang irisan piramida pada Contoh 6.1 adalah persegi-persegi

(Thomas’s Calculus, 11th pertama pada sudut dari pusat tabung. Temukan volume dari benda tersebut!

Jawaban

(3)

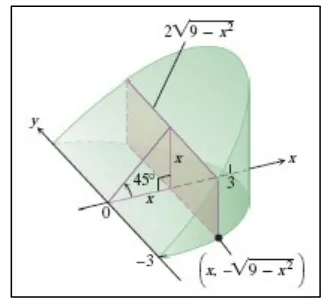
Gambar 6.2 Bangun pada Contoh 6.2

(Thomas’s Calculus, 11th

ed, p.398)

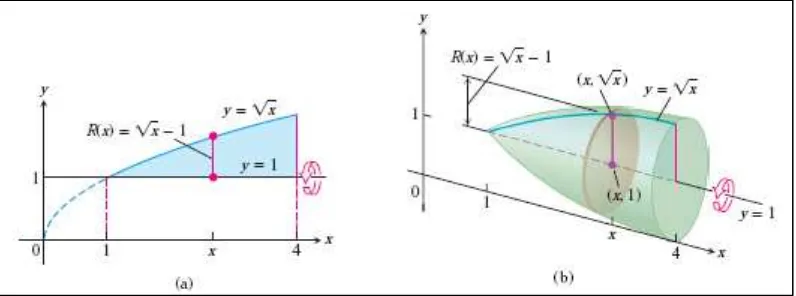
Bidang irisan pada adalah persegi panjang dengan area

( ) ( √ ) √

Persegi panjang-persegi panjang tersebut berjalan dari hingga , sehingga

∫ ( ) ∫ √ , ambil

( ) ⁄ _]

( ) ⁄

□

Solid of revolution: Metode Disk

Bangun yang dibentuk dengan merotasi suatu daerah bidang pada suatu sumbu dalam bidangnya disebut sebagai solid of revolution. Volumenya diberikan sebagai berikut.

∫ ( ) ∫ [ ( )]

Contoh 6.3 Solid of revolution

(4)

Jawaban

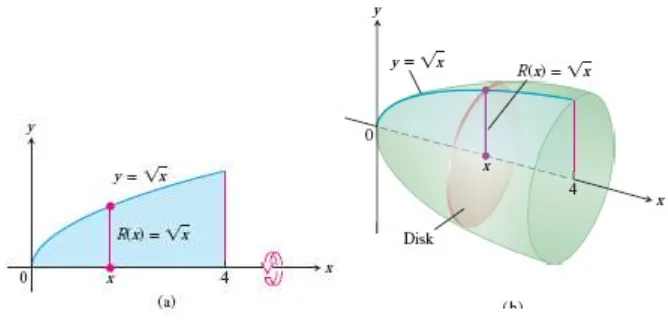
Kita gambarkan bangun yang dibentuk seperti pada gambar berikut.

Gambar 6.3 Daerah (a) dan bangun dari perputaran (b) untuk Contoh 6.3

(Thomas’s Calculus, 11th ed, p.400)

Volumenya adalah

∫ [ ( )]

∫ [√ ]

∫ ] □

Contoh 6.4 Volume sebuah bola

Lingkaran

diputar terhadap sumbu- untuk membentuk sebuah bola. Tentukan volumenya!

Jawaban

(5)

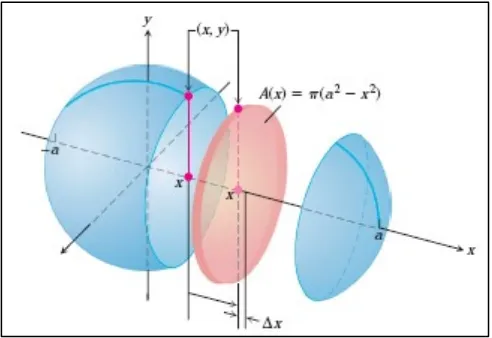
Gambar 6.4 Bola yang dibentuk dengan memutar lingkaran pada sumbu- .

Radiusnya adalah ( ) √

ed, p.400)

Luas area bidang irisan pada titik diantara dan adalah

( ) ( )

Sehingga volumenya adalah

∫ ( )

∫ ( ) [ ]

Contoh 6.5 Solid of revolution (rotasi pada garis )

Temukan volume sebuah bangun yang dibentuk dengan memutar daerah yang dibatasi oleh √ dan garis pada garis !

Jawaban

(6)

Gambar 6.5 Daerah (a) dan bangun revolusi (b) untuk Contoh 6.5

ed, p.401)

Volume bangun tersebut adalah

∫ [ ( )]

∫ [√ ]

∫ [ √ ]

[ ⁄ _] _□

Contoh 6.6 Rotasi pada

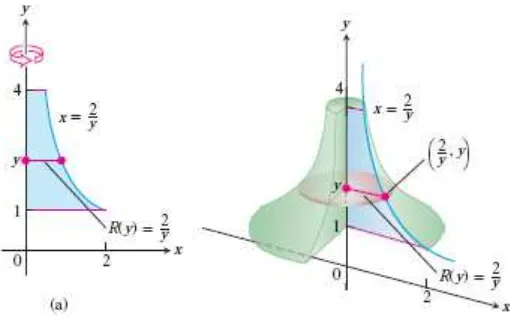
Temukan volume sebuah bangun yang dibentuk dengan memutar daerah diantara sumbu-dan kurva ⁄ , pada sumbu- !

Jawaban

(7)

Gambar 6.6 Daerah (a) dan bagian dari bangun revolusi (b) untuk Contoh 6.6

ed, p.402)

Volume bangun adalah

∫ [ ( )]

∫ ( )

∫

[ ] [ ] □

Contoh 6.7 Rotasi pada sumbu vertikal

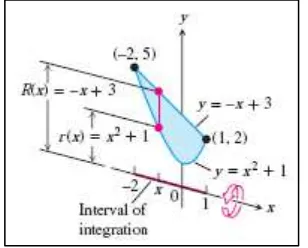
Temukan volume dari bangun yang dibentuk dengan memutar daerah diantara parabola dan garis pada garis !

Jawaban

(8)

Gambar 6.7 Daerah (a) dan bangun revolusi (b) untuk Contoh 6.7

ed, p.402)

Volume bangun adalah

∫ [ ( )]√

√

∫ [ ( _√√ )]

∫ [ _√√ ]

[ ]

√ √

√ □

Solid of revolution: Metode Washer

(9)

Gambar 6.8 Bidang irisan dari bangun revolusi yang dibentuk memiliki lubang di tengahnya

ed, p.403)

Volume untuk bangun seperti demikian adalah

∫ ( ) ∫ ([ ( )] [ ( )] )

Contoh 6.8 Bidang irisan metode washer (rotasi pada sumbu- )

Daerah yang dibatasi oleh kurva dan garis diputar terhadap untuk membentuk sebuah bangun solid. Tentukan volume dari bangun tersebut!

Jawaban

1. Pertama, kita gambarkan daerah dan kurva sebagaimana yang dimaksud dalam contoh soal.

Gambar 6.9 Daerah untuk Contoh 6.8

ed, p.403)

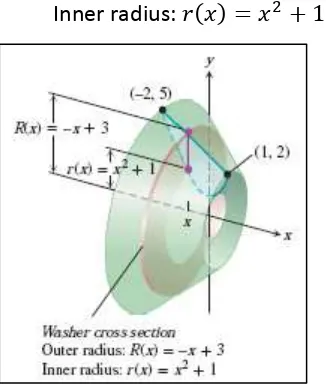
2. Temukan jari-jari luar dan dalam dari washer yang terbentuk dari ruas garis dari daerah tersebut jika diputar terhadap sumbu- .

(10)

Inner radius: ( )

Gambar 6.10 Saat daerah diputar sepanjang sumbu- diperoleh sebuah washer

ed, p.403)

3. Temukan batasan integral dengan mencari koordinat- dari titik-titik beririsan antara kurva dan garis pada Gambar 6.10 sebelumnya.

Contoh 6.9 Bidang irisan metode washer (rotasi pada sumbu- )

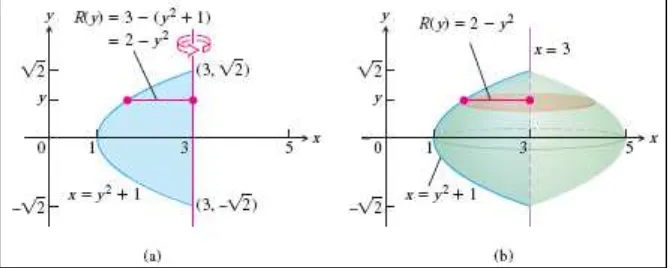
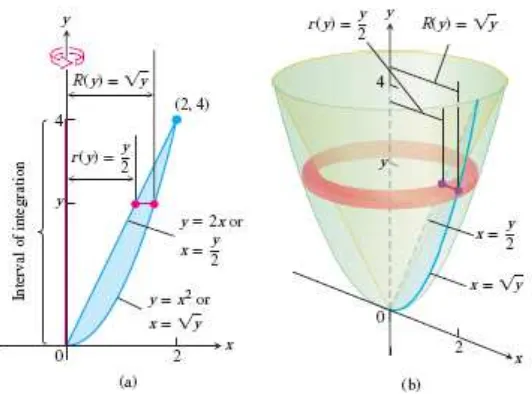
Daerah yang dibatasi parabola dan garis pada kuadran pertama diputar terhadap sumbu- untuk membentuk sebuah bangun. Tentukan volume bangun tersebut!

Jawaban

(11)

Gambar 6.11 (a) Daerah yang diputar terhadap sumbu- , (b) washer yang terbentuk

(Thomas’s Calculus, 11th ed, p.404)

Garis dan parabola beririsan pada dan , jadi batasan integrasi adalah dan . Kita integrasikan untuk menemukan volume:

∫ ([ ( )] [ ( )] )

∫ ([√ ] [ ] )

∫ ( ) [ ] □

Solid of revolution: Metode Shell

Volume dari sebuah bangun yang dibentuk dengan memutar daerah diantara sumbu- dan grafik dari sebuah fungsi kontinu ( ) , terhadap garis vertikal adalah

∫ ( )( )

Contoh 6.10 Selubung silinder yang berputar terhadap

(12)

Jawaban

Perhatikan gambar berikut.

Gambar 6.12 (a) Daerah, ukuran selubung, dan interval dari integrasi, (b) shell yang diputar

ed, p.412)

Variabel ketebalan selubung adalah , sehingga batasan integrasi untuk rumus shell adalah dan . Volumenya adalah

∫ ( )( )

∫ ( )(√ )

∫ ⁄ _[ ⁄ _] _□

Contoh 6.11 Selubung silinder yang berputar terhadap

sumbu-Daerah yang dibatasi oleh kurva √ , sumbu- , dan garis diputar sepanjang sumbu- untuk menghasilkan sebuah bangun. Tentukan volume bangun tersebut!

Jawaban

(13)

Gambar 6.13 (a) Daerah, ukuran selubung, dan interval dari integrasi, (b) shell yang diputar

ed, p.413)

Kali ini, variabel ketebalan selubung adalah , sehingga batasan integrasinya untuk rumus shell adalah dan . Volume dari bangun tersebut adalah

∫ ( )( )

∫ ( )

[ ] .□

6.3 Panjang Suatu Kurva

Definisi 6.2 Panjang suatu kurva parametric

Jika suatu kurva terdefinisi secara parameter dengan ( ) dan ( ) ,

dimana dan kontinu dan tidak berurutan nol pada [ ], dan ditelusuri tepat sekali

saat naik dari ke , maka panjang dari adalah integral tertentu

∫ √[ ( )] [ ( )]

Contoh 6.12 Keliling sebuah lingkaran

(14)

dan .

Jawaban

Saat bergerak dari ke , lingkaran ditelusuri tepat satu kali, sehingga kelilingnya adalah

∫ √( ₎ ( ₎

Kita tahu bahwa

dan

( ₎ ( ₎ ( )

Sehingga

∫ √ [ ]

Contoh 6.13 Menerapkan rumus parametric untuk panjang suatu kurva

Temukan panjang dari asteroid berikut jika

dan .

Gambar 6.14 Astroid Contoh 6.13

(15)

( ₎ [ ( )]

√( ₎ ( ₎ √ ( )

√

| |

Oleh karenanya,

Panjang kurva pada kuadran pertama ∫ ⁄

∫

⁄

] ⁄

Panjang dari asteroid adalah ( ⁄ ) □

Rumus untuk panjang dari ( )

Jika kontinu dan terdiferensiasi pada interval tertutup [ ], panjang dari kurva ( )

dari ke adalah

∫ √ ( ₎ ∫ √ [ ( )]

(16)

Temukan panjang dari kurva

Contoh 6.15 Panjang suatu grafik yang memiliki diskontinuitas pada ⁄

Temukan panjang dari kurva ( ⁄ ) ⁄ dari hingga .

Jawaban

(17)

(₎ ⁄

⁄

Kurva yang akan dicari panjangnya juga merupakan grafik dari ⁄ dari hingga . Turunannya

( ) ⁄ ⁄

kontinu pada [ ]. Sehingga dengan persamaan di atas diperoleh

∫ √ (₎ ∫ √

( ) ⁄ _]

( √ )

6.4 Momen dan Titik Pusat Massa

Momen, massa, dan titik pusat massa dari suatu batang tipis sepanjang sumbu- dengan fungsi density ( )

Momen pada titik pusat: ∫ ( )

(18)

Titik pusat massa: ̅

Contoh 6.16 Batang tipis dengan density konstan

Tunjukkan bahwa pusat massa dari suatu batang kecil dengan density konstan terletak pada titik tengah dari kedua ujungnya!

Jawaban

Kita modelkan batang tersebut sebagai bagian dari sumbu- dari ke (Gambar 6.15).

Gambar 6.15 Pusat massa dari suatu batang kecil terletak pada titik tengah diantara kedua ujungnya

ed, p.427)

Tujuan kita adalah menunjukkan bahwa ̅ ( ) ⁄ , titik tengah diantara dan . Kuncinya adalah density-nya memiliki suatu nilai konstan, sehingga memungkinkan kita untuk melihat fungsi ( ) dalam integral pada persamaan di atas sebagai suatu konstan

(19)

[ ]

Massa batang adalah

∫ ( ) ∫ ( ₎ [ _]

Pusat massa terletak pada

̅

Momen, massa, dan titik pusat massa dari suatu bidang tipis menutupi suatu daerah dalam bidang-

Momen pada titik pusat: ∫ ( )

Massa: ∫ ( )

Titik pusat massa: ̅

Contoh 6.18 Constant-density wire

Tentukan titik pusat massa dari sebuah kabel dengan density konstan berbentuk seperti setengah lingkaran dengan jari-jari !

Jawaban

(20)

Gambar 6.16 (a) Dimensi dan variabel digunakan untuk menemukan titik pusat massa, (b) Pusat massa tidak terletak pada kabel

ed, p.433)

Distribusi massa simetri terhadap sumbu- , sehingga ̅ . Untuk menemukan , kita imajinasikan kabel dibagi menjadi segmen-segmen pendek. Setiap segmen (Gambar 6.16a) memiliki

6.5 Area Permukaan Revolusi dan Teorema Pappus

Definisi 6.3 Luas permukaan revolusi terhadap

sumbu-Jika fungsi ( ) kontinu terdiferensiasi pada [ ], luas permukaan yang dibentuk

dengan memutar kurva ( ) sekitar sumbu- adalah

(21)

Gambar 6.17 Ilustrasi Contoh 6.19

ed, p.438)

Jawaban

Diketahui

√ √

√ ( ₎ √ ( √ )

√ √ √ _√

Dengan substitusi,

∫ √ √

√ ∫ √

( ) ⁄ _] _{( √ √ )}_□

(22)

sumbu-Jika ( ) kontinu terdiferensiasi pada [ ], luas permukaan yang dibentuk dengan memutar kurva ( ) sekitar sumbu- adalah

∫ √ ( ₎ ∫ ( )√ ( ( ))

Contoh 6.20 Menemukan luas perputaran terhadap

sumbu-Ruas garis , diputar terhadap sumbu- untuk membentuk kerucut

seperti pada Gambar 6.18. Tentukan luas permukaan selubungnya (tidak termasuk luas alasnya)!

ed, p.439)

Jawaban

Kita tahu dengan geometri sederhana bahwa

√

Kita ambil

(23)

Luas permukaan revolusi untuk kurva parametrik

Jika sebuah kurva ( ) ( ) , ditelusuri tepat satu kali saat naik dari ke , maka luas permukaan yang dibentuk dengan memutar kurva terhadap sumbu koordinat adalah

1. Perputaran terhadap sumbu- ( ):

∫ √( ₎ ( ₎

2. Perputaran terhadap sumbu- ( ):

∫ √( ₎ ( ₎

Contoh 6.21 Menerapkan rumus luas permukaan

Parameter standar dari sebuah lingkaran dengan jari-jari 1 dengan pusat ( ) dalam bidang- adalah

(24)

ed, p.440)

Jawaban

Kita evaluasi rumus

∫ √( ₎ ( ₎

∫ ( )√( ) ( )

∫ ( )

[ ] _□

Teorema 6.1 Teorema Pappus untuk volume

Jika daerah suatu bidang diputar sekali terhadap sebuah garis dalam bidang tersebut yang

tidak memotong melalui titik interior daerah, maka volume dari bangun yang terbentuk

sama dengan luas daerah dikali jarak yang dilalui pusat daerah selama perputaran. Jika

adalah jarak dari sumbu putar ke pusat, maka

(25)

Gambar 6.20 Dengan Teorema Pappus pertama, kita dapat menemukan volume sebuah torus tanpa harus menggunakan integral

ed, p.443)

Teorema 6.2 Teorema Pappus untuk luas permukaan

Jika suatu busur dari kurva diputar sekali terhadap sebuah garis dalam bidang yang tidak

memotong interior busur, maka luas permukaan yang dibentuk oleh busur sama dengan

panjang busur dikali jarak yang dilalui pusat busur selama perputaran. Jika adalah jarak

dari sumbu putar ke pusat, maka

Contoh 6.23 Luas permukaan sebuah torus (donut)

Luas permukaan dari donut pada Contoh 6.22 adalah

( )( )

6.6 Terapan Nyata

(26)

Usaha yang dilakukan oleh sebuah daya variabel ( ) sepanjang sumbu- dari ke

adalah

∫ ( )

Contoh 6.24 Menekan per

Tentukan usaha yang diperlukan untuk menekan per dari panjang aslinya 1 kaki ke panjang 0.75 kaki jika konstanta usaha adalah .

Jawaban

Kita ilustrasikan per yang tidak ditekan sepanjang sumbu- dengan satu ujungnya pada titik pusat dan titik ujung lainnya pada . Perhatikan Gambar 6.21 berikut.

Gambar 6.21 Usaha yang diperlukan untuk menahan sebuah per naik secara linear saat per makin ditekan

ed, p.449)

Hal ini memungkinkan kita untuk menggambarkan usaha yang diperlukan dalam menekan per dari ke dengan rumus . Untuk menekan per dari ke , usaha akan naik dari

(27)

tetap (Gambar 6.22). Bobot tali 0.08 lb/ft. Berapa banyak usaha yang digunakan untuk mengangkat kaleng dan tali?

ed, p.450)

Jawaban

Kaleng memiliki bobot tetap sehingga usaha untuk mengangkatnya adalah ft-lb.

Bobot dari tali berubah tergantung kenaikan kaleng, karena semakin sedikit tali yang tergantung. Saat kaleng ft dari tanah, sisa bagian dari tali yang masih ditarik memiliki bobot ( ) ( ) lb. Sehingga usaha untuk mengangkat tali adalah

∫ ( ) ( ) ∫ ( )

[ ] _ft-lb.

Total usaha untuk mengangkat kaleng dan tali adalah

(28)

6.7 Tekanan dan Daya Cairan

Persamaan tekanan-kedalaman

Dalam sebuah cairan yang tenang, tekanan pada kedalaman adalah density bobot cairan dikali :

Daya cairan pada suatu permukaan kedalaman konstan

Integral daya cairan terhadap suatu bidang datar

Misalkan bahwa sebuah bidang datar tenggelam secara vertikal dalam cairan dengan density bobot dari ke pada sumbu- . Misal ( ) adalah panjang dari garis horizontal diukur dari kiri ke kanan sepanjang permukaan bidang pada tingkat . Maka daya yang dikeluarkan cairan terhadap salah satu sisi bidang datar adalah

∫ ( ) ( )

Contoh 6.26 Menerapkan integral untuk daya cairan

Sebuah bidang segitiga dengan alas 6 ft dan tinggi 3 ft tenggelam secara vertikal, 2 ft ke bawah permukaan sebuah kolam renang. Temukan daya yang dikeluarkan oleh air melawan salah satu permukaan bidang tersebut!

Jawaban

(29)

ed, p.457)

Permukaan kolam terletak sepanjang garis dan rusuk atas bidang segitiga sepanjang garis . Rusuk sisi kanan bidang sepanjang garis , dengan titik kanan atas pada ( ). Panjang dari strip pada level adalah

( )

Kedalaman strip di bawah permukaan adalah ( ). Daya yang dikeluarkan oleh air melawan salah satu sisi bidang adalah

∫ ( ) ( )

∫ ( )

[ ] lb.□

Daya cairan dan centroids

Daya cairan dengan density bobot terhadap salah satu sisi dari bidang datar yang

tenggelam adalah hasil kali dari , jarak ̅ dari pusat bidang ke permukaan cairan, dan luas bidang:

̅

(30)

Gunakan persamaan di atas untuk menemukan daya pada Contoh 6.26.

Jawaban