BAB I PENDAHULUAN A. Latar belakang
Banyak orang yang beranggapan bahwa Matematika itu rumit, karena alasan itulah banyak orang yang menghindari Matematika. Padahal Matematika dapat kita jumpai di dalam kehidupan sehari-hari, dan mau tidak mau kita pasti menggunakan Matematika. Oleh karena itu saya membuat makalah ini dengan maksud membantu pemahaman agar mereka tidak menilai Matematika adalah sesuatu yang buruk. Secara khusus dalam ilmu pengetahuan Aljabar Linear.
B. Tujuan
Makalah ini dibuat dengan tujuan utama untuk memenuhi Tugas Mandiri mata kuliah Aljabar Linear Elementer, yang diberikan oleh dosen saya. Dan tujuan berikutnya adalah sebagai sumber informasi yang saya harapkan bermanfaat dan dapat menambah wawasan para pembaca makalah ini.
ISI
DETERMINAN
Determinan : Produk (hasil kali) bertanda dari unsur-unsur matriks sedemikian hingga berasal dari baris dan kolom yang berbeda, kemudian hasilnya di jumlahkan.
A = a11 a12 det (A) = a11 a22 – a12 – a21
a21 a22
A. Fungsi Determinan
Definisi:
Suatu permutasi dari bilangan-bilangan bulat {1, 2, 3, …, n} adalah penyusunan
bilangan bilangan tersebut dengan urutan tanpa pengulangan. Contoh:
Permutasi dari {1, 2, 3} adalah
(1, 2, 3) (2, 1, 3) (3, 1, 2)
(1, 3, 2) (2, 3, 1) (3, 2, 1)
Secara umum, bilangan-bilangan pada {1, 2, …, n} akan mempunyai n!
permutasi.
Sub Bahasan Determinan:
1. Menghitung determinan dengan perkalian elementer 2. Menghitung determinan dengan operasi baris elementer 3. Sifat-sifat determinan suatu matriks
4. Menghitung determinan dengan expansi kofaktor 5. Penyelesaian SPL dengan aturan cramer
1. Menghitung Determinan dengan Perkalian Elementer
Pada bagian ini kita akan membahas tentang determinan dan cara mencarinya. Determinan merupakan nilai yang paling penting dalam perhitungan matriks. Definisi-definisi maupun teorema yang penting yang berhubungan dengan pencarian matriks.
Sebuah permutasi dari himpunan bilangan bulat positif {1,2,3, . . . .,n} adalah susunan bilangan-bilangan bulat ini menurut aturan tertentu “tanpa menghilangkan” “tanpa mengurangi” bilangan bulat tersebut.
Contoh 1.
Permutasi dari {1,2} adalan (1,2) dan (2,1).
Permutasi dari {1,2,3} adalah (1,2,3),(3,1,2),(2,3,1),(2,1,3),
(1,3,2),dan (3,2,1).
Dari definisi permutasi, apabila ada 4 bagian, maka banyaknya permutasi adalah 24 buah. Hal ini dapat di hitung dari rumus n.
Dapat dilihat untuk n = 2, maka ada 2 permutasi. Untuk n = 3, maka ada 6 = 3.2.1 permutasi. Untuk n = 4, maka ada 24 = 4.3.2.1 permutasi.
Contoh 2.
Tentukan jumlah inversi dari permutasi berikut : a. (6,5,3,1,4,2) b. (2,4,1,3) c. (1,2,3,4) Penyelesaian : Jumlah inversi/pembalik : 5 + 4 + 2 + 0 + 1 + = 12 Jumlah inversi/pembalik : 1 + +2 + 0 =3
Tidak ada inversi/pembalik dalam permutasi ini
Definisi 2.
Dalam permutasi, di katakan terjadi sebuah inversi apabila sebuah bilangan bulat yang lebih besar mendahului sebuah bilangan yang lebih kecil.
Contoh :
Kita akan menghitung inversi dalam dalam permutasi (2,4,1,3). caranya sebuah berikut :
Banyak nya bilangan bulat lebih kecil daripada j1 = 2 dan mengikuti (yaitu j3 = 1),
dapat di lihat pada permutasi (2,4,1,3). Dalam permutasi tersebut j1 = 2 , j2 = 4, j3 =
Banyaknya bilangan bulat yang lebih kecil daripada j2 = 4 dan mengikutinya, ada
dua ( yaitu j3 = 1 dan j4 = 3).
Banyaknya bilangan bulat yang lebih kecil daripada j3 = 1 dan mengikutinya
adalah nol.
Sehingga banyaknya inversi dalam permutasi ini adalah 1 + 2 + 0 = 3 Definisi 3.
Sebuah permutasi di namakan permutasi genap jika banyaknya inversi dalam permutasi tersebut genap. Sebaliknya sebuah permutasi di namakan permutasi ganjil jika banyaknya inversi dalam permutasi tersebut ganjil.
Contoh :
Permutasi (2,4,1,3) adalah permutasi ganjil karena banyaknya inversi dalam permutasi tersebut ganjil.sementara itu ,permutasi (1,2,3,4,5,6) adalah permutasi genap.
Contoh :
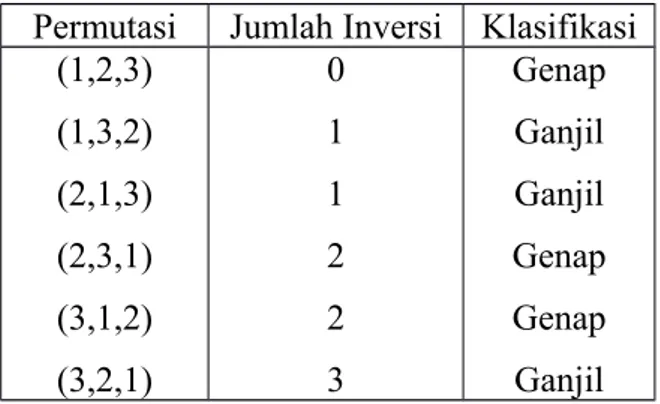
Tabel berikut merupakan klasifikasi berbagai permutasi dari {1,2,3} sebagai genap atau ganjil
Definisi 4.
Permutasi Jumlah Inversi Klasifikasi
(1,2,3) (1,3,2) (2,1,3) (2,3,1) (3,1,2) (3,2,1) 0 1 1 2 2 3 Genap Ganjil Ganjil Genap Genap Ganjil
Hasil perkalian elementer matriks A yang berukuran n x n adalah hasil perkalian elemen-elemen tersebut berasal dari baris yang sama atau kolom yang sama.
Contoh :
Hasil perkalian elemen matriks A yang berukuran 4 x 4 adalan a31 a22 a43 a14.
a11 a12 a13 a14
a21 a22 a23 a24
a31 a32 a33 a34
a41 a42 a43 a44
Sementara itu ,a11,a12,a23,a34 adalah bukan hasil perkalian elementer sebab bentuk
a11,a12,a23,a34 mempunnyai elemen pada baris yang sama, yaitu elemen a11 dan a12
terletak pada baris yang sama.
Cara mencari seluruh hasil perkalian elementer dalam matriks A yang berukuran n x n adalah sebagai berikut.
1. Tulislah bentuk a1.,a2.,a3.,....,an.
2. Tanda dalam bentuk tersebut di ganti dengan seluruh permutasi (j1,j2,j3,....jn)
maka tentulah di dapat n. Hasil perkalian elementer.
Contoh : a11 a12 a13
Dipunyai matriks a = a21 a22 a23 a31 a32 a33
maka kita tuliskan a1.,a2.,a3. Dan permutasi-permutasi dari n = 3 adalah :
(1,2,3,) (2,1,3) (3,1,2) (1,3,2) (2,3,1) (3,2,1)
Hasil perkalian elemennya adalah :
(1,2,3) a11 a22 a33
(2,1,3) a12 a21 a33
Sebuah hasil perkalian elementer bertanda dari A adalah sebuah hasil perkalian
elementer (a1.,a2.,...an) yang di kalikan dengan + 1 jika permutasinya genap dan
dikalikan dengan – 1 jika permutasinya ganjil. Contoh :
Untuk matrisk A yang berukuran 3 x 3,maka hasil perkalian bertanda dari a11 a23 a 32 adalah – a11 a23 a32 (karena permutasi yang bersesuaian adalah (1,3,2)
yang merupakan permutasi ganjil. Definisi 6.
A adalah matriks bujur sangkar. Determinan matriks A yang di simbolkan det (A) dapat di definisikan sebagai jumlahan semua hasil perkalian elementer bertanda dari matriks A.
Definisi di atas apabila di notasikan akan berbentuk : Det(A) = ∑ ± a1j1 a2j2 a3j3 . . .an jn
(j1j2jn)
Contoh :
Hasil untuk pencarian determinan akan di jabarkan dalam bagian berikut ini :
Untuk n = 2
permutasi invers hasil perkalian elementer
bertanda
(1,2) 0 a11 a22
(2,1) 1 -a12 a21
Jadi,det (A) = a11 a22 – a12 a21
2. Menghitung Determinan dengan Operasi Baris Elementer
Determinan suatu matriks dapat di hitung dengan menggunakan operasi baris elementer yang telah di perkenalkan pada bab sebelumnya .Perhitungan
A = A11 A12 A21 a22
determinan suatu matriks dapat di lakukan dengan mudah apabila kita mengenal sifat-sifat atau teorema yang berhubungan dengan determinan.
Teorema-teorema yang berhubungan denga determinan adalah sebagai berikut :
Teorema 1.
Apabila A adalah suatu matriks yang berukuran n x n dan memuat sebuah baris (kolom) yang elemenya semua nol,maka det(A) = 0.
Contoh : 1 2 1 -1 det 3 -1 2 0 = 0 0 0 0 0 -1 -1 2 1 Teorema 2.
Apabila A adalah suatu matriks yang berukuran n x n dan terdapat 2 baris (kolom) yang sama maka,det A = 0.
Contoh : 1 -2 3 4 det -2 2 4 4 = 0 1 1 -1 2 1 -2 3 4 Teorema 3.
Jika A adalah matriks segitiga (atas/bawah) yang berukuran n x n,maka det(A)
adalah hasil dari perkalian elemen-elemen di agonal utama,yaitu det (A) = a11 a22 a
33 ...ann.
Contoh :
1 0 0 0 0
0 3 2 -2 = (1)(2)(-3)(2) = - 12 det -3 2 -1 0 0
0 0 -3 1 2 3 -1 2 0
0 0 0 2 7 6 4 2 1
= (1)(-1)(-1)(2)(1) =2 Teorema 4.
Apabila A1 adalah matriks sebagai hasil dari matriks A yang sebuah
baris/kolomnya di kalikan dengan konstanta k,maka det A1) = kdet(A).
Contoh :
1 1 1
Bila A 2 -1 2 ,maka kita dapat menghitung det(B)
1 -2 2 1 1 1
Untuk B 4 -2 4
1 -2 -4
Jelas di hitung bahwa det (A) = 15,maka det (B) = 30 (sebab matriks B di peroleh dari A dengan baris ke dua dari matriks A di kalikan 2).
Teorema 5.
Apabila B1 adalah matriks sebagai hasil dari matriks B ( bila dua baris matriks B
di pertukarkan letak tempatnya,maka det(B1) = -det (B).
Contoh :
Coba tunjukkan dengan perkalian elementer bertanda apakah benar :
1 -2 -4 1 1 1
det 2 -1 2 = -det 2 -1 2 = 15
1 1 1 1 -2 -4
Teorema 6.
Jika C1 adalah matriks yang di hasilkan bila sebuah kelipatan suatu konstanta k ≠ 0
dari 1 baris (kolom) matriks C yang di tambahkan ke baris atau (kolom) yang
lain,maka det (C1) = det (C).
Contoh :
1 1 1 1 1 1
1 -2 -4 1 -2 -4
Sebab matriks di atas di hasilkan dari matriks A dengan operasi baris elementer
yang ke tiga, yaitu R2 R2 + (2) R1 atau perkalian konstanta (2) terhadap baris satu
yang di tambahkan ke baris 2.
Dan akhirnya dari teorema 1 sampai dengan teorema 6, kita akan dapat menghitung determinan matriks dengan lebih cepat secara manual.
3. Sifat-Sifat Determinan Suatu Matriks
Pada bagian berikut ini akan di bahas beberapa sifat determinan sebagai lanjutan dari ke enam sifat determinan yang telah di berikan pada bagian sebelumnya.
Teorema 1.
Bila A adalah matriks yang berukuran n x n,maka :
Det (AT) = det (A)
Contoh :
Elemen matriks ini menggunakan perkalian elementer bertanda
1 2 3 1 -1 2
det -1 0 -1 dan det 2 0 1
2 1 -2 3 -1 -2
Teorema 2.
Misalkan A,A1 dan A2 adalah matriks yang berukuran n x n yang berbeda di dalam
sebuah baris/kolom saja (katankanlah baris/kolom b) dan baris/kolom b dari A2 di
peroleh dari penjumlahan elemen-elemen yang bersesuaian di dalam baris/kolom
b dari matriks A dan matriks A1,maka :
Det (A2) = det (A) + det (A1)
Contoh :
A= 1 1 4 A1= 1 -1 -3 A2= 2 0 1
2 1 1 2 1 1 2 1 1
Teorema 3.
Jika A dan B adalah matriks bujur sangkar dengan ukuran n x n,maka det(AB) = det (A) + det (B).Contoh :
1 3 1 -1 3 1
A= -1 1 0 B = -1 0 0
0 -1 1 1 -1 2
Teorema 4.
Sebuah matriks A yang berukuran n x n merupakan matriks invertilbe jika dan hanya jika det (A) ≠ 0.
Teorema 5.
Jika A merupakan matriks invertible,maka det (A-1) = 1
det (A) Teorema 6.
Diberikan E adalah matriks elementer yang berukuran n x n.
a) Jika E di hasilkan dari pertukaran 2 baris In,maka det (E) = -1.
b) Jika E di hasilkan dari mengalikan satu baris In dengan konstanta k,maka
det (E) = k.
c) Jika E di hasilkan dari penambahan k kali baris kepada baris yang lain dari
In,maka det (E) = 1.
Nilai determinan suatu matriks dapat juga di hitung dengan menggunakan ekspansi kofaktor sebeelum kita menghitung determinan suatu matriks.Namun sebelum itu,perhatikan terlebih dahulu beberapa definisi dan istilah-istilah yang berhubungan dengan kosep perhitungan tersebut.
Definisi 1.
Bila A adalah sebuah matriks bujur sangkar,maka minor elemen aij (disimbolkan
dengan Mij) di definisikan sebagai determinan dari submatriks yang ada setelah
baris ke –i dan kolom ke –j di coret dari A. Nilai (-1)i+j di tuls sebagai C
ij dan dinamakan kofaktor elemen aij.
Jadi, Cij = (-1)i+j Mij.
Contoh : 1 2 1 Diberikan A -1 3 -3 ,maka 2 -2 1 1 2 1 M32 = det -1 3 -3 = det 1 1 = (1)(-3)-(1)(-1) = -3 += -2 2 2 1 -1 -3 Dan C32 = (-1)3+2 M32 = (-1)(-2) = 2 Jadi, C32 = 2 dan M32 = -2. Contoh lain :
Hitunglah determinan matriks A berikut ini : 1 2 1
A = 1 2 3
3 1 1
Dengan menggunakan ekspansi kofaktor baris 1 ekspansi kofaktor baris 2. Jawab :
Perhitungan determinan dengan ekspansi kofaktor baris 1 adalah sebagai berikut : Det(A) = (1) 2 3 -2 1 3 +1 1 2
= (-2)(-8) + 2(-2) -1(2) = 16-4-2 =10 Definisi 2. (Matriks Kofaktor)
Jika A adalah sembarang matriks n x n dan Cik adalah kofaktor dari aij,maka
matriks dengan bentuk : C11 C12 .... C1n
C21 C22 ....C2n
Cn1 Cn2 Cnn
Dinamakan matriks kofaktor dari matriks A. Reduksi Baris
Determinan sebuah matriks dapat di hitung dengan mereduksi matriks menggunakan operasi baris elementer sehingga matriks berada pada bentuk eselon baris.
Defenisi 3.
Matriks adjoin A di simbolkan dengan Ajd(A) adalah transpose dari matriks kofaktor A.
Definisi 4.
Jika A adalah matriks yang berukuran n x n dan A adalah matriks yang invertibel,maka :
A-1 = 1 adj(A)
det(A)
Denga kata lain kita dapat mencari A-1 dengan menggunakan det (A) dan adj (A).
Contoh 1. 3 1 -4
Tentukan A-1,bila A = 6 9 -2 Dengan menggunakan Adj (A).
Jawab : 3 1 -4 maka 6 9 -2 1 2 1
Sedangkan apabila di hitung,maka di dapat det (A) = 43 sehingga : 33 32 31 23 22 21 13 12 11 a a a a a a a a a Contoh 2. A =
Ekspansi melalui baris pertama :
Det(A) = a11C11 + a12C12 + a13C13
Atau ekspansi melalui baris ketiga :
Det(A) = a31 C31 + a32 C32 + a33 C33
Atau ekspansi melalui kolom kedua :
Det(A) = a12C12 + a22C22 + a32C32
5. Penyelesaian SPL dengan Aturan Cramer
Kita dapar menggunakan konsep determinan untuk mendapatkan penyelesaian SPL.caranya adalah dengan menggunakan aturan Cramer.
Aturan Cramer : 13 -9 34 13/43 -9/43 34/43 A-1=1/43 -8 7 -18 = -8/43 7/43 -18/43
Bila Ax = B adalah SPL yang terdiri dari n persaman linier dengan n variabel yang tidak di ketahui dan det (A) ≠ 0,maka SP; tersebut mempunyai penyelesaian tunggal dan penyelesaiaanya adalah :
x1 = det (A1) x2 = det (A2) x3 = det (An)
det (A) det(A) det(A)
Dengan matriks Aj,j = 1,2,4,. . . .,n adalah matriks yang di peroleh dengan
mengganti elemen kolom j dari matriks A dengan matriks : b1
b2
B= b3
bn
Contoh : Dipunyai SPL x + y -2z =1
SPL ini bersesuaian dengan SPL bentuk A x =B 2x – y + z = 2
x -2y – 4z = -4 1 1 -2 x1 1 Dengan A = 2 -1 1 x = x2 dan B = 2 1 -2 -4 x3 -4 1 1 -2
Det (A) = det 2 -1 1 =21 ;det(A1) = det 2 -2 1 = 26
1 -2 -4 -4 -2 -4
1 1 1 1 1 1
Det (A2)=det 2 2 1 =25 ;det(A3)=det 2 -4 2 = 15
1 -4 -4 1 -2 -4
Jadi dengan menggunakan aturan Cramer di dapat :
x = det(A1) = 26 y = det(A2) = 25 z = det(A3) = 15
BAB III PENUTUP
A. Kesimpulan
Determinan adalah suatu fungsi tertentu yang menghubungkan suatu bilangan real dengan suatu matriks bujursangkar. Determinan memiliki penyelesaian, yaitu himpunan angka yang akan memenuhi suatu determinan matriks. Ada beberapa macam penyelesaian determinan di antaranya dengan Ekspansi Kofaktor, Adjoin, Matirks Segitiga, Metode Cramer dan metode – metode lainnya, dan yang paling sering di gunakan yaitu dengan Ekspansi Kofaktor.
B. Saran
Dalam menyusun makalah ini, penulis menyadari sepenuhnya bahwa isi makalah ini belumlah sempurna dan masih kurang baik mengenai materi maupun cara penulisannya. Oleh karena itu, penulis sangat mengharapkan kritik dan saran yang sifatnya membangun dari pihak lain yang dapat menyempurnakan makalah ini. Dan alangkah baiknya juga apabila kita terus mengembangkan berbagai makalah-makalah tentang Pengetahuan Aljabar Linier Elementer di tengah-tengah masyarakat luas secara khusus dalam mahasiswa agar lebih mengerti bagaimana langkah-langkah yang lebih mudah dalam memecahkan suatu masalah dalam suatu determinan pada Aljabar Linier.
DAFTAR PUSTAKA
Buku :
Dasar-Dasar Aljabar Linear Jilid 1 Dasar-Dasar Aljabar Linear Jilid 2 Aljabar Linear Elementer
Sumber Lain :
www.wikipedia.com www.google.co .id