EKSEKUSI OPTIMAL TRANSAKSI PORTOFOLIO
DENGAN MODEL BIAYA LINEAR
RIMA FEBRIAN
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2009
ABSTRACT
RIMA FEBRIAN. Optimal Execution of Portfolio Transaction with Linear Cost Model. Supervised by RETNO BUDIARTI and DONNY CITRA LESMANA.
In investment, wealth is allocated by forming portfolio which consists of risk free and risky assets (stocks). There are some factors that influence portfolio transaction, i.e. volatility risk and transaction costs. The aim of portfolio transaction is to produce a future cash flow in terms of dividend and capital gain. The cash flow is obtained by constructing an optimal portfolio subject to minimum risk of trading strategies. Optimal portfolio can be formed by minimizing cost function, which is a combination of volatility risk and transaction costs arising from permanent and temporary market impact. This optimization can also generally be done by minimizing implementation of shortfall costs using linear market impact cost model. The construction of efficient strategies for optimal portfolio is obtained by a constrained optimization problem that minimize the expected value of implementation shortfall for any levels of maximum implemented shortfall variance. The constrained optimization problem can be solved using Lagrange multiplier, so that the unconstrained optimization problem will minimize cost function. Cost function is assumed to be a quadrature, which is strictly convex for any positive risk levels. Therefore, by solving the optimization problem, one can obtain explicit trajectories of optimal strategies. By solving initial value problem of difference equation, one can obtain the specific optimal solution of a trading trajectory, and for each risk aversion there is a unique corresponding trading trajectory that minimize cost function.
Key words: volatility risk, market impact, implementation shortfall, trading trajectory, trading strategy, cost function.
ABSTRAK
RIMA FEBRIAN. EKSEKUSI OPTIMAL TRANSAKSI PORTOFOLIO DENGAN MODEL BIAYA LINEAR. Dibimbing oleh RETNO BUDIARTI dan DONNY CITRA LESMANA.
Dalam melakukan investasi, kekayaan dialokasikan dengan membentuk portofolio yang terdiri atas aset bebas risiko dan aset berisiko (saham). Faktor-faktor yang mempengaruhi transaksi portofolio diantaranya risiko volatilitas dan biaya transaksi. Transaksi portofolio bertujuan untuk menghasilkan aliran pendapatan di masa depan baik dividen maupun capital gain, dan aliran pendapatan diperoleh dengan menghasilkan portofolio optimal yaitu mencari strategi perdagangan yang memiliki risiko minimum. Portofolio optimal dapat dibentuk dengan cara meminimumkan fungsi biaya yang terdiri atas kombinasi risiko volatilitas dan peningkatan biaya transaksi yang berasal dari dampak pasar permanen dan temporer atau secara umum meminimumkan biaya implementasi shortfall. Dengan asumsi model biaya dampak pasar linear, konstruksi suatu strategi efisien portofolio optimal dapat dilakukan dengan menyelesaikan masalah optimisasi berkendala yaitu meminimumkan nilai harapan implementasi shortfalluntuk setiap tingkat ragam implementasi shortfallmaksimum. Masalah kendala optimisasi tersebut dapat diselesaikan dengan menggunakan pengali lagrange, sehingga masalah optimisasi menjadi tak berkendala yaitu meminimumkan fungsi biaya. Fungsi biaya adalah fungsi kuadratur, berupa strictly convex untuk setiap tingkat risiko positif. Dari penyelesaian masalah optimisasi diperoleh konstruksi eksplisit strategi optimal transaksi portofolio. Dengan menyelesaikan masalah nilai awal suatu persamaan beda, didapat solusi spesifik trayektori perdagangan dan strategi perdagangan optimal dan untuk setiap tingkat risiko (risk aversion) yang diberikan ada korespondensi trayektori perdagangan yang unik dengan fungsi biaya adalah minimum.
EKSEKUSI OPTIMAL TRANSAKSI PORTOFOLIO
DENGAN MODEL BIAYA LINEAR
RIMA FEBRIAN
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2009
Judul Skripsi : Eksekusi Optimal Transaksi Portofolio dengan Model Biaya Linear
Nama
: Rima Febrian
NIM
: G54050424
Disetujui
Komisi Pembimbing
Ir. Retno Budiarti, MS.
Pembimbing I
Donny Citra Lesmana, S.Si., M.Fin.Math.
Pembimbing II
Diketahui
Dr. drh. Hasim, DEA.
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
PRAKATA
Segala puji bagi Allah SWT, subhanallah atas segala karunia dan nikmat-Nya yang agung sehingga penulis dapat menyelesaikan tugas akhir yang berjudul Eksekusi Optimal Transaksi Portofolio dengan Model Biaya Linear. Shalawat dan salam semoga senantiasa tercurah kepada junjungan kita Nabi Muhammad SAW yang membawa kebenaran bagi umat manusia dan rahmat bagi seluruh alam.
Kenangan yang mendalam terukir begitu indah di dalam mozaik perjalanan pembelajaran selama penyusunan tugas akhir ini, begitu banyak pihak yang telah memberikan kontribusi baik secara langsung maupun tidak langsung sehingga tugas akhir ini dapat diselesaikan. Untuk itu, penulis ingin mengucapkan terima kasih yang tidak terhingga kepada:
1. Allah SWT, sungguh tangan cinta dan kesempurnaan-Mu begitu syahdu kepada setiap hamba-Mu. 2. Ibu Retno Budiarti, sebagai pembimbing I yang begitu sabar, teliti, dan banyak berbagi ilmu
selama penyusunan tugas akhir ini. Berawal dari tulisan yang tidak jelas susunannya, sehingga tulisan ini menjadi bermakna. Bapak Donny Citra Lesmana, sebagai pembimbing II yang tetap bersemangat di tengah menjelang keberangkatan studynya direpotkan untuk memberikan bimbingan. Ibu Endar Hasafah Nugrahani, sebagai penguji atas kebaikan, saran dan masukan yang diberikan.
3. Bapak dan emak yang sangat aku sayangi, terima kasihku tiada terkira untuk semua yang telah dilakukan, doa, restu, kasih sayang, semangat, baik moral dan materil. Semoga Allah SWT membalas dengan surga-Nya. Amin. Hujan yang tetes-tetesnya tidak pernah berhenti memberikan kesegarannya dalam hidupku, kesegaran di tengah kegersangan hati. Tetes-tetes yang jatuhannya menyejukkan jiwa yang haus akan cinta, tetes-tetes yang memberikan tawa dan air mata, hingga hidup ini begitu lengkap penuh warna. Teh lulus, Teh Yayu, A Fiek, Bang Edi, atas doa, dukungan moral dan materil nya, serta seluruh keluarga besar ku.
4. Seluruh dosen Departemen Matematika IPB, yang telah memberikan ilmu yang tak ternilai semoga ilmu ini dapat diamalkan dan memberikan manfaat untuk hidup nantinya. Amin.
5. Bu Susi, Pak Yono, Bu Ade, Mas Bono, Mas Deni, Mas Hery, dan seluruh staf Tata Usaha Departemen Matematika untuk semua informasi, saran dan masukan yang telah diberikan.
6. Mba Mirani terima kasih untuk kasih dan sayangmu, doa dan motivasimu yang begitu tulus. Mb Mir yang menjadi sahabat sekaligus kakak untukku. Semoga Allah SWT senantiasa menyayangimu.
7. Mb Titi, Tia, Siti, Pipit, Lela, Mba Lina, Yuni, Nofita, Dewi, Ety, yang telah berbagi banyak hal selama ini, persahabatan ini semoga diridhai-Nya.
8. Lela, Dewi, dan Mas Awi yang bersedia menjadi pembahas pada saat seminar, terima kasih untuk waktu dan fikiran yang telah diberikan.
9. Keluarga besar Matematika ’42 : Mirani, Pipit, Lela, Tia, Bude, Siti, Lina, Nofi, Yuni, Dewi, Eko, Mocco, Mas Warno, Awi, Sapto, Qnun, Ardy, Danu, Dendi, Dian, Zil, Eyyi, Oby, Lisda, Ety, Yusep, Nyoman, Mega, Idha, Niken, Bima, Ilyas, Vera, Anto, Gita, Octa, Hikmah, Hap-hap, Ocoy, Nola, Agnes, Ricken, Vita, Luri, Ryu, Rita, Ridwan, Rendi, Djawa, Jane, Vino, Heri, Ayu, Achy, Hesti, Fachri, Bayu, Septian, mas Ayeep, Erlin, Boy, Yudi, Wiwi, Kak Mukhtar, dan Acuy terima kasih telah memberikan warna untuk pelangi hidupku ini.
10. Kakak dan Adik Kelas di Departemen Matematika, untuk semua bantuan, motivasi, dan informasinya. Serta semua pihak yang telah banyak membantu dalam penyelesaian tugas akhir ini, karena keterbatasan penulis haturkan maaf tidak dapat menyebutkan satu per satu.
Penulis menyadari masih ada kekurangan dalam penyusunan tugas akhir ini. Oleh karena itu, kritik dan saran dari berbagai pihak sangat membantu dalam penyempurnaan tugas akhir ini. Akhir kata, semoga karya ilmiah ini dapat memberikan manfaat bagi kita semua.
Bogor, September 2009
RIWAYAT HIDUP
Penulis dilahirkan di Bogor pada tanggal 08 Februari 1987 sebagai anak keempat dari empat bersaudara, anak dari pasangan Amir Hamzah dan Nyai Rosyidah.
Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1999 di Madrasah Ibtidaiyah Mathla’ul Anwar (MIMA) Pilar Kec. Leuwisadeng Kab. Bogor, Madrasah Tsanawiyah Negeri Model Babakansirna Kec. Leuwisadeng Kab. Bogor pada tahun 2002, Sekolah Menengah Atas Negeri 1 Leuwiliang Kab. Bogor pada tahun 2005, dan diterima menjadi mahasiswa Institut Pertanian Bogor melalui jalur Ujian Saringan Masuk IPB (USMI) pada tahun yang sama. Pada tahun 2006 diterima sebagai mahasiswa Departemen Matematika Fakultas Matematika dan IPA Institut Pertanian Bogor.
Selama menjadi mahasiswa, pada tahun pertama penulis tergabung dalam kepengurusan Kerohanian Islam (Rohis) Kelas Tingkat Persiapan Bersama sebagai bendahara, pada tahun kedua tergabung dalam kepengurusan Rohis Kelas Matematika angkatan 42 sebagai bendahara dan Himpunan Profesi Gugus Mahasiswa Matematika (GUMATIKA) sebagai anggota divisi kerohanian Lingkar Muslim Matematika (LIMIT) periode 2006-2007. Pada tahun ketiga, penulis tergabung dalam kepengurusan Serambi Ruhiyah Mahasiwa FMIPA (SERUM-G) sebagai anggota divisi keputerian periode 2007-2008. Selain mengikuti organisasi, penulis juga pernah menjadi pengajar privat mahasiswa Tingkat Persiapan Bersama untuk mata kuliah Pengantar Matematika dan Kalkulus. Pada tahun 2009 penulis menjadi pengajar SMP dan SMA pada lembaga bimbingan belajar di Bogor sampai sekarang.
DAFTAR ISI
Halaman DAFTAR ISI ... ix DAFTAR TABEL ... x DAFTAR GAMBAR ... x DAFTAR LAMPIRAN ... x I PENDAHULUAN ... 1 1.1. Latar Belakang ... 1 1.2. Tujuan penulisan ... 1 1.3. Metode Penulisan ... 1 1.4. Sistematika Penulisan ... 2 II LANDASAN TEORI ... 22.1 Sekuritas dan Portofolio ... 2
2.2 Percobaan Acak ... 2
2.3 Ruang Contoh ... 2
2.4 Peubah Acak ... 2
2.5 Fungsi Sebaran ... 3
2.6 Fungsi Massa Peluang ... 3
2.7 Nilai Harapan, Ragam, Peragam, dan Koefisien Korelasi Peubah Acak Diskret ... 3
2.8 Kebebasan ... 4
2.9 Convex dan Strictly Convex ... 4
2.10 Sign Function... 5 2.11 Pengali Lagrange ... 5 2.12 Persamaan Beda ... 5 2.13 Trigonometri Hiperbolik ... 7 III PEMODELAN ... 7 3.1 Model Perdagangan ... 7
3.1.1 Definisi Strategi Perdagangan ... 7
3.1.2 Dinamika Harga ... 8
3.1.3 Capturedan Biaya Trayektori Perdagangan ... 9
3.2 Efisien FrontierEksekusi Optimal ... 9
IV PEMBAHASAN ... 10
4.1 Dampak Pasar Permanen ... 10
4.2 Dampak Pasar Temporer ... 12
4.3 Konstruksi Eksplisit dari Strategi Optimal ... 12
V ILUSTRASI ... 13 5.1 Pemilihan Parameter ... 13 5.2 Struktur Frontier ... 17 VI SIMPULAN ... 17 DAFTAR PUSTAKA ... 18 LAMPIRAN ... 19
DAFTAR TABEL
Halaman
1. Parameter dan nilai yang dipilih untuk simulasi konstruksi portofolio optimal ... 14
2. Hasil simulasi konstruksi portofolio optimal dengan menggunakan parameter tertentu untuk
106 ... 143. Hasil simulasi konstruksi portofolio optimal dengan menggunakan parameter tertentu untuk 0 ... 15
4. Hasil simulasi konstruksi portofolio optimal dengan menggunakan parameter tertentu untuk
2 107 ... 16DAFTAR GAMBAR
Halaman 1. Ilustrasi Fungsi Convex... 52. Ilustrasi Fungsi Trigonometri Hiperbolik ... 7
3. Ilustrasi Dampak Pasar ... 8
4. Trayektori A optimal untuk
106 ... 155. Trayektori B optimal untuk 0 ... 15
6. Trayektori C optimal untuk
2 107 ... 167. Trayektori A, B, dan C optimal ... 16
8. FrontierEfisien ... 17
DAFTAR LAMPIRAN
Halaman 1. Penghitungan Nilai Harapan Implementasi Shortfall ... 192. Penghitungan Ragam Implementasi Shortfall ... 20
3. Penghitungan Nilai Harapan Total Implementasi Shortfalluntuk Fungsi Dampak Pasar Permanen dan Temporer ... 21
4. Konstruksi Eksplisit Strategi Optimal ... 22
5. Konstruksi Eksplisit Strategi Optimal ... 23
6. Konstruksi Eksplisit Strategi Optimal ... 24
7. Konstruksi Eksplisit Strategi Optimal untuk Solusi Spesifik Trayektori Perdagangan ... 25
8. Konstruksi Eksplisit Strategi Optimal untuk Solusi Spesifik Daftar Perdagangan ... 27
I. PENDAHULUAN
1.1 Latar Belakang
Dalam melakukan investasi, kekayaan dialokasikan dengan membentuk portofolio, yang terdiri atas aset bebas risiko dan aset berisiko (saham).
Ada beberapa faktor yang mempengaruhi transaksi portofolio, di antaranya risiko volatilitas dan biaya transaksi.
Risiko volatilitas yaitu risiko dalam nilai portofolio yang tidak dapat diprediksi dalam volatilitas aset yang mendasarinya (Bodie et al 2006). Adapun biaya transaksi ini terdiri atas biaya yang berasal dari dampak pasar permanen dan temporer.
Dalam kondisi normal, risiko investasi dapat diprediksi melalui kinerja perusahaan yang tercermin dalam harga saham. Jika aktivitas perusahaan menunjukkan pertumbuhan yang prospektif maka harga sahamnya akan mengalami kenaikan. Saham-saham dari perusahaan dengan pertumbuhan seperti itu dapat memberikan capital gain. Capital gain adalah keuntungan yang diperoleh pemegang saham selain dividen jika harga jual sahamnya melebihi harga belinya. Adapun dividen adalah bagian dari laba perusahaan yang dibagikan kepada pemegang saham.
Setiap waktu, harga saham berfluktuasi naik-turun. Fluktuasi harga saham inilah yang merupakan risiko investasi saham karena menjadikan ketidakpastian tingkat keuntungan (return).
Standar deviasi lebih dikenal dengan nama volatilitas. Secara intuitif, volatilitas adalah ukuran jumlah dan intensitas fluktuasi harga (Chriss NA 1997). Untuk harga saham yang bersifat volatil, maka fluktuasinya lebih sering dan lebih kuat. Ini berlawanan secara proporsional dengan jumlah informasi yang kita miliki mengenai harga saham yang akan datang.
Untuk memperoleh keuntungan, seorang investor yang akan membeli saham dari suatu perusahaan harus melakukan analisis terhadap nilai sahamnya. Analisis seperti ini terbagi atas dua bagian, yaitu
1. Analisis teknikal, yaitu metode analisis yang berdasarkan diagram/grafik dari harga saham. Metode ini dilakukan dengan cara membandingkan gerakan harga saham saat ini dengan gerakan harga saham di masa lalu untuk memprediksi harga saham di masa depan yang logis. Dasar dari analisis teknikal adalah diagram/grafik dari gerakan harga saham.
2. Analisis fundamental, yaitu metode analisis yang berdasarkan fundamental ekonomi suatu perusahaan. Metode ini menitikberatkan pada rasio finansial dan kejadian-kejadian yang secara langsung maupun tidak langsung mempengaruhi kinerja keuangan perusahaan.
Kedua analisis tersebut bertujuan untuk memprediksi aliran pendapatan di masa depan baik dividen maupun capital gain. Aliran pendapatan diperoleh dengan menghasilkan portofolio optimal, yaitu mencari strategi perdagangan yang memiliki risiko minimum di antara semua portofolio yang memiliki keuntungan (expected return) yang sama.
Dalam karya ilmiah ini, akan dibahas mengenai analisis eksekusi optimal suatu transaksi portofolio yang bertujuan untuk meminimumkan kombinasi risiko volatilitas dan peningkatan biaya transaksi dari dampak pasar permanen dan temporer, dengan asumsi model biaya linear.
1.2 Tujuan Penulisan
Tujuan dari penulisan karya ilmiah ini adalah untuk menunjukkan analisis fundamental eksekusi optimal dari transaksi portofolio dengan asumsi model biaya linear, sehingga diperoleh perumusan mengenai strategi eksekusi optimal suatu transaksi portofolio.
1.3 Metode Penulisan
Metode penulisan karya ilmiah ini berupa studi literatur. Untuk studi literatur, materi diperoleh dari jurnal ilmiah utama dan jurnal-jurnal ilmiah lain, serta buku-buku yang terkait dengan penyusunan karya ilmiah ini. Materi jurnal ilmiah utama diadaptasi dari jurnal ilmiah yang berjudul Optimal Execution
of Portfolio Transactions (Almgren & Chriss 2000).
1.4 Sistematika Penulisan
Karya ilmiah ini terdiri atas enam bagian. Bagian pertama berupa pendahuluan, terdiri atas latar belakang, tujuan penulisan, metode penulisan, dan sistematika penulisan. Bagian kedua adalah landasan teori yang menyajikan aspek teoritis penulisan karya ilmiah. Bagian ketiga merupakan pemodelan, yang menampilkan model perdagangan dan efisien
frontierstrategi optimal yang akan dilakukan analisis eksekusi optimal transaksi portofolio, bagian keempat adalah pembahasan yang membahas analisis fundamental eksekusi optimal suatu transaksi portofolio. Bagian kelima adalah ilustrasi, yang menampilkan hasil simulasi transaksi portofolio optimal untuk parameter yang dipilih, dan yang keenam adalah simpulan, merupakan hasil yang diperoleh dari pembahasan karya ilmiah.
II LANDASAN TEORI
Landasan teori menyajikan aspek teoritisyang menjadi landasan penulisan karya ilmiah ini. Landasan teori menjelaskan mengenai definisi-definisi dasar, lema, dan beberapa teori penting.
2.1 Sekuritas, dan Portofolio Definisi 2.1.1 (Sekuritas)
Sekuritas dalam pasar modal Indonesia dikenal dengan sebutan efek adalah instrumen yang menjanjikan pembayaran di masa depan.
Sekuritas atau efek diterbitkan oleh institusi yang dijual pertama kali ke publik dengan bantuan perantara keuangan seperti perbankan investasi (penjamin emisi) yang menjualkan sekuritas ke publik.
Sekuritas terdiri atas berbagai macam bentuk, yaitu surat utang (obligasi), kepemilikan perusahaan (saham), dan bentuk-bentuk turunan lain seperti kontrak berjangka, dan kontrak opsi.
(Bodieet al2006)
Definisi 2.1.2 (Portofolio)
Portofolio didefinisikan sebagai koleksi atau kumpulan dari berbagai macam sekuritas.
(Bodieet al2006)
2.2 Percobaan Acak
Definisi 2.2.1 (Percobaan Acak)
Percobaan acak adalah suatu percobaan yang dapat diulang dalam kondisi yang sama, yang hasil percobaannya tidak dapat ditebak dengan tepat, tetapi dapat diketahui semua kemungkinan hasil yang muncul.
(Craig, Hogg, & McKean 2005)
2.3 Ruang Contoh
Definisi 2.3.1 (Ruang Contoh)
Ruang contoh adalah himpunan semua kemungkinan yang dapat terjadi dari suatu percobaan acak, dinotasikan dengan .
(Ghahramani 2005)
2.4 Peubah Acak
Definisi 2.4.1 (Peubah Acak)
Misalkan adalah ruang contoh dari suatu percobaan acak. Fungsi X yang terdefinisi pada
yang memetakan setiap unsur ke satu dan hanya satu bilangan real X
x disebut peubah acak. Ruang dari X adalah himpunan bagi bilangan real A
x x: X
,
.Dalam melakukan analisis portofolio, para
investor berhadapan dengan ketidakpastian saat mereka berinvestasi. Karena banyak sekali kemungkinan yang akan terjadi, maka para investor tidak melihat setiap kemungkinan yang mempunyai peluang untuk terjadi secara rinci, tetapi cukup dengan melihat parameter, yaitu nilai-nilai yang menjadi ciri dari analisa yang mereka lakukan.
Peubah acak mempunyai parameter-parameter, di antaranya nilai tengah, ragam, peragam, dan koefisien korelasi. Dalam lingkup portofolio, jika analisis yang dimaksud adalah proses meminimumkan kombinasi risiko volatilitas dan peningkatan biaya transaksi dari dampak pasar permanen dan temporer, maka peubah acak berkaitan dengan biaya transaksi, adapun parameter-parameternya yaitu nilai harapan biaya transaksi, dan ragam biaya transaksi.
Definisi 2.4.2 (Peubah Acak Diskret)
Peubah acak X dikatakan peubah acak diskret jika nilai peubah acak
x x1, ,...2
merupakan himpunan tercacah.(Grimmett & Stirzaker 1992)
2.5 Fungsi Sebaran
Definisi 2.5.1 (Fungsi Sebaran)
Jika X suatu peubah acak, fungsi sebaran didefinisikan sebagai F xX( )P X( x) untuk setiap x
,
.(Ghahramani 2005)
2.6 Fungsi Massa Peluang
Definisi 2.6.1 (Fungsi Massa Peluang)
Fungsi massa peluang p suatu peubah acak X yang memiliki himpunan semua nilai kemungkinan
x x1, ,...2
didefinisikan sebagai suatu fungsi darike yang memenuhi sifat berikut : a. p x( ) 0 ; jika x
x x1, ,...2
b. p x( )i P X( xi) dan p x( ) 0i , (i1, 2,3,...) c. 1 ( ) 1i i p x
(Ghahramani 2005)2.7 Nilai Harapan, Ragam, Peragam, dan Koefisien Korelasi Peubah Acak Diskret Definisi 2.7.1 (Nilai Harapan)
Jika X adalah peubah acak yang memiliki fungsi massa peluang p xX( ), maka didefinisikan nilai harapan peubah acak
, ( ) X E X adalah: ( ) X( ) x E X
xp x (1) (Bain 1992) Definisi 2.7.2 (Ragam)Jika X adalah peubah acak yang memiliki nilai harapan E X( ), maka didefinisikan ragam peubah acak X, 2 X adalah:
2 2 ( ) X E X E X (2) (Bain 1992) Definisi 2.7.3 (Peragam)Jika X dan Y adalah peubah acak yang memiliki nilai harapan berturut-turut E X( )dan
( )
E Y , maka didefinisikan peragam antara peubah acak Xdan peubah acak Yadalah:
cov( , )X Y E X E X Y E Y[ ( )][ ( )] (3) atau
cov( , )X Y E XY( )E X E Y( ) ( ) (4) (Bain 1992)
Definisi 2.7.4 (Koefisien Korelasi)
Jika X dan Y adalah peubah acak yang memiliki standar deviasi berturut-turut X dan
Y
, serta peragam antara peubah acak X dan peubah acak Y adalah cov( , )X Y maka didefinisikan koefisien korelasi antara peubah acakX dan peubah acak Yadalah:
cov( , ) XY X Y X Y (5) (Bain 1992)
Teorema 2.7.5
Untuk peubah acak X X1, 2,...,Xn didefinisikan pada ruang contoh yang sama
1 1 ( n i i) n i ( )i i i E X E X
. (14) (Ghahramani 2005) CorollaryMisalkan X X1, 2,...Xn suatu peubah acak
pada ruang contoh yang sama, maka: 1 2 ( ... n) E X X X 1 2 ( ) ( ) ... ( n) E X E X E X . (15) (Ghahramani 2005) Teorema 2.7.6
Jika Xdan Y peubah acak yang saling bebas, maka:
a. E XY( )E X E Y( ) ( ) (7) b. Cov X Y( , ) 0 . (8) JikaXdan Y peubah acak dengan adan b konstanta maka :
c. E X Y( )E X( )E Y( ) (9) d. E aX b( )aE X( )b. (10) (Bain, 1992)
Teorema 2.7.7
Jika Xadalah suatu peubah acak yang bernilai konstan, maka jika P X( c) 1 untuk suatu konstanta cmaka
( )
E X c. (11) (Ghahramani 2005)
Teorema 2.7.8
Misalkan X adalah peubah acak diskret dengan himpunan nilai peluang A dan fungsi massa peluang p x( ), dan misalkan g adalah fungsi bernilai real maka g X( )adalah peubah acak dengan: [ ( )] ( ) ( ) x A E g X g x p x
. (12) (Ghahramani 2005) CorollaryMisalkan X adalah peubah acak diskret, 1, ,...,2 n
g g g adalah fungsi bernilai real dan
misalkan 1, 2,...,n adalah bilangan real, maka 1 1 2 2 [ ( ) ( ) ... n n( )] E g X g X g X 1E g X[ ( )]1 2E g X[ ( )] ...2 nE g X[ ( )].n (13) (Ghahramani 2005) 2.8 Kebebasan Definisi 2.8.1 (Kebebasan)
Peubah acak X1,...,Xn saling bebas jika
1,... n( ,..., )1 1( ) ...1 n( )
X X n X X n
f x x f x f x untuk semua x1,...,xn. (6)
(Helms 1997)
2.9 (Convexdan Strictly Convex)
Definisi 2.9.3 (Himpunan Convex)
Suatu himpunan S di n disebut
himpunan convex jika untuk setiap x dan y di S, segmen garis yang menghubungkan x dan y juga terletak di S.
(Peressini et al1988)
Definisi 2.9.4 (Convex)
Suatu fungsi f x( ) : n disebut
fungsi convexdi S jika
(1 )
( ) (1 ) ( ) f tx t y tf x t f y, n
x y
, dan t
0,1 .(Sydsaeter & Hammond 1995)
Definisi 2.9.5 (Strictly Convex)
Suatu fungsi ( ) : n
f x disebut
fungsi strictly convexdi S jika
(1 )
( ) (1 ) ( ) f tx t y tf x t f y xy dan t
0,1 .Gambar 1 Ilustrasi fungsi convex
2.10 Sign Function
Definisi 2.10.1 (Sign Function)
Sign function dari bilangan real x didefinisikan sebagai: 1, jika 0 sign( ) 0, jika 0 1, jika 0 x x x x (Shirokov 1979) 2.11 Pengali Lagrange
Suatu metode untuk memperoleh nilai-nilai maksimum relatif atau minimum relatif dari fungsi f x y( , ) yang dipengaruhi oleh kondisi persyaratan g x y( , ) 0 , terdiri atas pembentukan fungsi penolong.
( , , ) ( , ) ( , ) F x y f x y g x y dengan syarat: 0 F x , 0 F y , 0 F yang merupakan
syarat perlu untuk maksimum relatif maupun minimum relatif.
Parameter yang tidak bergantung pada x dan y disebut pengali lagrange.
Kasus dengan satu pengali lagrange
Untuk suatu masalah yang melibatkan satu persyaratan, diperlukan hanya satu parameter
sebagai pengalilagrange.
Jika f x y( , ) adalah fungsi yang ditentukan maksimum atau minimum relatifnya dan g x y( , ) 0 adalah persyaratan yang harus dipenuhi, maka fungsi penolongnya berbentuk :
( , , ) ( , ) ( , ) F x y f x y g x y
Fungsi penolong F x y( , , ) adalah fungsi dari tiga variabel x y, , dan .
Dapat ditunjukkan bahwa suatu maksimum relatif atau minimum relatif dari F adalah juga merupakan maksimum atau minimum relatif dari f x y( , ) dengan persyaratan g x y( , ) 0 , maka harus dipenuhi persyaratan: 0 0 ( , ) 0 F f g x x x F f g y y y F g x y
Setiap penyelesaian dari sistem persamaan ini adalah suatu nilai kritis dari fungsi
( , ). f x y
(Soemartojo 1987)
2.12 Persamaan Beda (Difference
Equation)
Konsep persamaan beda digunakan dalam analisis sistem dinamik dengan variabel diskret untuk menunjukkan dinamika/perubahan suatu variabel pada periode tertentu. Untuk fungsi y t
, nilaiyberubah bila nilai t berubah dari integer yang satu ke integer berikutnya, misalnya t1, t2, t3, dan seterusnya. Pola perubahan y digambarkan dengan istilah ‘beda’ (difference).Misalkan y menunjukkan besarnya perubahan y pada dua periode berurutan, sehingga dapat ditulis y yt1ytdengan
t
y adalah nilai ypada periode ke-t, dan yt1 adalah nilai y pada satu periode setelah periode ke-t. Bentuk di atas dapat ditulis
1 t t y y y 2 1 t t y y y 3 2 t t y y y dan seterusnya.
Misalkan 0 t T , maka kita dapat menyatakan yT dalam yT1hingga y0.
Hal yang sama berlaku juga sebaliknya, dalam hal ini jika persamaan berbentuk
1
t t
y y y.
Definisi 2.12.1 (Persamaan beda orde-1)
Persamaan beda orde-1 adalah persamaan beda yang melibatkan ekspresi yt yang
disebut beda ke-1, dan hanya melibatkan lag waktu satu periode.
(Chiang & Wainwright 2005)
Penyelesaian persamaan beda orde-1
Misalkan diberikan persamaan beda orde-1 1
t t
y ay c
dengan a dan c adalah konstanta. Solusi umum terdiri atas penjumlahan dua komponen, yaitu solusi partikular yp yang
merupakan solusi dari persamaan tak homogen lengkap, dan fungsi komplemen yc yang merupakan solusi umum dari persamaan
1 0.
t t
y ay
Penjumlahan yp dan ycmerupakan solusi
umum, dan diperlukan pemberian nilai awal untuk memperoleh solusi khusus persamaan beda.
Misalkan solusi persamaan beda berbentuk
t t y Ab (Abt 0), berarti 1 1 t t y Ab sehingga persamaan homogennya menjadi
1 0
t t
Ab aAb , dengan menghilangkan faktor taknol Abt diperoleh
0
b a atau b a
maka fungsi komplemennya dapat dituliskan sebagai
( t) ( )t c
y Ab A a
Untuk menentukan solusi partikular, misalkan solusi paling sederhana berbentuk
t
y k dan yt1 k dengan k suatu konstanta. Substitusikan nilai ini ke dalam persamaan yt1ayt c sehingga , ( 1) 1 k ak c c k a a
maka diperoleh solusi partikular ( ) ( 1). 1 p c y k a a
Solusi umum persamaan beda dapat dihitung dengan menjumlahkan solusi partikular yp dan fungsi komplemen yc
sehingga ( ) 1 t t c y A a a dengan a1.
(Chiang & Wainwright 2005)
Definisi 2.12.2 (Persamaan beda orde-2)
Persamaan beda orde-2 adalah persamaan beda yang melibatkan ekspresi 2
t
y
yang disebut beda ke-2 dari yt, tetapi tidak mengandung beda yang orde-nya lebih tinggi dari 2. Didefinisikan 2 1 2 1 1 2 1 ( ) ( ) = ( ) ( ) = 2 . t t t t t t t t t t t y y y y y y y y y y y
(Chiang & Wainwright 2005)
Penyelesaian persamaan beda orde-2
Misalkan persamaan beda orde-2 2 1 1 2
t t t
y a y a y c
merupakan persamaan beda linear tak homogen dengan koefisien konstan ( , )a a1 2 dan konstanta c.
Solusi partikular
Misalkan yt k dan yt1k. Substitusikan nilai konstanta y ke dalam persamaan yt2a y1 t1a y2 t c, diperoleh 1 2 1 2 1 2 (1 0) 1 k a k a k c c k a a a a sehingga 1 2 ( ) . 1 p c y k a a Fungsi komplemen
Persamaan beda homogen berbentuk
2 1 1 2 0
t t t
y a y a y
Misalkan solusi berbentuk t t y Ab maka 1 1 t t y Ab , dan 2 2 t t y Ab . Substitusikan t t y Ab , 1 1 t t y Ab dan 2 2 t t y Ab pada persamaan 2 1 1 2 0 t t t y a y a y
sehingga persamaan menjadi
2 1
1 2 0
t t t
Ab a Ab a Ab .
Dengan menghilangkan faktor taknol
t
Ab diperoleh persamaan karakteristik 2
1 2 0
b a b a , yang memiliki dua akar karakteristik 2 1 1 2 1 2 4 , . 2 a a a b b
Berdasarkan karakteristik akar pada akar
kuadrat dengan ekspresi
2 1 1 2 1 2 4 , 2 a a a
Kasus 1: Akar real berbeda
Ketika 2 1 4 2
a a , persamaan beda memiliki akar real berbeda. Fungsi komplemen dapat ditulis sebagai kombinasi linear berbentuk
1 1 2 2
t t
c
y A b A b
Kasus 2 : Akar real sama
Ketika 2 1 4 2
a a , persamaan beda memiliki akar real sama
1 1 2 ( ) 2 a b b b .
Fungsi komplemennya memiliki bentuk
3 4
t t
c
y A b A tb
Kasus 3 : Akar kompleks
Ketika 2 1 4 2
a a , persamaan beda memiliki akar kompleks b b1, 2 h vi dengan
2 2 1 1 dan 4 2 2 a a a h v
dan fungsi komplemennya berbentuk
5 6 2 2 2 2 1 2 1 2 5 1 2 6 1 2 ( cos sin ) 4 dengan 4 ( ) t c y R A t A t a a a R h v a A A A A A A i
(Chiang & Wainwright 2005)
2.13 Trigonometri Hiperbolik
Definisi 2.13.1 (Fungsi Trigonometri
Hiperbolik)
Fungsi sinus hiperbolik, kosinus hiperbolik, dan tangen hiperbolik didefinisikan sebagai:
1 sinh( ) 2 x x x e e
1 cosh( ) 2 sinh( ) tanh( ) cosh( )(Purcell & Varberg 1999)
x x x e e x x x 2 1 1 2 3 2 1 1 2 3 tanh
x coshx sinhxGambar 2. Ilustrasi fungsi trigonometri hiperbolik
III PEMODELAN
3.1 Model Perdagangan
Untuk memahami lebih lanjut mengenai model perdagangan, dalam hal ini diperlukan pemahaman mengenai definisi strategi perdagangan dan gambaran dinamika harga dalam kaitannya dengan model, diawali dengan definisi formal mengenai strategi perdagangan untuk eksekusi program penjualan yang terdiri atas likuidasi sekuritas tunggal. Definisi dan hasil untuk program pembelian dapat dianalogikan secara lengkap sama dengan program penjualan.
Di bawah ini akan dijelaskan mengenai definisi strategi perdagangan dan dinamika harga yang berperan dalam model perdagangan.
3.1.1 Definisi Strategi Perdagangan
Misalkan akan dilakukan eksekusi sebanyak X unit saham dari sebuah sekuritas yang secara lengkap akan dilikuidasi sebelum waktu T. T dibagi ke dalam N interval dengan panjang T
N
, dan didefinisikan waktu diskret tk k, untuk k0,...,N.
Suatu trayektori perdagangan didefinisikan sebagai x0,...,xN, dengan xk yaitu unit saham
yang direncanakan untuk dieksekusi pada waktu tk. Banyaknya saham awal adalah
0
x X, dan likuidasi pada waktu T adalah 0
N
x .
Dengan cara serupa seperti definisi pada trayektori perdagangan, secara spesifik strategi perdagangan terdiri atas n1,...,nN
dengan nkxk1xk yaitu unit saham yang dijual antara waktu tk1
dan
tk.
Secara jelas,hubungan xk
dan
nkadalah
sebagai berikut:1 1 k N k j j j j k x X n n
0,..., . k N (16)Dari perumusan di atas dapat didefinisikan strategi perdagangan sebagai aturan untuk menentukan nk yang tersedia pada waktu
1.
k
t Strategi ini terdiri atas strategi statik dan strategi dinamik. Strategi statik yaitu aturan untuk menentukan setiap nk hanya berdasarkan informasi yang tersedia pada waktu t0. Adapun strategi dinamik, merupakan kebalikan dari strategi statik yaitu aturan untuk menentukan setiap nk berdasarkan semua informasi, termasuk pada waktu tk1
.
3.1.2 Dinamika Harga
Misalkan harga saham awal adalah S0, sehingga nilai awal pasar adalah XS0. Harga saham dapat mengalami perubahan dari waktu ke waktu, hal tersebut dipengaruhi oleh dua faktor, yaitu:
a. Faktor eksogen, terdiri atas: 1. volatilitas
2. drift
b. Faktor endogen, yaitu dampak pasar. Volatilitas dan drift diasumsikan sebagai hasil dari pembentukan pasar yang terjadi secara acak dan saling bebas dari suatu perdagangan.
Dampak pasar dapat dibagi menjadi dua bagian, yaitu:
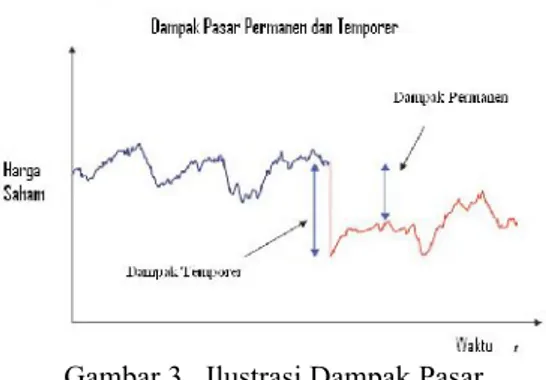
a. Dampak temporer, yang mengacu pada ketidakseimbangan sementara dalam penawaran (supply) dan permintaan (demand) yang disebabkan oleh perdagangan. Hal ini menunjukkan pergerakan harga yang bersifat sementara dari keseimbangan (ekuilibrium).
b. Dampak permanen, berarti perubahan dalam harga keseimbangan (ekuilibrium) perdagangan, sehingga menyebabkan adanya sisa setelah proses likuidasi.
Gambar 3. Ilustrasi Dampak Pasar Asumsi bahwa perubahan harga saham menurut discrete arithmetic random walk, untuk model yang dipengaruhi oleh dampak pasar permanen adalah sebagai berikut:
1/2 1 k k k k n S S g
,
k1,...,N (17)d
engan merepresentasikan volatilitas aset,k
menggambarkan peubah acak bebas dengan rataan nol dan ragam 1 untuk setiap
1,...,
k N, dan dampak permanen g v( ) merupakan fungsi dari rata-rata perdagangan selama interval waktu tk1 sampai tk, dan
didefinisikan v nk.
(18)
Adapun untuk model yang dipengaruhi oleh dampak pasar temporer adalah sebagai berikut: k k1 k n S S h
(19)
dengan h merupakan fungsi biaya dampak temporer dari rata-rata perdagangan selama interval waktu tk1 sampai tk. Dari model ini
dapat dilihat bahwa harga dipengaruhi oleh fungsi dampak sementara (temporer) yaitu
( )
h v . Harga rata-rata saham mengalami perubahan dan bersifat sementara yang disebabkan oleh perdagangan pada tingkat rata-rata v selama satu interval waktu. Sk merupakan harga sebenarnya per saham yang diterima pada penjualan ke-k.
3.1.3 Capture dan Biaya Trayektori
Perdagangan
Hasil dari perdagangan sepanjang trayektori tertentu menghasilkan capture trayektori, yaitu total pendapatan pada saat
perdagangan selesai, yang merupakan hasil
kali unit nk yang dijual dalam tiap interval waktu dikalikan harga efektif per saham Sk yang diterima pada saat penjualan.
1/ 2 0 1 1 1
N N k k k k k k k N k k k n n S XS g x n n h (20) dengan 0XS = Nilai awal saham 1/2 1 N k k k x
= Total efek volatilitas 1 N k k k n x g
= Dampak pasar permanen 1 N k k k n n h
= Dampak pasar temporer. Biaya total dari perdagangan adalah selisih 0 1 N k k k XS n S
, yaitu antara nilai awal dan total pendapatan perdagangan (capture). Ini adalah standar ukuran ex-post dari biaya transaksi yang digunakan dalam penilaian performa, dan disebut sebagai implementasishortfall(Perold 1988).
Dalam model ini, implementasi shortfall merupakan peubah acak, dengan E x( )sebagai nilai harapan shortfall dan V x( ) sebagai ragam shortfall,dengan
1 1 ( ) N k N k k k k k n n E x x g n h
(21)
(Bukti : lihat Lampiran 1) dan 2 2 1 ( ) N k. k V x x
(22)
(Bukti : lihat Lampiran 2)
Karena k menyebar Gauss maka
implementasi shortfall juga menyebar Gauss.
3.2 EfisienFrontierEksekusi Optimal
Pada bagian ini akan dibahas mengenai definisi efisien frontier dan penentuan
trayektori eksekusi optimal, serta akan diperlihatkan hubungan antara tingkat risiko (risk aversion) dan definisi pengoptimalan. Khususnya, akan ditunjukkan bahwa untuk setiap tingkat risiko, ada strategi eksekusi optimal tertentu.
Efisien frontier didefinisikan sebagai himpunan portofolio-portofolio yang menawarkan nilai harapan imbal hasil maksimum untuk risiko yang berbeda dan menawarkan risiko minimum untuk nilai harapan imbal hasil yang berbeda (Bodie 1993).
Model Markowitz menyatakan bahwa portofolio berisiko yang optimal terletak pada efisien frontier. Portofolio berisiko optimal ini dibentuk dari portofolio-portofolio yang berada di efisien frontier.
Kaitannya dengan implementasi shortfall seorang pedagang yang rasional akan selalu mencari cara untuk meminimumkan nilai harapan dari implementasi shortfall untuk setiap tingkat ragam shortfall yang diberikan.
Suatu strategi dikatakan efisien atau optimal jika tidak ada strategi lain yang memiliki ragam yang lebih rendah untuk nilai harapan implementasi shortfall pada tingkat yang sama atau lebih rendah, atau dengan kata lain tidak ada strategi yang memiliki tingkat lebih rendah dari nilai harapan implementasi shortfall untuk ragam sama atau lebih rendah.
Konstruksi suatu strategi efisien dapat dilakukan dengan menyelesaikan masalah optimisasi berkendala:
*
: ( )
min
( ).
x V x V
E x
(23)
Ini berarti, untuk suatu tingkat ragam maksimum yang diberikan V*0
,
dapat ditemukan strategi yang memiliki nilai harapan implementasi shortfall minimum. Karena V x( ) convex, maka himpunan*
{ ( )V x V} adalah convex, dan karena E x( ) adalah strictly convex, maka ada suatu nilai minimum yang unik (unique minimizer)
*( )* x V .
Begitu famili semua kemungkinan strategi efisien optimal memiliki parameter peubah tunggal V*, maka hal ini merepresentasikan mengenai semua kemungkinan maksimum tingkat ragam pada implementasishortfall. Ini
disebut sebagai famili efficient frontier strategi perdagangan optimal.
Untuk pembahasan selanjutnya, akan ditunjukkan bahwa untuk setiap nilai ada korespondensi trayektori perdagangan yang unik x sehingga E x( )V x( ) adalah minimum.
Akan diselesaikan masalah kendala optimisasi (23) dengan memperkenalkan pengali Lagrange , penyelesaian permasalahan menjadi tak berkendala sebagai berikut:
min( ( ) ( )).
x E x V x (24)
Jika 0 maka EV adalah strictly convex, dan persamaan (24) memiliki solusi unik x*( ) . Karena bervariasi, x*( ) meluas pada satu famili parameter yang sama. Persamaan (24) menunjukkan bahwa adalah ukuran tingkat risiko (risk-aversion), yang berarti berapa banyak perbandingan relatif ragam terhadap biaya rata-rata.
Untuk nilai parameter yang diberikan, masalah (24) dapat diselesaikan dengan teknik numerik yang bervariasi, bergantung pada bentuk fungsi yang dipilih untuk g v( ) dan
( )
h v . Dalam kasus khusus berupa fungsi linear, dapat dituliskan solusi eksplisit strategi perdagangan. Untuk mencari solusi eksplisit strategi perdagangan tersebut, dapat dikonstruksi dengan menyelesaikan turunan parsial persamaan (24) terhadap x dan memberikan nilai sama dengan nol.
Sebelum menyelesaikan solusi eksplisit strategi perdagangan, akan ditentukan terlebih dahulu nilai harapan dan ragam dari implementasi shortfall dengan asumsi fungsi dampak pasar yang linear.
Menghitung trayektori optimal secara signifikan akan lebih mudah jika mengambil fungsi dampak pasar permanen dan temporer berupa fungsi linear terhadap rata-rata perdagangan.
4.1 Dampak Pasar Permanen
Misalkan g v( )v
(25) Perhatikan persamaan (17), setiap n unit yang dijual menekan harga per saham sebesar
n . Dari persamaan (17): 1 2 1 k . k k k n S S g 1 1 2 1 0 1 1 2 2 2 1 2 1 1 1 2 2 2 0 1 2 1 1 2 2 0 1 2 1 2 2 2 0 1 1 Untuk 1 ( ) Untuk 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ).j j j j k n S S g k n S S g n n S g g n n S g g n S g
IV PEMBAHASAN
1 3 2 3 2 3 1 1 2 2 0 1 2 1 3 2 3 1 2 0 1 2 3 3 1 2 1 3 3 2 0 1 1 1 2 0 1 2 3 Untuk 3 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ). ( .. j j j j k k n S S g n n S g g n g S n n n g g g n S g S S
3 1 2 . ) ( ) ( ) ( ) ... ( ) . k k n n n n g g g g
1 2 0 1 1 1 2 0 1 1 ( ) ( ) k k j k j j j k k j j j j n S S g S g v
dengan j j n v .Substitusikan persamaan (25) sehingga 1 2 0 1 1 1 2 0 1 1 1 2 0 1 1 S . k k k j j j j k k j j j j k k j j j j S v n S S n
Substitusikan persamaan (16), didapat 1 2 0 1 Sk k j ( k) j S X x
(26)Dari persamaan (20) perhatikan bagian dari persamaan dampak pasar permanen, yaitu: 1 . N k k k n x g
(27)Substitusikan persamaan (25) ke dalam persamaan (27) sehingga diperoleh:
1 1 1 = . N N k k k k k N k k n x g x g v x v
Persamaan ini dapat diuraikan menjadi
1 N k k k n x g
1 1 1 1 1 1 2 1 1 2 2 2 1 1 1 2 2 2 1 1 1 2 2 2 1 1 1 1 2 1 1 ( ) ( ) 1[ ( ) ] 2 1 [ ( ) ] 2 1 ( ) 1 ( ) 2 2 1 ( 2 N k k N N k k k k k k N N k k k k k k k N k k k k N k k k k k N k k k k k N N k k k k k k N k k x v n x x n x n x x x x x x x x x x x x x x x x x x x
2 2 1 2 2 2 1 1 1 1 ) ( ) 2 1 1 = ( ) ( ) 2 2 N k k k N N k k k k k x n x x n
2 2 2 2 2 0 1 1 2 2 1 2 2 2 1 1 2 2 2 0 1 2 2 0 1 1 ( ) ( ) ...( ) 2 1 ( ) 2 1 1 ( ) 2 2 1 1 (karena , dan 0) 2 2 N N N N N k k N N k k N k N k x x x x x x x x n x x n X n x X x
sehingga untuk dampak pasar permanen menjadi: 2 2 1 1 1 1 . 2 2 N N k k k k k n x g X n
(28)Untuk tipe kasus program penjualan murni atau program pembelian murni, maka
.
k
n X
4.2 Dampak Pasar Temporer Misalkan k sign( ) k k n h n n (29)
dengan merupakan biaya tetap penjualan, dan
merupakan parameter biaya transaksi temporer yaitu rasio keragaman bid-ask dengan satu persen dari volume saham harian yang diperdagangkan.Model linear (29) sering disebut model biaya kuadratik karena biaya total yang terjadi oleh pembelian atau penjualan n unit dalam satuan waktu tunggal.
Dari persamaan (20) perhatikan untuk persamaan dampak pasar temporer yaitu:
1 . N k k k n n h
(30)Substitusikan persamaan (29) ke dalam persamaan (30) sehingga diperoleh:
1 1 2 1 sign( ) N N k k k k k k k N k k k n n h n n n n n
2 1 1 . N N k k k k n n
Sehingga persamaan untuk dampak pasar temporer menjadi: 2 1 1 1 . N N N k k k k k k k n n h n n
(31)Dengan asumsi model biaya yang linear untuk persamaan dampak pasar permanen dan temporer, yaitu persamaan (25) dan persamaan (29), nilai harapan dari biaya dampak pasar pada persamaan (21) menjadi
2 2 1 1 1 ( ) 2 N N k k k k E x X n n
(32) dengan 1 2
.
(Bukti : lihat Lampiran 3)
Nilai harapan E adalah fungsi strictly convexsepanjang 0
.
4.3 Konstruksi Eksplisit dari Strategi Optimal
Dengan E X( ) dari (32) dan V X( ) dari (22), dan asumsi bahwa njpositif, kombinasi
( ) ( ) ( )
U x E x V x adalah fungsi kuadratur dari x1,...,xN1 , berupa fungsi yang strictly convex untuk 0. Oleh karena itu akan ditentukan minimum global unik dengan mengatur turunan parsialnya sama dengan nol. Sehingga 1 1 2 2 2 2 j j j . j j x x x U x x (33)
(Bukti: lihat Lampiran 4)
Persamaan (33) berlaku untuk 1,..., 1 j N . 0 j U x adalah ekivalen dengan 2 1 1 2 1( 2 ) j j j j x x x x (34) dengan 2 2 2 . 1 2 (35)
(Bukti : lihat Lampiran 5)
Persamaan (34) adalah persamaan beda linear yang solusinya dapat ditulis sebagai kombinasi eksponensial exp(tj), dengan
memenuhi 2 2 2 (cosh( ) 1)
.
(36) (Bukti : lihat Lampiran 6)Simbol dan dinotasikan sebagai suatu faktor koreksi ( ) , karena 0 maka dan . Solusi spesifik dengan x0 X dan xN 0 adalah trayektori
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 4 4 4 4 2 2 2 2 2 2 4 2 N j j N j j N N X x(Bukti : lihat Lampiran 7)
Untuk strategi perdagangan tersebut diperoleh:
2 2 2 2 2 2 2 2 2 2 2 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 4 4 4 4 2 2 2 2 2 2 2 2 2 2 4 4 4 2 4 2 N j j N j j N N N j j j X n X
2 2 2 2 2 2 2 2 2 2 2 2 2 2untuk 1,..., dengan 0 untuk setiap
4 4 sepanjang 4 0 N N N j j N n j X
(Bukti : lihat Lampiran 8)
Untuk penjualan yang memiliki posisi awal bernilai besar, solusi akan menurun secara monoton dari nilai awal terhadap nol pada saat tarif ditentukan oleh parameter . Untuk yang sangat kecil, diperoleh ekspresi hampiran: 2 2 ( ) ( ), 0 (37)
Begitu interval perdagangan pendek, 2 secara esensial merupakan rasio dari hasil kali volatilitas dan risk-intolerance terhadap parameter biaya transaksi temporer.
Berikut ini akan diperlihatkan ilustrasi mengenai strategi optimal transaksi portofolio, dengan menggunakan parameter yang dipilih sesuai dengan analisis strategi optimal transaksi portofolio yang diperoleh pada pembahasan.
V ILUSTRASI
5.1 Pemilihan Parameter
Pada bagian ini akan diberikan contoh numerik dengan tujuan mengeksplorasi karakteristik frontier efisien secara kualitatif. Dipilih harga awal per saham S0 50, dan banyaknya saham awal sebesar satu juta saham, jadi nilai awal saham sebesar 50 juta. Saham ini memiliki volatilitas tahunan 30%, expected returntahunan sebesar 10%, bid-ask memiliki keragaman 1
8, dan median volume harian perdagangan sebesar 5 juta saham.
Dengan perdagangan tahunan selama 250 hari, ini memberikan volatilitas harian sebesar
0.3
0.019
250 , dan expected return harian sebesar 0.1 4 104
250
. Parameter mutlak
diperoleh dari perkalian volatilitas harian dengan harga awal sehingga diperoleh:
0.019 50 0.95
Likuidasi dilakukan dalam waktu satu minggu, sehingga T5 hari. Untuk memilih parameter fungsi biaya temporer pada persamaan (29) , merupakan biaya tetap dari biaya temporer yaitu setengah dari keragaman bid-ask, sehingga diperoleh
1 1 1
0.0625 2 8 16
. Untuk dimisalkan bahwa untuk setiap satu persen dari volume saham yang diperdagangkan, dibuat harga dampak sama dengan keragaman bid-ask. Sebagai contoh, perdagangan dengan tingkat 5% dari volume saham harian terjadi biaya satu waktu setiap perdagangan sebesar 58. Di bawah asumsi tersebut diperoleh:
6
6 1 8 2.5 10 0.01 5 10 .Untuk biaya permanen, aturan yang biasanya terjadi bahwa harga saham menjadi signifikan ketika menjual 10% dari harga harian, sehingga diperoleh:
7 6 1 8 2.5 10 (0.1 5 10 )
Telah dipilih bahwa 6 10
. Persamaan (37) diperoleh untuk strategi optimal,
0.6 /hari
sehingga T3. Untuk lebih jelas dapat dilihat pada tabel berikut:
Tabel 1 Parameter dan nilai yang dipilih untuk simulasi konstruksi portofolio optimal
Parameter Nilai T 5 N 5 1 X 0 S 50 0,95 0,0625 0,6
Tabel 2 Hasil simulasi konstruksi portofolio optimal dengan menggunakan parameter tertentu untuk
106 j 0 1 2 3 4 5 j t 0 1 2 3 4 5 j x 1.000.000 550.186 298.440 154.131 65.309,8 0 j n 0 449.814 251.746 144.309 88.821,2 65.309,8Gambar 4 Trayektori A optimal untuk
106Tabel 3 Hasil simulasi konstruksi portofolio optimal dengan menggunakan parameter tertentu untuk0 j 0 1 2 3 4 5 j t 0 1 2 3 4 5 j x 1.000.000 800.000 600.000 400.000 200.000 0 j n 0 200.000 200.000 200.000 200.000 200.000
Tabel 4 Hasil simulasi konstruksi portofolio optimal dengan menggunakan parameter tertentu untuk
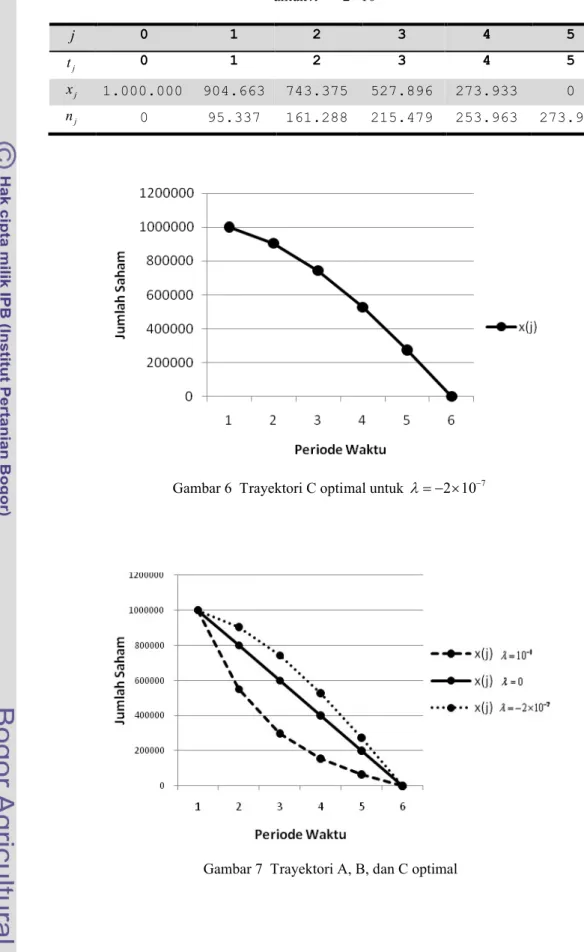
2 107 j 0 1 2 3 4 5 j t 0 1 2 3 4 5 j x 1.000.000 904.663 743.375 527.896 273.933 0 j n 0 95.337 161.288 215.479 253.963 273.933Gambar 6 Trayektori C optimal untuk
2 107
5.2 Struktur frontier
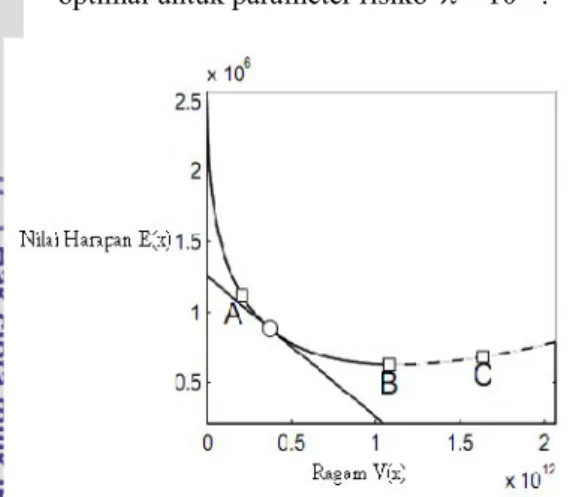
Sebuah contoh dari frontier efisien ditunjukkan pada Gambar 7.
Garis tangen mengindikasikan solusi optimal untuk parameter risiko
106.Gambar 8 Frontierefisien
Trayektori bersesuaian dengan indikasi titik pada frontier yang ditunjukkan pada trayektori A, B, dan C.
Trayektori A pada Gambar 4 memiliki 6
10
, itu dipilih oleh pedagang yang takut risiko (risk-averse) yang mengharapkan menjual dengan cepat untuk mengurangi risiko volatilitas, di samping biaya perdagangan .Trayektori B pada Gambar 5 memiliki 0
, disebut sebagai strategi naïve, karenanya merepresentasikan strategi optimal yang memimimumkan implementasi shortfalltanpa memperhitungkan ragam.
Trayektori C pada Gambar 6 memiliki 7
2 10
, itu dipilih oleh pedagang yang senang risiko yaitu seseorang yang menunda menjual sahamnya, dan menjual sahamnya dengan cepat pada akhir periodeDari gambar trayektori optimal, setiap parameter yang berbeda menunjukkan bahwa merupakan ukuran tingkat risiko (risk-aversion), dan ternyata untuk setiap nilai yang diberikan ada korespondensi trayektori perdagangan yang unik.
VI SIMPULAN
Pada pembahasan telah dilakukananalisis mengenai eksekusi optimal transaksi portofolio yang bertujuan untuk meminimumkan kombinasi risiko volatilitas dan peningkatan biaya transaksi dari dampak pasar permanen dan temporer, atau secara umum meminimumkan biaya implementasi shortfall.
Konstruksi suatu strategi efisien dapat dilakukan dengan menyelesaikan masalah optimisasi berkendala yaitu meminimumkan nilai harapan implementasi shortfall untuk setiap tingkat ragam implementasi shortfall maksimum.
Masalah kendala optimisasi tersebut dapat diselesaikan dengan menggunakan pengali lagrange dengan meminimumkan fungsi biaya.
Fungsi biaya yang dipilih merupakan fungsi kuadratur, berupa fungsi yang strictly convex untuk tingkat risiko positif. Oleh karena itu dapat ditentukan minimum global unik dengan mengatur turunan parsialnya sama dengan nol.
Dengan asumsi model biaya dampak pasar linear, diperoleh konstruksi eksplisit strategi optimal transaksi portofolio dengan menyelesaikan masalah nilai awal persamaan beda, dengan jumlah saham awal sebesar X dan sisa saham pada akhir periode sama dengan nol maka diperoleh solusi spesifik trayektori perdagangan optimal.
Dapat disimpulkan bahwa untuk setiap tingkat risiko (risk aversion) yang diberikan, ada korespondensi trayektori perdagangan yang unik dengan fungsi biaya yang minimum.