menentukan bentuk pengendali yang indeks perfomansinya adalah norm H 2.

BAB II

Teori Kontrol

H

2

Bab ini akan membahas teori kontrol H2 ,yang tujuannya adalah

menentukan bentuk pengendali yang indeks perfomansinya adalah norm H2.

Untuk itu pertama-tama akan dijelaskan tentang norm H2 selanjutnya akan

mencari plant diperumumnya, yang kemudian dilanjutkan dengan mencari fungsi transfer loop tertutupnya dan yang terakhir akan ditentukan kontrol yang diperkenankan dan optimal.

Secara ringkas suatu kontrol H2 dapat dinyatakan sebagai berikut : ”mencari pengontrol K yang proper dan real-rational yang menstabilkan

plant yang diperumum G secara internal dan meminimumkan norm H2

dari matriks transfer dari masukan w ke keluaran z, Tzw.”

2.1. Norm H2

Mula-mula pada subbagian ini dihitung norm H2 yang selanjutnya akan kita minimalkan. Oleh sebab itu pertama-tama kita butuhkan definisi yang berkaitan dengan norm H2.

Definisi 1:

Ruang Hardy H2 adalah ruang bagian (tertutup) dari H2(j ) dengan

fungsi matrik G(s) analitik pada bidang Re(s)>0, artinya setiap elemen matrik dari fungsi matrik G(s) analitik pada bidang Re(s)>0. Ruang bagian real rasional dari

H2, yang dinotasikan RH2 yang terdiri dari seluruh matrik transfer yang stabil,

… (2.1.1) Norma yang berkaitan dengan ruang H2 dari suatu fungsi G didefinisikan sebagai: 2 2 1 _* : sup [ ( ) ( )] 2 0 G trace G σ jω Gσ jω ωd π σ ∞ ⎛ ⎞ ⎜ ⎟ = _{⎜ ∫} + + _⎟ > ⎝ −∞ ⎠ , 2 2 1 _* : [ ( ) ( )] 2 G trace G jω G jω ωd π ∞ ⎛ ⎞ ⎜ ⎟ = _∫ ⎜ _−∞ ⎟ ⎝ ⎠ , 2 2 1 : [ ( ) ( )] 2 G trace G s G s ds j π ∞ ⎛ ⎞ ⎜ ⎟ =_⎜ ∫ _⎟ −∞ ⎝ ⎠ , 2 2 * { ( ) ( )} G trace g t g t ds ∞ = ∫ −∞ . Contoh 1:

Misalkan terdapat suatu sistem dinamik yang mempunyai G s( )=C sI( −A)−1B

dengan

[

]

0 1 1 ; ; 1 0 1 1 0 ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥} =_{⎢ ⎥} = − − ⎣ ⎦ ⎣ ⎦ A B C ,

dan akan dihitung 2

2 G . Jawab Diketahui

[

]

0 1 1 ; ; 1 0 1 1 0 A=⎡_⎢ ⎤_⎥ B=⎡ ⎤_{⎢ ⎥} C= − − ⎣ ⎦ ⎣ ⎦ ,

untuk mencari G 2₂, sebagai contoh akan digunakan dua buah cara:

1. Dengan menggunakan persamaan 2.1.3 dimana

2 2 1 : [ ( ) ( )] 2 G trace G s G s ds j π ∞ ⎛ ⎞ ⎜ ⎟ =_{⎜ ∫ ⎟} −∞ ⎝ ⎠ .

Untuk itu sebelumnya akan dicari ( )G s dan G ( )s terlebih dahulu. Mula-mula akan dihitung G s dimana ( )

… (2.1.2)

… (2.1.3)

… (2.1.4)

1

( ) ( )

G s =C sI−A − B

Dengan mensubstitusi A, B dan C sehingga

[

]

1 0 0 1 1 ( ) 1 0 0 1 1 0 s G s s − ⎛⎡ ⎤ ⎡ ⎤⎞ ⎡ ⎤ = _{⎜⎢ ⎥ ⎢}− _{⎥⎟ ⎢ ⎥} − − ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎝ ⎠ . Berikutnya didapat

[

]

1 1 1 ( ) 1 0 1 1 0 s G s s − − ⎡ ⎤ ⎡ ⎤ = _{⎢ ⎥ ⎢ ⎥} + ⎣ ⎦ ⎣ ⎦, dan karena 1 2 1 1 1 1 1 1 1 1 s s s s s s − − + ⎡ ⎤ ⎡ ⎤ = ⎢ ₊ ⎥ _{+ +} ⎢ ₋ ⎥ ⎣ ⎦ ⎣ ⎦, maka diperoleh

[

]

2 1 1 1 1 ( ) 1 0 1 0 1 s G s s s s + ⎡ ⎤ ⎡ ⎤ = _{⎢ ⎥ ⎢ ⎥} − + + ⎣ ⎦ ⎣ ⎦.

Dengan menggunakan operasi perkalian pada matriks

[

]

2 1 1 ( ) 1 1 0 1 G s s s s ⎡ ⎤ = + _{⎢ ⎥} + + _{⎣ ⎦}, diperoleh 2 1 ( ) 1 s G s s s + = + + .

Yang kedua akan dicari G ( )s dimana

( ) T( ) G s =G − , s sehingga 2 1 ( ) 1 s G s s s − + = − + .

Setelah ( )G s dan G ( )s didapat, G dapat dihitung. 2₂

Dari persamaan (2.1.3), diperoleh

2 2 1 : [ ( ) ( )] 2 G trace G s G s ds j π ∞ ⎛ ⎞ ⎜ ⎟ = _∫ ⎜ _−∞ ⎟ ⎝ ⎠ , … (2.1.6) … (2.1.7) … (2.1.8) … (2.1.9) … (2.1.10) … (2.1.11) … (2.1.12) … (2.1.13)

… (2.1.16) … (2.1.17) … (2.1.18) 2 2 2 2 1 1 1 2 1 1 s s G trace ds j s s s s π ∞ ⎛ _{⎡ − +⎛ ⎞⎛ + ⎞⎤} ⎞ ⎜ ⎟ =_⎜ ∫ ⎢⎜_{⎝ − +} ⎟⎜_{⎠⎝ + +} ⎟_⎠⎥ _⎟ ⎣ ⎦ −∞ ⎝ ⎠ , 2 2 4 2 2 1 1 2 1 s G trace ds j s s π ∞ ⎛ _{⎡⎛ − ⎞⎤} ⎞ ⎜ ⎟ =_{⎜ ∫ ⎢⎜ ⎟⎥ ⎟} + + ⎝ ⎠ ⎣ ⎦ −∞ ⎝ ⎠ , sehingga diperoleh 2 2 4 2 2 1 1 2 1 s G ds j s s π ∞ ⎛ _{⎡ − ⎤} ⎞ ⎜ ⎟ = _{∫ ⎢ ⎥} ⎜ _−∞⎣ + + _⎦ ⎟ ⎝ ⎠ .

Selanjutnya akan diselesaikan persamaan (2.1.15) dimana akan dipergunakan teorema residu.

Pole-pole 2 4 2 1 1 s s s − + + adalah 1 3 1 3 1 3 1 3 , , ,dan 2 2 2 2 i i i i + − − + − −

dimana semuanya itu berderajat satu.

Selanjutnya akan dihitung residu-residu dari masing pole

• Pada 1 3 2 i s= + adalah

(

)

2 1 1 3 2 2 1 3 1 lim 2 _{1 3 1 3} 1 2 2 i s i s a s i i s s s s − ₊ → ⎛ ⎞ ⎜ ⎟ ⎛ ⎛ ⎞⎞ ⎜ + − ⎟ = _⎜⎜_⎜ −⎜_⎜ ⎟_⎟⎟_{⎟ ⎛ ⎟} ⎞⎛ ⎞ ⎛ + ⎞ ⎛ − ⎞ ⎝ ⎠ ⎝ ⎠ ⎜ _{⎜ −⎜ ⎟⎟⎜ −⎜ ⎟⎟ + +} ⎟ ⎜ ⎟⎜ ⎟ ⎜ _{⎝ ⎝ ⎠⎠⎝ ⎝ ⎠⎠} ⎟ ⎝ ⎠ dimana diperoleh

(

)

1 3 3 1 3 2 2 2 2 3 1 3 (1) i i a i i − ⎛ ⎞⎛ ⎞ + − ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ = + . • Pada 1 3 2 i s= −

(

)

2 1 1 3 2 2 1 3 1 lim 2 _{1 3 1 3} 1 2 2 i s i s b s i i s s s s − ₋ → ⎛ ⎞ ⎜ ⎟ ⎛ ⎛ ⎞⎞ ⎜ − − ⎟ = ⎜⎜_⎜ −_⎜⎜ _⎟⎟⎟_{⎟ ⎛ ⎛ ⎞⎞⎛ ⎛ ⎞⎞} ⎟ + − ⎝ ⎠ ⎝ ⎠ ⎜ _{⎜ −⎜ ⎟⎟⎜ −⎜ ⎟⎟ + +} ⎟ ⎜ ⎟⎜ ⎟ ⎜ _{⎝ ⎝ ⎠⎠⎝ ⎝ ⎠⎠} ⎟ ⎝ ⎠ … (2.1.13) … (2.1.14) … (2.1.15)

… (2.1.19) … (2.1.20) … (2.1.21) … (2.1.22) … (2.1.23) dimana diperoleh

(

)

1 3 3 1 3 2 2 2 2 3 1 3 (1) i i b i i − ⎛ ⎞⎛ ⎞ − + ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ = − − . • Pada 1 3 2 i s= − +

(

)

2 1 1 3 2 2 1 3 1 lim 2 _{1 3 1 3} 1 2 2 i s i s c s i i s s s s − _{− +} → ⎛ ⎞ ⎜ ⎟ ⎛ ⎛ ⎞⎞ ⎜ − + − ⎟ = _⎜⎜_⎜ −⎜_⎜ ⎟_⎟⎟_{⎟ ⎟} ⎛ ⎛− + ⎞⎞⎛ ⎛− − ⎞⎞ ⎝ ⎠ ⎝ ⎠ ⎜ _{− + ⎜ −⎜ ⎟⎟⎜ −⎜ ⎟⎟}⎟ ⎜ ⎟⎜ ⎟ ⎜ _{⎝ ⎝ ⎠⎠⎝ ⎝ ⎠⎠}⎟ ⎝ ⎠ dimana diperoleh

(

)

1 3 3 1 3 2 2 2 2 3 1 3 ( 1) i i c i i − ⎛ ⎞⎛ ⎞ − + ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ = − + − . • Pada 1 3 2 i s= − −

(

)

2 1 1 3 2 2 1 3 1 lim 2 _{1 3 1 3} 1 2 2 i s i s d s i i s s s s − _{− −} → ⎛ ⎞ ⎜ ⎟ ⎛ ⎛ ⎞⎞ ⎜ − − − ⎟ = ⎜⎜_⎜ −_⎜⎜ _⎟⎟⎟_{⎟ ⎛ ⎛ ⎞⎞⎛ ⎛ ⎞⎞}⎟ − + − − ⎝ ⎠ ⎝ ⎠ ⎜ _{− + ⎜ −⎜ ⎟⎟⎜ −⎜ ⎟⎟}⎟ ⎜ ⎟⎜ ⎟ ⎜ _{⎝ ⎝ ⎠⎠⎝ ⎝ ⎠⎠}⎟ ⎝ ⎠ dimana diperoleh

(

)

1 3 3 1 3 2 2 2 2 3 1 3 ( 1) i i d i i − ⎛ ⎞⎛ ⎞ + − ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ = − − − .

… (2.1.24) … (2.1.25) … (2.1.26) … (2.1.27) … (2.1.28) … (2.1.29) … (2.1.30) … (2.1.31) Sehingga

[

]

2 1 1 1 1 4 2 1 2 1 s ds j a b c d s s π − − − − ∞ ⎡ − ⎤ _{= + + +} ∫ ⎢ _{+ +} ⎥ ⎣ ⎦ −∞ .

Dan setelah mensubstitusi dengan hasil dari persamaan (2.1.17), (2.1.19), (2.1.21), dan (2.1.23) maka diperoleh

[ ]

2 4 2 1 2 1 1 s ds j s s π ∞ ⎡ − ⎤ _{= −} ∫ ⎢ _{+ +} ⎥ ⎣ ⎦ −∞ , sehingga didapat 2 4 2 1 2 1 s ds j s s π ∞ ⎡ − ⎤ _{= −} ∫ ⎢ _{+ +} ⎥ ⎣ ⎦ −∞ .

Selanjutnya kembali ke persamaan (2.1.15)

2 2 4 2 2 1 1 2 1 s G ds j s s π ∞ ⎡ − ⎤ = _{∫ ⎢ ⎥} + + ⎣ ⎦ −∞

dan berikutnya mensubstitusi persamaan (2.1.26)

(

)

2 2 1 2 2 G j j π π = − , sehingga diperoleh 2 2 1 G = − , dimana 2 2 1 G = ,

dan normnya didapat sebagai

2 1

G = .

Perhitungan dengan menggunakan definisi di atas dirasakan cukup rumit sehingga untuk mempermudah dalam perhitungan, diperlukan lemma berikut

Lemma 1:

… (2.1.32) … (2.1.33) … (2.1.34) … (2.1.35) … (2.1.36) … (2.1.37) … (2.1.38) … (2.1.39) … (2.1.40) ( ) 0 A B G s C ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦

dengan A stabil. Maka, didapat

(

)

(

)

2 _{* *}

2

G =trace B QB =trace CPC ,

dimana Q merupakan matriks keteramatan Gramian dan P merupakan matriks

keterkontrolan Gramian yang didapat dari persamaan Lyapunov berikut ini:

* * * *

0, 0

AP+PA +BB = A Q QA C C+ + = .

Bukti

Karena G stabil, maka didapat

1( , 0 ( ) ) 0, 0 L Ce BAt t g t G t − ⎧ ≥ = _{= ⎨} < ⎩ . Matrik keterobservasian 0 _{A t}* _{* At} Q =

∫

∞e C Ce dt dan keterkontrolan 0 * A t * At

P=

∫

∞e BB e dt memenuhi persamaan Lyapunov sebagai berikut

* * 0 AP+PA +BB = , dan * * 0 A Q QA C C+ + = .

Hal ini dapat diperoleh sebagai berikut ini Pertama perhatikan matriks keteramatan Q

0

*

A t * At Q=

∫

∞e C Ce dt. Seperti yang telah diketahui bahwa

* _{* *} * _* * _* A t At A t At A t At d e C Ce A e C Ce e C Ce A dt ⎡ _{⎤ = +} ⎣ ⎦ .

Selanjutnya kedua ruas diintegralkan, diperoleh

* _{* *} * _* * _* 0 0 0 ( A t At) ( A t At) ( A t At) d e C Ce A e C Ce dt e C Ce dtA ∞ ∞ ∞ = +

∫

∫

∫

.

… (2.1.41)

… (2.1.42) Sekarang yang dikerjakan selanjutnya adalah menyelesaikan persamaan (2.1.40) diatas. Mula-mula menyelesaikan ruas kiri dari persamaan tersebut terlebih dahulu. * _* * _* 0 0 ( ) lim ( ) ∞ →∞ =

∫

A t At

∫

s A t At s d e C Ce d e C Ce , * _* * _* 0 0 ( ) lim( ) ∞ →∞ =

∫

A t At A t At s s d e C Ce e C Ce , * _* * _{* *} 0 ( ) lim( ) ∞ →∞ = −

∫

A t At A s As s d e C Ce e C Ce C C .

Karena A stabil, diperoleh

* _*

lim( ) 0

→∞ =

A s As s e C Ce .

Setelah mensubstitusi persamaan (2.1.44) ke dalam persamaan (2.1.43), maka hasil ruas kiri didapat

* _{* *} 0 ( A t At) d e C Ce C C ∞ = −

∫

.

Proses berikutnya adalah menyelesaikan ruas kanan dari persamaan (2.1.40) dengan mensubstitusi persamaan (2.1.38) ke ruas kanannya tersebut sehingga * * * * * * 0 0 ( A t At) ( A t At) A e C Ce dt e C Ce dtA A Q QA ∞ ∞ + = +

∫

∫

.

Selanjutnya setelah ruas kiri dan kanan dari persamaan (2.1.40) didapat maka menjadi

* *

C C A Q QA

− = + .

Setelah menambahkan C C pada kedua ruas , diperoleh *

* *

0

+ + =

A Q QA C C .

Kedua perhatikan matriks keterkontrolan P dimana

0

*

At * A t P=

∫

∞e BB e dt.

Seperti yang telah diketahui bahwa

… (2.1.47b) … (2.1.45) … (2.1.48a) … (2.1.43) … (2.1.44) … (2.1.47a) … (2.1.46)

* * * * * * * At A t At A t At A t d e BB e Ae BB e e BB e A dt ⎡ _{⎤ = +} ⎣ ⎦ .

Selanjutnya kedua ruasnya diintegralkan sehingga

* * * * * * * * 0 0 0 ( At A t) ( At A t) ( A t A t) d e BB e A e BB e dt e BB e dtA ∞ ∞ ∞ = +

∫

∫

∫

.

Dalam menyelesaikan persamaan (2.1.49) mula-mula menyelesaikan ruas kiri dari persamaan tersebut dimana

* * * * 0 0 ( ) lim ( ) ∞ →∞ =

∫

At A t

∫

s At A t s d e BB e d e BB e , * * * * 0 0 ( ) lim( ) ∞ →∞ =

∫

s At A t At A t s d e BB e e BB e , * * * * * 0 ( ) lim( ) ∞ →∞ = −

∫

At A t At A t s d e BB e e BB e BB .

Karena A stabil, diperoleh

* * lim( ) 0 →∞ = At A t s e BB e .

Setelah mensubstitusi persamaan (2.1.53) ke dalam persamaan (2.1.52), maka didapat * * * 0 ( At A t) d e BB e BB ∞ = −

∫

.

Proses berikutnya adalah menyelesaikan ruas kanan dari persamaan (2.1.49) dengan mensubstitusi persamaan (2.1.48) ke ruas kanannya tersebut sehingga * * * * * * * 0 0 ( At A t) ( A t A t) A e BB e dt e BB e dtA AP PA ∞ ∞ + = +

∫

∫

.

Selanjutnya setelah ruas kiri dan kanan dari persamaan (2.1.49) didapat maka diperoleh

* *

BB AP PA

− = + .

Setelah menambahkan BB pada kedua ruas pada persamaan (2.1.21), maka *

didapat … (2.1.49) … (2.1.56) … (2.1.48b) … (2.1.50) … (2.1.51) … (2.1.52) … (2.1.53) … (2.1.54) … (2.1.55)

* *

0= AP+PA +BB .

Setelah melihat dari pertama dan kedua di atas, matriks keteramatan Q dan matriks keterkontrolan P terbukti memenuhi

0 * * AP+PA +BB = , dan 0 * * A Q QA C C+ + = .

Dari persamaan (2.1.4) pada Definisi 1

2 _* 2 ₀ { ( ) ( )} G =

∫

∞trace g t g t dt, * 2 _{* *} 2 ₀ { } A t At G =

∫

∞trace B e C Ce B dt, * 2 * * 2 ₀ ( ) A t At G =trace

∫

∞ B e C Ce B dt, * 2 _{* *} 2 ( ₀ ( ) ) A t At G =trace B

∫

∞ e C Ce dtB , 2 _* 2 ( ) G =trace B QB . 2 _* 2 0 { ( ) ( )} G =

∫

∞trace g t g t dt, * 2 _{* *} 2 ₀ { } At A t G =

∫

∞trace Ce BB e C dt, * 2 _{* *} 2 ₀ { } At A t G =trace

∫

∞ Ce BB e C dt, * 2 _{* *} 2 ( 0 { } ) At A t G =trace C

∫

∞ e BB e dtC , 2 _* 2 ( ) G =trace CPC . Sehingga terpenuhi bahwa

(

)

(

)

2 * * 2 G =trace B QB =trace CPC . Contoh 2: … (2.1.57) … (2.1.58) … (2.1.59) … (2.1.60) … (2.1.61) … (2.1.62) … (2.1.63) … (2.1.64) … (2.1.65) … (2.1.66) … (2.1.67) … (2.1.68) … (2.1.69) … (2.1.70)

… (2.1.73)

… (2.1.74) Misalkan terdapat suatu sistem dinamik yang mempunyai G s( )=C sI( −A)−1B

dengan

[

]

0 1 1 ; ; 1 0 1 1 0 ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥} =_{⎢ ⎥} = − − ⎣ ⎦ ⎣ ⎦ A B C . Akan dihitung G . 2₂ Jawab: Diketahui

[

]

0 1 1 ; ; 1 0 1 1 0 ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥} =_{⎢ ⎥} = − − ⎣ ⎦ ⎣ ⎦ A B C .

Dari lemma 1, diperoleh

(

)

2 _*

2 =

G trace CPC ,

dimana P merupakan matrik keterkontrolan Gramian yang memenuhi

* * 0 + + = AP PA BB

[

]

11 12 11 12 12 22 12 22 0 1 0 1 1 0 0 1 0 1 1 1 1 0 0 0 − ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ + + = ⎢ ⎥ ⎢ ⎥ ⎢_{− −} ⎥ ⎢ ₋ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦ ⎣ ⎦ P P P P P P P P 12 22 12 11 12 11 12 12 22 22 12 22 1 0 0 0 − − − ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ + = ⎢_{− − − −} ⎥ ⎢ _{− −} ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ P P P P P P P P P P P P .

Selanjutnya dengan menyelesaikan persamaan didapat (2.1.74) sehingga diperoleh

11 12 22 1 1 1, , dan 2 2 = = − = P P P , dan karena 11 12 12 22 ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ P P P P P , maka 1 1 2 1 1 2 2 ⎡ ₋ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢₋ ⎥ ⎢ ⎥ ⎣ ⎦ P . Dari lemma 1 … (2.1.71) … (2.1.72) … (2.1.75) … (2.1.76)

… (2.2.2)

(

)

2 *

2 =

G trace CPC .

dengan mensubstitusi nilai C dan P kedalam persamaan tersebut maka diperoleh

[

]

2 2 1 1 1 2 1 0 1 1 0 2 2 G trace ⎛ ⎡ ₋ ⎤ ⎞ ⎜ ⎢ _{⎥ ⎡ ⎤}⎟ ⎜ ⎟ = ⎢ _{⎥ ⎢ ⎥} ⎜ ⎢₋ ⎥⎣ ⎦⎟ ⎜ _{⎢⎣ ⎥⎦} ⎟ ⎝ ⎠ . sehingga

[ ]

2 2 1 G =trace , dan didapat 2 1 G = .

2.2. Plant yang diperumum

Pada subbab ini akan dicari plant diperumum G(s) dari suatu model dinamik plant P dan beberapa fungsi bobotnya.

Pertama, misalkan suatu sistem dinamik P digambarkan persamaan diferensial berikut: 0 0 ( ) ( ) ( ) , ( ) ( ) ( ) ( ) x t A x t B u t x t x y t C x t D u t = + = = + &

dimana:x t( )∈ ℜndisebut variabel keadaan;x t( ₀ ) disebut kondisi awal sistem;

( ) r

y t ∈ ℜ adalah keluaran sistem; dan ( ) m

u t ∈ ℜ adalah masukan sistem. dengan: A merupakan matrik n x n merupakan matriks keadaan;

B merupakan matrik n x m merupakan matriks masukan; C merupakan matrik r x m merupakan matriks keluaran;

D merupakan matrik r x m merupakan matriks transmisi langsung masukan - keluaran … (2.2.1) … (2.1.77) … (2.1.78) … (2.1.79) … (2.1.80)

Seperti yang telah disebutkan diatas bahwa plant diperumum G terdiri dinamik P dan beberapa fungsi bobotnya. Untuk menggabungkannya, diperlukan operasi pada sistem. Oleh sebab itu selanjutnya akan diperkenalkan beberapa operasi pada sistem.

Operasi Pada Sistem

Pada bagian ini, kita akan menunjukan fakta-fakta mengenai interkoneksi pada sistem.

Misalkan terdapat suatu sistem dinamik P dengan diagram bloknya sebagai berikut

Gambar (2.2.1) : Diagram blok P

dan persamaan ruang keadaan dari sistem dinamik P tersebut seperti diuraikan pada persamaan (2.2.1) dan persamaan (2.2.2).

Keterhubungan antara persamaan ruang keadaan dengan matriks transfernya sebagai berikut

1 A B P( s ) C( sI A ) B D C D − ⎡ ⎤ =_{⎢ ⎥}= − + ⎣ ⎦ .

Misalkan P1 dan P2 merupakan dua subsistem dengan representasi ruang keadaannya 1 1 2 2 1 2 1 1 2 2 A B A B P P C D C D ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥} =_{⎢ ⎥} ⎣ ⎦, ⎣ ⎦.

Pertama kita akan memperkenalkan koneksi seri atau ”cascade”. Pada koneksi seri ini, output dari subsistem kedua menjadi input pada subsistem pertama seperti yang ditunjukan pada diagram blok berikut ini :

u s y P1 P2 u y P

Gambar (2.2.2) : Diagram blok untuk rangkaian seri atau “cascade”.

Untuk diagram blok pada gambar (2.2.2), persamaan ruang keadaan untuk plant P1 dinyatakan sebagai berikut:

1 1 1 1 1 1 1 , . x A x B s y C x D s = + = + & ;

dan persamaan ruang keadaan untuk plant P2 dinyatakan sebagai berikut :

2 2 2 2 2 2 2 , . s x A x B u C x D u = + = + & .

Diagram blok pada gambar (2.2.2) di atas akan dibentuk menjadi seperti diagram blok pada gambar (2.2.1).

Setelah mensubstitusi persamaan (2.2.6) pada persamaan ruang keadaan untuk plant P2 ke persamaan (2.2.3) dan (2.2.4) untuk persamaan ruang keadaan untuk plant P1, diperoleh

1 1 1 1 1 2 2 1 2 1 1 1 2 2 2 , . x A x B C x B D u y C x D C x D D u = + + = + + &

Representasi dari sistem seri ini merupakan gabungan persamaan (2.2.7), (2.2.5), dan (2.2.8) dimana berturut-turut ditunjukan sebagai

1 1 1 1 1 2 2 1 2 2 2 2 2 1 1 1 2 2 2 , , . x A x B C x B D u x A x B u y C x D C x D D u = + + = + = + + & &

maka persamaan – persamaan tersebut dapat ditulis dalam bentuk matriks yang dituliskan sebagai berikut :

1 2 2 2 2 1 1 2 1 2 1 1 1 2 1 2 0 x A B x y C D C D D u x A B C B D x ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢₌ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ & & .

Sehingga, representasi untuk sistem seri ini merupakan

1 1 2 2 1 2 1 1 2 2 A B A B P P C D C D ⎡ ⎤ ⎡ ⎤ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦,

dimana dapat ditunjukan pula sebagai:

… (2.2.3) … (2.2.5) … (2.2.4) … (2.2.6) … (2.2.7) … (2.2.8) … (2.2.8) … (2.2.9)

1 1 2 1 2 1 2 2 2 1 1 2 1 2 0 A B C B D P P A B C D C D D ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ .

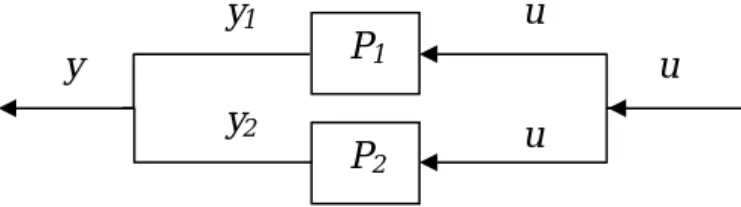
Yang kedua yang akan diperkenalkan adalah koneksi paralel atau penjumlahan dari P1 dan P2 dimana dapat ditunjukan dari diagram blok berikut ini:

Gambar 2.2.3 : Diagram blok untuk rangkaian paralel.

Untuk diagram blok pada gambar (2.2.3) di atas, persamaan ruang keadaan untuk plant P1 dinyatakan sebagai berikut:

1 1 1 1 1 1 1 1 , , x A x B u y C x D u = + = + &

dan persamaan ruang keadaan untuk plant P2 dinyatakan sebagai berikut :

2 2 2 2 2 2 2 2 , . y x A x B u C x D u = + = + &

Selanjutnya P1 dan P2 akan digabung dengan menggunakan operasi paralel atau penjumlahan. Adapun pada operasi paralel ini yang mengalami perubahan adalah pada outputnya dimana

1 2

y= +y y .

dan setelah mensubstitusi dengan persamaan (2.2.12) dan persamaan (2.2.14) maka outputnya diperoleh

2 2

1 1 ( 1 2)

y=C x +C x + D +D u.

Sedangkan untuk fungsi keadaan x&₁ dan x&₂ tidak mengalami perubahan seperti yang berturut – turut ditunjukan persamaan berikut ini

u u u y2 y1 y P1 P2 … (2.2.10) … (2.2.11) … (2.2.12) … (2.2.13) … (2.2.14) … (2.2.15) … (2.2.16) … (2.2.17)

1 1 1 1 2 2 2 2 , . u x A x B x A x B u = + = + & &

Berikutnya, persamaan (2.2.17), (2.2.18) dan (2.2.16) dapat dituliskan dalam bentuk matriks sebagai berikut

2 2 1 1 1 1 2 2 1 2 1 2 0 0 x x y u x A B x A B C C D D ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ + ⎦⎣ ⎦ & & , dimana 1 1 2 2 1 2 1 2 0 0 A B A B C C D D ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ + ⎦

merupakan hasil dari operasi paaralel dari P dan ₁ P . ₂

Sehingga secara umum, koneksi paralel atau penjumlahan dari P dan ₁ P ₂

didapat 1 1 2 2 1 2 1 1 2 2 A B A B P P C D C D ⎡ ⎤ ⎡ ⎤ + =_{⎢ ⎥ ⎢}+ _⎥ ⎣ ⎦ ⎣ ⎦, dimana diperoleh 1 1 1 2 2 2 1 2 1 2 0 0 A B P P A B C C D D ⎡ ⎤ ⎢ ⎥ + _{= ⎢ ⎥} ⎢ + ⎥ ⎣ ⎦ .

Selanjutnya akan digunakan operasi diatas untuk mencari plant

diperumum dari suatu sistem dinamik dengan beberapa fungsi bobotnya. Dalam hal ini dimisalkan ada plant P dengan fungsi bobot masukan Wi dan fungsi bobot keluaran Wo yang diilustrasikan seperti pada diagram blok berikut ini

Gambar 2.2.4 : Diagram blok P dan beberapa fungsi bobotnya

Dari diagram blok diatas, persamaan dinamik untuk Wi, sebagai berikut

w2 z s w u Wi P Wo … (2.2.18) … (2.2.19) … (2.2.20) … (2.2.21) … (2.2.22)

i i i i i i i x A x B u, w C x D u. = + = + &

Sedangkan persamaan dinamik untuk P dinyatakan sebagai berikut:

2 2 p p p p p p p p p x A x B w B w , s C x D w D w , = + + = + + &

dan persamaan dinamik untuk Wu dinyatakan sebagai berikut:

o o o o o o o x A x B s, z C x D s. = + = + &

Selanjutnya, akan disubstitusi persamaan (2.2.23) ke dalam persamaan (2.2.24)

(

)

2,

p p p p i i i p x& = A x +B C x +D u +B w

sehingga setelah diuraikan diperoleh

2,

p p p p i i p i p

x& = A x +B C x +B D u+B w

dan juga mensubstitusi persamaan (2.2.23) ke dalam persamaan (2.2.25)

(

)

2

p p p i i i p s=C x +D C x +D u +D w , sehingga setelah diuraikan juga diperoleh

2

p p p i i p i p

s=C x +D C x +D D u+D w .

Dari hasil di atas, selanjutnya akan disubstitusi hasil persamaan (2.2.31) tersebut ke persamaan (2.2.26) sehingga didapat.

(

2

)

o o o o p p p i i p i p

x& =A x +B C x +D C x +D D u+D w ,

dan setelah mengalikan dengan yang didalam kurung sehingga diperoleh

2

o o o o p p o p i i o p i o p

x& =A x +B C x +B D C x +B D D u+B D w .

Di samping itu, hasil persamaan (2.2.31) akan disubstitusi ke dalam persamaan (2.2.27)

(

2

)

o o o p p p i i p i p

z=C x +D C x +D C x +D D u+D w , dan setelah diuraikan maka persamaan (2.2.33) menjadi

… (2.2.23) … (2.2.24) … (2.2.25) … (2.2.26) … (2.2.27) … (2.2.28) … (2.2.29) … (2.2.30) … (2.2.31) … (2.2.31) … (2.2.32) … (2.2.33) … (2.2.34)

… (2.2.39)

2

o o o p p o p i i o p i o p

z=C x +D C x +D D C x +D D D u+D D w .

Persamaan (2.2.22), (2.2.29), (2.2.32), dan (2.2.33) akan digabung dimana

2 2 2 i i i i p p p p i i p i p o o o o p p o p i i o p i o p o o o p p o p i i o p i o p x A x B u, x A x B C x B D u B w , x A x B C x B D C x B D D u B D w , z C x D C x D D C x D D D u D D w . = + = + + + = + + + + = + + + + & & &

Dari keempat persamaan tersebut didapat persamaan ruang keadaan

2 0 0 0 0 i i i i p i p p i p p p o p i o p o o p i o p o o o p i o p o o p i o p A B x x B C A B D B x x w B D C B C A B D D B D x x D D C D C C D D D D D z u ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥₌ ⎢ ⎥₊ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦ & & & .

Persamaan (2.2.39) dapat dipecah menjadi

2 0 0 0 0 i i i i p p i p p p i p o o p i o p o o o p i o p x A x B x x B C A x B D u B w x B D C B C A x B D D B D ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ =_{⎢ ⎥} =_{⎢ ⎥⎢ ⎥}+_{⎢ ⎥} +_{⎢ ⎥} ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦ ⎣ ⎦ & & & & , dan 2. i o p i o p o p o p o p o x z D D C D C C x D D D u D D w x ⎡ ⎤ ⎢ ⎥ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ =_{⎣ ⎦⎢ ⎥}+_{⎣ ⎦} +_{⎣ ⎦} ⎢ ⎥ ⎣ ⎦ … (2.2.35) … (2.2.36) … (2.2.37) … (2.2.38) … (2.2.39) … (2.2.39)

2.3. Fungsi transfer loop tertutup

Subbab ini akan dicari fungsi transfer loop tertutup dari plant diperumum

G(s) dari suatu model dinamik plant dan beberapa fungsi bobotnya yang

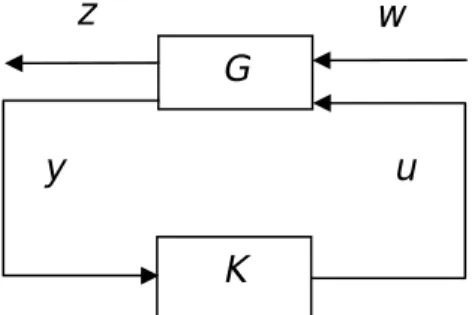
digabungkan dengan pengontrol K(s) seperti yang dilustrasikan seperti pada diagram blok berikut

Gambar 2.3.1 Diagram blok dari plant diperumum G yang digabungkan dengan

pengontrol K

Misalkan suatu plant diperumum G(s) dari suatu model dinamik plant dan beberapa fungsi bobotnya secara umum sebagai berikut

G K z y u w … (2.3.1)

1 2 ( ) ( ) ( ) ( ) x t& = Ax t +B w t +B u t , 1 11 12 ( ) ( ) ( ) ( ) z t =c x t +D w t +D u t , 2 21 22 ( ) ( ) ( ) ( ) y t =c x t +D w t +D u t .

Sedangkan pengontrol K(s) dari model tersebut dapat ditulis dalam bentuk berikut ˆ ˆ ˆ( ) _kˆ( ) _k ( ) x t& = A x t +B y t , ˆ ˆ ˆ ( ) _k ( ) _k ( ) u t =c x t +D y t . Dengan

merupakan variabel keadaan, merupakan keluaran,

merupakan keluaran terkontrol, merupakan masukan kontrol, merupakan gangguan,

merupakan pengontrol keadaan.

n p q m l k x y z u w v ∈ℜ ∈ℜ ∈ℜ ∈ℜ ∈ℜ ∈ℜ

Persamaan (2.3.1), (2.3.2), dan (2.3.3) dapat ditulis dalam bentuk matriks transfer sebagai berikut:

1 2 1 1 1 2 1 1 1 1 2 2 1 2 2 2 2 1 2 2 ( ) ( ) ( ) ( ) ( ) A B B G s G s G s C D D G s G s C D D ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ = _{⎢ ⎥ = ⎢ ⎥} ⎣ ⎦ ⎢ ⎥ ⎣ ⎦ .

Sehingga realisasi matriks transfer G dari persamaan (2.3.1), (2.3.2), dan (2.3.3) dapat dituliskan dalam bentuk ruang keadaan sebagai berikut:

1 2 11 12 1 11 12 21 22 2 21 22 ( ) ( ) ( ) ( ) ( ) A B B G s G s G s C D D G s G s C D D ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ =_{⎢ = ⎢ ⎥} ⎥ ⎣ ⎦ ⎢ ⎥ ⎣ ⎦ .

Dari plant diperumum G(s) dan pengontrol K(s) (Persamaan (2.3.1) sampai (2.3.5) ):

… (2.3.2) … (2.3.3)

… (2.3.4)

… (2.3.8) … (2.3.7) … (2.3.6)

… (2.3.9)

… (2.3.10)

• Substitusi persamaan (2.3.3) dan (2.3.5) ke persamaan (2.3.1) maka

diperoleh:

2 ˆ 2 2 ˆ ˆ 1 2 ˆ 21 2 ˆ 22

( ) ( _k ) ( ) _k ( ) ( _k ) ( ) _k ( )

x t& = A+B D C x t +B C x t + B +B D D w t +B D D u t .

• Substitusi persamaan (2.3.3) ke persamaan (2.3.4) maka diperoleh:

2 21 22

ˆ

ˆ( ) _k ( ) _kˆ( ) _k ( ) _k ( ) x t& =B C x t +A x t +B D w t +B D u t .

• Substitusi persamaan (2.3.3) dan (2.3.5) ke persamaan (2.3.2) maka

diperoleh:

(

11

)

1 12 ˆ 2 12 ˆ ˆ 12 ˆ 21 12 ˆ 22 ( )

( ) ( _k ) ( ) _k ( ) _k ( ) _k u t

z t = C +D D C x t +D C x t + D +D D D w t +D D D .

Dari persamaan (2.3.6), (2.3.7) dan (2.3.8) dapat dibentuk :

2 22 2 2 2 1 2 21 2 21 12 21 1 12 2 12 22 11 12 22 ˆ ˆ ˆ ˆ ( ) ( ) ˆ ˆ ˆ ˆ( ) ( ) ( ) ˆ( ) ˆ ˆ ˆ ( ) ˆ ˆ k k k k k k k k k k k k B D D A B D C B C x t B B D D x t x t B C A B D w t u t x t z t _{C D D C D C D D D} B D D D D D ⎡ ⎤ ⎡ + ⎤ ⎡ + ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎡ ⎤ =⎢ ⎥ +⎢ ⎥ + ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ _{+ +} ⎢ ⎥ ⎣ ⎦ ⎢_⎣ ⎥_⎦ ⎢_⎣ ⎥_{⎦ ⎣ ⎦} & & .

Persamaan (2.3.9) dapat pula dibentuk menjadi bentuk berikut ini

2 2 2 1 2 21 2 22 2 21 1 12 2 12 12 21 22 11 12 22 ( ) ˆ ˆ ˆ ˆ ( ) ˆ( ) ˆ ˆ ˆ ˆ( ) ( ) ˆ ( ) ˆ ˆ ( )

ˆ

ˆ

k k k k k k k k k k k k x t A B D C B C B B D D B D D x t x t x t B C A B D w t z t _{C D D C D C D D D} u t

B D

D

D D D

⎡ ⎤ ⎡ _{+ +} ⎤ ⎡ ⎤ _{⎢ ⎥} ⎢ ⎥ ⎢ ⎥ _{⎢ ⎥} = ⎢ ⎥ ⎢ ⎥ _{⎢ ⎥} ⎢ ⎥ ⎢ ⎥ _{+ + ⎢ ⎥} ⎢ ⎥ ⎣ _{⎦ ⎣ ⎦ ⎣ ⎦} & & _.

Sehingga ruang keadaan matriks transfer dari masukan w ke keluaran z yang dinotasikan Tzw didapat

… (2.3.19) … (2.3.18) … (2.3.17) … (2.3.11) 2 2 2 1 2 21 2 22 2 21 1 12 2 12 12 21 22 11 12 22 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ k k k k zw k k k k k k k k A B D C B C B B D D B D D T B C A B D C D D C D C D D D B D D D D D ⎡ + + ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ + + ⎢ ⎥ ⎣ ⎦ .

Setelah fungsi transfer untuk keeadaan umum, selanjutnya akan dicari fungsi transfer bentuk khusus dari model yang kita inginkan. Asumsikan plant diperumum G(s) dari suatu model khusus dari dinamik plant dan beberapa fungsi bobotnya tersebut sebagai berikut:

1 2 ( ) ( ) ( ) ( ) x t& = Ax t +B w t +B u t , 1 12 ( ) ( ) ( ) z t =c x t +D u t , 2 21 ( ) ( ) ( ) y t =c x t +D w t .

Sedangkan pengontrol K(s) dari model khusus tersebut

ˆ ˆ ˆ( ) kˆ( ) k ( ) x t& = A x t +B y t , ˆ ˆ ˆ ( ) _k ( ) _k ( ) u t =c x t +D y t .

Dari plant diperumum G(s) dan pengontrol K(s) dari bentuk khusus di atas (Persamaan (2.3.12) sampai (2.3.16) ):

• Substitusi persamaan (2.3.14) dan (2.3.16) ke persamaan (2.3.12) maka

diperoleh:

2 ˆ 2 2 ˆ ˆ 1 2 ˆ 21

( ) ( _k ) ( ) _k ( ) ( _k ) ( )

x t_& = A+B D C x t +B C x t + B +B D D w t .

• Substitusi persamaan (2.3.14) ke persamaan (2.3.15) maka diperoleh:

2 ˆ 21

ˆ ˆ

ˆ( ) _k ( ) _kˆ( ) _k ( ) x t& =B C x t +A x t +B D w t .

• Substitusi persamaan (2.3.14) dan (2.3.16) ke persamaan (2.3.13) maka

diperoleh:

1 12 ˆ 2 12 ˆ ˆ 12 ˆ 21

( ) ( _k ) ( ) _k ( ) _k ( )

z t = C +D D C x t +D C x t +D D D w t .

Dari persamaan (2.3.6), (2.3.7) dan (2.3.8) dapat dibentuk :

… (2.3.13) … (2.3.14)

… (2.3.15) … (2.3.16) … (2.3.12)

… (2.3.20) … (2.3.21) … (2.3.22) 2 2 2 1 2 21 2 21 12 21 1 12 2 12 ˆ ˆ ˆ ( ) ( ) ˆ ˆ ˆ ˆ( ) ( ) ˆ( ) ˆ ˆ ˆ ( ) k k k k k k k k k A B D C B C x t B B D D x t x t B C A B D w t x t z t _{C D D C D C D D D} ⎡ + ⎤ ⎡ + ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎡ ⎤ =⎢ ⎥ +⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ₊ ⎣ ⎦ ⎢_⎣ ⎥_⎦ ⎢_⎣ ⎥_⎦ & & _.

Persamaan (2.3.20) dapat dibentuk menjadi persamaan berikut

2 2 2 1 2 21 2 21 1 12 2 12 12 21 ˆ ˆ ˆ ( ) _{( )} ˆ ˆ ˆ ˆ( ) ˆ( ) ˆ ˆ ˆ ( ) ( ) k k k k k k k k k A B D C B C B B D D x t _{x t} x t B C A B D x t z t _{C D D C D C D D D} w t ⎡ _{+ +} ⎤ ⎡ ⎤ _{⎡ ⎤} ⎢ ⎥ ⎢ ⎥ _{⎢ ⎥} = ⎢ ⎥ ⎢ ⎥ _{⎢ ⎥} ⎢ ⎥ ⎢ ⎥ _{+ ⎢⎣ ⎥⎦} ⎣ ⎦ ⎢_⎣ ⎥_⎦ & & _.

Sehingga ruang keadaan matriks transfer dari masukan w ke keluaran z yang dinotasikan Tzw didapat

2 2 2 1 2 21 2 21 1 12 2 12 12 21 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ k k k k k k k k k zw A B D C B C B B D D B C A B D C D D C D C D D D T ⎡ + + ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ + ⎢ ⎥ ⎣ ⎦ .

2.4. Penentuan kontrol yang diperkenankan dan optimal

Setelah matriks transfer didapat selanjutnya akan masuk ke dalam penentuan kontrol yang diperkenankan dan optimal yang meliputi kestabilan internal, eksistensi keterkontrolan, dan pembahasan mengenai transformasi fraksional linier

Seperti yang telah diuraikan diatas mengenai permasalahan kontrol H2 dimana akan mencari pengontrol K yang bersifat proper dan real-rational. Maka selanjutnya akan diterangkan terlebih dahulu mengenai proper dan strictly-proper

Definisi Proper dan Strictly Proper :

• G(s) dikatakan proper jika (G j∞ terbatas atau jika derajat tertinggi ) penyebut dari G(s) lebih besar atau sama dengan derajat tertinggi pembilang G(s)

… (2.4.1.1)

… (2.4.1.2) • G(s) dikatakan strictly proper jika (G j∞ =0 atau jika derajat tertinggi )

pembilang G(s) sama dengan derajat tertinggi penyebut G(s).

2.4.1. Kestabilan Internal

Sebelum membahas lebih lanjut mengenai stabil internal akan dijelaskan dulu beberapa istilah berikut ini

(A,B2) dapat distabilkan ekivalen dengan pernyataan berikut

i. Matrik [A−λI B, ₂] memiliki rank baris penuh untuk semua Re( )λ ≥ 0

ii. Untuk semua

x

dan

λ

sedemikian sehingga x A* =x*λ dan

R e ( )λ ≥ maka 0 x*B ≠ 0

iii. Terdapat matrik F sedemikian rupa sehingga A + B2F stabil

(C2,A) dapat dideteksi ekivalen dengan pernyataan berikut ini:

i. Matrik 2 A I C λ − ⎡ ⎤ ⎢ ⎥

⎣ ⎦ memiliki rank kolom penuh untuk semua Re( )λ ≥ 0 ii. Untuk semua x dan λ sedemikian sehingga A x = λ dan Re( ) 0x λ ≥

maka Cx≠0

iii. Terdapat matrik L sedemikian sehingga A + LC stabil iv. (A C stabil *, *₂)

Definisi 2 :

Suatu sistem seperti diagram blok di atas dikatakan stabil secara internal jika pada matrik transfer :

1 _{1 1} 1 1 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) = ( ) ( ) − _{− −} − − − − − − − ⎡ − − ⎤ ⎡ ⎤ = ⎢ ⎥ ⎢₋ ⎥ _{− −} ⎣ ⎦ ⎣ ⎦ ⎡ + − − ⎤ ⎢ _{− −} ⎥ ⎣ ⎦ I K I KG K I KG G I G I KG I KG I K I GK G K I GK I GK G I GK

… (2.4.2.3)

2.4.2. Eksistensi Pengontrol

Eksistensi pengontrol dinyatakan dengan lemma berikut ini :

Lemma 2:

Terdapat pengontrol K (Proper) yang mencapai stabilitas secara internal

jika dan hanya jika ( ,A B dapat distabilkan dan ₂) (C A dapat dideteksi. Lebih ₂, ) lanjut, misalkan terdapat F dan L sedemikian sehingga A+B F₂ dan A+LC₂

stabil maka pengontrol dinyatakan oleh

2 2 ( ) 0 + + − ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥ ⎢}= _⎥ ⎣ ⎦ ⎣ ⎦ c c c c A B A B F LC L K s C D F Bukti Lemma 2 :

• (=>) Jika ( ,A B tidak dapat distabilkan dan ₂) (C A tidak dapat dideteksi ₂, )

maka terdapat beberapa nilai eigen dari A% yang berada di bidang Re(s)>0 sehingga tidak ada L dan F sedemikian sehingga A+LC₂ dan A+B F₂

stabil.

• (<=) Dengan asumsi dapat distabilkan dan dapat dideteksi, terdapat F dan

L sedemikian sehingga A+B F₂ dan A LC+ ₂ stabil. Misalkan K(s) adalah pengontrol yang diberikan pada lemma, maka matriks transfer dari w ke

… (2.4.3.1)

2.4.3. Transformasi Fraksional Linier

Pada bagian ini akan dibahas mengenai transformasi fraksional linier yang akan digunakan untuk parameterisasi pengontrol. Parameterisasi pengontrol merupakan salah satu cara yang digunakan untuk memperoleh bentuk pengontrol

K yang optimal dan tunggal.

Sebelum melangkah ke penentuan pengontrol yang optimal dan tunggal maka akan diberikan terlebih dahulu mengenai pengertian transformasi fraksional linier terlebih dahulu.

Definisi 3 :

Misalkan M adalah matriks yang dipartisi sebagai berikut:

1 2 1 2 11 12 ( ) ( ) 21 22 , + × + ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ = M M ∈ p p q q M M M

M z2 w2 y2 u2 … (2.4.3.2) dan misalkan q2 p2 l ×

Δ ∈

dan q1 p1 u ×

Δ ∈

adalah dua buah matrik yang

lain,

maka:

• Lower LFT yang terkait dengan Δ adalah pemetaan yang didefinisikan _l sebagai: _{( , ) :} q2 p2 q1 p1 l F M • × → × dengan: F Ml( , l) M11 M12 l(I M22 l) 1M21 − Δ = + Δ − Δ jika (I M22 l) 1 − − Δ ada.

• Upper LFT yang terkait dengan Δ adalah pemetaan yang didefinisikan _u sebagai: _{( , ) :} q1 p1 q2 p2 u F M • × → × , dengan: F Mu( , u) M22 M21 u(I M11 u) 1M12 − Δ = + Δ − Δ jika (I M11 l) 1 − − Δ ada.

Terminologi lower LFT dan upper LFT diperoleh dari diagram berikut yang merupakan representasi dari F M_l( ,Δ dan ( , )_l) F M_u Δ _u

Gambar 2.4.3.1 : a. F M_l( ,Δ , b. ( , )_l) F M_u Δ _u

Selanjutnya dengan mensubstitusi kembali Ac,Bc,Cc,Dc diperoleh:

2 2 2 2 2 2 2 0 A B F A LC A LC A B F LC LC A B F + ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥ ⎢}= _⎥ − + + − + ⎣ ⎦ ⎣ ⎦ %

karena seluruh elemen matriksA%stabil, makaA% stabil.

Untuk penentuan pengontrol ini diperlukan beberapa asumsi berikut:

a. ( ,A B dapat di stabilkan dan ₂) (C A dapat dideteksi, ₂, )

b. R₁ =D D₁₂* ₁₂>0 dan R₁ =D D_{21 21}* >0, M l Δ z1 w1 y1 u1 Δ_u a. b.

… (2.4.3.3) … (2.4.3.4) … (2.4.3.4) … (2.4.3.5) … (2.4.3.6) … (2.4.3.7) … (2.4.3.8) … (2.4.3.9) … (2.4.3.10) c. 2 1 12 A j I B C D ω − ⎡ ⎤ ⎢ ⎥

⎣ ⎦mempunyai rank kolom penuh untuk semua

ω

,

d. 1 2 21 A j I B C D ω − ⎡ ⎤ ⎢ ⎥

⎣ ⎦mempunyai rank baris penuh untuk semua

ω

,

Akibat dari keempat asumsi diatas maka diperoleh dua buah matrik Hamiltonian berikut: 1 * 1 * 2 1 12 1 2 1 2 2 * 1 * 1 * * 1 12 1 12 1 2 1 12 1 * 1 * * 1 1 21 2 2 2 2 2 2 * 1 * * 1 1 21 2 21 1 1 21 2 2 : , ( ) ( ) ( ) : , ( ) ( ) A B R D C B R B H C I D R D C A B R D C A B D R C C R C J B I D R D B A B D R C − − − − − − − − ⎡ − − ⎤ = ⎢_{− − − −} ⎥ ⎣ ⎦ ⎡ − − ⎤ = ⎢_{− − − −} ⎥ ⎣ ⎦

dimana H dan J₂ 2 ∈ dom(Ric) dan lebih jauh, X2 := Ric(H2) ≥ 0 dan

Y2:=Ric(J2)≥ 0 Definisikan 1 * * 2: 1 ( 2 2 12 1) F = −R− B X +D C , dan * * 1 2: ( 2 2 1 21) 2 L = − Y C +B D R− , dan juga 2 2 2 2 2 2 1 1 12 2 2 2 1 1 2 21 2 2 2 2 2 : , : , : , : , ˆ : . F F L L A A B F C C D F A A L C B B L D A A B F L C = + + = + = + = + = + +

Sebelum masuk ke dalam teorema yang utama maka diperlukan lemma berikut ini :

Lemma 3:

… (2.4.3.11) … (2.4.3.12) … (2.4.3.13) … (2.4.3.14) … (2.4.3.15) … (2.4.3.16) … (2.4.3.17) 2 2 1 2 2 1 1 2 1 12 1 / F / F A B R U , C D R − − ⎡ ⎤ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ dan 2 1 2 1 2 1 2 2 2 2 21 L L / / A B V R − C R − D ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦

dimana U adalah inner dan V adalah co-inner, U G~ _c∈RH₂⊥ dan G V_f ~∈RH₂⊥

Bukti :

Pembuktian menggunakan sifat-sifat dasar aljabar dari perkalian matriks blok. Dari U diperoleh: 2 1 2 1 2 1 2 1 2 1 12 − − ⎡ − − ⎤ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ * * F F ~ / * / * A C U ( s ) R B R D .

Sehingga selanjutnya didapat

1 1 1 1 2 2 1 1 2 1 2 1 2 1 12 1 0 − − − ⎡ − − − ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ * * * F F F F ~ / F / * / * F A C C C U U( s ) A B R R B R D C I , dan 1 1 1 2 1 2 1 2 1 12 1 0 0 0 − − ⎡ − − ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ * * F F F ~ c F / * / * F A C C U G ( s ) A I R B R D C .

Dengan menggunakan transformasi similaritas

2 0 − ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ I X I ,

pada U U maupun pada ~ U G dan akibat persamaan ~ _c

2 2 2 2 * * 2 2 1 1 0 F F F F A X +X A +C C = , diperoleh 1 2 2 1 1 2 1 2 0 0 0 0 * F ~ / F / * A U U( s ) A B R I R B I − − ⎡ − ⎤ ⎢ ⎥ =_{⎢ ⎥}= ⎢ ⎥ ⎣ ⎦ , dan

… (2.4.3.18) … (2.4.3.19) … (2.4.3.20) … (2.4.3.21) … (2.4.3.22) … (2.4.3.23) 2 2 2 1 2 1 2 1 2 1 2 0 0 0 0 0 * F * ~ F c F / * / * A X A X U G ( s ) A I R R B R B ⊥ − − ⎡ − − ⎤ ⎡ − − ⎤ ⎢ ⎥ =_{⎢ ⎥}=_{⎢ ⎥}∈ ⎣ ⎦ ⎢ ⎥ ⎣ ⎦ H ,

dengan sifat dualitas, maka G Vf ~ R 2 ⊥

∈ H dan V adalah co-inner

Dengan menggunakan lemma ini selanjutnya kita akan masuk ke teorema yang utama.

Teorema 1:

Terdapat kontrol optimal yang tunggal

2 2 2

ˆ

( ) :

0

opt

A

L

K

s

F

⎡

₋

⎤

= ⎢

⎥

⎣

⎦

, dengan: 2 2 2 _{1/ 2 * *} 1 1 2 1 2 1 1 2 2 2 2 2 2

min T_zw = G B_c + R F G_f =trace B X B( )+trace R F Y F( ).

Bukti:

Misalkan parameterisasi pengontrol K( s )=F ( M ,Q )_{l 2} ,Q∈RH₂ dengan

2 2 2 2 0 0 ⎡ − ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ˆA L B M ( s ) F I C I , maka T_zw=F N Q₁

(

,

)

dengan 2 1 2 1 1 12 12 2 21 0 0 0 0 0 − ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ = ⎢ − ⎥ ⎢ ⎥ ⎣ ⎦ F L L F A B F B B A B N C D F D C D .

Berdasarkan teorema di atas, diperoleh bahwa F G K1

(

,

)

=Tzw =N11+N QN12 21,

dengan

11 11 12 2 2 21

… (2.4.3.24) … (2.4.3.25) … (2.4.3.26) … (2.4.3.27) … (2.4.3.28) … (2.4.3.29) … (2.4.3.30) … (2.4.3.31) … (2.4.3.32) … (2.4.3.33) … (2.4.3.34) … (2.4.3.35) 12 12 2 N =G M , 21 2 21 N = %M G ,

( )

2 2 F A B M s F I ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦,

( )

2 L A L M s C I ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ % ,

( )

1 F F A L X s C I − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦,

( )

AL B1L X s F I − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ % ,

( )

0 F A L Y s F − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦,

( )

0 L A L Y s F − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ % . Sehingga diperoleh 11 12 21 zw T =N +N QN 1 2 2 1 1 0 1 12 0 2 21 F L A B A B A B A L A B C C D F I F C D ⎧⎡ ⎤ ⎡ ⎤⎡ ⎤ ⎡ − ⎤⎡ ⎤⎫ ⎪ ⎪ =_{⎨⎢ ⎥ ⎢}+ _{⎥⎢ ⎥ ⎢ ⎥⎢ ⎥⎬} ⎪⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦⎣ ⎦⎪ ⎩ ⎭ 2 2 1 1 12 2 21 2 21 L F A B A B A L A B Q C D F I C D C D ⎡ ⎤⎡ ⎤ ⎡ ⎤ ⎡ ⎤ + ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦. 2 2 2 21 1 2 1 1 1 12 12 0 0 0 0 0 L F A B F B A LC LD A B A B A B C C D F D F ⎧ ⎡ ⎤ ⎡ − − ⎤⎫ ⎡ ⎤ ⎪ ⎢ ⎥ ⎢ ⎥⎪ =_{⎨⎢ ⎥ ⎢}+ _{⎥ ⎢ ⎥⎬} ⎣ ⎦ ⎪ _{⎢⎣ ⎥ ⎢⎦ ⎣ ⎥⎦}⎪ ⎩ ⎭ 2 2 2 21 2 1 1 12 12 2 2 21 0 0 L F A B F B A LC LD A B Q A B C D F D C C D ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ + ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ 1 2 1 2 1 1 0 1 12 0 1 12 2 21 F F L L F L L F F F A B A B A B A B A B Q C C D F C D C D ⎡ ⎤ ⎡ ⎤⎡ ⎤ ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥ ⎢}+ _{⎥⎢ ⎥}+_{⎢ ⎥ ⎢ ⎥} ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦

… (2.4.3.36) … (2.4.3.37) … (2.4.3.38) … (2.4.3.39) … (2.4.3.40) … (2.4.3.41) 1 2 1 2 1 1 0 1 12 0 1 12 2 21 F F L L F L L F F F A B A B A B A B A B F Q C C D F C D C D ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ =_{⎢ ⎥ ⎢}+ _{⎥ ⎢ ⎥}+_{⎢ ⎥ ⎢ ⎥} ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦. 1/ 2 1/ 2 1/ 2 1 1 1 2 zw c f T =G B −UR FG +UR QR V

Dari lemma 3 diperoleh bahwa G B dan _{c 1} U saling orthogonal. Sehingga

2 2 2 _{1/ 2 1/ 2 1/ 2} 1 1 1 2 2 2 2 zw c f T = G B + UR FG −UR QR V , 2 2 2 _{1/ 2 1/ 2 1/ 2} 1 1 1 2 2 2 2 zw c f T = G B + R FG −UR QR V .

Dan karena G dan _f V juga orthogonal menurut lemma 3 di atas, maka:

2 2 2 1/ 2 1/ 2 1/ 2 1 1 1 2 2 2 ₂ zw c f T = G B + R FG −R QR V , 2 2 2 2 _{1/ 2 1/ 2 1/ 2} 1 1 1 2 2 2 2 2 zw c f T = G B + R FG + R QR V .

Persamaan di atas jelas menunjukkan bahwa Q= memberikan kontrol 0

2

H yang optimal dan tunggal. Maka K =F M₁

(

₂, 0

)

adalah pengontrol yang optimal dan tunggal.