MAKALAH
DISTRIBUSI PROBABILITAS DISKRIT (BINOMIAL DAN
POISSON)
diajukan untuk memenuhi salah satu tugas mata kuliah Statistika yang di bina oleh Bapak Slamet Abadi M.Si.
Disusun oleh :
Agung Dwi Julianto (1610631090007) Dean Rezfy Pratama (1610631090042)
Iyana Nasrudin (1610631090082)
Rio Rinaldi (1610631090130)
UNIVERSITAS SINGAPERBANGSA KARAWANG
FAKULTAS PERTANIAN
AGROTEKNOLOGI
KARAWANG
2016
KATA PENGANTAR
Puji syukur kami panjatkan kehadirat Tuhan Yang Maha Esa karena dengan rahmat, karunia, serta taufik dan hidayah-Nya saya dapat menyelesaikan makalah tentang Distribusi Probabilitas Diskrit ini dengan baik meskipun banyak kekurangan didalamnya. Dan juga saya berterima kasih pada Bapak Slamet Abadi M.Si. selaku Dosen mata kuliah Statistika, UNSIKA yang telah memberikan tugas ini kepada saya.
Saya sangat berharap makalah ini dapat berguna dalam rangka menambah wawasan serta pengetahuan kita mengenai Distribusi Probabilitas Diskrit Binomial dan Poisson. Saya juga menyadari sepenuhnya bahwa di dalam makalah ini terdapat kekurangan dan jauh dari kata sempurna. Oleh sebab itu, saya berharap adanya kritik, saran dan usulan demi perbaikan makalah yang telah saya buat di masa yang akan datang, mengingat tidak ada sesuatu yang sempurna tanpa saran yang membangun.
Semoga makalah sederhana ini dapat dipahami bagi siapapun yang membacanya. Sekiranya laporan yang telah disusun ini dapat berguna bagi saya sendiri maupun orang yang membacanya. Sebelumnya kami mohon maaf apabila terdapat kesalahan kata-kata yang kurang berkenan dan kami memohon kritik dan saran yang membangun dari anda demi perbaikan makalah ini di waktu yang akan datang.
Karawang, 19 Februari 2017
DAFTAR ISI
KATA PENGANTAR...2 DAFTAR ISI...3 BAB I PENDAHULUAN...4 1.1 Latar Belakang...4 1.2 Rumusan Masalah...5 1.3 Tujuan...5 BAB II PEMBAHASAN...6 2.1 Pengertian Probabilitas...62.3 Manfaat Probabilitas dalam Penelitian...8
2.4 Menghitung Probabilitas atau Peluang Suatu Kejadian...9
3.1 Definisi Distribusi Binomial...10
3.2 Ciri-ciri Distribusi Binomial...11
3.3 Penerapan Distribusi Binomial...11
3.4 Contoh Soal Distribusi Binomial dan Cara Penyelesaiannya...12
4.1 Definisi Distribusi Poisson...16
4.2 Ciri-ciri Distribusi Poisson...17
4.3 Penerapan Distribusi Poisson...19
4.4 Contoh Soal Distribusi Poisson dan Cara Penyelesaiannya...20
BAB III PENUTUP...21
5.1 Kesimpulan...21
BAB I
PENDAHULUAN
1.1 Latar Belakang
Baik di dalam dunia pertanian, ekonomi, sosial budaya maupun dunia teoritis (termasuk dunia komputer tentunya), kita sering menghadapi suatu yang sering disebut sebagai “ketidakpastian”. Ketidakpastian terjadi akibat keterbatsan manusia itu sendiri di dalam dunianya dalam mengukur/menghitung/menalar/melamar sesuatu hal yang lebih baik yang akan datang maupun yang ada di depan mata, termasuk yang telah terjadi. Sudah sejak awal dari awal zaman, ketidakpastian diantisipasi manusia dengan berbagai cara. Ada yang bersifat prophecy dan supranatural, ada pula yang lebih rasional dengan mempelajari periodisitas (pengulangan) gejala alam untuk mengurangi tingkat ketidakpastian itu hingga sampai ke tingkat yang lebih manageble. Namun, ketidakpastian itu tetap mewarnai kehidupan manusia karena ketidakpastian itu mungkin menjadi faktor pemicu dinamika roda kehidupan itu sendiri. Dengan kata lain, walau ketidakpastian itu seringkali menjadi sumber kesulitan, tetapi juga sekaligus merupakan blessing.
Teori probabilitas bisa dikatakan merupakan salah satu ilmu untuk
“mengukur” ketidakpastian hingga ke tingkat yang lebih manageble dan predictable. Teori probabilitas digunakan bukan hanya untuk hal-hal yang praktis, bahkan juga untuk hal-hal yang teoritis ketika model-model matematis tidak dapat lagi disusun secara komprehensif untuk memecahkan suatu masalah.
kebohongan (dikenal sebagai kebohongan statistika) ketika statistika
digunakan sementara model dasar probabilitas yang terkait tidak sesuai atau relevan dengan situasi yang sebenarnya. Simulasi dan teori antrian dapat dikatakan juga sebagi turunan dan teori probabilitas. Dengan simulasi maka perilaku suatu sistem atau rancangan dapat dipelajari. Teori probabilitas digunakan dalam menentukan perilaku secara lebih kuantitatif dari apa yang disimulasikan.
Kejadian yang sering atau jarang terjadi dikatakan mempunyai peluang terjadi yang besar atau kecil. Keseluruhan nilai-nilai peluang biasa digunakan dalam
kehidupan sehari-hari. Dalam mengaplikasikan statistika terhadap permasalahan sains, industri, atau sosial, pertama-tama dimulai dari mempelajari populasi.
Tiga buah sebaran teoritis yang paling terkenal, diantaranya dua buah sebaran peluang yang diskrit dan sebaran yang kontinyue Kedua sebaran yang teoritis yang diskrit itu ialah sebaran binomial dan sebaran Poisson. Sebaran kontinyu nya adalah sebaran normal.
1.2 Rumusan Masalah
Berdasarkan latar belakang masalah tersebut di atas, maka masalah pokok yang dirumuskan untuk makalah ini adalah:
1. Apa itu probabilitas?
2. Bagaimana pengaplikasian probabilitas dalam bidang pertanian? 3. Apa manfaat probabilitas dalam penelitian?
4. Bagaimana cara menghitung probabilitas dalam suatu kejadian? 1.3 Tujuan
Tujuan pembuatan makalah ini selain untuk melengkapi tugas mata kuliah Statistika, yaitu untuk mengetahui probabilitas lebih jauh, mulai dari cara
menghitungnya, dan memahami konsep distribusi binomial yang merupakan bagian dari probabilitas itu sendiri.
BAB II
2.1 Pengertian Probabilitas
Dalam kehidupan sehari-hari kita sering dihadapkan dengan beberapa pilihan yang harus kita tentukan memilih yang mana. Biasanya kita dihadapkan dengan kemungkinan-kemungkinan suatu kejadian yang mungkin terjadi dan kita harus pintar-pintar mengambil sikap jika menemukan keadaan seperti ini, misalkan saja pada saat kita ingin bepergian, kita melihat langit terlihat mendung. Dalam keadaaan ini kita dihadapkan antara 2 permasalahan, yaitu kemungkinan terjadinya hujan serta kemungkinan langit hanya mendung saja dan tidak akan turun hujan. Statistik yang membantu permasalahan dalam hal ini adalah probabilitas.
Probabilitas didefinisikan sebagai peluang atau kemungkinan suatu kejadian, suatu ukuran tentang kemungkinan atau derajat ketidakpastian suatu peristiwa (event) yang akan terjadi di masa mendatang. Rentangan probabilitas antara 0 sampai dengan 1. Jika kita mengatakan probabilitas sebuah peristiwa adalah 0, maka peristiwa tersebut tidak mungkin terjadi. Dan jika kita mengatakan bahwa probabilitas sebuah peristiwa adalah 1 maka peristiwa tersebut pasti terjadi. Serta jumlah antara peluang suatu kejadian yang mungkin terjadi dan peluang suatu kejadian yang mungkin tidak terjadi adalah satu, jika kejadian tersebut hanya memiliki 2 kemungkinan kejadian yang mungkin akan terjadi.
Contoh: Ketika David ingin pergi kerumah temannya, dia melihat langit dalam keadaan mendung, awan berubah warna menjadi gelap, angin lebih kencang dari biasanya serta sinar matahari tidak seterang biasanya. Bagaimanakah tindakan David sebaiknya?
Ketika David melihat keadaan seperti itu, maka sejenak dia berpikir untuk membatalkan niatnya yang akan pergi ke rumah temannya. Ini dikarenakan dia berhipotesis bahwa sebentar lagi akan turun hujan dan kecil kemungkinan bahwa hari ini akan tidak hujan, mengingat gejala-gejala alam yang mulai nampak.
Probabilitas dalam cerita tadi adalah peluang kemungkinan turunnya hujan dan peluang tidak turunnya hujan. Selain definisi di atas ada juga definisi klasiknya yaitu:
Eksperimen : semua aktivitas yang dapat menghasilkan out comes. Sample space set of all possible out comes.
Out comes: sesuatu yang diamati / hasil observasi.
Event: Sample space (bagian dari himpunan dari seluruh out comes yang mungkin muncul dalam satu set eksperimen). Contoh : Pelemparan mata uang (2 titik), dadu (6 titik). Bila terdapat n kejadian setara yang salah satunya harus terjadi dan S dinyatakan sebagai kejadian sukses, maka probabilitas sukses adalah S/n.
Mutually Exclusive (bertentangan) : munculnya event yang satu, menyebabkan tidak munculnya event yang lain.
Collectively exhausive (Lengkap) : munculnya head and tail pada sebuah lemparan koin dan tidak ada lagi out comes yang muncul ( salah satu harus terjadi).
2.2 Pengaplikasian probabilitas dalam bidang pertanian
Dalam bidang pertanian terkadang hal peluang sering terjadi pada saat pembibitan, penanaman, pengendalian hama, dan panen. Hal tersebut terjadi karena dampak kegagalan dari susunan pertanian itu tidak ditekankan dengan baik oleh petani. Maka dari itu rancangan peluang harus dibuat secara demikian agar suatu kejadian yang akan datang bisa diperkirakan walaupun tidak 100 persen terjadi.
Berikut contoh probabilitas peluang di bidang pertanian:
Petani dapat memperkirakan waktu panen berdasarkan keadaan cuaca,
seringkali petani salah memperkirakannya. Tetapi di sini yang di maksud yaitu di saat cuaca cerah, contohnya tanaman kedelai sebentar lagi akan dipanen lalu kemudian tiba-tiba hujan lebat, akibatnya tanaman kedelai banyak yang membusuk. Karena tanaman ini lebih cocok ditanam pada musim panas.
Pada saat petani melakukan penyemprotan insektisida pada tanaman padi seluas 500m² dengan volume air pada tangki sebesar 5 liter, petani harus bisa memperkirakan volume larutan air pada tangki tersebut habis secara rata.
2.3 Manfaat Probabilitas dalam Penelitian
Manfaat probabilitas dalam kehidupan sehari-hari adalah membantu kita dalam mengambil suatu keputusan, serta meramalkan kejadian yang mungkin terjadi. Jika kita tinjau pada saat kita melakukan penelitian, probabilitas memiliki beberapa fungsi antara lain:
Membantu peneliti dalam pengambilan keputusan yang lebih tepat.
Pengambilan keputusan yang lebih tepat dimaksudkan tidak ada keputusan yang sudah pasti karena kehidupan mendatang tidak ada yang pasti kita ketahui dari sekarang, karena informasi yang didapat tidaklah sempurna. Dengan teori probabilitas kita dapat menarik kesimpulan secara tepat atas
hipotesis yang terkait tentang karakteristik populasi. Menarik kesimpulan secara tepat atas hipotesis (perkiraan sementara yang belum teruji
kebenarannya) yang terkait tentang karakteristik populasi pada situasi ini kita hanya mengambil atau menarik kesimpulan dari hipotesis bukan berarti kejadian yang akan datang kita sudah ketehaui apa yang akan tertjadi. Mengukur derajat ketidakpastian dari analisis sampel hasil penelitian dari
suatu populasi. Contoh:
Ketika diadakannya minat petani penggunaan pupuk dari tahun 2000, pemerintah mendapatkan data perbandingan antara jumlah penggunaan pupuk organik berbanding jumlah penggunaan pupuk urea adalah memiliki perbandingan 5:6, sedangkan hasil data minat petani pada tahun 2010 menunjukan hasil
perbandingan jumlah penggunaan pupuk organik berbanding jumlah penggunaan pupuk urea adalah 5:7. Maka pemerintah dapat mengambil keputusan bahwa setiap tahunnya dari tahun 2000 hingga 2010 jumlah pengunaan pupuk urea berkembang lebih pesat dari pada jumlah penggunaan pupuk organik.
2.4 Menghitung Probabilitas atau Peluang Suatu Kejadian
Jika tadi kita hanya memperhatikan peluang suatu kejadian secara kualitatif, hanya memperhatikan apakah kejadian tersebut memiliki peluang besar akan terjadi atau tidak. Disini kita akan membahas nilai dari probabilitas suatu kejadian secara kuantitatif. Kita bisa melihat apakah suatu kejadian berpotensi terjadi ataukah tidak. Misalkan kita memiliki sebuah koin yang memiliki muka gambar dan angka, jika koin tersebut kita lemparkan keatas secara sembarang, maka kita memiliki 2 pilihan yang sama besar dan kuat yaitu peluang munculnya angka dan peluang munculnya gambar. Jika kita perhatikan secara seksaama, pada satu koin hanya terdiri dari satu muka gambar dan satu muka angka, maka peluang munculnya angka dan gambar adalah sama kuat yaitu ½. 1 menyatakan hanya satu dari muka pada koin yang mungkin muncul, entah itu gambar maupun angka sedangkan 2 menyatakan banyaknya kejadian yang mungkin terjadi pada pelemparan koin, yaitu munculnya gambar + munculnya angka.
Jika kita berbicara tidak lagi 2 kejadian yaitu menyangkut banyak kejadian yang mungkin terjadi, mengingat dan dari hasil pengumpulan dan penelitian data diperoleh suatu rumus sebagai berikut. Jika terdapat N peristiwa, dan nA dari N peristiwa tersebut membentuk kejadian A, maka probabilitas A adalah : P(A) = nA N
Dimana:
n = banyaknya kejadian
N = kejadian seluruhnya/peristiwa yang mungkin terjadi Contoh 1:
Suatu mata uang logam yang masing-masing sisinya berisi gambar dan angka dilemparkan secara bebas sebanyak 1 kali. Berapakah probabilitas munculnya gambar atau angka?
Jawab :
n = 1; N = 2 P(gambar atau angka) = n N= 1 2 atau 50%
Contoh 2: Berapa peluang munculnya dadu mata satu pada satu kali pelemparan? Jika kita tinjau pada sebuah dadu hanya memiliki 1 buah mata dadu bermata 1, sedangkan pada dadu terdapat 6 mata yaitu mata 1 sampai mata 6.
Maka P ( A )=n
N
¿1 6
Probabilitas mempunyai beberapa aturan, diantaranya:
Jika n = 0 maka peluang terjadinya suatu kejadian pada keadaan ini adalah sebesar P(A)= 0 atau tidak mungkin terjadi.
Jika n merupakan semua anggota N maka probabilitasnya adalah satu, atau kejadian tersebut pasti akan terjadi.
Probabilitas suatu kejadian memiliki rentangan nilai. Jika E menyatakan bukan peristiwa E maka berlaku.
3.1 Definisi Distribusi Binomial
Dalam statistik probabilitas dikenal dengan distribusi. Salah satu jenis
distribusi variabel random diskrit yang paling sederhana adalah distribusi binomial. Distribusi Binomial adalah distribusi untuk proses Bernoulli. Distribusi ini dikemukakan pertama kali oleh seorang ahli matematika bangsa Swiss yang bernama J. Bernoulli (1654-1705).
Distribusi Binomial adalah suatu distribusi probabilitas yang dapat digunakan bilamana suatu proses sampling dapat diasumsikan sesuai dengan proses Bernoulli. Misalnya, dalam perlemparan sekeping uang logam sebanyak 5 kali, hasil setiap ulangan mungkin muncul sisi gambar atau sisi angka. Begitu pula, bila kartu diambil berturut-turut, kita dapat memberi label “berhasil” bila kartu yang terambil adalah kartu merah atau “gagal” bila yang terambil adalah kartu hitam. Ulangan-ulangan tersebut bersifat bebas dan peluang keberhasilan setiap ulangan tetap sama, yaitu sebasar ½..(Ronald E. Walpole).
1. Jumlah percobaan merupakan bilangan bulat. Contoh melambungkan koin 2 kali, tidak mungkin 2½ kali.
2. Setiap eksperimen mempunyai dua outcome (hasil). Contoh: sukses atau gagal, laki-laki atau perempuan, sehat atau sakit.
3. Peluang sukses sama setiap ekperimen. Contoh: Jika pada lambungan pertama peluang keluar mata H/sukses adalah ½, pada lambungan seterusnya juga ½. Jika sebuah dadu, yang diharapkan adalah keluar mata lima, maka dikatakan peluang sukses adalah 1/6, sedangkan peluang gagal adalah 5/6.Untuk itu peluang sukses dilambangkan p, sedangkan peluang gagal adalah (1-p) atau biasa juga dilambangkan q, di mana q = 1-p.
3.2 Ciri-ciri Distribusi Binomial
Distribusi Binomial dapat diterapkan pada peristiwa yang memiliki ciri-ciri percobaan Binomial atau Bernoulli trial sebagai berikut :
1. Setiap percobaan hanya mempunyai 2 (dua) kemungkinan hasil: sukses (hasil yang dikehendaki) dan gagal (hasil yang tidak dikehendaki).
2. Setiap percobaan beersifat independen atau dengan pengembalian.
3. Probabilita sukses setiap percobaan harus sama, dinyatakan dengan p. Sedangkan probabilita gagal dinyatakan dengan q, dan jumlah p dan q harus sama dengan satu.
4. Jumlah percobaan, dinyatakan dengan n, harus tertentu jumlahnya. 3.3 Penerapan Distribusi Binomial
Beberapa kasus dimana distribusi normal dapat diterapkan yaitu:
1. Jumlah pertanyaan dimana anda dapat mengharapkan bahwa terkanan anda benar dalam ujian pilihan ganda.
2. Jumlah asuransi kecelakaan yang harus dibayar oleh perusahaan asuransi. 3. Jumlah lemparan bebas yang dilakukan oleh pemain basket selama satu
musim.
b(x ;n ; p)=C n xp x qn−x= n ! x !(n−x)! p x qn−x Keterangan: x = 0,1,2,3,…,n n = banyaknya ulangan
x = banyaknya keberhasilan dalam peubah acak x p = peluang berhasil dalam setiap ulangan
q = peluang gagal, dimana q = 1-p dalam setiap ulangan 3.4 Contoh Soal Distribusi Binomial dan Cara Penyelesaiannya
Berdasarkan data biro perjalanan PT Mandala Wisata air, yang khusus menangani perjalanan wisata turis manca negara, 20% dari turis menyatakan sangat puas berkunjung ke Indonesia, 40% menyatakan puas, 25% menyatakan biasa saja dan sisanya menyatakan kurang puas. Apabila kita bertemu dengan 5 orang dari peserta wisata turis manca negara yang pernah berkunjung ke Indonesia, berapakah probabilitas :
a) Paling banyak 2 di antaranya menyatakan sangat puas. b) Paling sedikit 1 di antaranya menyatakan kurang puas c) Tepat 2 diantaranya menyatakan biasa saja
d) Ada 2 sampai 4 yang menyatakan puas. Jawab :
Diketahui n = 5; Ditanyatakan:
a) Paling banyak 2 di antaranya menyatakan sangat puas (p(x) ≤ 2). p=0,20; b(x; n, p) = b(0; 5; 0,20) + b(1; 5; 0,20) + b(2; 5; 0,20)
= 0.32768 + 0.40960 + 0.20480 = 0.94208
Maka hasil p(x) ≤ 2 = 0.94208
Jadi: p(x) ≥ 1 = b(1; 5; 0,15) + b(2; 5; 0,15) + b(3; 5; 0,15) + b(4; 5; 0,15) + b(5; 5; 0,15)
= 0,3915 + 0,1382 + 0,0244 + 0,002 +0,0001 = 0,5562
c) Tepat 2 diantaranya menyatakan biasa saja (p(x)=2). p=0,25
d) Ada 2 sampai 4 yang menyatakan puas (x ≤ 2 x ≤ 4) P=0,40;
Jadi (x ≤ 2 x ≤ 4) = b(2; 5;0.40) + b(3; 5, 0.40) + b(4; 5, 0.40) = 0.3456 +
0.2304 + 0.0768 = 0.6528 Analisis masing – masing point :
a) Sebanyak paling banyak 2 dari 5 orang dengan jumlah 0.94208 atau 94,28% yang menyatakan sangat puas adalah sangat besar.
b) Paling sedikit 1 dari 5 orang (berarti semuanya) dengan jumlah 0,5563 atau 55,63% yang menyatakan kurang puas dapat dikatakan cukup besar (karena lebih dari 50%).
c) Tepat 2 dari 5 orang yang menyatakan biasa saja dengan jumlah 0,2637 atau 26,37% adalah kecil (karena dibawah 50%).
d) Ada 2 sampai 4 yang menyatakan puas dengan jumlah 0,6528% atau 65,28% dapat dikatakan cukup besar.
Analisis keseluruhan :
a) Persentase Jika diambil persentase terbesar tanpa memperhatikan jumlah X, maka persentase terbesar ada di point pertama (a) yaitu 94,28% yang menyatakan sangat puas. Hal tersebut menandakan banyak turis manca negara yang sangat menyukai Indonesia.
b) Nilai x Jika dilihat dari jumlah x, maka perlu diperhatikan point kedua (b). Jumlah x adalah paling sedikit 1 dari 5 orang (berarti x>=1) yaitu 55,63% yang menyatakan kurang puas.Hal tersebut berarti kelima (semua) turis manca negara kurang puas terhadap kunjungannya ke Indonesia.
4.1 Definisi Distribusi Poisson
Distribusi Poisson disebut juga distribusi peristiwa yang jarang
terjadi,Distribusi Poisson diberi nama sesuai dengan penemunya yaitu Siemon D. Poisson (1781-1841), seorang ahli matematika bangsa Perancis. Distribusi Poisson termasuk distribusi teoritis yang memakai variable random (variable acak) diskrit.
Distribusi poisson adalah,
Distribusi nilai-nilai bagi suatu variabel random X (X diskret), yaitu
banyaknya hasil percobaan yang terjadi dalam suatu interval waktu tertentu atau di suatu daerah tertentu.
Distribusi probabilitas diskret yang menyatakan peluang jumlah peristiwa yang terjadi pada periode waktu tertentu apabila rata-rata kejadian tersebut diketahui dan dalam waktu yang saling bebas sejak kejadian terakhir. Distibusi Poisson merupakan distribusi probabilitas untuk variabel diskrit
acak yang mempunyai nilai 0,1, 2, 3 dst. Distribusi Poisson adalah distribusi nilai-nilai bagi suatu variabel random X (X diskrit), yaitu banyaknya hasil percobaan yang terjadi dalam suatu interval waktu tertentu atau disuatu daerah tertentu. fungsi
distribusi probabilitas diskrit yang sangat penting dalam beberapa aplikasi praktis. Poisson memperhatikan bahwa distribusi binomial sangat bermanfaat dan dapat menjelaskan dengan sangat memuaskan terhadap probabilitas Binomial b(X│n.p) untuk X= 1,2,3 …n. namun demikian, untuk suatu kejadian dimana n sangat besar (lebih besar dari 50) sedangkan probabilitas sukses (p) sangat kecil seperti 0,1 atau kurang, maka nilai binomialnya sangat sulit dicari. Suatu bentuk dari distribusi ini adalah rumus pendekatan peluang Poisson untuk peluang Binomial yang dapat digunakan untuk pendekatan probabilitas Binomial dalam situasi tertentu.
Distribusi Poisson sering digunakan untuk menentukan peluang sebuah peristiwa yang dalam area kesempatan tertentu diharapkan terjadinya sangat jarang. Distribusi ini juga bisa dianggap sebagai pendekatan kepada distribusi binom, N cukup besar sedangkan = peluang terjadinya peristiwa A, sangat dekat dengan nol sedemikian sehingga λ = Np tetap, maka distribusi binom didekati oleh distribusi Poisson.
4.2 Ciri-ciri Distribusi Poisson
Satu-satunya parameter distribusi Poisson adalah λ, yaitu mean dan variansi, menyatakan derajat hitungan dalam satuan waktu atau tempat. Apabila satuan tempat atau waktu berubah dengan derajat relatif tetap, maka harga λ berubah secara
proporsional.
Asumsi sebaran Poisson :
1. Terdapat n tindakan bebas dimana n sangat besar, 2. Hanya satu keluaran yang dipelajari,
3. Terdapat peluang yang konstan dari munculnya kejadian setiap tindakan, 4. Peluang lebih dari satu keluaran pada setiap tindakan sangat kecil atau
Sebaran Poisson merupakan sebaran peluang dari peubah acak Poisson X, yang menyatakan jumlah keberhasilan dalam suatu selang waktu atau daerah tertentu, adalah :
P ( X : μ ) = , x = 0,1,2,...
Dimana µ adalah rata-rata keberhasilan selama selang waktu atau daerah tertentu dan e = 2,71828 .. (bilangan alami).
Percobaan Poisson memiliki ciri-ciri berikut :
1. Hasil percobaan pada suatu selang waktu dan tempat tidak tergantung dari hasil percobaan di selang waktu dan tempat yang lain yang terpisah
2. Peluang terjadinya suatu hasil percobaan sebanding dengan panjang selang waktu dan luas tempat percobaan terjadi. Hal ini berlaku hanya untuk selang waktu yang singkat dan luas daerah yang sempit
3. Peluang bahwa lebih dari satu hasil percobaan akan terjadi pada satu selang waktu dan luasan tempat yang sama diabaikan
Definisi Distribusi Peluang Poisson : e : bilangan natural = 2.71828...
x : banyaknya unsur BERHASIL dalam sampel m : rata-rata keberhasilan
Perhatikan rumus yang digunakan! Peluang suatu kejadian Poisson hitung dari rata-rata populasi (m)
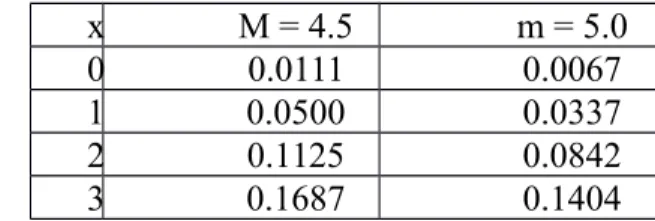
Tabel Peluang Poisson
Seperti halnya peluang binomial, soal-soal peluang Poisson dapat diselesaikan dengan Tabel Poisson (Statistika 2, hal 163-164). Cara membaca dan menggunakan Tabel ini tidak jauh berbeda dengan Tabel Binomial
x M = 4.5 m = 5.0 0 0.0111 0.0067 1 0.0500 0.0337 2 0.1125 0.0842 3 0.1687 0.1404 poisson(2; 4.5) = 0.1125
poisson(x < 3; 4.5) = poisson(0;4.5) + poisson(1; 4.5)+ poisson(2; 4.5) = 0.0111 + 0.0500 + 0.1125 = 0.1736
poisson(x > 2;4.5) = poisson(3; 4.5) + poisson(4; 4.5) +...+ poisson(15;4.5) atau
= 1 - poisson(x £ 2)
= 1 - [poisson(0;4.5) + poisson(1; 4.5)+ poisson(2; 4.5)] = 1 – [0.0111 + 0.0500 + 0.1125 ] = 1 – 0.1736 = 0.8264 4.3 Penerapan Distribusi Poisson
Distribusi poisson banyak digunakan dalam hal:
A. Menghitung Probabilitas terjadinya peristiwa menurut satuan waktu, ruang atau isi, luas, panjang tertentu, saeperti menghitung probabilitas dari:
Kemungkinan kesalahan pemasukan data atau kemungkinan cek ditolak oleh bank
Jumlah pelanggan yang harus antri pada pelayanan rumah sakit, restaurant cepat saji atau antrian yang panjang bila ke ancol.
Banyaknya bintang dalam suatu area acak di ruangangkasa atau banyaknya bakteri dalam 1 tetes atau 1 liter air.
Jumlah salah cetak dalam suatu halaman ketik
Banyaknya penggunaan telepon per menit atau banyaknya mobil yang lewat selama 5 menit di suatu ruas jalan.
Distribusi bakteri di permukaan beberapa rumput liar di ladang.
Semua contoh ini merupakan beberapa hal yang menggambarkan tentang suatu distribusi Poisson.
B. Menghitung distribusi binomial apabila nilai n besar (n ≥ 30) dan p kecil (p<0,1). Jika kita menghitung sejumlah benda acak dalam suatu daerah tertentu T, maka proses penghitungan ini dilakukan sebagai berikut :
Jumlah rata-rata benda di daerah S T adalah sebanding terhadap ukuran S, yaitu E Count(S)= λ S. Di sini melambangkan ukuran S, yaitu panjang, luas, volume, dan lain lain. Parameter λ > 0 menggambarkankan intensitas proses. Menghitung di daerah terpisah adalah bebas.
Kesempatan untuk mengamati lebih dari satu benda di dalam suatu daerah kecil adalah sangat kecil, yaitu P(Count(S)2) menjadi kecil ketika ukuran menjadi kecil.
Rumus Poisson dapat digunakan untuk menghitung probabilitas dari jumlah kedatangan, misalnya :
probabilitas jumlah kedatangan nasabah pada suatu bank pada jam kantor. Distribusi Poisson ini digunakan untuk menghitung probabilitas menurut satuan waktu.
Rumus Probabilitas Poisson suatu peristiwa yang berdistribusi Poisson dirumuskan:
P(X) = µ_X . e_µ / x!
Keterangan: P(x) = Nilai probabilitas distribusi poisson µ = Rata-rata hitung dan jumlah nilai sukses, dimana µ = n . p e = Bilangan konstan = 2,71828
X = Jumlah nilai sukses
P = Probabilitas sukses suatu kejadian ! = lambang faktorial
4.4 Contoh Soal Distribusi Poisson dan Cara Penyelesaiannya
1. Rata – rata pengunjung di kios itu tiap jam adalah 8 pengunjung. Berapakah probabilitas akan ada 6 pengunjung dalam satu jam tertentu?
Jawab :
sukses (x) = 6 Mean sukses = 8
P(x = 6|8) = (86) (2,7183-8) / 6! = 0, 122
Jadi, probabilitas akan ada 6 pengunjung dalam 1 jam tertentu adalah 0, 122 2. Dari pusat penelitian Menteri Pertanian, tercatat bahwa rata – rata kasus
serangan OPT yang terjadi di suatu daerah tiap hari adalah 7 kasus. Berapakah probabilitas terdapat 4 kasus dalam 1 hari tertentu?
sukses (x) = 4 Mean sukses = 7
P(x = 4|7) = (74) (2,7183-7) / 4! = 0, 091
Jadi, probabilitas terdapat 4 kasus penyerangan OPT dalam satu hari tertentu adalah 0,091
3. Rata-rata truk pembawa padi yang lewat di suatu daerah tiap jam adalah 6 buah. Berapakah probabilitas 5 truk pembawa padi lewat dalam satu jam tertentu?
Jawab : sukses (x) = 5 Mean sukses = 6
P(x = 5|6) = (65 ) (2,7183-6) / 4! = 0, 1606
Jadi, probabilitas 5 truk pembawa padi lewat dalam satu jam tertentu adalah 0, 01606
BAB III
PENUTUP
5.1 Kesimpulan
Dari uraian di atas dapat disimpulkan bahwa probabilitas sangatlah membantu manusia dalam mengambil sebuah keputusan. Misalkan untuk memperkirakan apakah peluang lebih banyak gagal atatu sukses dari sebuah usaha.
Distribusi binomial dan poisson merupakan suatu performans dari suatu percobaan, percobaan itu hanya memiliki dua macam keluaran yaitu “Sukses” atau “Gagal”.
Tentunya penggunaan metode tersebut dapat diaplikasikan pada bidang pertanian, dan akan sangat bermanfaat untuk membantu pemerintah, petani, penyuluh, maupun saya sebagai calon sarjana pertanian nantinya.
DAFTAR PUSTAKA
1. Dasari D. [Internet]. [diunduh 2017 19 Februari]. Tersedia pada:
http://www.statistikdasar.com/files/materi/distribusi_peluang_diskrit.pdf 2. Syamsul R. [Internet]. [diunduh 2017 19 Februari]. Tersedia pada:
https://www.academia.edu/6769745/MAKALAH_DISTRIBUSI_BINOMI AL
3. Arlim A. [Internet]. [diunduh 2017 19 Februari]. Tersedia pada:
4. Lestari, T., 2009. Dampak Konversi Lahan Pertanian Bagi Taraf Hidup
Petani. Makalah Kolokium. Departemen Sains Komunikasi dan Pengembangan Masyarakat. Intitut Pertanian Bogor.
5. Prof. Dr. Sudjana, M.A., M.Sc. (1996) Metoda Statistika . Bandung: Tarsito.
6. Nurd D. [Internet]. [diunduh 2017 20 Februari]. Tersedia pada: